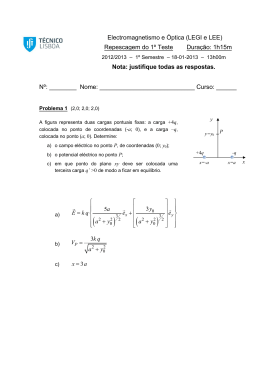
7.3. Potencial Eléctrico e Energia Potencial Eléctrica de Cargas Pontuais
Ao estabelecer o conceito de potencial eléctrico, imaginamos colocar uma partícula de
prova num campo eléctrico produzido por algumas cargas – fonte não descritas. Por
uma questão de simplificação foi suposto anteriormente que o campo era uniforme para
fixar a ideia do potencial eléctrico em nossas mentes. Vamos agora focalizar nossa
atenção nas cargas pontuais, que sabemos que produzem campos eléctricos que não são
uniformes.
Considere uma carga pontual positiva isolada q (Figura 7.3). Recorde que tal
carga é uma fonte de um campo eléctrico que está direccionado radialmente para fora da
carga. Para encontrar o potencial eléctrico a uma distância r da carga, começamos com a
expressão geral para a diferença de potencial, a equação 7.3:
B r
r
V B − V A = − ∫ E ⋅ ds
A
r
r
r
Como o campo eléctrico devido à carga pontual é dado por E = k e qrˆ / r 2 , onde r̂ é um
r r
vector unitário dirigido da carga para o ponto do campo, a grandeza E ⋅ ds pode ser
expressa como
r r
q r r
E ⋅ ds = k e 2 rˆ ⋅ ds
r
Figura 7.3. A diferença de potencial entre os pontos A e B devida a uma carga pontual q
depende apenas das coordenadas radiais inicial e final rA e rB. Os dois círculos
tracejados representam secções transversais das superfícies equipotenciais esféricas.
r
r r
r
O produto escalar rˆ ⋅ ds = ds cos θ , onde θ é o ângulo entre r̂ e ds como na Figura
r
r
7.3. Além disso, observe que ds cos θ é a projecção de ds em r , de modo que
r r
ds cos θ = dr. Com essas substituições, descobrimos que E ⋅ ds = k e q / r 2 dr , de tal
forma que a expressão para a diferença de potencial se torna
(
)
116
(7.10)
r r
A integral de linha E ⋅ ds é independente da trajectória entre A e B – como tem de ser,
porque o campo eléctrico de uma carga pontual é conservativo1. Além disso, a equação
7.10 expressa o importante resultado de que a diferença de potencial entre quaisquer
dois pontos A e B depende somente das coordenadas radiais rA e rB. Como já vimos é
habitual definir o potencial de referência como sendo zero em rA = ∞. Com essa escolha,
o potencial eléctrico devido a uma carga pontual a qualquer distância r da carga é
(7.11)
A partir disso, vemos que V é constante sobre uma superfície esférica de raio r centrado
na carga pontual. Assim, concluímos que as superfícies equipotenciais para uma carga
pontual isolada consistem numa família de cascas esféricas concêntricas com a carga,
como mostrado na Figura 7.3. Observe que as superfícies equipotenciais são
perpendiculares às linhas de força eléctrica, como é o caso para um campo eléctrico
uniforme.
O potencial eléctrico de duas ou mais cargas pontuais é obtido aplicando-se o
princípio da superposição. Isto é, o potencial total em algum ponto P em decorrência
das cargas pontuais múltiplas é a soma dos potenciais das cargas individuais. Para um
grupo de cargas, podemos escrever o potencial total em P na forma
(7.12)
onde o potencial novamente é considerado como zero no infinito e ri é a distância do
ponto P à carga qi. Observe que a soma na equação 7.12 é uma soma algébrica de
grandezas escalares em vez de uma soma vectorial (que é utilizada para calcular o
campo eléctrico de um grupo de cargas). Assim, é muito mais fácil calcular V para
r
muitas cargas do que calcular E .
Consideraremos agora a energia potencial eléctrica de interacção de um sistema
de partículas carregadas. Se V1 for o potencial eléctrico no ponto P devido à carga q1, o
trabalho necessário para trazer uma segunda carga q2 do infinito ao ponto P sem
aceleração será q 2 ∆V = q 2V1 . Por definição, esse trabalho iguala a energia potencial U
do sistema das duas partículas (Figura 7.4) quando as partículas estão separadas por
uma distância r12 – o agente externo mudou a energia do sistema fazendo trabalho sobre
ele. Podemos, consequentemente, expressar a energia potencial como
1
Um campo conservativo é aquele que exerce uma força conservativa sobre um corpo colocado nele.
Tanto os campos gravitacionais quanto os eléctricos são conservativos.
117
(7.13)
Figura 7.4. Se duas cargas pontuais estão separadas por uma distância r12, a energia
potencial eléctrica do par de cargas é dada por
.
Observe que, se as cargas forem do mesmo sinal, U é positiva. Isso é consistente com o
facto de que cargas de mesmo sinal se repelem e, dessa forma, trabalho positivo deve
ser feito sobre o sistema para aproximar as duas cargas, e a energia potencial do sistema
aumenta por causa desse trabalho. Se as cargas forem de sinais opostos, a força é
atractiva e U é negativa, o que significa que trabalho negativo é feito quando se
aproximam cargas de sinais opostos. Como a força é atractiva, as partículas se
aproximarão naturalmente. Neste caso, o sistema realiza trabalho sobre o agente externo
(ou o agente externo faz trabalho negativo) enquanto as partículas se aproximam. Isso
representa energia saindo do sistema e a energia potencial do sistema diminui.
Se o sistema consiste em mais de duas partículas carregadas, a energia potencial
eléctrica total pode ser obtida calculando-se U para cada par de cargas e somando – se
os termos algebricamente. A energia potencial eléctrica total de um sistema de cargas
pontuais é igual ao trabalho necessário para trazer as cargas, uma de cada vez, de uma
distância infinita até suas posições finais.
______________________________________________________________________
Exemplo 7.1. Potencial devido a duas cargas pontuais (resolvido na aula teórica).
______________________________________________________________________
7.4. Obtenção do Campo Eléctrico pelo Potencial Eléctrico
r
O campo eléctrico E e o potencial eléctrico V estão relacionados pela equação 7.3.
Ambas as grandezas são determinadas por uma distribuição específica de cargas – fonte.
Mostraremos agora como calcular o campo eléctrico se o potencial eléctrico for
conhecido numa determinada região.
A partir da equação 7.3 podemos expressar a diferença de potencial dV entre
dois pontos a uma distância ds um do outro como sendo
r r
dV = − E ⋅ ds
(7.14)
118
Se o campo eléctrico tiver somente uma componente, Ex, por exemplo, então
r r
E ⋅ ds =Exdx. Consequentemente, a equação 7.14 torna-se dV = – Exdx, ou
Ex = −
dV
dx
(7.15)
Isto é, o campo eléctrico é igual ao negativo da derivada do potencial eléctrico com
respeito a alguma coordenada. A variação no potencial é nula para qualquer
deslocamento perpendicular ao campo eléctrico. Isso é consistente com a noção de que
as superfícies equipotenciais são perpendiculares ao campo, como mostra a Figura 7.5a.
Figura 7.5. Superfícies equipotenciais (linhas tracejadas) e linhas do campo eléctrico
(linhas contínuas). As superfícies equipotenciais são perpendiculares às linhas do campo
eléctrico em todos os pontos.
119
Se a distribuição de carga tem simetria esférica, de tal forma que a densidade de
carga dependa apenas da distância radial r, o campo eléctrico é radial. Neste caso,
r r
E ⋅ ds = Er dr, e podemos expressar dV como dV = – Er dr. Consequentemente
Er = −
dV
dr
(7.16)
Por exemplo, o potencial de uma carga pontual é V = keq/r. Como V é uma função
somente de r, a função potencial tem simetria esférica. Aplicando a equação 7.16,
descobrimos que a magnitude do campo eléctrico devido à carga pontual é Er = keq/r2,
um resultado familiar. Observe que o potencial muda somente no sentido radial, não
numa direcção perpendicular a r. Assim, V (como Er) é uma função somente de r.
Novamente, isso é consistente com a ideia de que as superfícies equipotenciais são
perpendiculares às linhas do campo. Neste caso, as superfícies equipotenciais são uma
família de cascas esféricas concêntricas com a distribuição esfericamente simétrica da
carga (Figura 7.5b). As superfícies equipotenciais para o dipolo eléctrico são
esquematizadas na Figura 7.5c.
Em geral, o potencial eléctrico é uma função de todas as três coordenadas
espaciais. Se V é dado em termos de coordenadas rectangulares, as componentes do
campo eléctrico Ex, Ey e Ez podem ser encontradas a partir de V (x, y, z) como derivadas
parciais
Ex = −
dV
dx
Ey = −
dV
dy
Ez = −
dV
dz
Por exemplo, se V = 3x2y + y2 + yz, então
Ex = −
∂V
∂
3 x 2 y + y 2 + yz = −6 xy
=−
∂x
∂x
(
)
7.5. Potencial Eléctrico devido a Distribuições Contínuas de Carga
O potencial eléctrico devido a uma distribuição contínua de carga pode ser calculado de
duas maneiras. Se a distribuição de carga for conhecida, podemos começar com a
equação 7.11 para o potencial de uma carga pontual. Consideramos, então, o potencial
devido a um pequeno elemento de carga dq, tratando esse elemento como uma carga
pontual (Figura 7.6). O potencial dV em qualquer ponto P devido ao elemento de carga
dq é
(7.17)
onde r é a distância do elemento de carga a P. Para encontrar o potencial total em P,
integramos a equação 7.17 para incluir contribuições de todos os elementos da
distribuição de carga. Como cada elemento está, em geral, a uma distância diferente de
P e como ke é uma constante, podemos expressar V como
120
(718)
onde substituímos a soma na equação 7.12 pela integral.
Figura 7.6. O potencial eléctrico no ponto P devido a uma distribuição contínua de
carga pode ser calculado dividindo-se a distribuição de carga em segmentos de carga dq
e somando-se as contribuições para o potencial de todos os segmentos.
O segundo método para calcular o potencial de uma distribuição contínua de
carga emprega a equação 7.3. Esse procedimento é útil quando o campo eléctrico já é
conhecido a partir de outras considerações, tais como a lei de Gauss. Neste caso,
substituímos o campo eléctrico na equação7.3 para determinar a diferença de potencial
entre dois pontos quaisquer. Escolhemos, então, V como zero em algum ponto
conveniente.
7.6. Potencial Eléctrico dum Condutor Carregado
Já vimos que, quando um condutor sólido em equilíbrio electrostático tem uma carga
líquida, a carga fica na superfície externa do condutor. Além disso, mostramos que o
campo eléctrico na face externa de um condutor em equilíbrio é perpendicular à
superfície, enquanto o campo dentro do condutor é nulo.
Devemos agora demonstrar que todo ponto na superfície de um condutor
carregado em equilíbrio electrostático está no mesmo potencial eléctrico. Considere dois
pontos A e B na superfície de um condutor carregado, como na Figura 7.7.Ao longo de
r
uma trajectória de superfície conectando esses pontos, o campo E sempre é
r r
r
perpendicular ao deslocamento ds ; consequentemente, E ⋅ ds = 0 . Usando esse
resultado e a equação 7.3, concluímos que a diferença de potencial entre A e ,B é
necessariamente zero. Assim
121
Figura 7.7. Um condutor de formato arbitrário com um excesso de carga positiva.
Quando o condutor está em equilíbrio electrostático, toda a carga permanece na
r
superfície, E = 0 dentro do condutor e o campo eléctrico na face externa do condutor é
perpendicular à superfície. O potencial é constante dentro do condutor e é igual ao
potencial na superfície. A densidade superficial de carga não é uniforme.
Esse resultado se aplica a quaisquer dois pontos na superfície. Desse modo, V é
constante em todo lugar na superfície de um condutor carregado em equilíbrio e, assim,
tal superfície é uma superfície equipotencial. Além disso, como o campo eléctrico é
zero dentro do condutor, concluímos que o potencial é constante em todo lugar dentro
do condutor e igual a seu valor na superfície. Conclui-se que nenhum trabalho é
necessário para mover uma carga de prova do interior de um condutor carregado para
sua superfície.
Figura 7.8. (a) O excesso de carga na superfície de uma
esfera condutora de raio R está uniformemente distribuído
em sua superfície. (b) Potencial eléctrico em função da
distância r a partir do centro da esfera condutora carregada.
(c) Intensidade do campo eléctrico em função da distância
r a partir do centro da esfera condutora carregada.
Por exemplo, considere uma esfera metálica maciça de raio R e carga total
positiva Q; como indicado na Figura 7.8a. Como temos um condutor esférico a
distribuição de carga é uniforme. O campo eléctrico fora da esfera tem magnitude keQ/r2
122
e aponta radialmente para fora. Vemos que o potencial no interior e na superfície da
esfera deve ser keQ/R em relação ao infinito. O potencial fora da esfera é keQ/r. A
Figura 7.8b é um gráfico do potencial em função de r e a Figura 7.8c mostra as
variações do campo eléctrico com r.
Uma cavidade dentro de um condutor em equilíbrio
Agora considere um condutor de formato arbitrário contendo uma cavidade como na
Figura 7.9. Vamos pressupor que não há cargas dentro da cavidade.
Figura 7.9. Um condutor em equilíbrio electrostático contendo uma cavidade vazia. O
campo eléctrico na cavidade é nulo. Independentemente da carga no condutor.
Demonstraremos que o campo eléctrico dentro da cavidade tem de ser zero,
independentemente da distribuição de carga na superfície externa do condutor. Além
disso, o campo na cavidade é nulo, mesmo que exista um campo eléctrico do lado de
fora do condutor.
Para provar este ponto, usaremos o fato de que todo ponto no condutor está no
mesmo potencial e, dessa forma, quaisquer dois pontos A e B na superfície da cavidade
r
têm de estar no mesmo potencial. Agora imagine que um campo E existe na cavidade e
calcule a diferença de potencial VB – VA, definida pela expressão
r
Se E é diferente de zero, podemos invariavelmente encontrar um caminho entre A e B
r r
para o qual E ⋅ ds é sempre um número positivo (uma trajectória ao longo da direcção
r
de E ) e, assim, a integral tem de ser positiva. Contudo, como VB – VA = 0, a integral
r
também tem de ser zero. Essa contradição pode ser resolvida apenas se E =0 dentro da
cavidade. Assim, concluímos que uma cavidade rodeada por paredes condutoras é uma
região livre de campo enquanto não houver cargas dentro da cavidade.
Esse resultado tem algumas aplicações interessantes. Por exemplo, é possível
blindar um equipamento electrónico ou até mesmo todo um laboratório dos campos
externos cercando-o com paredes condutoras. A blindagem frequentemente é necessária
durante a realização de medidas eléctricas altamente sensíveis. Durante uma tempestade
com raios, a localização mais segura é dentro de um automóvel. Mesmo que um raio
atinja o carro, o corpo de metal garante que você não irá receber um choque dentro dele,
r
onde E =0.
123