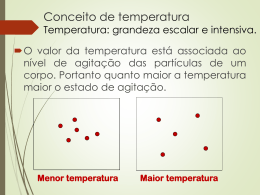
TEMPERATURA E ESCALAS TERMOMÉTRICAS - TEORIA
Freqüentemente, usamos a temperatura para indicar quando um corpo está mais quente ou mais frio que outro.
Para entender o conceito de temperatura, vamos pensar em um exemplo simples. Um estudante retira do freezer um pedaço de
metal e um pedaço de madeira, após os dois terem ficado muito tempo lá dentro. Quando o estudante segura os dois corpos,
ele tem a impressão que o pedaço de metal está mais frio que a madeira, embora os dois pedaços estivessem com a mesma
temperatura (a do interior do freezer). Isso ocorre porque o metal é um bom condutor, e por isso retira energia da mão do
estudante mais rapidamente que a madeira. A partir deste simples exemplo, percebemos que é necessário o uso de um método
de medição mais preciso para determinarmos a temperatura de um corpo.
Podemos dizer que a temperatura de um sistema determina o estado térmico deste sistema. Em outras palavras, a temperatura
nos fornece uma medida da agitação das moléculas deste sistema.
Observe que todos os sistemas são compostos por moléculas. Considere um sistema gasoso, em um recipiente rígido, como a
seguir:
As moléculas deste sistema podem ter energia pelas três maneiras a seguir: (a) translação; (b) rotação e (c) vibração.
Quando um sistema recebe energia, a agitação de suas moléculas aumenta, segundo uma das três formas citadas acima. Como
a temperatura é uma medida do grau de agitação das moléculas, nesta situação, sua temperatura aumenta.
Como a medição da agitação é difícil, os aparelhos de medição de temperatura (termômetros) normalmente associam a
temperatura a alguma outra grandeza do sistema em questão. Por exemplo, pressão (devido às colisões entre as moléculas e as
paredes do recipiente) e comprimento (devido à dilatação térmica do corpo).
Equilíbrio Térmico
O equilíbrio térmico entre dois ou mais sistemas ocorre quando todos eles apresentam a mesma temperatura.
È importante lembrar que a temperatura final de equilíbrio estará no intervalo entre as temperaturas extremas da situação
inicial.
Lei Zero da Termodinâmica
A Lei Zero da Termodinâmica formaliza um conceito que é bastante intuitivo. Embora bastante simples, sua formulação só
aconteceu em 1931, por R. H. Fowler. Como já haviam sido propostas a Primeira Lei e a Segunda Lei da Termodinâmica, que
dependem do conceito de temperatura, foi dado a ela o nome de Lei Zero.
Se dois corpos A e B estão, separadamente, em equilíbrio térmico com um terceiro corpo C, então
A e B estão em equilíbrio entre si.
A partir do enunciado da Lei Zero, pode ser redefinido o equilíbrio térmico: dois corpos estão em equilíbrio térmico se eles
apresentarem a mesma temperatura mesmo não estando em contato entre si.
Escalas Termométricas
As escalas termométricas são formas diferentes de se indicar a temperatura de um corpo. Podemos interpretá-las como
idiomas, que são diferentes entre si, mas têm como objetivo passar alguma informação. Claramente, precisamos saber como
transformar a informação de temperatura de uma escala para outra, como se estivéssemos fazendo a tradução de um idioma
para outro. Para encontrarmos uma equação que relacione duas escalas, precisamos de dois pontos de equivalência conhecida
entre elas. Normalmente, os pontos de equivalência usados são os pontos de fusão do gelo e de ebulição da água.
As escalas mais comuns são a Celsius, a Fahrenheit e a Kelvin, esta também chamada de escala absoluta.
•
Celsius
Proposta por Anders Celsius, atribui o valor 0˚C ao ponto de fusão do gelo, sob pressão normal, e 100˚C ao ponto de ebulição
da água, também sobre pressão normal. É a escala usada no Brasil.
•
Fahrenheit
Proposta por D. G. Fahrenheit, que se baseou na temperatura ambiente de um dia frio no inverno europeu e a temperatura
corporal de sua esposa. Nesta escala, o ponto de gelo corresponde a 32°F e o ponto de vapor, a 212°F.
•
Kelvin
Proposta por Lord Kelvin, associa o 0K ao grau mínimo de agitação das moléculas de um gás. Nessa situação, as moléculas
exerceriam pressão nula sobre as paredes do recipiente e se alcançaria a menor excitação possível delas. Chamamos a
temperatura nesta situação de zero absoluto. Um kelvin é a 273,16ª parte da distância entre o zero absoluto e o ponto triplo da
água, que é o ponto onde coexistem em equilíbrio os estados sólido, líquido e gasoso da água.
Assim, o ponto de fusão do gelo corresponde a 273K e a ebulição da água, a 373K.
A escala Kelvin é dita uma escala absoluta porque relaciona a pressão e a temperatura de uma amostra de gás ideal
(usualmente Hidrogênio ou Nitrogênio a baixas pressões) confinado em recipiente rígido. Verifica-se que a relação entre
pressão e temperatura é linear, da forma:
T = aP + b
em que a e b são parâmetros determinados experimentalmente.
Uma escala de temperatura baseada no comportamento de um gás ideal pode ser criada medindo-se a pressão em duas
temperaturas conhecidas, como o ponto de gelo e o ponto de vapor. Como só existe uma reta que passa pelos dois pontos,
pode ser gerado um gráfico que relaciona temperatura e pressão como a seguir.
Agora vamos encontrar as equações de conversão entre as principais escalas. A figura abaixo mostra a correspondência entre
os pontos de gelo e vapor nas três escalas.
Precisamos agora aprender a converter as leituras de uma escala para as outras. Para isso, seguiremos os seguintes passos:
1.
2.
3.
Arbitrar uma leitura em uma escala e marcar o seu correspondente na outra escala.
Manter a proporcionalidade entre os intervalos nas duas escalas.
Resolver a igualdade encontrada até chegar a uma equação de conversão.
Vamos seguir os passos descritos para encontrar as equações de conversão entre as três escalas citadas: Celsius, Fahrenheit e
Kelvin.
Celsius e Fahrenheit
c−0
f − 32
=
100 − 0 212 − 32
⇒
c
f − 32
=
100
180
Celsius e Kelvin
c−0
k − 273
=
100 − 0 373 − 273
⇒
c
k − 273
=
100
100
Kelvin e Fahrenheit
f − 32
k − 273
=
212 − 32 373 − 273
⇒
f − 32 k − 273
=
180
100
Assim, podemos resumir as três relações encontradas no quadro abaixo:
Variações de Temperatura
Até agora, aprendemos a converter leituras pontuais de temperatura. Porém, é comum precisarmos converter intervalos de
temperatura, como a temperatura ao longo do dia em determinada cidade. Nestes casos, o raciocínio é semelhante ao
empregado nas conversões pontuais de temperatura. Não é difícil perceber que precisamos adaptar a conversão de variações
de temperatura, uma vez que, entre o ponto de gelo e o ponto de vapor, temos 100 divisões nas escalas Celsius e Kelvin e 180
divisões na escala Fahrenheit. Logo, uma variação de 10 divisões na escala Celsius não pode ser equivalente a uma variação
de 10 divisões na escala Fahrenheit.
O que fizemos até agora foi manter as proporções entre os intervalos nas duas escalas. Faremos o mesmo, porém,
considerando como intervalo pequeno a variação de temperatura considerada.
ΔC
ΔF
ΔK
=
=
100 − 0 212 − 32 373 − 273
⇒
ΔC ΔF ΔK
=
=
100 180 100