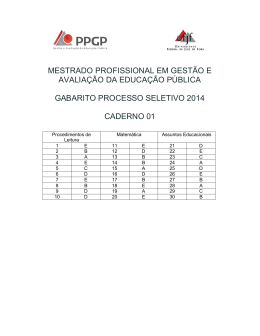
| Agrupamento de Escolas de Vouzela e Campia
Projeto Testes Intermédios de Agrupamento
Teste Intermédio a nível de Escola
MATEMÁTICA
Época Especial
Duração do Teste: 35 min (Caderno 1) + 55 min (Caderno 2)
21.04.2015
9.º Ano de Escolaridade – 3.º Ciclo do Ensino Básico
16 páginas
O teste é constituído por dois cadernos (Caderno 1 e Caderno 2).
Utiliza apenas caneta ou esferográfica de tinta indelével, azul ou preta.
É permitido o uso de calculadora no Caderno 1.
Não é permitido o uso de corretor. Deves riscar aquilo que pretendes que não seja
classificado.
Para cada resposta, indica a numeração do item.
Apresenta as tuas respostas de forma legível.
Apresenta apenas uma resposta para cada item.
Para responderes aos itens de escolha múltipla, escreve, na folha de respostas:
 O número do item;
 A letra que identifica a opção escolhida.
O teste inclui um formulário.
As cotações dos itens encontram-se no final do enunciado de cada caderno.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 1/16
Formulário
Números
Valor aproximado de  (pi): 3,14159 .
Geometria
Áreas
Paralelogramo: Base  Altura .
Losango:
Diagonal maior  Diagonal menor
.
2
Trapézio:
Base maior  Base menor
 Altura .
2
Superfície esférica: 4r , sendo r o raio da esfera.
2
Volumes
Prisma e cilindro: Área da base  Altura.
Pirâmide e cone:
Esfera:
Área da base  Altura
.
3
4 3
r , sendo r o raio da esfera.
3
Álgebra
Fórmula resolvente de uma equação do segundo grau da forma
ax  bx  c  0 : x 
2
 b  b 2  4ac
.
2a
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 2/16
CADERNO 1
Neste caderno, é permitido o uso de calculadora.
1. Numa turma recolheu-se a informação sobre o número de crianças em cada
uma das famílias dos alunos.
A informação foi organizada num gráfico de barras. No entanto, não se consegue
visualizar toda a informação.
Sabe-se que foram inquiridos 25 alunos, ou seja 25 famílias.
1.1.
Qual é a média do número de crianças por família
Apresenta todos os cálculos que efetuares.
1.2.
Escolhido um aluno ao acaso, qual é a probabilidade de a sua família
ter mais de três crianças?
Apresenta o resultado na forma de fração irredutível.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 3/16
2. Na figura estão representados os triângulos retângulos [ABC] e [ADE].
xm
De acordo com os dados, determina x.
Apresenta todos os cálculos que efetuares.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 4/16
3.
Na figura seguinte está representado um paralelepípedo retângulo [ACDFGIJL]
formado por dois paralelepípedos retângulos geometricamente iguais.
Sabe-se que o volume da pirâmide [BDEK] é igual a 1728 cm3.
3.1. Mostra que x = 12 cm.
Apresenta todos os cálculos que efetuares.
3.2. Qual das seguintes afirmações é verdadeira?
(A) As retas GL e BD são paralelas.
(B) As retas AE e HI são não complanares.
(C) Os planos ABE e EJI são paralelos.
(D) As retas BK e CD são concorrentes.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 5/16
4. Um êmbolo colocado num cilindro empurra o ar debaixo dele.
Quando um peso de
x
gramas é colocado no êmbolo, a altura do êmbolo à base
do cilindro é h cm.
h é inversamente proporcional a
x.
4.1.A tabela seguinte relaciona o peso, x , colocado no êmbolo e a altura, h,
do êmbolo à base do cilindro.
Peso em gramas
250
Altura do êmbolo em centímetros
45
300
a
Determina o valor de a.
4.2.Qual dos seguintes gráficos pode, por exclusão de partes, relacionar as
variáveis x e y?
(A)
(B)
y
(C)
y
(D)
y
y
x
xx
x
x
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 6/16
x
5. Na figura, está representada uma circunferência de centro O e raio 9 cm .
Calcula o comprimento do setor circular AOB.
Apresenta o resultado, em cm, arredondado às centésimas.
6. Observa a seguinte sequência de figuras.
Figura 1
Figura 2
Figura 3
Figura 4
Admite que se mantém esta regularidade.
A que é igual a diferença entre o número de círculos da figura 11 e o número de
círculos da figura 9?
(A) 2
(B) 23
(C) 11
(D) 21
FIM do CADERNO 1
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 7/16
COTAÇÕES
1.
1.1. ………………………………………………..………………………...……… 6 pontos
1.2. …………………………………………………...…………..………………… 4 pontos
2. ………………………………..………………………………………………………. 4 pontos
3.
3.1. ………………………………….…………………………….………………..
8 pontos
3.2. …………………………………………………...………………..…………… 3 pontos
4.
4.1. ………………………………….…………………………….………………..
4 pontos
4.2. …………………………………………………...………………..…………… 3 pontos
5. ……………………………………………..………………………………………..... 5 pontos
6. ……………………………………………..………………………………………..... 3 pontos
Subtotal (Caderno 1) ………………... 40 pontos
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 8/16
CADERNO 2
Neste caderno, não é permitido o uso de calculadora.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 9/16
7. Um técnico de eletricidade faz serviços ao domicílio. Da deslocação a casa do
cliente cobra 10 euros e o custo da mão-de-obra é 22,50 euros à hora.
7.1. Se o técnico de eletricidade trabalhou 30 minutos, quanto é que recebeu de
honorários?
7.2. Sabendo que o técnico recebeu 55 euros quando foi à casa da Maria,
quantas horas lá trabalhou?
7.3. Indica a fórmula que relaciona o valor dos honorários a pagar ao técnico de
eletricidade (H) com o número de horas de trabalho (t).
(A) H = 22,50×t
(B) H = 10×t + 22,5
(C) H = 22,50×t + 10
(D) H = 10×t
8. Em qual opções seguintes o número 0,002015 está escrito em notação
científica?
(A) 2,015  10 .
3
(B) 2,015  10
3
.
4
(C) 20,15  10 .
2
(D) 0,2015  10 .
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 10/16
9. Na figura, está representada uma circunferência de centro O.
Sabe-se que:
 A, B, C e D são pontos da circunferência;
 BFA  100 º ;
 DC  70 º ;
 ABD  60º ;
Determina a amplitude, em graus, do ângulo AED.
Apresenta todos os cálculos que efetuares.
1  3x
y
 x
2
10. Considera o seguinte sistema de equações:  2
.
2x  1  2  3 y
Determina o par ordenado x, y  que é a solução do sistema.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 11/16
11. Na figura, está representado um retângulo [ABCD]. Os vértices A e B são
pontos da reta real.
Sabe-se ainda que:
 o ponto E é um ponto da reta real;

AB  5

BC  2

EB  DB
 ao ponto B corresponde o número 2  29
Qual é o número que corresponde ao ponto E?
(A)
29
(B)  29
(C) 2  29
(D) 2
12. Resolve a equação  2x  12  3x  3 utilizando a fórmula resolvente.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 12/16
13. Os triângulos [ABC] e [MNO] são semelhantes.
Admite que:
- AB  3  MN ;
2
- a área do triângulo [ABC] é 72 m .
Qual é a área do triângulo [MNO]?
2
(A) 216 m .
2
(B) 648 m .
2
(C) 8 m .
2
(D) 24 m .
2
14.
8
 1  2 
 1
Calcula o valor numérico da expressão     2 4     usando, sempre
 2
 2  
que possível, as regras operatórias das potências.
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 13/16
15. Na figura estão representados, num referencial cartesiano de origem
O, partes dos gráficos de duas funções, f e g , e o triângulo [ABC].
y
x
f
g
Sabe-se que:
 O ponto C pertence aos eixos das abcissas e tem a mesma abcissa que o
ponto B;
 A função f é definida por f x    x  1 ;
 A função g é uma função quadrática da forma g ( x)  ax 2 , com a  0 ;
 Os pontos A e B são pontos de interseção dos gráficos de f e g e B tem
abcissa 1.
15.1. Mostra que a função g é definida por g ( x)  2 x 2 .
15.2. Em qual das opções seguintes estão as coordenadas do ponto A?
(A)  1;  2 .
 1 1
(B)   ,  .
 2 2
 1 2
(C)   ,  .
 3 3
(D)  1,0  .
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 14/16
16. A Sofia, o Pedro e o Jorge vão fazer um jogo, para decidirem qual dos três
será o Presidente da Associação de Estudantes da Escola.
O jogo consiste em lançar, uma só vez, um dado, como o da Figura 1, e adicionar
os três números da face que fica voltada para cima.
A Figura 2 representa uma planificação do dado.
Os amigos combinaram que:
 se a soma dos três números fosse um número par maior do que 2, o portavoz seria o Pedro;
 se a soma dos três números fosse um número ímpar, o porta-voz seria a
Sofia;
 se a soma dos três números fosse 1, o porta-voz seria o Jorge.
Os três amigos têm a mesma probabilidade de ser porta-voz do grupo?
Mostra como chegaste à tua resposta.
FIM
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 15/16
COTAÇÕES
Subtotal (Caderno 1) ………………... 40 pontos
7.
7.1. …………………………………………………………….………………….... 3 pontos
7.2. …………………………………………………...………..…………………… 3 pontos
7.3. …………………………………………………………….………………….... 3 pontos
8. …………………………..……………………..……………………………………… 3 pontos
9. ……………………………………………………………………..………………….. 7 pontos
10. ……………………………………………………………………..……..………….. 7 pontos
11. ………….……………………………………………..…………………..…………. 3 pontos
12. ………………………………………………………………………………………... 8 pontos
13. ………………………………………………………………………………….……… 3 pontos
14. ………………………………………………………………...………….…………... 6 pontos
15.
15.1. ……………..…………………………………...……….………………….... 5 pontos
15.2. …………..………………………………......…………..…………………… 3 pontos
16. ……………………………………………………………….……………...………... 6 pontos
Subtotal (Caderno 2) ……………….. 60 pontos
TOTAL ………..…. 100 pontos
TI de Matemática (AGEVC) | 9.º Ano – 3.º Ciclo | Abril de 2015 – Página 16/16