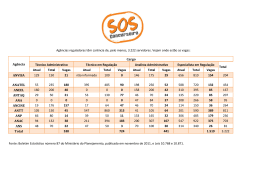
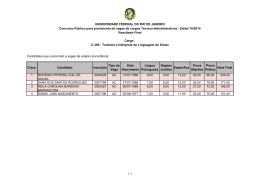
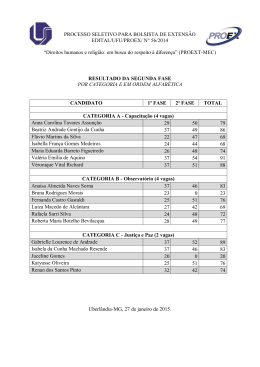
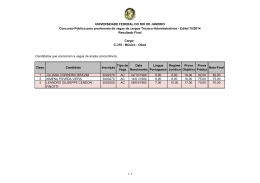
Estatística - aulasEstContagem.doc
04/09/10
Contagem
Princípio Fundamental de Contagem
‰
Se algum procedimento pode ser realizado de n1 maneiras diferentes; se,
seguindo este, um segundo procedimento pode ser realizado de n2
maneiras diferentes; se ainda, seguinte este segundo, um terceiro
procedimento pode ser realizado de n3 maneiras diferentes, e assim por
diante; então o número de maneiras nas quais podemos realizar os
procedimentos na ordem dada é o produto n1 * n2 * n3...
‰
Exemplo: Suponhamos que uma placa de carro contenha 2 letras distintas,
seguidas por três dígitos, com o primeiro dígito diferente de zero. Quantas
placas podem ser impressas?
Solução: Teremos a seguinte solução:
10 opções
10 opções
9 opções
22 opções
23 opções
Resposta: 10 x 10 x 9 x 22 x 23 = 455400 placas
Notação Fatorial
‰
O produto dos inteiros positivos de 1 a n, inclusive, aparece frequentemente
em matemática e, por isso, é representado pelo símbolo especial n!.
n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1
‰
É conveniente definir, também, 0!=1.
‰
Exemplo:
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4! = 5 * 24 = 120
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
7! = 7 * 6 * 5 * 4! = 5040
i)
ii)
iii)
iv)
E Nemer
1/7
Estatística - aulasEstContagem.doc
04/09/10
Permutação
‰
Um arranjo de um conjunto de n objetos, em dada ordem, é chamado
permutação dos objetos (tomados todos ao mesmo tempo).
‰
Um arranjo de quaisquer r desses n objetos, em dada ordem, é chamado
de r-permutação ou permutação dos n objetos, tomados r a r.
‰ Exemplo: Consideremos o conjunto de letras a, b, c e d. Então:
i) BDCA, DCBA e ACDB são permutações das 4 letras (tomadas todas ao
mesmo tempo).
ii) BAD, ADB, CBD e BCA são permutações das 4 letras, tomadas 3 a 3.
iii) AD, CB, DA e BD são permutações das 4 letras, tomadas 2 a 2.
‰
Exemplo: Encontre o número de permutações de 6 objetos: a, b, c, d, e, f;
tomadas 3 a 3. Em outras palavras, encontre o número de “palavras de 3
letras”, com letras distintas, que podem ser formadas com as 6 letras
acima.
Solução:
4 opções
5 opções
6 opções
Então, pelo princípio fundamental de contagem, existem 6*5*4 = 120 palavras de
três letras distintas, formadas com as 6 letras dadas; ou existem 120 permutações
de 6 objetos tomadas 3 a 3. Portanto,
P(6,3) = 120
A dedução da fórmula para P(n,r) segue o processo executado no exemplo
anterior:
• O primeiro elemento numa r-permutação de n objetos pode ser escolhido
de n maneiras diferentes;
• O segundo elemento pode ser escolhido de n-1 maneiras;
• O terceiro pode ser escolhido de n-2 maneiras.
• Continuando assim, temos que o r-ésimo (último) elemento da rpermutação pode ser escolhido de n-(r-1) = n-r+1 maneiras.
Assim, temos que:
E Nemer
2/7
Estatística - aulasEstContagem.doc
04/09/10
n!
(n − r )!
n ∗ (n − 1) ∗ (n − 2) ∗K∗ (n − r + 1) ∗ (n − r )!
n!
=
Obs: n * (n-1) * (n-2) *...* (n-r+1) =
(n − r )!
(n − r )!
Teorema 1: P(n,r) = n * (n-1) * (n-2) * (n-3) *...* (n-r+1) =
obs: No caso particular de r=n, temos:
P(n, n) = n ∗ (n − 1) ∗ (n − 2) ∗K∗ 3 ∗ 2 ∗1 = n!
‰
Exemplo: Quantas permutações de 3 objetos: a, b, c, existem?
Solução: Existem 3! = 3 * 2 * 1 = 6 permutações, ou seja:
abc
acb
bac
bca
cab
cba
Permutações com Repetições
‰
‰
‰
Frequentemente queremos saber o número de permutações de objetos, alguns
dos quais são aparecem repetidos.
n!
onde, n1 é o número de
n1!∗ n2 !∗K∗ nr !
vezes que o objeto A aparece repetido, n2 é o número de vezes que o objeto B
aparece repetido, n3 é o número de vezes que o objeto C aparece repetido, e
assim em diante.
A fórmula geral para esse caso é:
Exemplo: Suponha que se queira formar todas as palavras de 5 letras
possíveis, usando as letras da palavra DADDY. Observe que, caso não
tivéssemos letras repetidas, teríamos 5! = 120 permutações das letras. Como a
letra D aparece três vezes, temos que descontar 3! = 3 * 2 * 1 = 6 maneiras de
permutar as três letras D. Portanto, o resultado final é
5! 120
=
= 20
3!
6
Ou seja, existem 20 palavras diferentes de 5 letras que podem ser formadas
com as letras da palavra DADDY.
‰
Exemplo: Quantos anagramas podem ser formados com as letras a, a, b, c.
E Nemer
3/7
Estatística - aulasEstContagem.doc
04/09/10
Solução: Se não houvesse letras repetidas, teríamos 4! = 24 anagramas.
Entretanto, como temos 2 letras repetidas, teremos:
4! 4 ∗ 3 ∗ 2
=
= 12 anagramas
2!
2
Verificação:
aabc
aacb
abac
abca
acab
acba
‰
baac
baca
bcaa
caab
caba
cbaa
Exemplo: Quantos sinais diferentes, cada qual composto por 8 bandeiras
penduradas numa linha vertical, podem ser formadas com um conjunto de 4
bandeiras vermelhas indistinguíveis, 3 brancas indistinguíveis e uma azul?
V
V
V
V
B
B
B
A
Solução: Procuramos o número de permutações de 8 objetos, dos quais 4 são
iguais (as bandeiras vermelhas) e 3 também são iguais (brancas). Pelo teorema
anterior, existem
8!
8 ∗ 7 ∗ 6 ∗ 5 ∗ 4 ∗ 3 ∗ 2 ∗1
=
= 280 sinais diferentes
4! 3!
4 ∗ 3 ∗ 2 ∗1 ∗ 3 ∗ 2 ∗ 1
Amostras ordenadas
‰
‰
Muitos problemas de análise combinatória e, em particular, de probabilidade,
estão ligados á escolha de uma bola de uma urna contendo n bolas (ou uma
carta de baralho, ou uma pessoa da população).
Quando escolhemos uma bola após outra da urna, digamos r vezes,
chamamos a escolha de amostra ordenada de tamanho r. E, são consideradas
duas possibilidades:
o Amostragem com reposição: Neste caso, a bola é recolocada na urna,
antes da escolha da próxima. Portanto, pelo princípio fundamental de
contagem, existem amostras ordenadas diferentes, com reposição, de
tamanho r. Logo:
n ∗ n ∗ n ∗K∗ n = n r
E Nemer
4/7
Estatística - aulasEstContagem.doc
04/09/10
o Amostragem sem reposição: Neste caso, a bola não é recolocada na urna,
antes da escolha da próxima bola. Assim, não há repetição na amostra
ordenada. Ou seja, uma amostra ordenada, sem reposição, de tamanho r, é
simplesmente uma r-permutação dos objetos da urna. Logo, há
P(n,r) = n * (n-1) * (n-2) * (n-3) *...* (n-r+1) =
n!
(n − r )!
amostras ordenadas diferentes sem reposição, de tamanho r, de uma
população de n objetos.
‰
Exemplo:
De
quantas
maneiras
diferentes
podemos
escolher,
sucessivamente,3 cartas de um baralho de 52 cartas com reposição, e sem
reposição ?
Solução: i) Se cada carta é colocada no baralho antes da próxima ser escolhida,
então cada uma carta pode ser escolhida de 52 maneiras diferentes.
52
52
52
Ou seja, há 52 * 52 * 52 = 523 = 140.608 amostras ordenadas diferentes de
tamanho 3, com reposição.
ii) Por outro lado, se não há reposição, podemos escolher a primeira carta de 52
maneiras diferentes, a segunda de 51 maneiras e a terceira de 50.
52
51
50
Ou seja, há 52 * 51 * 50 = 132.600 amostras ordenadas diferentes de tamanho 3,
sem reposição.
Combinação
‰
Suponha um conjunto com n objetos. Uma combinação destes n objetos
tomados r a r, ou uma r-combinação, é qualquer subconjunto de r elementos.
‰
Em outras palavras, uma r-combinação é qualquer seleção r dos n objetos,
sem considerar sua ordem.
‰
Como exemplo, as combinações das letras A, B, C e D, tomadas 3 a 3, são
{A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}, ou simplesmente, ABC, ABD, ACD, BCD.
‰
Observe que ABC, ACB, BAC, BCA, CAB e CBA, embora representem 6
permutações, são combinações iguais, isto é, cada uma representa o mesmo
conjunto {A,B,C}.
E Nemer
5/7
Estatística - aulasEstContagem.doc
‰
O número de combinações de n objetos, tomados r a r, é obtido a partir da
seguinte fórmula:
C (n, r ) =
‰
n!
P(n, r )
=
r!
r ! (n − r ) !
Como um outro exemplo, de um grupo de 8 pessoas, quantas comissões
podem ser formadas com 3 delas?
C (8,3) =
‰
04/09/10
8!
= 56
3 ! (8 − 3) !
Como um exemplo mais genérico, suponha um grupo formado por 6 homens e
7 mulheres. Quantas comissões podem ser formadas com:
o 6 pessoas?
ƒ Solução:Temos 6 vagas para formar a comissão. Como não houve
nenhuma restrição quanto a sexo, significa que temos 13 pessoas (6
homens e 7 mulheres) para distribuir pelas 6 vagas. Como a ordem não
importa, temos um problema de combinação. Logo, temos como
resposta:
13 !
= 1716
6 ! (13 − 6) !
o 6 pessoas, onde 3 são homens e 3 são mulheres?
ƒ Solução:Temos 6 vagas para formar a comissão. Temos que 3 vagas
deverão ser preenchidas com homens, e são 6 homens para as 3
vagas. As outras 3 vagas deverão ser preenchidas por 3 mulheres, e
temos 7 mulheres para essas 3 vagas. Como a ordem não importa,
temos um problema de combinação. Logo, temos como resposta:
C (13,6) =
Homem
Homem
Homem
Mulher
6 homens
C (6,3) =
E Nemer
6!
= 20
3 ! (6 − 3) !
Mulher
Mulher
7 mulheres
x
6/7
C (7,3) =
7!
= 35
3 ! (7 − 3) !
= 700
Estatística - aulasEstContagem.doc
04/09/10
o 6 pessoas, onde 3 são homens e 3 são mulheres, onde o homem A
participa mas os homens B e C não, e onde a mulher X participa mas a
mulher Y não?
ƒ Solução:Temos 6 vagas para formar a comissão. Temos que 3 vagas
deverão ser preenchidas com homens, e são 6 homens para as 3
vagas. Entretanto, como o homem A tem que participar, isto significa
que uma vaga já está reservada para ele. Logo, sobram 2 vagas para os
outros 5. Mas como os homens B e C não podem participar, teremos,
então, somente 3 homens para distribuir pelas 2 vagas restantes. As
outras 3 vagas deverão ser preenchidas por 3 mulheres, e temos 7
mulheres para essas 3 vagas. Como a mulher X tem que participar,
sobram 6 mulheres para as outras 2 vagas. Mas como a mulher Y não
pode participar, sobram 5 mulheres para distribuir entre as 2 vagas
restantes. Como a ordem não importa, temos um problema de
combinação. Logo, temos como resposta:
A
Homem
Homem
X
3 homens
C (3,2) =
E Nemer
3!
=3
2 ! (3 − 2) !
Mulher
Mulher
5 mulheres
x
7/7
C (5,2) =
5!
= 10
2 ! (5 − 2) !
= 30