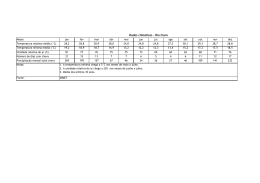
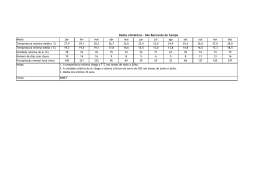
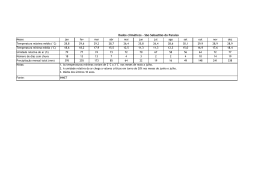
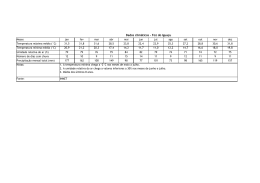
Análise da sensibilidade do Modelo BRAMS a
variações na umidade do solo
Edvânia Pereira dos Santos, Argemiro Lucena Araújo, Enilson Palmeira Cavalcanti
Universidade Federal de Campina Grande, UFCG
[email protected], [email protected],
[email protected]
Resumo
Neste estudo foi avaliada a sensibilidade do modelo BRAMS em relação às variações
de umidade do solo. O modelo foi alimentado com dados do Modelo Global T126 obtidos
para o dia 12 de novembro de 2009. Foram caracterizados 5 tipos de condições de umidade do
solo: padrão, seco, muito úmido, umidade decrescente e umidade crescente. O modelo foi
integrado por 24h e analisados os campos de calor latente e calor sensível após 15 horas de
integração. Foi observado que a umidade da camada mais próxima da superfície é a que tem
maior influência no comportamento dos fluxos de calor sensível e do calor latente. Estes são
também influenciados quando se tem umidade crescente em relação à profundidade do solo
implicando em fluxo de umidade das camadas mais profundas para a superfície. Simulações
com o BRAMS devem utilizar a umidade do solo a mais realista possível.
Palavras Chave: Modelo BRAMS, Fluxo de calor latente (LE), Fluxo de calor sensível (H).
Abstract
This study has evaluated the sensitivity of BRAMS for variations in soil moisture. The
model was fed data from the Global Model T126 obtained on November 12, 2009. We
characterized five types of soil moisture conditions: standard, dry, too wet, moisture
decreasing and increasing humidity. The model was integrated for 24 hours and analyzed the
fields of latent and sensible heat after 15 hours of integration. It was observed that the
moisture from the layer nearest the surface is having the biggest influence on the flow of
sensible heat and latent heat. These are also affected when there is increased moisture in
relation to soil depth resulting in flow of moisture from deeper layers to the surface.
Simulations with the BRAMS should use soil moisture to realistic as possible.
Keywords: BRAMS Model, Latent heat flux (LE), Sensible heat flux (H).
1. Introdução
As determinações dos fluxos de calor latente e sensível em superfície são de
fundamental importância, representam a troca de calor e a perda de água pela superfície em
condições de solo nu ou coberto por vegetação. Esses fatores são fundamentais na avaliação
do balanço de energia e estresse hídrico de culturas e da evapotranspiração. Baldochi et al.
(1983) relata que condições de estresse hídrico influenciam a divisão da radiação líquida em
calor latente e sensível. Para uma cultura em boas condições hídricas todo saldo de radiação é
consumido como fluxo de calor latente.
A umidade do solo afeta diretamente a quantidade de calor em cada um dos fluxos
mencionados anteriormente. Segundo Sellers et al. (1989) o conteúdo de água no solo é o
elemento mais importante na variabilidade das transferências de calor sensível e latente. Um
exemplo bem difundido atualmente a respeito da importância da umidade do solo nos fluxos
radiativos é a calibração do algoritmo SEBAL - Surface Energy Balance Algorithm for Land,
(Bastiaanssen et al., 1998). Nele a escolha dos chamados pixels âncora se baseia no fato de
que sobre áreas bem irrigadas, em condições ideais de evapotranspiração, o fluxo de calor
sensível é nulo, ou seja, toda energia disponível é utilizada para evaporação da água. Já para
áreas sem umidade no solo e sem vegetação o fluxo de calor latente é considerado nulo, ou
seja, toda radiação foi utilizada para aquecimento do ar próximo à superfície.
Neste sentido, objetiva nesse trabalho avaliar a influência da umidade do solo na
obtenção dos fluxos de calor latente e calor sensível através de simulações com o modelo
atmosférico BRAMS - Brazilian developments on the Regional Atmospheric Modelling
System.
2. Material e Métodos.
Os fluxos de calor sensível e calor latente foram obtidos a partir de simulações
utilizando-se o modelo BRAMS. Os dados referentes à grande escala, utilizados para
alimentação do modelo, foram obtidos do CPTEC – Centro de Previsão do Tempo e Estudos
Climáticos, modelo global T126.
Foi realizada uma integração de 24h, iniciada no dia 12 de novembro de 2009 às 0h e
com término no dia 13 de novembro de 2009 às 0h (horários UTC). A grade do modelo
corresponde a 27x27 espaçados de 112 km, centrada em 9º de latitude Sul e 41º de longitude
Norte. Foram ativadas as parametrizações de radiação (Chen e Cotton, 1983; 1987),
convecção (Grell, 1993), turbulenta (Mellor e Yamada, 1974) e de microfísica (Walko et al.,
1995).
Foram realizadas cinco rodadas do modelo com diferentes aspectos da umidade do
solo e profundidades. A primeira rodada foi realizada com as condições pré-estabelecidas do
modelo BRAMS para os valores de umidade do solo nos níveis indicados. Para a segunda
rodada a umidade foi considerada como constante e com valor 0,10 para todos os níveis
(condição de solo seco). Para a terceira rodada utilizou-se como valor de umidade 0,90
(condição de solo muito úmido), também constante para todos os níveis. Para a quarta rodada
foi estabelecido um gradiente decrescente de umidade iniciado em 0,90 com término em 0,10.
Por fim, foi utilizou-se um gradiente crescente em relação a profundidade com umidade
inicial de 0,10 e termino 0,90. A Tabela 1 mostra os níveis de profundidades escolhidos e os
respectivos valores de umidade do solo para cada rodada do modelo.
Tabela 1. Níveis de profundidade e seus respectivos valores de umidade do solo para cada
rodada do modelo
Nível
-0,05
-0,25
-0,50
-0,75
-1,00
-1,25
-1,50
-1,75
-2,00
Rodada 1
0,15
0,18
0,20
0,20
0,25
0,25
0,30
0,30
0,30
Rodada 2
0,10
0,10
0,10
0,10
0,10
0,10
0,10
0,10
0,10
Rodada 3
0,90
0,90
0,90
0,90
0,90
0,90
0,90
0,90
0,90
Rodada 4
0,90
0,80
0,70
0,60
0,50
0,40
0,30
0,20
0,10
Rodada 5
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
Os resultados serão analisados a partir de figuras que representam o comportamento
dos fluxos de calor sensível e calor latente obtidos após 15h de integração do modelo, Esses
campos foram gerados pelo aplicativo GrADS – Grid Analysis and Display System,
3. Resultados e Discussão
As análises dos campos dos fluxos de calor latente (LE) e calor sensível (H) para as
condições de umidade de solo estabelecidas na Tabela 1 são apresentadas após 15h (UTC) de
integração do modelo, correspondente às 12h local são apresentadas a seguir.
A
B
C
D
E
Figura 1 – Campos do fluxo de calor latente (W/m²) após 15h de integração, para condição
de solo padrão (A), seco (B), muito úmido (C), umidade decrescente (D) e umidade crescente
(E).
De acordo com a Figura 1 observa-se que praticamente não houve diferença entre as
condições A e B, ou seja, a umidade do solo padrão e a umidade constante de 0,10 oferecem
resultados aparentemente semelhantes. Pequena diferença nos fluxos máximos de calor latente
que chegam a atingir 800 Wm-2 no caso da umidade padrão, esse fato demonstra a
contribuição do fluxo de umidade no sentido para cima na camada de solo.
A
B
C
D
E
Figura 2 – Campos do fluxo de calor sensível (W/m²) após 15h de integração, para condição
de solo padrão (A), seco (B), muito úmido (C), umidade decrescente (D) e umidade crescente
(E).
O mesmo se observa para o caso das condições C e D que também não tiveram
diferenças consideráveis. Portanto, ao se utilizar uma umidade constante de 0,90 e uma
umidade decrescente de 0,90 a 0,10 produzem o mesmo efeito visto que, neste caso, não há
contribuição do solo já que o transporte de umidade é no sentido das camadas mais profundas.
O efeito da contribuição do fluxo de umidade pelo solo para os fluxos de calor latente são
bem evidenciados no caso C em que o gradiente no sentido da superfície é muito forte de 0,10
na superfície para 0.90 na parte mais profunda do solo.
Para o fluxo de calor sensível (Figura 2) o comportamento e semelhante no que diz
respeito às comparações entre rodadas. No entanto, observa-se que para a condição padrão
(A) e seco (B) o saldo de energia foi utilizado principalmente para aquecer a atmosfera, ou
seja, fluxo de calor sensível maior que o fluxo de calor latente. Já para os casos em foram
considerados muito úmido (C) e gradiente decrescente iniciando com 0,90 (D) ocorreu o
inverso, fluxo de calor latente maior que fluxo de calor sensível. O caso (E) apresenta fluxo
de calor sensível maior que fluxo de calor latente, embora evidencie a contribuição do fluxo
de umidade no solo.
4. Conclusões
Com o exposto foi possível observar que o modelo não possui sensibilidade
significativa para alterações no gradiente de umidade do solo e que a umidade mais próxima
da superfície é a que determina a tendência do calor sensível e do calor latente, reduzindo a
interferência da umidade conforme se aumenta a profundidade.
5. Referências Bibliográficas
Baldocchi, D. D. et al. “Influence of water stress on the diurnal Exchange of mass and energy
between the atmosphere and a soybean canopy.” Agronomy Journal, Madison, v,75, p,543548, 1983.
Bastiaanssen, W G. M., et al. “A remote sensing surface energy balance algorithm for land
(SEBAL). 1: Formulation,” J. Hydrol., 212–213., 198–212, 1998.
Chen, C., Cotton, W. R. A one-dimensional simulation of the stratocumulus-capped mixed
layer. Boundary Layer Meteorology, Dordrecht, Netherlands, 25, 289-321, 1983.
Chen, C., Cotton, W. R. The physics of the marine stratocumulus-capped mixed layer.
Journal of the Atmospheric Sciences, AMS, Boston, USA, 44, 20, 2951-2977, 1987.
Grell, G. A. Prognostic evaluation of assumptions used by cumulus parametrizations. Monthly
Weather Review, v,121, 764-787, 1993.
Mellor, G. L.; Yamada, T. A hierarchy of turbulence closure models for planetary boundary
layers. Journal of the Atmospheric Sciences, AMS, Boston, USA, 31, 7, 1791-1806, 1974.
Sellers, P. J. et al. “A Simple Biosphere Model (SiB) for use whithin General Circulation
Models.” J. Atmos. Sci., v,43, p,505-531, 1989.
Walko, R. L.; Tremback, J. C.; Hertenstein, R. F. A. The regional atmospheric modeling
system. Version 3b, User's Guide, Fort Collins: ASTER Division, 1995, 121 p.