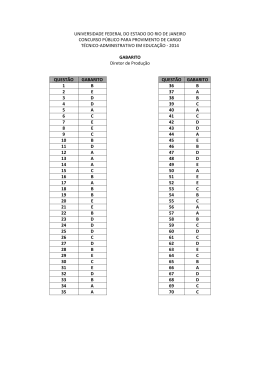
Lista de exercícios – 06
Aluno (a) : ____________________________
Série: 3º ano (Ensino médio)
Professor: Flávio
Disciplina: Matemática
No Anhanguera você é + Enem
Observações:
Data da entrega: 25/09/2015.
A lista deverá apresentar capa, enunciados e as respectivas resoluções das questões.
1.
Resolva as seguintes equações fatoriais:
(Gabarito: a) { }
2.
b) {60})
Simplifique a expressão:
(Gabarito: 1/(n + 1))
3.
4.
Se
a)
b)
c)
d)
e)
então n é igual a:
13
11
9
8
6
Simplifique a expressão
(Gabarito: n + 3)
5.
Simplifique a expressão a seguir de acordo com as regras do Fatorial de um número:
a) 1/(n + 2)
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
b) n/(n + 2)
c) 1/(n + 2)
d) 1/n
e) 1/n – 1
(Gabarito: A)
6.
Calcule:
a) 5!
b) 6! + 4!
2
2
c) (3!) – (2 )!
d) 10! / 7!
e) 100! / 98!
(Gabarito: a) 120
7.
b) 744
c) 12
d) 720
e)9900
Calcule a soma das raízes da equação (5x – 7)! = 1
(Gabarito: 3)
8.
Resolva a equação (2x – 3)! = 120
(Gabarito: 4)
9.
Resolva as expressões:
a) (n – 2)! = 720
b) (n – 2)! = 2(n – 4)!
c) (n – 9)! = 1
(Gabarito: a) 8
b) 4 c) 9 e 10)
10. (Unitau – SP – Adaptada) Sendo n ≠ 0, assinale a alternativa que possui o(s) valor(es) que satisfaz(em) a
equação abaixo:
a)
b) 0 e 7
c) 0 e 10
d) 1
e) 0 e 2
(Gabarito: B)
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
11. Resolva as equações a seguir:
(Gabarito: a) 7
b) 4)
12. Resolva a equação:
(Gabarito: 5)
13. De quantas maneiras 5 pessoas podem viajar em um automóvel com 5 lugares, se apenas uma delas sabe
dirigir?
(Gabarito: 24 maneiras)
14.
1 2 −1 0
2 5 0 1
O valor do determinante
é:
3 0 1 2
0 2
3
2
a) -24
b) 16
c) 12
d) 8
e) 32
6 1 1 4
3 2 1 3
15. O valor do determinante de
4 3 1 2
é:
5 4 1 1
a) 10
b) 1
c) 15
d) 23
e) 0
16.
a
x y
Sabendo que
=4 e d
z w
g
b
c
e
h
f = −10 , encontre o valor de:
i
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
a)
5x 5 y
z
b
c)
w
a
e d
h g
= b)
5 y 5x
5w 5 z
4c
4f =
4i
=
a
d)
b
c
2d 2e 2 f =
3g 3h 3i
17. Encontre o valor de n.
15   n + 10 
  = 

 6   n+4 
18. Resolva as seguintes equações:
a)
n
  = 84
 3
b)
 15  15 

 =  
 3x − 3   9 
19. Calcule o valor de n, sabendo que:
15   15  16 
  + 
 =  .
 7   n + 3  7 
20. Resolva a equação
n n n
 n 
  +   +   + ... + 
 = 1022.
1
2
3
n
−
1
     


21. Resolva a equação:
n n n
n
n n
  +   +  ... +   = 8192 −   −  .
 2  3  4
n
1 0
22. Classifique cada igualdade seguinte em verdadeira ou falsa:
a)
10  10  10 
10 
  +   +   + ... +   = 210
1 2 3
10 
b)
 3  4   5 
8  9 
  +   +   + ... +   =  .
 3  3   3 
 3  4 
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.
23. (UNI – RIO) Calcule o valor de
n n n n
 n  n
  −   +   −   + ... + 
 −   , onde n é impar, justificando a
0   1  2  3
 n − 1  n 
sua resposta.
24. Dê o desenvolvimento de:
 x y2 
 +

2 3 
6
25. Calcule a soma dos coeficientes do desenvolvimento de:
a) (x² + 2y)
b) (3x – y²)
9
12
1/3 8
c) (x + y )
x y 
d)  −
 4 5 


10
2
n
26. O desenvolvimento de ( 2x - y ) tem 6 termos. O terceiro termo é:
6 2
a) -80 x y
3 2
b) 80 x y
2 3
c) 80 x y
6 2
d) 80 x y
2 3
e) -80 x y
27. ( UFMA ) O quarto termo no desenvolvimento de
a) 20x
3
b) 12x
2
c) 15x
-6
d) 6x
-6
e) 2x
3
é:
6
28. (UFES ) Qual é o termo central de ( x - 3 ) ?
a) -540x
3
b) -3240x
c) 3240x
d) 540x
3
e) 540x
4
3
3
Pré-Universitário Colégio Anhanguera – Há 37 anos educando gerações.