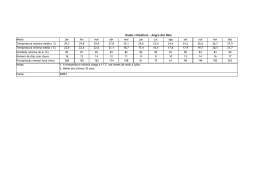
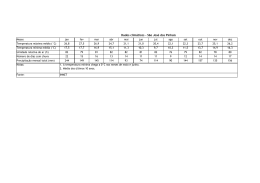
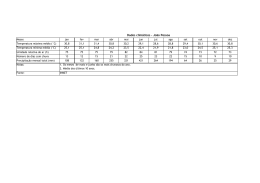
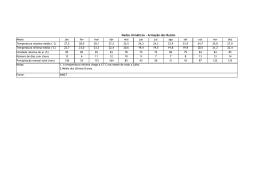
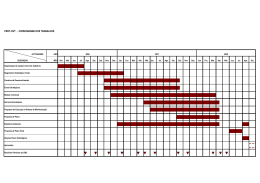
RAIZ UNITÁRIA E COINTEGRAÇÃO: TR.
.S
APLICA*
*VES
Marina Silva Cunha
1. INTRODUÇÃO
Segundo Fava & Cati (1995) a origem da discussão sobre a existência de raiz
unitária nas séries econômicas está no debate sobre a estacionaridade ou não da
tendência, sendo que grande parte dos dados utilizados na análise empírica em
economia é em forma de uma série temporal.
Uma série com uma tendência estocástica se diferencia de outra com uma
tendência determinística, pois as mudanças na mesma deixam de ter um caráter
transitório e passam a apresentar um caráter permanente [(Pereira, 1988) e (Gujarati,
2000)].
"A presença de uma tendência estocástica implica que flutuações em
uma série temporal são o resultado de choques não somente no
componente transitório ou cíclico, mas também no componente de
tendência." [Balke (1991) apud Gujarati (2000, p. 730)]1
Portanto, a determinação da presença de raiz unitária é relevante para a
economia pois auxilia no processo de verificação de várias teorias. Uma das
1
Balke, N. S. Modelling trends in macroeconomic times series. Economic review, Federal ReserveBank
de Dallas, maio de 1991, p. 81.
2
aplicações dessa análise constitui-se na verificação da passividade das políticas
econômicas. Além disso, a presença de raiz unitária pode ser utilizada como um
indicativo de que os agentes econômicos possuem um comportamento racional,
utilizando todas informações disponíveis [ver Pereira (1988) e Perron et al. (1995)].
A utilização dos modelos de regressão envolvendo séries temporais não
estacionárias pode conduzir ao problema que se convencionou chamar de regressão
espúria, isto é quando temos um alto R2 sem uma relação significativa entre as
variáveis (Harris, 1995). Isto ocorre devido ao fato de que a presença de uma
tendência, decrescente ou crescente, em ambas as séries leva a um alto valor do R2,
mas não necessariamente, a presença de uma relação verdadeira entre séries (Gujarati,
2000).
Neste contexto, a importância da análise de cointegração surge de seu uso para
aquelas séries econômicas não estacionárias. Basicamente, a presença de raiz unitária
na série temporal conduz a resultados viesados, invalidando os pressupostos da
estatística clássica de que a média e a variância são constantes ao longo do tempo, e,
com isto, mascarando o relacionamento entre duas, ou mais, variáveis. Detectada a
presença de raiz unitária, então se deve trabalhar com as séries temporais diferenciadas
e não em nível, ou seja, a tendência precisa ser removida. Assim, quando uma série
econômica apresentar uma tendência estocástica tornar-se-á estacionária após a
aplicação de uma ou mais diferenças, pois terá pelo menos uma raiz unitária. No
entanto, ao se remover a tendência, elementos de longo prazo entre as variáveis são
eliminados.
2
3
A interpretação econômica da cointegração é que se duas (ou mais) variáveis
possuem uma relação de equilíbrio de longo prazo, então mesmo que as séries possam
conter tendências estocásticas (isto é, serem não estacionárias), elas irão mover-se
juntas no tempo e a diferença entre elas será estável (isto é, estacionária). Em suma, o
conceito de cointegração indica a existência de um equilíbrio de longo prazo, para o
qual o sistema econômico converge no tempo (Harris, 1995).
Neste contexto, o objetivo deste trabalho é analisar a presença de raiz unitária e
realizar análises de cointegração entre algumas séries econômicas brasileiras.
Especificamente, buscar-se-á aplicar esta metodologia para se testar a passividade da
política monetária, a teoria da Paridade do Poder de Compra (PPC) e a curva de
Phillips.
2. MATERIAL e MÉTODOS
2.1 MATERIAL
Neste trabalho foram utilizadas seis séries mensais, relativas ao período de agosto de
1994 até dezembro de 2000: (1) a base monetária, obtida junto ao Banco Central; (2) o
índice de inflação representado pelo IGP/DI da Fundação Getúlio Vargas; (3) o
rendimento médio mensal nominal das pessoas ocupadas, da Pesquisa Mensal do Emprego
realizada pelo IBGE; (4) a taxa de desemprego aberto do IBGE; (5) taxa de câmbio
nominal; e (6) o índice de preços estrangeiros (IPA-EUA). Todos os testes realizados no
trabalho foram obtidos utilizando-se o pacote econométrico Regression Analysis of Times
Series- RATS versão 4.0. No caso do procedimento de Johansen foi utilizada a rotina
CATS do RATS.
3
4
2.2 MÉTODOS
A seguir serão discutidos os testes para detectar raiz unitária e as técnicas de
cointegração, pois como discutido anteriormente:
"Com uma tendência determinística, as variáveis podem ser
transformadas em estacionárias pela inclusão de uma tendência
temporal em qualquer regressão ou fazendo uma regressão preliminar
sobre o tempo e subtraindo a tendência estimada. Com uma tendência
estocástica, são necessários testes quanto à cointegração e não
estacionaridade." [Holde et al.(1990) Apud Gujarati (2000, p. 730)]2
Deve ser enfatizado que além do teste de cointegração de Engle e
Granger foi incluído o procedimento de Johansen, que é mais consistente para
os casos em que existem mais de um vetor de cointegração.
Por fim, serão apresentados os modelos empíricos analisados no presente
trabalho.
2.2.1 Raiz Unitária
Nesse trabalho foram utilizados as estatísticas denominadas Dickey-Fuller (DF)
e Dickey-Fuller Aumentado (ADF) [Dickey e Fuller (1979 e 1981)] e Dickey e Pantula
[Dickey e Pantula (1987)] para testar a presença ou não de raiz unitária na série.
O teste Dickey-Fuller baseia-se no seguinte modelo de regressão
∆y t = α + βt + ηy t −1 + et
(1)
2
Holden, K; Peel, D. A. Thompson, J. L. Economic Forecasting: an introduction. Cambridge University
Press, Nova York, 1990, p. 81.
4
5
p
η = ∑ ρi − 1
sendo que,
i =1
Y denota a variável dependente e ∆ denota o operador de diferença (∆yt = yt - yt-1). Os
parâmetros a serem estimados são α, β e η. As estatísticas ττ e τµ e τ apresentadas por
Dickey & Fuller (1981) correspondem ao teste t para a estimativa do coeficiente da
variável Yt-1 da equação (1). Essas estatísticas são especificadas para um modelo que
inclui uma constante e uma tendência (ττ), um modelo incluindo apenas constante (τµ) e
um modelo sem constante e sem tendência (τ). As hipóteses testadas nesses modelos
correspondem a uma hipótese nula de que a série não é estacionária (H0 : yt não é I(0)
ou η = 0); contra a hipótese alternativa de que a série não é integrada, ou seja, trata-se
de uma série estacionária (H1: yt é I(0)).
Foram utilizadas também as estatísticas φ3 e φ1, obtidas por Dickey & Fuller
(1979 e 1981), que testam se o coeficiente da variável tendência e o coeficiente da
variável yt
- 1
e se a constante e o coeficiente da variável yt
- 1,
respectivamente, são
estatisticamente iguais a zero na eq. (1).
Pode-se incorporar na eq. (1) valores defasados da variável endógena (yt) a fim
de se eliminar a presença autocorrelação entre os termos de erro, ou seja,
p −1
∆y t = α + βt + ηy t −1 + ∑ λ i ∆y t − i +e t
(2)
i =1
sendo que,
p
λi = − ∑ ρ j
j = i +1
sendo p a ordem do modelo auto-regressivo ou o número de defasagens suficientes para
que os resíduos resultantes sejam não correlacionados (white noise). Neste caso, temos
5
6
o teste denominado de Dickey-Fuller Aumentado (ADF). Para a determinação do
número de defasagens foram utilizados os testes AIC (AKAIKE Information Criterion)
e SBC (SCHWARZ Bayesian Criterion).
Para se testar a existência de mais de uma raiz unitária foi utilizado o teste de
Dickey e Pantula (1987), obtido a partir da reformulação do modelo anterior:
p −2
∆2 y t = α + η∆y t −1 + ∑ λi ∆2 yt −i +et
(3)
i =1
2.2.2. Cointegração
Segundo Harris (1995, p.22), se uma série deve ser diferenciada d vezes antes de
tornar-se estacionária, então ela contém d ra5zes unitárias e é dita ser integrada de
ordem d, denotada I(d). Considere duas séries de tempo yt e xt, ambas I(d), em geral,
qualquer combinação linear dessas duas séries também será I(d). Por exemplo, os
resíduos obtidos da regressão de yt contra xt serão I(d). Se, entretanto, existir um vetor
β, tal que o termo de erro da regressão (µt = yt −β xt) é de menor ordem de integração,
I(d−b), onde b > 0, então Engle & Granger (1982) define yt e xt como integradas de
ordem (d, b). Portanto, se yt e xt são ambas I(1) e µt ~ I(0), as duas séries serão cointegradas de ordem CI (1,1). Assim, para estimar a relação de equilíbrio de longo
prazo entre yt e xt é necessário apenas estimar o seguinte modelo
yt = β xt + µt
ou
yt =β 1 + β 2 xt + µt
(4)
Uma estimativa consistente dessa relação pode ser obtida utilizando o método de
mínimos quadrados. Resumidamente, estima-se uma regressão com as variáveis em
6
7
nível e aplica-se o teste de raiz unitária sobre os resíduos dessa regressão, sendo
consideradas séries co-integradas aquelas variáveis cuja série dos resíduos seja
estacionária. Para verificar a estacionaridade dos resíduos foram utilizados os testes
∆eˆt = a1eˆt −1 + et
(5)
e
∆eˆt = a1eˆt −1 +
∑ ai +1∆eˆt −i +et
(6)
i
Deve-se testar a hipótese de que a1=0, utilizando os valores tabelados por Engle & Yoo
(1987). Se este hipótese não for rejeitada, pode-se concluir que os resíduos são não
estacionários. Caso os resíduos sejam estacionários, tem-se a indicação de que as
variáveis analisadas possuem relacionamento de longo prazo e de que existe um modelo
de correção de erro (MCE). Este modelo faz a ligação entre aspectos relacionados com a
dinâmica de curto prazo com os de longo prazo, isto é, permite combinar as vantagens
de se modelar tanto nas diferenças quanto em nível.
Para Harris (1995), os valores correntes da variável dependente Y são
determinados não somente pelos valores correntes da variável explicativa X, mas
também pelos seus valores passados, devido aos custos de ajustamento. A variável X
defasada pode ser indicada por Xt-i (i = 0,..., q). Por outro lado, valores defasados de Y
[Yt-i (i = 0,..., p)] podem ser incluídos também no modelo, tornando-o um modelo
dinâmico de curto-prazo. Um modelo dinâmico simples pode ser dado considerando p
= q = 1, dessa forma tem-se
yt = α0 + γ0xt + γ1xt-1 + αyt-1 + ut
7
(7)
8
sendo que os resíduos são ruídos brancos [ut ~ IN(0,)]. Esta formulação de um modelo
dinâmico pode ser facilmente generalizada, tornando-se mais realista, pela incorporação
de mais lags de p e q. Contudo, existem vários problemas que podem ocorrer com este
modelo dinâmico, tais como multicolinearidade, erro de especificação e regressão
espúria. Uma solução para este último problema é trabalhar com um modelo dinâmico
nas (primeiras) diferenças. Contudo, este procedimento remove informações de longo
prazo do modelo, o que impede a utilização do modelo para previsão.
Um recurso mais apropriado é fornecido pela formulação do modelo de correção
de erro (MCE) de um modelo dinâmico. Rearranjando e reparamentrizando (7) , obtemse:
∆ yt = γ0 ∆xt −(1− α1) uˆ t −1 + ut
ou
∆ yt = γ0 ∆xt −(1− α1)[ y t −1 − βˆ 0 − βˆ1 x t −1 ] + ut
(8)
αˆ 0
γ +γ1
e βˆ1 = 0
. Assim, as equações (7) e (8) são equivalentes,
em que βˆ 0 =
1 − α1
1 − α1
contudo o MCE possui várias vantagens. Primeiro, assumindo que X e Y são
cointegradas, o MCE incorpora os efeitos de curto prazo e de longo prazo. O equilíbrio
de longo prazo, apresentado na equação (4), está incorporada no modelo. Dessa forma,
se existe equilíbrio para qualquer período de tempo, então [ y t −1 − βˆ 0 − βˆ1 x t −1 ]=0. Para
períodos de desequilíbrio, este termo é diferente de zero e mensura a distância que o
sistema está de seu equilíbrio no período t. Assim, a estimativa de (1 −α1) fornece
informações sobre o processo de ajustamento de variável y ou sobre sua resposta ao
8
9
desequilíbrio. Uma segunda característica do MCE é que todos os seus termos são
estacionários, considerando que as variáveis y e x são cointegradas e que os termos β 1 e
β 2 foram estimados. Por fim, uma terceira característica do MCE é que o mesmo está
de acordo com o conceito de cointegração de Engle & Granger (1982). Assim, a
formulação do MCE está imune ao problema de regressão espúria. (Harris, 1995)
O MCE pode ser generalizado, incluindo mais lags tanto em p quanto em q. Um
MCE mais geral pode ser dado por:
A(L)∆yt = B(L) ∆xt −(1− π)[ y t − p − βˆ 0 − βˆ1 x t − p ] + ut
(9)
sendo que
A(L) = 1 − α1L− α2L2−... − αp Lp
B(L) = 1 − γ1L− γ2L2−... − γp Lp
π = 1 − α1− α2 −... − αp
que corresponde ao seguinte modelo dinâmico
A(L)∆yt = B(L) ∆xt + ut
(10)
O MCE pode ser estendido também para um contexto multivariado, em que o
vetor de variáveis é dado por xt, como segue:
xt = A1xt + …+ Ak xt - k + ut
(11)
Como anteriormente, reparametrizando este modelo, pode-se obter o MCE para um
contexto multivariado, definido por:
∆xt = Γ1 ∆ xt - 1 + …+ Γk - 1 ∆ xt – k
+1
sendo que ut ~ IIN (0, Λ)
9
+ Π xt - 1 + u t
(12)
10
Γi = − (I − A1 − ... − Ai),
i= 1, …, k −1
Π = − (I − A1 − ... − Ai)
A matriz Π
n xn
contém as informações de longo-prazo correspondente a Π = αβ’,
em que α representa o ajustamento do desequilíbrio, enquanto β constitui-se em uma
matriz
dos
coeficientes
de
longo
prazo.
Assim,
βxt–1,
representaria
( y t − p − βˆ 0 − βˆ1 x t − p ) em (9), contudo aqui este termo constitui-se em um vetor com
n – 1 componentes. Para Harris (1995), uma melhor visualização da equação (12)
pode ser obtida considerando que existem 3 variáveis (n = 3) ou zt’ = [ y1t, y2t, x1t ]’ e
k = 2. Desse modo, pode-se escrever
 ∆y1t 
 ∆y1t −1  α 11 α 12 
∆y  = Γ ∆y  + α
  β11
α
22  
1
2 t −1 
 2t 
 21
β
 ∆xt 
 ∆xt −1  α 31 α 32   12
β 21
β 22
y 
β 31   1t −1 
(13)
y
β 32   2t −1 
 xt −1 
Apesar das vantagens do método de Engle e Granger, quando se utiliza mais de
duas variáveis no modelo ou um modelo multivariado podem ocorrer problemas.
Neste caso, podem existir múltiplos vetores de cointegração e o resultado produzido
por este procedimento seria uma combinação linear dos diferentes vetores de
cointegração.
Procurando solucionar esse problema da possível existência de vários vetores de
cointegração, Johansen (1988) propôs um procedimento a partir do uso do método de
máxima verossimilhança (ver também Johansen & Juscelius (1990)).
No modelo descrito na equação (12), o termo Π possui um papel fundamental,
uma vez que contém as informações de longo prazo e de realimentação ou de ajuste
10
11
de desequilíbrio do modelo. Dessa forma, esse método consiste em testar se os
coeficientes da matriz Π contêm as informações de longo prazo sobre as variáveis
envolvidas. Existem três casos possíveis, considerando o rank ou posto (r) dessa
matriz. Primeiro, se esta matriz for de posto completo ou posto (Π
Π) = n, ou se
existem n colunas linearmente independentes, as variáveis em xt serão I (0) ou
estacionárias. Segundo, se o posto dessa matriz for igual a zero ou posto (Π
Π) = 0,
então não existe nenhum vetor de cointegração. Estes dois casos não são
particularmente interessantes. Terceiro, se posto (Π
Π) = r ≤ n − 1 existem n − 1
vetores de cointegração, ou seja, o posto de Π indica o número de relações que cointegram.
Este número pode ser obtido utilizando dois testes de razão de verossimilhança,
o teste Traço e o de Máximo Valor. A hipótese nula do primeiro teste é de que o
número de vetores de cointegração é r ≤ p (em que p = 1, 2, 3, ..., n − 1), e a hipótese
alternativa é de que r = n, uma hipótese mais genérica. A idéia básica do segundo
teste é de verificar a significância do maior autovalor, confrontando a hipótese nula
de que r vetores de cointegração são significativos contra a alternativa de que o
número de vetores significativos seja r +1, ou seja, r = 0 contra r = 1; r = 1 contra r =
2 e assim por diante. Estes testes são dados respectivamente por:
λtrace = −T
∑ ln(1 − λˆi )
p
p = 1, 2, 3, ..., n − 1
(14)
p = 1, 2, 3, ..., n − 1
(15)
i = r +1
e
(
λ max = −T ln 1 − λˆr +1
)
11
12
Conforme Harris (1995), não é incomum os resultados desses dois testes
divergirem, não indicando o mesmo número de vetores de cointegração, o que pode ser
uma conseqüência de amostras pequenas. Além disso, quando estes testes divergirem,
Enders (1995) sugere utilizar o teste máximo valor.
2.2.4. Modelos empíricos
Como salientado na introdução, este trabalho tem por finalidade verificar a
existência de três relações discutidas pela teoria econômica, utilizando a análise de
cointegração.
A primeira relação a ser testada é a passividade da política monetária, ou seja, se
a variação da base monetária (BM) responde apenas a aumentos no nível da inflação
(P). Esta relação foi analisada por Pereira (1988), sendo que foi rejeitada a hipótese de
cointegração entre as séries.
A segunda relação a ser testada refere-se à curva de Phillips, que estabelece uma
relação entre a taxa de desemprego e as variações nas taxas dos salários nominais.
Teoricamente, existem três versões para a curva de Phillips. A curva de Phillips original
foi formulada por A.W. Phillips em 1958 e aperfeiçoada por R. Lipsey em 1960.
Posteriormente, em 1968/69, Edmund Phelps e Milton Friedman modificaram a versão
original, nesta formulação as taxas de desemprego menores podiam ser obtidas através
de políticas expansionistas às custas dos salários nominais. Portanto, assumiu-se a
presença de um trade-off entre desemprego e inflação, com a incorporação das
expectativas da inflação no modelo. Por fim, no início da década de 70, surge o
12
13
pensamento ‘novo clássico’, cujos principais representantes eram Robert Lucas e
Tomas Sargent. A principal inovação proposta por estes autores à segunda versão da
curva de Phillips é a utilização de expectativas racionais.
Este trabalho procurou verificar empiricamente a validade da versão original da
curva de Phillps, ou seja, da relação entre a taxa de variação dos salários nominais (W) e
a taxa de desemprego (D), discutida em Gujarati (2000) e Griffits et alli (1999).
Por fim, será testada a validade da Paridade do Poder de Compra (PPC), para o
Brasil, que pode ser apresentada em sua versão absoluta (ou forte) e relativa (ou fraca)
ver os trabalhos de Rossi (1996) e Holland (1996). Na versão absoluta a taxa de câmbio
real deve ser igual à unidade e na versão relativa deve se manter constante ao longo do
tempo. Na versão absoluta espera-se que a lei do preço único se verifique. Assim, se um
bem i é vendido a um preço único, tem-se
Pi BR = E BR / EUA Pi EUA
em que E
BR/EUA
(16)
é a taxa de câmbio nominal e PBR e PEUA são os respectivos níveis
gerais de preços. Considerando,
E tPPC = E t
Pt EUA
(17)
Pt BR
se observa que EPPC deve ser igual a 1, dado (16). Rearranjando (17)
E t = E tPPC
Pt BR
(17’)
Pt EUA
Aplicando logaritmo, tem-se
log E t = log E tPPC + log Pt BR − log Pt EUA
13
(17’’)
14
mas, como E tPPC é igual a 1, log E tPPC será zero.
3. RESULTADOS E DISCUSSÕES
Na figura 1 estão apresentadas as séries analisadas na pesquisa. De início, foram
aplicados os testes de Akaike e Schuartz para indicar a ordem de defasagem de cada
série, quando os resultados dos mesmos divergiram foi utilizado o critério da
parcimônia, adotando-se a menor ordem indicada. Posteriormente, foram utilizados os
testes descritos anteriormente para testar a presença de raiz unitária nas séries. Os
resultados tanto dos testes de Akaike e Schwarz quando de raiz unitária estão
apresentados na tabela 1. Pode-se observar que, com exceção da taxa de variação dos
salários nominais, todas as séries apresentaram uma raiz unitária.
Dessa forma, o modelo 2 ou a curva de Phillips não passa para as fazes seguintes
dos testes, uma vez que para a aplicação dos testes de cointegração as séries devem ser
integradas de mesma ordem. Contudo, nestes casos pode ser realizado o exame da
causalidade entre as séries, utilizando-se a série do desemprego em primeira diferença,
uma vez que é uma série não-estacionária. Contudo, isto causa a perda de algumas
informações de longo prazo.3
Portanto, a seguir serão analisados os modelos 1 ou da passividade da política
monetária e o modelo 3 referente à PPC. Os resultados dos testes de cointegração
3
Para mais detalhes do procedimento para analisar a causalidade entre as séries ver Judge et alli (1999) e
Gujarati (2000). Deve-se ressaltar que a aplicação de testes de causalidade não faz parte do objetivo do
presente trabalho.
14
-0,05
0,05
15
2,04
2,03
2,02
1,99
0,00
1,98
1,97
Mai/96
Fev/96
Nov/97
Ago/97
Mai/97
Fev/97
Nov/96
Ago/96
Nov/98
Fev/99
Mai/99
Ago/99
Nov/99
Fev/00
Mai/00
Ago/00
Nov/00
Nov/98
Fev/99
Mai/99
Ago/99
Nov/99
Fev/00
Mai/00
Ago/00
Nov/00
Mai/98
0,25
Fev/98
2,05
Ago/98
2,06
Mai/98
d) D
Fev/98
-15,00
Ago/98
Nov/97
2,00
Mai/97
c) W
Fev/97
0,10
Nov/95
a) LBM
Ago/97
2,01
Nov/96
0,15
Mai/96
0,20
Fev/96
0,30
Ago/96
0,35
Ago/95
-5,00
Nov/95
5,00
Ago/95
10,00
Mai/95
15,00
Fev/95
-0,10
e) LTC
f) LPE
Figura 1. Séries do W e D e do logaritmo da BM, P, TC e PE, ago/94 a dez/00.
Nov/00
Ago/00
Mai/00
Fev/00
Nov/99
Ago/99
Mai/99
Fev/99
Nov/98
Ago/98
Mai/98
Fev/98
Nov/97
Ago/97
Mai/97
Fev/97
Nov/96
Ago/96
Mai/96
Fev/96
Nov/95
Ago/95
Mai/95
Fev/95
Nov/94
Ago/94
3,60
Nov/94
3,80
Mai/95
-10,00
Ago/94
4,20
Fev/95
4,40
Nov/94
Ag
o/
94
N
ov
/9
4
Fe
v/
95
M
ai/
95
Ag
o/
95
N
ov
/9
5
Fe
v/
96
M
ai/
96
Ag
o/
96
N
ov
/9
6
Fe
v/
97
M
ai/
97
Ag
o/
97
N
ov
/9
7
Fe
v/
98
M
ai/
98
Ag
o/
98
N
ov
/9
8
Fe
v/
99
M
ai/
99
Ag
o/
99
N
ov
/9
9
Fe
v/
00
M
ai/
00
Ag
o/
00
N
ov
/0
0
4,60
Ago/94
Nov/00
Ago/00
Mai/00
Fev/00
Nov/99
Ago/99
Mai/99
Fev/99
Nov/98
Ago/98
Mai/98
Fev/98
Nov/97
Ago/97
Mai/97
Fev/97
Nov/96
Ago/96
Mai/96
Fev/96
Nov/95
Ago/95
Mai/95
Fev/95
Nov/94
Ago/94
Ag
o/
9
D 4
ez
/9
4
Ab
r/9
Ag 5
o/
9
D 5
ez
/9
5
Ab
r/9
Ag 6
o/
9
D 6
ez
/9
6
Ab
r/9
Ag 7
o/
9
D 7
ez
/9
7
Ab
r/9
Ag 8
o/
9
D 8
ez
/9
8
Ab
r/9
Ag 9
o/
9
D 9
ez
/9
9
Ab
r/0
Ag 0
o/
0
D 0
ez
/0
0
15
utilizando a metodologia desenvolvida por Engle e Granger estão apresentados na
tabela 3 e os resultados do procedimento de Johansen estão na tabela 4.
2,35
2,30
4,80
2,25
2,20
2,15
2,10
2,05
4,00
2,00
1,95
1,90
1,85
b) LP
9,00
8,00
7,00
6,00
5,00
0,00
4,00
3,00
2,00
1,00
0,00
16
Tabela 1. Resultados dos testes de raiz unitária.
Estatística DF
ττ
τ
φ3
τµ
φ1
LBM
2,52323
7,82969**
6,16619**
−3,69014**
−2,25655
LP
8,42438
27,61486**
37,81291**
−2,25314
−1,41184
W
51,28611**
−10,60351** −10,12766** −9,14564** 37,65862**
D
1,43206
1,52595
−1,91565
−1,74122
−0,49521
LTC
0,00643
1,18229
3,35857
2,22191
−2,16286
LPE
0,35289
2,51465
2,39167
3,18197
−0,22238
Estatística ADF
Lags
ττ
τµ
τ
φ3
φ1
Total
LBM
12
3,27771
4,54953
6,95806**
−0,28490 −1,50232
LP
2
0,88516
3,60816
6,88430*
7,06937**
−2,49708
W
2
24,29539**
−7,59118 −6,97052** −5,95354** 19,35483**
D
10
0,07013 −1,52302
0,35456
1,04195
1,37272
LE
3
1,23329
3,24820
2,93595
−1,82168 −0,06920
LP*
3
2,09884
1,69322
2,17282
−0,48211 −0,03808
Estatística Dickey – Pantula
τµ
τ
φ1
1
LBM
8,89082**
−4,21338**
−2,31542**
1
LP
13,33426**
−5,15636**
−3,29403**
W
72,25314**
−12,01499**
−12,10355**
D
6,32501**
−3,51533**
−3,51542**
LE
34,95956**
−8,36136**
−7,73649**
LP*
17,50746**
−5,91568**
−5,40612**
Obs.: ** indica que a hipótese nula é rejeitada no nível de significância de 5%.
*indica que a hipótese nula é rejeitada no nível de significância de 10%.
1
foi utilizado uma defasagem para a aplicação do teste de Dickey-Pantula.
Fonte: dados da pesquisa.
Tabela 2. Ordem de Integração das séries
Variável
Integração
LBM
I(1)
LP
I(1)
W
I(0)
D
I(1)
LE
I(1)
LP*
I(1)
Fonte: dados da pesquisa
16
17
Para o primeiro método, aplicou-se o teste de raiz unitária nos resíduos das
regressões dos modelos 1 e 2. Desse modo, para o modelo 1 tem-se duas regressões e
para o modelo 3, três regressões. Os testes indicaram que os resíduos das regressões
tanto do modelo 1 quanto do modelo 2 são não estacionários, indicando que as séries
não são cointegradas, utilizando os valores tabelados por Engle & Yoo (1987).
O procedimento de Johansen indicou os mesmos resultados que a metodologia
de Engle e Granger apenas para o modelo 1. Observando-se os resultados dos testes
Traço e do Máximo Valor, nota-se que para o modelo 1 não é rejeitada a hipótese de
que não existe nenhum vetor de cointegração ou r = 0. No caso do modelo 3, não é
rejeitada a hipótese de r = 1, ou seja, os testes sugerem a existência de um vetor de
cointegração.
Tabela 3. Teste de Cointegração – Procedimento de Engle e Granger, teste de raiz
unitária para os resíduos.
Estatística DF
Variável
dependente
LBM
LP
−2,4542
−1,68021
LE
LP
LP*
−2,69232
−3,22769
−3,24719
Estatística ADF
Lags
Modelo 1
1
1
Modelo 3
2
2
2
Integração
−2,21297
−1,91177
I(1)
I(1)
−2,87110
−3,02938
−3,03559
I(1)
I(1)
I(1)
Obs.: ** indica que a hipótese nula é rejeitada no nível de significância de 5%.
* indica que a hipótese nula é rejeitada no nível de significância de 10%.
Fonte: dados da pesquisa.
17
18
Tabela 4. Procedimento de Johansen.
H0: r
n − r λ̂
− T ln 1 − λˆ
i
0
1
2
1
0
1
2
3
2
1
(
r +1
)λ
max(0,95)
Modelo 1
15,18
8,09
Modelo 3
0,55199 61,02342**
22,29
0,05454 4,26236
15,18
0,01367 1,04609
8,09
0,09189 7,32567
0,02253 1,73186
(
)
− T ∑ ln 1 − λ̂i λtrace(0,95)
9,05748
1,73186
18,25
8,09
66,33187**
5,308447
1,04609
32,94
18,25
8,09
Obs.: ** indica que a hipótese nula é rejeitada no nível de significância de 5%.
Fonte: dados da pesquisa.
Contudo, como salientado por Jacinto (1997), como no caso do modelo 2, para o
modelo 1 é possível ser aplicado os testes de causalidade, trabalhando, no caso do
modelo 1, com as duas variáveis em diferenças de primeira ordem. Deve-se ressaltar
que os resultados do modelo 1, coincidem com os obtidos por Pereira (1988), que
analisou esta relação em um outro período.
O vetor β estimado pelo procedimento de Johansen, que corresponde à relação
de longo prazo entre as variáveis, normalizando em termos de LE, foi [ 1 − 1,969 2,644
−1,132], sendo que o último valor corresponde à constante. Assim, tem-se:
LE − 1,969 LP + 2,644 LP* −1,132 = 0
ou
LE = 1,132 + 1,969 LP −2,644 LP*
18
19
que está de acordo com os sinais esperados teoricamente, ver eq. (17’’). Por fim,
seguindo o trabalho de Rossi (1996) e, considerando β1 LE, β2 LP e β3 LP*, foi
imposto a seguinte restrição ao vetor β :
Restrição:
χ2 = 35,28
1 = β1 = β2 = − β3
(0,000)
A estatística qui-quadrado (χ2), utilizada para testar esta hipótese, rejeitou a
restrição imposta ao modelo. O que está de acordo com o procedimento de Engle e
Granger, ou seja, não foi possível obter um bom ajuste. O trabalho de Rossi (1996)
obteve os mesmos resultados, contudo o seu período de análise foi de janeiro de 1980 a
julho de 1994. O presente trabalho trata do período subseqüente.
4. CONSIDERAÇÕES FINAIS
O presente trabalho analisou empiricamente três relações estabelecidas pela
teoria econômica, para o período após a implementação do plano real, utilizando a
metodologia de cointegração de Engle e Granger e de Johansen.
Assim, foi analisada a passividade da política monetária, a curva de Phillips e a
PPC. Não foi possível testar a existência de cointegração na relação estabelecida pela
curva de Phillips, uma vez que as séries não foram integradas de mesma ordem. No que
se refere à relação entre a base monetária e o nível de preços os dois procedimentos
19
20
indicaram os mesmos resultados, ou seja, a não existência de um vetor de cointegração.
Contudo, com relação à PPC a metodologia de Engle e Granger indicou que não existe
uma relação de longo prazo entre as séries, ao contrário do procedimento de Johansen
que sugere a existência de um vetor de cointegração no período. Contudo,
estatisticamente a relação estabelecida pela PPC não obteve um bom ajuste, neste
último caso.
5. REFERÊNCIAS BIBLIOGRÁFICAS
DICKEY, D.A. & FULLER, W.A. Likelihood ratio statistics for autoregressive time
series with a unit root. Econometrica, 49:1057-1072, 1981.
DICKEY, D.A & FULLER, W.A. Distribution of the estimator for auto-regressive time
series with a unit root. Journal of the American Statistical Association, 74:427-31,
1979.
ENGLE, Robert F; W. J. GRANGER. Cointegration and error correction:
representation, estimation, and testing. Econometrica, v. 50, p. 987-1007, 1982.
ENGLE, Robert F.; YOO, B. Forecasting and testing in cointegrated systems. Journal
of econometrics, v. 35, p. 143-59, 1987.
FAVA, V.L, CATI, R.C. Mudanças no comportamento do PIB brasileiro: uma
abordagem econométrica. Pesquisa e planejamento econômico,. 25(2), ago, 1995.
HILL, R. Carter; GRIFFITHS, JUDGE, G. Judge. Econometria. São Paulo: Saraiva, 1999,
408p.
20
21
HOLLAND, Márcio. Taxa de câmbio real e paridade de poder de compra no Brasil. In:
Anais do XXVI encontro nacional de economia. Vitória, v. 2, p.963-982, 1988.
GUJARATI, Damodar N. Econometria básica. São Paulo: Makron Books, 3a ed., 2000,
846p.
HARRIS, R.I.D. Using cointegration analysis in econometric modelling. London,
1995, 176p.
HAUGH, L. D. & BOX, G. E. P. Identification of dynamic regression (distributed lag)
models connecting two time series.
Journal of the American Statistical
Association, 72: 121-30, mar. 1977.
JACINTO, Paulo de Andrade. Comportamento do investimento agregado no Brasil,
período 1975 a 1995. Porto Alegre, 1997, 94p (Dissertação de Mestrado).
JOHANSEN, Soren. Statistical analysis of cointegration vectors. Journal of economic
dynamics and control, v. 12, p, 231-254, 1988.
JOHANSEN, Soren; JUSELIUS; Katerina. Maximum likelihood estimation and inference
on cointegration with application to the demand for money. Oxford bulletin of
economics and statistics, v. 52, 169-209, 1990.
JUDGE, G. Judge; HILL, R. Carter; GRIFFITHS, Willian E.; HELMUT, Lutkepahl;
TSUNG-CHAO, Lee. Introduction to the theory and practice of econometrics. Jonh
Wiley & Sons, 2 ed., 1988, 850p.
PEREIRA, P. L. V. Cointegração: Uma resenha com aplicações a séries brasileiras.
Revista de econometria, v.8, n.2, 1988.
21
22
PERRON, P.; CATI, R.C. & GARCIA, M. G. P. Unit roots in the presence of abrupt
governamental interventions with an application to Brazilian data. Texto para
discussão n. 349. Departamento de Economia PUC-RIO, dez., 1995.
ROSSI, José W. O modelo monetário de determinação da taxa de câmbio: teste para o
Brasil. Pesquisa e planejamento econômico, v. 26, n.2, p. 155-182, 1996.
22