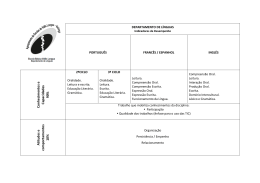
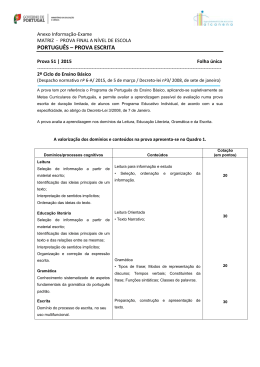
Linguagens Formais e Autómatos
Semana 9
October, 11 2011, 02:18
Nesta aula :
• Pumping lema para as linguagens livre de contexto.
• Utilização do lema para mostrar que uma gramática não é livre de contexto.
1. Pumping lemma para CFL
Se L for uma linguagem livre de contexto, então existe um número p tal que ∀s ∈ L, |s| ≥ p ⇒ s = uvxyz tal
que
• ∀i ≥ 0, uvi xyi z ∈ L
• |vy| > 0
• |vxy| ≤ p
Seja G uma gramática livre de contexto. Seja b o comprimento maximo das regras (comprimento do
lado direito).Se efectuamos um primeiro passo de derivação a partir do símbolo inicial S ⇒ α onde |α| ≤ b.
Podemos a seguir expandir cada um dos símbolos de α. S ⇒ α ⇒ β1 β2 . . . βi i ≤ b. O comprimento desta
sequência é menor ou igual a b2 . Se repetimos esta operação n vezes, o comprimento da sequência obtida
será menor ou igual a bn . Qualquer sequência com comprimento maior ou igual a b|V|+1 (com |V| igual
ao número de símbolos não terminais) terá que conter na sua sequência de derivações um símbolo não
terminal repetido. Vamos portanto escolher p = b|V|+1 .
A título de exemplo consideramos a gramática G :
S →
A →
B →
AB
aA | bb
xz
(1)
Para esta gramática temos p = 23+1 = 16. As sequências que podem ser derivadas são (por ordem crescente
de comprimento até p) são :
S ⇒ AB ⇒ bbB ⇒ bbxz
S ⇒ AB ⇒ aAB ⇒ abbxz
S ⇒ AB ⇒ aAB ⇒ aaAxz ⇒ aabbxz
S ⇒ AB ⇒ aAB ⇒ aaAxz ⇒ aaaAxz ⇒ aaabbxz
...
S ⇒ AB ⇒ aAB ⇒ aaAxz ⇒ aaaAxz . . . ⇒ aaaaaaaaaaaabbxz
A primeira sequência com comprimento maior ou igual a p pode ser decomposta em cinco partes : u =
aaaaaaaaaaa, v = a, x = bbxz, y = , z = tal que ∀i ≥ 0 uvi xyi z ∈ L(G).
Seja τ a mais curta sequência de derivações para gerar s. Nesta sequência τ haverá necessáriamente
um dos símbolos não terminais que será expandido (substituido) duas vezes. Vamos chamar R este
símbolo.
Podemos dividir s em cinco sub-cadeias a sequência de derivações ficando assim :
∗
∗
∗
T ⇒ uRz ⇒ uvRyz ⇒ uvxyz
(2)
O símbolo não terminal R é responsável por gerar as sequências vxy (primeira ocorência) e x na segunda
ocorência. Essas duas sequências foram geradas pelo mesmo símbolo não terminal, podem portanto ser
trocadas o resultado será sempre uma sequência que pertence à linguagem. Logo a primeira condição do
lema está provada.
A segunda condição do lema implica que as sequências v e y não podem ser ambas vazias. Se fosse o
caso teriamos a sequência de derivações :
∗
∗
∗
T ⇒ uRz ⇒ uRz ⇒ s
1
(3)
∗
o que implica que R ⇒ R que pode acontecer só se a gramática tiver aluma patologia (ciclos infinitos e/ou
regras inuteis).
Uma outra maneira de chegar a mesma conclusão é notar que uma das regras de R é recursiva (porque
o símbolo R foi escolhido assim). Uma regra recursiva (ou indirectamente recursiva) tem de contribuir
com símbolos terminais para a sequência final. Logo os terminais adicinados em cada recursão fazem
parte de v ou y (ou ambos). Essas cadeias não podem portanto ser ambas vazias.
A terceira condição implica que |vxy| ≤ p. O comprimento da sequência vxy tem de ser menor que |V| +
1caso contrário haveria outro símbolo repetido dentro de vxy. Não é possível porque entra en contradição
com a escolha de R.
2. Exemplo 1
Seja a linguagem L = {an bn cn , n ≥ 0}. Para mostrar que não é livre de contexto vamos assumir que é e
mortrar que chegamos a uma contradição (o pumping lema não se aplica). Para isso é preciso mostrar
que existe pelo menos uma sequência tal que qualquer que seja a partição (em cinco sub-cadeias), pelo
menos uma das condições do lema não se verifica.
Sendo p o parâmetro do lema, escolemos a sequência s = ap bp cp . O comprimento da sequência é
maior que p deve portanto existir u, v, x, y, ztal que s = uvxyz com uvi xyi z ∈ L ∀i ≥ 0. Consideramos duas
hipoteses quanto a composição de v e y :
• v e y contêm um só tipo de caracter. Neste caso uvi xyi z não pode conter tantos as, bs, e cs. Logo a
sequência não pode fazer parte de L.
• v e/ou y contêm mais de um tipo de caracter. Neste caso a sequência pode conter um número igual
de cada um dos caracteres mas não vão aparecer na ordem desejada.
Em conclusão, a linguagem não pode ser livre de contexto.
3. Exemplo 2
Seja a linguagem M = {ai bj ck 0 ≤ i ≤ j ≤ k}. Vamos usar novamente a sequência s = ap bp cp . Temos
novamente duas hipoteses :
• v e y contêm um só tipo de caracter. Neste caso não podemos usar o mesmo raciocínio porque o
número de elementos nas sequências de caracteres não devem ser iguais. Um dos três caracteres
não deve aparecer nem em v nem em y vejamos os casos possíveis :
– Os as são ausentes. Neste caso, para i = 0 uvi xyi z = uxz contém mais as do que bs ou de cs
logo não faz parte da linguagem.
– Os bs são ausentes. Neste caso, se v ou y estiverem compostos de as, a sequência uvi xyi z vai
conter mais as do que bs. Se v ou y estiverem compostos de cs então uv0 xy0 z vai conter mais
bs do que cs. Em ambos os casos a sequência não pode fazer parte da linguagem.
– Os cs são ausentes. Neste caso, uvi xyi z vai conter mais as ou bs do que c neste caso também a
sequência não pertence à linguagem.
• v e/ou y contêm mais de um tipo de caracter. Neste caso a sequência pode conter um número igual
de cada um dos caracteres mas não vão aparecer na ordem desejada.
Em conclusão, a linguagem M não é livre de contexto.
4. Exercícios
4.1. Propriedades de fecho nas linguagens LC
Mostre que o conjunto das linguagens livre de contexto é fechado para as operações regulares (concatenação, alternativa e repetição).
2
4.2. Definição de CFG (2)
Define gramáticas livre de contexto para as linguagens seguintes :
1. O conjunto das cadeias sobre o alfabeto {a, b} que contêm mais as do que bs.
2. O complemento da linguagem {an bn |n ≥ 0}.
3. {w#x|wR é uma sub-cadeia de x e w ∈ {0, 1}∗ }. wR representa a cadeia w invertida.
4. {x1 #x2 # . . . #xk |k ≥ 1, xi ∈ {a, b}∗ , ∃i, jxi = xR
j }.
4.3. Derivações (2)
Considere a gramática livre de contexto G = ({S, A, B}, {a, b}, S, P) onde P é
S → aB | bA | a | aS | bAA
B → b | bS | aBB
Verifique se abaabba, aabaab e baaabba fazem parte de L(G).
4.4. Definição de CFG (3)
Define uma gramática livre de contexto que gera a linguagem :A = {ai bj ck | i = j ou j = k, i, j, k ≥ 0}
A gramática obtida é ambigua ? Justifique.
4.5. Definição de CFG (4)
Determine para cada uma das seguintes linguagens uma gramática que gere as lingugens seguintes :
1. L1 = {an bm |n ≥ 0, m > n}
2. L2 = {an b2n |n ≥ 0}
3. L3 = {an+2 bn |n ≥ 1}
4. L4 = {an bn−2 |n ≥ 2}
5. L5 = L1 ∪ L2
6. L6 = L21
3
(4)
Download