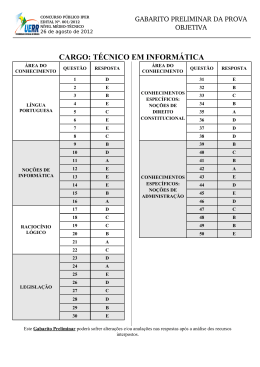
Análise e Resolução da prova de Analista
do Tesouro Estadual – SEFAZ/PI
Disciplinas: Matemática Financeira e
Raciocínio Lógico
Professor: Custódio Nascimento
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
1- Análise da prova
Neste artigo, faremos a análise das questões de Matemática Financeira
e Raciocínio Lógico cobradas na prova de Analista do Tesouro Estadual da
SEFAZ/Piauí, por serem as nossas disciplinas no Exponencial Concursos.
Primeiramente, seguem alguns comentários gerais sobre a prova.
A prova de Matemática Financeira trouxe uma boa distribuição dos
assuntos pedidos no edital. A maioria das questões era de esquematização
simples, porém de cálculos complexos, como já é praxe na FCC. Os nossos
alunos devem ter tido um desempenho muito bom na prova, pois todos os
assuntos cobrados na prova foram trabalhados em nossos cursos.
As questões de Raciocínio Lógico estavam bem simples e tranquilas,
além de rápidas para resolver.
Após resolvermos todas as questões, não visualizamos recurso para
as questões da prova.
2- Resolução das questões
Matemática Financeira
Vamos resolver cada questão, com comentários. A teoria foi abordada no
nosso curso de Matemática Financeira para ATE – SEFAZ/PI, focado na
banca FCC, lançado no site do Exponencial Concursos.
Eis as questões da prova, com a devida resolução:
21. Se Ricardo aplicar 75% de seu capital, durante 6 meses, poderá resgatar
no final de 6 meses o montante correspondente a R$ 16.302,00. Se ele aplicar
o restante do capital, durante 8 meses, poderá resgatar no final de 8 meses o
montante correspondente a R$ 5.512,00. Ricardo, então, decide aplicar todo o
capital, durante 10 meses, resgatando todo o montante no final de 10 meses.
Considerando que as aplicações são realizadas sob o regime de capitalização
simples e com a mesma taxa de juros, o montante que ele resgatará no final de
10 meses será de
(A) R$ 21.500,00
(B) R$ 22.037,50
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
2 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
(C) R$ 22.198,75
(D) R$ 22.360,00
(E) R$ 23.650,00
Resolução:
Chamaremos o capita aplicado de C, os montantes de M1, M2 e M3 e os
prazos de n1, n2 e n3. Eis os dados da questão:
𝐶1 = 0,75 ∙ 𝐶
𝐶2 = 0,25 ∙ 𝐶
𝐶3 = 𝐶
𝑀1 = 16302
𝑀2 = 5512
𝑛3 = 10 𝑚.
𝑛1 = 6 𝑚.
𝑛2 = 8 𝑚.
Inserindo os valores nas equações que representam os montantes de
cada operação:
𝑀1 = 𝐶1 ∙ (1 + 𝑖 ∙ 𝑛1 ) ⟹ 16302 = 0,75 ∙ 𝐶 ∙ (1 + 𝑖 ∙ 6) ⟹ 𝐶 =
16302
0,75 ∙ (1 + 6𝑖)
𝑀2 = 𝐶2 ∙ (1 + 𝑖 ∙ 𝑛2 ) ⟹ 5512 = 0,25 ∙ 𝐶 ∙ (1 + 𝑖 ∙ 8) ⟹ 𝐶 =
5512
0,25 ∙ (1 + 8𝑖)
Igualando os valores de C, temos:
16302
5512
=
0,75 ∙ (1 + 6𝑖) 0,25 ∙ (1 + 8𝑖)
16302
5512
=
3 ∙ (1 + 6𝑖) (1 + 8𝑖)
Note que 16302 é múltiplo de 3, então podemos realizar a simplificação:
5434 ∙ (1 + 8𝑖) = 5512 ∙ (1 + 6𝑖)
5434 + 43472𝑖 = 5512 + 33072𝑖
10400𝑖 = 78 ⟹ 𝑖 = 0,0075
Substituindo em qualquer uma das equações de C, temos:
𝐶=
16302
16302
16302
=
=
= 20800
0,75 ∙ (1 + 6𝑖) 0,75 ∙ (1 + 6 ∙ 0,0075) 0,75 ∙ 1,045
Agora que já sabemos o valor do capital e da taxa de juros, basta
aplicarmos na fórmula do montante para sabermos o que pede a questão:
𝑀3 = 𝐶 ∙ (1 + 𝑖 ∙ 𝑛3 ) = 20800 ∙ (1 + 0,0075 ∙ 10) = 22360
A alternativa D é a resposta correta. (gabarito preliminar OK)
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
3 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
22. Sabe-se que o valor dos juros correspondente a uma dívida que vence daqui
a 3 anos é igual a R$ 3.972,00, considerando uma taxa de juros compostos de
10% ao ano. Esta mesma dívida, considerando uma taxa de juros compostos
de 5% ao semestre e com vencimento daqui a 1 ano, apresentaria um valor de
juros (J), em reais, tal que
(A) J ≤ 1.100
(B) 1.100 < J ≤ 1.200
(C) 1.200 < J ≤ 1.300
(D) 1.300 < J ≤ 1.400
(E) J > 1.400
Resolução:
Vimos em nossas aulas que os juros de uma aplicação a juros compostos
podem ser calculados por:
𝐽 = 𝐶 ∙ [(1 + 𝑖)𝑛 − 1]
Inserindo na equação os dados da questão, temos:
3972 = 𝐶 ∙ [(1 + 0,1)3 − 1]
3972 = 𝐶 ∙ (1,331 − 1) ⟹ 𝐶 =
3972
= 12000
0,331
Aplicando tal valor à segunda opção de juros, temos:
𝐽 = 12000 ∙ [(1 + 0,05)2 − 1] = 12000 ∙ (1,1025 − 1) = 1230
A alternativa C é a resposta correta. (gabarito preliminar OK)
23. Um investidor aplica, em uma mesma data, os seguintes capitais:
I. R$ 11.600,00, durante 15 meses, sob o regime de capitalização simples.
II. R$ 20.000,00, durante 1 semestre, sob o regime de capitalização composta,
a uma taxa de juros de 3% ao trimestre.
Se os valores dos juros das duas aplicações são iguais, então a taxa de juros
anual da primeira aplicação é de
(A) 8,4%
(B) 9,0%
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
4 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
(C) 9,6%
(D) 10,5%
(E) 10,8%
Resolução:
Vamos aos dados da questão:
𝐶1 = 11600
𝐶2 = 20000
𝑛1 = 15 𝑚.
𝑖2 = 3% 𝑎. 𝑡.
𝑛2 = 1 𝑠. = 2 𝑡.
O juro da aplicação simples será:
𝐽1 = 𝐶1 ∙ 𝑖1 ∙ 𝑛1 = 11600 ∙ 𝑖1 ∙ 15
O juro da aplicação composta será:
𝐽2 = 𝐶2 ∙ [(1 + 𝑖2 )𝑛2 − 1] = 20000 ∙ (1,032 − 1) = 20000 ∙ 0,0609 = 1218
Igualando ambos os valores, temos:
11600 ∙ 𝑖1 ∙ 15 = 1218 ⟹ 𝑖1 = 0,007 = 0,7% 𝑎. 𝑚.
Note que, como calculamos o prazo dos juros simples em meses, a taxa
de juros será mensal. No entanto, queremos a taxa anual, então temos que
calcular a taxa proporcional:
𝑖𝑎 = 12 ∙ 𝑖𝑚 = 12 ∙ 0,7 = 8,4% 𝑎. 𝑎.
A alternativa A é a resposta correta. (gabarito preliminar OK)
24. Suponha que a taxa de inflação apresentada em um determinado período
foi de 5%. Se uma pessoa investiu R$ 25.000,00 no início deste período e
resgatou no respectivo final todo o correspondente montante no valor de R$
26.827,50, significa que a taxa real de juros obtida por esta pessoa no período
foi de
(A) 2,00%
(B) 2,20%
(C) 2,31%
(D) 2,57%
(E) 2,75%
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
5 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
Resolução:
Eis uma questão clássica da FCC, que foi resolvida em nosso curso de
Matemática Financeira para ATE – SEFAZ/PI.
Como a questão trata de juros com influência da inflação, utilizamos a
seguinte fórmula:
(1 + 𝑖𝑎𝑝𝑎𝑟 ) = (1 + 𝑖𝑟𝑒𝑎𝑙 ) ∙ (1 + 𝑖𝑖𝑛𝑓 )
Os dados da questão são:
𝑖𝑖𝑛𝑓 = 5% = 0,05
𝑀 = 𝐶 ∙ (1 + 𝑖𝑎𝑝𝑎𝑟 ) ⟹ 26827,5 = 25000 ∙ (1 + 𝑖𝑎𝑝𝑎𝑟 )
(1 + 𝑖𝑎𝑝𝑎𝑟 ) = 1,0731 ⟹ 𝑖𝑎𝑝𝑎𝑟 = 0,0731
Aplicando a fórmula, temos:
(1 + 𝑖𝑎𝑝𝑎𝑟 ) = (1 + 𝑖𝑟𝑒𝑎𝑙 ) ∙ (1 + 𝑖𝑖𝑛𝑓 )
1,0731 = (1 + 𝑖𝑟𝑒𝑎𝑙 ) ∙ (1 + 0,05) ⟹ 1 + 𝑖𝑟𝑒𝑎𝑙 =
1,0731
= 1,022 ⟹ 𝑖𝑟𝑒𝑎𝑙 = 2,2%
1,05
A alternativa B é a resposta correta. (gabarito preliminar OK)
25. Um capital de R$ 15.000,00 é aplicado, durante 2 anos, à taxa de 5% ao
semestre com capitalização contínua. Dos valores abaixo, o mais próximo do
valor dos juros desta aplicação é
(A) R$ 3.076,00
(B) R$ 3.155,00
(C) R$ 3.321,00
(D) R$ 3.487,00
(E) R$ 3.653,00
Dados: ln(1,051271) = 0,05; ln(1,105171) = 0,10; ln(1,161834) = 0,15 e
ln(1,221403) = 0,20; em que ln é o logarítmo neperiano, tal que ln(e) = 1.
Resolução:
Como vimos na nossa aula 03 de Matemática Financeira para ATE –
SEFAZ/PI, a fórmula geral de cálculo do montante de um capital que sofre
capitalização contínua, é dada por:
𝑀 = 𝐶 ∙ 𝑒 𝑖∙𝑛
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
6 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
Colocando o tempo e a taxa na mesma base temporal, temos 2 anos, a
taxa de 10% ao ano, o que dá: 𝑖 ∙ 𝑛 = 2 ∙ 0,10 = 0,20. Assim, temos:
𝑀 = 15000 ∙ 𝑒 0,20 = 15000 ∙ 𝑒 𝑙𝑛1,221403 = 15000 ∙ 1,221403 = 18321,04
Logo, o juro foi de:
𝐽 = 𝑀 − 𝐶 = 18321,04 − 15000 = 3321,04
A alternativa C é a resposta correta. (gabarito preliminar OK)
26. A taxa de desconto utilizada em um banco para as operações de desconto
de títulos é de 24% ao ano. Se um título é descontado neste banco 3 meses
antes de seu vencimento, verifica-se que o valor do desconto comercial simples
supera o valor do desconto racional simples em R$ 73,80. O valor atual do título,
considerando o desconto comercial simples, é igual a
(A) R$ 19.768,20
(B) R$ 20.238,20
(C) R$ 20.285,20
(D) R$ 20.332,20
(E) R$ 20.426,20
Resolução:
Como dissemos em nosso curso de curso de Matemática Financeira
para ATE – SEFAZ/PI, esta é uma questão clássica da FCC.
Como é de nosso costume, começamos listando os dados do enunciado:
𝑛 = 3 𝑚.
𝑖 ∙ 𝑛 = 0,02 ∙ 3 = 0,06
𝑖 = 24% 𝑎. 𝑎. = 2% 𝑎. 𝑚.
𝐷𝐶 − 𝐷𝑅 = 73,8
Calculando o desconto comercial simples, com a fórmula 𝐷𝐶 = 𝑁 ∙ 𝑖 ∙ 𝑛 ,
temos:
𝐷𝐶 = 𝑁 ∙ 0,06
Já o cálculo do desconto racional simples é com a fórmula 𝐷𝑅 = 𝐴𝑅 ∙ 𝑖 ∙ 𝑛,
e ficamos com:
𝐷𝑅 = 𝐴𝑅 ∙ 𝑖 ∙ 𝑛 = 𝐴𝑅 ∙ 0,06
Mas 𝑁 = 𝐴𝑅 ∙ (1 + 𝑖 ∙ 𝑛) logo podemos substituir os valores:
𝐷𝑅 =
Prof. Custódio Nascimento
𝑁
𝑁 ∙ 0,06
∙ 0,06 =
(1 + 0,06)
1,06
www.exponencialconcursos.com.br
7 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
Logo, temos:
𝐷𝐶 − 𝐷𝑅 = 73,8 ⟹ 𝑁 ∙ 0,06 −
𝑁 ∙ 0,06
= 73,8
1,06
𝑁 ∙ 1,06 ∙ 0,06 − 𝑁 ∙ 0,06 = 73,8 ∙ 1,06 ⟹ 𝑁 =
73,8 ∙ 1,06
= 21730
0,0036
Calculando o valor atual pelo desconto comercial simples, temos:
𝐷𝐶 = 𝑁 ∙ 0,06 = 21730 ∙ 0,06 = 1303,8
𝐴𝐶 = 𝑁 − 𝐷𝐶 = 21730 − 1303,8 = 20426,2
A alternativa E é a resposta correta. (gabarito preliminar OK)
27. Para quitar uma dívida que apresenta na data de hoje o valor de R$
77.000,00, um empresário deverá efetuar um pagamento de P reais daqui a um
ano e outro de 2P reais daqui a 2 anos. Considerando o critério do desconto
racional composto a uma taxa de 8% ao ano, obtém-se que P é igual a
(A) R$ 27.000,00
(B) R$ 29.160,00
(C) R$ 30.326,40
(D) R$ 31.492,80
(E) R$ 32.659,20
Resolução:
Trazendo todos os valores ao valor presente, temos:
𝑃
2∙𝑃
+
= 77000
1,08 1,082
Multiplicando todas as parcelas por 1,082, temos:
1,08 ∙ 𝑃 + 2 ∙ 𝑃 = 77000 ∙ 1,082
3,08 ∙ 𝑃 = 77000 ∙ 1,1664 = 89812,8 ⟹ 𝑃 =
89812,8
= 29160
3,08
A alternativa B é a resposta correta. (gabarito preliminar OK)
28. O adquirente de um imóvel deverá quitar a respectiva dívida por meio de
60 prestações mensais e consecutivas, com a primeira prestação vencendo 1
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
8 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
mês após a data de aquisição do imóvel. Sabe-se que foi adotado o sistema de
amortização constante a uma taxa de 1,2% ao mês com o valor da décima
prestação igual a R$ 4.030,00. O valor da vigésima prestação é igual a
(A) R$ 3.640,00
(B) R$ 3.670,00
(C) R$ 3.700,00
(D) R$ 3.730,00
(E) R$ 3.760,00
Resolução:
Eis uma questão diferente do que a banca usualmente cobra, pois não foi
informado o valor da dívida. Logo, temos que empregar um pouco de raciocínio
matemático para podermos resolvê-la.
Estudando o modelo SAC, vimos que cada prestação é a soma de uma
parcela de amortização com outra de juro:
𝑃 =𝐴+𝐽
Lembramos que a amortização é constante, e que o juro pago é
proporcional ao valor devido (saldo devedor). Assim, a décima prestação é dada
por:
𝐴 + 𝐽10 = 4030
Mas o valor de cada parcela de juro é dado por:
𝐽𝑘 = 𝑖 ∙ 𝑆𝐷𝑘−1
Além disso, o saldo devedor é calculado com a fórmula:
𝑆𝐷𝑘 = (𝑛 − 𝑘) ∙ 𝐴
Assim, temos:
𝐽𝑘 = 𝑖 ∙ (𝑛 − (𝑘 − 1)) ∙ 𝐴
Calculando o valor de J10, temos:
𝐽10 = 𝑖 ∙ (60 − (10 − 1)) ∙ 𝐴 = 0,012 ∙ 51 ∙ 𝐴 = 0,612 ∙ 𝐴
Inserindo o valor do juro na equação que já montamos anteriormente
para a prestação, temos:
𝐴 + 0,612 ∙ 𝐴 = 4030 ⟹ 1,615 ∙ 𝐴 = 4030 ⟹ 𝐴 = 2500
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
9 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
Agora, podemos calcular todos os valores
financiamento. O juro da vigésima prestação será:
que
quisermos
do
𝐽20 = 𝑖 ∙ (60 − (20 − 1)) ∙ 𝐴 = 0,012 ∙ 41 ∙ 2500 = 1230
Logo, a vigésima prestação será dada por:
𝑃20 = 𝐴 + 𝐽20 = 2500 + 1230 = 3730
A alternativa D é a resposta correta. (gabarito preliminar OK)
29. Uma dívida no valor de R$ 20.000,00 vai ser paga em 30 prestações
mensais, iguais e consecutivas, vencendo a primeira prestação 1 mês após a
data de formação da dívida. Utilizou-se o sistema de amortização francês com
uma taxa de 2% ao mês. Pelo quadro de amortização, obtém-se que o saldo
devedor imediatamente após o pagamento da primeira prestação é de R$
19.507,00. O valor da cota de amortização incluído no valor da segunda
prestação é de
(A) R$ 502,86
(B) R$ 512,72
(C) R$ 522,58
(D) R$ 532,44
(E) R$ 542,30
Resolução:
Se o saldo devedor após a primeira parcela é de R$ 19.507,00, isso
significa que a amortização da primeira parcela é de:
𝐴1 = 20000 − 19507 = 493
O juro da primeira parcela será:
𝐽1 = 0,02 ∙ 20000 = 400
Como vimos no nosso curso, no sistema de amortização francês todas as
parcelas possuem valores iguais. Logo, todas as prestações terão o valor:
𝑃 = 𝐴1 + 𝐽1 = 493 + 400 = 893
Para calcularmos a segunda parcela, basta tomarmos o novo saldo
devedor, e sobre ele calcularmos o juro:
𝐽2 = 0,02 ∙ 19507 = 390,14
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
10 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
Como as prestações são iguais, temos que a segunda amortização será:
𝐴2 = 𝑃 − 𝐽2 = 893 − 390,14 = 502,86
A alternativa A é a resposta correta. (gabarito preliminar OK)
30. Os dois fluxos de caixa abaixo, referentes aos projetos X e Y, apresentam
a mesma taxa interna de retorno positiva anual.
O desembolso inicial (D) do projeto Y é igual a
(A) R$ 1.750,00
(B) R$ 1.800,00
(C) R$ 1.850,00
(D) R$ 1.900,00
(E) R$ 1.950,00
Resolução:
Vamos começar calculando a taxa interna de retorno do projeto X, o que
é feito quando igualamos o VPL a zero:
𝑉𝑃𝐿𝑋 = −2000 +
550
1815
+
=0
(1 + 𝑖) (1 + 𝑖)2
Na aula 04 do nosso curso de Matemática Financeira para ATE –
SEFAZ/PI, ensinamos como resolver este tipo de equação.
Como (1 + 𝑖) ≠ 0, podemos multiplicar todos os termos por (1 + 𝑖)2 :
−2000 ∙ (1 + 𝑖)2 + 550 ∙ (1 + 𝑖) + 1815 = 0
Vamos empregar uma substituição de variáveis, fazendo (1 + 𝑖) = 𝑥 :
−2000 ∙ 𝑥 2 + 550 ∙ 𝑥 + 1815 = 0
Simplificando por 5, temos:
−400 ∙ 𝑥 2 + 110 ∙ 𝑥 + 363 = 0
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
11 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
𝑥=
−110 ± √1102 − 4 ∙ (−400) ∙ 363 −110 ± √12100 + 580800 −110 ± 770
=
=
2 ∙ (−400)
−800
−800
Logo, as respostas são 𝑥1 = −0,825 e 𝑥2 = 1,1.
Queremos apenas a resposta positiva, logo
𝑥 = 1,1 ⟹ 1 + 𝑖 = 1,1 ⟹ 𝑖 = 0,1 = 10%
Agora, basta aplicarmos tal taxa ao fluxo de caixa do Projeto Y:
𝑉𝑃𝐿𝑌 = −𝐷 +
275 968 1197,9
+
+
=0
1,1 1,12
1,13
𝐷 = 250 + 800 + 900 = 1950
A alternativa E é a resposta correta. (gabarito preliminar OK)
Raciocínio Lógico
Vamos resolver cada questão, com comentários. A teoria foi abordada no
nosso curso de Raciocínio Lógico para ATE – SEFAZ/PI, focado na banca
FCC, lançado no site do Exponencial Concursos.
Lembramos que as questões 31 a 36 foram abordadas no curso de
Estatística, e serão tratadas pelo respectivo professor. As demais questões estão
a seguir:
37. Uma empresa fabrica dois tipos de latas cilíndricas para embalar alimentos.
O volume da lata tipo I é o dobro do volume da lata tipo II, mas a quantidade
de material gasta para fabricar a superfície lateral dos dois tipos de latas é igual.
Dessa forma, a altura da lata tipo I é igual
(A) ao quádruplo da altura da lata tipo II.
(B) ao dobro da altura da lata tipo II.
(C) à altura da lata tipo II.
(D) à metade da altura da lata tipo II.
(E) à quarta parte da altura da lata tipo II.
Dados: Em uma lata cilíndrica qualquer:
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
12 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
− o volume é diretamente proporcional à altura e também diretamente
proporcional ao quadrado do diâmetro da lata;
− a quantidade de material gasta para fabricar a superfície lateral é diretamente
proporcional à altura e também diretamente proporcional ao diâmetro da lata.
Resolução:
Chamaremos de V1, A1, D1 e Q1, respectivamente, o volume, altura,
diâmetro e quantidade de material da primeira lata, e de V2, A2, D2 e Q2 as
respectivas variáveis da segunda lata. Pelos dados da questão, temos:
𝑉1 = 2 ∙ 𝑉2
𝑄1 = 𝑄2
Mas a questão afirma que o volume é diretamente proporcional à altura
e também diretamente proporcional ao quadrado do diâmetro da lata, logo
sendo k a constante de proporcionalidade, temos:
𝑉1 = 𝑘 ∙ 𝐴1 ∙ 𝐷12
𝑉2 = 𝑘 ∙ 𝐴2 ∙ 𝐷22
Dividindo uma equação pela outra, temo:
𝑉1 𝑘 ∙ 𝐴1 ∙ 𝐷12
𝑉1 𝐴1 𝐷1 2
=
⟹
=
∙( )
𝑉2 𝑘 ∙ 𝐴2 ∙ 𝐷22
𝑉2 𝐴2 𝐷2
Mas 𝑉1 = 2 ∙ 𝑉2 , logo:
2 ∙ 𝑉2 𝐴1 𝐷1 2
𝐴1 𝐷1 2
=
∙( ) ⟹
∙( ) =2
𝑉2
𝐴2 𝐷2
𝐴2 𝐷2
A questão afirma, ainda, que a quantidade de material gasta para fabricar
a superfície lateral é diretamente proporcional à altura e também diretamente
proporcional ao diâmetro da lata. Empregando o mesmo raciocínio anterior,
chegamos a:
𝑄1 𝐴1 𝐷1
𝐴1 𝐷1
𝐷1 𝐴2
=
∙
⟹
∙
=1⟹
=
𝑄2 𝐴2 𝐷2
𝐴2 𝐷2
𝐷2 𝐴1
Substituindo tal valor na equação dos volumes, temos:
𝐴1 𝐴2 2
𝐴2
𝐴
∙( ) =2⟹
= 2 ⟹ 𝐴1 =
𝐴2 𝐴1
𝐴1
2
A alternativa D é a resposta correta. (gabarito preliminar OK)
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
13 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
38. Em uma sequência de números inteiros, o primeiro elemento vale 1 e o
segundo elemento vale − 1. A partir do terceiro, cada elemento é igual ao
produto dos dois elementos imediatamente anteriores a ele. A soma dos
primeiros 2015 elementos dessa sequência é igual a
(A) − 671.
(B) − 673.
(C) − 1.
(D) − 2013.
(E) − 2015.
Resolução:
Seguindo a lei de formação da sequência, teremos:
1, -1, -1, 1, -1, -1, 1, -1, -1, 1 ...
Ou seja, há repetição do seguinte argumento: 1, -1, -1
Logo, a cada 3 elementos que somamos, o resultado dá -1. Sendo assim,
basta calcularmos o quociente e o resto da divisão de 2015 por 3, para sabermos
o comportamento final da sequência. Ora, a divisão de 2015 por 3 dá quociente
de 671 e resto 2.
Logo, a soma até o 2013º termo dá -671, e os últimos dois termos são 1
e -1, que dão soma zero. Assim, o resultado da questão é -671.
A alternativa A é a resposta correta. (gabarito preliminar OK)
39. As afirmações a seguir, todas verdadeiras, foram feitas pelo chefe do
departamento de Imunologia de uma faculdade de medicina, referindo-se a
eventos que poderiam acontecer no ano de 2014.
1. Se o projeto for aprovado, o departamento receberá novos computadores e
terá seu laboratório reformado.
2 . Se o laboratório for reformado, passará a ter capacidade para processar o
sangue de 50 pacientes por dia.
3. Se for possível processar o sangue de 50 pacientes por dia, o número de
atendimentos diários no ambulatório será duplicado.
A partir dessas informações, é correto concluir que, se a capacidade de
processamento de sangue do laboratório do departamento de Imunologia, em
2015, é de apenas 25 pacientes por dia, então, necessariamente,
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
14 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
(A) o departamento não recebeu novos computadores.
(B) o número de atendimentos diários no ambulatório não foi duplicado.
(C) o laboratório do departamento foi reformado.
(D) o projeto citado pelo chefe do departamento não foi aprovado.
(E) a capacidade de processamento de sangue do laboratório manteve-se
constante.
Resolução:
Se a capacidade de processamento do laboratório é de 25 pacientes por
dia em 2015, isso significa que é falsa a proposição “o laboratório passará a ter
capacidade para processar o sangue de 50 pacientes por dia”. Logo,
empregando os conceitos da proposição condicional, temos:
2 . Se o laboratório for reformado, passará a ter capacidade para processar o
sangue de 50 pacientes por dia.
F
F
1. Se o projeto for aprovado, o departamento receberá novos computadores e
terá seu laboratório reformado.
V/F
F
F
3. Se for possível processar o sangue de 50 pacientes por dia, o número de
atendimentos diários no ambulatório será duplicado.
F
V/F
Assim, a única alternativa possível é a letra D.
A alternativa D é a resposta correta. (gabarito preliminar OK)
40. Na eleição para síndico de um edifício, houve cinco candidatos e um total
de 186 votos. O vencedor e o último colocado obtiveram 42 e 34 votos,
respectivamente. Sabendo que não houve empate entre quaisquer dois
candidatos, o número de votos obtido pelo terceiro colocado
(A) certamente foi 36.
(B) pode ter sido 36 ou 37.
(C) certamente foi 37.
(D) certamente foi 38.
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
15 de 16
Análise e Resolução da prova de ATE – SEFAZ/PI
Matemática Financeira e Raciocínio Lógico
Prof. Custódio Nascimento
(E) pode ter sido 38 ou 39.
Resolução:
Subtraindo os votos do primeiro e do último colocados, temos que sobram
110 votos para os três demais candidatos. Como a média de votos desses três
candidatos é de 36,7 votos, temos um ponto de partida, pois sabemos que a
quantidade orbitou em torno desse número. Como não houve empate, temos
que a quantidade possível de votos para cada candidato variou de 35 a 41.
Vamos estudar algumas hipóteses de votação:
4º colocado
35
35
3º colocado
36
37
2º colocado
39
38
Soma
110
110
Note que não há outras possibilidades, pois a soma seria diferente de
110. Logo, o terceiro colocado pode ter tido 36 ou 37 votos.
A alternativa B é a resposta correta. (gabarito preliminar OK)
Prof. Custódio Nascimento
www.exponencialconcursos.com.br
16 de 16