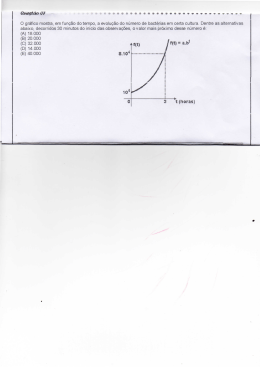
UNIVERSIDADE DOS AÇORES
Aplicações da Matemática
Curso: Bioinformática
2º Ano 1º Semestre
Ficha 2.
1. A taxa de crescimento de uma colónia de bactérias, num qualquer momento, é
proporcional ao número total de bactérias nesse momento. Sob condições ideais,
uma colónia de bactérias Eschrichia coli cresce com factor 100 em cada 2 horas. Se
inicialmente estiverem presentes 4 000 bactérias, ao fim de quanto tempo é que a
colónia tem 1 000 000 de bactérias?
2. Aproximadamente 10 000 bactérias são colocadas numa cultura. Seja P(t) o número
de bactérias presentes na cultura após t horas, e suponha que P(t) satisfaz a equação
P’(t) = 0.55P(t).
2.1. Encontre a fórmula para P(t).
2.2. O que é P(0)?
2.3. Quantas bactérias estão presentes após 5 horas?
2.4. Quando irá dobrar a população?
2.5. Qual é a constante de crescimento?
2.6. Determine a rapidez com que a cultura está crescendo quando ela atinge 100 000
bactérias?
2.7. Qual é a população da cultura quando a taxa de crescimento é de 34 000 bactérias
por hora?
3.
Determine a constante de crescimento de uma população que cresce com uma taxa
proporcional ao seu tamanho, sabendo que a população dobra a cada 40 dias?
4. A taxa de crescimento de uma cultura de células é proporcional ao seu tamanho. Em
10 horas uma população de um milhão de células cresce para 9 milhões. Qual será o
tamanho da cultura após 15 horas?
5. Uma amostra com 8 gramas de um material radioactivo é colocada num cofre. Seja
P(t) a quantidade de material radioactivo que permanece após t anos, e suponha que
P(t) satisfaz a equação P’(t) = -0.021P(t).
5.1. Encontre a fórmula para P(t).
5.2. Indique o valor de P0, e da constante de decrescimento.
5.3. Após 10 anos que quantidade de material radioactivo permanece?
5.4. Determine a rapidez com que a amostra está se desintegrando quando resta 1
grama.
5.5. Qual é a quantidade de material radioactivo que ainda permanece quando ele se está
desintegrando a uma taxa de 0.105 gramas por ano?
5.6. O material tem uma meia - vida de 33 anos. Quanto material irá permanecer após
33 anos, 66 anos e 99 anos?
6. Suponha que uma pessoa recebe uma injecção de 300 mg de penicilina no instante
t=0 e seja f(t) a quantidade (em miligramas) de penicilina presente na corrente
sanguínea da pessoa, t horas após a injecção. A quantidade de penicilina presente
0.6 t
decresce exponencialmente de acordo com a equação f(t) = 300 e-
.
6.1. Quanta penicilina irá permanecer após 5 horas?
6.2. Determine a rapidez com que a quantidade de penicilina está decrescendo na
corrente sanguínea quando estão presentes 20 mg.
6.3. Qual é a meia – vida biológica da penicilina neste caso?
7. Num hospital veterinário 8 unidades de sulfato são injectadas num cão. Depois de
50 minutos apenas permanecem 4 unidades nesse animal. Seja f(t) a quantidade de
sulfato presente após t minutos. Para qualquer valor do tempo a taxa de variação de
f(t) é proporcional ao valor de f(t). Encontre uma fórmula para f(t).