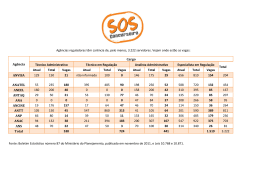
Comentário do simulado – 2015
Prof : Paulo
QUESTÃO 01
Comprimento :28m = 2800 cm  2800 : 250 = 11,2 cm
Largura : 12m = 1200 cm  1200 : 250 = 4,8
Resposta: alternativa: C
QUESTÃO 02
N
20 000 000 habitantes
DM =

=25 hab /km²
área
800 000 km²
Resposta: alternativa: B
QUESTÃO 03
32000 mulheres 8000 mulheres
=
 32 000x = 224 000 000 
28000 homens
x homens
x=7 000 homens
Como são 5 anos temos: 5 x 7 000 = 35 000
Resposta: alternativa: D
QUESTÃO 04
x representa o número total de vagas oferecidas
x
 vagas destinadas para sonoplastia
2
x
 vagas destinadas para iluminação
4
10  vagas destinadas para cenotécnica
x x
Logo: x= + +10
2 4
4x – 2x – x = 40
x = 40
Resposta: alternativa: A
QUESTÃO 05
S  números de shorts
C  números de camisas
n ( S x C ) = 10 . 12 = 120
Respostas: alternativa: E
x=
224 000 000
32 000
QUESTÃO 06
N =0,05. 10²+0,1 .10+3,4=9,4 partes por milhões
Respostas: alternativa: D
QUESTÃO 07
Para T = 4, temos que: 4=3+
12
 n = 12, ou seja, a partir da 13ª tentativa
n
Resposta: alternativa: B
QUESTÃO 08
(172−13)+164
+8,5=170  H máx =170m
2
Resposta: alternativa: D
H máx =
QUESTÃO 09
5
C= (F−32) 9C=5F−160  5f =9C+ 160
9
9C+160
Logo : F =
5
Resposta: alternativa: C
QUESTÃO 10
0,1.0
Noinício ,(t=0) q (0)=q0 .2 =q0
q
q
t
−1
−0,1t
q (t)= 0  0 =q−0,1
−0,1t =−1
0.2 2 =2
2
2
Logo,t = 10 meses.
Resposta: alternativa: E
QUESTÃO 11
Para o forno chegar a 48º C, temos:
7
48= t+ 20 t=20
5
Para o forno chegar a 200ºC, temos :
2
16
200=
t²− t+320  t²−200t+7500=0
125
5
Resolvendo a equação do 2º grau, temos: t = 50 ( não convém) ou t = 150.
Logo o tempo, em minutos, necessários para aumentar a temperatura de 48º C para
250º C é dado por 150 – 20 = 130
Resposta: alternativa: D
QUESTÃO 12
Podemos atribuir a cada letra um número, de acordo com a sua posição no alfabeto, por
exemplo : A = 1 , B = 2 , C = 3 e assim por diante.
Assim temos:
1
2,
3,
4,
5
f (A)= f (1)=3 , f (B)= f ( 2)=3 f (C)= f (3)=3 f ( D)= f ($)=3 f (E)= f (5)=3 , ...
2x−1
Portanto de maneira geral, temos que f (x )=3
, sendo x a posição da letra no nosso
alfabeto.
31=32x−1  x=1 , assim f 1 (31)= A
323=32x−1  x=12 , assim f 1 (323)= L
9
2x−1
1
5
3 =3  x=5 , assim f = f (3 )=E
325=32x−1  x=13 , assim f 1 (325)=M
Portanto a palavra é ALEM
resposta: alternativa: C
QUESTÃO 13
Contrato I : f(x)= 0,40x + 90
Contrato II : f(x) = 0,80x + 77,20
Para que seja mais vantajoso optar pelo contrato I, devemos ter:
0,40x + 90 < 0,80x + 77,20  - 0,40x < -12,80
12,80
 x > 32
0,40x > 12,80  x >
0,40
Logo, o contrato I é mais vantajoso a partir de 33 minutos
Resposta: alternativa: A
QUESTÃO 14
Em 4 anos, o valor aumentou em R$ 2 000,00, então o valor é de R$ 500,00 por ano.
4
Em 6 anos e 4 meses, o valor será 4000+ 6+
.500=43 166,00
12
Resposta: alternativa: D
(
)
QUESTÃO 15
b
−m
x v =− =150 −
=150 m=300
a
2.1
2
y v =C (150)=7500  150 −300 . 150+n=7500  n=3000
Logo m + n = 30 300
Resposta: alternativa: D