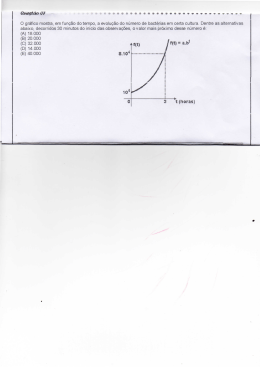
Resolução - Lista 3 – Cálculo I
Exercício 1 – página 61: Encontre as funções compostas , , , e
determine o domínio de cada uma delas, para cada par de funções e dados:
c) = e = + 2
Calculando :
= ï
=
1
= ï
Encontrando o domínio de :
Não existem restrições para a função = , logo o domínio da função será:
= ℝ
Calculando :
= ï
+ 2 = + 2 + 2 + 2
Encontrando o domínio de :
Não existem restrições para a função + 2 = + 2 + 2 + 2, logo
o domínio da função + 2 será:
= ℝ
Calculando :
= ï
+ 2=
Encontrando o domínio da função + 2=
:
Neste caso existe uma restrição. O denominador da fração deve ser diferente de 0.
Logo temos:
+ 2 ≠ 0
ï
+ 2) ≠ 0
Como neste curso estamos interessados em domínios que estejam contidos nos reais,
temos que o domínio da função será:
= ∈ ℝ| ≠ 0!
Calculando :
= 1
1 2
= +
ï
Neste caso existe uma restrição. O denominador da fração deve ser diferente de 0.
Logo temos:
≠0
e
≠0
Logo temos que ≠ 0.
Portanto o domínio da função será:
= ∈ ℝ| ≠ 0!
Exercício 2 – página 62: Expresse cada uma das funções dadas como composição de
duas outras funções.
a) " = 7 − Podemos observar que o fator 7 − pode ser representado por uma função %
ficando:
% = 7 − A outra parte da função " que é a parte que tem o expoente pode ser
representada por uma função &', onde &' será:
&' = ' Quando fazemos &% obtemos a função ":
&7 − = 7 − = "
Logo as funções que compostas formam " são &' = ' e % = 7 − .
b)( = cos √
Podemos observar que √ pode ser representada por uma função - tal que:
- = √
A outra parte da função, a parte que tem cosseno, pode ser representada por uma
função ./ tal que:
./ = cos /
Quando fazemos a composição de funções .-, obtemos a função (:
.√ = cos √ = (
Logo as funções que quando compostas formam ( são - = √ e ./ = cos /
c) % = 0
Podemos observar que − 2 pode ser representada por uma função 1 tal que:
1 = − 2
A outra parte da função pode ser representada por uma função 23 tal que:
23 = 1
3
Quando as funções 1 e 23 são compostas, obtemos a função %:
21 = 2 − 2 = 0 = %
d) 45 = √sin 5
Podemos representar sin 5 por uma função 85 tal que:
85 = sin 5
Também podemos representar a outra parte da função 45 como uma função 9,
tal que:
9 = :9
Quando compostas as funções 9 e 85, obtemos a função 45:
85 = sin 5 = :sin 5 = 45
Exercício 3 – página 77: Determine a inversa de cada função dada e dê sua expressão
como uma função de x.
b) = √ + 2
Para encontrar a inversa, devemos isolar . Para facilitar a álgebra, = ;:
; = √ + 2
ï
√ = ; − 2 ï
ï
; = √ + 2
; − 2 = √
ï
ï
; = :; − 2
Escrevendo a função em termos de x, obtemos:
0 = √ − 2
c) = 3 + − 2=
Novamente, para encontrar a inversa, devemos isolar . Para facilitar a álgebra,
= ;:
; = 3 + − 2=
2 + :; − 3 = ;
>
ï ; − 3 = − 2=
ï
:; − 3 = − 2
>
ï
Escrevendo a função em termos de x, obtemos:
>
0 = √ − 3 + 2
Exercício 9 – página 78: Uma cultura de bactérias cresce segundo a lei 15 = ?10@A ,
onde 15 é o número de bactérias em 5 horas, 5 ≥ 0, e ? e C são constantes
estritamente positivas. Se após 2 horas o número inicial de bactérias, 10, é
duplicado, após 6 horas qual será o número de bactérias?
A função 15 = ?10@A nos diz quantas bactérias existem numa cultura em função do
tempo t. Segundo enunciado,? e C são constantes positivas e o tempo deve ser 5 ≥ 0.
Para a resolução deste exercício, devemos descobrir os valores das constantes? e C
antes de encontrar o número de bactérias na cultura após 6 horas.
Primeiramente, pode-se encontrar quantas bactérias existiam na cultura no instante
inicial, tomando como o início 5 = 0 e assim encontrando10:
15 = ?10@A Para 5 = 0 horas temos:
10 = ?10@D
10 = ?
Portanto a constante ? é igual ao número inicial de bactérias na cultura. A função pode
ser reescrita como:
15 = 1010@A Agora, o enunciado nos diz que a quantidade de bactérias na cultura após 2 horas será
o dobro da quantidade inicial, em outras palavras:
12 = 210
Através dessa informação, conseguimos encontrar o valor da constante C fazendo:
12 = 1010@ ï
210 = 1010@ ï
2 = 10@
Aplicando o logaritmo de base 10 para retirar C do expoente:
log 2 = log 10@
ï
log 2 = 2C ï
GHI =C ï
C = 0,150514997
Obs: Quando omitida a base do logaritmo, normalmente trata-se da base 10.
Agora que conhecemos os valores das constantes ? e C, podemos encontrar a
quantidade de bactérias na cultura após 6 horas em termos de 10:
16 = 1010D,=D=LMMN.P
ï
16 = 810
Resposta: Após 6 horas, o número de bactérias é 8 vezes maior do que a quantidade
inicial de bactérias.
Exercício 10 – página 78: Suponha que uma determinada substância radioativa se
desintegre de acordo com a função 95 = 9D 20D,D=A , onde 95 é a quantidade após 5
anos, 9D é a quantidade inicial e 5 é o tempo decorrido, em anos. Sabemos que a
quantidade da substância está reduzida à metade da quantidade inicial. Quanto tempo
já passou?
Segundo o enunciado, a função 95 = 9D 20D,D=A representa a quantidade de uma
substância radioativa que varia com o tempo. O enunciado nos diz que a quantidade
de substância se reduziu pela metade, portanto:
9 5U =
ï
VW
ï
=2
0D,D=AU
X
9 5U = 9D 2
ï
0D,D=AU
20 = 2
X
VW
= 9D 2
0D,D=AU
X
0D,D=AU
Por propriedade de exponenciais, sabemos que
20 = 2
ï
X
= 20 , logo podemos fazer:
0D,D=AU
X
Utilizando a propriedade de potências de mesma base, podemos igualar os expoentes:
−1 = −0,05 5U
5U = 20 anos
Resposta: O tempo necessário para que a massa da substância radioativa diminua pela
metade é de 20 anos.