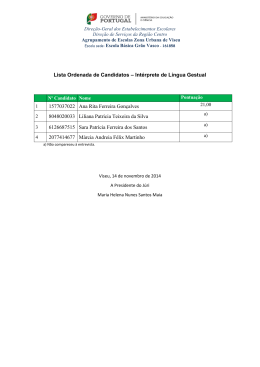
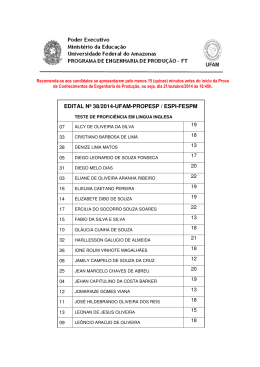
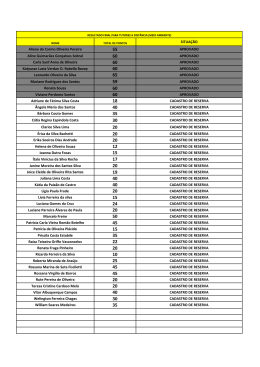
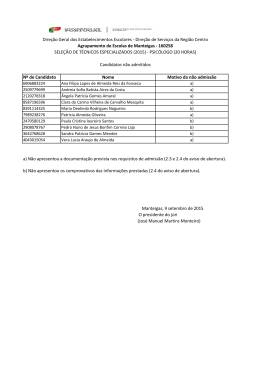
90
APÊNDICE A
Síntese da Revisão Bibliográfica
Título
Autores
Instituição Tipo
/ Evento
Conjunto
dos
Números Keiji Nakamura
PUC SP
dissertação
Os alunos de 5ª. série/6º. Ano Lucimeire Omoti PUC SP
Dissertação
Irracionais: A trajetória de um
conteúdo não incorporado às
práticas escolares
frente
a
atividades
sobre de Aquino
observação e generalização
de padrões
Números Inteiros nos Ensinos Aguinaldo José PUC SP
Fundamental e Médio
Rama
Um Estudo sobre o Cálculo Aparecida
Operatório
no
Dissertação
de PUC SP
Dissertação
Cruz PUC SP
Dissertação
Maria PUC SP
Dissertação
Campo Lourdes
Multiplicativo com alunos de Bonanno
5ª.
série
do
Ensino
Fundamental
Resolução de Problemas em Ivan
aulas
de
Matemática
para Rodrigues
alunos de 1ª. a 4ª. séries do
Ensino
Fundamental
e
a
Atuação dos Professores
Investigações sobre Números Icléa
Naturais
e
Processos
de Bonaldo
Ensino e Aprendizagem desse
tema
no
Escolaridade
início
da
91
Parâmetros
Curriculares Mutsu-Ko
PUC SP
Dissertação
PUC SP
Dissertação
Martins PUC SP
Dissertação
Investigação em Sala de Aula: Mari Emilia dos PUC SP
Dissertação
Nacionais de Matemática para Kobashigawa
o Ensino Fundamental: das
Prescrições
ao
Currículo
praticado pelos Professores
Um Estudo com os Números Humberto
Inteiros nas Séries Iniciais: Todesco
Re-aplicação da Pesquisa de
Passoni
O Professor, o Ensino de Aléxis
Fração e o Livro Didático: Um Teixeira
Estudo Investigativo
Uma Proposta de Atividade Santos Calhau
em Salas de Aula no Ensino
Fundamental
Análise
de
Situações
PUC SP
Dissertação
PUC SP
Dissertação
Envolvendo Eduardo Pereira
Aprendizagem
Números
de Marcelo
Racionais:
Uma
abordagem para o ensino de
argumentações e provas na
Matemática Escolar
Construção do Termo Geral Sebastião
da Progressão Aritmética pela Archilia
Observação e Generalização
de Padrões
Produzindo Significados aos Thais de Oliveira IX ENEM
Comunica-
Números
ção
Reais
Contexto
Em
um e
Dario
Exploratório- Fiorentini
Científica
Investigativo
Um Estudo sobre a Produção Viviane C A de IX ENEM
Comunica-
de Significados para Números Oliveira e
ção
Relativos
Ana
Clara S Araújo
Científica
92
Números e Operações: Uma Gracivane
IX ENEM
Minicurso
de Norma Suely G IX ENEM
Minicurso
reflexão sobre os Significados Pessoa, Cristina
das
Operações
Algoritmos
e
no
dos A Rocha, José A
Ensino A Pereira e José
Fundamental
M Silva Filho
Diferentes
Tipos
Problemas
no Allevato
Desenvolvimento
de
Diferentes
de
Habilidades
Pensamento
Tratamento da Informação na Ilydio Pereira de IX ENEM
Minicurso
Educação Básica: Aritmética Sá
Modular e os Códigos de
Identificação do Cotidiano
Buscando Significados para a Marilene Ribeiro IX ENEM
Minicurso
Teoria dos Números como Resende
Saber
a
Ensinar
na
Licenciatura em Matemática
Pensamento
Reverso
Ensino de Matemática
Psicologia
e
Matemática
no Antonio
Carlos IX ENEM
Minicurso
Brolezzi
Educação David
A
da IX ENEM
Pôster
Escola Costa e Wagner
na
Primária: do Contar para a Valente
Aritmética
das Marlene
Apropriação
Significações do Conceito de Amorim
Divisão
de
P ANPED
Grupo
e
Trabalho
de
Números Ademir Damazio
Racionais
Contando Histórias nas Aulas Débora
de
Matemática: Andrade
Produção/Mobilização
de Regina
Conceitos na Perspectiva da Grando
Resolução de Problemas
O ANPED
Grupo
e
Trabalho
Célia
de
93
Discursos sobre a Matemática Cláudio José de ANPED
Grupo
Escolar: Um Estudo a partir Oliveira
Trabalho
de
da Revista Nova Escola
Análise
Exploratória
Dados:
Um
Diagnóstico
de Cileda Q Silva e ANPED
Estudo Maria
Inez
Grupo
Trabalho
sobre Miguel
Concepções de Professores
Números
Racionais: Plínio C Moreira UNESP
Conhecimentos da Formação e Maria Manuela
Inicial e Prática Docente na M S David
Escola Básica
bolema
de
94
APÊNDICE B
Caderno de Atividades Reformulado
Atividade 01 – O Sentido dos Números e as Intuições
1ª. Parte
Leia o texto abaixo e depois responda o que se pede.
“A imprensa muitas vezes utiliza formas diferentes de escrita na publicação de suas
notícias”. Observe duas notícias divulgadas recentemente:
“... Uma famosa cantora internacional tem um patrimônio de 25 mi de dólares...”
“...Uma bolsa de uma grife de luxo pode custar até 40 mil reais...”
Ao observar as notícias você pode informar:
I – Se o patrimônio da cantora tem valor muito alto?
II – Se um automóvel importado da montadora alemã Audi é vendido por 250.000
reais, você acha que ela poderá comprar muitos desses veículos? Justifique
III – Quando a notícia foi editada e publicada o dólar estava cotado em R$2,00, qual
o valor do patrimônio da cantora em reais?
IV – Quantos dólares custa a bolsa pela cotação do item anterior?
V – Você pensou que o valor de cotação do dólar em R$2,00 serviu como uma
unidade de medida?
Você seria capaz de criar uma tabela de conversão das duas moedas, na ordem de
real para dólar?
VI – Num sentido de reta numérica faça a representação conjunta das unidades
monetárias, real e dólar, isto é, numa reta só você tem que marcar as unidades do
real e as do dólar sem dizer qual é qual, mas colocando o real na parte debaixo da
reta e o dólar na parte de cima.
VII – Observando uma “trena”, instrumento utilizado em medições, justifique a
demarcação de dois tipos de numeração no objeto.
VIII – Usando a trena, faça a medida da diagonal da tela do notebook que o
professor José Ricardo levou para a sala de aula e veja as descrições das
95
características que estão em sua etiqueta que avistamos quando abrimos o
computador.
O que você associa quanto à medida realizada e o conteúdo da etiqueta, que veio
da fábrica que produziu o equipamento?
2ª. Parte
O professor Ricardo anotou no quadro os seguintes números: 0,495; 0,6 e 0,08,
depois pediu para que seus alunos colocassem os números em ordem crescente.
I – Qual seria a resposta correta?Relate como você resolveu a questão
Observe os três quadrinhos abaixo, que mostram o troco que cada menino de uma
turma do colégio recebeu depois de pagar um lanche na cantina.
II – Represente cada troco na forma decimal e diga qual deles recebeu o menor e o
maior troco. Relate como você resolveu a questão.
Você consegue dizer quem gastou mais dinheiro na lanchonete? Como você justifica
sua resposta?
Observando-se um atleta de salto em trampolim, tem-se:
96
- 1º. Salto: o trampolim tinha 5 metros de altura em relação ao nível da água na
piscina e ele alcançou 3 metros de profundidade nesta piscina;
- 2º. Salto: o trampolim tinha 4 metros de altura em relação ao nível da água na
piscina e ele percorreu um total de 6 metros, dentro e fora da água.
III – Responda:
a) Faça uma ilustração sobre cada salto
b) Represente a profundidade na água de cada salto com um número inteiro e diga
qual dos saltos teve maior profundidade na piscina.Justifique o motivo de você ter
utilizado o sinal de positivo ou negativo para o número inteiro.
Observando o placar de pontuação do atleta no segundo salto, tinha-se notas
maiores do que as registradas no primeiro salto, isso porque essa pontuação não se
relaciona com a profundidade obtida na piscina ou até mesmo com a altura do
trampolim. O interessante quando se observa a nota é que elas apareceram da
seguinte maneira: 89.8 no primeiro salto e 92.0 no segundo salto.
IV – Responda:
a) Essas notas são altas? Justifique sua resposta.
b) O que significam os pontos que aparecem nas notas?
Atividade 02 – Estimar Ações tem significados
Raiz: sf. 1. Bot. Porção do eixo da planta que cresce para baixo, ger.dentro do solo,
fixando-a e fornecendo-lhe água e nutrientes. 2. Parte inferior;base.3. Anat. A parte
do dente implantada na maxila. 4. Princípio, origem.5.Gram. A parte básica da
estrutura da palavra. 6. Mat. Potência fracionária de um número. [Pl.:raízes]
Fonte: Mini Aurélio Século XXI
97
Observe as significações dos números 2 e 6 extraídas de um dicionário, sobre a
palavra raiz.
I – Responda:
a)A palavra raiz você já ouviu falar em Matemática e por isso pergunto qual a
resposta para
36 ?
b) Qual o significado que você dá para a resposta?
Não foi explicado o porquê se colocou um significado do dicionário numa atividade
de Matemática.
II – Responda:
a) Você saberia explicar porque se falou de raiz e depois pediu para se calcular
36 ? Em sua opinião, por que foi destacado o significado número 2 para a palavra
raiz, que diz base, além do referente à Matemática?
b)E no significado número 6 que se refere à Matemática você sabe dizer o motivo de
potência fracionária de um número? Explique o que você entende desse significado,
se quiser exemplifique.
III – Mais um pouco sobre “raiz”...
Um professor propôs aos alunos o cálculo da seguinte raiz quadrada
961 , mas que
explicassem como acharam a resposta. Um aluno tentou fazer o cálculo da raiz
quadrada por decomposição em fatores primos e não conseguiu. Seu colega fez o
cálculo por tentativas e chegou à resposta.
Veja o que professor observou no rascunho de cada aluno:
98
1º. aluno
961 não divide por 2, pois não é par
961 não divide por 3, pois a soma de seus algarismos não é um número divisível por
3
961 não divide por 5, pois não termina em 5 e nem em zero
961 não divide por 7, fez a conta e viu resto
961 não divide por 11, fez a conta e viu resto
961 não divide por 13, fez a conta e viu resto
961 não divide por 17, fez a conta e viu resto E assim o aluno desistiu...
2º. aluno
10 . 10 = 100
20 . 20 = 400
30 . 30 = 900
Vou tentar 31 . 31 ... como a unidade do produto dá 1, ele estimou que o resultado
seria certo... armou a conta e viu que 31.31 dava 961 então escreveu que a resposta
seria 31.
Você acha que o 2º. aluno fez a questão corretamente? Você acha que ele fez uma
estimativa do resultado? Justifique a sua resposta.
Uma caixa de pisos vem com a seguinte descrição de medidas para cada unidade
de piso: 31 cm x 31 cm.
IV – O que significa isso, a caixa está informando para gente multiplicar 31 por 31?
Qual o formato desse piso?Justifique suas respostas.
Em cada caixa de piso vem 10 unidades. O chão de um quarto quadrado que mede
3,1 m por 3,1 m.
V – Você seria capaz de estimar quantas caixas seriam usadas para cobrir o chão
do quarto com pisos? Justifique sua resolução como você quiser... desenhando,
calculando, pensando, etc.
99
Num show de um cantor famoso foi estimada uma presença de 35.000
espectadores. Para assistir o show não foi colocado nenhum tipo de cadeira, todos
os presentes estariam de pé.
VI – Explique como se chegou a este número de pessoas para a platéia.
Atividade 03 – Números e Operações: Pensando e Raciocinando
UM DIA NO COMÉRCIO
No bairro de Patrícia tem uma padaria onde sua mãe compra sempre alguma coisa
para o lanche. Essa padaria fica um pouco distante de sua casa, e às vezes, a mãe
de Patrícia compra num barzinho em frente à sua casa, o que precisa para o lanche,
principalmente em dias de chuva. A Patrícia é uma estudante muito dedicada e
observadora. Vamos conhecer algumas situações que a Patrícia vivenciou...
Um dia ela foi a padaria com sua mãe e ficou observando como a moça do caixa
dava o troco... a máquina registradora já dizia para a moça qual era o troco a ser
dado numa tela igual de um computador...primeiro a moça registrou os itens que sua
mãe comprou e depois ela registrou o dinheiro que foi dado para pagamento das
despesas. Em seguida, no visor apareceu o valor do troco a ser dado. A mãe de
Patrícia gastou nas compras R$3,40 com pães e R$4,95 com outros produtos,
dando uma nota de 10 reais para pagamento.
I – Agora pense e responda:
a) Qual foi o troco recebido pela mãe de Patrícia?
b) Que operações você acha que foram feitas pela máquina do caixa nestas
compras para apresentar o valor do troco?
c) Se você tivesse que fazer o cálculo mentalmente para dar o troco, como faria da
maneira mais rápida possível?
d) Você acha que a máquina poderia fazer um cálculo igual ao seu? Justifique
100
Continuando a história...
Outro dia a Patrícia foi ao barzinho com sua mãe e observou que lá a
máquina registradora não informava o valor do troco, sua tela era pequena e preta
com números verdes, mas ela ficou impressionada como a moça do caixa fez a
conta rapidamente para dar o troco à sua mãe. A situação da compra foi a seguinte:
a mãe de Patrícia comprou refrigerantes por R$4,15 e outros produtos que custaram
R$2,95, e depois deu uma nota de 10 reais para pagamento dos gastos.
Curiosa, perguntou a moça como ela tinha feito a conta... A moça explicou:
- peguei R$2,95 e coloquei os R$0,05 dos R$4,15... aí deu R$3,00 que eu somei
com R$4,10 que sobrou, pronto deu R$7,10. Na hora de dar o troco para R$10,00,
peguei R$0,40 centavos em moeda e pensei R$7,50, depois peguei R$0,50 e pensei
R$8,00 e depois peguei uma nota de 2 reais e pensei R$10,00.
Patrícia adorou o jeito de fazer conta da moça... muito diferente do que ela costuma
fazer na escola quando tem um problema desse tipo...
II – Agora é sua vez de responder... você acha que a moça fez a conta
corretamente? Você usaria quais operações para dar o troco à mãe de Patrícia? Por
que você pensou nessas contas?
III – Você seria capaz de dar o troco da padaria fazendo de outra maneira a conta?
Explique como faria.
... a Patrícia agora observa tudo... vamos continuar...
Patrícia agora fica observando a moça do caixa do barzinho e outro dia se
deparou com outra situação interessante...
Ela foi comprar 8 pãezinhos que custavam R$0,15 cada um... e levou uma nota de 2
reais. Num instante a moça fez as contas e entregou o troco para Patrícia. Patrícia
olhou para ela e disse :
- sei como você fez as contas...
A moça abriu um sorriso e perguntou para a menina:
- Como?
A menina respondeu como pensou:
- Você fez R$0,10 vezes 8 é igual a R$0,80 centavos, mais R$0,05 vezes 8 que é
igual a R$0,40... depois somou R$0,80 + R$0,40, total R$1,20... e o troco você
pegou R$0,30 e pensou R$1,50, depois pegou R$0,50 e pensou R$2,00.
101
Patrícia olhou para a moça com triunfo de saber fazer contas mentalmente.
A moça sorriu novamente para Patrícia e disse calmamente:
- Minha querida menina, você pensou corretamente... mas eu não pensei assim.
Patrícia se assustou e perguntou:
- Como você pensou????
A moça explicou:
- Como 1 pão custa R$0,15, pensei 2 pães custam R$0,30, então 4 pães R$0,60 e
finalmente 8 pães R$1,20...
A moça deu um novo sorriso para a menina e completou:
- Eu pensei em somas que fossem o dobro...
A menina logo perguntou:
- E o troco???
A moça respondeu:
- Você me deu R$2,00 e a conta era R$1,20... logo pensei R$2,00 menos R$1,00 é
igual a R$1,00 e daí eu tirei os R$0,20, pronto troco de R$0,80.
Aí foi a vez de Patrícia sorrir e dizer:
- legal, agora já sei que posso pensar de maneiras diferentes em situações
parecidas.
Patrícia saiu feliz do barzinho.
Agora é com você, pensa um pouco e responda:
IV – Você entendeu como a moça do caixa fez as contas? Você achou correto fazer
assim? Diga o que você achou da forma que a moça fez as contas.
V – Como você faria essas contas mentalmente?
VI – Responda:
a)Quando você multiplica algum valor por 8, você já pensou em somar dobros como
a moça fez? Se você for além da adição e pensar em multiplicar por 2, depois por 2
novamente, e depois por 2, no final dá certo?
b) Tenta multiplicar o número 35 por 8 sem armar a conta, faz um cálculo mental, e
escreva como foi seu raciocínio.
VII – Do jeito que a moça fez as contas, se pensarmos de forma mais complexa
como uma multiplicação, temos que: multiplicar por 8 é como se multiplicarmos por 2
e depois por 2 e depois por 2... isso lembra alguma outra operação que você
conheceu em Matemática? Se lembrar diga qual e porque você acha que lembra.
Atividade 04 – Propor Ação
102
Observe a história abaixo e depois pense um pouco para responder as questões
pedidas:
Dona Giselda vai fazer um refresco para seu filho e três amigos que vão
estudar para a prova de Matemática, mas na hora de fazer ela ficou com uma
dúvida, pois achou duas receitas e não sabia qual delas usar. A única coisa que
Dona Giselda sabia era que o refresco ficasse com um gosto bem forte de fruta.
Veja as receitas que ela encontrou:
1ª. receita:
Despejar numa jarra 6 partes de suco concentrado e 8 partes de água. Adoce a
gosto.
2ª. receita:
Despejar numa jarra 12 partes de suco concentrado e 14 partes de água. Adoce a
gosto.
Como Dona Giselda gosta muito de Matemática e também entende muito
bem como lidar com receitas, ela rapidinho eliminou a dúvida... Agora eu não vou lhe
contar qual receita Dona Giselda fez, pois você vai ter que pensar ... e muito mais do
que escolher a receita, você vai responder algumas questões de Matemática e tirar
suas próprias conclusões sobre as receitas e outras situações...
I – Você sabe explicar porque a mãe do menino teve dúvida sobre qual receita
fazer?
II – O refresco em cada receita ficará com o mesmo sabor? Se você acha que não,
diga qual refresco ficará com o sabor mais forte. Justifique sua resposta.
III – Se a mãe do menino fizer a 2ª. receita, você acha que cada criança poderá
tomar 4 copos de refresco? Justifique sua resposta
IV – Repare que existe uma mudança na quantidade de partes entre a 1ª receita e a
2ª receita, que representa um aumento de 6 partes de suco e 6 partes de água. Isso
garante o mesmo sabor? Justifique
V – Pensando de forma a relacionar as quantidades do problema descrito em caráter
de comparação entre partes, tem-se: na 1ª receita se usarmos 1 parte de suco, qual
deve ser a utilização aproximada de água? Que operação ou pensamento você usou
para encontrar sua resposta? Explique como resolveu esta situação.
Na 2ª receita qual a quantidade de água a ser utilizada para uma parte de suco?
103
Após os cálculos você é capaz de indicar qual seria uma solução para a dúvida da
Dona Giselda?
VI – Se pensássemos em frações em cada receita:
a) A fração 6/8 na 1ª. receita tem qual significado para você?
b) E a fração 12/14 na 2ª. receita?
VII – Para resolver o problema da história, ou seja, qual receita fazer e justificar a
resposta, vou mostrar a resolução apresentada por 3 alunos, identificados pelo
nome, e quero que você pense em cada uma delas e depois responda ou justifique o
que se pede:
a)Paulinho
o aluno resolveu o problema assim:
Leu a 1ª. receita e pensou assim:
coposdesuco 6 7 42
= X =
coposdeágua 8 7 56
Leu a 2ª. receita e pensou assim:
coposdesuco 12 4 48
=
X =
coposdeágua 14 4 56
Depois respondeu que a 2ª. receita tem mais sabor.
Você concorda com a forma que esse aluno resolveu a questão? Se você acha que
ele deu a resposta certa ou errada, justifique como você pensou para tirar sua
conclusão.
b) Jorginho
O aluno resolveu o problema assim:
Leu a 1ª. receita e pensou assim:
Nesta receita olhando os copos de água tenho que metade de 8 é igual a 4, então se
eu colocar mais metade de 4, que é 2, fico com 6. Isso é a quantidade de suco
usado na receita.
Leu a 2ª. receita e pensou assim:
Nesta receita olhando os copos de água tenho que metade de 14 é igual a 7, então
se eu colocar mais metade de 7, que é 3,5, fico com 10,5. Isso é menos que a
quantidade de suco usado na receita.
Concluo então que a 2ª. receita tem mais sabor.
Você entendeu as contas do aluno? Explique o que entendeu
104
c) Pedrinho
o outro aluno resolveu o problema assim:
Leu a 1ª. receita e pensou assim:
Tenho 6 partes de suco e 14 partes de refresco (6 de suco e 8 de água) que forma a
fração 6/14 que dividindo o número de cima pelo número de baixo dá
aproximadamente 0,42.
Leu a 2ª. receita e pensou assim:
Tenho 12 partes de suco e 26 partes de refresco (12 de suco e 14 de água) que
forma a fração 12/26 que dividindo o número de cima pelo número de baixo dá
aproximadamente 0,46.
Concluo que a 2ª. Receita tem mais sabor.
Você entendeu as contas do aluno? Explique o que entendeu