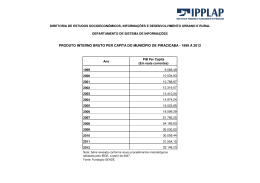
MODELOS NEOCLÁSSICOS DE CRESCIMENTO ECONÔMICO1
SOUZA, Nali de Jesus.
Desenvolvimento Econômico. 5a ed. São Paulo: Atlas, 2005.
Após a Segunda Guerra Mundial, a maioria dos países procurou acelerar o crescimento
econômico, visando aumentar a renda e reduzir a pobreza. Os economistas passaram a formular
teorias e modelos para identificar os fatores de crescimento das economias. O modelo neoclássico
fundamenta-se em algumas equações simples e adota um conjunto de pressupostos: (a) concorrência
perfeita e pleno emprego em todos os mercados; (b) economia fechada e sem governo; (c) função de
produção com rendimentos constantes à escala (quando variam simultaneamente todos os fatores) e
rendimentos decrescentes quando se altera apenas um dos fatores; (d) economia produzindo um
único bem com apenas três fatores: capital fixo (K), trabalho (L) e terra (N); e (e) os fatores de
produção são homogêneos, divisíveis e imperfeitamente substituíveis entre si (Paz e Rodrigues,
1972, p. 107).
1 - Modelo de Meade
Na versão de Meade, o nível do produto (Y) aparece como função do emprego de capital,
trabalho, terra e das inovações tecnológicas, incluídas na variável temporal (t):
Y = f (K, L, N, t)
(1)
A variação do produto (∆Y) será igual à soma das variações do estoque de capital (∆K) e do
emprego de trabalho (∆L), multiplicadas pelas produtividades marginais respectivas (Pmg), além do
crescimento residual do produto (∆Y’), atribuído ao progresso técnico, T (toda terra estando ocupada,
sua variação seria nula), ou seja:
∆Y = PmgK ∆K + PmgL ∆L + ∆Y’
(2)
No equilíbrio concorrencial, as produtividades marginais do capital e do trabalho serão iguais
a suas remunerações respectivas (PmgK = ∆Y/∆K = r; PmgL = ∆Y/∆L = w). Dividindo-se toda a
equação (2) por Y e acrescentando-se K no numerador e no denominador da parcela relativa ao
capital e L na parcela do trabalho, tem-se que:
∆Y/Y = (rK/Y) (∆K/K) + (wL/Y) (∆L/L) + (∆Y’/Y)
(3)
A taxa de crescimento do produto (∆Y/Y) depende das taxas de crescimento do estoque de
capital (∆K/K), do crescimento demográfico (∆L/L) e do progresso tecnológico (∆Y’/Y = ∆T/T), bem
como da participação da renda do capital e do trabalho no produto total (rK/Y = Ky e wL/Y = Ly).
Desse modo, a equação (3) pode ser representada de uma forma mais simples (Paz e Rodrigues,
1972, p. 115):
1
Esta é uma versão ampliada da seção 11.3 do livro Desenvolvimento Econômico (Souza, 2005).
∆Y/Y = Ky (∆K/K) + Ly (∆L/L) + (∆Y’/Y)
(4)
O ritmo do crescimento econômico de uma economia dependerá das hipóteses que se fizer
acerca das variáveis envolvidas. Considerando-se nulos o crescimento demográfico e o progresso
técnico e os mesmos valores para Ky e Ly, o crescimento econômico passará a depender da
produtividade marginal do capital e do ritmo de seu crescimento, bem como da propensão a poupar
(s = S/Y). No equilíbrio, o investimento torna-se igual à poupança (∆K = S = sY). Substituindo-se Ky
em (4) por rK/Y, tem-se que ∆Y/Y = (rK/Y) (∆K/K). Sabendo-se que ∆K/Y = s, então:
(5)
∆Y/Y = rs
A relação (5) diz que, sem progresso técnico e crescimento demográfico nulo, o crescimento
equilibrado exige que o produto cresça a uma taxa igual ao produto entre a propensão a poupar e a
produtividade marginal do capital (PmgK = ∆Y/∆K = r). Quanto maiores a propensão a poupar e a
produtividade do capital, tanto mais crescerá a economia. Com propensão a poupar constante, o
crescimento dependerá apenas da produtividade marginal do capital; porém, com um único fator
variável (rendimentos decrescentes), a economia tenderá ao estado estacionário; isso ocorrerá mais
rapidamente se a propensão a poupar for decrescente. Entretanto, os rendimentos decrescentes da
produtividade do capital poderão ser compensados por propensões a poupar crescentes (Paz e
Rodrigues, 1972, p. 117).
Com a hipótese de crescimento demográfico positivo e progresso técnico nulo, a economia
precisa crescer no mesmo ritmo do crescimento demográfico e da acumulação de capital, para manter
o crescimento equilibrado, isto é, sem desemprego ou hiperemprego. Isso pode ser demonstrado a
partir da equação (4), sabendo-se que toda a renda se distribui entre capitalistas e trabalhadores, isto
é, que (wL + rK) = Y, então (wL/Y + rK/Y) = 1, ou (Ky + Ly ) = 1. Supondo-se ∆Y/Y = ∆L/L, e
sabendo-se que Ky = (1 – Ly), a equação (4) torna-se igual a ∆Y/Y = (1 – Ly) (∆K/K) + Ly ∆Y/Y, ou:
(∆Y/Y)(1 – Ly) = (1 – Ly) (∆K/K)
(6)
Segue-se que, com ∆T/T = 0, então ∆Y/Y = ∆K/K = ∆L/L. Sem progresso técnico, taxas de
crescimento diferentes para o capital e a população conduzem a variações tanto nas remunerações
dos fatores capital e trabalho, como nas participações desses fatores na renda nacional. Logo, o
crescimento equilibrado depende da igualdade entre essas taxas. Maior crescimento demográfico
requer acumulação de capital na mesma proporção, para manter no longo prazo o crescimento de Y,
K e L em equilíbrio estável. Crescimento demográfico menor aumenta os salários e o crescimento
econômico se reduz. Nesse caso, é necessário que o progresso técnico e o capital aumentem sua
contribuição no crescimento econômico.
2 - Modelo de Solow
O modelo de Solow chega a conclusões semelhantes ao do modelo de Meade, usando
relações per capita. Relacionando poupança, acumulação de capital e crescimento demográfico, ele
2
procura explicar a variação do produto per capita. A função de produção Y = T f(K,L), é
transformada em termos per capita, Y/L = T f(K/L,L/L), ou seja:
y = T f(k),
(1)
onde y é a produção per capita, k é o capital per capita (a relação capital/trabalho) e T é o nível
tecnológico, que afeta as produtividades marginais do capital e do trabalho (Sachs e Larrain, 1995, p.
624).
No equilíbrio, I = S = sY; porém, uma parcela do investimento bruto, I, destina-se à
depreciação do capital fixo (dK), sendo d a taxa de depreciação, de sorte que ∆K = I – dK:
∆K = sY – dK
(2)
Como Solow trabalha em termos per capita, a equação (2) precisa ser dividida por L:
∆K/L = sy – dk
(3)
A suposição básica de Solow é a de que, no equilíbrio estável, existe uma relação k = K/L
constante, de sorte que ∆Y/Y = ∆K/K = ∆L/L = n. A taxa natural de crescimento demográfico, n,
como em Harrod, apresenta-se como uma variável exógena, que depende de fatores biológicos e
culturais e não das variáveis do modelo. Considerando o progresso técnico nulo, o equilíbrio estável
exige que uma variação positiva da relação k = K/L (maior quantidade de capital por trabalhador)
seja acompanhada por uma variação superior do estoque de capital, em relação ao crescimento
demográfico, n, ou seja:
∆k/k = ∆K/K – n
(4)
Dividindo-se (4) por L, obtém-se que ∆K/L = ∆k + nk ; substituindo-se o segundo membro
desta equação em (3), chega-se à equação fundamental de Solow:
∆k = sy – (n + d)k
(5)
Esta equação fundamental afirma que o aumento do capital por trabalhador (∆k), o
aprofundamento do capital, precisa ser igual à poupança per capita (sy), menos a ampliação do
capital, (n + d)k. A proporção nk da poupança serve para equipar os novos trabalhadores que
ingressam no mercado de trabalho, com a mesma relação K/L dos que já se encontram empregados; a
parcela dk precisa ser usada para depreciar o capital per capita adicional (Sachs e Larrain, 1995, p.
633).
No estado estável de longo prazo (logo, o aprofundamento do capital ∆k é nulo), a poupança
per capita sy torna-se igual à ampliação do capital (n + d)k, sendo a relação K/L constante:
sy = (n + d)k.
(6)
Neste caso, a poupança agregada é suficiente para fornecer capital à população que cresce a
uma taxa n = ∆Y/Y e para a depreciação do capital existente.
A Figura 11.1 mostra o equilíbrio da economia no ponto E, o estado estável. O formato da
3
curva y indica que a função de produção apresenta rendimentos decrescentes. A curva sy possui a
mesma declividade da função de produção, y. A reta da ampliação do capital, que passa por E,
mostrando a igualdade entre sy e (n + d)k, tem como declividade o termo constante (n + d), a taxa de
crescimento natural, n, mais a taxa de depreciação, d. Pontos a esquerda de E (sy > (n + d)k)
mostram o aprofundamento do capital (∆k > 0) e crescimento econômico superior ao crescimento
demográfico (∆Y/Y > ∆L/L).
Figura 11.1 Equilíbrio da economia no estado estável.2
A tendência ao aprofundamento do capital pode ser explicada do seguinte modo. Suponha
que o capital per capita da economia seja k1, inferior ao capital requerido de pleno emprego (ke). A
quantidade de capital necessária para equipar os trabalhadores adicionais com a mesma relação K/L
existente e substituir o capital gasto no processo produtivo é k1R, o que é inferior à poupança per
capita disponível k1S. O excesso de poupança por trabalhador, igual a SR, tenderá a expandir o
capital per capita até o ponto E; isso ocorrerá enquanto SR for positivo. À direita do ponto E, a
poupança disponível seria insuficiente para equipar os trabalhadores adicionais com a mesma relação
K/L dos trabalhadores já empregados e realizar a depreciação do capital existente.
Percebe-se que as nações em desenvolvimento, com desemprego de trabalhadores,
encontrando-se em pontos à esquerda de E, tendem a crescer a taxas superiores às das nações mais
ricas, situadas à proximidade de E, o equilíbrio estável. A conclusão do modelo é a de que a elevação
da taxa de poupança, s, expande a relação capital/trabalho, k, e a renda per capita, y, até a economia
atingir o equilíbrio estável de longo prazo, quando a taxa de crescimento y manter-se-á constante e
igual a n. Porém, uma vez atingido o equilíbrio estável, o aumento da poupança não influenciará
mais a taxa de crescimento do produto, a ponto de elevá-la acima da taxa do crescimento
demográfico.
Desconsiderando-se a depreciação dK, no ponto de equilíbrio estável E, com nk = sy, ter-se-ia
que n = sy/k = s(Y/L)/(K/L) = sY/K = s/v, isto é, a taxa natural de crescimento demográfico (sem
progresso técnico) é igual à propensão a poupar (s), dividida pela relação capital/produto (v). Essa
2
Adaptado de Sachs e Larrain, 1995, p. 634.
4
conclusão é idêntica a que se chega por meio dos modelos de Harrod e Domar, como foi visto no
Capítulo 5. Em outras palavras, no equilíbrio de pleno emprego é a taxa de crescimento demográfico,
n, quem determina a taxa de crescimento do emprego de trabalho, do capital e do produto. Valores
diferentes para s e v não modificam a taxa requerida de pleno emprego n, dada de forma
independente das variáveis do modelo.3
Esse modelo descreve perfeitamente o ritmo de crescimento do fluxo circular
schumpeteriano, como foi visto no Capítulo 6 de Souza (2005). Na ausência de inovações
tecnológicas nesse fluxo circular, será o crescimento demográfico quem determinará o ritmo do
crescimento econômico. Um aumento da taxa de crescimento demográfico, n, eleva as taxas de
crescimento de Y, K e L, mas diminui a produção per capita. Na Figura 11.1, a reta (n + d)k
deslocar-se-ia para cima e para a esquerda. Como se observa, a igualdade entre sy = (n’ + d)k
ocorreria em um ponto à esquerda de E, como em S, reduzindo a produção per capita de ye para y1.4
A produção per capita se reduz porque a função de produção y mantém-se a mesma (tecnologia
constante). Inversamente, quando o crescimento demográfico se reduz, a reta desloca-se para a
direita. As necessidades de ampliação de capital para atender aos novos trabalhadores se reduzem,
sobrando mais poupança (sy) para o aprofundamento do capital (∆k). Embora ∆Y/Y diminua, a
produção per capita aumenta (Sachs e Larrain, 1995, p. 640).
A introdução do progresso tecnológico no modelo de Solow (∆T/T > 0), deslocando a função
de produção per capita y para cima, implica que o mesmo número de trabalhadores e idêntico
estoque de capital exercem um impacto maior sobre o nível de produção, do que na situação anterior.
Em outras palavras, na prática, para uma dada taxa de crescimento demográfico, n, precisa-se
acrescentar a taxa do progresso técnico ∆T/T = t, para se obter a taxa efetiva de crescimento do
produto real, ou seja:
∆Y/Y = (n + t).
(7)
As produtividades do trabalho e do capital aumentam com maiores conhecimentos, mais
educação e melhor saúde para os trabalhadores, assim como pelo uso de processos e máquinas mais
eficientes, o que eleva o ritmo do crescimento econômico. Tendo em vista que ∆K/K = ∆Y/Y = (n +
t) e ∆L/L = n, constata-se que o capital por trabalhador (K/L) e a produtividade do trabalho (Y/L)
crescem no ritmo do progresso técnico t, e que a relação K/Y permanece constante. Quanto maior o
crescimento do progresso técnico em relação ao número de trabalhadores, maior será a produtividade
do trabalho e tanto mais altas serão as taxas da acumulação de capital e do crescimento econômico.
Finalmente, a importante conclusão do modelo neoclássico, tanto na versão de Meade, como
na de Solow, é a de que o ritmo do progresso técnico determina o crescimento da renda per capita no
equilíbrio estável de longo prazo. Isso pode ser visto ao se subtrair a taxa de crescimento
demográfico da taxa efetiva de crescimento da renda, conforme a equação (7), ou seja, ∆Y/Y – n = t,
tal que:
3
Solow usou a suposição de Harrod de que o crescimento da população é exógeno e de que a força de trabalho, L(t), cresce no tempo t
a uma taxa constante n, isto é, L(t) = Lo ent (Solow, 1956, p. 67).
4
Imagine que a nova reta (n’ + d)k, partindo da origem, passe pelo ponto S.
5
∆y/y = t.
(8)
Conclui-se que a contribuição neoclássica à teoria do crescimento econômico é inegável e
continua muito atual. O modelo de Solow mostra a dinâmica de longo prazo de uma economia
capitalista desenvolvida, que se dirige a um estado de equilíbrio estável. Nesse ponto, o crescimento
demográfico e a tecnologia determinam o ritmo de crescimento equilibrado. As críticas afirmam,
contudo, que o modelo neoclássico, pressupondo perfeita flexibilidade de preços dos fatores, é muito
mecanicista e harmonioso; que ele não considera as expectativas empresariais, ao excluir a função
investimento, fator que pode afetar o crescimento equilibrado. Pelas hipóteses de flexibilidade de
salários e preços, mercados concorrenciais, perfeita informação e capital maleável, “as expectativas
nunca poderiam frustrar-se” (Jones, 1979, p. 109).5 Além disso, o progresso técnico aparece como
elemento exógeno e formado de modo independente dos parâmetros do modelo.
3 - Teoria de crescimento com progresso técnico endógeno
A nova teoria que trata o progresso técnico como elemento ativo no processo de crescimento,
afirma que ele exerce efeitos expansivos sobre o produto ao elevar a produtividade dos fatores e ao
retransmitir esses efeitos entre as unidades produtivas. A teoria do crescimento com progresso
técnico endógeno tomou impulso nos anos de 1980, por não haver uma tendência à convergência dos
produtos per capita entre áreas com diferentes níveis de desenvolvimento iniciais. Pelo contrário, as
desigualdades entre regiões ou países ricos e pobres tendem a aumentar. Na ausência de perfeita
mobilidade dos fatores de produção K e L entre países ou regiões, as desigualdades aumentam. O
crescimento do produto não se explica apenas por K e L, permanecendo uma parte importante não
explicada, atribuída no modelo neoclássico à tecnologia, A(t), a qual varia lentamente no tempo.
A teoria do crescimento endógeno não procura medir a parte não explicada A(t), mas
encontrar as fontes desse crescimento, as quais se encontram no interior do sistema produtivo.
Embora essa teoria tenha sido popularizada por Romer (1986), sua origem é mais antiga, podendo ser
encontrada nos artigos pioneiros: Investimento em capital humano, de Schultz (1961); Implicações
econômicas do aprender fazendo, de Arrow (1962); Investimento humano, difusão tecnológica e
crescimento econômico, de Nelson e Phelps (1966); A taxa de retorno do investimento alocado na
educação, de Schultz (1967); Uma teoria econômica da mudança tecnológica, de Nordhaus (1969)
etc.
Estudando outras fontes de crescimento, além de K e L, Langoni (1976) mostrou que a
contribuição líquida da educação para o crescimento do produto foi de 15,7% no Brasil (1960/1970),
23% nos EUA (1950/1962) e de 10% na França (1950/1962). Com relação ao Brasil, a contribuição
do capital físico, entre 1960/1970, foi de 32%, contra 47% do trabalho (incluído os 15,7% da
educação), sendo de 21% a parcela do crescimento do produto não explicada por K nem por L, sendo
5
Esses pontos foram discutidos no Capítulo 5, através dos modelos de Domar, Harrod e de Kaldor.
6
atribuída ao progresso técnico [A(t)] (Langoni, 1976, p. 27). Essa parcela não explicada por K, nem
por L, é muito importante para ser ignorada. Outras fontes explicativas do crescimento econômico
seriam investimentos em capacitação tecnológica e geração de conhecimento. Os países
subdesenvolvidos podem importar tecnologias, além de investir em pesquisa tecnológica, gerando
maior crescimento do produto.
Outras fontes de crescimento são: (a) economias de escala, derivadas do aumento do tamanho
do mercado e do nível da produção; (b) elevação da produtividade, decorrente da transferência de
trabalhadores e atividades de setores menos eficientes, como a agricultura, para os mais produtivos,
como a indústria de transformação; (c) economias externas, geradas pelas infra-estruturas criadas
pelo Estado e pela difusão do conhecimento entre os agentes produtivos. Melhorias dos portos e das
comunicações, reduzindo os custos das empresas, são economias externas por não dependerem
diretamente da ação da empresa, mas de outras unidades produtivas, ou órgãos do governo.
Privatizações e reformas institucionais são outros exemplos de economias externas, podendo
aumentar a oferta de produtos, melhorar a eficiência dos serviços e reduzir seus custos.
Deseconomias externas também podem ocorrer, como uma desvalorização cambial, que aumenta os
preços dos insumos importados e os custos das empresas, gerando impactos depreciativos sobre o
nível do produto.6
3.1 Convergência espacial da renda per capita
1-β
β
Seja Y = A(t) K L o produto de uma economia, β a elasticidade do produto em relação ao
trabalho e (1 – β) a elasticidade do produto em relação ao capital. Dividindo-se esta função por L,
1-β
β
1-β
1-β
obtém-se Y/L = A(t) K L L-1 = A(t) (K/L) , ou y = A(t) k , conforme definição da seção
anterior. Derivando-se esta última relação, chega-se a:
(1)
dy/y = (1 – β) dk/k + A’
A taxa de crescimento do produto per capita (dy/y) depende da taxa de crescimento do capital
per capita (dk/k) e de um crescimento residual (A’), atribuído ao progresso tecnológico.
Substituindo-se k por K/L na equação (1), e depois dK por sY e Y pela função de Cobb-Douglas,
chega-se ao seguinte resultado (Romer, 1994, p. 5):
1/(1-β)
dy/y = (1 – β) [s A(t)
y
(-β )/(1-β )
– n] + A’
(2)
Observa-se que a taxa de crescimento do produto per capita dependerá da elasticidade do
produto em relação ao trabalho (β), da propensão a poupar, do nível tecnológico inicial [A(t)], do
nível do produto per capita, do crescimento demográfico e do progresso técnico residual (A’). O
parâmetro β é fundamental, porque vai influenciar o tempo em que ocorrerá a convergência dos
produtos per capita entre um país desenvolvido e um país subdesenvolvido. Considerando-se dois
países com os mesmos parâmetros [A(t)], β, n e A’ = 0 e conhecendo-se os produtos per capita, pode6
Há, contudo, um efeito oposto ao estimular as exportações e o crescimento do produto total.
7
se calcular a propensão a poupar de cada país para que eles cresçam à mesma taxa. Neste caso, é
preciso que o país com maior produto per capita tenha maior propensão a poupar.
Sendo β = 0,6, o expoente (-β)/(1 – β) do produto per capita y da equação (2) será igual a –
1,5. Considerando-se as suposições acima, um país com produto per capita dez vezes menor, como
as Filipinas em relação aos EUA (1960), deveria crescer de modo mais acelerado.7 Para que os EUA
cresçam no ritmo das Filipinas seria preciso que sua taxa de poupança (e a taxa dos investimentos)
fosse 31,62 vezes maior.8 Como os países desenvolvidos não possuem propensão a poupar dessa
magnitude, a conclusão do modelo neoclássico é a de que o país mais pobre terá taxas de
crescimento mais altas, levando à convergência do produto per capita no longo prazo.9 Porém, os
países desenvolvidos serão mais produtivos se o estoque inicial de conhecimento for maior. Desse
modo, eles crescerão mais do que os países pobres, porque “cada unidade do capital investido
aumenta tanto o estoque de capital físico, como o nível da tecnologia de todas as firmas da economia,
através da difusão do conhecimento” (Romer, 1994, p. 7). Isso contribuirá para o aumento das
desigualdades econômicas.
Pela equação (1), verifica-se que, se β = 0,6 e considerando-se A’ = 0, a contribuição do
crescimento do capital per capita no produto per capita será de 0,4 vezes dk/k. Se a contribuição do
trabalho no produto β cair para 0,3, uma variação do capital per capita (dk/k) expandirá 0,7 vezes o
produto per capita. A presença de retornos decrescentes mais fracos, decorrentes da acumulação de
capital, pode ser o resultado de economias externas, fruto da difusão de conhecimentos na economia.
Barro e Martin estudaram dois conjuntos de Estados dos EUA; o conjunto mais pobre
(Carolina do Norte, Carolina do Sul, Virgínia e Geórgia) possuía renda per capita igual a 1/3 daquela
do conjunto mais rico (Nova Iorque, Massachusetts e Rhode Island). Seu trabalho considerou β =
0,6, -β /(1 – β) = -1,5 e (1/3)-1,5 = 5,2; isso significa haver uma diferença de cinco vezes na
produtividade marginal do capital, em favor dos Estados mais pobres (Sul). Entretanto, os Estados
mais ricos (Norte) vêm crescendo de modo mais acelerado há décadas, o que explica o aumento da
divergência do produto per capita no longo prazo. A explicação encontra-se na dotação desigual do
estoque de conhecimentos inicial, em favor do Norte, que tende a se ampliar no longo prazo. Essas
diferenças de tecnologia tendem a gerar importantes economias externas no Norte e fatores
desfavoráveis no Sul, que ampliam as desigualdades regionais (Romer, 1994, p. 9).
1/3
1/3
1/3
Introduzindo-se o capital humano (H) na função de produção Y = A(t) K H L , o
coeficiente – β /(1 – β) se reduz para 0,5 e a taxa de retorno dos capitais físico e humano se reduzem
para (1/3)0,5 = 1,73 vezes maior no Sul em comparação ao Norte, o que não seria substancialmente
7
Supondo, para ambos os países, que: s = 0,15; n = 0,02; A(t) = 2, β = 0,6, A’ = 0. Então, para as Filipinas
dy/y = 0,4 (0,15. 22,5.0,1-1,5 – 0,02) = 10,7%; para os EUA, dy/y = 0,4 (0,15. 22,5.1-1,5 – 0,02) = 0,32.
8
Sendo y-β/1-β = 0,1-0,6/1-0,6 = 0,1-1,5 = 31,62. Multiplicando-se a taxa de poupança dos EUA (0,15) por 31,62 na fórmula da nota
anterior, chega-se a uma taxa de crescimento para a renda per capita desse país de 10,7%, a mesma das Filipinas. Se β = 2/3, então β/1−β = -2 e a taxa de poupança dos EUA precisaria ser 100 vezes maior: 0,1-2 = 100.
9
Em 1990, a relação investimento interno bruto/PIB foi de 17% nos EUA e 24% nas Filipinas. Entre 1990/1999, o investimento
interno bruto cresceu 7% nos EUA e 4,1% nas Filipinas, expandindo o PIB em 3,4% no primeiro país e em 3,2% no segundo. Nos
anos de 1980, o PIB dos EUA cresceu 3%, contra apenas 1% para as Filipinas. Como se observa, esses dados não favorecem a
hipótese da convergência do PIB per capita dos dois países entre 1980/1999.
8
muito elevado ao ponto de atrair o capital do Norte e levar à convergência das rendas regionais per
capita. Desse modo, no longo prazo as desigualdades entre países e regiões tendem a aumentar. A
conclusão é a de que o modelo neoclássico de crescimento não consegue captar os efeitos externos,
endógenos, sobre o crescimento da produtividade.
Para captar esses efeitos externos, Romer (1994, p. 7) supôs que cada unidade de capital
aumenta tanto o estoque do capital físico, como o nível tecnológico das firmas, por meio da difusão
do conhecimento técnico. O progresso técnico aparece como função do capital e do trabalho, isto é,
1-α
α
A(K, L). Desse modo, a função de produção da firma j será: Yj = A(K, L) Kj Lj . O parâmetro α
representa o efeito privado e indica que a produção da firma j aumentará a %, quando ela aumentar
1% o emprego de trabalho.
O estoque de conhecimentos A, como função do capital e do trabalho, foi colocado por
γ
- γ
Romer na forma A(K, L) = K L . O parâmetro γ > 0 representa o efeito externo. A elasticidade
negativa para o trabalho indica que o emprego de mais mão-de-obra diminui o incentivo a adotar
inovações, o que se traduz em menor difusão do conhecimento na economia. Os efeitos privados que
os diferentes α’s do conjunto de firmas exercem na economia ficam captados pelo parâmetro β da
função de produção agregada Y, ao qual devem ser acrescidos os efeitos externos, isto é, β = α – γ,
sendo β o efeito agregado no conjunto das firmas. Desse modo, no modelo neoclássico, os efeitos do
capital sobre a expansão do produto (1 – β) ficam subestimados ao não se considerar a contribuição
do progresso técnico e dos efeitos externos. As empresas difundem externalidades sobre as demais,
ao realizarem gastos em treinamento de trabalhadores e na pesquisa tecnológica. Esses efeitos
repercutem-se em toda a economia, aumentando as produtividades marginais de K e L e elevando a
contribuição do progresso técnico A no produto Y.
Outros estudos mostraram que a convergência do produto per capita ocorre muito
lentamente, pela existência de externalidades mais importantes nos países ou regiões mais ricas. No
longo prazo, a difusão do conhecimento de regiões ou países com mais altos A(K, L) deverá ocorrer
em direção de países ou regiões com mais baixos A(K, L), principalmente pelo surgimento de efeitos
externos mais importantes nas áreas mais pobres.
3.2 Abandonando a hipótese de concorrência perfeita
Na hipótese de concorrência perfeita, existe um número muito grande de firmas, produzindo
um bem homogêneo com um custo mínimo. Os preços pm são dados pelo mercado e os lucros são
normais. A função de produção Y = A(t) f(K, H, L) é homogênea de grau um (rendimentos constantes
à escala), significando que, para dobrar a produção, necessita-se duplicar todos os insumos K, H, L.
A tecnologia A(t) é uma variável temporal e determinada independentemente das variáveis do
modelo. No entanto, o conhecimento pode ser usado por muitas pessoas ao mesmo tempo, isto é, a
informação é um bem não rival. Nesse caso, para dobrar a produção, não é necessário duplicar a
tecnologia A(t). Um mesmo processo conhecido, Ai, pode ser usado simultaneamente por um
conjunto de firmas.
9
Enquanto cada fator é remunerado segundo suas produtividades marginais, o conhecimento
que uma firma assimila tende a produzir um retorno maior do que os gastos efetuados para a sua
apreensão. Porém, quanto mais a firma investir na produção de conhecimento, tanto maior ele será e
mais importantes serão os efeitos desencadeados no conjunto da economia. Desse modo, no
agregado, a tecnologia aparece como um fator endógeno, dependente da aplicação de trabalho,
capital físico e capital humano, isto é, A = A (K, L, H). Além disso, como as descobertas são
protegidas por direito autoral, durante algum tempo, a informação não pode ser considerada como
um bem público típico. Firmas e indivíduos adquirem poder de mercado e auferem rendas de
monopólio decorrentes de descobertas. Essa imperfeição de mercado, inserida no espírito do modelo
schumpeteriano, reduz a peculiaridade de bem não rival da informação (Romer, 1994, p. 13).
Para considerar todos esses fatores, Romer (1986) estabeleceu uma função de produção Y =
A(R) f(Rj, Kj, Lj), em que Rj são os gastos em pesquisa e desenvolvimento realizados pela firma j. Os
conhecimentos que eles geram acabam sendo difundidos no conjunto da economia. Ao serem
internalizados pelas firmas i, eles contribuem para aumentar sua produção e seus lucros, sem
realizarem os gastos correspondentes. Desse modo, como Rj é um bem não rival, ele melhora a
produtividade dos fatores K, L e H, gerando, portanto, rendimentos crescentes à escala. Em
conclusão, as contribuições do capital físico e do capital humano sobre o produto ficam subestimadas
quando se consideram apenas seus efeitos sobre a empresa que o aplicou. Contudo, esses
investimentos beneficiam direta e indiretamente outras unidades produtivas. Tais efeitos indiretos
podem elevar substancialmente a contribuição do capital no crescimento do produto, o que explicaria
grande parte do fator residual de crescimento (A’) do modelo neoclássico.
Desse modo, o conhecimento aparece como um fator de produção, como o capital físico, o
capital humano e a mão-de-obra. Conclui-se que a sociedade precisa investir na geração de
conhecimento, como investe em capital fixo e na educação dos trabalhadores. Investimentos em
novos conhecimentos geram externalidades, como explicou Romer:
“A criação de novos conhecimentos por uma firma produz efeitos externos positivos sobre
as possibilidades de produção de outras firmas, porque o conhecimento não pode ser
perfeitamente patenteado ou mantido secreto. E o que é mais importante: a produção de
bens de consumo como uma função do estoque de conhecimento e outros insumos exibe
retornos crescentes; mais precisamente, o conhecimento pode ter um produto marginal
crescente” (Romer, 1986, p. 1003).
Em outras palavras, determinado percentual aplicado na expansão do estoque de
conhecimentos gera um aumento mais do que proporcional no nível do produto, pelas
interdependências entre os produtores. Dessa forma, os fatores externos dos investimentos em
ciência e tecnologia produzem retornos crescentes de escala, implicando crescimento econômico
superior ao crescimento demográfico e à variação tecnológica inicial.
O capital humano, H, o capital físico, K, e a força de trabalho, L, estão intimamente
10
associados pelo conhecimento técnico, gerado internamente, ou importado, e que se difunde entre os
agentes produtivos, produzindo externalidades positivas e que são captadas pelas empresas. Desse
modo, o conhecimento surge como um insumo na função de produção como o capital físico, o capital
humano e a força de trabalho. Para aumentar o produto per capita, além de aumentar o capital físico,
a sociedade precisa investir também em saúde, educação e treinamento dos trabalhadores, assim
como na geração de novos conhecimentos técnicos. Estes produzem externalidades positivas, que são
apropriadas pelos agentes produtivos e elevam o nível da produção agregada. Isso se explica porque
o saber gerado pelas novas tecnologias não pode ser totalmente patenteado, podendo ser
internalizado e aperfeiçoado por empresas rivais da comunidade.
As regiões ou países que mantiverem investimentos crescentes na ciência básica e aplicada,
na descoberta de novos produtos e processos de trabalho, bem como em educação e saúde de sua
população, deverão crescer mais rapidamente. Os rendimentos crescentes da produção de
conhecimentos deverão neutralizar os rendimentos decrescentes em alguns setores de atividade,
principalmente na agricultura. Os países não inovadores poderão se beneficiar da difusão
internacional do conhecimento técnico, se conseguirem importar tecnologia e, sobretudo, se forem
capazes de adaptá-las e produzir conhecimento próprio. Desse modo, eles também poderão crescer a
taxas mais elevadas, com melhoria dos indicadores de desenvolvimento.
4 - Conclusão
Partindo-se das análises de Meade e de Solow, constatou-se que o modelo neoclássico é um
instrumento simples e eficiente para mostrar a trajetória de crescimento de uma economia no longo
prazo. Constatou-se que as produtividades do capital e do trabalho aumentam com maiores
conhecimentos e que a renda per capita cresce com o progresso técnico no equilíbrio estável de
longo prazo. Porém, considerando-se duas regiões ou países com desigual nível inicial de renda per
capita e conhecimento técnico, as desigualdades entre eles deverão aumentar pela imperfeita
mobilidade espacial de fatores. A área com estoque inicial superior de conhecimentos deverá crescer
de modo mais acelerado pela existência de importantes economias externas e pela adoção mais
intensa de novas tecnologias. A conclusão é a de que a convergência somente começará quando
surgirem novos conhecimentos e economias externas importantes nas regiões ou países mais pobres.
Isso poderá acelerar-se pela adoção de medidas favoráveis, que estimulem a difusão espacial do
capital e do progresso técnico.
A introdução do capital humano (H) na função de produção, reduzindo a elasticidade do
produto em relação ao trabalho, torna o modelo neoclássico mais próximo da realidade. Contudo, o
progresso técnico, considerado exógeno no modelo neoclássico, na verdade depende dos próprios
fatores K, L e H. Assim, quanto maior a acumulação de capital físico e o investimento em capital
humano, tanto maior será a geração de conhecimentos, o que se repercutirá em maiores taxas de
crescimento econômico.
11
A criação de novos conhecimentos pelas firmas produz efeitos externos positivos sobre as
demais firmas, que elevam sua produção sem a realização de gastos adicionais. Isso se explica
porque as novas tecnologias não podem ser perfeitamente patenteadas. O surgimento de imitadores
aumenta a produção total, gera novos lucros e novos investimentos. Isso implica em rendimentos
crescentes na economia, pois um dado investimento inicial em pesquisa tecnológica gera retornos
mais do que proporcionais, em virtude das interdependências existentes entre as firmas e pela
possibilidade da imitação entre as empresas. Desse modo, embora as exportações, do lado da
demanda, sejam importantes fatores do desenvolvimento, principalmente aquelas de produtos
manufaturados; do lado da oferta, a geração de novos conhecimentos, os investimentos em capital
humano e no treinamento de trabalhadores, na pesquisa de novos produtos e novos processos são os
elementos básicos para completar o elenco dos fatores do desenvolvimento econômico moderno.
QUESTÕES PARA REFLEXÃO E DISCUSSÃO
1. Explique a condição de Meade para que o crescimento do produto ocorra de modo equilibrado
com a acumulação de capital e emprego de trabalho.
2. Explique o significado do equilíbrio estável e por que as economias subdesenvolvidas deverão
crescer mais do que as economias desenvolvidas antes de atingirem esse ponto.
3. Por que no equilíbrio estável a poupança não influencia o crescimento econômico acima do
crescimento demográfico.
4. Do que depende o crescimento da renda per capita no modelo neoclássico e o que significa dizer
que a tecnologia é exógena?
5. Por que o modelo neoclássico de crescimento não produz a convergência das rendas regionais
per capita? E quando isso poderá ocorrer?
6. O que significa elasticidade da produção em relação ao trabalho muito alta e por que a
elasticidade do conhecimento tecnológico em relação ao trabalho é negativa?
7. Por que a contribuição do capital no crescimento econômico fica subestimada no modelo
neoclássico?
8. O que significa crescimento econômico com progresso técnico endógeno? Por que o
conhecimento é um bem não rival?
9. Qual a principal conclusão destes modelos de crescimento?
REFERÂNCIAS BIBLIOGRÁFICAS
JONES, Hywel G. Modernas teorias do crescimento econômico. São Paulo : Atlas, 1979.
LANGONI, Carlos Geraldo. A economia da transformação. Rio de Janeiro : Biblioteca do Exército,
1976.
12
NELSON, Richard R., PHELPS, Edmund S. Investment in Humans, technological diffusion and
economic growth. American Economic Review, v. 56, May 1966.
NORDHAUS, William D. An economic theory of technological change. American Economic
Review, v. 59, n. 2, May 1969.
PAZ, Pedro, RODRIGUES, Octávio. Modelos de crescimento econômico. Rio de Janeiro : Forum,
1972.
ROMER, Paul M. Increasing returns and long-run growth. Journal od Political Economy, v. 94, n. 5,
1986.
_____. The origins of endogenous growth. Journal of Economic Perspectives, v. 8, n. 1, Winter
1994.
SACHS, Jeffrey D., LARRAIN, Felipe B. Macroeconomia. São Paulo : Makron, 1995.
SCHULTZ, T. W. Reflections on investment in human capital. American Economic Review, v. LI,
March 1961.
SOLOW, Robert M. A contribution to the theory of economic growth. The Quarterly Journal of
Economics, v. LXX, Feb. 1956.
SOUZA, Nali de Jesus. Desenvolvimento Econômico. 5a ed. São Paulo: Atlas, 2005.
13