Codificação neural
Natureza da Informação
UFABC
Prof. João Henrique Kleinschmidt
Material elaborado pelos professores de NI
1
Princípios gerais do Sistema Nervoso
Neurônio: unidade funcional do SNC
Introdução ao Sistema Nervoso
Central
Tálamo
4
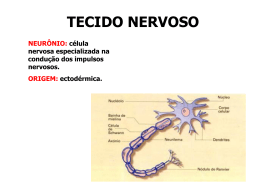
Neurônio
Célula do sistema nervoso responsável pela
condução do impulso nervoso
Há cerca de 86 bilhões de neurônios no sistema
nervoso humano
Constituído pelas seguintes partes: corpo celular
(onde se encontra o núcleo celular), dendritos,
axônio e telodendritos.
Considerado a unidade básica da estrutura do
cérebro e do sistema nervoso.
5
6
Sinapses
Dendritos
Corpo
(Soma)
Voltagem pós-sináptica
Promontório
axónico
Sinapses
Axônio
Terminal
axónico
7
8
Processamento do sinal: dendritos e soma
9
Processamento do sinal: dendritos e soma
10
Propriedades do Potencial de Ação (PA)
EVENTO TUDO-OU-NADA
- Estímulo sublimiar (E1, E2): não causa PA
-Estimulo limiar (E3): causa um único PA
Conversão Analógico/Digital: potencial de ação em
mV transformado para “TUDO” ou “NADA” (0 ou 1)
11
Potencial tudo ou nada no axônio: Potencial de ação
• O potencial de ação pode ser entendido como “1”, e a ausência de
potencial de ação, como “0”
• Uma série temporal pode ser codificada como uma série digital binária
Ex: 01110100101; 01010101010
…onde provavelmente cada padrão pode assumir um “significado”
fisiológico!
12
Efeitos das sinapses excitatórias e inibitórias
Agonista: substância que se liga ao receptor e o
ativa
Analogia com chave/fechadura: fechadura seria
o receptor e chave seria o agonista
Quando a chave é girada na fechadura, significa
que o agonista se ligou ao receptor e quando a
porta é aberta, o receptor é ativado
13
Efeitos das sinapses excitatórias e inibitórias
Antagonista: substância que se liga ao receptor e não o
ativa
Impede que o agonista se ligue
Exemplo: Muitos anestésicos utilizados nas cirurgias
possuem antagonistas de receptores nicotínicos
impede que a Acetilcolina (agonista) se ligue
músculo não se contrai, fazendo com que a pessoa fique imóvel
Analogia chave/fechadura: chave incorreta tenta abrir a
fechadura e quebra um pedaço dentro
14
Lógica Booleana
Os efeitos das sinapses excitatórias e inibitórias
podem seguir um padrão de lógica booleana
Excitatória
Inibitória
Agonismo
+
-
Antagonismo
-
+
15
O neurônio de McCulloch-Pitts
“Conjuntos de neurônios podem realizar qualquer função aritmética ou lógica”
oi
i1
wi1
i2
1
wi2
neti
wij
ij
win
in
j n
wiji j
j 1
oi f neti si
net
si=0
oi
Onde f(x) = 1 se x >= 0
ou f(x) = 0 caso contrário
1
Neurônio i
si=1
net
Implementação da função AND com modelo
de neurônio de McCulloch-Pitts
Função AND
o
f (net-2)
i1 i2 net f(net-2)
0 0
0 1
0
1
0
1
i1
Wi1=1
s=2
0
1 0
1
0
1 1
2
1
net i1 1 i2 1
Wi2=1
i2
net
o f net 2
Implementação de função OR com modelo de
neurônio de McCulloch-Pitts
Função OR
o
f(net-1)
i1 i2 net f(net-1)
0 0
0 1
0
1
0
1
i1
Wi1=1
s=1
1
1 0
1
1
1 1
2
1
net i1 1 i2 1
Wi2=1
i2
net
o f net 1
Exercício) Se colocarmos um agonista que dobra o valor de cada peso
sináptico, quais seriam as novas funções lógicas dos neurônios de
McCulloch-Pitts descritas abaixo? E o que acontece com as funções
lógicas desses neurônios se colocarmos um antagonista que corta o valor
de cada peso sináptico pela metade?
Exercício: A seguinte rede neural é composta por neurônios do tipo
McCulloth-Pitts, com limiar de ativação 2. Os neurônios de 1 a 4 representam
as entradas e o neurônio 5 representa a saída da rede. Os pesos são dados
por wij, onde i representa o neurônio pré-sináptico e j o neurônio pós-sináptico.
Seja n = {n1, n2, n3, n4} os valores dos neurônios de entrada e w = {w15, w25,
w35, w45}.
1
2
3
4
5
Determine qual a saída do neurônio 5 para as seguintes entradas e pesos
sinápticos:
a) n = {1,1,1,1} e w = {2,-1,1,-1}
b) n = {1,0,0,0} e w = {2,-1,1,-1}
c) n = {0,1,1,1} e w = {2,-1,2,-1}
d) n = {1,0,1,0} e w = {2,-1,2,-1}
Como a informação é
transmitida pelos neurônios?
Será que a informação é
transmitida como no código
morse?
Ou o que importa é somente
a taxa, r, de disparos
r1
r2
r3
21
3 tipos de codificação neural
1.
2.
3.
Codificação frequencial: As diferentes frequências de
disparo do neurônio representam respostas a diferentes
estímulos.
Codificação vetorial ou populacional: Um estímulo
pode ser codificado como um vetor cujos componentes
são as taxas de disparo de vários neurônios.
Codificação temporal: O neurônio codifica a
informação mediante a duração dos intervalos entre os
disparos.
Veremos o primeiro e o segundo (o terceiro é análogo
ao primeiro, mas com o tempo no lugar da frequência)
22
1. Codificação frequencial (“rate coding”)
-
A frequência de disparos dos neurônios é proporcional à
voltagem pós-sináptica.
r1
r2
s1
r3
S2
S3
Injetando uma corrente s1, s2, s3 produzimos voltagens cada vez maiores
no interior do neurônio
No último caso, S3, não da para juntar mais os potenciais de ação. A
distância (tempo) mínima entre dois potenciais sucessivos é o período
refratário absoluto.
23
1. Codificação frequencial
Decodificação dos sinais em frequência
dos impulsos elétricos
Os neurônios decodificam o aumento ou redução na intensidade do
estimulo em frequência de impulsos elétricos.
A amplitude do P.A. de cada célula excitável é invariável.
24
1. Codificação frequencial
Aplicação prática da codificação de frequências:
HAL-5 (Hybrid Assistive Limb-5)
Exoesqueleto robótico.
Multiplica por cinco a força
muscular de uma pessoa normal.
Sensores colocados acima da pele
registram código de frequências
que movimentam os músculos.
Ver (a partir do minuto 3):
http://www.youtube.com/watch?v=G4evlxq34og
25
1. Codificação frequencial
Hardiman 1 (1965)
General Electric
Jacob Rosen Universidade de
Washington
Kanagawa Power Suite
26
1. Codificação frequencial
Cálculo de Informação transmitida com
codificação de frequências
Sejam E = {e1,e2,...,em} o conjunto de estímulos para um
neurônio e R = {r1,r2,...,rn} o conjunto de possíveis
respostas do mesmo neurônio
P(ei) é a probabilidade de apresentar um determinado
estímulo, ei, para o neurônio.
P(rj) é probabilidade de termos uma determinada
resposta, rj, do neurônio. Por exemplo, r1 pode significar
resposta de 50 Hz e r2 uma resposta de 100 Hz.
P(rj|ei) é a probabilidade condicional de termos uma
resposta, rj, no neurônio quando apresentamos o
estímulo, ei.
27
1. Codificação frequencial
Cálculo da entropia de Shannon
S Prj log 2 ( P(rj )) P(r1 ) log 2 ( P(r1 )) P(rn ) log( P(rn ))
j
Representa o grau de imprevisibilidade da
resposta do neurônio.
Quanto mais uniforme é a distribuição de
respostas, rj, mais imprevisível é a
resposta do neurônio.
28
1. Codificação frequencial
Exemplo de cálculo de entropia de Shannon
para a resposta de frequencia do neurônio
Caso A: O neurônio responde sempre com a mesma frequência.
S Prj log 2 ( P(rj )) P(r1 ) log 2 ( P(r1 )) 1x log 2 (1) 1x0 0
j
Significa que o grau de imprevisibilidade da resposta do neurônio é zero.
Caso B: Dois tipos de resposta r1 e r2, onde P(r1)+P( r2)=1.
S Prj log 2 ( P(rj )) P(r1 ) log 2 ( P(r1 )) P(r2 ) log 2 ( P(r2 ))
j
P(r1 ) log 2 ( P(r1 )) (1 P(r1 ) log 2 (1 P(r1 ))
29
1. Codificação frequencial
1 bit
S
0,5
1 P(r1)
Quando ambas as frequências de disparo têm a mesma
probabilidade de acontecer P(r1)=P(r2)=0,5 a entropia ou
imprevisibilidade é máxima, e igual a 1 bit.
30
1. Codificação frequencial
Exemplo: Qual é a informação em bits que
pode transmitir um neurônio se 60% das
vezes dispara na frequência lenta e 40%
do tempo na frequência rápida
S 0,6 log2 (0,6) (0,4) log2 (0,4) 0,97 bits
31
1. Codificação frequencial
Eletroencefalograma
32
1. Codificação frequencial
Experimentos com biofeedback
O sujeito tenta controlar suas ondas cerebrais
enquanto um aparelho mostra seu grau de
relaxação.
Atualmente os aparelhos de bio-feedback são
usados para permitir que um sujeito controle
algum aparelho “com a mente”.
33
1. Codificação frequencial
Exemplo: Neurosky
http://www.youtube.com/watch?v=hQWBfCg91CU
34
1. Codificação frequencial
Diferenciar 3 estados:
parado, esquerda e direita
Vídeo BBCI Berlin:
Pinball com o cérebro
http://www.youtube.com/watch?v=ZIIffTH5D-E
• Ainda é melhor usar as mãos, mas já é rápido o
suficiente
35
2. Codificação vetorial ou
populacional
As respostas a um padrão ei compõem um
vetor no qual cada componente
representa a taxa de disparo de um
determinado neurônio.
[ r1 , r2 , rn ]
36
2. Codificação vetorial ou populacional
Exemplo:
Codificação
vetorial
ou populacional
no epitélio
olfativo
37
2. Codificação vetorial ou populacional
Outros exemplos de codificação
populacional ou vetorial
Codificação vetorial da aceleração da
cabeça nos canais semi-circulares do
ouvido.
Codificação vetorial das cores
38
2. Codificação vetorial ou populacional
Entrada do sistema visual
Entrada é um padrão de luz em um arranjo bidimensional
Ondas capturadas por fotoreceptores
Bastonetes: sensível à luz de baixa intensidade
Cones: sensíveis a frequências específicas (cores)
39
2. Codificação vetorial ou populacional
Resposta relativa
Codificação vetorial nos cones
=[ 0, 27, 75]
Comprimento de onda (nm)
40
2. Codificação vetorial ou populacional
Experimentos de Miguel Nicolelis
Múltiplos
eletrodos no
cérebro.
Codificação
populacional
Feedback
sensorial
Ver:
http://www.youtube.com/watch?v=PTVVYYxY9Cs
http://www.youtube.com/watch?v=gnWSah4RD2E
41
2. Codificação vetorial ou populacional
Processamento dos vetores neurais no
experimento de Nicolelis
Aplicam-se técnicas de reconhecimento de padrões
para reconhecer cada vetor de frequências de
disparo.
Exemplo: Extração de características com
componentes principais
Depois estabelecem-se correlações (mediante
redes neurais artificiais) entre as características
extraídas e os movimentos dos membros.
Posteriormente a sequência de características
produzirá o movimento dos membros do robô.
42
Download