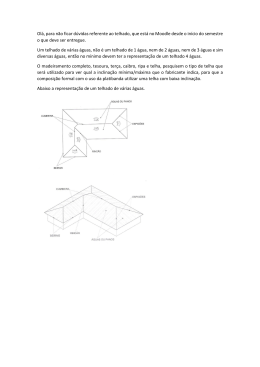
01.
Leia o texto a seguir.
A família das abelhas
Existem fatos sobre a família das abelhas que devemos
conhecer: por exemplo, algumas abelhas não têm pai e
mãe!
 Na colônia das abelhas existe uma especial: a rainha.
 Há muitas abelhas trabalhadoras que embora sejam
fêmeas não põem ovos.
 Os zangões são machos. Alguns deles não
trabalham. Os machos são produzidos pelos ovos
infertilizados da rainha. Logo, só têm uma mãe e não
têm pai.
 Todas as fêmeas são produzidas quando a rainha
acasalou com um macho e assim têm pai e mãe. As
fêmeas geralmente acabam como trabalhadoras, mas
algumas são alimentadas com uma substância especial,
chamada geleia real, que faz com que elas se tornem
rainhas. Elas estão prontas para irem embora e formar a
sua colônia, assim que as abelhas construírem um
enxame e deixarem a sua casa (colmeia) à procura de
um novo lugar para construírem sua colmeia.
 Concluímos que as fêmeas têm pai e mãe, e os
machos só mãe.
também foi construída uma pista de caminhada, com 4
metros de largura, como demonstra a figura a seguir.
As áreas aproximadas da praça central e da
pista são, respectivamente:
2
2
50 m e 491 m .
2
2
50 m e 346 m .
2
2
491 m e 855 m .
2
2
491 m e 364 m .
2
2
855 m e 419 m .
03. Hoje em dia, diversos
jogos matemáticos são disponibilizados na internet
com o intuito de que os alunos pratiquem os
conteúdos aprendidos em sala de aula de maneira
lúdica.
O jogo “Pontos em Batalha” é um desses e trabalha
com
conceitos
de
geometria
analítica.
O jogo consiste em preencher a localização dos barcos
e calcular a distância da bala que sairá do barco A e
deverá atingir, perpendicularmente, o segmento BC
(uma corrente que liga os barcos inimigos). Veja a
figura a seguir.
Disponível em:
<www.sbem.com.br/files/ix_enem/Relato.../RE21461236053T.doc>.
Acesso em: 29 fev. 2012. (Adapt.).
A figura a seguir ilustra cinco níveis da “árvore
genealógica” de uma abelha, na qual as letras F e M
indicam fêmea e macho, respectivamente.
Disponível em: <www.proativa.vdl.ufc.br/oa/pontos/pontos.html>. Acesso em: 21
mar. 2012. (Adapt.).
Considerando o texto e o esquema, assinale a
alternativa que corresponde ao total de fêmeas
encontrado no nível 8.
(A) 5
(B) 8
(C) 13
(D) 21
(E) 34
02. Na cidade de Três Laguinhos, o prefeito inaugurou
uma praça com aparelhos de ginástica para a
comunidade. A praça tem formato circular, cuja medida
do raio é 12,5 metros. Ao seu redor, formando um anel,
Com base na figura, suponha que os três
barcos estejam na disputa por um tesouro localizado
no baricentro do triângulo formado por suas
localizações. Pode-se afirmar corretamente que o
tesouro encontra-se no ponto de coordenadas:
(A) (– 4, 3)
(B) (0, 0)
 4

(C)   ,  1
 3

(D) (–1, –1)

3
(E)  2,  

2
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
04. Paulo queria comparar os pneus do carro de seu
pai com os do carro de seu avô; para isso, mediu a
distância do chão até o ponto mais alto do pneu,
conforme a figura a seguir.
Paulo
encontrou
as
seguintes medidas: 45 cm
no carro do pai e 72 cm no
carro do avô; com isso,
concluiu que, em uma volta,
o pneu maior percorre:
(A) o dobro de espaço do pneu menor.
(B) o mesmo espaço que o pneu menor.
(C) 160% a mais de espaço que o pneu menor.
(D) 50% a mais de espaço que o pneu menor.
(E) 60% a mais de espaço que o pneu menor.
05. Uma empresa deseja encomendar tortas salgadas
para uma comemoração. O preço das tortas varia
apenas em função do raio, visto que os três tipos
vendidos têm a mesma altura e o mesmo tipo de
recheio, conforme tabela a seguir.
Preço (R$)
Raio (cm)
Pequena
10,00
10
Média
20,00
20
Grande
25,00
25
Desse modo, o menor preço pago, por kg, ocorrerá na
compra de tortas:
(A) grandes.
(B) médias.
(C) pequenas.
(D) médias ou grandes.
(E) pequenas ou médias.
06. Para fazer os enfeites de mesa de uma festa de
aniversário com motivo circense, uma pessoa utilizou
latas de leite em pó revestidas de E.V.A (Etil Vinil
Acetado) – material emborrachado muito utilizado em
decoração de festas infantis – para produzir cartolas,
conforme a figura.
Para a produção de cada cartola, foi necessário cortar o
E.V.A conforme as indicações a seguir:
 um círculo, de raio R, para encapar o fundo da lata;
 um retângulo cuja largura corresponde à medida da
altura H da lata para encapar a sua lateral;
 uma coroa circular para fazer a aba da cartola, cujas
medidas estão indicadas na figura.
Considere:
 R = 5 cm;
 H = 12,5 cm;
   3;
 cada folha retangular de E.V.A possui dimensões de
80 cm de comprimento e 60 cm de largura.
Desse modo, considerando que a folha de E.V.A seja
aproveitada ao máximo, visando o mínimo desperdício,
para a construção de cada cartola, deve-se utilizar:
(A) menos de 10% da folha de E.V.A.
(B) entre 10% e 11% da folha de E.V.A.
(C) entre 11% e 12% da folha de E.V.A.
(D) entre 12% e 13% da folha de E.V.A.
(E) mais de 13% da folha de E.V.A.
07. Um condomínio residencial está sendo construído
em um bairro em que uma praça com alguns pontos
comerciais separa a rua principal em duas partes iguais.
No plano cartesiano, a rua principal é representada por
um segmento AB, cuja reta suporte r passa pelos
pontos C(8, –1) e D(–4, 05), e a praça é representada
pelo ponto P, ponto médio do segmento AB.
Considerando que os pontos A e B são as interseções
da reta r com os eixos coordenados, a localização da
praça, no plano cartesiano, é indicada pelas
coordenadas:
(A) x = 3 e y = 3/2
(B) x = 1 e y = 3
2
(C) x = 0 e y = 3
3
4
(D) x = e y =
3
2
(E) x = 6 e y = 0
08. Mariana vai fazer uma festa em sua casa, e para
que seus amigos consigam chegar até lá, ela resolveu
construir um mapa indicando o caminho desde a
escola até sua casa. Sabendo que o caminho percorrido
neste trajeto é de 1,2 km e que, no mapa, esse caminho
mede 10 cm, a escala utilizada por Mariana foi de:
(A) 1: 12
(B) 1: 120
(C) 1: 1.200
(D) 1: 12.000
(E) 1: 120.000
09. As bactérias são organismos que se reproduzem
por divisão celular, processo no qual cada célula se
divide em duas, sequencialmente, em intervalos de
tempo regulares, crescendo em ritmo exponencial.
Considere determinada colônia de bactérias cujo
processo de reprodução obedece à função
t
y(t)  2 8 ; sabendo que t é medido em horas, a
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
quantidade de bactérias dessa colônia, após quatro
dias, será igual a:
(A) 256
(B) 512
(C) 2.048
(D) 3.906
(E) 4.096
10. Samuel fez uma pesquisa com todos os alunos do
o
3 ano do Ensino Médio de sua escola para decidirem
como seria a confraternização de fim de ano. Com as
respostas obtidas, ele elaborou a seguinte tabela.
Para expor os dados aos alunos, ele construiu um
gráfico de setores de raio r cm. As áreas dos setores
relacionados ao churrasco e à festa temática serão,
respectivamente:
(A)
(B)
(C)
(D)
(E)
9
1
r² e r²
20
8
3
1
r² e r²
10
8
3
1
r² e r²
10
4
9
1
r² e r²
10
4
9
1
r² e r²
20
25
Tipo de
confraternização
Almoço comunitário
Festa temática
Noite no boliche
Churrasco
o
N de
alunos
30
25
55
90
Como calcular a renda familiar por pessoa?
A renda familiar por pessoa é calculada somandose a renda bruta dos componentes do grupo familiar e
dividindo-se pelo número de pessoas que formam este
grupo familiar. Se o resultado for até um salário mínimo
e meio, o estudante poderá concorrer a uma bolsa
integral. Se o resultado for maior que um salário mínimo
e meio e menor ou igual a três salários mínimos, o
estudante poderá concorrer a uma bolsa parcial de 50%.
Entende-se como grupo familiar a unidade nuclear
composta por uma ou mais pessoas, eventualmente
ampliada por outras pessoas que contribuam para o
rendimento ou tenham suas despesas atendidas por
aquela unidade familiar, todas moradoras em um
mesmo domicílio.
Portal do Programa Universidade Para Todos - ProUni. Disponível em:
<http://prouniportal.mec.gov.br/>.
11. Se a renda de certa família for de 6 salários
mínimos, para que um de seus membros possa
concorrer a uma bolsa integral pelo ProUni, esse grupo
familiar deve ter, no mínimo:
(A) 3 pessoas.
(B) 4 pessoas.
(C) 5 pessoas.
(D) 6 pessoas.
(E) 7 pessoas.
12. Paulo tem um tetraedro regular oco de plástico,
como o mostra a figura a seguir, e quer determinar o
valor de sua aresta. Desprovido de um instrumento de
medição, ele realizou os seguintes procedimentos:
encheu um béquer com 500 mL de água e, com uma
seringa, injetou o líquido através do plástico, até encher
completamente o tetraedro. Quando isso ocorreu, a
água restante no béquer correspondia a 150 mL.
Considerando que os cálculos de Paulo estavam
corretos, ele determinou
que a aresta do tetraedro
media:
Dado: 2  1,4.
256
512
2.048
3.906
4.096
13. Leia o texto a seguir.
Matemática e Administração
Função custo: em Administração, custo é o gasto
pertinente à produção de um produto por uma fábrica
ou indústria: mão de obra de trabalhadores, impostos,
encargos sociais, transporte, telefone, internet, água,
energia elétrica, entre outros gastos diretos ou opcionais.
Um custo pode ser considerado fixo ou variável, a
maioria das empresas trabalham com os dois tipos.
Função receita: Receita é o valor arrecadado com a
venda do produto no mercado.
Função lucro: Lucro é o valor calculado entre a diferença
da receita e do custo. Caso esse cálculo tenha como
resultado um número positivo, verificamos a ocorrência
de lucro; caso seja um número negativo, existe a
ocorrência de prejuízo. Na ocorrência de valor nulo,
concluímos que houve receita igual ao custo da
produção.
Disponível em: <http://educador.brasilescola.com/estrategiasensino/interdisciplinarizando-matematica-administracao-financeira.htm>.
Acesso em: 7 mar. 2012. (Adapt.).
Uma doceira tem um custo fixo de R$ 4,00 por semana
para a produção de brigadeiros, além do custo de R$
7,00 por quilograma de brigadeiro produzido. O preço
de venda de 100 gramas de brigadeiro é R$ 2,50.
Considere que em quatro semanas a doceira precisa
lucrar pelo menos R$ 1.064,00. Para saber a quantia
mínima de brigadeiro que ela deverá vender para obter
esse lucro, a doceira deve resolver a inequação:
(A) 25x – (7x – 16) ≥ 1.064
(B) 25x – (7x + 4) ≥ 1.064
(C) 25x – (7x + 16) ≥ 1.064
(D) 25x – (4x + 7) ≥ 1.064
(E) 25x – (4x + 28) ≥ 1.064
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
14. Uma artesã deseja produzir colchas utilizando
faixas de mesmo tamanho de dois tecidos diferentes,
um tecido liso, com 6,5 metros, e um estampado, com
4,8 metros. O comprimento dessas faixas, de forma que
tenham o maior comprimento possível, para que a
artesã aproveite totalmente os dois tecidos, deve ser:
(A) 10 cm
(B) 20 cm
(C) 30 cm
(D) 40 cm
(E) 50 cm
15. Em uma família, cinco irmãos têm as suas idades
consecutivas.
Sabendo que a média aritmética de todas as idades é
19, a razão do produto pela soma das cinco idades é:
(A) 1.224
(B) 1.615
(C) 1.805
(D) 25.704
(E) 136.001
16. Em determinada instituição financeira, foi aplicada
uma importância de R$ 1.200,00, a uma taxa de 2,5%
ao mês, em regime de juros compostos.
O tempo estimado necessário para chegar ao
montante de R$ 9.600,00 é de:
Dados: log 8 = 0,9; log 1,025 = 0,01.
(A) 36 meses.
(B) 48 meses.
(C) 90 meses.
(D) 120 meses.
(E) 180 meses.
Leia o texto a seguir e observe a figura.
Os Tijolos de Encaixe de solo cimento são modulares,
ecológicos, estruturais, que garantem ao consumidor
inúmeras vantagens ao construir, pois o sistema de
encaixe é muito simples, rápido e seguro. Esses tijolos
têm o formato de paralelepípedo retângulo, com
dimensões, em centímetros, de 15 x 30 x 7,5 e dois
furos com diâmetros de 8,8 centímetros para passagem
da parte elétrica, hidráulica e esgoto na vertical sem
precisar cortar as paredes.
17. Considerando a ilustração, os dados do texto e
π = 3, tem-se que o volume de cada tijolo é de,
aproximadamente:
(A) 2.375 cm³
(B) 2.503,8 cm³
(C) 2.939,4 cm³
(D) 3.810,6 cm³
(E) 4.246,2 cm³
18. Leia o texto a seguir.
A função principal de um telhado é proteger a
casa da chuva. Por isso, todo telhado precisa ter um
caimento para escoar a água da chuva.
Entende-se por caimento a inclinação do plano da água
do telhado, ou seja, representa o quociente entre a
altura H e a largura L da água do telhado. Quanto
maior o caimento, mais inclinado será o telhado.
Deve-se ter o cuidado de escolher um caimento mínimo,
que depende do desenho da telha e das ranhuras
projetadas pelo fabricante para evitar a penetração da
água da chuva em dias de vento forte. Telhas de um
mesmo modelo podem apresentar caimentos mínimos
diferentes dependendo do fabricante.
Veja, por exemplo, o caimento mínimo recomendado por
fabricantes diferentes para a telha do tipo francesa:
Fabricante
A
B
C
Caimento mínimo
do telhado
30%
45%
40%
<www.ebanataw.com.br/roberto/telhado/tlh5.htm> (Adapt.)
Acesso em: 1° fev. 2012.
A figura a seguir (sem escala) ilustra um telhado com
medidas, em metros, que utilizará telha do tipo
francesa.
Disponível em: <http://www.monteirotijolos.com/index-historico.htm>.
Acesso em: 12 mar. 2012. (Adapt.).
De acordo com a figura e com o texto, pode-se afirmar
que o telhado:
www.davidmachado.com.br
EXCELÊNCIA NO ENSINO DA MATEMÁTICA
(A) atende às especificações dos três fabricantes.
(B) atende apenas à especificação do fabricante A.
(C) atende apenas às especificações dos fabricantes A
e B.
(D) atende apenas às especificações dos fabricantes A
e C.
(E) não atende às especificações de nenhum dos três
fabricantes.
19.
Uma
empresa
produz
embalagens
paralelepipédicas de papel com diversas medidas.
Observe, a seguir, dois modelos produzidos.
Essa empresa recebeu uma encomenda de caixas que
devem ter:
 comprimento da caixa B acrescido em x
centímetros.

mesma altura da caixa do modelo A.

largura da caixa B acrescido em x centímetros.

volume da caixa A aumentado em 200%.
Desse modo, para que a empresa atenda às exigências
da encomenda, a nova caixa deverá ter comprimento,
largura e altura iguais, respectivamente, a:
(A) 18 cm, 17 cm e 10 cm
(B) 13 cm, 13 cm e 10 cm
(C) 10 cm, 9 cm e 8 cm
(D) 4 cm, 4 cm e 10 cm
(E) 9 cm, 8 cm e 10 cm
www.davidmachado.com.br