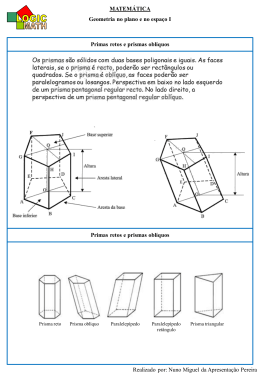
Marcio Rogério do Nascimento
O USO DE ARGAMASSA DE ASSENTAMENTO COMO
PREENCHIMENTO DE ALVENARIA ESTRUTURAL
CERÂMICA
Tese submetida ao Programa de Pós
Graduação em Engenharia Civil da
Universidade Federal de Santa
Catarina para a obtenção do Grau de
Doutor em Engenharia Civil.
Orientador: Prof. Ph.D. Humberto
Ramos Roman.
Florianópolis
2015
Ficha de identificação da obra elaborada pelo autor através do
Programa de Geração Automática da Biblioteca Universitária da UFSC.
Nascimento, Marcio Rogério do
O uso de argamassa de assentamento como preenchimento de
alvenaria estrutural cerâmica / Marcio Rogério do Nascimento; orientador,
Humberto Ramos Roman - Florianópolis, SC, 2015.
265 p.
Tese (doutorado) - Universidade Federal de Santa Catarina, Centro
Tecnológico. Programa de Pós-Graduação em Engenharia Civil.
Inclui referências
1. Engenharia Civil. 2. Alvenaria Estrutural. 3. Bloco cerâmico. 4.
Argamassa. 5. Graute. I. Roman, Humberto Ramos. II. Universidade Federal
de Santa Catarina. Programa de Pós-Graduação em Engenharia Civil. III.
Título.
Marcio Rogério do Nascimento
O USO DE ARGAMASSA DE ASSENTAMENTO COMO
PREENCHIMENTO DE ALVENARIA ESTRUTURAL
CERÂMICA
Esta Tese foi julgada adequada para obtenção do Título de Doutor em
Engenharia Civil, e aprovada em sua forma final pelo Programa de PósGraduação em Engenharia Civil da Universidade Federal de Santa
Catarina.
Florianópolis, 20 de março de 2015.
______________________________________________
Prof. Roberto Caldas de Andrade Pinto, Ph.D.
Coordenador do PPGEC/UFSC
Banca Examinadora:
_______________________
Prof. Humberto Ramos Roman, Ph.D. - ECV/UFSC - Orientador
_______________________
Prof.ª Márcio Roberto Silva Côrrea, Dr. - USP
_______________________
Prof. Guilherme Aris Parsekian, Dr. - UFSCar
_______________________
Prof. Luis Alberto Gómez, Dr. - ECV/UFSC
_______________________
Prof. Philippe Jean Paul Gleize, Dr. - ECV/UFSC
_______________________
Profª. Fernanda Fernandes Marchiori, Drª. - ECV/UFSC
Eu dedico este trabalho a minha esposa Roberta, minha
filha Antônia e minha mãe Silvia, pela vida, exemplo e
amor.
AGRADECIMENTOS
Ao professor Humberto Ramos Roman, pela orientação e apoio
durante todo o período de pesquisa e redação desta tese.
Ao professor Itamar Ribeiro Gomes, pela coorientação, paciência
e apoio durante parte da pesquisa e redação desta tese.
Ao professor e amigo, João Batista Rodrigues Neto, pelo
incentivo e amizade.
Ao professor Luís Gómez, pelo auxilio na instrumentação dos
ensaios.
Ao PPGEC e a todos os Professores do Curso, os quais, direta e
indiretamente tornaram este trabalho possível.
Aos funcionários do laboratório de materiais de construção, Luiz,
Renato e Roque, pelo companheirismo e disposição.
Aos colegas da pós-graduação, Fabiano, Glêdes, Giovana,
Fabíola, Roberta, Viviany, Ronaldo, Rudiele, César, Lidiane, Julio, José
Marcos, Carlos Quintero, Mariana, Flávia, Lourenço, Elisabeth e,
principalmente, Francisco Morato Leite pela ajuda e discussões que
foram vitais para o desenvolvimento do trabalho.
Aos bolsistas, Roberto, Gabriel, Marcelo, Darvil e Edilberto, pelo
auxilio durante a execução do programa experimental.
À minha esposa Roberta e minha filha Antônia, pela paciência,
amor e incentivo.
À minha mãe, Sílvia e meus irmãos, Marcos, Marcel e Elaine,
pelo apoio e carinho.
À Cerâmica Constrular, pelo fornecimento dos blocos utilizados
nos trabalhos experimentais.
À empresa Votorantim Cimentos, pelo fornecimento do cimento e
da argamassa industrializada.
À CAPES – Coordenação de Aperfeiçoamento de Pessoal de
Nível Superior, pelo financiamento deste trabalho.
RESUMO
Este trabalho tem como objetivo investigar o comportamento estrutural
à compressão da alvenaria de blocos estruturais cerâmicos considerando
o preenchimento dos furos com a argamassa de assentamento, como
componente integrante do sistema construtivo em alvenaria estrutural.
Para atingir o objetivo do trabalho, realizou-se a análise das
propriedades mecânicas dos prismas, correlacionando-as com as
propriedades obtidas com a caracterização dos blocos, argamassas e
grautes. Para tanto, a análise foi dividida em três Etapas: Referência,
Argamassa Mista e Argamassa Industrializada. Para a moldagem dos
prismas, utilizaram-se três blocos de geometrias distintas; três traços de
argamassas mistas; três traços de argamassas industrializadas e três
traços de grautes, com resistências distintas. Como conclusões gerais do
trabalho, podem destacar as seguintes: para os prismas preenchidos, em
ambas as etapas, o fator com maior influência na resistência à
compressão dos prismas foi o bloco; para os prismas preenchidos e
moldados com os blocos de 6 MPa, da Etapa Argamassa Mista, o
aumento na resistência da argamassa não gera aumento significativo na
resistência dos prismas, constatando-se que a utilização dos blocos de 6
MPa e a argamassa C (traço 1:1:6), como assentamento e
preenchimento, demonstra-se como a melhor combinação de blocoargamassa, pois além deste traço apresentar o menor consumo de
cimento, esta série de prismas quando preenchida com argamassa
apresenta aumento efetivo da carga de ruptura, no valor de 60%,
viabilizando a utilização da técnica prescrita na norma ABNT NBR
15812-2 (2010); para os prismas preenchidos da Etapa com Argamassa
Industrializada, somente os prismas moldados com os blocos de 6 MPa
apresentam aumento significativo na resistência à compressão com o
aumento da resistência das argamassas, onde a melhor combinação de
bloco-argamassa ocorre para o prisma moldado com a argamassa
industrializada de 10 MPa, que apresenta aumento efetivo da carga de
ruptura, no valor 40,5%. Diante do exposto, observa-se que o aumento
na resistência à compressão dos prismas com a utilização da argamassa
como preenchimento estrutural evidencia a viabilidade de utilização
desta técnica, desde que a escolha entre os componentes dos prismas
seja adequada.
Palavras chave: Alvenaria estrutural, graute, argamassa, bloco
cerâmico.
ABSTRACT
This study aims to investigate the behavior of structural masonry clay
blocks in structural compression considering the filling of their holes
with bedding mortar, as part of a constructive system in structural
masonry. In order to achieve this aim, the mechanical properties of the
prisms were analyzed in relation to the properties obtained with the
characterization of the blocks, mortars and grouts. The analysis was
separated in three stages: References, Mixed Mortar and Industrial
Mortar. Three blocks with different geometries were used for molding
the prisms, as well as three mixes of mixed mortar, three mixes of
industrial mortar and three mixes of grout, with different strength. The
following stand out as general conclusions: for the filled prisms, in both
stages the factor with highest influence on the prisms' strength was the
block; for the filled prisms molded with 6 MPa blocks, on the Mixed
Mortar stage, increasing the mortar strength does not increase the
strength of the prisms significantly, having that the use of 6 MPa blocks
and C mortar (mix 1:1:6) as bedding and filling, is the best block-mortar
combination, because aside from presenting the lowest consume of
cement, this series of prisms presents a significant increase in failure
strength when filled with mortar, with a value of 60%, which makes the
use of the technique prescribed by the ABNT NBR 15812-2 (2010)
standard viable. For the filled prisms in the Industrial mortar stage, only
the prisms molded with 6 MPa blocks present significant increase in
compressive strength when the strength of the mortars is increased,
where the best block-mortar combination occurs for the prism molded
with the 10 MPa industrial mortar, which presents significant increase in
failure strength, with a value of 40,5%. Having these results, it is noticed
that the increase in compressive strength of prisms using mortar as
structural bedding evidences the viability of such technique as long as
the choice regarding the components is adequate.
Keywords: Structural masonry, grout, mortar, clay block.
LISTA DE FIGURAS
Figura 2.1 – Valores de espessuras mínimas para as paredes externas e
septos dos blocos cerâmicos estruturais (a) de paredes
vazadas e (b) com paredes maciças, em milímetros. ....... 37
Figura 2.2 - Esquema de ensaio de resistência à tração indireta do bloco.
......................................................................................... 39
Figura 2.3 - Modelos de prismas utilizados experimentalmente. .......... 52
Figura 2.4 - Geometrias e dimensões dos blocos estudados.................. 60
Figura 2.5 - Geometrias e dimensões dos blocos estudados.................. 61
Figura 2.6 - Resistência à compressão simples de blocos, argamassas e
prismas. ............................................................................ 63
Figura 2.7 - Resultados médios de resistência à compressão. ............... 65
Figura 2.8 - Resultados de resistência à compressão dos prismas......... 67
Figura 2.9 – Resultados de resistências dos grautes versus prismas. .... 70
Figura 2.10 – Secções transversais dos prismas adotados com os
diferentes percentuais de grauteamento. .......................... 71
Figura 2.11 - Tipos de assentamento utilizados na construção dos
prismas: (a) assentamento total e (b) assentamento nas
faces laterais dos blocos................................................... 77
Figura 2.12 - Tensões nas unidades e na argamassa submetidas a
compressão simples. ........................................................ 80
Figura 2.13 - Representação gráfica de tensões e critérios de ruptura
para tijolos e alvenaria. .................................................... 80
Figura 2.14 - Estado multiaxial de tensões da alvenaria sob compressão.
......................................................................................... 81
Figura 2.15 - Deformação lateral dos blocos e da argamassa submetidos
à compressão simples....................................................... 83
Figura 2.16 - Distribuição de tensões, segundo modelo de Atckinson e
Nolan. .............................................................................. 83
Figura 2.17 – Curvas de ruptura para prismas de blocos não grauteados.
......................................................................................... 87
Figura 3.1 - Programa de caracterização dos materiais, argamassas,
blocos e prismas. .............................................................. 95
Figura 3.2 - Curva granulométrica da areia utilizada e zonas de
utilização conforme ABNT NBR 7211 (2005). ............... 97
Figura 3.3 - Curva granulométrica da areia utilizada e limites de
utilização conforme BS 1200 (1976) e ASTM C-144
(1987)............................................................................... 97
Figura 3.4 - Curva granulométrica da brita utilizada e limites de
utilização conforme ABNT NBR 7211 (2005). ............... 99
Figura 3.5 - Geometria e respectivas resistências nominais dos blocos
utilizados. .......................................................................102
Figura 3.6 - Corte dos corpos-de-prova do material dos blocos. .........103
Figura 3.7 – Corpo-de-prova após a fixação dos strain gauges............104
Figura 3.8 – Configuração do ensaio com amostra, célula de carga e
prensa..............................................................................106
Figura 3.9 –Corpo-de-prova após a fixação dos strain gauges.............111
Figura 3.10 – Disposição da fixação dos transdutores de deslocamento
nos corpos-de-prova. ......................................................115
Figura 3.11 – Configuração do ensaio com o corpo-de-prova com strain
gauges, célula de carga e prensa. ....................................117
Figura 3.12 - Prismas de 3 fiadas com junta a prumo. .........................118
Figura 3.13 - Capeamento superior dos blocos para a moldagem dos
prismas............................................................................121
Figura 3.14 - Blocos sendo umedecidos antes da moldagem do prisma.
........................................................................................122
Figura 3.15 - Armazenamento e cuidados com os prismas após
moldagem. ......................................................................123
Figura 3.16 – Detalhe de fixação dos transdutores de deslocamento no
prisma. ............................................................................124
Figura 3.17 – Configuração do ensaio com o prisma, célula de carga e
prensa..............................................................................125
Figura 4.1 – Gráfico Tensão x Deformação do material dos blocos. ...138
Figura 4.2 – Gráfico Tensão x Deformação das argamassas. ..............140
Figura 4.3 – Gráfico Tensão x Deformação dos grautes. .....................141
Figura 4.4 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus resistência média à compressão
dos grautes (fg). ..............................................................144
Figura 4.5 - Carga de ruptura média (Fp) versus resistência média à
compressão dos grautes (fg). ...........................................148
Figura 4.6 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus relação entre os valores de
resistência média à compressão do graute/resistência do
bloco na área líquida (fg/fbliq).........................................151
Figura 4.7 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus relação entre os valores médios
de módulo de elasticidade do graute/módulo de
elasticidade do bloco (Eg/Eb). .........................................151
Figura 4.8 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus relação entre os valores de
resistência média à compressão do graute/resistência da
argamassa (fg/farg)........................................................... 152
Figura 4.9 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus relação entre os valores médios
de módulo de elasticidade do graute/módulo de
elasticidade da argamassa (Eg/Earg). ............................... 152
Figura 4.10 – Módulos e áreas utilizados na análise de prismas
grauteados. ..................................................................... 155
Figura 4.11 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus resistência média à compressão
das argamassas de assentamento ou de preenchimento
(farg = fg) – Etapa com Arg. Mista................................ 161
Figura 4.12 – Gráfico da resistência média à compressão dos prismas na
área líquida (fpliq) versus resistência média à compressão
das argamassas de assentamento ou de preenchimento
(farg = fg) – Etapa com Arg. Industrializada. ................ 165
Figura 4.13 – Gráfico da relação entre fp liq/farg e fb liq/farg, para os
prismas vazios – Etapa Arg. Mista. ............................... 178
Figura 4.14 – Gráfico da relação entre fp liq/farg e fb liq/farg, para os
prismas grauteados – Etapa Arg. Mista. ........................ 179
Figura 4.15 – Gráfico da relação entre fp liq/farg e fb liq/arg, para os
prismas vazios – Etapa Arg. Industrializada. ................. 181
Figura 4.16 – Gráfico da relação entre fp liq/farg e fb liq/arg, para os
prismas grauteados – Etapa Arg. Industrializada. .......... 181
Figura 4.17 – Carga de ruptura média (Fp) versus resistência média à
compressão das argamassas de assentamento ou de
preenchimento (farg = fg) – Etapa Argamassa Mista. ... 183
Figura 4.18 – Comparação entre os diagramas tensão-deformação
obtidos para as argamassas e prismas vazios. ................ 185
Figura 4.19 – Gráfico da carga de ruptura dos prismas (Fp) versus
relação entre os valores médios de módulo de elasticidade
da argamassa/módulo de elasticidade do bloco (Earg/Eb) –
Etapa Arg. Mista. ........................................................... 188
Figura 4.20 – Gráfico da carga de ruptura dos prismas (Fp) versus
relação entre os valores médios de módulo de elasticidade
da argamassa/módulo de elasticidade do prisma vazio na
área líquida [Earg/Ep vazio(área líquida)] – Etapa Argamassa
Mista. ............................................................................. 189
Figura 4.21 - Carga de ruptura média (Fp) versus resistência média à
compressão das argamassas de assentamento ou de
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
Figura
preenchimento (farg = fg) – Etapa Argamassa
Industrializada. ...............................................................191
4.22 – Comparação entre os diagramas tensão-deformação
obtidos para as argamassas e prismas vazios. .................193
4.23 – Gráfico da carga de ruptura dos prismas (Fp) versus
relação entre os valores médios de módulo de elasticidade
da argamassa/módulo de elasticidade do bloco (Earg/Eb) –
Etapa Arg. Industrializada. .............................................196
4.24 – Gráfico da carga de ruptura dos prismas (Fp) versus
relação entre os valores médios de módulo de elasticidade
da argamassa/módulo de elasticidade do prisma vazio na
área líquida [Earg/Ep vazio(área líquida)] – Etapa Argamassa
Industrializada. ...............................................................196
4.25 – Ruptura característica dos prismas vazios com os blocos
B6 - Etapa Arg. Mista. ....................................................198
4.26 – Ruptura característica dos prismas vazios com os blocos
B12 – Etapa Arg. Mista. .................................................198
4.27 – Ruptura característica dos prismas vazios com os blocos
B15 – Etapa Arg. Mista. .................................................198
4.28 – Ruptura característica dos prismas vazios moldados com
os blocos B6 – Etapa Arg. Industrial. .............................199
4.29 – Ruptura característica dos prismas vazios moldados com
os blocos B12 – Etapa Arg. Industrial. ...........................199
4.30 – Ruptura característica dos prismas vazios moldados com
os blocos B15 – Etapa Arg. Industrial. ...........................200
4.31 – Ruptura característica dos prismas grauteados moldados
com os blocos B6 e argamassa C – Etapa Referência. ...201
4.32 – Ruptura característica dos prismas grauteados moldados
com os blocos B12 e argamassa B – Etapa Referência. .201
4.33 – Ruptura característica dos prismas grauteados moldados
com os blocos B15 e argamassa C – Etapa Referência. .202
4.34 – Ruptura característica dos prismas grauteados moldados
com os blocos B15 e argamassa A – Etapa Referência. .203
4.35 – Ruptura característica dos prismas grauteados moldados
com os blocos B6 – Etapa Arg. Mista. ...........................204
4.36 – Ruptura característica dos prismas grauteados moldados
com os blocos B12 – Etapa Arg. Mista. .........................204
4.37 – Ruptura característica dos prismas grauteados moldados
com os blocos B15 – Etapa Arg. Mista. .........................205
4.38 – Ruptura característica dos prismas grauteados moldados
com os blocos B6 – Etapa Arg. Industrial. .....................205
Figura 4.39 – Ruptura característica dos prismas grauteados moldados
com os blocos B12 – Etapa Arg. Industrial. .................. 206
Figura 4.40 – Ruptura característica dos prismas grauteados moldados
com os blocos B15 – Etapa Arg. Industrial. .................. 206
Figura 5.1 - Estratégias de modelagem para estruturas de alvenaria: (a)
alvenaria;
(b)
micromodelagem
detalhada;
(c)
micromodelagem simplificada; (d) macromodelagem... 209
Figura 5.2 – Critério de Mohr-Coulomb no plano. ............................. 214
Figura 5.3 - Representação gráfica da superfície de ruptura do critério de
Mohr-Coulomb no espaço das tensões principais. ......... 215
Figura 5.4 - Representação gráfica da superfície de ruptura no plano
desviador. ....................................................................... 215
Figura 5.5 – Características geométricas dos prismas. ........................ 220
Figura 5.6 – Critério limite de plasticidade Mohr-Coulomb Parabólico.
....................................................................................... 221
Figura 5.7 – Diagramas tensão-deformação obtidos para o prisma MG6C..................................................................................... 224
Figura 5.8 – Distribuição de tensão para o prisma MG6-C e o graute
para carga de 4,3 MPa, extraída do programa Marc Mentat.
....................................................................................... 225
Figura 5.9 – Distribuição de tensão para o prisma MG6-C e o graute
para carga de 8,7 MPa, extraída do programa Marc Mentat.
....................................................................................... 226
Figura 5.10 – Diagramas tensão-deformação obtidos para o prisma
MG6-B. .......................................................................... 227
Figura 5.11 – Distribuição de tensão para o prisma MG6-B e o graute
para carga de 4,3 MPa, extraída do programa Marc Mentat.
....................................................................................... 228
Figura 5.12 – Distribuição de tensão para o prisma MG6-B e o graute
para carga de 8,7 MPa, extraída do programa Marc Mentat.
....................................................................................... 229
Figura 5.13 – Diagramas tensão-deformação obtidos para o prisma
MG6-A........................................................................... 230
Figura 5.14 – Distribuição de tensão para o prisma MG6-A e o graute
para carga de 4,3 MPa, extraída do programa Marc Mentat.
....................................................................................... 231
Figura 5.15 – Distribuição de tensão para o prisma MG6-A e o graute
para carga de 8,7 MPa, extraída do programa Marc Mentat.
....................................................................................... 232
Figura 5.16 – Distribuição de tensão para o prisma MG6-A e o graute
para carga de 10,1 MPa, extraída do programa Marc
Mentat. ............................................................................233
Figura 5.17 – Pontos da seção transversal para a análise da distribuição
de tensão ao longo da altura. ..........................................236
Figura 5.18 – Distribuição de tensão ao longo da altura para o Prisma
MG6-C............................................................................238
Figura 5.19 – Distribuição de tensão ao longo da altura para o Prisma
MG6-B............................................................................239
Figura 5.20 – Distribuição de tensão ao longo da altura para o Prisma
MG6-A. ..........................................................................240
Figura 5.21 – Distribuição de tensões principais máximas para o graute
do prisma MG6-C, extraída do programa Marc Mentat. 241
Figura 5.22 – Distribuição de tensões principais máximas para o graute
do prisma MG6-B, extraída do programa Marc Mentat. 241
Figura 5.23 – Distribuição de tensões principais máximas para o graute
do prisma MG6-A, extraída do programa Marc Mentat. 242
LISTA DE TABELAS
Tabela 2.1 - Tolerâncias dimensionais para blocos cerâmicos. ............... 36
Tabela 2.2 – Características mecânicas e físicas para blocos cerâmicos
estruturais. .......................................................................... 37
Tabela 2.3 - Valores de Ø em função da quantidade de blocos. .............. 38
Tabela 2.4 – Traços dos grautes em volume conforme BS 5628: Part 2. 42
Tabela 2.5 – Traços dos grautes em volume conforme ASTM C 476-83.43
Tabela 2.6 - Exigências mecânicas e reológicas para argamassas. .......... 47
Tabela 2.7 - Especificações dos traços e propriedades das argamassas. .. 47
Tabela 2.8 - Especificações dos traços e propriedades das argamassas. .. 48
Tabela 2.9 - Limites da composição granulométrica do agregado miúdo
para argamassas de assentamento. ...................................... 49
Tabela 2.10- Propriedades mecânicas das argamassas obtidas no estudo de
Khalaf et al.. ....................................................................... 51
Tabela 2.11 – Valores de Ø em função da quantidade de elementos da
alvenaria. ............................................................................ 54
Tabela 2.12 – Valores de k para diferentes grupos de unidades cerâmicas
e argamassas. ...................................................................... 55
Tabela 2.13 – Modelos matemáticos para a determinação da resistência à
compressão da alvenaria para blocos de concreto. ............. 56
Tabela 2.14 – Resultados de resistência à compressão. ........................... 57
Tabela 2.15 – Valores de eficiência para prisma-bloco e parede-bloco ... 58
Tabela 2.16 - Valores de resistência para blocos e paredes. .................... 60
Tabela 2.17 – Resultados de resistência dos prismas. .............................. 69
Tabela 2.18 – Normas e autores internacionais pesquisados, referentes a
blocos cerâmicos. ............................................................... 75
Tabela 2.19 - Propriedades elásticas da alvenaria estrutural de blocos
cerâmicos. ........................................................................... 76
Tabela 2.20 – Resistência das pequenas paredes em função do
assentamento. ..................................................................... 78
Tabela 3.1 – Composição granulométrica do agregado miúdo utilizado. 96
Tabela 3.2 – Composição granulométrica do agregado graúdo utilizado. 98
Tabela 3.3 - Características físicas dos materiais utilizados nas argamassas
de assentamento e grautes. ............................................... 100
Tabela 3.4 - Caracterização química do Cimento Portland CP II Z-32. 100
Tabela 3.5 - Composição da Cal CH III. ................................................ 101
Tabela 3.6 - Características físicas dos materiais utilizados nas argamassas
de assentamento e grautes. ............................................... 101
Tabela 3.7 - Denominação das argamassas. ........................................... 107
Tabela 3.8 - Denominação e características das argamassas mistas. ..... 108
Tabela
3.9
- Denominação e características das argamassas
industrializadas..................................................................109
Tabela 3.10 - Denominação e resistências esperadas dos grautes. .........113
Tabela 3.11 - Denominação dos prismas da Etapa de Referência. .........120
Tabela 3.12 - Denominação dos prismas da Etapa com Argamassa Mista.
...........................................................................................120
Tabela 3.13 - Denominação dos prismas da Etapa com Argamassa
Industrializada. ..................................................................120
Tabela 4.1 – Características físicas dos blocos dos Lotes 1 e 2. .............127
Tabela 4.2 – Resistência à compressão dos blocos dos Lotes 1 e 2........128
Tabela 4.3 – Resistência à tração indireta dos blocos dos Lotes 1 e 2....128
Tabela 4.4 - Análise de variância para a resistência à compressão dos
blocos dos Lotes 1 e 2 . .....................................................129
Tabela 4.5 – Característica mecânicas dos blocos para corpos-de-prova
prismáticos (20x40) mm. ..................................................130
Tabela 4.6 – Característica mecânicas dos blocos cerâmicos utilizados por
Cesar (2007) e Santos (2208). ...........................................131
Tabela 4.7 – Característica mecânicas das argamassas para corpos-deprova prismático (4x4x16) cm. .........................................133
Tabela 4.8 – Característica mecânicas das argamassas para corpos-deprova (ϕ5X10) cm. ............................................................133
Tabela 4.9 - Análise de variância para a resistência à compressão para as
duas geometrias de corpos-de-prova . ...............................133
Tabela 4.10 – Características mecânicas dos grautes para corpos-de-prova
(ϕ10X20) cm, utilizando transdutores de deslocamento. ..135
Tabela 4.11 – Características mecânicas dos grautes para corpos-de-prova
(ϕ10X20) cm, utilizando strain gauge. ..............................135
Tabela 4.12 - Análise de variância para a resistência à compressão para as
duas geometrias de corpos-de-prova . ...............................136
Tabela 4.13 – Valores de resistência à compressão dos blocos. .............137
Tabela 4.14 – Valores de resistência à tração dos blocos. ......................137
Tabela 4.15 – Valores de módulo de elasticidade e coeficiente de Poisson
dos blocos..........................................................................138
Tabela 4.16 – Resumo das propriedades mecânicas das argamassas. ....139
Tabela 4.17 – Resumo das propriedades mecânicas dos grautes. ...........141
Tabela 4.18 – Característica mecânicas dos prismas da Etapa Referência.
...........................................................................................143
Tabela 4.19 – Análise de variância para o grautes e blocos na resistência à
compressão dos prismas moldados com a argamassa da
classe C. ............................................................................146
Tabela 4.20 – Análise de variância para o grautes e argamassas na
resistência à compressão dos prismas moldados com os
blocos da classe B15......................................................... 147
Tabela 4.21 – Aumento efetivo da capacidade de carga dos prismas
preenchidos....................................................................... 150
Tabela 4.22 – Porcentagem estimada dos carregamentos absorvidos pelos
grautes. ............................................................................. 158
Tabela 4.23 – Características mecânicas dos prismas da Etapa com
Argamassa Mista. ............................................................. 160
Tabela 4.24 – Característica mecânicas dos prismas da Etapa com
Argamassa Industrializada................................................ 164
Tabela 4.25 – Análise de variância para a argamassa e bloco na resistência
à compressão dos prismas. ............................................... 167
Tabela 4.26 – Análise de variância para a argamassa e preenchimento na
resistência à compressão dos prismas. .............................. 170
Tabela 4.27 – Análise de múltiplas médias entre a resistência à
compressão dos prismas – Etapa com Argamassa Mista.. 172
Tabela 4.28 – Análise de múltiplas médias entre a resistência à
compressão dos prismas – Etapa com Argamassa Industrial.
.......................................................................................... 175
Tabela 4.29 – Valores experimentais e calculados de resistência média à
compressão, na área líquida.............................................. 180
Tabela 4.30 – Valores experimentais e calculados de resistência média à
compressão, na área líquida.............................................. 182
Tabela 4.31 – Efeito relativo da capacidade de carga dos prismas
preenchidos....................................................................... 184
Tabela 4.32 – Porcentagem estimada dos carregamentos absorvidos pelos
grautes. ............................................................................. 187
Tabela 4.33 – Efeito relativo da capacidade de carga dos prismas
preenchidos....................................................................... 192
Tabela 4.34 – Porcentagem estimada dos carregamentos absorvidos pelos
grautes. ............................................................................. 194
Tabela 5.1 – Vantagens e desvantagens dos modelos discretos e
homogeneizados. .............................................................. 211
Tabela 5.2 – Efeito relativo da capacidade de carga dos prismas
preenchidos ...................................................................... 218
Tabela 5.3 – Características mecânicas lineares dos materiais. ............. 222
Tabela 5.4 – Características mecânicas não lineares dos materiais. ...... 222
LISTA DE SÍMBOLOS
fb – resistência média à compressão do bloco;
fbk – resistência característica do bloco;
fbT – resistência a tração do bloco;
farg – resistência média à compressão da argamassa;
fargk – resistência característica à compressão da argamassa;
fargT - resistência à tração na flexão da argamassa;
fg – resistência média à compressão do graute;
fgk – resistência característica à compressão do graute;
fp – resistência média à compressão do prisma na área bruta (área da
seção de assentamento sem desconto das áreas dos furos);
fb liq – resistência média à compressão do prisma na área líquida (área da
seção de assentamento com desconto das áreas dos furos);
Fp – carga de ruptura do prisma ou força última de ruptura;
Eb – módulo de elasticidade secante do bloco;
Earg – módulo de elasticidade secante da argamassa;
Eg – módulo de elasticidade secante do graute;
Ep – módulo de elasticidade secante do prisma na área bruta;
Ep liq – módulo de elasticidade secante do prisma na área líquida;
νb – coeficiente de Poisson do bloco;
νarg – coeficiente de Poisson da argamassa;
νg – coeficiente de Poisson do graute;
η – fator de eficiência prisma/bloco;
SUMÁRIO
1.
1.1.
1.2.
1.2.1.
1.2.2.
1.3.
1.4.
2.
2.1.
2.1.1.
2.1.2.
2.1.3.
2.1.4.
2.1.5.
2.2.
2.2.1.
2.2.2.
2.2.3.
2.2.4.
2.2.5.
2.2.6.
2.2.7.
2.2.8.
2.2.9.
2.3.
2.4.
3.
3.1.
3.1.1.
3.1.2.
3.1.3.
3.2.
3.3.
3.4.
INTRODUÇÃO ................................................................... 29
JUSTIFICATIVA DO TRABALHO .................................... 30
OBJETIVOS ......................................................................... 32
Objetivo Geral ..................................................................... 32
Objetivos Específicos .......................................................... 32
METODOLOGIA DO TRABALHO .................................... 32
ESTRUTURA DO TRABALHO .......................................... 33
CARACTERÍSTICAS,
ESPECIFICAÇÕES
E
COMPORTAMENTO
SOB
COMPRESSÃO
DA
ALVENARIA ESTRUTURAL .......................................... 35
CARACTERÍSTICAS
E
ESPECIFICAÇÕES
DA
ALVENARIA ESTRUTURAL ............................................ 35
Bloco cerâmico..................................................................... 35
Graute .................................................................................. 40
Argamassa de assentamento............................................... 43
Prismas ................................................................................. 51
Resistência à compressão na alvenaria.............................. 53
FATORES QUE INFLUENCIAM NA RESISTÊNCIA À
COMPRESSÃO DA ALVENARIA ESTRUTURAL .......... 56
Resistência à compressão dos blocos ................................. 57
Resistência à tração dos blocos .......................................... 59
Geometria do bloco ............................................................. 59
Argamassa de assentamento............................................... 62
Graute .................................................................................. 64
Módulo de elasticidade ....................................................... 72
Espessura da junta de assentamento ................................. 76
Tipo de assentamento.......................................................... 77
Absorção de água inicial dos blocos................................... 79
COMPORTAMENTO DA ALVENARIA SUBMETIDA À
COMPRESSÃO .................................................................... 79
CONSIDERAÇÕES DO CAPÍTULO .................................. 88
PROGRAMA EXPERIMENTAL ..................................... 93
MATERIAIS UTILIZADOS ................................................ 96
Agregados ............................................................................ 96
Aglomerantes ..................................................................... 100
Água ................................................................................... 101
BLOCOS CERÂMICOS..................................................... 102
ARGAMASSAS DE ASSENTAMENTO .......................... 106
GRAUTES .......................................................................... 112
3.5.
4.
4.1.
4.2.
4.3.
4.4.
4.5.
4.5.1.
4.5.1.1
4.5.1.2
4.5.2.
4.5.2.1
4.5.2.2
4.5.2.3
4.5.3.
5.
5.1.
5.2.
5.3.
5.3.1.
5.3.2.
5.3.3.
5.3.4.
6.
6.1
6.1.1
6.1.1.1
6.1.1.2
6.1.2
6.1.2.1
PRISMAS ............................................................................117
RESULTADOS E DISCUSSÃO .......................................127
RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA E FÍSICA DOS BLOCOS .............................127
RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA DAS ARGAMASSAS ...................................132
RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA DOS GRAUTES ............................................135
RESUMO DAS PROPRIEDADES MECÂNICAS DOS
COMPONENTES ................................................................137
RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA DOS PRISMAS .............................................142
Resultados dos ensaios da Etapa Referência ...................142
Análise da influência dos componentes na resistência à
compressão dos prismas.......................................................145
Análise da capacidade de carga dos prismas grauteados .....147
Resultados dos ensaios das Etapas com Argamassa Mista e
Argamassa Industrializada ...............................................159
Análise da influência dos componentes na resistência à
compressão dos prismas.......................................................166
Análise da capacidade de carga dos prismas grauteados da
Etapa com Argamassa Mista................................................182
Análise da capacidade de carga dos prismas grauteados das
Etapas com Argamassa Industrializada ...............................190
Análise do modo de ruptura dos prismas ........................197
ANÁLISE NUMÉRICA ....................................................207
NÃO LINEARIDADE DOS MATERIAIS .........................212
SIMULAÇÃO NUMÉRICA ...............................................217
ANÁLISE DOS RESULTADOS DA SIMULAÇÃO .........223
Resultados para o prisma MG6-C ....................................223
Resultados para o prisma MG6-B ....................................227
Resultados para o prisma MG6-A ....................................230
Discussão dos resultados ...................................................234
CONCLUSÕES E RECOMENDAÇÕES FUTURAS ....243
ENSAIO DE CARACTERIZAÇÃO MECÂNICA DOS
PRISMAS ............................................................................243
Etapa Referência .................................................................243
Influência dos componentes na resistência dos prismas .......243
Análise da capacidade de carga dos prismas grauteados ......244
Etapas com Argamassa Mista e Industrializada ..............245
Influência dos componentes na resistência dos prismas .......245
6.1.2.2 Aumento efetivo da capacidade de carga dos prismas das Etapas
com argamassa mista e industrializada ............................... 247
6.2
MODO DE RUPTURA DOS PRISMAS............................ 248
6.3
SIMULAÇÃO DOS PRISMAS .......................................... 250
6.4
RECOMENDAÇÕES PARA TRABALHOS FUTUROS .. 252
REFERÊNCIAS ................................................................................ 253
29
1. INTRODUÇÃO
A alvenaria estrutural pode ser definida como um sistema construtivo
em que paredes atuam simultaneamente como elemento de vedação e
estrutural, podendo ser armada ou não, executada com tijolos ou blocos
cerâmicos, blocos de concreto ou blocos silico-cálcareos. Este sistema
construtivo é o mais antigo em utilização, e vem se modificando ao
longo dos anos de acordo com a evolução tecnológica e industrial,
mediante as necessidades de mercado.
No passado, as obras possuíam estética simplificada e os projetos não
eram arrojados, em consequência das limitações de conhecimentos
técnicos. Não existia estudos ou normalização que estabelecessem
parâmetros para a elaboração de projetos ou na execução dessas obras,
resultando em edificações de custo oneroso e que não exploravam a
potencialidade de seus materiais. A era industrial trouxe mudanças nos
padrões das construções que, aliadas a competitividade de mercado,
exigiu construções mais rápidas e de menor custo.
No Brasil, o início da alvenaria estrutural ocorreu no estado de São
Paulo, no fim da década de 60, na construção de habitações populares
em edifícios com quatro ou cinco pavimentos empregando blocos de
concreto. Mas a má qualidade dos materiais empregados, o uso de
técnicas construtivas inapropriadas e a falta de controle durante a obra
geraram, em alguns empreendimentos, muitas patologias,
comportamento térmico inadequado, etc. Além disso, a ideia de que esse
tipo de sistema construtivo se destinava apenas a construções populares
provocou uma retração no mercado e dificultou as pesquisas no
desenvolvimento e melhorias deste sistema. Neste período aparecem às
primeiras normas técnicas de controle e execução de alvenaria, resultado
do esforço da IBRACON (Instituto Brasileiro do Concreto) em agrupar
os conhecimentos sobre materiais e métodos utilizados na execução de
alvenaria de blocos vazados de concreto (SÁNCHEZ, 1994).
A partir da década de 1980 começaram a ser desenvolvidas pesquisas
em universidades brasileiras, aprofundando os estudos sobre o
comportamento estrutural, influência da mão-de-obra e técnicas
utilizadas para aumentar a produtividade neste tipo de construção.
Também nesse período, os blocos cerâmicos começaram a ser
produzidos.
Segundo Roman (1991), este sistema construtivo apresenta grandes
vantagens, como a economia que resulta quando comparadas com as
estruturas de aço ou concreto, maior rapidez, facilidade de execução e
propriedade para usos com grandes variedades funcionais; o que torna
30
essa técnica viável e de grande potencial econômico a ser explorado
pelas empresas da construção.
Dessa forma a alvenaria estrutural passou a ter maior aceitação nacional,
principalmente quando grandes empresas da construção que visando
obter maior produtividade e redução de custos a adotaram em suas
obras, em virtude da flexibilidade e racionalização de seus sistemas.
Esta preocupação com a redução de custo, produtividade e qualidade do
produto final, tem sido uma constante em todas as empresas atuantes no
setor da construção civil, para se manterem competitivas e atuantes
neste ramo industrial.
A partir deste contexto observa-se o crescente desenvolvimento de
pesquisas na área, evidenciado pelo aumento no número de publicações
científicas. Porém, em virtude à grande variabilidade e condições
especificas do Brasil, a realização de uma quantidade maior de
pesquisas para a caracterização dos materiais e comportamento
mecânico da alvenaria estrutural ainda se faz necessária. Essas
contribuições estabeleceriam parâmetros mais confiáveis para a
elaboração e atualização das normas específicas para alvenaria estrutural
de blocos cerâmicos, ampliando, ainda mais, o seu emprego.
1.1. JUSTIFICATIVA DO TRABALHO
Nos sistemas construtivos em alvenaria estrutural, as paredes
atuam simultaneamente como vedação e como elementos resistentes às
cargas verticais (peso próprio e ocupação) e cargas horizontais (vento).
Quanto à resistência, as paredes devem atuar predominantemente sob
compressão e quando ocorrer o aparecimento de tensões como
consequência de esforços de tração, estas devem ser restringidas a
pontos específicos da estrutura e não apresentar valores elevados
(CORRÊA e RAMALHO, 2003).
Em algumas situações de projeto, em função dos carregamentos e
tensões atuantes, torna-se necessário o aumento da capacidade resistente
das paredes construídas. Tal exigência estrutural pode ser atingida com
o grauteamento destas paredes, que consiste no preenchimento dos seus
vazios por um componente denominado graute. O graute é um concreto
com agregados de pequena dimensão e relativa fluidez que, lançado nos
vazios dos blocos da alvenaria, proporciona o aumento de área da seção
transversal resistente e solidariza estes blocos com eventuais armaduras
posicionadas no seu interior. Desta forma aumenta-se a capacidade
resistente da alvenaria à compressão ou permite-se que as armaduras
31
colocadas combatam tensões de tração que a alvenaria por si só não
resistiria.
Quando necessário, o grauteamento das paredes é realizado logo
após 24 h do assentamento das unidades, conforme prescrito na norma
ABNT NBR 15812-2 (2010). Entretanto, a mesma norma técnica
especifica que o grauteamento pode ser realizado com a própria
argamassa de assentamento, logo após o assentamento das unidades,
desde que a alvenaria não seja armada. Sendo a racionalização
característica de um sistema construtivo em alvenaria estrutural
(PARSEKIAN e FURLAN JUNIOR, 2003), a utilização da argamassa
de assentamento como preenchimento das unidades logo após o
assentamento elimina o uso e controle dos materiais utilizados na
fabricação do graute, aumentando com isso a agilidade e flexibilidade na
execução da obra.
Contudo, nota-se uma carência em pesquisas a cerca do
comportamento das paredes em alvenaria estrutural utilizando-se da
técnica de preenchimento destas paredes com a própria argamassa de
assentamento. Praticamente não há trabalhos sobre o tema, embora o
Grupo de Desenvolvimento de Sistema em Alvenaria da Universidade
Federal de Santa Catarina (GDA), no trabalho realizado por Mendes
(1998), tenha apontado para a potencialidade na utilização desta técnica.
Desta forma, a utilização mais segura desta técnica para aumento
do desempenho estrutural, já permitida por norma, requer pesquisas
acerca da sua influência no comportamento e na qualidade do produto
final construído. Sendo o bom desempenho da alvenaria estrutural
dependente dos materiais empregados neste tipo de sistema construtivo,
melhorar este desempenho está intimamente ligado à busca de materiais
e técnicas que permitam um melhor comportamento em uso do
conjunto. Neste aspecto, a compatibilização e o conhecimento das
características de todos os componentes constituintes da alvenaria
estrutural (bloco, argamassa, graute e armadura) são indispensáveis para
maximizar e aperfeiçoar todo o potencial deste sistema construtivo.
Além dos aspectos técnicos favoráveis, pesquisas visando o
desenvolvimento deste sistema construtivo têm relevância econômica
bastante clara no contexto brasileiro, pois a abundância e a qualidade
das jazidas existentes no país, especialmente na região sul, tornam os
produtos cerâmicos bastante competitivos dentro do setor construtivo.
Assim, o desenvolvimento de pesquisas que aperfeiçoem o uso de
produtos cerâmicos para a alvenaria estrutural potencializa o
desenvolvimento deste setor industrial em constante crescimento.
32
1.2. OBJETIVOS
1.2.1. Objetivo Geral
O objetivo principal deste trabalho é o de investigar o
comportamento estrutural à compressão da alvenaria de blocos
cerâmicos considerando o preenchimento dos furos com a argamassa de
assentamento, substituindo o graute tradicionalmente utilizado, como
componente integrante do sistema construtivo em alvenaria cerâmica
estrutural.
1.2.2. Objetivos Específicos
O presente trabalho tem como objetivos específicos os seguintes
pontos:
- Comparar o comportamento sob compressão uniaxial de
prismas de blocos cerâmicos, quando preenchidos com graute e
argamassa de assentamento.
- Analisar o modo de ruptura dos prismas de blocos cerâmicos
submetidos à compressão uniaxial, quando preenchidos com graute e
argamassa de assentamento.
- Comparar o comportamento sob compressão uniaxial entre os
prismas de blocos cerâmicos, obtido na análise numérica e obtido no
programa experimental.
1.3. METODOLOGIA DO TRABALHO
A fim de atingir os objetivos gerais e específicos, este trabalho
consistiu-se nas seguintes etapas:
a) Apresentação dos conceitos básicos de alvenaria estrutural e
revisão bibliográfica. Na revisão bibliográfica apresentam-se as
principais características (mecânica, física e geométrica) e
especificações nacionais e internacionais dos componentes e elementos
da alvenaria estrutural, o comportamento da alvenaria não grauteada e
grauteada sob compressão, fatores que interferem na sua resistência e o
modo e tipo de ruptura que ocorrem na alvenaria;
b) Na sequência determinou-se a metodologia utilizada no
programa experimental do trabalho. Nesta etapa são apresentados a
caracterização dos materiais e componentes utilizados, os traços em
volume e massa das argamassas de assentamento e grautes, os
procedimentos de moldagem e métodos de ensaios utilizados para os
33
blocos, argamassas, grautes e prismas, bem como os equipamentos
utilizados para os ensaios de resistência à compressão e módulo de
elasticidade.
c) Com o desenvolvimento do programa experimental, realizouse a análise dos resultados obtidos nos ensaios de caracterização
mecânica dos prismas e demais componentes utilizados, com o objetivo
de investigar o comportamento estrutural à compressão da alvenaria de
blocos cerâmicos considerando o preenchimento dos furos com a
argamassa de assentamento.
d) Após a análise dos resultados obtidos com o programa
experimental realizou-se a análise numérica. Nesta etapa apresentam-se
os conceitos, metodologia empregada e os resultados obtidos com a
análise numérica através do método dos elementos finitos. Esta parte do
trabalho tem a finalidade de avaliar o comportamento dos prismas sob
compressão considerando a não linearidade dos materiais, com a
utilização do programa computacional Marc Mentat 2012, completando
a análise realizada com o programa experimental.
e) Por último, são elaboradas as conclusões e sugestões para
pesquisas futuras.
1.4. ESTRUTURA DO TRABALHO
No Capítulo 1 descreve-se a introdução à alvenaria estrutural, os
aspectos históricos, os objetivos deste trabalho e a metodologia
empregada.
No Capítulo 2 apresenta uma revisão bibliográfica acerca do
comportamento da alvenaria estrutural não grauteada e grauteada
submetida à compressão, fatores que interferem na sua resistência, o
modo e o tipo de ruptura que ocorre na alvenaria, assim como
especificações e propriedades físico-mecânicas de seus componentes e
elementos.
O Capítulo 3 apresenta o programa experimental, onde se
estabelece a metodologia de caracterização dos componentes da
alvenaria estrutural, prismas, blocos, argamassa e grautes.
No Capítulo 4, são apresentados e discutidos os resultados
obtidos no programa experimental.
O Capítulo 5 apresenta a análise numérica realizada através do
método dos elementos finitos.
Finalmente, no capítulo 6 são apresentadas as conclusões e
sugestões para pesquisas futuras.
34
35
2. CARACTERÍSTICAS,
ESPECIFICAÇÕES
E
COMPORTAMENTO SOB COMPRESSÃO DA ALVENARIA
ESTRUTURAL
2.1. CARACTERÍSTICAS E ESPECIFICAÇÕES DA ALVENARIA
ESTRUTURAL
Neste item da revisão bibliográfica apresentam-se as principais
características (mecânica, física e geométrica) e especificações nacionais
e internacionais dos componentes e elementos da alvenaria estrutural, de
interesse neste estudo, quais sejam: bloco cerâmico, graute, argamassa
de assentamento e prismas.
2.1.1. Bloco cerâmico
A matéria prima utilizada na confecção dos blocos cerâmicos é a
argila. Todas as propriedades físicas e mecânicas do bloco são afetadas
pela sua composição e pelo processo de fabricação. Segundo Rizzatti
(2003), a argila para a fabricação de blocos deve ter plasticidade quando
misturada com água, de maneira que possa ser moldada, deve ter
suficiente resistência à tração para manter o formato depois de moldada
e, ainda, deve ser capaz de fundir as partículas quando queimada a altas
temperaturas. Ainda segundo o autor, a plasticidade, a água de
moldagem e o comportamento na secagem e na queima dependem da
granulometria e dos diversos minerais presentes. Para Gomes (1983), a
produção de blocos cerâmicos deve reunir a experiência estrutural e a
tecnologia das argilas, de forma que estes componentes apresentem
resistência e durabilidade necessária e proporcionem o conforto
ambiental desejado.
As normas ABNT NBR 15270 - Partes 1 e 2 (2005), classificam
os blocos cerâmicos basicamente em dois grupos:
a) Bloco de vedação: componente da alvenaria de vedação que
possui furos prismáticos perpendiculares às faces que os
contêm. O bloco cerâmico para vedação é produzido para ser
assentado especificamente com furos na horizontal, mas
também pode ser produzido para utilização com furos na
vertical;
b) Bloco estrutural: componente da alvenaria estrutural que
possui furos prismáticos perpendiculares às faces que os
contêm, produzidos para serem assentados com furos na
36
vertical. Estes ainda podem ser classificados em bloco
estrutural de paredes vazadas, de paredes maciças e
perfurados.
Para a norma EN 1996-1-1 (2005), as unidades de alvenaria são
classificadas conforme os tipos e os grupos correspondentes, de acordo
com a porcentagem de vazios. As unidades com porcentagens de vazios
menores que 25% são considerados do Grupo 1 (tijolos cerâmicos,
tijolos vazados e pedras de origem natural e artificial). Para os Grupos 2
e 3 a porcentagem de vazio na vertical fica entre os 25% e os 70%. No
Grupo 4 a unidade de alvenaria do possui furo na horizontal, com
porcentagem de vazio menor que 70%. Essa classificação ainda
estabelece limites geométricos para a disposição de furos e espessuras
mínimas de parede, sendo uma referência para a produção de unidades
para fins estruturais.
A norma ABNT NBR 15270-2 (2005), para blocos estruturais,
também estabelece requisitos dimensionais para a utilização destes
componentes, conforme se observa na Tabela 2.1.
Tabela 2.1 - Tolerâncias dimensionais para blocos cerâmicos.
Grandezas Controladas
Tolerância (mm)
Largura (L)
Altura (H)
± 3*
Comprimento (C)
Planeza das faces (F)
<3
Desvio em relação ao esquadro (D)
<3
Nota: *Tolerâncias dimensionais em relação à média das dimensões efetivas.
Fonte: ABNT NBR 1527-2 (2005).
Para a espessura das paredes externas e septos, a norma traz as
seguintes exigências de valores mínimos para blocos cerâmicos
estruturais de paredes vazadas e com paredes maciças, conforme a
Figura 2.1.
37
Figura 2.1 – Valores de espessuras mínimas para as paredes externas e septos
dos blocos cerâmicos estruturais (a) de paredes vazadas e (b) com paredes
maciças, em milímetros.
(a)
(b)
Fonte: ABNT NBR 1527-2 (2005).
Quanto às características físicas e mecânicas, a mesma norma
determina alguns valores para índice de absorção de água (AA) e
resistência característica à compressão (fbk), indicados na Tabela 2.2.
Tabela 2.2 – Características mecânicas e físicas para blocos cerâmicos
estruturais.
Resistência característica à compressão,
na área bruta – fbk (MPa)
Índice de absorção de
água - AA (%)
> 3,0
8 < AA < 22
Fonte: ABNT NBR 1527-2 (2005).
A mesma norma também estabelece que o bloco cerâmico
estrutural não deve apresentar defeitos sistemáticos, tais como quebras,
superfícies irregulares ou deformações que impeçam seu emprego na
função especificada.
Para o cálculo da resistência característica à compressão dos
blocos, na área bruta, a ABNT NBR 15270-2 (2005) especifica o
seguinte procedimento:
38
1) Inicialmente, a resistência característica é estimada através da
Equação 2.1.
fbk,est = 2
fb 1
+ f b 2 + ⬚…
fb i-1
i-1
(2.1)
- fbi
Onde:
fbk,est = resistência característica estimada da amostra, em MPa;
fb(1), fb(2),…, fbi = valores de resistência à compressão individual
dos corpos-de-prova da amostra, ordenados crescentemente;
i = n/2, se n for par;
i = (n -1)/2, se n for ímpar;
n = quantidade de blocos da amostra.
2) Após o cálculo do fbk,est deve-se proceder à seguinte análise:
a) se o valor do fbk,est ≥ fbm (média da resistência à compressão de
todos os corpos-de-prova da amostra), adota-se fbm como a resistência
característica do lote (fbk);
b) se o valor do fbk,est < Ø x fb(1) (menor valor da resistência à
compressão de todos os corpos-de-prova da amostra), adota-se a
resistência característica à compressão (fbk) determinada pela expressão
Ø x fb(1), estando os valores de Ø indicados na Tabela 2.3.
c) caso o valor calculado de fbk,est esteja entre os limites
mencionados acima (Ø x fb(1) e fbm ), adota-se este valor como a
resistência característica à compressão (fbk).
Tabela 2.3 - Valores de Ø em função da quantidade de blocos.
Nº de
Blocos
6
7
8
9
10
11
12
13
14
15
16
≥
18
Ø
0,89
0,91
0,93
0,94
0,96
0,97
0,98
0,99
1,00
1,01
1,02
1,04
Nota: Recomenda-se adotar n ≥ 13.
Fonte: ABNT NBR 1527-2 (2005).
Ainda em relação ao ensaio para a determinação da resistência à
compressão dos blocos cerâmicos estruturais, a velocidade de
carregamento aplicada, segundo a ABNT NBR 15270-2, deve ser de
0,05 ± 0,01 MPa/s.
Outra característica mecânica importante do bloco é sua
resistência à tração. Embora a alvenaria atue predominantemente sob
esforços de compressão, dependendo da rigidez dos seus materiais
39
constituintes, podem surgir tensões de tração nos blocos, tornando
importante a determinação da sua resistência à tração. Conforme a
norma ASTM C 1006 (1984), a determinação desta propriedade pode
ser realizada de forma indireta por meio de ensaio de compressão,
similar ao ensaio de compressão diametral realizado em corpos-de-prova
de concreto. No ensaio, para a aplicação da carga de compressão, são
posicionadas barras de aço de seção transversal cilíndrica com diâmetro
entre 1/12 a 1/8 da altura da amostra e com comprimento maior que a
largura do bloco, conforme apresentado na Figura 2.2.
Figura 2.2 - Esquema de ensaio de resistência à tração indireta do bloco.
F
H
L
Fonte: adaptado de Leão (2008).
Conforme a norma, para o cálculo da resistência à tração dos
blocos por compressão diametral utiliza-se a Equação 2.2.
T=
2.F
π.L.H
(2.2)
Onde:
T = resistência à tração indireta por compressão, em MPa;
F = carga máxima aplicada, em Newton;
L = largura do bloco, para área bruta, ou soma das espessuras das
paredes do bloco, quando considerada a área líquida, em milímetros;
H = altura do bloco, em milímetros.
Ainda segundo a norma, a velocidade de carregamento aplicada
para o ensaio não deve exceder 0,15 kN/s.
Entretanto de acordo com Chema e Klingner (1986), a resistência
à tração dos blocos pode ser determinada mediante a seguinte equação:
40
T = 0,41 x (fb)1/2
(2.3)
Onde:
T = resistência à tração do bloco, em MPa;
fb = resistência à compressão do bloco na área bruta, em MPa;
Entretanto, o ensaio preconizado pela ASTM C 1006 (1984) tem
sido o método mais utilizado por pesquisadores para a determinação da
resistência à tração dos blocos.
Quanto à determinação do módulo de elasticidade para blocos
cerâmicos não existem ensaios normalizados com esta finalidade. Para
blocos de concreto, tanto o CEB-FIP Mode Code (1990) como o ACI –
Buildin Code 318 (1999) especificam métodos e equações para o cálculo
do módulo de elasticidade dos blocos. Entretanto para blocos cerâmicos,
a ABNT NBR 15270-3 (2005) recomenda a utilização da ABNT NBR
8522 (2008) para a determinação do módulo de deformação longitudinal
desse componente.
2.1.2. Graute
A norma ABNT NBR 15812-1 (2010) define graute como o
componente utilizado no preenchimento dos espaços vazios dos blocos
cerâmicos, com a finalidade de solidarizar armaduras à alvenaria ou
aumentar sua capacidade resistente. Ainda segundo a norma, o graute
deve ter características no estado fresco que garantam o completo
preenchimento dos espaços vazios dos blocos e não deve apresentar
retração que provoque o descolamento do graute das paredes dos blocos.
Segundo Gomes (1983), o graute desempenha várias funções,
entre as quais se destacam:
- para alvenaria armada, permitir o posicionamento correto das
armaduras nos furos e transmissão de esforço entre o graute e o bloco;
- absorver parcela dos esforços verticais;
- aumentar a rigidez global do conjunto, especialmente em
relação às cargas horizontais.
Basicamente, o graute é utilizado como reforço estrutural em
paredes de alvenaria, aumentando sua capacidade resistente, absorvendo
uma parcela dos esforços verticais as quais são submetidas,
proporcionando maior estabilidade e rigidez ao conjunto, além de
solidarizar a armadura à estrutura, permitindo seu posicionamento.
41
Tradicionalmente, o graute utilizado tem as mesmas
características que o concreto e, de acordo com a norma ABNT NBR
15812-2 (2010), deve ser utilizado no mínimo 24 h após a execução da
alvenaria. Entretanto, conforme a ABNT NBR 15812-2 (2010), quando
não usado em alvenaria armada, o graute pode ser substituído pela
argamassa de assentamento das unidades logo após a execução da
alvenaria, desde que os ensaios de prisma apresentem os resultados
especificados pelo projetista.
Segundo Cunha (2001), o graute consiste em um microconcreto,
formado de cimento, água, agregado miúdo e agregados graúdos de
pequenas dimensões (até 9,5 mm) com alta fluidez. Essa fluidez é
fundamental para que o graute possa preencher os furos dos blocos sem
sofrer segregação. Além de sua alta fluidez, o graute deve apresentar
boa trabalhabilidade e boa capacidade de reter água, evitando perdas
excessivas de água para o bloco.
A trabalhabilidade consiste em uma das propriedades relevantes
para a utilização do graute, que está ligada a outras propriedades como a
consistência e plasticidade. Com isto, um dos parâmetros usados para se
medir a trabalhabilidade do graute é a sua consistência, que é
determinada através do ensaio de abatimento do tronco de cone.
Entretanto, a norma para alvenaria de blocos cerâmicos, ABNT NBR
15812-2 (2010), não indica valores de abatimento para aplicação do
graute. A norma somente recomenda que a trabalhabilidade deve ser
compatível com o método de adensamento utilizado e adequada para
preencher todos os vazios dos blocos sem que haja segregação. Em
alvenaria de blocos de concreto, de acordo com a antiga ABNT NBR
8798 (1985), o abatimento indicado deveria ser de 200 ± 30 mm.
A norma britânica BS 5628: Part 2 (1985) especifica valores de
abatimento compreendidos entre 75 a 175 mm para a utilização do
graute. Mas para Oliveira (1986), o graute deve apresentar abatimento
de 200 mm para blocos com baixa absorção e 250 mm para blocos com
alta absorção. Para blocos cerâmicos, valores abaixo de 8% consideramse baixa sucção e valores acima de 22%, considera-se alta sucção
(ABNT NBR 1570-2, 2005).
Outro fator de grande importância é a resistência à compressão do
graute para a resistência final da alvenaria. Segundo a ABNT NBR
15812-2 (2010), o graute deve apresentar resistência à compressão de
modo que a resistência do prisma grauteado atinja a especificada pelo
projetista. Entretanto, não especifica valores mínimos ou máximos de
resistência à compressão de utilização para o graute. Na antiga ABNT
NBR 8798 (1985), para alvenaria de blocos de concreto, o graute
42
deveria apresentar valores de resistência à compressão superiores a 14
MPa. Para a antiga norma ABNT NBR 10837 (1989), a resistência
característica à compressão do graute (fgk) deveria ser igual ou maior
que duas vezes a resistência característica à compressão do bloco (fbk).
Ramalho e Corrêa (2003) comentam que essa recomendação é fácil de
entender quando se recorda que a resistência característica do bloco é
referida à área bruta e que o índice de vazios para os blocos é
usualmente 50%. Para os autores, seria mais claro se a norma
mencionasse que a resistência característica do graute fosse no mínimo o
mesmo valor da resistência característica do bloco em relação à área
liquida.
A determinação da resistência à compressão do graute, quando o
graute apresenta as mesmas características que o concreto, segue a
ABNT NBR 5739 (2007) – Concreto: Ensaio de corpos-de-prova
cilíndricos.
Para a determinação do módulo de elasticidade do graute,
conforme recomendação da ABNT NBR 15270-3 (2005) utiliza-se a
mesma norma para concreto, a ABNT NBR 8522 (2008) – Concreto:
Determinação do Módulo Estático de Elasticidade à Compressão. A
determinação do módulo de deformação do graute é realizada, portanto,
através dos dados extraídos do diagrama tensão x deformação traçado
para os corpos-de-prova ensaiados.
Para satisfazer as exigências de propriedades mecânicas e
trabalhabilidade estabelecidas pelo projetista, de acordo com a obra a ser
executada, a dosagem do traço do graute pode ser realizada
experimentalmente por qualquer método desenvolvido para dosagem de
concreto convencional. A norma ABNT NBR 15912-2 (2010) somente
determina que a dosagem deve levar em consideração a absorção dos
blocos e das juntas de argamassa, que pode proporcionar uma redução
na relação água/cimento.
Entretanto, a norma britânica BS 5628: Part 2 (1985), recomenda
o traço em volume para a dosagem do graute, nas seguintes proporções
apresentadas na Tabela 2.4.
Tabela 2.4 – Traços dos grautes em volume conforme BS 5628: Part 2.
Partes em volume
Cimento
Cal
Areia
Agregado Graúdo
1
0 a 0,25
3
2
Fonte: BS 5628: Part 2 (1985).
43
A norma britânica também recomenda para o diâmetro máximo
do agregado graúdo o valor de 10 mm.
A norma americana ASTM C 476-83 (1987) também faz algumas
recomendações para os traços em volume dos grautes, conforme
apresentado na Tabela 2.5.
Tabela 2.5 – Traços dos grautes em volume conforme ASTM C 476-83.
Partes em volume
Tipo de
Graute
Cimento
Portland
Cal hidratada ou pasta
de cal
Graute
1
0 a 1/10
Fino
Graute
1
0 a 1/10
Grosso
Fonte: ASTM C 476-83 (1987).
Agregados secos
Finos
Graúdos
2¼a3
-
2¼a3
1a2
Quanto às exigências granulométricas dos agregados utilizados na
composição dos traços dos grautes, a ABNT NBR 15812-2 (2010)
especifica somente que os agregados devem ter dimensão inferior a 1/3
da menor dimensão dos espaços vazios a serem preenchidos pelo graute.
Entretanto, quando o graute tem as mesmas características que um
concreto, as exigências granulométricas dos agregados baseiam-se nas
especificações estabelecidas pela norma ABNT NBR 7211 (2009).
2.1.3. Argamassa de assentamento
A argamassa de assentamento é o componente utilizado na
ligação entre os blocos, garantindo distribuição uniforme de esforços
(ABNT NBR 15812-1, 2010).
É composta por um ou mais aglomerantes (cimento Portland e
cal), agregados inertes (areia), água ou outra adição cuja finalidade é
aumentar a retenção da água durante a hidratação e, consequentemente,
melhorar a trabalhabilidade da mistura; podendo ser dosada em obra ou
em instalação própria (argamassa industrializada).
Para Sabbatini (1984) e Gallegos (1989), o grande interesse na
argamassa de assentamento de alvenaria estrutural está relacionado à
trabalhabilidade, consistência, aderência e deformabilidade. A
resistência à compressão da argamassa assume aspecto secundário,
44
exigindo-se que a argamassa resista aos esforços a que for submetida
sem comprometer seu desempenho quando parte do conjunto.
Ainda segundo Roman et al. (1999), uma grande resistência para
a argamassa não é necessariamente sinônimo de uma melhor solução
estrutural. A argamassa deve ser resistente o suficiente para suportar os
esforços que a parede está submetida. Os autores afirmam que a
resistência da argamassa não deve exceder a resistência dos blocos da
parede, de maneira que as fissuras que venham a ocorrer em razão de
expansões térmicas ou outros movimentos da parede ocorram na junta.
Na norma britânica BS 5628-3 (1985), as principais funções da
argamassa de assentamento em uma parede de alvenaria são:
- unir as unidades e ajudá-las a resistir aos esforços normais e
laterais;
- distribuir uniformemente as cargas atuantes na parede por toda a
área resistente das unidades, evitando assim concentrações de tensões
por causa de imperfeições geométricas;
- absorver as deformações naturais a que a alvenaria estiver
sujeita;
- selar as juntas contra a penetração de água da chuva.
Para assegurar o desempenho das argamassas, algumas
propriedades no estado fresco devem ser levadas em consideração além
da sua resistência à compressão simples. Conforme Camarini e Ishikawa
(2004), de acordo com características e solicitações exigidas em obra, às
seguintes propriedades das argamassas no estado fresco devem ser
consideradas: trabalhabilidade, plasticidade, coesão, retenção de água e
teor de ar incorporado. Neste estudo, no intuito de explicar estas
propriedades, os autores fazem um resumo das principais observações
relatadas por alguns pesquisadores, conforme pode ser observado na
sequência:
a) Trabalhabilidade: consiste na síntese de diversas propriedades
reológicas da argamassa como a consistência, plasticidade, retenção e
exsudação de água, coesão interna, adesão inicial, massa específica e
retenção da consistência (RILEM, 1982; CAVANI, ANTUNES e
JOHN, 1997). A consistência pode ser associada à medida de
trabalhabilidade. A trabalhabilidade é entendida, subjetivamente, como
facilidade de manuseio e aplicação. Em termos de elementos que
compõem uma argamassa, pode-se dizer que a trabalhabilidade melhora
quando o módulo de finura do agregado diminui, mantendo-se a
continuidade da granulometria, e piora quando se tem agregado de grãos
angulosos. Em relação aos aglomerantes, a adição de cal melhora a
trabalhabilidade, sendo necessário verificar a sua influência em outras
45
propriedades. Quanto aos cimentos, as diferentes classes não influem,
significativamente, na trabalhabilidade. Entretanto, cimentos mais finos
podem produzir argamassas mais trabalháveis e com maior retenção de
água. A plasticidade e a trabalhabilidade são termos subjetivos, que só
podem ser avaliados por quem manuseia e aplica a argamassa, sendo a
consistência uma medida de avaliar essas duas propriedades em
conjunto (CINCOTTO; SILVA e CASCUDO 1995).
b) Plasticidade: esta propriedade consiste em que a argamassa
tende a manter a sua deformação sem ruptura, após a redução do esforço
que a originou (RILEM, 1982). A plasticidade é influenciada pelo teor
de ar incorporado, natureza e teor de aglomerante e da intensidade da
energia de mistura. A plasticidade está ligada à coesão interna da
mistura, ou seja, às forças de tensão superficial dos materiais e da água
de amassamento. No estado plástico, a argamassa deve apresentar-se
trabalhável, isto é, no manuseio da argamassa com a colher de pedreiro
ela deve se manter coesa, e quando da aplicação sobre a unidade da
alvenaria, a argamassa deve fluir sem aderir na colher de pedreiro, sendo
de fácil espalhamento sobre a unidade (SABBATINI, 1986).
c) Coesão: a coesão da argamassa é caracterizada pelas forças de
atração física existentes entre as partículas sólidas inertes e a pasta de
aglomerante. A cal atua positivamente na coesão interna da argamassa,
influindo na melhoria das propriedades de consistência e
trabalhabilidade (CINCOTTO; SILVA e CASCUDO 1995). A coesão é
influenciada pelo teor de finos, tanto do aglomerante como do agregado
miúdo (RAGO e CINCOTTO, 1997).
d) Retenção de água: a retenção de água é a propriedade da
argamassa em fixar a água no meio da mistura, quando colocada em
contato com bloco de alta sucção (SABBATINI, 1986). Uma das
características da cal é a capacidade de retenção de água, e esta
característica também é adquirida pela argamassa (CARASEK,
CASCUDO e SCARTEZINI, 2001). As argamassas devem apresentar a
propriedade de retenção de água na mistura para que mantenha a
trabalhabilidade requerida durante a sua aplicação, minimizando, desta
forma, a exsudação. Uma argamassa deve possuir capacidade de reter
água em seu meio, molhando a superfície dos grãos do agregado e do
aglomerante. Portanto, a capacidade de retenção de água da argamassa
está ligada à área específica de seus constituintes. A cal, além de ser um
aglomerante, possui capacidade de adsorção e área específica elevada, e
assim cumpre também a função de reter água na mistura
(GUIMARÃES, 2002). A cal, pelas suas características físicas,
apresenta boas condições de retenção de água, em virtude da grande
46
capacidade de adsorção de seus cristais, adsorvendo até 100% do seu
volume (SABBATINI, 1986). É prática usual, em obra, a mistura da
pasta de cal com areia, em proporção definida, para maturação da cal,
isto é, para a hidratação dos óxidos não hidratados possivelmente
existentes na cal hidratada. Esse procedimento melhora a capacidade de
retenção da água na argamassa, em relação à adição da cal em pó na
mistura, para aplicação de imediato. A cal dolomítica apresenta
resultados melhores de retenção de água em relação à cal cálcica, para
mesmo traço e trabalhabilidade. O teor de cal na mistura também influi
na capacidade de retenção de água na argamassa. Para tal, o teor de cal
na mistura deve ser, no mínimo, na mesma proporção do cimento. Com
relação ao traço, aumentando-se a relação agregado/aglomerante e
mantendo a relação cal/cimento fixa, a retenção de água decresce
(CINCOTTO; SILVA e CASCUDO, 1995).
e) Teor de ar incorporado: o teor de ar incorporado influi na
trabalhabilidade das argamassas e concretos. Segundo Yoshida e Barros
(1995), o ar incorporado serve de lubrificante entre os grãos sólidos da
argamassa, melhorando a sua trabalhabilidade e capacidade de retenção
de água. Entretanto, quanto maior o teor de ar incorporado, maior o
volume de vazios, o que implica uma maior porosidade e, por
conseguinte, uma diminuição da resistência à compressão da argamassa.
A ABNT NBR 13281 (2005) especifica alguns valores quanto ao
desempenho mecânico e reológico das argamassas, classificando-as em
função destes valores (Tabela 2.6). Entretanto, a mesma norma não
especifica aplicações ou restrições para cada uma das classes de
argamassas em função das propriedades que apresentam. A norma
ABNT NBR 15812-1 (2010) especifica que argamassas de
assentamento, quando utilizadas em alvenaria estrutural de blocos
cerâmicos, devem apresentar resistência à compressão com valor
mínimo de 1,5 MPa e máximo limitado a 70% da resistência
característica à compressão do bloco (fbk), referida na área liquida.
Quanto à trabalhabilidade, a norma ABNT NBR 8798 (1985) indica o
valor de 230 ± 10 mm para a consistência das argamassas de
assentamento, quando utilizadas em alvenaria estrutural de blocos
vazados de concreto.
47
Tabela 2.6 - Exigências mecânicas e reológicas para argamassas.
Características
Estado
Fresco
Identificação1)
Limites
Método
Normal
Alta
≥ 80 e ≤ 90
> 90
NBR
13277
Capacidade de
retenção de água
(%)
a
<8
b
≥ 8 e ≤ 18
c
> 18
I
≥ 0,1 e < 4,0
Resistência à
Estado
compressão aos
II
≥ 4,0 e ≤ 8,0
Endurecido
28 dias (MPa)
III
> 8,0
1)
Exemplo de identificação de argamassa: I-Normal-a.
Fonte: ABNT NBR 13281 (2005).
NBR
13278
Teor de ar
incorporado (%)
NBR
13279
A norma americana ASTM C-270-86b (1987), entretanto,
especifica o uso das argamassas de assentamento para alvenaria quanto
ao traço e propriedades mecânicas e reológicas, conforme Tabela 2.7.
Enquanto que a norma britânica BS 5628-1 (1992) determina a produção
e o uso das argamassas de assentamento para a alvenaria estrutural tendo
por referência os requisitos estruturais e as características dos
componentes escolhidos para a execução das alvenarias, conforme
apresentado na Tabela 2.8.
Tabela 2.7 - Especificações dos traços e propriedades das argamassas.
Traço em Volume
Tipo de
Argamassa
Cim.
Cal
Areia
M
1
0,25
S
1
0,25 a
0,50
N
1
0,50 a
1,25
O
1
1,25 a
2,25
De 2,25
a3
vezes a
soma
dos
volumes
de
aglomerantes
Resistência
média à
compressão
28 dias (MPa)
Retenção
de água
(%)
Ar
incorporado
(%)
17,2
75
12
12,4
75
12
5,2
75
14*
2,4
75
14*
Somente para argamassas de laboratório. * Quando existir armadura incorporada à junta de
argamassas, a quantidade de ar incorporado não deve ser maior que 12 %.
Fonte: ASTM C 270-86b (1987).
48
Tabela 2.8 - Especificações dos traços e propriedades das argamassas.
Traço da argamassa (em volume)
Ar incorporado na
mistura
Aumenta a capacidade de
acomodar deformações.
Aumenta a resistência à
compressão e durabilidade.
Classe
Cim.:
cal :
areia
Resistência média à
compressão 28 dias
(MPa)
Cimento de
alvenaria:
areia
Cim.:
areia c/
plastificante
Ensaios
em
laboratório
Ensaios
em obra
(i)
1:0 até
0,25:3
-
-
16,0
11,0
(ii)
1:0,5:4
até 4,5
1:2,5 até 3,5
1:3 até
4
6,5
4,5
(iii)
1:1:5 até
6
1:4 até 5
1:5 até
6
3,6
2,5
(iv)
1:2:8 até
9
1:5,5 até 6,5
1:7 até
8
1,5
1,0
Aumenta a resistência ao ataque do
frio durante a construção.
Aumenta a resistência e
consequentemente a resistência à
penetração da chuva.
Fonte: (BS 5628-1, 1992)
A norma brasileira ABNT NBR 13281 (2001) também não
determina limites granulométricos de utilização para agregados miúdos
para as argamassas. A distribuição granulometria do agregado miúdo
utilizado na fabricação de argamassas pode influenciar suas
propriedades no estado fresco. Desta forma, o estabelecimento de
exigências ou limites granulométricos é de fundamental importância
para a especificação de argamassas adequadas para o uso em alvenaria
estrutural (MOHAMAD, 2007).
No Brasil existem apenas especificações granulométricas para
agregados miúdos quando estes são utilizados para concretos, conforme
a norma ABNT NBR 7211 (2009) - Agregados para concreto.
Entretanto as normas BS 1200 (1976) e ASTM C-144 (1987)
49
especificam limites de utilização adequados para argamassas de
assentamento de alvenaria, conforme pode ser observado na Tabela 2.9.
Tabela 2.9 - Limites da composição granulométrica do agregado miúdo para
argamassas de assentamento.
Peneira
(abertura
em mm)
4,75
2,36
1,20
0,60
0,30
0,15
Porcentagem Retida
BS 1200 (1976)
Limite
Limite
Inferior
Superior
0
0
0
10
0
30
20
60
60
95
90
100
Porcentagem Retida
ASTM C-144 (1987)
Limite
Limite
Inferior
Superior
0
0
0
5
0
30
25
60
65
90
85
98
Fonte: BS 1200 (1976) e ASTM C-144 (1987).
Quanto à determinação das propriedades mecânicas das
argamassas, especificamente para a determinação dos valores de
resistência à compressão e tração na flexão, são utilizados os ensaios de
caracterização conforme a ABNT NBR 13279 (2005) para corpos-deprova prismáticos de dimensões (4x4x16) cm. A resistência à
compressão é calculada conforme equação 2.4.
Rc =
Fc
1600
(2.4)
Onde:
Rc = resistência à compressão, em megapascals;
Fc = carga máxima aplicada, em newton.
A velocidade de carregamento utilizada para este ensaio deve ser
de 500 ± 50 N/s, até a ruptura do corpo-de-prova.
Para a o cálculo da resistência à tração na flexão, segundo a
mesma norma, utiliza-se a equação 2.5.
Rf =
1,5.L. Fc
403
(2.5)
50
Onde:
Rf = resistência à tração na flexão, em Megapascals;
Fc = carga aplicada verticalmente no centro do corpo-de-prova
prismático, em Newton.
L = distância entre os suportes, em milímetros.
Quanto à determinação do módulo de elasticidade das
argamassas, a norma ABNT NBR 15270-3 (2005) recomenda a mesma
metodologia utilizada pela ABNT NBR 8522 (2008), para concreto, na
qual o modulo é determinado através do gráfico tensão-deformação,
entre os pontos com 0,5 MPa e 30% da carga de ruptura.
Para Cheema e Klingner (1986), o módulo de elasticidade
tangente (Etg) e o módulo de elasticidade secante (Esec), respectivamente
obtidos para níveis de tensão de 30% e 60% da resistência à compressão
da argamassa (fag), podem ser estimados através das equações 2.6 e 2.7.
Etg = 1000. farg
(2.6)
Esec = 500. farg
(2.7)
No mesmo trabalho, os valores encontrados para o coeficiente de
Poisson foram de 0,20 na fase inicial de deformação e 0,50 na tensão de
esmagamento.
Khalaf et al. (1992) apud Mohamad (2007), realizaram estudos
de caracterização das argamassas de assentamento, obtendo as
propriedades mecânicas para três traços diferentes, em volume. Os
resultados de Khalaf et al. (1992) não mostraram uma boa aproximação
quando comparados com a estimativa do módulo de elasticidade das
equações 2.6 e 2.7 proposta por Cheema e Klingner (1986), tanto para o
módulo tangente como para o secante. As equações que melhor
representaram os resultados experimentais da Tabela 2.10, foram Etg =
600. farg e Esec = 340.farg, para os módulos de elasticidade tangente e
secante, respectivamente.
51
Tabela 2.10- Propriedades mecânicas das argamassas obtidas no estudo de
Khalaf et al..
Etg (MPa)
Traço
(em
volume)
fag
(MPa)
1:1:6
1:0,5:4,5
Esec * (MPa)
Khalaf
et al.
1000.farg
Khalaf
et al.
500.farg
8,0
5603
8000
3696
4000
14,6
10250
14600
5000
7300
Coeficiente de
Poisson
Tesões
Tensões
finais
iniciais
**
0,26
0,40
0,22
0,35
1:0,25:3
25,0
14119
25000
8140
12500
0,18
0,25
Nota: * O módulo de elasticidade secante foi determinado a 2/3 da resistência à
compressão do corpo de prova. ** O coeficiente de Poisson para tensões finais é aquele
medido quando a argamassa está próximo da tensão de ruptura.
Fonte: Khalaf et al. (1992).
2.1.4. Prismas
Prismas de alvenaria são simulações mais simples e econômicas
para a verificação das propriedades mecânicas de uma parede de
alvenaria estrutural. Ensaios em paredes em escala natural seriam ideais,
porém são muitas vezes técnica e economicamente inviáveis
comparados com ensaios utilizando primas (MENDES, 1998). Para
Silva Junior (2007), os prismas de alvenaria são corpos-de-prova usados
para prever as propriedades básicas dos elementos a serem empregados
efetivamente em uma construção executada em alvenaria estrutural.
Os prismas podem ter formas, tamanhos e modos de
assentamento diferentes (Figura 2.3). Os prismas são compostos por
dois ou mais blocos estruturais, assentados com argamassa na superfície
total ou apenas na face lateral da seção transversal dos blocos. E
conforme solicitação de projeto, os prismas podem ser grauteados ou
não (GROHMANN, 2006).
52
Figura 2.3 - Modelos de prismas utilizados experimentalmente.
Fonte: Grohmann (2006).
Segundo Drysdale et al. (1994), os prismas tem geralmente uma
unidade de largura, uma unidade de comprimento e altura variando entre
1,5 e 5 vezes a espessura. Na maioria das vezes são construídos com
junta a prumo, mas podem ter junta amarrada, que representam melhor
as condições da obra.
A norma brasileira ABNT NBR 15812-2 (2010), prescreve a
utilização de prismas de 2 blocos de altura e argamassamento total na
face de assentamento, com juntas de assentamento com espessura de 10
± 3 mm. Ainda segundo a norma, para prismas grauteados, o
grauteamento deve ser realizado após 24 ± 2 h após o assentamento dos
prismas. Entretanto, quando utilizada a própria argamassa de
assentamento em substituição ao graute, o preenchimento dos prismas
pode ser executado logo após seu assentamento.
A norma americana ASTM E 447-84 (1987) recomenda que os
prismas possuam três blocos assentados a prumo, com duas juntas de
argamassa. Para Page (1991), Colville (1991), La Rovere e Rodrigues
(1997), Rizzati (2003), os prismas devem ser os mais representativos
possíveis das paredes de alvenaria para a verificação de suas
propriedades mecânicas. Os autores afirmam que ensaios em prismas
devem ter pelo menos três unidades para representar com melhor
eficácia a parede e minimizar o confinamento imposto pelos pratos da
prensa. Pois nestes prismas, o bloco central, geralmente livre do efeito
de confinamento dos pratos da prensa, representa melhor o tipo de
ruptura da alvenaria.
Quanto ao comportamento mecânico, os prismas, assim como as
paredes, apresentam comportamento mecânico diferente da unidade
(bloco). Isso ocorre principalmente a presença da junta horizontal de
53
argamassa, que é mais deformável que o bloco. Ao ser comprimida
axialmente, a parede tende a se deformar lateralmente, devido ao efeito
de Poisson, e a argamassa, por ter em geral módulo de elasticidade
menor do que a do bloco tende a ter maior deformação. No entanto, por
causa da aderência entre os blocos e a argamassa, esta deformação é
impedida, surgindo tensões laterais de tração no bloco e de compressão
na argamassa (LA ROVERE, 2001 apud MATA, 2006).
Quanto à representatividade dos prismas como corpo-de-prova
das paredes de alvenaria, tomando-se um amplo conjunto de ensaios já
realizados no Brasil, verifica-se que a resistência das paredes equivale
em torno de 70 % da resistência dos prismas, tanto para blocos de
concreto como para blocos cerâmicos (RAMALHO e CORRÊA, 2003).
Este comportamento está de acordo com a norma ABNT NBR 15812-1
(2010). Segundo a norma, na falta de ensaios de resistência a
compressão de paredes, a resistência característica à compressão da
alvenaria pode ser estimada como 70 % da resistência característica de
compressão simples de prismas.
2.1.5. Resistência à compressão na alvenaria
A resistência a compressão é, obviamente, o parâmetro de
resistência mais importante para a alvenaria estrutural, pois suas paredes
atuam basicamente sob compressão. Desta forma, muitos trabalhos e
normas foram desenvolvidos com o objetivo de quantificá-la utilizandose principalmente de prismas ou pequenas paredes, uma vez que ensaios
com paredes em escala real são difíceis de serem executados.
De acordo com a norma ABNT NBR 15812-2 (2010), o valor da
resistência à compressão característica dos elementos da alvenaria pode
ser calculado através da seguinte equação:
fek,est = 2
fe 1
+ fe 2 + ⬚…
i-1
fe i-1
- fei
(2.8)
Onde:
fek,est = resistência característica estimada da amostra, em MPa;
fb(1), fb(2),…, fbi = valores de resistência à compressão individual
dos corpos-de-prova da amostra, ordenados crescentemente;
fem = média de todos os resultados da amostra;
n = número de corpos-de-prova da amostra;
i = n/2, se n for par;
i = (n – 1)/2, se n for ímpar.
54
O valor de fek não deve ser superior a 0,85 x fem e nem inferior a
Ø x fe(1), sendo o valor de Ø indicado na Tabela 2.11.
Tabela 2.11 – Valores de Ø em função da quantidade de elementos da alvenaria.
Nº de
elementos
3
4
5
6
7
8
9
10
11
12
13
Ø
0,80
0,84
0,87
0,89
0,91
0,93
0,94
0,96
0,97
0,98
0,99
Fonte: ABNT NBR 15812-2 (2010).
Na norma britânica BS 5628-1 (1992), a resistência característica
à compressão da alvenaria pode ser determinada experimentalmente,
tanto para blocos de concreto como cerâmicos, com teste em painéis
cujas dimensões devem ser de 1,20 m a 1,80 m de comprimento por 2,40
m de altura, com área mínima da seção transversal de 0,125 m2,
conforme a equação 2.9.
fk =
Fm ψu ψm
x
A
1,2
(2.9)
Onde:
fk = resistência característica à compressão da parede;
Fm = média da carga máxima de dois painéis teste;
ψm = fator de redução da resistência da argamassa, dado na
Tabela 15 da BS 5628-1;
ψu = fator de redução para amostras de elementos estruturais;
A = área da seção transversal de qualquer painel.
O código europeu EN 1996-1-1 (2005) determina a resistência
característica à compressão da alvenaria conforme equação 2.10.
β
fk = k .fbα . farg
(2.10)
Onde:
fk = resistência característica à compressão da parede, em MPa;
k, α, β = constantes;
farg = resistência média à compressão da argamassa, em MPa;
fb = resistência à compressão normalizada da unidade, em MPa.
55
A resistência normalizada é o valor da resistência à compressão
da unidade convertida no equivalente seco ao ar de uma amostra de 100
mm de largura por 100 mm de altura.
Para alvenarias executadas com argamassas correntes e leves,
conforme o EN 1996-1-1, a equação 2.10 pode ser reescrita da seguinte
forma:
0,3
fk = k .fb0,7 . farg
(2.11)
O valor da constante k é determinado em função da argamassa
utilizada na parede, do tipo de unidade e do grupo em que está
classificada esta unidade. Na Tabela 2.12, encontram-se os valores de k
para blocos cerâmicos. Para determinar a resistência característica da
alvenaria utilizando-se da equação 2.11, alguns requisitos para a
especificação da resistência do bloco e argamassa devem ser
considerados:
a) para argamassa de uso geral: a resistência à compressão do
bloco (fb) não pode ser maior que 75 MPa, enquanto que a resistência da
argamassa (farg) não pode ser maior que 20 MPa nem maior que duas
vezes a resistência média à compressão dos bloco (2.fb);
b) para argamassa de camada fina: a resistência média à
compressão do bloco (fb) não pode ser maior que 50 MPa;
c) para argamassas leves: a resistência da argamassa (farg) não
pode ser maior que 10 MPa.
Tabela 2.12 – Valores de k para diferentes grupos de unidades cerâmicas e
argamassas.
Grupo de
Blocos
Cerâmicos
Argamassa
de uso
geral
Grupo 1
0,55
Grupo 2
0,45
Grupo 3
0,35
Grupo 4
0,35
Fonte: EN 1996-1-1 (2005).
Argamassa de
camada fina
(espessura da
junta entre 0,5
mm a 3 mm)
0,75
0,70
0,50
0,35
Argamassas Leves de
densidade (kgf/m3) entre:
600 ≤ ρ ≤ 800
800 < ρ ≤ 1300
0,30
0,25
0,20
0,20
0,40
0,30
0,25
0,25
Alguns pesquisadores com o intuito de determinar a capacidade
de resistência da alvenaria e explicar seu comportamento, também
desenvolveram modelos matemáticos para estimar a resistência à
56
compressão da alvenaria. Assim em suas pesquisas, Rizzatti (2003) e
Grohmann (2006) reuniram os principais modelos obtidos por
pesquisadores para a determinação da resistência à compressão da
alvenaria grauteada, para blocos de concreto, conforme Tabela 2.13.
Tabela 2.13 – Modelos matemáticos para a determinação da resistência à
compressão da alvenaria para blocos de concreto.
Fonte
Priestley e Yuk (1984)
f (MPa)
fp = {(p/1,5).([ [(0,1.fb’) + (α.fa)]/(0,1 + α)]} +
{ 0,9375.(1-a).fg}
fp = 0,6.{[fb’.(%sólidos/100) + [fg.(1%sólidos/100]}
Colville e Wolde-Tinsea
(1991)
Hamid e Chandrakeerthy
fp = [0,64.fb’(a-b)] + [1,07.b.fg]
(1994)
Khalaf et al. (1994)
fm = 0,3.fb + 0,2.fa + 0,25.fg
fm = resistência à compressão da
%sólidos = porcentagem da área de
alvenaria;
sólidos do bloco;
fp = resistência à compressão do
p = percentual de sólidos do bloco;
prisma;
α = ha/(4,1 . hb);
fb = resistência à compressão do
ha = altura da junta de argamassa;
bloco (área bruta);
hb = altura do bloco;
fb’ = resistência à compressão do
a = relação entre área líquida e área
bloco (área líquida);
bruta;
fb = resistência à compressão do
b = relação entre área grauteada e
bloco (área bruta);
área bruta.
fa = resistência à compressão da
argamassa;
fg = resistência à compressão do
graute;
Fonte: Rizzati (2003) e Grohmann (2006).
2.2. FATORES QUE INFLUENCIAM NA RESISTÊNCIA À
COMPRESSÃO DA ALVENARIA ESTRUTURAL
Vários fatores influenciam a resistência à compressão da
alvenaria e devem ser levados em consideração quando esta é analisada.
Neste item serão abordados apenas os fatores principais de interesse do
desenvolvimento desta tese.
57
2.2.1. Resistência à compressão dos blocos
A resistência à compressão do bloco é a principal característica
na resistência dos prismas e paredes, sendo que esta característica é
valida principalmente quando estes não são grauteados. Fahmy e
Ghoneim (1995), em estudo experimental, observaram que um
acréscimo de 50 % na resistência à compressão do bloco pode aumentar
em 15 % a resistência à compressão de prismas não grauteados, porém
para prismas grauteados, o ganho de resistência é menor, da ordem de 6
a 8%.
Romagna (2000) ao ensaiar prismas não grauteados com blocos
de concreto com três diferentes resistências e argamassa de traço 1: 1: 6
(em volume), com resistência media à compressão de 4,84 MPa, obteve
os seguintes valores de resistência à compressão para prismas, conforme
Tabela 2.14.
Tabela 2.14 – Resultados de resistência à compressão.
Resistência do Bloco área bruta (MPa)
Resistência do Prisma –
área bruta (MPa)
10,23
15,86
7,22
9,10
16,77
Fonte: Romagna (2000).
9,87
De acordo com o estudo de Romagna (2000), ao aumentar a
resistência do bloco em 64%, obteve-se um aumento na resistência dos
prismas de 37%. No entanto, segundo o autor, o aumento da resistência
à compressão da alvenaria não é proporcional ao aumento da resistência
à compressão do bloco.
Para La Rovere (2001) apud Mata (2006), quanto maior a
resistência da unidade, maior será a resistência à compressão da
alvenaria. Porém a autora ressalta que, a resistência à compressão da
alvenaria será menor do que a resistência à compressão da unidade por
dois motivos:
1) a resistência medida da unidade não é a verdadeira resistência
uniaxial, e sim um valor superior ao verdadeiro, pois a restrição nas
extremidades das unidades causada pelos pratos da prensa de ensaio,
que dependerá da geometria da unidade, gera tensões de compressão
transversais, como em um ensaio tri-axial à compressão;
58
2) devido ao fato da argamassa ser mais deformável do que as
unidades, ela tenderá a deformar-se mais do que as unidades,
deformação esta impedida pela aderência entre a argamassa e as
unidades o que provoca o surgimento de tensões de tração nas unidades
transversalmente ao eixo vertical de compressão.
Segundo Ramalho e Corrêa (2003), a resistência do bloco tem
caráter predominante dentre os fatores que exercem influência direta na
resistência à compressão de painéis de parede. De uma forma geral,
quanto mais resistente o bloco, mais resistente será a alvenaria.
Ainda segundo os autores, existe um conceito muito importante
quande se trata da influência da resistência dos blocos na resistência à
compressão das paredes. Trata-se da eficiência (η), ou seja, a relação
existente entre a resistência da parede ou prisma e a resistência do bloco,
onde quanto maior a resistência do bloco menor será a eficiência e viceversa. Desta forma, o fator de eficiência que relaciona a resistência da
parede e prisma com a resistência do bloco, pode ser expresso pela
equação 2.12.
fp
η=
(2.12)
fb
Onde:
η = eficiência parede-bloco ou prisma-bloco;
fp = resistência do prisma ou parede;
fb = resistência do bloco.
Assim, Ramalho e Corrêa (2003), conforme prática corrente no
Brasil, apresentam-se na Tabela 2.15, valores de eficiência entre
prismas, paredes e blocos cerâmicos e de concreto com resistência entre
4,5 MPa e 20 MPa, sendo as paredes e prismas não grauteados e com
argamassas usuais.
Tabela 2.15 – Valores de eficiência para prisma-bloco e parede-bloco
Fator de Eficiência (η)
Bloco
Cerâmico
Prisma-bloco
Valor
Valor
mínimo
máximo
0,30
0,60
Concreto
0,50
Fonte: Ramalho e Corrêa (2003).
0,90
Parede-bloco
Valor
Valor
mínimo
máximo
0,20
0,50
0,40
0,60
59
2.2.2. Resistência à tração dos blocos
Na alvenaria, o esforço predominante é o de compressão, mas
dependendo da rigidez dos seus materiais constituintes, surgem sempre
tensões de tração nos blocos, em consequência principalmente da
deformação da argamassa que leva as paredes dos blocos a uma tensão
de tração superior à suportada por eles.
Shivre (1982) afirma que as tensões de tração que se concentram
nas paredes dos blocos são responsáveis pela ruptura da alvenaria
carregada axialmente. Assim, Forrest et al. (1986) observam que o
conhecimento da resistência à tração dos blocos se torna um fator
importante para o entendimento do comportamento da alvenaria, em
virtude da ruptura das paredes ser atribuída a estas tensões de tração
geradas nos blocos.
Entretanto, grande parte das pesquisas realizadas com prismas e
paredes apontam a resistência à compressão de seus componentes como
um dos principais fatores responsáveis pelo comportamento mecânico
da alvenaria e que o aumento da capacidade resistente das paredes está
relacionada ao aumento da resistencia à compressão de suas unidades.
Mas segundo Drysdale et al (1994), o aumento da resistência à
compressão de prismas e paredes pode ser proporcionado pelo aumento
de resistência à tração no bloco que decorre do acréscimo de sua
resistência à compressão, sendo esta tomada como parâmetro por ser um
ensaio de fácil execução. Entretanto Sahlin apud Gomes (1983) sugere
que a resistência à tração nos blocos cerâmicos seja em torno de 3 a 5%
da sua resistência à compressão.
2.2.3. Geometria do bloco
A geometria do bloco também tem influencia na resistência à
compressão das paredes de alvenaria. Segundo Shrive (1983), a busca de
uma geometria adequada para o bloco é importante para que se consiga
um melhor desempenho mecânico de ambos, bloco e alvenaria quando
submetidos à compressão. Esta conclusão foi observada após o autor
estudar o mecanismo de ruptura da alvenaria e a distribuição de tensões
no bloco e na alvenaria. Em seu estudo o autor propõe três tipos de
blocos, testando unidades, prismas de três blocos e paredes de três
blocos de largura e seis de altura, utilizando argamassa somente nas
paredes laterais, com junta alternada. Neste estudo o autor conclui que
existem vantagens em aumentar a espessura dos septos, reduzir o
afunilamento dos furos e alinhar os furos.
60
Ganesan et al (1988) afirmam que o fator de eficiência varia com
a forma do bloco e o tipo de assentamento. Em algumas formas de
blocos e tipos de arranjo aparecem concentrações de tensões que
reduzem a resistência à compressão da alvenaria. Em seus estudos foram
testadas três formas diferentes de blocos. Os blocos tipo A foram
assentados com argamassa apenas nas faces e os demais foram
argamassados nas faces e septos. A Figura 2.4 mostra os tipos de blocos
estudados, sendo que os valores de resistência para blocos (fb) e paredes
(fw) estão mostrados na Tabela 2.16.
Figura 2.4 - Geometrias e dimensões dos blocos estudados.
Fonte: Ganesan et al. (1988).
Tabela 2.16 - Valores de resistência para blocos e paredes.
Bloco
fb (MPa)
fw (MPa)
A
3,30
1,46
Fator de Eficiência
(fw/fb)
44,24 %
B
5,10
3,33
65,29 %
2,91
58,91 %
C
4,94
Fonte: Ganesan et al. (1988).
Conforme se observou nos resultados obtidos no estudo, o bloco
“racionalizado” tipo B apresentou melhor desempenho que os outros. A
análise de tensões indica concentração de tensões e variações bruscas
das mesmas nos blocos convencionais, enquanto que nos blocos
“racionais” a variação é suave.
Ainda, segundo os autores, é necessário que a forma do bloco seja
repensada a fim de que se aumente a eficiência de blocos estruturais. Os
autores propõem que sejam utilizados blocos cujo septo central seja
igual ao dobro da lateral mais a espessura da junta, conseguindo-se desta
forma o alinhamento dos furos.
Ganesan e Ramamurthy (1992), através do método dos elementos
finitos, realizaram um estudo analítico sobre o comportamento da
61
alvenaria de blocos de concreto considerando a influência de: diferentes
geometrias, diferentes arranjos e propriedades das argamassas. Segundo
os autores a forma do bloco influencia as tensões que se desenvolvem,
tanto na sua distribuição, quanto na sua magnitude. Foi observado
também que a geometria dos blocos influencia no comportamento dos
prismas, através da superposição dos septos e faces, ocasionando níveis
críticos de tensão.
Rizzatti (2003) investigou a resistência à compressão de quatro
blocos cerâmicos com geometrias diferentes (Figura 2.5), e de prismas e
paredes confeccionadas com estas unidades, em paredes não armadas. O
estudo foi realizado através de análise experimental e análise numérica
pelo método dos elementos finitos.
Figura 2.5 - Geometrias e dimensões dos blocos estudados.
Fonte: Rizzatti (2003).
Em termos de resistência à compressão, o bloco tipo D destacouse em relação aos demais blocos estudados, proporcionando uma melhor
capacidade de absorver esforços nas paredes, devido à coincidência de
todos os septos entre as fiadas subsequentes provocada pela existência
de um duplo septo central, proporcionando uma melhor transmissão de
carregamentos. No entanto, este desempenho não se verificou nos
ensaios de blocos e prismas. O autor conclui que, quando utilizado
blocos vazados, a disposição e os tipos de furos podem ocasionar
grandes concentrações de tensões, reduzindo a resistência das paredes e
conduzindo a falhas frágeis das mesmas. Porém, embora o bloco tipo D
tenha demonstrado desempenho superior nos ensaios de compressão de
62
paredes, existem outros parâmetros a serem considerados para a escolha
de um bloco ideal, como por exemplo, a ocorrência de trincas, melhor
queima, facilidade de manuseio e a qualidade da argila.
2.2.4. Argamassa de assentamento
A resistência da argamassa não é tão significativa para a
resistência da parede quanto à resistência do bloco, principalmente na
alvenaria grauteada. Gomes (1983), em estudo com alvenaria de blocos
cerâmicos, concluiu que nas paredes submetidas à compressão simples,
a resistência da argamassa de assentamento não precisa ultrapassar a
resistência à compressão dos blocos, pois pode produzir uma argamassa
muito rígida a qual não é adequada para o desempenho das paredes.
Mohamad (1998), pesquisando prismas não grauteados de blocos
de concreto, verificou que quando usou uma argamassa com menor
resistência do que a resistência do bloco, a ruptura do prisma foi dúctil,
ocorrendo um esfacelamento da parte externa das paredes dos blocos,
propagando-se da junta para o restante do bloco. Quando utilizou uma
argamassa com a mesma resistência do bloco na área liquida, a ruptura
foi essencialmente frágil, ocorrendo no sentido da seção transversal do
prisma.
Ainda em seu estudo, reunindo dados de outros pesquisadores e
comparando as resistências de blocos, argamassas e prismas (Figura
2.6), Mohamad observou que a maioria dos pesquisadores trabalha com
níveis de resistência à compressão de argamassa da ordem de 40 a 60%
da resistência do bloco na área líquida. Entretanto para o autor,
conforme resultado de sua pesquisa deve existir a compatibilidade entre
a argamassa e o tipo de bloco, na qual a resistência à compressão da
argamassa esteja entre 0,70 à 1 vezes a resistência à compressão do
bloco na área bruta.
63
Figura 2.6 - Resistência à compressão simples de blocos, argamassas e prismas.
Fonte: Mohamad (1998).
Garcia (2000) também realizou uma compilação de resultados de
pesquisas de vários autores os quais observaram que a utilização de
argamassas muito mais resistentes do que os blocos é antieconômica,
pois o ganho de resistência obtido nos painéis de parede é irrelevante.
Como exemplo os ensaios desenvolvidos na EESC, a pedido da
Cerâmica Selecta, no qual se aumentou 79% da resistência da
argamassa, e obteve-se um aumento de 1,9% na resistência dos painéis
de parede; e os ensaios realizados por Franco (1987), quando o aumento
de 45% da resistência da argamassa, produziu um aumento de apenas
3,2% na resistência das paredes.
Romagna (2000), trabalhando com prismas de blocos de
concreto, também constatou que a influência da resistência da argamassa
na resistência dos prismas é, de maneira geral, menos importante para
prismas grauteados do que para não grauteados.
Para Cunha (2001), o aumento de resistência da argamassa não
influiu na resistência de prismas, não grauteados e grauteados, uma vez
que grandes aumentos na resistência das argamassas proporcionam
acréscimos muito pequenos na resistência à compressão dos prismas de
alvenaria.
Juste (2001) em seu trabalho utilizando blocos de concreto com
baixa resistência à compressão, confirmou que a afirmação feita por
64
diversos pesquisadores de que a resistência à compressão de prismas
depende principalmente da resistência e característica do bloco utilizado
e em bem menor proporção das características da argamassa. Assim,
segundo a autora para esta situação, deve-se escolher um tipo de
argamassa com traço adequado, de modo a aperfeiçoar outras
propriedades da argamassa, tais como trabalhabilidade e capacidade de
absorver deformações. Porém, ao serem utilizados blocos de resistência
à compressão elevada, a autora recomenda cuidado especial na escolha
da argamassa, para que a mesma não interfira na resistência à
compressão da alvenaria.
Steil (2003) também observou que as propriedades da argamassa
têm influência sobre a resistência de prismas. Em seu trabalho, o autor
notou que argamassas com praticamente a mesma resistência e rigidez,
diferindo na capacidade de retenção de água e composição, podem
produzir prismas que apresentem, além de diferentes tipos de ruptura,
resistências à compressão e fatores de eficiência distintos. Assim para o
autor, a especificação de argamassas para alvenaria estrutural não deve
ser baseada unicamente em sua resistência à compressão. Deve-se dar
especial atenção às demais propriedades da argamassa, tais como
aderência ao bloco e retenção de água, principalmente quando do uso de
argamassas industrializadas, já que, pela presença de aditivos, podem
apresentar comportamento completamente distinto do comportamento
de argamassas mistas de cimento e cal, mesmo que tenham algumas
propriedades semelhantes.
Para Grohmann (2006), em trabalho realizado com prismas não
grauteados e grauteados de blocos cerâmicos utilizando dois traços de
argamassa, constatou influência significativa da resistência da
argamassa na resistência à compressão dos prismas. E para o autor, esta
influência se torna mais evidente à medida que se utilizam grautes com
maiores resistências à compressão.
2.2.5. Graute
Quanto a influência do graute, Gomes (1983) realizou um estudo
em alvenaria estrutural de blocos cerâmicos, procurando estabelecer a
influência da resistência do graute nas paredes, além de analisar a
utilização de emendas na armadura e o módulo de deformação dos
painéis. Na parte específica de comparação entre grautes foram
utilizados blocos cerâmicos de resistência à compressão de 15,3 MPa e
argamassa de 4,83 MPa. Os resultados obtidos para paredes grauteadas
65
com taxa de armadura igual a 0,2% são apresentados no gráfico da
Figura 2.7.
Figura 2.7 - Resultados médios de resistência à compressão.
Resistência à Compressão Parede
(MPa)
3,8
3,68
3,6
3,4
3,2
3,08
3
2,8
2,77
2,6
2,47
2,4
0
3,13
11,23
14,83
Resistência à Compressão Graute (MPa)
Fonte: Gomes (1983).
No trabalho, o autor concluiu que, para o graute colaborar no
aumento da resistência das paredes, é necessário que sua resistência seja,
no mínimo, igual a dos blocos. Nota-se que, se a resistência do graute se
situa entre 3,0 e 11,0 MPa, o aumento de resistência destas paredes é
pequeno, podendo se tornar desprezível. A norma americana Uniform
Building Code (UBC) da Califórnia, genericamente, recomenda que a
resistência do graute não deva ser inferior a 13,7 MPa, para o bloco
cerâmico e para o tipo de parede ensaiada. Esta recomendação se
justificou experimentalmente.
Khalifa e Magzoub (1994) apud Mendes (1998), em seu trabalho,
relatam duas conclusões que são apresentados por diversos
pesquisadores sobre os efeitos do grautes e da sua resistência na
alvenaria. A primeira afirma que a resistência à compressão do prisma
grauteado é maior que a média das resistências separadas do bloco e do
grautes. Segundo os autores, tem-se que o grautes interno aos blocos
providenciaria contraventamento lateral às paredes do bloco impedindo
sua flambagem e por sua vez, o graute teria resistência à compressão
aumentada em consequência ao fato de se encontrar confinado no
interior do bloco. Em contraposição a primeira afirmativa, segundo
66
Khalifa e Magzoub (1994), outros pesquisadores afirmam que a
presença do grautes reduziria significativamente a resistência à
compressão do prisma, em razão das deformações incompatíveis entre
bloco e graute. Ou seja, grautes muito deformáveis provocariam o
aumento de tração nas paredes do bloco levando o mesmo ao colapso.
Ainda, segundo Khalifa e Magzoub (1994), o melhor
desempenho da alvenaria grauteada é obtido quando os módulos de
elasticidade do bloco e grautes são similares. Se o bloco é mais flexível
do que o grautes, tensões de tração lateral seriam introduzidas na
argamassa e a tensão vertical máxima no bloco aumentaria tanto quanto
a tensão lateral máxima no grautes. E assim, tensões de tração
horizontais seriam criadas nas paredes dos blocos por causa da restrição
da expansão lateral de um graute mais flexível. Entretanto, por outro
lado, quando a rigidez do graute é mais baixa que a do bloco, tensões
explosivas seriam criadas no bloco e como consequência a resistência do
prisma reduzida. Contudo, o aumento da resistência do graute não causa
um aumento significante na resistência do prisma, podendo causar uma
alta concentração de tensões na interface de adesão graute/bloco,
levando a ruptura prematura do prisma.
Khalaf (1996), avaliando os fatores que influenciam a resistência
de prismas grauteados e não grauteados de blocos de concreto, também
observou que o maior desempenho dos prismas grauteados ocorre
quando as características de deformação do bloco e do graute são as
mesmas. O autor ainda observa que o aumento da resistência da
argamassa para prismas grauteados apresenta efeito insignificante.
Segundo o autor, uma explicação seria a influencia de tensões de
confinamento horizontal exercida sobre a junta de argamassa pelo
grautes, que aumenta a resistência aparente da argamassa. Estas tensões
de confinamento são inversamente proporcionais a resistência da
argamassa em consequência ao alto coeficiente de Poisson da mesma.
Assim, de seus resultados o autor conclui que, para o aumento da
resistência dos prismas, as propriedades de deformação do bloco e do
grautes devem ser iguais.
Mendes (1998) teve conclusões similares estudando o
comportamento mecânico de prismas grauteados e não grauteados de
blocos cerâmicos com três blocos de altura. O pesquisador utilizou
blocos com 22,89 MPa e dois tipos de argamassa, a argamassa (iii) com
6,64 MPa e a argamassa (i) com 20,18 MPa. Na fabricação dos prismas
grauteados com três blocos de altura, para cada tipo de argamassa de
assentamento, foi realizado o grauteamento com três grautes com
resistências distintas. Os resultados obtidos no trabalho podem ser
67
observados na Figura 2.8. Observando os resultados obtidos nota-se que,
com a argamassa com menor resistência à compressão, os prismas
apresentam um melhor desempenho com grautes com menor resistência
à compressão; já na utilização de argamassa com maiores valores de
resistência à compressão, os prismas não apresentam resultados
significativamente distintos com a variação dos grautes.
Figura 2.8 - Resultados de resistência à compressão dos prismas.
Prisma com Argamassa (i)
Prisma com Argamassa (iii)
Resistência à compressão Prisma (MPa)
23
21,3
21
20,8
19,5
19
17,9
17
14,7
15
13
12,6
12,7
11
9
8,1
7
0,0
13,2
26,7
49,7
Resistência à compressão Graute (MPa)
Fonte: Mendes (1998).
Através da análise dos resultados, Mendes (1998) concluiu que os
prismas que apresentaram o melhor desempenho são aqueles
preenchidos com grautes com módulos de deformação próximos ao
módulo de deformação da argamassa e próximos ao módulo de
deformação dos prismas não grauteados. Foi observada uma relação de
resistência ótima entre argamassa e graute de 0,5. Segundo o autor,
razões menores parecem levar à diminuição de resistência à compressão
e maiores não implicam em aumento da mesma.
Camacho e Rodrigues (1999), em seu estudo sobre a influência
do graute na resistência da alvenaria, verificaram que o grauteamento
permite o aumento de resistência da alvenaria na mesma relação entre a
área bruta e a área líquida do bloco, desde que graute e bloco
apresentem aproximadamente a mesma resistência. Além de afirmarem
68
que a adoção de grautes cada vez mais resistentes representa elevação de
custo e não contribui muito para o aumento da resistência da alvenaria.
Romagna (2000), em trabalho experimental realizado, estudou a
influência dos materiais constituintes na resistência à compressão da
alvenaria de blocos de concreto grauteados e não grauteados. No
trabalho foram moldados 60 tipos de prismas com três blocos de
diferentes resistências à compressão, dois tipos de argamassas (1:1:6) e
(1:0,5:4,5), quatro tipos de grautes com diferentes resistências à
compressão e dois tipos de assentamento, total e lateral.
Segundo o autor, para prismas não grauteados, tanto no
argamassamento total quanto lateral, para um mesmo traço, à medida
que se aumenta a resistência à compressão do bloco, aumenta a
resistência à compressão do prisma. Porém, este aumento da resistência
à compressão do prisma não é diretamente proporcional ao aumento da
resistência à compressão do bloco. Já para os prismas grauteados, a
partir de um determinado nível de resistência à compressão do bloco, na
medida em que se aumenta a resistência à compressão do graute, quando
utilizada argamassa menos resistente, não se obtém aumento de
resistência à compressão nos prismas. Os resultados obtidos no trabalho
mostraram que o uso de grautes com resistência à compressão acima da
resistência do bloco medida na área líquida, não trouxe ganhos de
resistência à compressão para a alvenaria. Os melhores resultados foram
obtidos com grautes e blocos de resistências à compressão
aproximadamente iguais. Entretanto, este fato pode não ocorrer somente
como consequência ao aumento dos valores de resistência à compressão,
mas também em razão dos valores de módulo de elasticidade dos
componentes. O que reforça a necessidade de compatibilização dos
materiais constituintes da alvenaria para o aumento de sua resistência
mecânica à compressão.
Cunha (2001), apud Reis (2010), estudou prismas grauteados de
concreto avaliando a resistência à compressão em função da resistência
da argamassa e da absorção de água no graute. No seu programa
experimental, o autor usou um tipo de bloco com dimensões de
14x19x39 cm, com resistência à compressão nominal de 4,5 MPa, três
tipos de argamassas e três tipos de grautes, com resistências à
compressão de 15 MPa, 25 MPa e 35 MPa. Segundo Cunha (2001), a
resistência à compressão da argamassa não exerce influência na
resistência à compressão dos prismas vazios e grauteados. Como em
outros trabalhos, constatou-se que a resistência à compressão dos
prismas aumenta com o acréscimo de resistência à compressão do
graute.
69
O autor conclui também que a perda de água do graute para o
bloco pode causar dois tipos de fenomenos: o primeiro é o aumento da
resistencia à compressão nos grautes que tem uma relação agua/cimento
maior; o segundo ocasiona a redução da resistencia à compressão do
graute de até 28,6%. Essa redução pode ser explicada pela perda de
aderencia na interface bloco/graute em razão do aumento de porosidade
daquela região. O fato também pode ser entendido como a baixa relação
água/cimento do graute em consequência da perde água para o bloco,
sem a retenção de água suficiente para uma correta hidratação do
cimento.
Arantes (2003), apud Grohmann (2006), realizou sua pesquisa
com o objetivo de estudar a influência do graute no aumento da
capacidade de carga da alvenaria, através de ensaios de compressão de
prismas contrafiados de alvenaria cerâmica, grauteados, parcialmente
grauteados e não grauteados. Os prismas foram executados com um
bloco e meio de largura por três blocos de altura, utilizando bloco de
13,08 MPa de resistência à compressão, dois tipos de argamassa, com
6,50 MPa e 18,80 MPa, e três tipos de grautes. Os resultados
encontrados pelo autor, para prismas grauteados e não grauteados são
mostrados na Tabela 2.17.
Tabela 2.17 – Resultados de resistência dos prismas.
Resistência à Compressão (MPa)
Prisma
Graute
Prisma A1
Prisma A2
Vazio
-
7,35
7,66
G1
8,93
11,58
13,30
G2
15,36
12,61
13,74
G3
26,66
13,59
15,25
Fonte: Arantes (2003 apud GROHMANN, 2006).
Através dos resultados de Arantes (2003), percebe-se um
aumento médio na resistência à compressão dos prismas de 6% quando
a resistência à compressão do graute é aumentada em 72%, e um
aumento médio de 16% quando se aumenta a resistência à compressão
do graute em 199%, indicando que a resistência à compressão do prisma
é influenciada pela resistência à compressão do graute, de forma
relativamente proporcional. O gráfico da Figura 2.9 mostra o
desempenho dos prismas estudados pelo autor. Com a análise dos
70
resultados o pesquisador concluiu que o melhor desempenho foi obtido
para prismas com graute de resistência à compressão aproximadamente
igual a do bloco e que é perfeitamente viável a utilização da técnica do
grauteamento da alvenaria cerâmica para ganho de resistência mecânica
das estruturas.
Figura 2.9 – Resultados de resistências dos grautes versus prismas.
Fonte: Arantes (2003 apud GROHMANN, 2006).
Grohmann (2006), em estudo experimental com blocos
cerâmicos, também avaliou da influência do graute na resistência à
compressão de prismas, utilizando diferentes três tipos de grautes - G1,
G2 e G3, dois tipos de argamassas - A1 e A2 e quatro porcentagens de
grauteamento de 0%, 33%, 66% e 100% (Figura 2.10).
71
Figura 2.10 – Secções transversais dos prismas adotados com os diferentes
percentuais de grauteamento.
Prisma 0% Grauteado
Prisma 33% Grauteado
Prisma 66% Grauteado
Prisma 100% Grauteado
Fonte: Grohmann (2006).
Na comparação entre os prismas grauteados com diferentes tipos
de grautes, o autor concluiu que o aumento de resistência à compressão
dos grautes não gera um aumento significativo na resistência à
compressão dos prismas. De forma geral, há um pequeno aumento na
resistência à compressão dos prismas com o aumento da resistência à
compressão dos grautes, mas em prismas com a totalidade dos furos
grauteados a utilização de grautes de maior resistência à compressão
pode gerar um decréscimo de resistência à compressão nos prismas. Este
fato foi constatado somente nas séries de prismas em que se utilizou a
argamassa de resistência à compressão menor. Os prismas com 100%
dos furos grauteados sofrem maior influência das tensões geradas pelo
graute em função do estado de confinamento do mesmo.
Segundo Grohmann (2006), para prismas parcialmente
grauteados o aumento da porcentagem dos furos grauteados não gera um
aumento significativo na resistência à compressão dos prismas.
Entretanto, os prismas totalmente grauteados na sua maioria, têm um
ganho significativo de resistência à compressão, principalmente na
utilização de argamassas mais fortes.
Quanto à análise da ruptura do comportamento dos prismas à
compressão, o autor relata que a ruptura da alvenaria grauteada ocorre
em consequência da expansão do graute, que transmite tensões aos
demais componentes do prisma, bloco e junta de argamassa, que tendem
72
a confinar o graute. A ação do graute sobre o prisma gera tensões de
tração na interface bloco/argamassa, zona mais frágil do prisma,
levando-o à ruína. Segundo o autor, quando o graute não atinge sua
resistência máxima antes do conjunto bloco/argamassa, as faces do
bloco são tracionadas ao restringirem as deformações da argamassa, que
tem a tendência de se expandir lateralmente, ocasionando a ruptura do
bloco por estas tensões de tração geradas. Ainda segundo o autor,
prismas com argamassas mais fracas, na maioria das vezes, rompem de
forma lenta, pois as argamassas mais fracas são mais dúcteis, com maior
capacidade de absorver deformações. Já os prismas com argamassas
mais fortes, geralmente, têm ruptura explosiva, fissurando subitamente.
Prismas com grautes de resistência à compressão mais elevada são mais
influenciados pelas tensões geradas pelo graute nos demais
componentes. No caso de prismas totalmente grauteados esta situação se
agrava pelo maior confinamento do graute.
No estudo realizado por Leão (2008), caracterizou-se o
desempenho da alvenaria de blocos cerâmicos estruturais grauteada e
não grauteada, investigando a resistência à compressão e à tração na
flexão de prismas. O autor concluiu que o aumento no valor da
proporção Resistência da argamassa/Resistência do bloco provoca um
aumento na resistência à compressão do prisma sem graute. Porém, essa
relação não é linear, apresentando um valor máximo de resistência à
compressão do prisma quando a resistência à compressão da argamassa
é próxima da resistência do bloco na área bruta. Ainda segundo o autor,
a resistência de prismas grauteados, não é significativamente
influenciada pela variação na resistência a compressão da argamassa.
Isso porque o modo de ruptura do prisma grauteado é diferente do modo
do não grauteado. Ou seja, mesmo que a resistência a compressão da
alvenaria (bloco/argamassa) aumente com o aumento a resistência da
argamassa, essa mesma alvenaria, quando grauteada rompe por tração
provocada pela deformação transversal do graute no seu interior e não
por compressão. Assim, o aumento na resistência do graute pode
aumentar a resistência do prisma ou até mesmo reduzir a resistência do
prisma. Concluindo-se com isso, a necessidade de compatibilização dos
materiais utilizados na construção da alvenaria grauteada para melhor
desempenho da mesma.
2.2.6. Módulo de elasticidade
O módulo de elasticidade dos materiais constituintes dos prismas
e paredes também são fatores importantes no desempenho mecânico da
73
alvenaria. O módulo de elasticidade é um parâmetro mecânico que
proporciona uma medida da rigidez ou capacidade de deformação para o
material ou componente ensaiado. Para a alvenaria, a deformabilidade
ou capacidade de acomodar deformações é definida como “a capacidade
que a parede de alvenaria possui de manter-se íntegra ao longo do
tempo, distribuindo as deformações internas ou externas impostas em
microfissuras não prejudiciais ao seu desempenho” (FRANCO,1987).
Para alvenaria estrutural é recomendado o emprego de
argamassas com baixos módulos de elasticidade, com a finalidade de
absorver as deformações da estrutura (ISHIKAWA, 2001). Entretanto,
segundo Rizzatti (2003), quanto maior a diferença de deformação
específica entre a unidade e a argamassa, maior o diferencial de
deformação entre os materiais, ocasionando um aumento das tensões de
tração nas unidades e com isso uma ruptura da alvenaria com cargas
menores.
O módulo de elasticidade dos elementos da alvenaria pode ser
determinado através do traçado do diagrama tensão-deformação, obtido
na compressão, a fim de avaliar e quantificar a deformação ocorrida
durante a realização do ensaio. Normalmente, o modulo é determinado
para os valores correspondentes de 40% a 60% da carga de ruptura para
o módulo secante, e ao valor carrespondente a 30% da carga de ruptura
para o modulo tangente inicial. Isto acontece por ocorrer nestre trecho
um comportamento linear dos elementos (MOHAMAD, 2007).
Para o ACI 530-92 (1995) o módulo de elasticidade da alvenaria
de unidades de concreto pode ser obtido em função da resistência do
bloco e da argamassa por meio de ensaios com prismas, a partir da
inclinação da reta secante entre os pontos correspondentes a 5% e 33%
da máxima resistência à compressão dos prismas ensaiados.
Para Drysdale et al. (1994), ao se alcançar em torno de 50% da
tensão máxima a não linearidade já é evidente nos ensaios à compressão
realizados com prismas. Mas apesar dos prismas representarem melhor o
comportamento da alvenaria, os autores citam que ensaios com a
argamassa, graute e blocos isolados são também realizados para a
aquisição de informações mais completas de suas características.
Garcia (2000), em sua pesquisa, considerou para a determinação
do modulo de elasticidade os valores correspondentes entre 30% e 40%
da carga de ruptura, de blocos, argamassas, prismas e painéis de parede.
Segundo a autora, isto se deve ao fato que neste trecho o comportamento
do gráfico tende a se manter linear. Para a obtenção do módulo, na
realização do ensaio foi considerado pela autora o terço médio do corpode-prova, por esse possuir menor influência dos pratos da prensa. O
74
mesmo procedimento de ensaio também foi utilizado por Mohamad
(2007), pois segundo o autor os resultados são afetados pelos pratos da
prensa quando se considera o deslocamento total do corpo-de-prova.
Para Dhanasekar (1985) apud Mohamad (2007), o valor do
modulo de elasticidade da alvenaria pode ser determinado em função da
sua resistência à compressão (fc), conforme a equação abaixo:
Ealv = 1180 . fc0,83
(2.13)
Segundo a norma européia EN 1996 1-1 (2005), na ausência de
valores obtidos por ensaios, o módulo pode ser determinado de forma
aproximada pela equação 2.14, onde fk é a resistência característica à
compressão da alvenaria, sendo que o valor recomendado para a
constante K é 1000.
Ealv = K . fk
(2.14)
Parsekian (2002) apud Santos (2008), em sua pesquisa reuniu
várias normas e autores nacionais e internacionais, relacionando em sua
maioria, o módulo de elasticidade com a tensão de ruptura do elemento
ou um coeficiente multiplicador da resistência da alvenaria ou do
próprio bloco, conforme pode ser observado na Tabela 2.18.
75
Tabela 2.18 – Normas e autores internacionais pesquisados, referentes a blocos
cerâmicos.
Fonte
AS 3700
(1998)
BS 5628
(1995)
Tipo de
bloco
cerâmico
Resistência
entre 5 a 30
MPa
Resistência
superior a
30 MPa
-
Argamassa
Ealv
(MPa)
M2, M3
700.fp
Observações
Carga de curta
duração
M3, M4
1000.fp
-
900.fp
-
Norma
Americana
-
-
700.fp
Especifica o
módulo de
elasticidade de
acordo com a
corda dos pontos
de 5% e 33% de
fp do diagrama
tensãodeformação
LECZNE
R (1986)
Padrão
Britânico
(i) e (ii)
3750.(f
bk –
1000)1/2
-
WOLDET
INSAE et
Vazados
550.fp
al (1993)
Fonte: Parsekian (2002 apud SANTOS, 2008).
Grauteados ou
não
A norma brasileira ABNT NBR 15812-1 (2010), para alvenaria
de blocos cerâmicos, estabelece que na falta de valores experimentais os
valores de módulo de elasticidade e coeficiente de Poisson da alvenaria
podem ser adotados de acordo com a Tabela 2.19.
76
Tabela 2.19 - Propriedades elásticas da alvenaria estrutural de blocos cerâmicos.
Propriedade
Valor
Valor Máximo
Módulo de Elasticidade
600 fpk
12 GPa
Coeficiente de Poisson
0,15
-
Fonte: ABNT NBR 15812-1 (2010).
Mas, para Juste (2001) torna-se necessário uma norma específica
para a obtenção do módulo de elasticidade das unidades e componentes
da alvenaria, decorrente da não existência de nenhum método de ensaio
padronizado. A autora relata ainda que os valores obtidos nas pesquisas
já realizadas são afetados por vários fatores, tais como velocidade de
carregamento, intensidade de carregamento, dimensões dos corpos-deprova, prejudicando assim a comparação direta dos resultados entre os
estudos realizados pelos pesquisadores.
2.2.7. Espessura da junta de assentamento
A norma ABNT NBR 8215 (1983) estabelece a espessura da
junta de assentamento em alvenaria estrutural em 10 mm, com
tolerância de mais ou menos 3 mm, pois valores fora deste intervalo
prejudicam o desempenho da alvenaria. Valores inferiores, que
teoricamente levariam a alvenarias mais resistentes, não são
recomendáveis, pois a junta não conseguiria absorver as imperfeições
que ocorrem nas unidades. Entretanto, o aumento da espessura da junta
provoca redução na resistência do prisma. Segundo Roman (1991), a
resistência da alvenaria diminui, em aproximadamente 15%, para cada
aumento de 3 mm na espessura e vice-versa, considerando como base
uma junta de 10 mm.
Esse comportamento também foi verificado por Mohamad
(1998). Segundo o autor, a espessura da junta de argamassa influi
significativamente na resistência à compressão da alvenaria e seu
aumento impõe diminuição significativa na eficiência da mesma. Em
estudo com prismas confeccionados com blocos de concreto,
executando-se juntas de assentamento de 7 e 10 mm de espessura,
Mohamad observou um aumento na resistência à compressão da
alvenaria de 32,3 %, quando utilizado juntas com espessura de 7 mm.
Carvalho et al. (2006) também constatou que a diminuição da
espessura das juntas de assentamento interfere na resistência dos
77
prismas. Em seu estudo com prismas de blocos cerâmicos, com juntas
de 10 e 25 mm de espessura, o autor observou uma diminuição de 28 %
na resistência dos prismas com o aumento da espessura de suas juntas de
assentamento.
2.2.8. Tipo de assentamento
Sobre a forma de assentamento, os prismas podem ter argamassa
de assentamento em toda superfície transversal do bloco ou somente nas
paredes ou faces laterais (face shell), conforme Figura 2.11. O tipo de
assentamento é um fator que também pode alterar a resistência do
prisma.
Em estudo utilizando o método dos elementos finitos para estudar
o comportamento de prismas com diferentes tipos de assentamento,
Ganesan e Ramamurthy (1992) concluíram que a colocação de
argamassa de assentamento somente nas paredes laterais dos blocos
(face shell) implica no surgimento de grandes concentrações de tensões
nas paredes transversais dos blocos, causando a redução na resistência à
compressão do prisma ou parede. Ainda segundo os autores, através da
simulação computacional, puderam observar que se a aplicação da
argamassa em todo o bloco levou a eliminação dessas concentrações de
tensões.
Figura 2.11 - Tipos de assentamento utilizados na construção dos prismas: (a)
assentamento total e (b) assentamento nas faces laterais dos blocos.
(a)
(b)
Fonte: Leão (2008).
Pasquali (2006), apud Santos (2008), estudou o comportamento
de pequenas paredes com dois tipos de geometria de blocos cerâmicos
vazados, sendo um tipo com paredes vazadas e outro com paredes
maciças. Foram utilizados três tipos de argamassas industrializadas a
base de cal e areia calcária e dois tipos de assentamento (total e lateral).
78
Os resultados encontrados pelo autor são apresentados na Tabela 2.20.
Analisando os dados da Tabela 2.20, conclui-se que as duas geometrias
de blocos vazados apresentam uma redução significativa na resistência
das pequenas paredes quando utilizado assentamento lateral. Esta
redução varia de 16,1% a 25,9% para as paredes vazadas e de 38% a
49,3% para as paredes maciças.
Tabela 2.20 – Resistência das pequenas paredes em função do assentamento.
Tipo de
Parede
Resistência
Média da
Argamassa
(MPa)
Tipo de
Assentamento
Total
Lateral
Total
Vazada
4,25
Lateral
Total
12,56
Lateral
Total
2,51
Lateral
Total
Maciça
4,25
Lateral
Total
12,56
Lateral
Fonte: Pasquali (2006 apud SANTOS, 2006).
2,51
Resistência
Pequenas
Paredes –
Área Bruta
(MPa)
4,32
3,53
4,34
3,64
5,71
4,23
4,68
2,90
5,60
3,19
6,57
3,33
Redução
(%)
18,3
16,1
25,9
38,0
43,0
49,3
Entretanto, Colville e Woldetinsae (1990), também estudando a
influência do tipo de assentamento na resistência à compressão de
prismas moldados com blocos de concreto, concluíram que a resistência
à compressão dos prismas vazados é aproximadamente 8% menor para
prismas com assentamento total do que para prismas com assentamento
lateral. É importante ressaltar que os autores chegaram a estes resultados
considerando a resistência à compressão dos prismas quando calculada
em relação à área de assentamento da argamassa. Segundo os autores, a
resistência à compressão dos prismas vazados deve ser calculada em
relação à área de assentamento e não de acordo com a área dos blocos
utilizados.
79
2.2.9. Absorção de água inicial dos blocos
Outro fator a ser considerado na resistência das paredes de
alvenaria é a absorção de água inicial ou sucção dos blocos. Blocos com
altas taxas de absorção retiram a água da argamassa de assentamento,
interferindo na resistência à compressão da argamassa e na aderência da
mesma às unidades da alvenaria.
Conforme Franco (1993), blocos com altas taxas de absorção de
água inicial provocam, quando em contato com a argamassa, diminuição
da plasticidade da argamassa durante o assentamento, ocasionando
perda da capacidade da alvenaria de absorver pequenas deformações
pertinentes ao assentamento.
De acordo com a ABNT NBR 15270-3 (2005), caso o índice de
absorção de água inicial (AAI) para os blocos cerâmicos estruturais seja
superior a 30 g/193,55 cm² por minuto, os blocos devem ser umedecidos
antes do assentamento para melhorar o seu melhor desempenho no
momento do assentamento. Segundo Carvalho (2003), prismas
construídos com blocos umedecidos apresentam uma tendência de
aumento de resistência à compressão. Entretanto, conforme a ABNT
NBR 15270-3 (2005), se o valor do índice de absorção inicial (AAI)
resultar menor que o limite recomendado, os blocos podem ser
assentados sem ser previamente umedecidos.
2.3. COMPORTAMENTO DA ALVENARIA SUBMETIDA À
COMPRESSÃO
Segundo Hilsdorf (1969) apud Sabbatini (1984), a alvenaria é
constituída por materiais (argamassa e bloco) com diferentes
características mecânicas, onde a resistência à compressão uniaxial e o
módulo de elasticidade da argamassa de assentamento são geralmente
menores que os do bloco. Porém, a aderência e o atrito entre os
materiais constituintes impedem que a deformação lateral da argamassa
seja maior que a dos blocos, criando um estado de tensão de compressão
triaxial na argamassa e tração axial lateral nos blocos (Figura 2.12).
Com isso, a alvenaria pode ser submetida a esforços maiores que os
suportados pela argamassa em estado uniaxial.
Observando o comportamento dos tijolos sob este estado triaxial
de tensões, o autor desenvolveu um critério de ruptura para um tijolo
sob esta situação, como mostrado na Figura 2.13, para argamassas com
menor módulo de elasticidade (mais deformáveis) em relação ao bloco.
Conforme a teoria do autor, os fatores que afetam a resistência à
80
compressão da alvenaria são a resistência à compressão uniaxial do
tijolo, a resistência à tração biaxial do tijolo, a resistência a compressão
uniaxial da argamassa (inicio da linha C), o comportamento da
argamassa sob um estado de compressão triaxial (linha C) e um
coeficiente de não uniformidade U (uma medida de tensões adicionais
devidas a não uniformidade de juntas e tijolos e suas propriedades).
Figura 2.12 - Tensões nas unidades e na argamassa submetidas a compressão
simples.
Fonte: HILSDORF (1969).
Figura 2.13 - Representação gráfica de tensões e critérios de ruptura para tijolos
e alvenaria.
Fonte: HILSDORF (1969).
81
Hamid e Drysdale (1979) apud Grohmann (2006), estudando
prismas grauteados de concreto, analisaram a interação entre bloco,
argamassa e graute sob estado multiaxial de tensões (Figura 2.14),
desenvolvendo um modelo de ruptura para a alvenaria. Os autores
basearam-se nas seguintes hipóteses: aderência na interface
bloco/argamassa/graute, distribuição proporcional de esforços verticais
entre os componentes, distribuição uniforme de tensões ao longo da
altura, teoria de Mohr e adoção das características do graute como sendo
um concreto convencional.
Figura 2.14 - Estado multiaxial de tensões da alvenaria sob compressão.
Fonte: Hamid e Drysdale (1979).
Segundo os autores, ao se aplicar o carregamento à alvenaria o
graute atinge sua capacidade resistente de compressão não confinado,
expandindo em razão de suas deformações inelásticas ocasionadas pela
microfissuração. Assim, como o bloco tende a restringir estas
deformações e a confinar o graute, gera tensões de tração em suas
paredes. No caso do graute não atingir a sua capacidade de resistência
antes do conjunto bloco-argamassa, as faces do bloco são tracionadas ao
restringirem as deformações da argamassa. Desta forma, o bloco sempre
romperá em consequência às tensões de tração geradas pela deformação
dos demais componentes.
Hamid e Drysdale (1979) também observaram que, quando os
prismas eram submetidos à compressão axial surgiam fissuras verticais
nos blocos que aumentava em função da carga aplicada. As fissuras
82
eram formadas em virtude da maior deformação lateral do graute e da
argamassa em relação aos blocos.
Para analisar a ruptura dos prismas grauteados, os pesquisadores
igualaram elasticamente as deformações do graute e do conjunto blocoargamassa. Os autores partiram do pressuposto que a resistência à
compressão da alvenaria grauteada e não grauteada está em função dos
seguintes fatores: resistência uniaxial do bloco, resistência à compressão
não confinada da argamassa e do graute, módulos de deformação do
graute e do bloco, proporção entre a área líquida e a área bruta do bloco,
altura do bloco e espessura da junta de argamassa.
Assim, com suas pesquisas, Hamid e Drysdale (1979) chegaram
as seguintes conclusões para prismas, quando grauteados:
- a resistência do prisma (na área líquida) diminui para prismas
grauteados;
- a influência do tipo de bloco e de argamassa diminui para
prismas grauteados;
- a ruptura para prismas grauteados ocorre pela ruptura à tração
do bloco induzido pela deformação lateral do graute;
- grandes aumentos na resistência dos grautes têm pouco efeito na
resistência dos prismas;
- a ruptura do graute governa a ruptura dos prismas.
O modelo de ruptura de Lenczner, apud Gomes (1983), leva em
consideração a contribuição da argamassa de assentamento na
resistência da alvenaria, considerando a compatibilidade de deformações
entre bloco e argamassa, conforme Figura 2.15. Neste modelo, a
argamassa por possuir módulo de elasticidade menor que o do bloco, é
submetida a esforços de compressão e os blocos são submetidos a
esforços de tração, ocasionando a ruptura por tração no bloco devido sua
baixa resistência à tração.
83
Figura 2.15 - Deformação lateral dos blocos e da argamassa submetidos à
compressão simples.
Deformação dos
blocos tracionados
Deformação da
argamassa comprimida
Deformação lateral
livre dos blocos
Deformação lateral
livre da argamassa
Fonte: Gomes (1983).
Atckinson e Nolan (1985), baseando-se no critério de ruptura de
Hilsdorf (1969), também relacionaram as propriedades de resistência e
deformação de prismas submetidos à compressão. Segundo os autores, o
prisma atua como um conjunto bloco/argamassa sujeito a uma tensão de
compressão vertical uniforme, gerando tensões laterais de compressão e
tração, também uniformes em ambos os componentes (Figura 2.16).
Figura 2.16 - Distribuição de tensões, segundo modelo de Atckinson e Nolan.
Fonte: Atckinson e Nolan (1985).
McNary e Abrams (1985), a partir do modelo proposto por
Atckinson e Noland (1985), realizaram ensaio com prismas de blocos
cerâmicos maciços e diferentes argamassas, para comparar os dados
experimentais com os valores teóricos. Na realização dos procedimentos
84
experimentais foram feitos ensaios de compressão triaxial da argamassa,
compressão uniaxial dos blocos e dos prismas.
Segundo os autores, como a argamassa tem a tendência a
expandir lateralmente e como está aderida mecanicamente ao bloco, ela
é restringida lateralmente, ocasionando tensões laterais de tração no
bloco e de compressão na argamassa. Sendo assim, a resistência dos
prismas é governada pela resistência à tração do bloco e pelas
propriedades de deformação da argamassa.
Cheema e Klingner (1986), realizando ensaios experimentais com
1 tipo de bloco de concreto, 2 grautes de resistências diferentes e 2 tipos
de argamassas de mesmo traço, porém de resistências diferentes,
também desenvolveram um modelo de ruptura para a alvenaria. A partir
dos resultados experimentais, os autores desenvolveram modelagem
elástica em elementos finitos para a previsão da resistência do prisma e
tipo de ruptura devido aos carregamentos. Com a modelagem foi
determinada uma metodologia com equações e gráficos baseados nas
características mecânicas dos materiais, que apontam qual o tipo de
tensão gera a ruptura dos prismas. Esta metodologia determina se a
ruptura no prisma ocorrerá por tração nos blocos, ou se pelas
resistências à compressão dos materiais. Porém os gráficos e equações
utilizados pelos autores são válidos apenas para os materiais
empregados pelos autores, em virtude da grande variação existente entre
aos materiais para alvenaria de país para país e até mesmo de região
para região, restringindo a imediata utilização do modelo matemático
proposto pelos autores.
Entretanto, nos resultados obtidos por Cheema e Klingner (1986),
dois importantes fatos foram observados: a ocorrência de melhor
desempenho à compressão do prisma grauteado com graute de menor
resistência a compressão; para prismas não grauteados, o aumento da
espessura da junta em 2,7 mm, diminuiu a resistência do prisma.
Ainda segundo os autores, os prismas grauteados usualmente
atingem a ruptura quando a tensão de tração transversal perto da
interface bloco/argamassa fendilha o bloco, mas também pode ocorrer a
ruptura do prisma quando a tensão de compressão no bloco, argamassa
ou graute esmaga o correspondente material.
Assim, os autores classificam e nomeiam as formas de ruptura
que podem ocorrer na alvenaria grauteada de blocos de concreto em
cinco tipos, em ordem decrescente de possibilidade de ocorrência:
- Fendilhamento lateral do bloco: ocorre quando a resistência à
tração do bloco é alcançada, levando a ruptura da alvenaria por tração
no bloco;
85
- Esmagamento da argamassa: ocorre quando a máxima tensão de
compressão atuante na argamassa atinge a resistência de compressão da
argamassa confinada;
- Esmagamento do bloco: ocorre quando é atingida a resistência à
compressão do bloco;
- Fendilhamento da argamassa: ocorre quando é atingida a
resistência à tração máxima da argamassa;
- Esmagamento do graute: ocorre quando a máxima tensão de
compressão atuante no graute atinge a resistência à compressão
confinada do graute.
Para a alvenaria não grauteada, os autores dividem as formas de
ruptura das paredes de alvenaria em três tipos característicos:
- Tração no bloco: ocorre onde a tensão de tração principal no
bloco supera a resistência à tração do bloco;
- Esmagamento do bloco: ocorre quando a tensão principal de
compressão no bloco supera a resistência à compressão do bloco;
- Esmagamento da argamassa: ocorre quando a tensão de
compressão axial na argamassa é maior que a resistência da argamassa
confinada.
A partir dos modos de ruptura observados para a alvenaria não
grauteada, os autores desenvolveram várias expressões utilizando as
características dos materiais utilizados, que procuravam prever a tensão
de compressão necessária para a ocorrência de cada tipo de ruptura, em
função da relação entre o módulo de elasticidade da argamassa e do
bloco.
Deste modo, no caso de ruptura por tração no bloco, a equação
proposta é dada por:
ftb = (1/ς) . fhb1
(2.15)
Onde:
ftb = tensão de tração transversal principal no bloco;
fhb1 = tensão de compressão aplicada no prisma quando a ruptura
é dada pela tração no bloco;
ς = coeficiente de influência, obtido a partir da Figura 2.17.
Para a ocorrência de ruptura quando a tensão de compressão
nominal no bloco alcançar a resistência à compressão uniaxial do bloco,
a equação proposta será:
86
fhb = ς . ftb
Onde:
fhb < fb
fhb = tensão de compressão aplicado no prisma;
fb = resistência à compressão uniaxial do bloco;
(2.16)
Para o caso de ruptura por esmagamento da argamassa, a equação
é definida da seguinte forma:
fhm = γ . fm
(2.17)
Onde:
fhm = tensão de compressão máxima do prisma quando a ruptura
ocorre pelo esmagamento da junta de assentamento;
fm = resistência à compressão uniaxial do bloco;
γ = coeficiente de influência, obtido a partir do gráfico da Figura
2.17.
Cheema e Klingner (1986) concluíram também que, para uma
dada relação entre módulos de elasticidade da argamassa (Ea) e do bloco
(Eb), a ruptura ocorre preferencialmente por tração no bloco ou por
esmagamento da argamassa. Assim, tem-se que:
Ea/Eb ≥ 0,66 → ruptura por esmagamento da argamassa;
Ea/Eb < 0,66 → ruptura por tração no bloco.
87
Figura 2.17 – Curvas de ruptura para prismas de blocos não grauteados.
Fonte: Cheema e Klingner (1986).
Mohamad (1998) estudou o comportamento da alvenaria
estrutural de blocos de concreto não grauteados em relação às
características mecânicas de diferentes traços de argamassas confinadas
triaxialmente. O autor verificou que quando submetida a esforços de
compressão a ruptura dos blocos de concreto ocorreu em razão dos
seguintes fatores: esmagamento da argamassa, tração na argamassa e
tração no bloco. O autor também observou que, quando utilizada
argamassa com resistência à compressão inferior à do bloco, a ruptura
foi dúctil, ocorrendo um esfacelamento da parte externa das paredes dos
blocos. Quando foi utilizada argamassa com resistência à compressão do
mesmo nível de resistência do bloco na área liquida, o tipo de ruptura foi
frágil, no mesmo sentido da seção transversal do bloco.
O mesmo autor em seu trabalho desenvolvido em 2007, chegou
as seguintes conclusões para prismas de três blocos de concreto
assentados com duas juntas de argamassas: o surgimento das nãolinearidades da alvenaria corresponde ao aumento das deformações
laterais, em consequência à extensiva fissuração do material e a um
aumento progressivo do coeficiente de Poisson.
88
Ainda, segundo Mohamad (2007), para prismas de três blocos
construídos com a argamassa de traço I (1:0,25:3), com maior rigidez, as
fissuras apresentam-se de forma vertical, acontecendo de forma
simétrica em ambos os lados. Em nenhuma das amostras foram
verificados pontos de esmagamento da junta de assentamento sendo que
as trincas foram, para este tipo de prisma, simétricas, verticais e
dispersas.
Para os prismas construídos com argamassa do tipo II (1:0,5:4,5),
de menor rigidez, tiveram, por consequência do esmagamento
localizado, uma associação de trincas verticais em razão da
concentração de tensões em alguns pontos. No processo de ruptura,
verificou-se o início da perda de coesão da argamassa, o esmagamento
da junta de argamassa e o esfacelamento da superfície inferior e superior
do bloco.
Ainda, de acordo com as análises efetuadas por Mohamad (2007),
verificou-se que a alvenaria (bloco e argamassa) tende a igualar a
rigidez dos materiais, ou seja, a junta de argamassa horizontal e o bloco
passam a comportar-se como únicos. Partindo-se da hipótese de que os
resultados obtidos nas deformações do conjunto (bloco e argamassa) são
governados pela deformação da junta de argamassa, até níveis de tensão
igual a 0,3 da resistência à compressão do prisma, o autor conclui que: a
relação entre o módulo de elasticidade confinado e o uniaxial variou de
0,9 a 2,56 e depende da resistência da argamassa. Criou-se um modelo
do comportamento da proporção entre os módulos de elasticidade da
argamassa e do bloco, cuja proporção de rigidez foi de 0,75 e 1,
respectivamente, até a relação tensão/resistência atingir 0,30. Após isso,
para diferentes tipos de composição entre o bloco e a argamassa, ocorre
uma diminuição na proporção de rigidez entre a argamassa e o bloco,
por causa do esmagamento da junta de assentamento ou do
desenvolvimento de tensões de tração localizadas.
2.4. CONSIDERAÇÕES DO CAPÍTULO
Este texto tem como objetivo levantar alguns questionamentos e
fazer algumas observações sobre o que já foi desenvolvido em pesquisas
relacionadas à alvenaria estrutural, mais especificamente, de blocos
cerâmicos.
De acordo com as normas técnicas de projeto para alvenaria
estrutural de blocos cerâmicos, ABNT NBR 15812-1 (2010), a escolha
dos componentes é uma decisão que fica sob responsabilidade dos
projetistas. Estas escolhas de projeto baseiam-se em normas, anos de
89
experiência em desenvolvimento de projetos e execução de obras e estão
fundamentadas, principalmente, nos valores de resistência à compressão
da alvenaria ou de seus componentes.
Entretanto, alguns autores observam que se torna necessária a
compatibilização das propriedades dos componentes da alvenaria
estrutural. Nesse caso, as decisões de projeto deveriam levar em conta
os valores de módulo de elasticidade dos componentes. Por essa razão,
são formuladas as seguintes questões: o que isto implicaria? Qual a
relação entre os custos elevados versus maior confiabilidade de
comportamento estrutural? Qual a melhor escolha a ser tomada pelos
projetistas? Em vista disso, prevê-se a alteração dos custos
(aumentariam) em função da dificuldade de obtenção destes valores de
módulo em ensaios.
Outra questão que pode ser levantada: qual o método mais
adequado para obtenção destes valores de módulo, tendo em vista que
muitos destes ensaios são adaptados à alvenaria estrutural de blocos
cerâmicos? Observa-se que muitos dos ensaios utilizados são adaptados
por questões de facilidade, praticidade e custos. Isto não
necessariamente implica em resultados confiáveis para análise do
comportamento do conjunto, tendo em vista que em muitas
metodologias leva-se em consideração o tipo de material que se está
analisando.
Assim, encontra-se outro campo de pesquisa e diversas
discussões, que não se entende como o objetivo deste trabalho. O
presente trabalho visa analisar o comportamento da alvenaria e não
novas metodologias de ensaios.
Outro ponto a ser discutido: para todos os autores, basicamente a
ruptura da alvenaria ocorre por tensões de tração no bloco, ocasionada
pela deformação da argamassa e/ou graute. Todavia, poucos trabalhos
utilizam-se dos valores de tração dos blocos para comparação e análise
do comportamento da alvenaria estrutural. Entende-se que isto se deve
ao fato que a alvenaria estrutural funcione basicamente sobre
compressão, daí a comparação de valores de resistência à compressão.
Mas também se entende que a dificuldade de realização do ensaio para
obtenção dos valores de resistência à tração faz com que boa parte dos
pesquisadores opte por ensaios de compressão.
Para o ensaio de resistência a tração utiliza-se do mesmo método
empregado para os corpos-de-prova de concreto, ou seja, ensaio de
tração indireta por compressão; desenvolvido para o concreto e não para
um bloco, cuja geometria e material são diferentes.
90
Para alguns autores o aumento da resistência à compressão dos
blocos implica no aumento das suas resistências à tração. O que tornaria
importante a normatização deste ensaio para blocos de alvenaria. Mas
qual seria a relação/taxa de aumento no aumento da resistência à tração
quando do aumento em sua resistência à compressão? Mostra-se,
portanto, outra lacuna para investigação.
Voltando-se para o objetivo principal do trabalho, a norma
técnica brasileira ABNT NBR 15812-2 (2010) permite o grauteamento
das paredes com a própria argamassa de assentamento logo após o
assentamento das unidades, desde que a alvenaria não seja armada.
Contudo, nenhuma pesquisa foi encontrada para alvenaria de blocos
cerâmicos para fundamentar tal especificação. O que leva a formulação
de novas questões: a pressão de adensamento da argamassa utilizada
como preenchimento não provocaria a expulsão desta quando fresca,
ocasionando danos ao desempenho da parede? Seria melhor algum
ensaio ou tempo mínimo de preenchimento com a argamassa? O que
pode ocasionar esta decisão técnica no comportamento mecânico do
conjunto bloco-argamassa de assentamento e argamassa como
preenchimento estrutural?
Tendo em vista que todas as pesquisas com alvenaria grauteada
baseiam-se na utilização de graute convencional, ou seja, de concreto e
este obviamente, sob solicitação mecânica, tem função e comportamento
distinto das argamassas, abre-se aqui precedentes para novas discussões
e pesquisas.
Também se entende que devem ser consideradas em decisões de
projeto, não somente as relações entre resistência à compressão dos
blocos e da argamassa como preenchimento, mas também os valores de
módulo de elasticidade destes componentes. Pois, sabe-se que
propriedades mecânicas como módulo de elasticidade são fatores
importantes no que diz respeito ao comportamento do conjunto. Este
detalhe implicaria também na padronização de ensaios para
componentes de alvenaria em função de suas características e também
aplicação.
A norma técnica brasileira para a argamassa de assentamento,
ABNT NBR 13281 (2005), classifica as argamassas em faixas de
resistência quanto ao desempenho mecânico. Entretanto, não indica qual
a aplicação mais adequada destas argamassas em função destes valores.
Portanto, qual o objetivo de classificação se não há indicação de qual
melhor aplicação deste componente? Adequar esta norma conforme o
tipo de aplicação da argamassa seja para revestimento, assentamento ou
91
preenchimento torna-se também um desafio a ser encarado pelos
pesquisadores.
Face ao exposto, há uma lacuna para investigação e discussões, o
que justifica o objetivo principal deste trabalho.
92
93
3. PROGRAMA EXPERIMENTAL
Neste capítulo será descrito o procedimento experimental adotado
no trabalho. São apresentados os procedimentos de caracterização dos
materiais e componentes utilizados na moldagem dos prismas, os traços
em volume e massa das argamassas de assentamento e grautes, os
procedimentos de moldagem bem como os equipamentos utilizados para
os ensaios de caracterização física e mecânica dos materiais e
componentes.
O primeiro objetivo dos ensaios de caracterização é permitir a
comparação das propriedades dos prismas e os seus componentes,
procurando semelhanças e diferenças entre suas propriedades físicas e
mecânicas, estudando desta forma a viabilidade de utilização da técnica
de preenchimento das paredes de alvenaria com a argamassa de
assentamento.
O objetivo secundário é a obtenção das principais propriedades
mecânicas dos materiais e os diagramas tensão-deformação dos prismas,
que viabilizam as análises numéricas pelo Método dos Elementos
Finitos. Esta análise tem a finalidade de avaliar o comportamento de
algumas séries de prismas, através de análise de tensões sob compressão
axial, com a utilização do programa computacional Marc Mentat 2012.
A análise numérica realizada é baseada no comportamento não linear
dos materiais, sendo utilizado para os prismas a micromodelagem.
A caracterização se deu com a análise das resistências e
propriedades elásticas dos blocos, das argamassas, dos grautes e dos
prismas. Os ensaios em blocos e prismas foram conduzidos até a
ruptura, para que através dos parâmetros obtidos, ou seja, medição dos
deslocamentos, deformações e modo de ruptura, possibilite a
comparação de comportamento e resistência entre as diferentes séries de
prismas analisadas.
Para tanto, utilizaram-se três blocos de geometrias distintas,
designados blocos tipo B6, B12 e B15. Para a realização do estudo
utilizaram-se dois lotes de blocos produzidos em datas diferentes. Para a
determinação da resistência à compressão dos prismas foram utilizados
os blocos do lote 1, e para a determinação do módulo de elasticidade
foram utilizados os blocos do lote 2, conforme 2ª e 3ª Etapas do
fluxograma da Figura 3.1.
Para as argamassas, utilizaram-se seis traços com resistências
distintas, sendo três traços de argamassas mistas, designadas argamassas
94
tipo A, B e C; três traços de argamassas industrializadas, designadas
argamassas tipo M, 5 e 10.
Utilizaram-se também três traços de grautes, com resistências
distintas, designados G1, G2 e G3.
Para este trabalho foram moldados prismas de três fiadas à
prumo, com argamassamento total. Na 2ª Etapa do programa
experimental, os prismas moldados foram utilizados para obtenção dos
valores de resistência à compressão e os prismas moldados na 3ª Etapa
do programa experimental, foram utilizados para obtenção dos valores
de módulo de elasticidade. Divididos entre estas duas etapas do trabalho,
foram moldados cinco prismas para cada combinação bloco-argamassagraute, sendo 48 tipos de prismas com características distintas,
totalizando 240 prismas.
Basicamente, o programa experimental constitui-se de três etapas.
Inicialmente, na primeira etapa, caracterizam-se os materiais
empregados na produção das argamassas, grautes e os blocos utilizados
na moldagem dos prismas. Nesta etapa também se realizou a definição e
conversão dos traços das argamassas e grautes utilizados, conforme é
apresentado no fluxograma da Figura 3.1.
Na segunda e terceira etapas do programa experimental realizouse a caracterização mecânica dos blocos, argamassas, grautes, e prismas
empregados no trabalho, conforme o fluxograma da Figura 3.1. De
acordo com a Figura 3.1, fb, fbk e Eb, representam respectivamente,
resistência média à compressão, resistência característica à compressão
e módulo de elasticidade do bloco; farg e Earg representam resistência
média à compressão e módulo de elasticidade da argamassa; para os
grautes, fg e Eg, representam resistência média à compressão e módulo
de elasticidade dos grautes; fp e Ep representam a resistência média à
compressão e módulo de elasticidade dos prismas.
A caracterização mecânica dividiu-se entre estas duas etapas em
virtude das limitações do espaço físico e disponibilidade de
equipamentos para a realização dos ensaios no laboratório. Entretanto, a
terceira etapa do programa experimental realizou-se somente com a
constatação de nenhuma diferença significativa entre os valores das
propriedades mecânicas obtidas para os blocos dos dois lotes recebidos.
Todos os ensaios foram realizados no Laboratório de Materiais de
Construção Civil – LMCC, da Universidade Federal de Santa Catarina –
UFSC.
95
Figura 3.1 - Programa de caracterização dos materiais, argamassas, blocos e
prismas.
Fonte: Autor (2015).
96
3.1. MATERIAIS UTILIZADOS
Para o desenvolvimento do trabalho utilizaram-se materiais
disponíveis na região da Grande Florianópolis e habitualmente
utilizados em alvenaria estrutural. As propriedades e metodologias
empregadas em suas caracterizações são descritos a seguir.
3.1.1. Agregados
Neste trabalho, para a produção das argamassas mistas e dos
grautes, como agregado miúdo, utilizou-se areia quartzosa de origem
natural. Em estudo prévio, realizou-se a análise granulométrica das
areias comercializadas na região da Grande Florianópolis.
Para manter o padrão granulométrico em todo estudo, realizou-se
a composição granulométrica da areia, conforme ABNT NBR 7211
(2009), BS 1200 (1976) e ASTM C-144 (1987), normas estas
específicas para argamassas e concreto.
A caracterização granulométrica da areia realizou-se de acordo
com a norma ABNT NBR NM 248 (2003): Agregados - Determinação
da composição granulométrica. As porcentagens retidas acumuladas em
cada peneira para a areia utilizada se encontram na Tabela 3.1, sendo
que a curva granulométrica da areia e os limites granulométricos
indicados pela ABNT NBR 7211 (2009), específica para concreto, estão
apresentados na Figura 3.2. Na Figura 3.3, encontra-se a curva
granulométrica da areia utilizada e os limites inferiores (LI) e superiores
(LS) especificados pelas normas BS 1200 (1976) e ASTM C-144
(1987), indicadas para argamassas de assentamento.
Tabela 3.1 – Composição granulométrica do agregado miúdo utilizado.
Peneira
% Retida Acumulada
(abertura em mm)
4,75
0
2,36
2
1,20
10
0,60
35
0,30
70
0,15
90
0,075
97
Fundo
100
Fonte: Autor (2015).
97
Figura 3.2 - Curva granulométrica da areia utilizada e zonas de utilização
conforme ABNT NBR 7211 (2005).
100
97
Porcentagem Retida Acumulada (%)
90
Zona Ótima Inferior
Zona Ótima Superior
Zona Utilizável Inferior
Zona Utilizável Superior
Areia Utilizada
90
80
70
70
60
50
40
35
30
20
10
10
0
Fundo 0,075
2
0,15
0,3
0,6
1,2
2,4
4,8
6,3
9,5
Abertura das Peneiras (mm)
Fonte: Autor (2015).
Figura 3.3 - Curva granulométrica da areia utilizada e limites de utilização
conforme BS 1200 (1976) e ASTM C-144 (1987).
100
97
Porcentagem Retida Acumulada (%)
90
LI BS 1200
LS BS 1200
LI ASTM C144
LS ASTM C144
Areia Utilizada
90
80
70
70
60
50
40
35
30
20
10
10
0
Fundo 0,075
2
0,15
0,3
0,6
1,2
2,4
4,8
6,3
9,5
Abertura das Peneiras (mm)
Fonte: Autor (2015).
98
Para a produção dos grautes, como agregado graúdo, utilizou-se
brita de origem granítica comercializada na região da Grande
Florianópolis. Durante todo o estudo, foi mantido o mesmo padrão
granulométrico do agregado graúdo para a confecção dos grautes.
As porcentagens retidas acumuladas em cada peneira, da brita
utilizada no estudo, se encontram na Tabela 3.2, sendo que sua curva
granulométrica e os limites granulométricos indicados pela ABNT NBR
7211 (2009) estão apresentados na Figura 3.4. Conforme pode ser
observado na Figura 3.4, a brita utilizada no estudo se encontra dentro
dos limites granulométricos especificados pela norma ABNT NBR 7211
(2009), para uso em concretos, e situa-se na zona granulométrica
4,75/12,5. A dimensão máxima encontrada para o agregado graúdo foi
de 12,5 mm, valor este dentro do limite de 1/3 da menor dimensão dos
furos a serem preenchidos pelos grautes, preconizado pela norma ABNT
NBR 15812-2 (2010).
Tabela 3.2 – Composição granulométrica do agregado graúdo utilizado.
Peneira
(abertura em mm)
% Retida
Acumulada
12,50
0
9,50
6
6,30
53
4,75
86
2,36
97
Fundo
100
Fonte: Autor (2015).
99
Figura 3.4 - Curva granulométrica da brita utilizada e limites de utilização
conforme ABNT NBR 7211 (2005).
Porcentagem Retida Acumulada (%)
100
90
97
97
86
80
70
60
53
50
40
30
20
Limite Inferior
Limite Superior
10
Brita Utilizada
0
Fundo 0,075 0,15 0,3
6
0,6
1,2
2,4
4,8
6,3
9,5
12,5
Abertura das Peneiras (mm)
Fonte: Autor (2015).
As determinações das massas específicas, massas unitárias e teor
de material fino (material pulverulento) dos agregados realizaram-se de
acordo com as normas ABNT NBR NM 52 (2003) – Agregado miúdo –
Determinação de massa especifica e massa especifica aparente, ABNT
NBR NM 53 (2003) – Agregado graúdo – Determinação de massa
especifica, massa especifica aparente e absorção de água, ABNT NBR
NM 45 (2006) – Agregados - Determinação da massa unitária, ABNT
NBR NM 46 (2003) – Agregados – Determinação do material fino que
passa através da peneira 75 µm, por lavagem. As massas específicas e
unitárias são características importantes na transformação de traços de
argamassas e grautes em massa para volume e vice-versa.
Assim, os valores de massas específicas, massas unitárias e teores
de material fino encontrados para os agregados utilizados encontram-se
na Tabela 3.3.
100
Tabela 3.3 - Características físicas dos materiais utilizados nas argamassas de
assentamento e grautes.
Massa
Específica
Material
Aparente
(kg/dm³)
Areia
2,55
Brita
2,69
Fonte: Autor (2015).
Massa
Unitária
(kg/dm³)
Módulo
de
Finura
1,40
1,45
2,1
5,75
Teor de
Material
Fino
(%)
3,5
1,1
Dimensão
Máxima
Característica
(mm)
2,4
12,5
3.1.2. Aglomerantes
O cimento utilizado neste estudo foi o cimento Portland CP II Z32, proveniente da empresa Votorantim Cimentos Brasil S.A., indicado
para argamassas e disponível no mercado. A caracterização química do
cimento Portland CPII Z-23, cedida pela empresa Votorantim, encontrase na Tabela 3.4. De acordo a ABNT NBR 11578 (1991): Cimento
Portland composto – Especificação, o cimento utilizado encontra-se de
acordo com os limites estabelecidos por norma.
Tabela 3.4 - Caracterização química do Cimento Portland CP II Z-32.
Limites de Norma
Ensaio
Teores (%)
≤ 4,0
Trióxido de enxofre – SO3
2,66
≤ 6,50
Óxido de magnésio - MgO
5,97
≤ 6,50
Perda ao Fogo
5,35
≤ 16,0
Resíduo insolúvel
7,80
Fonte: Empresa Votorantim Cimentos Brasil S.A. (2012).
A cal utilizada para o estudo foi do tipo hidratada CH III,
proveniente da empresa Cal Cem, e que estava disponível no mercado.
A caracterização química da cal hidratada CH III, cedida pela empresa
Cal Cem, encontra-se na Tabela 3.5. De acordo com a ABNT NBR 7175
(2003): Cal hidratada para argamassas – Requisitos, a cal utilizada
encontra-se dentro do especificado por norma.
101
Tabela 3.5 - Composição da Cal CH III.
Ensaio
Teores (%)
Óxidos Totais (CaO total + MgO
total)
Anidrido Carbônico (Co2)
Óxidos Totais não hidratados
(CaO + MgO)
Granulometria # 30 (0,600 mm)
Granulometria # 200 (0,075 mm)
Fonte: Empresa Cal Cem (2012).
96,6
2,8
5,7
0,0
12,0
Limites de
Norma
≤ 88,0
≤ 13,0
≤ 15,0
≤ 0,5
≤ 15,0
Para os ambos aglomerantes, a determinação de suas massas
específicas foi realizada conforme a norma ABNT NBR NM 23 (2000)
– Cimento Portland e outros materiais em pó – Determinação da massa
específica. Para a obtenção das massas unitárias realizou-se o mesmo
procedimento utilizado para os agregados. As massas unitárias são
características importantes na transformação de traços de argamassas e
grautes em massa para volume e vice-versa.
Assim, os resultados da caracterização física encontrados para
cada um dos aglomerantes utilizados na produção das argamassas e
grautes são apresentados na Tabela 3.6.
Tabela 3.6 - Características físicas dos materiais utilizados nas argamassas de
assentamento e grautes.
Material
Cimento CP II Z 32
Cal Hidratada CH III
Fonte: Autor (2015).
Massa Específica
Aparente (kg/dm³)
Massa Unitária
(kg/dm³)
2,82
2,35
1,13
0,70
3.1.3. Água
A água utilizada no desenvolvimento do trabalho foi proveniente
da rede de abastecimento local, CASAN – Companhia Catarinense de
Águas e Saneamento.
102
3.2. BLOCOS CERÂMICOS
Para a realização do trabalho utilizou-se blocos cerâmicos
estruturais da classe T29, com dimensões nominais 14x19x29 cm com
resistências nominais declaradas pelo fabricante de 6 MPa, 12 MPa e 15
MPa, com geometrias distintas conforme Figura 3.5. Para facilitar o
entendimento ao longo do trabalho, as três classes de blocos foram
denominadas de acordo com as suas resistências nominais, ou seja,
como B6, B12 e B15.
Figura 3.5 - Geometria e respectivas resistências nominais dos blocos utilizados.
B6
B12
B15
Fonte: Autor (2015).
Foram recebidos blocos de dois lotes (L1 e L2), produzidos em
datas diferentes por uma mesma empresa da região do Alto Vale do
Itajaí em Santa Catarina. Inicialmente, para ambos os lotes, fez-se a
verificação das variações dimensionais dos blocos estudados de acordo
com a ABNT NBR 15270-3 (2005). Para a determinação das dimensões,
áreas bruta e líquida, índice de absorção d’água (AA) e índice de
absorção inicial (AAI), utilizou-se uma amostra com treze blocos para
cada lote recebido, de acordo com a norma ABNT NBR 15270-3
(2005).
Logo após, iniciando a 2ª Etapa do programa experimental,
realizou-se o ensaio de resistência à compressão para cada um dos treze
blocos que constituíam a amostra, também conforme especificações da
ABNT NBR 15270-3 (2005). Para os ensaios de resistência à
compressão a velocidade de carregamento foi de 0,05 ± 0,01 MPa/s,
conforme norma ABNT NBR 15270-3 (2005), e para os ensaios de
tração indireta utilizou-se a velocidade de 0,15 kN/s, conforme ASTM C
1006 (1984).
103
Conforme prescrito em norma, os blocos foram capeados com
pasta de cimento, com no mínimo 48 h antes do ensaio, com espessura
variando entre 1 e 3 mm. O capeamento foi utilizado para corrigir
imperfeições das superfícies dos blocos, gerados pelo processo de
fabricação, e para a melhor distribuição do carregamento em toda a área
da seção do bloco, durante a realização dos ensaios. Para todos os
ensaios de resistência à compressão e tração dos blocos, utilizou-se a
prensa de sistema hidráulico SHIMADZU, com capacidade máxima de
2000 kN, do Laboratório de Materiais e Construção Civil –
LMCC/UFSC.
Para a determinação do módulo de elasticidade e coeficiente de
Poisson do material do bloco, referente à 3ª Etapa do programa
experimental, foram extraídos três corpos-de-prova prismáticos de cada
uma das classes de bloco, com dimensões de (20x40) mm e espessura
variável de acordo com suas respectivas geometrias. Os corpos-de-prova
foram extraídos das paredes localizadas na região central do bloco
(septo) em razão da maior facilidade em cortá-las e a menor variação
existente entre as espessuras das paredes desta região entre as três
classes de blocos utilizadas, tentando-se assim padronizar o máximo
possível estas dimensões.
Inicialmente cortaram-se os blocos em porções menores com uma
serra circular, para posteriormente, os corpos-de-prova prismáticos
serem cortadas nas dimensões finais com um disco de corte diamantado
(Figura 3.6), que proporcionou melhor acabamento e maior controle nas
dimensões dos corpos-de-prova.
Figura 3.6 - Corte dos corpos-de-prova do material dos blocos.
Fonte: Autor (2015).
104
Após esta etapa do processo, com os corpos-de-prova limpos e
secos, realizou-se a preparação de suas superfícies para a fixação dos
strain gauges, com cola da marca Loctite (Figura 3.7). Estes strain
gauges foram utilizados na obtenção dos valores de deformação dos
corpos-de-prova, utilizados na determinação dos valores de módulo de
elasticidade e coeficiente de Poisson para as respectivas classes de
blocos. Os strain gauges estavam conectados a um sistema de aquisição
de dados composto por um Dataloger Spider 8 da marca HBM e
software CATMAN, do mesmo fabricante.
Para a obtenção de dados confiáveis para a determinação dos
valores de módulo de elasticidade e coeficiente de Poisson, utilizaram-se
dois strain gauges fixados em cada um dos lados do corpo-de-prova,
para compensar possíveis deformações excessivas apresentadas durante
o ensaio, em cada um dos seus lados. Cada strain gauge fornecia valores
de deformações longitudinal e transversal. Os valores de deformação
utilizados na construção do diagrama tensão x deformação, foram
obtidos com a média dos valores de deformação longitudinal e
transversal registrados para cada um dos corpos-de-prova.
Figura 3.7 – Corpo-de-prova após a fixação dos strain gauges.
Fonte: Autor (2015).
105
Neste ensaio adotaram-se os procedimentos da norma ABNT
NBR 8522 (2008), de acordo com as recomendações ABNT NBR
15270-3 (2005), devida a falta de ensaios normalizados utilizando estes
corpos-de-prova para o material do bloco cerâmicos. Desta forma,
adotou-se a velocidade de carregamento de 0,45 ± 0,15 MPa/s,
conforme a ABNT NBR 8522 (2008). A aplicação da carga foi realizada
em um único ciclo, de forma lenta e contínua. Assim, de acordo com
esta norma, calculou-se o módulo de elasticidade secante obtido para as
tensões de 0,5 MPa e 30% da carga de ruptura, para todas os corpos-deprova prismáticos.
Para a realização dos ensaios para obtenção do módulo de
elasticidade e coeficiente de Poisson dos materiais dos blocos utilizou-se
a prensa de sistema hidráulico INSTRON, com capacidade máxima de
50 kN, do Laboratório Nanotec – LMCC/UFSC, e uma célula de carga
de 50 kN conectada ao equipamento de aquisição de dados (Figura 3.8),
ambas com capacidade de carga adequada aos corpos-de-prova
ensaiados, conforme observado em ensaios prévios. Foi necessária a
utilização da célula de carga por causa da impossibilidade de aquisição
direta dos dados de carregamento aplicada pela prensa hidráulica,
durante os ensaios.
Para este ensaio, inicialmente fez-se a calibração da célula de
carga, para a aquisição de dados compatíveis com os apresentados pela
prensa e pelo software CATMAN. Os valores de carga mostrados pela
prensa e da célula de carga foram filmados para correções, caso
necessário. Durante a realização do ensaio, tomou-se o cuidado para que
realmente estivessem sendo registrados pelo programa os dados de
deformação dos strain gauges e de aplicação do carregamento pela
célula de carga. Caso a diferença nos valores de deformação vertical
fosse superior a 20%, o corpo-de-prova era reposicionado e inicia-se
novamente o ensaio.
106
Figura 3.8 – Configuração do ensaio com amostra, célula de carga e prensa.
Fonte: Autor (2015).
3.3. ARGAMASSAS DE ASSENTAMENTO
Para o desenvolvimento do trabalho, foram utilizadas seis tipos
de argamassas com diferentes resistências à compressão, sendo três
traços de argamassas mistas (cimento, cal e areia) e três argamassas
industrializadas, com dosagens e resistências distintas.
Os traços utilizados para a confecção das argamassas mistas
foram os especificados pela norma britânica BS 5628: Part 1 (1992),
como classe (i), (ii) e (iii). Esta classificação e o traço em volume
correspondente pela norma britânica, bem como a denominação das
argamassas utilizadas neste estudo, encontram-se na Tabela 3.7.
107
Tabela 3.7 - Denominação das argamassas.
Traço (em
volume)
1 : 1/4 : 3
1 : 1/2 :4,5
1:1:6
Classe
(i)
(ii)
(iii)
Fonte: Autor (2015).
Denominação
A
B
C
Os traços prescritos pela BS 5628: Part 1 (1992), que são
apresentados em volume, foram convertidos para massa para diminuir
no processo de produção das argamassas as variações em razão de
medições volumétricas imprecisas. Para esta conversão utilizou-se a
seguinte equação:
1:
Vch .γch
Va .γa
:
Vh
γc
.γ
V0 c
(3.1)
Onde:
Vch = proporção da cal hidratada no traço da argamassa, em
volume unitário (dm³);
Va = proporção do agregado miúdo no traço da argamassa, em
volume unitário (dm³);
γc = massa unitária do cimento no estado solto (kg/dm³);
γch = massa unitária da cal hidratada no estado solto (kg/dm³);
γa = massa unitária da areia no estado solto (kg/dm³);
Vh/V0 = coeficiente médio de inchamento do agregado, conforme
ABNT NBR 6467 (2006). Adotou-se coeficiente igual a 1, para areia
seca.
Em estudo preliminar, para cada traço utilizado, definiram-se o
índice de consistência e a relação água/cimento (Fa/c) em função da
coesão e trabalhabilidade das argamassas e características dos materiais
empregados em sua produção, procurando-se manter a mesma
consistência para os seis traços durante todo o estudo. O procedimento
para a determinação da consistência seguiram os procedimentos
estabelecidos na norma ABNT NBR 13276 (2002). O teor de
incorporação de ar e a capacidade de retenção de água também foram
determinados para cada um dos traços de argamassas, respectivamente,
conforme as normas EN 1015-7:1999 e ABNT NBR 13277 (2005).
Estas características, depois de definidas, foram mantidas durante todo o
estudo.
108
A Tabela 3.8 mostra os traços convertidos de volume para massa,
a relação água/cimento (Fa/c), teor de ar incorporado, potencial de
retenção de água e o índice de consistência das argamassas mistas
utilizadas no estudo.
Tabela 3.8 - Denominação e características das argamassas mistas.
Tipo
Traço em
volume
(cim. : cal :
areia)
A
1 : 1/4 : 3
B
1 : 1/2 :4,5
C
1:1:6
Traço em
massa (cim.
: cal : areia)
1 : 0,15 :
3,72
1 : 0,31 :
5,58
1 : 0,62 :
7,43
Teor
de Ar
Incorp.
(%)
Retenção
de Água
(%)
Fa/c
Consistência (mm)
5,8
80
0,95
± 260
6,0
75
1,45
± 275
5,2
80
1,95
± 285
Fonte: Autor (2015).
Para as argamassas industrializadas foram utilizadas argamassas
do tipo Múltiplo Uso, de assentamento estrutural de 5 MPa e 10 MPa,
produzidas por uma empresa atuante no mercado nacional. Na
caracterização no estado fresco das argamassas industrializadas, foram
realizados os mesmos ensaios utilizados na caracterização das
argamassas mistas.
Assim a denominação para os três classes de argamassas
industrializadas, a relação água/argamassa anidra (Fa/arg) e as demais
propriedades determinadas em estudo preliminar, em função da coesão e
trabalhabilidade desejada e que foram mantidas durante todo o estudo,
encontram-se na Tabela 3.9.
109
Tabela 3.9 - Denominação e características das argamassas industrializadas.
Tipo de
Argamassa
Industrializa
Denominação
Teor de Ar
Incorporado
(%)
Retenção
de Água
(%)
Fa/arg
Consistência
(mm)
Múltiplo Uso
M
11,0
89,5
0,13
4
± 175
5
5,8
85,9
0,14
4
± 210
10
5,0
85,5
0,15
5
± 220
Assentamento
Estrutural de
5 MPa
Assentamento
Estrutural de
10 MPa
Fonte: Autor (2015).
As argamassas mistas e industrializadas apresentaram todos os
requisitos exigidos pela norma NBR 13281 (2005), exceto a argamassa
mista do tipo B, que apresentou valor de retenção de água abaixo dos
limites desta norma. Entretanto, conforme observado em laboratório,
esta diferença não inviabilizou sua utilização na moldagem e
preenchimento dos prismas, não interferindo assim no objetivo principal
do estudo.
A preparação das argamassas mistas, de acordo com a antiga
ABNT NBR 8798 (1985), foi executada em misturador mecânico de
eixo inclinado (betoneira), conforme a seguinte metodologia:
1) Colocava-se parte da água de amassamento e todo o agregado
miúdo no misturador em funcionamento;
2) Em seguida, colocava-se todo o cimento no misturador,
também em funcionamento;
3) Logo em seguida, adicionava-se a cal hidratada e o resto da
água.
A mistura dos materiais, durante a preparação das argamassas
mistas, foi realizada durante ± 5 min, com a quantidade de água
necessária para conferir à mistura a consistência e trabalhabilidade
determinadas em ensaios prévios.
Para a preparação das argamassas industrializadas foi utilizada
uma argamassadeira de eixo vertical, em razão de indisponibilidade do
equipamento indicado pelo fabricante. Mesmo assim, em ensaios
preliminares, o uso deste equipamento demonstrou-se mais adequado do
que o utilizado para a preparação das argamassas mistas, em
consequência aos aditivos incorporadores de ar existentes na
composição das argamassas industrializadas. Assim, a mistura das
110
argamassas industrializadas foi executada de acordo com a seguinte
metodologia:
1) Colocava-se metade da água de amassamento na
argamassadeira;
2) Em seguida, colocava-se toda a argamassa anidra na
argamassadeira, em movimento;
3) Depois era realizada a mistura na argamassadeira por 3 min.
Após esta etapa, quando necessário, era desligado o equipamento e
retirava-se parte da argamassa aderida na parede da cuba da
argamassadeira, por não mais do que 3 min;
4) Na sequência, colocava-se a outra metade da água na cuba e
realizava-se novamente a mistura por 1 min, tempo necessário para
conferir à mistura a consistência e trabalhabilidade determinadas em
ensaios prévios.
Na 2ª Etapa do programa experimental, para cada moldagem de
prismas vazios ou grauteados com as argamassas A, B, C, M, 5 e 10,
foram moldados no mínimo três corpos-de-prova prismáticos (4x4x16)
cm³, em moldes metálicos, para a determinação das propriedades
mecânicas das argamassas, por meio de ensaio de resistência à
compressão e resistência à tração na flexão, aos 28 dias, de acordo com
as recomendações da norma ABNT NBR 13279 (2005).
Na a realização de todos os ensaios de compressão e tração na
flexão dos corpos-de-prova prismáticos das argamassas utilizou-se a
prensa de sistema hidráulico da marca SOLOTEST, com capacidade
máxima de 196 kN para o ensaio de compressão e 19,6 kN para o ensaio
de tração na flexão, do Laboratório de Materiais e Construção Civil –
LMCC/UFSC.
As velocidades de carga utilizadas para todos os ensaios
resistência à compressão e tração na flexão foram, respectivamente, de
500 ± 50 N/s e 50 ± 10 N/s, conforme ABNT NBR 13279 (2005).
Para a determinação do módulo de elasticidade e coeficiente de
Poisson, ensaios referentes à 3ª Etapa do programa experimental, foram
moldados três corpos-de-prova cilíndricos (ϕ5x10) cm para cada tipo de
argamassa, adotando os procedimentos da norma ABNT NBR 8522
(2008), de acordo com as recomendações da norma ABNT NBR 152703 (2005).
Nesta 3ª Etapa, após o processo de cura em sala climatizada,
realizou-se a preparação da superfície dos corpos-de-prova para a
fixação dos strain gauges, com cola da marca Loctite (Figura 3.9). Os
strain gauges estavam conectados a um sistema de aquisição de dados
111
composto por um Dataloger Spider 8 da marca HBM e software
CATMAN, do mesmo fabricante.
Figura 3.9 –Corpo-de-prova após a fixação dos strain gauges.
Fonte: Autor (2015).
Para a obtenção de dados confiáveis para a determinação dos
valores de módulo de elasticidade e coeficiente de Poisson, utilizaram-se
dois strain gauges fixados em cada um dos lados da amostra, para
compensar possíveis deformações excessivas apresentadas durante o
ensaio, em cada um dos lados da amostra. Cada strain gauge fornecia
valores de deformações longitudinal e transversal. Os valores de
deformação utilizados na construção do diagrama tensão x deformação
cada classe de argamassa, foram obtidos com a média dos valores de
deformação longitudinal e transversal registrados para cada corpo-deprova.
Nestes estes ensaios de determinação do módulo de elasticidade e
coeficiente de Poisson das argamassas, utilizou-se a prensa de sistema
hidráulico SHIMADZU com capacidade máxima de 2000 kN, entretanto
112
configurada na escala de 100 kN, e uma célula de carga de 50 kN
conectada ao equipamento de aquisição de dados, ambas com
capacidade de carga adequada aos corpos-de-prova utilizados, conforme
observado nos ensaios de resistência a compressão. Foi necessária a
utilização da célula de carga por causa da impossibilidade de aquisição
direta dos dados de carregamento aplicados pela prensa hidráulica,
durante os ensaios.
Para este ensaio, inicialmente fez-se a calibração da célula de
carga, para a aquisição de dados compatíveis com os apresentados pela
prensa e pelo software CATMAN. Os valores de carga registrados pela
prensa e pela célula de carga foram filmados para correções, caso
necessário. Durante a realização do ensaio, tomou-se o cuidado para que
realmente estivessem sendo registrados pelo programa os dados de
deformação dos strain gauges e de aplicação do carregamento pela
célula de carga. Caso a diferença nos valores de deformação vertical
fosse superior a 20%, o corpo-de-prova era reposicionado e inicia-se
novamente o ensaio.
Para os ensaios de módulo de elasticidade e Poisson utilizou-se a
velocidade de carregamento de 0,45 ± 0,15 MPa/s, conforme ABNT
NBR 8522 (2008), com a aplicação da carga ocorrendo em um único
ciclo, de forma lenta e contínua. Assim, Assim, de acordo com esta
norma, calculou-se o módulo de elasticidade secante obtido para as
tensões de 0,5 MPa e 30% da carga de ruptura, para todas os corpos-deprova de argamassas. Todos os equipamentos utilizados pertenciam ao
Laboratório de Materiais e Construção Civil – UFSC.
3.4. GRAUTES
Neste trabalho foram utilizados três traços de grautes, de
resistência e módulos de elasticidade distintos, para posterior
comparação com o grauteamento utilizando-se a própria argamassa de
assentamento. A dosagem dos grautes foi realizada de acordo com o
método IPT/EPUSP. Com este procedimento de dosagem foram
determinados os dois traços de menor resistência, que foram mantidos
em todo o estudo. O cálculo da dosagem não será apresentado, pois o
objetivo do estudo não era estudar a dosagem dos grautes, mas sim,
utilizar traços que resultariam em resistências médias à compressão
distintas.
Para obtenção do graute de maior resistência, foi utilizada uma
mistura industrializada de base cimentícia, tradicionalmente empregado
em reforços estruturais, com nome comercial Sika Grout, produzido pela
113
Empresa Sika S.A. Essa mistura consiste basicamente de cimento
Portland, areia de quartzo de granulometria selecionada e aditivos
especiais. Para a produção deste traço de maior resistência, foi seguida a
recomendação do fabricante de incorporação de 30% de pedrisco, em
massa, ao sika grout.
Assim, a Tabela 3.10 apresenta as denominações dos grautes,
traços utilizados (em massa), relação água/cimento (Fa/c) e as
resistências médias à compressão esperadas para cada um dos traços,
que foram mantidas durante todo o estudo.
Tabela 3.10 - Denominação e resistências esperadas dos grautes.
G1*
Traço (em massa)
(cimento : areia :
brita)
1 : 0 : 0,3
0,13
Resistência Média à
Compressão Esperada
(MPa)
40
G2
1 : 1,82 : 2,04
0,60
25
G3
1 : 2,56 : 2,58
0,80
15
Denominação
Fa/c
Nota: *Traço em massa (sika grout : areia : brita)
Fonte: Autor (2015).
Neste trabalho, para os grautes, adotaram-se estes valores de
resistência médios à compressão tomando-se como referência trabalhos
já realizados pelo grupo GDA da UFSC. Para o menor valor de
resistência à compressão adotou-se o maior valor nominal de resistência
à compressão dos blocos utilizados na moldagem dos prismas, neste
caso, utilizou-se o valor de 15 MPa, referente ao bloco B15.
O abatimento do tronco de cone (slump) fixado para o estudo foi
de 210 ± 10 mm, em função das características dos materiais
empregados e da trabalhabilidade necessária para o grauteamento dos
prismas. O slump para cada traço foi determinado, conforme a norma
ABNT NBR NM 67 (1998).
A preparação dos três traços de grautes foi executada em
misturador mecânico (betoneira de queda livre de 120 l de capacidade)
de eixo inclinado, de acordo com a seguinte metodologia:
1) Inicialmente colocava-se 80% da água de amassamento na
betoneira;
2) Depois, era colocado todo o agregado graúdo;
3) Na sequência, com a betoneira em movimento, se colocava
todo o cimento;
114
4) Depois, todo o agregado miúdo;
5) Por último, adicionava-se o restante de água.
A mistura dos materiais, durante a preparação dos grautes, era
realizada durante 3 a 5 min, com a quantidade de água necessária para
conferir à mistura a consistência e trabalhabilidade, conforme
determinado em ensaios prévios.
Durante a moldagem dos prismas grauteados, para cada graute do
tipo G1, G2 e G3, foram moldados seis corpos-de-prova cilíndricos de
(ϕ10x20) cm, em moldes metálicos, para a determinação de suas
propriedades mecânicas, ou seja, para os ensaios de resistência à
compressão, de módulo de elasticidade e coeficiente Poisson, após 28
dias de moldagem.
As moldagens dos corpos-de-prova, os ensaios de resistências à
compressão, os ensaios de módulo de elasticidade e Poisson para os três
traços de grautes foram realizadas de acordo com as normas ABNT
NBR 5738 (2003), ABNT NBR 5739 (2007) e ABNT NBR 8522
(2008). Para a realização de todos os ensaios de caracterização mecânica
dos corpos-de-prova utilizou-se a prensa de sistema hidráulico
SHIMADZU, com capacidade máxima de 2000 kN, do Laboratório de
Materiais e Construção Civil – UFSC.
Na 2ª Etapa do programa experimental, os corpos-de-prova
moldados para os três tipos de grautes foram utilizados para obtenção
dos valores de resistência à compressão e os corpos-de-prova moldados
na 3ª Etapa do programa experimental, foram utilizados para obtenção
dos valores de módulo de elasticidade e coeficiente de Poisson.
A velocidade de carga utilizada para todos os ensaios de
caracterização mecânica dos grautes foi de 0,45 ± 0,15 MPa/s, conforme
as normas ABNT NBR 5739 (2007) e ABNT NBR 8522 (2008).
Na 3ª Etapa do programa experimental, realizaram-se dois
ensaios diferentes para a determinação dos valores de modulo de
elasticidade e coeficiente de Poisson.
No primeiro ensaio utilizou-se um compressômetro para a
determinação dos módulos de elasticidade e coeficiente de Poisson.
Basicamente, o compressômetro consta de dois anéis metálicos fixados
na base e no topo do corpo-de-prova para a determinação da deformação
longitudinal e um anel diametral, para a determinação da deformação
transversal (Figura 3.10). Este equipamento foi adaptado para a
utilização de transdutores de deslocamento para as leituras dos
deslocamentos, utilizados no cálculo das deformações. Estes
transdutores de deslocamento estavam conectados a um sistema de
115
aquisição de dados composto por um Dataloger Spider 8 da marca HBM
e software CATMAN, do mesmo fabricante.
Assim foram utilizados dois transdutores de deslocamento para a
medição do deslocamento longitudinal e um para o transversal,
conforme Figura 3.10. Para a construção do diagrama tensão x
deformação foi utilizada a média dos valores de deformações
longitudinais determinadas para as duas leituras de deslocamento
vertical.
Figura 3.10 – Disposição da fixação dos transdutores de deslocamento nos
corpos-de-prova.
Fonte: Autor (2015).
Entretanto, em virtude da dificuldade de realização do ensaio e o
desgaste do equipamento, a leitura obtida no deslocamento diametral foi
maior que a deformação observada no corpo-de-prova durante o ensaio.
Após o tratamento dos dados, esse problema observado foi comprovado
com os elevados valores de coeficiente de Poisson obtidos para os três
traços de grautes, prejudicando a determinação experimental destes
valores.
116
Assim, como segunda tentativa, optou-se pela utilização de strain
gauges para a obtenção dos valores de deformação dos grautes,
utilizados na determinação dos valores de módulo de elasticidade e
coeficiente de Poisson. Após o processo de cura em sala climatizada,
realizou-se a limpeza e preparação da superfície dos corpos-de-prova
para a fixação dos strain gauges, com cola da marca Loctite (Figura
3.11). Estes strain gauges estavam conectados a um sistema de aquisição
de dados composto por um Dataloger Spider 8 da marca HBM e
software CATMAN, do mesmo fabricante.
Para a obtenção de dados confiáveis para a determinação dos
valores de módulo de elasticidade e coeficiente de Poisson, utilizaram-se
dois strain gauges fixados em cada um dos lados dos corpos-de-prova,
para compensar possíveis deformações excessivas apresentadas durante
o ensaio, em cada um dos lados da amostra. Cada strain gauge fornecia
valores de deformações longitudinal e transversal. Os valores de
deformação utilizados na construção do diagrama tensão x deformação
para cada um dos três traços de graute, foram obtidos com a média dos
valores de deformação longitudinal e transversal registrados para cada
corpo-de-prova.
Nestes ensaios de determinação dos valores de módulo de
elasticidade e Poisson dos grautes, utilizou-se uma prensa de sistema
hidráulico da marca SHIMADZU, com capacidade máxima de 2000 kN,
entretanto configurada na escala de 400 kN, e uma célula de carga de
500 kN conectada ao equipamento de aquisição de dados (Figura 3.11),
ambas com capacidade de carga adequada aos corpors-de-prova
utilizados, conforme observado nos ensaios de resistência à compressão.
Foi necessária a utilização da célula de carga por causa da
impossibilidade de aquisição direta dos dados de carregamento
aplicados pela prensa hidráulica, durante os ensaios.
Para este ensaio, inicialmente fez-se a calibração da célula de
carga, para a aquisição de dados compatíveis com os apresentados pela
prensa e pelo software CATMAN. Os valores de carga registrados pela
prensa e pela célula de carga foram filmados para correções, caso
necessário. Durante a realização do ensaio, tomou-se o cuidado para que
realmente estivessem sendo registrados pelo programa os dados de
deformação dos strain gauges e de aplicação do carregamento pela
célula de carga. Caso a diferença nos valores de deformação vertical
fosse superior a 20%, o corpo-de-prova era reposicionado e inicia-se
novamente o ensaio.
Para os ensaios de módulo de elasticidade e Poisson utilizou-se a
velocidade de carregamento de 0,45 ± 0,15 MPa/s, conforme ABNT
117
NBR 8522 (2008), com a aplicação da carga ocorrendo em um único
ciclo, de forma lenta e contínua. Assim, Assim, de acordo com esta
norma, calculou-se o módulo de elasticidade secante obtido para as
tensões de 0,5 MPa e 30% da carga de ruptura, para todas os corpos-deprova de argamassas. Todos os equipamentos utilizados pertenciam ao
Laboratório de Materiais e Construção Civil – UFSC.
Figura 3.11 – Configuração do ensaio com o corpo-de-prova com strain gauges,
célula de carga e prensa.
Fonte: Autor (2015).
3.5. PRISMAS
Para o desenvolvimento do trabalho, a moldagem dos prismas foi
dividida em três etapas:
- Etapa Referência (R): etapa na qual foram utilizados três tipos
de argamassas de assentamento e três tipos de grautes, de resistências
distintas;
118
- Etapa Argamassa Industrializada (I): etapa na qual foram
utilizados três tipos de argamassas industrializadas, de resistências
distintas, como argamassa de assentamento e preenchimento;
- Etapa Argamassa Mista (M): etapa na qual foram utilizados três
tipos de argamassas de assentamento mistas, de resistências distintas,
como argamassa de assentamento e preenchimento.
Para este trabalho foram moldados prismas de três fiadas à prumo
com argamassamento total, em razão da economia e facilidade de
execução, conforme Figura 3.12. Optou-se pelo emprego de prismas
com três blocos por estes amenizarem os efeitos gerados pelo
confinamento dos pratos da prensa aos blocos das extremidades e por
terem boa correlação com o comportamento das paredes. Nestes
prismas, o bloco central, geralmente livre do efeito de confinamento dos
pratos da prensa, representa melhor o tipo de ruptura da alvenaria
(PAGE, 1991; COLVILLE, 1991; LA ROVERE E RODRIGUES,1997;
RIZZATI, 2003).
Figura 3.12 - Prismas de 3 fiadas com junta a prumo.
Fonte: Autor (2015).
Na 2ª Etapa do programa experimental, os prismas moldados
foram utilizados para obtenção dos valores de resistência à compressão e
os prismas moldados na 3ª Etapa do programa experimental, foram
utilizados para obtenção dos valores de módulo de elasticidade.
119
Divididos entre estas duas etapas do trabalho, foram moldados
cinco prismas para cada combinação bloco-argamassa-graute,
totalizando 48 tipos de prismas de características distintas. Os blocos do
Lote 1 foram utilizados para a moldagem dos prismas empregados nos
ensaios de determinação da resistência à compressão, sendo que os
blocos do Lote 2 foram utilizados nos prismas empregados nos ensaios
de determinação do módulos de elasticidade.
Para a determinação da resistência à compressão, foram moldados
cinco prismas para cada combinação bloco-argamassa-graute,
totalizando 240 prismas. Dentre estes prismas, para a determinação do
módulo de elasticidade, foram utilizados apenas dois prismas para cada
combinação, em virtude da dificuldade de execução do ensaio,
totalizando 96 prismas para este ensaio. Os prismas foram denominados
em função da etapa (R, I ou M), prisma grauteado (G) ou prisma vazio
(V), tipo de bloco (6, 12 e 15), tipo de argamassa de assentamento ou
preenchimento (A, B, C, M, 5 e 10) e o tipo de graute (G1, G2 e G3),
conforme exemplo a seguir:
Desta forma, as denominações e combinações utilizadas no
trabalho para cada etapa são apresentadas na Tabela 3.11, Tabela 3.12 e
Tabela 3.13.
120
Bloco
Tabela 3.11 - Denominação dos prismas da Etapa de Referência.
Nomenclatura dos Prismas
Arg. A (1:1/4:3)
G1
G2
Arg. B (1:0,5:4,5)
G3
B6
-
-
-
B12
-
-
-
RG15- RG15 RG15
AG1 -AG2 -AG3
Fonte: Autor (2015).
B15
G1
-
G2
-
G3
-
RG12 RG12 RG12
-BG1 -BG2 -BG3
-
-
-
Arg. C (1:1:6)
G1
G2
G3
RG6- RG6- RG6CG1 CG2 CG3
-
-
-
RG15 RG15 RG15
-CG1 -CG2 -CG3
Tabela 3.12 - Denominação dos prismas da Etapa com Argamassa Mista.
Nomenclatura dos Prismas
Arg. A (1:1/4:3)
Arg. B (1:0,5:4,5)
Arg. C (1:1:6)
Bloco
Com
Com
Com
Vazio
Vazio
Vazio
Graute
Graute
Graute
B6
MV6-A MG6-A MV6-B MG6-B MV6-C MG6-C
B12 MV12-A MG12-A MV12-B MG12-B MV12-C MG12-C
B15 MV15-A MG15-A MV15-B MG15-B MV15-C MG15-C
Fonte: Autor (2015).
Tabela 3.13 - Denominação dos prismas da Etapa com Argamassa
Industrializada.
Nomenclatura dos Prismas
Arg. Multiplouso
Arg. 5 MPa
Arg. 10 MPa
Bloco
Com
Com
Com
Vazio
Vazio
Vazio
Graute
Graute
Graute
B6
IV6-M
IG6-M
IV6-5
IG6-5
IV6-10
IG6-10
B12 IV12-M IG12-M IV12-5
IG12-5 IV12-10 IG12-10
B15 IV15-M IG15-M IV15-5
IG15-5 IV15-10 IG15-10
Fonte: Autor (2015).
A moldagem dos prismas foi executada sobre uma mesa de
granito, nivelada, coberta com uma manta plástica untada com óleo
mineral. A espessura das juntas de assentamento dos prismas foi
executada com 10 ± 3 mm. Para a realização dos ensaios de
caracterização mecânica dos prismas não grauteados, os blocos das
extremidades foram capeados em uma das faces com pasta de cimento
para corrigir as imperfeições do bloco e distribuir homogeneamente o
121
carregamento em toda a área da seção transversal (Figura 3.13), no
mínimo dois dias antes do assentamento dos prismas. Procedimento este
análogo ao utilizado para a caracterização mecânica dos blocos. Para os
prismas grauteados, o capeamento dos blocos das extremidades foi
realizado com no mínimo 48 h antes do ensaio de resistência, facilitando
a preparação dos prismas para os ensaios.
Para a Etapa Referência, o grauteamento dos prismas foi
realizado 24 ± 2 horas após o assentamento dos mesmos, em três
camadas, sendo o adensamento realizado com 30 golpes/camada com
haste de adensamento metálica, de acordo com as recomendações da
ABNT NBR 8215 (1983), pois este procedimento não é definido na
norma ABNT NBR 15812 (2010).
Para os prismas preenchidos com argamassas, Etapas Argamassa
Mista e Industrializada, o preenchimento dos prismas não ocorreu logo
após o assentamento dos blocos, conforme indicado pela norma ABNT
NBR 15812-2 (2010). Durante as moldagens, realizando o
preenchimento dos prismas logo após o assentamento dos blocos,
constatou-se que com o adensamento do preenchimento provocava-se a
“expulsão” das juntas de argamassas, que ainda não apresentavam
resistência necessária para combater este fenômeno. Assim, o
preenchimento dos prismas com a argamassa se deu 1 h após o
assentamento dos blocos, tempo este constatado como o mínimo
necessário para que não ocorresse a expulsão das juntas de argamassa
com o adensamento do preenchimento.
Figura 3.13 - Capeamento superior dos blocos para a moldagem dos prismas.
Fonte: Autor (2015).
122
Todos os blocos tiveram suas faces umedecidas pouco antes do
assentamento, sendo mergulhados em uma lamina de água de 5 a 10 mm
por cerca de 5 min antes do assentamento dos blocos (Figura 3.14).
Segundo CARVALHO (2003), prismas construídos com blocos
umedecidos apresentaram uma tendência de aumento de resistência à
compressão.
Figura 3.14 - Blocos sendo umedecidos antes da moldagem do prisma.
Fonte: Autor (2015).
Após a moldagem dos prismas, os mesmos foram cobertos com
capas plásticas, para minimizar a ação das intempéries do ambiente não
controlado do laboratório, conforme Figura 3.15, para após 28 dias de
moldagem serem realizados os ensaios de caracterização mecânica.
123
Figura 3.15 - Armazenamento e cuidados com os prismas após moldagem.
Fonte: Autor (2015).
Os ensaios de resistência à compressão e módulo de elasticidade
para os prismas não grauteados foram realizados 28 dias após o
assentamento, enquanto que os ensaios dos prismas grauteados foram
realizados 28 dias após o grauteamento, já que essa seria a idade em que
o graute obteria a resistência esperada.
Na 3ª Etapa do programa experimental, para o ensaio do módulo
de elasticidade, utilizou-se uma prensa hidráulica da marca SHIMADZU
com capacidade máxima de 2000 kN, entretanto configurada na escala
de 1000 kN, uma célula de carga de 500 kN e dois transdutores de
deslocamento de curso de 20 mm. Novamente foi necessária a utilização
da célula de carga, por causa da impossibilidade de aquisição direta dos
dados de carregamento aplicados pela prensa hidráulica, durante os
ensaios.
Os transdutores de deslocamento estavam conectados a um
sistema de aquisição de dados composto por um Dataloger Spider 8 da
marca HBM e software CATMAN, do mesmo fabricante. Os dois
transdutores de deslocamento e as hastes ajustáveis para a leitura de
deformação foram posicionados em cada um dos lados dos prismas
através de fixadores metálicos desenvolvidos para estes ensaios, que
foram fixados nas superfícies dos blocos com cola epóxi, conforme
Figura 3.16.
124
Figura 3.16 – Detalhe de fixação dos transdutores de deslocamento no prisma.
Fonte: Autor (2015).
Inicialmente fez a calibração dos transdutores de deslocamento e
da célula de carga, para a aquisição de dados compatíveis com os
apresentados pela prensa e pelo software CATMAN. Os valores de
carga registrados pela prensa e pela célula de carga foram filmados para
correções, caso necessário.
Logo após a calibração do equipamento, para a realização do
ensaio posicionou-se a célula de carga acima de um dos pratos da
prensa, e o prisma ficou confinado entre os pratos, conforme se observa
na Figura 3.17. Os pratos utilizados para o ensaio eram de uso especifico
para prismas, para a distribuição correta de tensões sobre toda a
superfície de contato do prisma.
Após a calibração, fixação dos transdutores de deslocamento,
posicionamento da célula de carga e do prisma na prensa, iniciou-se o
ensaio. O ensaio de módulo de elasticidade foi realizado até a carga
referente a 50% da tensão de ruptura dos prismas, determinada na 2ª
Etapa do programa experimental, em virtude da capacidade da célula de
carga utilizada, evitando-se assim possíveis danos aos equipamentos.
Durante a realização do ensaio, tomou-se o cuidado para que
realmente estivessem sendo registrados pelo programa os dados de
deslocamento dos transdutores e de aplicação do carregamento pela
125
célula de carga. Caso a diferença nos valores de deslocamento vertical
fosse superior a 20%, o prisma era reposicionado e inicia-se novamente
o ensaio.
Para os ensaios de resistência à compressão e módulo de
elasticidade dos prismas utilizou-se a velocidade de carregamento de
0,05 ± 0,01 MPa/s, conforme ABNT NBR 15270-3 (2005) e ABNT
NBR 15812-2 (2010), com a aplicação da carga ocorrendo em um único
ciclo, de forma lenta e contínua. Assim, de acordo com esta norma,
calculou-se o módulo de elasticidade secante obtido para as tensões de
0,5% e 30% da carga de ruptura, para os prismas. Todos os
equipamentos utilizados pertenciam ao Laboratório de Materiais e
Construção Civil – UFSC.
Figura 3.17 – Configuração do ensaio com o prisma, célula de carga e prensa.
Fonte: Autor (2015).
126
127
4. RESULTADOS E DISCUSSÃO
Neste capítulo apresentam-se e discutem-se os resultados obtidos
nos ensaios de caracterização mecânica e física dos prismas e demais
componentes utilizados no programa experimental, visando atingir o
objetivo principal e objetivos específicos deste trabalho.
4.1. RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA E FÍSICA DOS BLOCOS
Os valores de caracterização geométrica e mecânica dos blocos
dos dois lotes recebidos, utilizados no programa experimental,
encontram-se a seguir na Tabela 4.1, Tabela 4.2 e Tabela 4.3.
Tabela 4.1 – Características físicas dos blocos dos Lotes 1 e 2.
Classe
de
Bloco
LOTE 1
B6
B12
B15
LOTE 2
B6
B12
B15
CARACTERÍSTICAS FÍSICAS
Dimensões (mm)
Área
Área
e (CV - %)
Bruta
Líquida
Nº de
exem(cm2)
(cm2)
plares
Larg.
Altura
Comp.
e (C.V.
e (C.V.
- %)
- %)
137,3
188,8
288,2
396,3
158,3
13
(0,2)
(0,3)
(0,2)
(0,4)
(0,8)
141,0
191,3
290,4
409,5
204,1
13
(0,3)
(0,3)
(0,2)
(0,5)
(0,4)
140,8
191,1
288,3
408,2
221,0
13
(0,6)
(0,6)
(0,6)
(1,0)
(0,9)
137,2
189,1
286,9
393,5
152,4
13
(0,4)
(0,3)
(0,2)
(0.4)
(0,5)
140,6
192,4
289,4
407,1
204,3
13
(0,4)
(1,1)
(0,5)
(0,9)
(0,8)
139,4
188,5
287,1
400,2
214,4
13
(0,6)
(0,5)
(0,6)
(1,1)
(1,4)
C.V. = coeficiente de variação; * AAI em g/193.55cm²/min.
Fonte: Autor (2015).
AAI (*)
e (C.V.
- %)
12,6
(14,8)
16,1
(10,6)
16,6
(13,6)
12,3
(14,1)
14,8
(19,1)
16,7
(15,1)
128
Tabela 4.2 – Resistência à compressão dos blocos dos Lotes 1 e 2.
RESISTÊNCIA À COMPRESSÃO
LOTE 2
LOTE 1
Classe
de
Bloco
Nº de
Exemplares
Área Bruta
fbk
C.V.
(MPa)
(%)
9,2
11,3
Área Líquida
fb
fbk
C.V.
(MPa)
(MPa)
(%)
27,0
22,6
13,1
B6
13
fb
(MPa)
11,0
B12
13
14,8
10,2
15,0
30,3
23,2
11,8
B15
13
16,1
12,9
14,0
32,7
24,9
11,3
B6
13
10,5
8,5
13,8
26,8
19,5
14,7
B12
13
14,1
11,2
17,0
29,0
22,5
10,0
16,7
13,6
15,3
32,8
23,6
15,5
B15
13
Fonte: Autor (2015).
Tabela 4.3 – Resistência à tração indireta dos blocos dos Lotes 1 e 2.
LOTE 2
LOTE 1
RESISTÊNCIA À TRAÇÃO
Área Bruta
Classe de
Nº de
f
bT
Bloco
Exemplares
C.V. (%)
(MPa)
B6
6
0,46
13,2
B12
6
0,46
13,5
B15
6
0,68
10,7
B6
6
0,48
16,00
B12
6
0,49
15,35
B15
6
0,71
8,36
Fonte: Autor (2015).
Área Líquida
fbT
C.V.
(MPa)
(%)
0,56
13,2
1,21
12,2
1,43
10,9
0,59
15,94
1,32
14,52
1,47
8,10
Inicialmente realizou-se uma análise de variância (ANOVA),
para a verificação se há diferença estatisticamente significativa entre os
valores de propriedades mecânicas dos blocos dos Lotes 1 e 2. A análise
de variância é um teste de distribuição F, que determina se as médias de
duas ou mais populações podem ser consideradas estatisticamente
iguais, analisando suas variâncias. A análise mostrou que, tanto para os
resultados de resistência à compressão como para os de tração indireta,
não há diferença significativa para um nível de confiança de 95%,
conforme Tabela 4.4. Deste modo, seguiu-se com as etapas seguintes de
moldagens e caracterização mecânica dos prismas.
129
Entretanto, constata-se que a resistência característica à
compressão (fbk) para as amostras coletadas para cada uma das três
classes de blocos cerâmicos, resulta em valores menores que os
nominais declarados pela indústria cerâmica fornecedora, exceto para a
classe B6. Os blocos das classes B12 e B15 apresentam,
respectivamente, valores de resistência característica à compressão em
média 14% abaixo do declarado.
Tabela 4.4 - Análise de variância para a resistência à compressão dos blocos dos
Lotes 1 e 2 .
Blocos
Lotes
Comparados
F
Fα
(calculado) (crítico)
B6
Lote 1 e Lote 2
1,03
2,064
B12
Lote 1 e Lote 2
0,748
2,064
B15
Lote 1 e Lote 2
0,586
2,064
Resultado
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
Fonte: Autor (2015).
A resistência média à tração obtida para os blocos ficaram entre
3% a 4,2% da resistência à compressão. Esses baixos resultados eram
esperados, em virtude das características do material e processo de
fabricação para blocos cerâmicos.
Quanto à caracterização física, os resultados obtidos para os dois
lotes de blocos apresentam-se na Tabela 4.1. Observa-se que as
dimensões reais dos blocos (largura, altura e comprimento) estão em
conformidade com a norma brasileira ABNT NBR 15270-2 (2005), ou
seja, dentro da variação de ± 3,0 mm para as médias das dimensões
efetivas. Os valores do AAI verificados para os blocos encontram-se
abaixo do valor de 30 g/193,55cm² x min, que de acordo com a ABNT
NBR 15270-3 (2005) não implica no prévio umedecimento dos blocos
antes da moldagem dos prismas. Entretanto, conforme descrito no item
3.6 do programa experimental, todos os blocos foram umedecidos antes
da moldagem para o aumento do desempenho dos prismas.
Na Tabela 4.5 encontram-se os valores de resistência à
compressão (fb), módulo de elasticidade (Eb) e coeficiente de Poisson
(νb) do material dos blocos, para cada uma das três classes de blocos.
Conforme descrito no item 3.3 do programa experimental, foram
extraídos corpos-de-prova prismáticos com dimensões de (20x40) mm e
espessura variável, de acordo com suas respectivas geometrias.
130
Bloco
Tabela 4.5 – Característica mecânicas dos blocos para corpos-de-prova
prismáticos (20x40) mm.
Nº de
Exemplares
Espessura
(mm)
C.V.
(%)
(MPa)
C.V.
(%)
Eb (MPa)
B6
3
7,7
0,8
32,8
14,2
8243,9
8,1
0,05 12,5
B12
3
10,5
6,3
50,7
8,2
11864,4
8,7
0,09
8,9
B15
3
8,1
5,4
34,9
11,5
8111,1
6,4
0,05
8,8
fb
C.V.
(%)
νb
C.V.
(%)
Fonte: Autor (2015).
Conforme a Tabela 4.2 e Tabela 4.5, os valores médios obtidos de
resistência à compressão para os corpos-de-prova prismáticos dos blocos
B6, B12 e B15 em comparação com os valores de fb dos blocos, na área
líquida, apresentaram um aumento de 21,5%, 67,3% e 6,7%
respectivamente. Sendo que o resultado encontrado para o bloco B12
apresentou a maior diferença em relação aos demais resultados. Esses
aumentos explicam-se pela diferença existente entre as geometrias dos
blocos e dos corpos-de-prova prismáticos, onde os resultados
encontrados para estes últimos podem ter sido afetados pelo
confinamento gerado pelos contatos da prensa. Além da geometria, a
porosidade da massa, processo e temperatura de queima e grau de
vitrificação dos blocos interferem diretamente nas propriedades do
material, o que também pode explicar as diferenças entre os resultados
de resistência encontrados para os três tipos de blocos. Isto explicaria
também a grande diferença no valor de módulo de elasticidade
encontrado para o material do bloco B12, em relação aos blocos B6 e
B15, mesmo este último apresentando o maior valor de fb.
Ainda em relação aos valores de módulo de elasticidade, estes
ficaram abaixo do esperado. Entretanto correspondem a valores
intermediários, quando comparados aos valores de módulo de
elasticidade dos blocos, na área líquida, para os trabalhos realizados por
CESAR (2007) e SANTOS (2008), conforme Tabela 4.6. Em ambas as
pesquisas utilizaram-se blocos cerâmicos com (14x19x29) cm de
dimensão. Para o cálculo do módulo de elasticidade, utilizou-se o bloco
inteiro, cuja aquisição dos dados de deformação foi realizada com strain
gauges (CESAR, 2007) e transdutores de deslocamento (SANTOS,
2008).
131
Tabela 4.6 – Característica mecânicas dos blocos cerâmicos utilizados por Cesar
(2007) e Santos (2208).
Área Bruta
Geometria
Santos (2008)
Cesar (2007)
Fonte
fb
Eb
Área Líquida
fb liq
Eb liq
(MPa)
C.V
(%)
(GPa)
C.V
(%)
(MPa)
C.V
(%)
(GPa)
C.V
(%)
8,3
13,7
1,9
24,0
20,8
13,7
4,7
24,0
11,7
9,9
4,1
15,7
28,5
9,9
10,4
15,7
15,1
12,1
6,1
25,9
30,8
12,1
12,4
25,4
Fonte: Autor (2015).
Para Cesar (2007), o resultado encontrado para o módulo de
elasticidade do bloco se mostrou relativamente baixo e disperso com
coeficiente de variação em torno de 24%, o que segundo a autora, é
comum em se tratando de materiais cerâmicos. A natureza frágil dos
materiais cerâmicos, que é em consequência dos defeitos e imperfeições
inerentes à estrutura do material ou gerado pelo processo de fabricação,
tem a tendência em ser distribuídos aleatoriamente tanto em orientação
quanto em tamanho, e por consequência as resistências à fratura exibirão
uma grande variabilidade (GLEIZE, 2003 apud CESAR, 2007).
O mesmo observa-se para os valores obtidos na pesquisa
realizada por Santos (2008), que apresentaram coeficientes de variação
entre 15,7% e 25,4%. Entretanto, os valores de módulo de elasticidade
do bloco, na área líquida, foram maiores quando comparados com os
valores encontrados para os corpos-de-prova prismáticos da Tabela 4.5.
Ainda, verificando a relevância dos dados levantados pelos
autores, os valores de módulo de elasticidade do bloco obtidos por Cesar
(2007), na área líquida, foram utilizados no trabalho desenvolvido por
Manzano (2013). O autor estudou o comportamento de um modelo de
132
conexão vertical concebido para atuar em conjunto com os painéis
estruturais cerâmicos pré-fabricados, utilizando análise numérica com
elementos finitos. Para esta análise, Manzano (2013) utilizou os dados
experimentais obtidos Cesar (2007), para calibrar o modelo utilizado em
sua pesquisa.
Os valores de Coeficiente de Poisson obtidos para o material dos
blocos, também ficou abaixo do esperado, tomando-se por base o valor
de 0,15 para alvenaria de blocos cerâmicos, conforme indicado pela
norma ABNT NBR 15812-1 (2010). Cesar (2007) e Manzano (2013)
adotaram em seus trabalhos, respectivamente, os valores de 0,20 e 0,15
para o Coeficiente de Poisson, valores estes próximos ao indicado pela
norma ABNT NBR 15812-1, entretanto estes valores se referem a
alvenaria e não ao material dos blocos.
Assim, os valores de caracterização mecânica dos blocos
adotados para este trabalho, são os obtidos com os blocos do Lote 1,
mostrados na Tabela 4.2 e Tabela 4.3. Somente na análise numérica,
serão utilizados os valores de Módulo de Elasticidade encontrados nos
ensaios com os corpos-de-prova prismáticos (20x40) mm, mostrados na
Tabela 4.5.
4.2. RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA DAS ARGAMASSAS
A Tabela 4.7 e Tabela 4.8 apresentam os valores de
caracterização mecânica das argamassas utilizadas no programa
experimental, para os corpos-de-prova cilíndricos e prismáticos.
Conforme a Tabela 4.7 e Tabela 4.8, para as mesmas classes de
argamassas, observa-se que os valores de resistências média à
compressão obtidos para cada geometria de corpo-de-prova não
apresentam grande diferença. Em uma análise de variância (ANOVA),
os valores de resistência média à compressão encontrados para as duas
geometrias de corpo-de-prova de cada classe de argamassa, com um
nível de confiança de 95%, não apresentam diferença significativa,
conforme Tabela 4.9. De um modo geral os corpos-de-prova (ϕ5x10) cm
tiveram um acréscimo médio de aproximadamente 10% nos valores de
resistência, quando comparados aos corpos-de-prova prismáticos de
(4x4x16) cm. Isto se deve ao fato, que os ensaios de caracterização dos
corpos-de-prova ocorreram com tempos de cura e equipamento
diferentes, em virtude da complexidade na preparação corpos-de-prova
(ϕ5x10)cm utilizados nos ensaios de módulo de elasticidade.
133
Tabela 4.7 – Característica mecânicas das argamassas para corpos-de-prova
prismático (4x4x16) cm.
A
Nº de
Exemplares
12
farg
(MPa)
12,7
fargk
(MPa)
10,7
C.V.
(%)
9,2
B
12
6,4
5,6
7,7
2,1
9,7
C
12
3,1
2,6
9,6
1,3
7,6
10
12
9,5
7,3
13,9
3,7
7,7
M
12
6,8
6,1
5,9
2,9
11,3
12
4,8
4,0
10,2
1,2
13,5
Argamassa
5
Fonte: Autor (2015).
fargT C.V.
(MPa) (%)
3,9
13,1
Tabela 4.8 – Característica mecânicas das argamassas para corpos-de-prova
(ϕ5X10) cm.
Nº de
Exemplares
3
3
3
3
3
3
Argamassa
A
B
C
10
M
5
farg
(MPa)
14,4
6,7
2,7
10,9
7,4
5,5
fargk
(MPa)
11,4
6,0
2,1
8,8
6,0
4,3
C.V.
(%)
13,0
6,4
13,5
11,4
11,7
13,1
Earg
(MPa)
12554,2
7120,1
2529,6
12299,3
8717,1
7890,8
C.V.
(%)
11,2
11,0
13,0
6,4
6,3
7,9
νarg
0,17
0,14
0,14
0,13
0,21
0,13
C.V.
(%)
13,0
13,0
11,2
15,1
13,0
9,8
Fonte: Autor (2015).
Tabela 4.9 - Análise de variância para a resistência à compressão para as duas
geometrias de corpos-de-prova .
A
F
(calculado)
2,14
Fα
(crítico)
2,16
F > Fα (Não Há Diferença)
B
0,99
2,16
F > Fα (Não Há Diferença)
C
2,13
2,16
F > Fα (Não Há Diferença)
10
1,66
2,16
F > Fα (Não Há Diferença)
M
1,23
4,30
F > Fα (Não Há Diferença)
5
2,08
2,16
F > Fα (Não Há Diferença)
Argamassa
Fonte: Autor (2015).
Resultado
134
Observa-se que os valores de resistência média à compressão das
seis classes de argamassas (mistas e industrializadas) encontram-se
abaixo de 70 a 100% da resistência dos blocos, indicados por
pesquisadores como Mohamad (1998) e Ramalho e Corrêa (2003) para
argamassas mistas, exceto o valor de farg da argamassa da classe A se
comparado ao valor de fb do bloco do tipo B6. Entretanto, essa faixa de
utilização indicada pelos pesquisadores refere-se a argamassas de
assentamento mistas, ou seja, argamassas de cimento, cal e areia.
Para as argamassas mistas, os valores de resistência média à
compressão encontram-se abaixo dos indicados pela norma BS 5628-1
(1992), para as classes (i), (ii) e (iii). Estes resultados justificam-se por
causa das propriedades dos materiais constituintes das argamassas e,
como consequência, as relações água/cimento (Fa/c) necessária para
atingir a trabalhabilidade adequada para o assentamento dos blocos, que
resultariam nestes valores de resistências abaixo do indicado pela
norma.
Para as argamassas industrializadas, visando atingir a
consistência e trabalhabilidade adequada para o trabalho, utilizou-se na
mistura um percentual de água abaixo do indicado pelo fabricante.
Mesmo utilizando uma reação água/argamassa anidra (Fa/arg) abaixo do
indicado, os valores encontrados de resistência média à compressão para
as argamassas foram menores do que o esperado para as argamassas de
assentamento estrutural de 5 e 10 MPa. Isto pode ser explicado pelo teor
de ar incorporado das argamassas, que pode ter aumentado em
consequência dos aditivos em sua composição e o equipamento utilizado
na mistura durante a moldagem dos prismas, que foi diferente do
equipamento utilizado na determinação dos teores de ar incorporado das
argamassas, aumentando assim sua porosidade e consequentemente
diminuindo sua resistência.
Assim, os valores de resistência mecânica das argamassas
adotados para este trabalho, são os mostrados na Tabela 4.7, obtidos
para os corpos-de-prova prismáticos, de acordo com a norma ABNT
NBR 13281 (2005). Entretanto, para os valores de módulo de
elasticidade e coeficiente de Poisson, serão utilizados os valores obtidos
nos ensaios com os corpos-de-prova cilíndricos, apresentados na Tabela
4.8.
135
4.3. RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA DOS GRAUTES
A Tabela 4.10 e a Tabela 4.11 apresentam os valores de
caracterização mecânica dos grautes utilizados no programa
experimental.
Observa-se na Tabela 4.10 e Tabela 4.11, para cada traço de
grautes, que os valores de resistência média à compressão obtidos para
cada tipo de corpo-de-prova não apresentam grande diferença. Adotando
o mesmo procedimento utilizado com as argamassas, ou seja, fazendo
uma análise de variância (ANOVA), os valores de resistência à
compressão e módulo de elasticidade obtidos para cada traço de graute
nos ensaios com transdutores de deslocamento e strain gauges, com um
nível de confiança de 95%, não apresentam diferença significativa,
conforme Tabela 4.12.
Tabela 4.10 – Características mecânicas dos grautes para corpos-de-prova
(ϕ10X20) cm, utilizando transdutores de deslocamento.
G1
Nº de
Exemplares
12
G2
12
Graute
G3
12
Fonte: Autor (2015).
40,3
36,7
5,5
Nº de
Exemplares
6
24,4
20,2
10,3
6
30657,8
10,3
14,3
11,7
10,9
6
22375,9
5,3
fg
fgk
C.V.
(MPa) (MPa) (%)
Eg
(MPa)
C.V.
(%)
47490,2
9,6
Tabela 4.11 – Características mecânicas dos grautes para corpos-de-prova
(ϕ10X20) cm, utilizando strain gauge.
Graute
Nº de
Exemplares
Nº de
fgk
C.V.
Exem(MPa) (MPa) (%)
plares
G1
3
44,2
34,7
13,0
G2
3
28,1
22,1
G3
3
16,2
13,2
Eg
(MPa)
C.V.
(%)
νg
C.V.
(%)
3
52229,6
12,5
0,17
12,5
12,9
3
33403,7
2,1
0,27
7,7
13,2
3
28459,1
14,3
0,23
9,5
fg
Fonte: Autor (2015).
136
Tabela 4.12 - Análise de variância para a resistência à compressão para as duas
geometrias de corpos-de-prova .
Graute
F(calculado)
G1
1,99
G2
2,14
G3
1,92
Fonte: Autor (2015).
Fα
(crítico)
2,16
2,16
2,16
Resultado
F > Fα (Não Há Diferença)
F > Fα (Não Há Diferença)
F > Fα (Não Há Diferença)
De um modo geral os ensaios realizados com strain gauges
tiveram um acréscimo médio de aproximadamente 20% nos valores de
resistência, quando comparados aos valores obtidos com os ensaios
realizados com transdutores de deslocamento. Isto se deve ao fato, que
os ensaios de caracterização dos corpos-de-prova ocorreram com tempos
de cura e teores de umidades diferentes, em virtude da complexidade na
preparação corpos-de-prova utilizados nos ensaios com strain gauges.
Para os ensaios com transdutores de deslocamento utilizaram-se os
corpos-de-prova úmidos, conforme ABNT NBR 8522. Para os corposde-prova com strain gauges os ensaios foram realizados 7 dias após a
cura de 28 dias em câmara úmida, pois a fixação dos strain gauges e a
realização ensaio somente eram possíveis com os corpos-de-prova
secos.
Os valores de Coeficiente de Poisson obtidos nos ensaio com
transdutores de deslocamento foram descartados, em virtude dos
elevados valores obtidos. Como apontado no programa experimental,
nos ensaios com transdutores de deslocamento, em virtude da
dificuldade de realização do ensaio e desgaste do equipamento, a leitura
obtida no deslocamento diametral foi maior que a deformação observada
no corpo-de-prova durante o ensaio, gerando valores elevados de
Poisson para os três traços de grautes.
Todavia, os valores encontrados nos ensaios com strain gauges
encontram-se próximos ao valor indicado pela norma ABNT NBR 6118
(2007) para concreto no caso da ausência de dados experimentais, ou
seja, 0,20.
Assim, os valores de caracterização mecânica dos grautes
adotados para este trabalho, são os mostrados na Tabela 4.10, obtidos
nos ensaios com transdutores de deslocamento. Entretanto, para os
valores de coeficiente de Poisson, serão utilizados os valores obtidos nos
ensaios com strain gauge, conforme Tabela 4.11.
137
4.4. RESUMO DAS
COMPONENTES
PROPRIEDADES
MECÂNICAS
DOS
Neste item apresentam-se os valores de caracterização mecânica
dos blocos, grautes e argamassas utilizadas na confecção dos prismas.
Estes valores são utilizados como referência para análise dos resultados
experimentais e na análise numérica.
Na Tabela 4.13 à Tabela 4.15apresenta-se o resumo dos valores
das propriedades mecânicas obtidos para os blocos B6, B12 e B15. Na
Figura 4.1 apresentam-se os diagramas tensão versus deformação para
cada classe de bloco utilizado no programa experimental.
Tabela 4.13 – Valores de resistência à compressão dos blocos.
RESISTÊNCIA À COMPRESSÃO
Área Bruta
Área Líquida
Nº de
Classe de
Exemfb
fbk
C.V.
fb
fbk
C.V.
Bloco
plares
(MPa) (MPa) (%) (MPa) (MPa) (%)
B6
13
11,0
9,2
11,3
27,0
22,6
13,1
B12
13
14,8
10,2
15,0
30,3
23,2
11,8
B15
13
16,1
12,9
14,0
32,7
24,9
11,3
Fonte: Autor (2015).
Tabela 4.14 – Valores de resistência à tração dos blocos.
Classe de
Bloco
B6
B12
B15
Fonte: Autor (2015).
RESISTÊNCIA À TRAÇÃO
Área Bruta
Nº de
f
C.V.
bT
Exemplares
(MPa)
(%)
6
0,46
13,2
6
0,46
13,5
6
0,68
10,7
Área Líquida
fbT
C.V.
(MPa)
(%)
0,56
13,2
1,21
12,2
1,43
10,9
138
Tabela 4.15 – Valores de módulo de elasticidade e coeficiente de Poisson dos
blocos.
Classe de
Bloco
B6
Nº de
Exemplares
3
8243,9
C.V.
(%)
8,1
0,05
C.V.
(%)
12,5
B12
3
11864,4
8,7
0,09
8,9
B15
Fonte: Autor (2015).
3
8111,1
6,4
0,05
8,8
Eb (MPa)
νb
Figura 4.1 – Gráfico Tensão x Deformação do material dos blocos.
50
45
40
Tensão (MPa)
35
30
25
20
15
10
BLOCO B15
5
0
0,0000
0,0010
0,0020
0,0030
0,0040
BLOCO B12
0,0050
0,0060
0,0070
0,0080
Deformação Específica (mm/mm)
Fonte: Autor (2015).
Com os valores de expostos na Tabela 4.13, fazendo uma análise
de variância (ANOVA) para os valores de resistência à compressão, na
área bruta e líquida, obtidos para as três classes de bloco, com um nível
de confiança de 95%, constata-se que os blocos B12 e B15 não
apresentam diferença significativa estes valores, sendo que estes valores
diferem significativamente do valor de resistência à compressão
encontrado para o bloco B6. Analisando os valores da Tabela 4.14,
também se constatou para os valores de resistência à tração na área
líquida, para as três classes de bloco, que não há diferença significativa.
Entretanto, para os blocos B6 e B12, os valores de resistência à tração
na área bruta, não apresentam diferença significativa.
139
Quanto aos valores de módulo de elasticidade, analisando a
Tabela 4.15 e a Figura 4.1, observa-se que os blocos B15 e B6 não
apresentam grande diferença entre estes valores, além de apresentarem
comportamento similar na deformação.
Fazendo uma análise de variância (ANOVA) com os valores de
expostos na Tabela 4.12, com um nível de confiança de 95%, constatase que os valores de módulo de elasticidade obtidos para os blocos B6 e
B15 não apresentam diferença significativa, sendo que estes valores
diferem significativamente do valor de módulo obtido para o bloco B12.
Mesmo sem diferença significativa entre os valores de módulo de
elasticidade, os blocos B6 e B15 apresentam valores distintos de
resistências à compressão e tração. Isto ocorre em consequência das
diferenças apresentadas em suas geometrias. O mesmo acontece com os
valores de resistência à compressão dos blocos B12 e B15, que não
apresentam diferença significativa, porém estas duas classes de blocos
apresentam valores de resistência à tração e de módulo de elasticidade
distintos. Este comportamento evidencia a influência da geometria nos
valores de resistência dos blocos, conforme já constatado por outros
pesquisadores.
Para as argamassas, na Tabela 4.16 apresenta-se o resumo dos
valores das propriedades mecânicas obtidos para as seis classes de
argamassas. Na Figura 4.2 apresentam-se os diagramas tensão versus
deformação para cada classe de argamassa utilizada no programa
experimental.
Tabela 4.16 – Resumo das propriedades mecânicas das argamassas.
Arg.
Nº de
Exemplares
A
12
12,7
10,7
9,2
3,9
B
12
6,4
5,6
7,7
C
12
3,1
2,6
10
12
9,5
M
12
5
12
Earg
(MPa)
C.V.
(%)
νarg
13,1
12554,2
11,2
0,17 13,0
2,1
9,7
7120,1
11,0
0,14 13,0
9,6
1,3
7,6
2529,6
13,0
0,14 11,2
7,3
13,9
3,7
7,7
12299,3
6,4
0,13 15,1
6,8
6,1
5,9
2,9
11,3
8717,1
6,3
0,21 13,0
4,8
4,0
10,2
1,2
13,5
7890,8
7,9
0,13
farg
fargk
C . V.
(MPa) (MPa) (%)
Fonte: Autor (2015).
fargT
C.V.
(MPa) (%)
C.V.
(%)
9,8
140
Figura 4.2 – Gráfico Tensão x Deformação das argamassas.
50
ARGAMASSA B
ARGAMASSA C
ARGAMASSA 10
ARGAMASSA 5
ARGAMASSA M
Tensão (MPa)
40
ARGAMASSA A
30
20
10
0
0,0000
0,0020
0,0040
0,0060
0,0080
Deformação Específica (mm/mm)
Fonte: Autor (2015).
Analisando a Tabela 4.16 observa-se que as argamassas das
classes B, 5 e M não apresentam grande diferença entre seus valores de
módulo de elasticidade e apresentam comportamento similar na
deformação (Figura 4.2). As argamassas das classes A e 10 também não
apresentam grandes diferenças ente seus valores de resistência e módulo
de elasticidade, bem como seu comportamento na deformação (Figura
4.2). Somente a argamassa C apresenta valores distintos de resistência e
módulo, bem como comportamento distinto na deformação em relação
às demais classes de argamassa (Figura 4.2).
Fazendo uma análise de variância (ANOVA) com os valores
expostos na Tabela 4.16, com um nível de confiança de 95%, verifica-se
que as argamassas B, 5 e M apresentam diferença significativa entre
seus valores de resistência à compressão. Entretanto, como se observa
na Figura 4.2, constata-se que estas classes de argamassas não
apresentaram diferenças significativas entres seus valores de módulo de
elasticidade, ou seja, encontram-se dentro de um mesmo grupo de
valores de módulo de elasticidade.
Para as argamassas das classes A e 10, com um nível de
confiança de 95%, verifica-se que os seus valores de resistência à
compressão apresentam diferenças significativas. Entretanto, os valores
de módulo de elasticidade encontrado para estas duas classes de
141
argamassas
não
apresentam
diferença
significativa.
Este
comportamento, provavelmente, está relacionado com o traço e aditivos
utilizados para a fabricação da argamassa industrializada do tipo 10, não
revelados pelo fabricante.
Para os grautes, na Tabela 4.17 apresenta-se o resumo dos valores
das propriedades mecânicas obtidos para os três traços de grautes. Na
Figura 4.3 apresentam-se os diagramas tensão versus deformação para
cada traço de graute utilizado no programa experimental.
Graute
Tabela 4.17 – Resumo das propriedades mecânicas dos grautes.
Nº de
fg
Exem(MPa)
plares
(MPa)
C.V.
(%)
Nº de
Exemplares
Eg (MPa)
C.V.
(%)
fgk
νg
C.V.
(%)
G1
12
40,3
36,7
5,5
6
47490,2
9,6
0,17 12,5
G2
12
24,4
20,2
10,3
6
30657,8
10,3 0,27
7,7
G3
12
14,3
11,7
10,9
6
22375,9
5,3
9,5
0,23
Fonte: Autor (2015).
Figura 4.3 – Gráfico Tensão x Deformação dos grautes.
50
45
GRAUTE G1
GRAUTE G2
GRAUTE G3
40
Tensão (MPa)
35
30
25
20
15
10
5
0
0,0000
Fonte: Autor (2015).
0,0010
0,0020
0,0030
0,0040
Deformação Específica (mm/mm)
142
Analisando os valores expostos na Tabela 4.17, observa-se que os
três traços de grautes apresentam diferentes valores em suas
propriedades mecânicas, além de comportamento distinto na deformação
(Figura 4.3). Em uma análise de variância (ANOVA), com um nível de
confiança de 95%, constata-se que realmente existe diferença
significativa entre os valores de resistência e módulo de elasticidade dos
grautes. Estas diferenças entre os valores das propriedades mecânicas
dos três traços de grautes eram esperadas, tendo em vista que os traços
foram dosados com este objetivo.
4.5. RESULTADOS DOS ENSAIOS DE CARACTERIZAÇÃO
MECÂNICA DOS PRISMAS
Nesta parte do trabalho apresentam-se e discutem-se os resultados
obtidos nos ensaios de caracterização mecânica realizados com os
prismas, divididos nas três etapas definidas no programa experimental.
4.5.1. Resultados dos ensaios da Etapa Referência
Esta etapa teve como objetivo investigar e comparar os resultados
obtidos para os prismas sob compressão uniaxial, preenchidos com
graute e com a argamassa de assentamento.
Na Tabela 4.18 apresentam-se os valores da caracterização
mecânica obtidos para os prismas na Etapa Referência. Para a
comparação, foram utilizados também os resultados obtidos para os
prismas vazios e preenchidos com a própria argamassa da Etapa
Argamassa Mista, moldados com os respectivos blocos e argamassas de
assentamento utilizado em cada uma das quatro séries da Etapa de
Referência. A partir destes resultados, construiu-se o gráfico da
resistência média à compressão dos prismas (fpliq), na área líquida,
versus resistência média à compressão dos grautes (fg), conforme Figura
4.4, a fim de facilitar a identificação de tendências de comportamento
para cada uma das séries de prismas.
143
Tabela 4.18 – Característica mecânicas dos prismas da Etapa Referência.
Nº de Exemplares = 5
Bloco B15
Bloco B15
Bloco B12
Eficiência
Ep
(GPa)
Ep Liq
(GPa)
C.V.
(%)
(η) –
Área
Bruta
12,2
36,5
41,4
14,4
0,85
11,3
19,5
25,2
1,6
0,68
5,4
15,0
14,5
7,0
0,67
14,5
6,1
7,0
8,1
4,7
0,80
22,2
15,3
6,3
11,7
5,1
0,74
14,1
17,2
6,8
20,8
25,4
2,5
0,88
6,6
9,6
11,6
7,2
19,8
24,0
5,7
0,59
11,6
9,3
11,3
11,5
12,4
15,2
14,3
0,58
6,9
9,3
10,9
10,0
4,1
7,6
8,2
0,58
375,3
9,7
9,3
17,3
10,0
4,1
7,7
8,2
0,58
RG12-BG1
477,0
11,9
11,8
15,0
12,1
19,4
24,8
9,0
0,80
RG12-BG2
337,6
9,2
8,4
10,6
9,0
16,7
21,5
10,1
0,57
RG12-BG3
329,9
10,0
8,2
10,4
9,8
13,0
16,9
2,6
0,55
MG12-B
389,2
13,0
9,5
12,1
14,3
7,4
9,5
6,7
0,64
MV12-B
333,6
11,1
8,1
16,3
11,8
5,6
11,5
8,1
0,55
RG6-CG1
689,5
11,0
17,1
24,3
10,9
20,9
29,4
7,5
1,55
RG6-CG2
216,6
9,6
5,3
7,6
9,1
10,7
16,6
11,8
0,48
RG6-CG3
184,0
10,1
4,5
6,5
10,0
7,8
12,8
9,0
0,41
MG6-C
262,2
7,7
6,6
9,3
7,7
2,8
3,9
7,3
0,60
MV6-C
164,1
9,5
4,1
10,6
10,2
2,0
4,9
11,4
0,38
Prismas
Bloco B6
Nº de Exemplares = 2
Fp
(kN)
C.V.
RG15-AG1
550,3
11,9
13,6
15,8
RG15-AG2
439,7
10,9
10,9
12,7
RG15-AG3
437,3
5,0
10,8
12,6
MG15-A
503,0
6,9
12,5
MV15-A
482,9
15,0
12,0
RG15-CG1
567,2
6,4
RG15-CG2
381,7
RG15-CG3
372,8
MG15-C
382,3
MV15-C
Fonte: Autor (2015).
(%)
fp
fp liq C.V.
(MPa) (MPa) (%)
144
Figura 4.4 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus resistência média à compressão dos grautes (fg).
25
23
Prisma Bloco B15 Arg A
Prisma Bloco 12 Arg B
Prisma Bloco B15 Arg C
Prisma Bloco B6 Arg C
MV15-A
21
19
MV15-C
MV12-B
fp liq (MPa)
17
MG15-A
15
MG12-B
MG15-C
13
11
MG6-C
MV6-C
9
RG15-CG1
RG6-CG1
RG15-AG1
RG12-BG2
RG12-BG3
RG6-CG2
RG6-CG3
7
RG12-BG1
RG15-AG3 RG15-AG2
RG15-CG2
RG15-CG3
5
0
5
10
15
20
25
30
35
40
45
fg (MPa)
Fonte: Autor (2015).
Analisando a Tabela 4.18 e o gráfico da Figura 4.4, observa-se
que quando preenchidos com a argamassa de assentamento, os prismas
apresentam um pequeno aumento em suas resistências à compressão, em
comparação aos prismas grauteados com os grautes G2 e G3, exceto
para os prismas da série MG15-C, moldado com a argamassa da classe
C. Isto se deve ao fato que a argamassa da classe C, com o menor valor
de resistência à compressão, apresenta resistência abaixo do
recomendado para o grauteamento de paredes de alvenaria. Ainda, os
prismas preenchidos com os grautes G2 e G3, aparentemente, não
apresentam diferença entre seus valores de resistência à compressão,
exceto para os prismas moldados com os blocos B6. Os prismas
grauteados que apresentam os maiores valores de resistência, com o
aumento da resistência do grautes, são aqueles moldados com as
argamassas de menor valor de resistência à compressão, neste caso a
argamassa da classe C. Este comportamento condiz com os trabalhos
desenvolvidos por outros pesquisadores, na qual o aumento da
resistência da argamassa contribui pouco para o aumento da resistência
dos prismas quando grauteados (Garcia, 2000; Romagna, 2000; Cunha,
2001; Juste, 2001), evidenciando a hipótese que o enrijecimento da
145
alvenaria com argamassas mais resistentes pode representar uma solução
antieconômica e com pouca influencia no resistência final das paredes.
Observa-se também, que os fatores de eficiência para os prismas
vazios encontram-se em conformidade com os valores observados por
Ramalho e Corrêa (2003) para prismas de blocos cerâmicos, variando
entre 0,3 e 0,6; exceto para a série de prismas MV15-A que apresentam
fator de eficiência de aproximadamente 0,74.
Para os prismas grauteados, os maiores valores encontrados
foram para os prismas das séries RG15-AG1, RG15-CG1, RG12-BG1,
RG6-CG1, preenchidos com os grautes da classe G1 de maior rigidez, e
os prismas da série MG15-A, preenchido com a argamassa da classe A,
também de maior rigidez entre as argamassas utilizadas.
A princípio nota-se que com o aumento da resistência dos grautes
aumenta-se a eficiência dos prismas. Entretanto, para algumas séries de
prismas (RG15-AG1 e MG15-A), isto não significa que ocorreu um
aumento efetivo da carga de ruptura dos mesmos, tendo em vista que os
valores de carga de ruptura obtidos para os prismas grauteados
encontram-se próximos dos valores obtidos para os prismas vazios,
assentados com a mesma classe de argamassa.
4.5.1.1 Análise da influência dos componentes na resistência à
compressão dos prismas
Com o propósito de verificar a influência da variação da
argamassa, bloco e o efeito conjunto do bloco e argamassa na resistência
dos prismas, foi realizadas análises fatoriais de 2 fatores (ANOVA) para
as séries de prismas grauteados, moldados com os blocos B15, B6 e
argamassas das classes A e C.
Na primeira análise, para os prismas moldados com os blocos B6,
B15 e argamassa classe C, os fatores avaliados foram os valores médios
de resistência à compressão dos grautes e a resistência à compressão dos
blocos (2 fatores). Para o graute utilizou-se 4 níveis de variação, ou seja,
utilizou-se o grautes G1 (primeiro nível), G2 (segundo nível), G3
(terceiro nível) e argamassa C (quarto nível). Para os blocos, utilizaramse os blocos da classe B6 (primeiro nível) e B15 (segundo nível). Todos
os níveis de variação possuem valores distintos de resistência à
compressão.
Os resultados encontrados com esta análise fatorial para os
prismas grauteados, com um nível de confiança de 95%, apresentam-se
na Tabela 4.19. Constata-se que a resistência média à compressão do
graute, do bloco e a interação entre estes dois fatores, influenciam
146
significativamente na resistência média à compressão dos prismas, na
área líquida. Ainda, o graute foi o fator com maior influência na
resistência à compressão dos prismas, seguido da interação entre o bloco
e graute, e por último pelo bloco. Este último fator apresenta pequena
influência, em comparação aos demais fatores.
Tabela 4.19 – Análise de variância para o grautes e blocos na resistência à
compressão dos prismas moldados com a argamassa da classe C.
Variável
PRISMAS GRAUTEADOS
F
Fα (crítico)
(calculado)
Resultado
Graute
201,439
2,90
F > Fα (Há influência)
Bloco
4,275
4,15
F > Fα (Há influência)
Graute x Bloco
47,603
2,90
F > Fα (Há influência)
Fonte: Autor (2015).
Na segunda análise, para os prismas moldados somente com os
blocos B15 e as argamassas das classes A e C, os fatores avaliados
foram os valores médios de resistência à compressão dos grautes e a
resistência à compressão das argamassas (2 fatores). Para o graute
utilizou-se 5 níveis de variação, ou seja, utilizou-se o grautes G1
(primeiro nível), G2 (segundo nível), G3 (terceiro nível), argamassa A
(quarto nível) e argamassa C (quinto nível). Para as argamassas,
utilizaram-se argamassas da classe A (primeiro nível) e classe C
(segundo nível). Todos os níveis de variação possuem valores distintos
de resistência à compressão.
Os resultados encontrados com esta análise fatorial para os
prismas grauteados, com um nível de confiança de 95%, apresentam-se
na Tabela 4.20. Constata-se que a resistência média à compressão do
graute, da argamassa e a interação entre estes dois fatores, influenciam
significativamente na resistência média à compressão dos prismas, na
área líquida. Ainda, o graute foi o fator com maior influência na
resistência dos prismas, seguido da argamassa e por último, da interação
entre o graute e argamassa.
147
Tabela 4.20 – Análise de variância para o grautes e argamassas na resistência à
compressão dos prismas moldados com os blocos da classe B15.
PRISMAS GRAUTEADOS
Variável
F (calculado)
Fα (crítico)
Resultado
Graute
33,472
2,90
F > Fα (Há influência)
Argamassa
9,348
4,15
F > Fα (Há influência)
Graute x Argamassa
7,228
2,90
F > Fα (Há influência)
Fonte: Autor (2015).
Observa-se que em ambas as análises, tanto o bloco, argamassa,
graute e a combinações destes componentes influenciam na resistência
dos prismas. Este comportamento já fora constatado em trabalhos
realizados por outros pesquisadores. Entretanto, o aumento da
resistência da argamassa possui pouca influência no aumento da
resistência à compressão dos prismas. Isto é evidenciado quando
comparados os valores de resistência dos prismas preenchidos moldados
com o bloco B15, preenchidos com a mesma classe de grautes (Tabela
4.18). Enquanto que a argamassa A possui uma resistência cinco vezes
maior que a da argamassa C, observa-se que os valores de resistências
dos prismas moldados com a argamassa A não aumentaram
proporcionalmente seus valores de resistência quando comparados com
os prismas moldados com a argamassa C. Conforme Cunha (2001), o
aumento de resistência da argamassa não influiu na resistência de
prismas, não grauteados e grauteados, uma vez que grandes aumentos na
resistência das argamassas proporcionam acréscimos muito pequenos na
resistência à compressão dos prismas de alvenaria, evidenciado aqui
com os resultados encontrados para os prismas moldados com o bloco
B15 e argamassas A e C. Conforme os resultados expostos na Tabela
4.19 e Tabela 4.20, este aumento na resistência dos prismas está
relacionado principalmente ao graute e na interação entre bloco e graute.
4.5.1.2 Análise da capacidade de carga dos prismas grauteados
Com o objetivo de identificar o aumento efetivo da capacidade de
carga dos prismas quando grauteados, o gráfico da Figura 4.5 mostra as
cargas de ruptura em função do aumento do preenchimento, para os
prismas vazios e grauteados moldados com os grautes G1, G2, G3 e
argamassas A, B e C, bem como os prismas preenchidos com suas
respectivas argamassas de assentamento (MG6-C, MG12-B, MG15-C e
148
MG15-A). Conforme se observa na Figura 4.5, o preenchimento dos
prismas com a argamassa de assentamento leva a um pequeno aumento
na carga de ruptura dos prismas, quando comparados com os prismas
vazios (MV6-C, MV12-B, MV15-C e MV15-A). Este aumento é mais
evidente com os prismas moldados com os blocos B6 e com a argamassa
classe C, de menores valores de fb e farg. Conforme prismas moldados
com os blocos B15 e argamassas A e C, não se observa aumento
acentuado da carga de ruptura com o enrijecimento da argamassa e do
grautes. Observa-se a principio que o enrijecimento da alvenaria, com o
aumento da resistência da argamassa, não representa aumento
proporcional para a resistência dos prismas grauteados.
Figura 4.5 - Carga de ruptura média (Fp) versus resistência média à compressão
dos grautes (fg).
700
Prisma Bloco B15 Arg A
Prisma Bloco B12 Arg B
Prisma Bloco B15 Arg C
Prisma Bloco B6 Arg C
650
600
550
RG15-CG1
MG15-A
500
Fp (kN)
RG6-CG1
RG15-AG1
MV15-A
RG15-AG3 RG15-AG2
450
MG15-C
MV15-C
400
350
MG12-B
MV12-B
300
RG12-BG2
RG12-BG3
MG6-C
RG12-BG1
RG15-CG2
RG15-CG3
250
RG6-CG2
RG6-CG3
200
MV6-C
150
0
10
20
30
40
fg (MPa)
Fonte: Autor (2015).
Assim, com a intenção de verificar a eficácia da utilização dos
grautes para estes prismas, novamente foi realizada uma análise de
variância (ANOVA), utilizando os valores de resistência média à
compressão dos prismas, na área bruta. Este procedimento teve como
objetivo verificar se houve aumento efetivo nos valores de carga de
ruptura dos prismas (forças últimas de ruptura dos prismas), com a
utilização da argamassa de assentamento (como preenchimento
estrutural) e os grautes G1, G2 e G3, quando comparados com os
prismas vazios. Também se determinou o Efeito Relativo, ou seja, o
149
valor percentual de aumento ou não na carga de ruptura dos prismas
quando preenchidos.
De acordo com Leão (2008), a comparação entre a resistência de
prismas grauteados e não-grauteados levando-se em conta área líquida é
feita para áreas diferentes, e eventualmente pode resultar que a
resistência do prisma grauteado é inferior a resistência do prisma vazio.
Essa consideração não leva em conta o efetivo aumento da carga de
ruptura resistida pelos prismas grauteados. O meio técnico nacional
trabalha com resistência bruta dos prismas, que faz com que se
considere o efetivo aumento de resistência dos prismas com graute.
Neste trabalho, assim como na pesquisa realizada por Mendes
(1998) e Leão (2008), a análise estatística de comparação entre a
resistência média à compressão de prismas grauteados e não grauteados
foi feita com os dados referidos à área bruta dos mesmos, visando
verificar o efetivo aumento da carga de ruptura resistida pelos prismas.
Desta forma, com um nível de confiança de 95%, o resultado da
análise de múltiplas médias obtida para os valores de resistência média à
compressão dos prismas (fp), na área bruta, bem como o Efeito Relativo,
encontra-se na Tabela 4.21.
Analisando os resultados dispostos na Tabela 4.21, somente os
prismas RG15-CG1, RG12-BG1, RG6-CG1 e RG6-CG2, preenchidos
com os grautes G1 e G2, e os prismas MG6-C, preenchidos com a
argamassa classe C, apresentam aumento significativo em suas
resistências na área bruta, ou seja, em sua capacidade de carga. Este
aumento, em média, nos valores de resistência à compressão (fp), e
consequentemente nas cargas de ruptura, observa-se para os prismas
grauteados que apresentam valores de fp superiores a 29,3%, em
comparação aos valores de fp dos prismas vazios (Efeito relativo >
29,3%). Este aumento significativo nos valores de carga de ruptura está
relacionado com as diferenças existentes entre os valores das
propriedades mecânicas dos materiais que o constituem (GOMES, 1983;
MOHAMAD 1998; MENDES, 1998; CAMACHO E RODRIGUES,
1999; CUNHA, 2001; GROHMANN, 2006; LEÃO, 2008).
De acordo com o objetivo deste trabalho, somente a família de
prismas MG6-C, preenchidos com a própria argamassa de assentamento,
apresentam aumento significativo em sua capacidade de carga, aumento
este de 61,0%. Esse aumento na resistência dos prismas, na área bruta,
com a utilização da argamassa assentamento como preenchimento
estrutural levanta a hipótese da viabilidade de utilização. Entretanto, as
combinações MG15-A, MG15-C e MG12-B não apresentam esse
mesmo comportamento.
150
Tabela 4.21 – Aumento efetivo da capacidade de carga dos prismas
preenchidos.
F
Bloco B6
Bloco B12
Bloco B15
Bloco B15
Prismas
Fα
(calculado) (crítico)
Conclusão
F < Fα
(Não há diferença)
F < Fα
(Não há diferença)
Efeito
Relativo
(%)
MV15-A
RG15-AG1
1,489
2,306
MV15-A
RG15-AG2
1,081
2,306
MV15-A
RG15-AG3
1,326
2,571
F < Fα (Não há diferença)
- 10,0
+ 4,2
+ 51,6
MV15-A
MG15-A
0,535
2,306
F < Fα
(Não há diferença)
MV15-C
RG15-CG1
9,440
2,306
F > Fα (Há diferença)
F < Fα
(Não há diferença)
F < Fα
(Não há diferença)
F < Fα
(Não há diferença)
+ 13,3
- 9,2
MV15-C
RG15-CG2
0,471
2,306
MV15-C
RG15-CG3
0,065
2,306
MV15-C
MG15-C
0,110
2,306
MV12-B
RG12-BG1
6,343
2,306
F > Fα (Há diferença)
+ 45,7
MV12-B
RG12-BG2
0,529
2,776
F < Fα (Não há diferença)
+ 3,7
MV12-B
RG12-BG3
0,088
2,306
F < Fα (Não há diferença)
+ 1,2
MV12-B
MG12-B
1,852
2,306
F < Fα (Não há diferença)
+ 17,3
MV6-C
RG6-CG1
19,725
2,571
F > Fα (Há diferença)
+ 317,1
MV6-C
RG6-CG2
3,426
2,306
F > Fα (Há diferença)
+ 29,3
+ 9,8
+ 61,0
MV6-C
RG6-CG3
1,367
2,306
F < Fα
(Não há diferença)
MV6-C
MG6-C
4,512
2,306
F > Fα (Há diferença)
+ 3,2
0,0
0,0
Fonte: Autor (2015).
Assim, visando compreender este comportamento, construíram-se
gráficos correlacionando as propriedades mecânicas dos materiais
constituintes dos prismas. Mais especificamente, traçaram-se gráficos
para a resistência média à compressão dos prismas (fpliq) versus as
relações entre as resistências dos grautes e blocos (fg/fbliq), entre as
resistências das argamassas e blocos (farg/fbliq), entre os módulos de
elasticidade do graute e bloco (Eg/Eb) e entre os módulos de elasticidade
da argamassa e bloco (Earg/Eb), todos na área líquida, conforme Figura
4.6 à Figura 4.9.
151
Figura 4.6 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus relação entre os valores de resistência média à compressão
do graute/resistência do bloco na área líquida (fg/fbliq).
25
21
19
fpliq (MPa)
RG6-CG1
Prismas Blocos B15 Arg A
Prismas Blocos B12 Arg B
Prismas Blocos B15 Arg C
Prismas Blocos B6 Arg C
23
RG15-CG1
17
RG15-AG1
MG15-A
15
13
MG12-B
MV15-C
11
RG12-BG1
RG15-AG2
RG15-AG3
TG15-C RG15-CG3
RG12-BG2
RG12-BG3
9
MG6-C
7
RG6-CG2
RG6-CG3
5
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
fg/fbliq
Fonte: Autor (2015).
Figura 4.7 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus relação entre os valores médios de módulo de elasticidade
do graute/módulo de elasticidade do bloco (Eg/Eb).
25
23
Prismas Blocos B15 Arg A
21
Prismas Blocos B12 Arg B
Prismas Blocos B15 Arg C
19
Prismas Blocos B6 Arg C
17
fpliq (MPa)
RG6-CG1
RG12-BG1
MG15-A
15
13
11
MG12-B
MG15-C
9
MG6-C
RG15-CG1
RG15-AG3
RG15-AG1
RG15-AG2
RG15-CG3
RG12-BG3 RG12-BG2
RG15-CG2
RG6-CG2
7
RG6-CG3
5
0,0
1,0
Fonte: Autor (2015).
2,0
3,0
4,0
5,0
6,0
Eg/Eb
152
Figura 4.8 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus relação entre os valores de resistência média à compressão
do graute/resistência da argamassa (fg/farg).
25
Prismas Blocos B12 Arg B
21
Prismas Blocos B15 Arg C
fpliq (MPa)
19
Prismas Blocos B6 Arg C
17
RG15-AG1
11
9
RG15-AG3
RG15-AG2
RG15-CG3
MG12-B
MG15-C RG12-BG3 RG12-BG2
RG15-CG2
MG6-C
RG6-CG2
RG6-CG3
7
RG15-CG1
RG12-BG1
MG15-A
15
13
RG6-CG1
Prismas Blocos B15 Arg A
23
5
0,0
2,0
4,0
6,0
8,0
10,0
12,0
14,0
fg/farg
Fonte: Autor (2015).
Figura 4.9 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus relação entre os valores médios de módulo de elasticidade
do graute/módulo de elasticidade da argamassa (Eg/Earg).
25
Prismas Blocos B12 Arg B
21
Prismas Blocos B15 Arg C
19
fpliq (MPa)
RG6-CG1
Prismas Blocos B15 Arg A
23
Prismas Blocos B6 Arg C
17
RG15-AG1
MG15-A
15
RG12-BG1
RG15-AG3
MG12-B RG15-AG2
13
11
RG12-BG2
MG15-C
RG12-BG3
MG6-C
9
7
RG15-CG1
RG15-CG3RG15-CG2
RG6-CG3
RG6-CG2
5
0,0
Fonte: Autor (2015).
5,0
10,0
15,0
20,0
Eg/Earg
153
Analisando os resultados da Tabela 4.21 e os gráficos da Figura
4.6 à Figura 4.9, observa-se que com o aumento das relações fg/fbliq,
Eg/Eb, fg/farg e Eg/Earg, os prismas grauteados que apresentam maior
desempenho (aumento na carga de ruptura), foram aqueles moldados
com argamassa de assentamento com os menores valores de resistência
à compressão e módulo de elasticidade, neste caso, os prismas RG15CG1, RG12-BG1, RG6-CG1 e RG6-CG2, assentados com as
argamassas das classes B e C. Esse comportamento fica evidente quando
comparados os prismas moldados com os blocos B15, com argamassas
das classes A e C, na qual o aumento no valor da resistência à
compressão da argamassa não representou aumento significativo
proporcional na resistência dos prismas, quando preenchidos com os
grautes, ou seja, não ocorreu aumento efetivo em sua carga de ruptura.
Em alguns casos, para os prismas RG15-AG2 e RG15-AG3,
aparentemente ocorreu um decréscimo no valor da resistência quando
preenchidos com os grautes G2 e G3. Entretanto, como se demonstra na
Tabela 4.21, não se constata diferença significativa entre os valores de
resistência para estas duas séries de prismas, em relação ao prisma vazio
da família MV15-A, ou seja, não há aumento efetivo na carga de
ruptura.
Este aumento, ou não, efetivo das cargas de ruptura dos prismas
pode ser explicado pelas diferenças existentes entre os valores de
resistência característica à compressão dos grautes e blocos, na área
líquida. Geralmente, recomenda-se que a resistência característica do
graute apresente no mínimo o mesmo valor da resistência característica
do bloco, em relação à área líquida (RAMALHO e CORRÊA, 2003;
PARSEKIAN et al, 2012). Para Dhanasekar (1994), a resistência ideal
para o grautes devem ser igual a resistência da alvenaria, na área líquida,
comportamento este também evidenciado por Mendes (1998). Ainda, de
acordo com Ramalho e Corrêa (2003), o comportamento do prisma pode
ser influenciado negativamente em razão das diferentes características
elásticas dos materiais que compõem os prismas, o que foi observado
para os prismas RG15-AG2 e RG15-AG3. Este comportamento
evidencia-se por causa da grande diferença entre os valores de módulos
de elasticidade da argamassa de assentamento e do material do bloco
para estes prismas, que são da ordem de 54,8%, sendo que o material do
bloco apresenta o menor valor de módulo de elasticidade. Os valores de
resistência característica à compressão dos grautes G2 e G3 em relação
ao fbk do bloco B15, na área líquida, são menores, o que pode ter
contribuído para o decréscimo nos valores de resistência dos prismas
quando preenchidos com estes grautes.
154
Comparando-se os valores característicos de resistência dos
blocos e grautes, Tabela 4.13 e Tabela 4.17, evidencia-se este
comportamento, onde as séries de prismas que apresentam aumento
significativo nos valores de carga de ruptura foram aquelas na qual os
valores de resistência característicos à compressão dos grautes são
próximos ou superiores aos valores de fbk dos blocos que constituem
estes prismas, neste caso os prismas das séries RG15-CG1, RG12-BG1,
RG6-CG1 e RG6-CG2.
Desta forma evidencia-se que, para determinadas combinações de
materiais, o aumento das relações entre as propriedades da argamassa,
graute e bloco podem gerar o aumento nas resistências dos prismas,
como visualizado anteriormente com os gráficos da Figura 4.6 à Figura
4.9.
Observa-se também que os prismas MG6-C não apresentam as
maiores relações fg/fbliq, Eg/Eb, fg/farg e Eg/Earg, entretanto apresentam
aumento significativo em sua carga de ruptura quando preenchidos com
a argamassa de assentamento. Comparando os valores característicos de
resistência à compressão do bloco (fbk liq) e da argamassa (fargk),
utilizados na moldagem dos prismas MG6-C, observa-se a argamassa
apresenta valor de resistência em torno de 90,7% menor que o valor de
resistência do bloco, o que conforme observado por Ramalho e Corrêa
(2003) e Parsekian et al. (2012), esta diferença entre os valores de
resistência da argamassa e bloco não é indicada, e como consequência
ocasionariam um decréscimo nos valores de carga a ser resistida para a
série MG6-C, comportamento este não observado.
Mas de acordo com Mendes (1998), prismas grauteados que
apresentam melhor desempenho são aqueles que são preenchidos com
grautes com módulos de elasticidade próximos ao módulo de
elasticidade da argamassa e dos prismas não grauteados.
Comportamento este, também observado por Dhanasekar e Kumar
(1994) e Khalifa e Magzoub (1994).
Para Mendes (1998), quanto maior o módulo de elasticidade do
grautes, maior será a parcela de carregamento total por ele absorvido.
Ainda, segundo o autor, para os grautes que apresentam pouca diferença
entre seus coeficientes de Poisson, com o aumento da tensão vertical nos
grautes maior será a tensão lateral gerada nestes e consequentemente
maior será a possibilidade de ocorrer tensões de tração e cisalhamento
no bloco. Contudo, para grautes que apresentam menores módulos de
elasticidade, o conjunto de alvenaria (bloco e argamassa), absorve uma
parcela maior do carregamento total. Deste modo, com o aumento do
carregamento absorvido pelo bloco e, consequentemente, da tensão de
155
compressão efetiva nos blocos, há a diminuição de tensões laterais e o
aumento da resistência ao cisalhamento dos blocos, tendo como
consequência, o aumento na resistência à compressão dos prismas.
Desta maneira, visando identificar a parcela de carregamento
suportado pelo graute e pelo prisma, foi adotado o mesmo procedimento
teórico utilizado por Gomes (1983), Mendes (1998) e Leão (2008), ou
seja, igualaram-se as deformações dos materiais do prisma grauteado de
acordo com a Lei de Hooke. Como nos trabalhos desenvolvidos
anteriormente pelos autores, aqui neste trabalho não se busca determinar
valores absolutos, mas sim obter uma possível explicação do
comportamento da alvenaria de blocos cerâmicos grauteados. Ressaltase, que esse procedimento analisa a alvenaria dentro do seu regime
elástico, diferente do comportamento que será analisado na análise
numérica, ou seja, considerando a não linearidade do material dos
componentes dos prismas.
Assim, como nos trabalhos desenvolvidos pelos pesquisadores
citados, a Figura 4.10 exemplifica o sistema composto por graute e
alvenaria, sendo esta última composta do conjunto bloco e argamassa.
Figura 4.10 – Módulos e áreas utilizados na análise de prismas grauteados.
bloco
Argamassa
bloco
Prisma após
carregamento
Fonte: adaptado de Mendes (1998).
Onde, de acordo com a Figura 4.10, tem-se que:
Fg e Falv são, respectivamente, as parcelas de carregamento
absorvido pelo graute e pela alvenaria;
156
Aalv, Ealv e νalv são, respectivamente, a área resistente, o
módulo de elasticidade e o coeficiente de Poisson da alvenaria;
Ag, Eg e νg são, respectivamente, a área resistente, o módulo de
elasticidade e o coeficiente de Poisson do graute;
εg e εalv são, respectivamente, as deformações específicas do
graute e da alvenaria.
Assim, partindo da Equação 4.1 (Lei de Hooke) e igualando-se as
deformações dos materiais, obtêm-se as Equações 4.2 e 4.3, que
relacionam e fornecem as parcelas do carregamento total absorvidas
pelo grautes e pela alvenaria.
(4.1)
Fazendo a soma dos carregamento absorvidas pelo graute e pela
alvenaria, igual ao carregamento total Ft, e igualando as deformações
específicas do graute (εg) e da alvenaria (εalv) tem-se:
e
Ft = Fg + Falv
Logo, as parcelas de carregamento absorvidos pela alvenaria e
pelo grautes são dadas pelas seguintes equações:
(4.2)
(4.3)
Para o cálculo das parcelas de carregamentos absorvidos, de
acordo com o proposto por Mendes (1998) e Leão (2008), neste trabalho
também foram utilizados os módulos de elasticidade do graute e dos
prismas não grauteados, obtidos na área líquida. Diferente do proposto
por Gomes (1983), que utilizou o módulo de elasticidade do bloco ao
invés do módulo da alvenaria. O procedimento aqui adotado, segundo
Mendes (1998), faz com que a análise seja mais representativa do que
realmente ocorre no prisma grauteado, já que o carregamento absorvido
pelo bloco é influenciado pelas propriedades da argamassa de
157
assentamento. Na Tabela 4.22 encontram-se os valores percentuais
estimados dos carregamentos absorvidos pelos grautes e alvenarias,
calculados com as Equações 4.2 e 4.3, para as diferentes séries de
prismas da Etapa Referência.
De acordo com os resultados da Tabela 4.22, percebe-se que com
o aumento da rigidez do graute aumenta-se a parcela de carregamento
deste em relação ao carregamento total do prisma, consequentemente,
diminuindo a parcela de carregamento suportada pela alvenaria (blocoargamassa). De acordo com Mendes (1998), ao se permitir uma menor
sobrecarga na alvenaria, pela utilização de grautes mais resistentes e/ou
argamassas mais deformáveis, dois efeitos somam-se e influenciam
negativamente para um melhor desempenho à compressão do prisma
grauteado: quando o bloco absorve uma menor parcela do carregamento
total, o graute, por estar mais carregado, desenvolve maiores tensões
laterais sobre o bloco; ao absorver uma menor parcela do carregamento
total que incide sobre o prisma, o bloco fica sujeito a uma tensão de
compressão menor, diminuindo sua resistência ao cisalhamento. Assim,
este aumento de carregamento sob os grautes implica no aumento da
tensão lateral sobre as paredes internas dos blocos, e como
consequência, ocasiona a ruptura prematura do prisma.
Diferente dos resultados encontrados pelo pesquisador, conforme
os valores expostos na Tabela 4.21 e Tabela 4.22, observa-se que o
aumento na rigidez do graute não ocasiona a diminuição da resistência
dos prismas. Entretanto, constata-se que não existe diferença
significativa entre as cargas de ruptura dos prismas, com o aumento da
rigidez do grautes, ou seja, não ocorre a diminuição da capacidade de
carga dos prismas. Entretanto, também não ocorre o aumento de sua
capacidade de carga, exceto para os prismas RG15-CG1, RG12-BG1,
RG6-CG1, RG6-CG2 e MG6-C, que apresentaram aumento
significativo em suas cargas de ruptura quando grauteados. Esta
diferença observada em relação aos trabalhos de Mendes (1998) e
também de Leão (2008), se deve ao fato que nos trabalhos destes dois
pesquisadores adotaram-se blocos com geometrias e valores de
resistências à compressão diferentes dos utilizados neste trabalho, onde
a distribuição de tensão de um componente para o outro se comportando
de forma distinta sob compressão.
158
Bloco B6
Bloco B12
Bloco B15
Tabela 4.22 – Porcentagem estimada dos carregamentos absorvidos pelos
grautes.
ETAPA REFERÊNCIA
Área Líquida alvenaria =
Área Graute = 129,5 cm²
221,1 cm²
Ep liq prisma
% Carga
% Carga
Prismas
Eg (MPa)
vazio
Graute
Alvenaria
(MPa)
RG15-AG1 47490,2 11720,6
70,4
29,6
RG15-AG2 30657,8 11720,6
60,5
39,5
RG15-AG3 22375,9 11720,6
52,8
47,2
MG15-A
12554,2 11720,6
38,6
61,4
MV15-A
11720,6
0
100
RG15-CG1 47490,2
7662,0
78,4
21,6
RG15-CG2 30657,8
7662,0
70,1
29,9
RG15-CG3 22375,9
7662,0
63,1
36,9
MG15-C
2529,6
7662,0
16,2
83,8
MV15-C
7662,0
0
100
Área Líquida alvenaria =
Área Graute = 116,8 cm²
204,1 cm²
Ep liq prisma
% Carga
% Carga
Prismas
Eg (MPa)
vazio
Graute
Alvenaria
(MPa)
RG12-BG1 47490,2 11511,5
70,2
29,8
RG12-BG2 30657,8 11511,5
60,4
39,6
RG12-BG3 22375,9 11511,5
52,7
47,3
MG12-B
7120,1
11511,5
26,1
73,9
MV12-B
11511,5
0
100
Área Líquida alvenaria =
Área Graute = 126,4 cm²
158,3 cm²
Ep liq prisma
% Carga
% Carga
Prismas
Eg (MPa)
vazio
Graute
Alvenaria
(MPa)
RG6-CG1 47490,2
4890,0
88,6
11,4
RG6-CG2 30657,8
4890,0
83,3
16,7
RG6-CG3 22375,9
4890,0
78,5
21,5
MG6-C
2529,6
4890,0
29,2
70,8
MV6-C
4890,0
0
100
fp liq
(MPa)
15,8
12,7
12,6
14,5
22,2
17,2
11,6
11,3
10,9
17,3
fp liq
(MPa)
15,0
10,6
10,4
12,1
16,3
fp liq
(MPa)
24,3
7,6
6,5
9,3
10,6
Fonte: Autor (2015).
Desta maneira, para os resultados encontrados neste trabalho, o
enrijecimento das argamassas e dos grautes não proporcionam aumento
significativo nas cargas de ruptura dos prismas, exceto para as séries
RG15-CG1, RG12-BG1, RG6-CG1 e RG6-CG2, moldados com as
159
argamassas de menor rigidez. Isto se evidencia com os prismas
moldados com os blocos B15, na qual o aumento na resistência da
argamassa, ou seja, com a utilização da argamassa A, não ocorreu
diferença significativa entre os valores de resistência dos prismas
grauteados e vazio (Tabela 4.21). Este comportamento também foi
observado por Mendes (1998) e Leão (2008), ou seja, com o
enrijecimento da argamassa e consequentemente da alvenaria, não
ocorre aumento significativo dos valores de resistência dos prismas
quando grauteados. Comportamento similar foi observado anteriormente
com os gráficos da Figura 4.6 à Figura 4.9, na qual os prismas
grauteados RG15-CG1 assentados com as argamassas das classes C, de
menor rigidez, apresentam aumento significativo em su capacidade de
carga, quando comparados com os prismas vazios.
Para os prismas MG6-C, a diminuição da rigidez do graute, neste
caso a argamassa C, contribui para o aumento da carga de ruptura do
prisma. Nesta série de prismas, a diminuição da parcela de carga
suportada pelo preenchimento em razão de sua baixa rigidez, provoca o
aparecimento de baixas tensões sobre as paredes internas dos blocos,
contribuindo para o aumento da capacidade de carga dos prismas.
Desta forma, o aumento na resistência à compressão dos prismas
com a utilização da argamassa como preenchimento estrutural, neste
caso para a série MG6-C, levanta a hipótese da viabilidade de utilização
desta técnica, desde que a escolha entre os materiais seja adequada.
Entretanto, ressalta-se que este aumento não se observa nas demais
séries de prismas preenchidos com argamassa, gerando-se dúvidas
quanto ao desempenho mecânico dos prismas com a utilização desta
técnica, o que se espera esclarecer ao longo das próximas etapas deste
trabalho.
4.5.2. Resultados dos ensaios das Etapas com Argamassa
Mista e Argamassa Industrializada
Estas etapas têm como objetivo investigar o comportamento de
prismas sob compressão uniaxial com a utilização da argamassa de
assentamento dos tipos mista e industrializada, como preenchimento
estrutural dos prismas, conforme prescrito na norma ABNT NBR
15812-2 (2010).
Assim, na Tabela 4.23 apresentam-se os valores de caracterização
mecânica obtidos para a Etapa com Argamassa Mista. A partir destes
resultados, conforme Figura 4.11, construiu-se o gráfico da resistência
média à compressão dos prismas (fpliq), na área líquida, versus
160
resistência média à compressão das argamassas, que para os prismas
grauteados desempenham a mesma função do graute (farg = fg). A
construção deste gráfico teve como objetivo a identificação de
tendências de comportamento para cada uma das séries de prismas.
Tabela 4.23 – Características mecânicas dos prismas da Etapa com Argamassa
Mista.
ETAPA COM ARGAMASSA MISTA
Nº de Exemplares = 5
Bloco B15
Bloco B12
Bloco B6
Prismas
Fp
(kN)
C.V.
(%)
fp
fp liq
(MPa) (MPa)
Nº de Exemplares = 2
Eficiência
Ep liq
(GPa)
C.V.
(%)
Ep
(GPa)
(%)
(η) –
Área
Bruta
C.V.
MV6-C
164,1
9,5
4,1
10,6
10,2
2,0
4,9
11,4
0,38
MV6-B
214,5
13,6
5,4
13,9
13,9
3,4
9,5
4,3
0,49
MV6-A
276,5
9,0
7,0
17,9
9,4
2,9
7,7
3,8
0,63
MG6-C
262,2
7,7
6,6
9,3
7,7
2,8
3,9
7,3
0,60
MG6-B
258,8
7,6
6,6
9,2
7,9
3,7
5,3
4,7
0,59
MG6-A
300,2
13,6
7,6
10,7
12,9
3,7
5,3
3,5
0,69
MV12-C
281,1
13,0
6,9
13,9
12,5
4,4
8,9
5,8
0,47
MV12-B
333,6
11,1
8,1
16,3
11,8
5,6
11,5
8,1
0,55
MV12-A
393,1
10,0
9,6
19,1
9,1
5,0
10,2
6,7
0,65
MG12-C
326,7
6,6
8,0
10,2
7,2
4,5
5,5
9,2
0,54
MG12-B
389,2
13,0
9,5
12,1
14,3
7,4
9,5
6,7
0,64
MG12-A
442,8
9,6
10,9
13,8
9,7
6,1
8,0
6,7
0,74
MV15-C
375,3
9,7
9,3
17,3
10,0
4,1
7,7
8,2
0,58
MV15-B
335,0
6,9
8,4
15,5
7,8
5,2
9,6
6,7
0,52
MV15-A
482,9
15,0
12,0
22,2
15,3
6,3
11,7
5,1
0,74
MG15-C
382,3
6,9
9,4
11,0
5,9
6,6
7,6
8,9
0,58
MG15-B
455,2
8,6
11,3
13,1
8,5
9,0
10,6
6,4
0,68
MG15-A
503,0
6,9
12,5
14,5
6,1
7,0
8,1
4,7
0,80
Fonte: Autor (2015).
161
Figura 4.11 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus resistência média à compressão das argamassas de
assentamento ou de preenchimento (farg = fg) – Etapa com Arg. Mista.
25
Prisma Vazio Bloco B6
Prisma Garuteado Bloco B6
Prisma Vazio Bloco B12
Prisma Grauteado Bloco B12
Prisma Vazio Bloco B15
Prisma Grauteado Bloco B15
23
21
fpliq (MPa)
19
17
15
13
11
9
7
2,0
4,0
6,0
8,0
10,0
12,0
14,0
farg = fg (MPa)
Fonte: Autor (2015).
Analisando os valores da Tabela 4.23 e o gráfico da Figura 4.11,
com o aumento da resistência à compressão da argamassa, os prismas
apresentam um pequeno aumento em suas resistências, tanto para os
prismas vazios como para os prismas preenchidos com a argamassa de
assentamento. Este aumento na resistência dos prismas vazios e
grauteados com o aumento da resistência da argamassa divergem com as
conclusões de outros pesquisadores, no qual a resistência à compressão
da argamassa não representa influencia significativa na resistência à
compressão dos prismas vazios (Garcia, 2000; Romagna, 2000; Cunha,
2001; Juste, 2001).
Porém, para os prismas vazios MV15-B assentado com a
argamassa da Classe B, o valor de resistência à compressão não
apresenta o mesmo comportamento que os demais grupos de prismas. O
valor de resistência à compressão destes prismas apresenta uma pequena
queda quando comparado com os prismas MV15-C, moldados com a
argamassa da Classe C, com menor valor de resistência. Entretanto,
estes valores de resistência à compressão dos prismas encontram-se
muito próximos, o que pode significar que não ocorre diferença significa
entre estes valores.
162
Observa-se, também, que os fatores de eficiência para os prismas
vazios aumentam com o aumento da resistência da argamassa. Estes
valores encontram-se próximos dos valores observados por Ramalho e
Corrêa (2003), para prismas de blocos cerâmicos, variando entre 0,3 e
0,6; exceto para algumas séries de prismas, como a série MV15-A, que
apresenta o maior fator de eficiência, no valor de 0,74, como já
observado na Etapa de Referência. Para os prismas grauteados, os
maiores valores encontrados foram para os prismas das séries
preenchidas com a argamassa da classe A, de maior rigidez entre as
argamassas utilizadas.
Para a Etapa com Argamassa Industrializada, diferente do
observado na Etapa com Argamassa Mista, analisando os valores da
Tabela 4.24 e o gráfico da Figura 4.12, com o aumento da resistência à
compressão da argamassa ocorre um decréscimo na resistência dos
prismas com a utilização da argamassa de resistência intermediária,
neste caso a argamassa classe M. Esta tendência observada na Figura
4.12 para os prismas moldados com a argamassa M ocorre tanto para os
prismas vazios como para os prismas preenchidos com esta classe de
argamassa, exceto para os prismas IG6-M.
Este comportamento pode ser justificado em consequência da
composição da argamassa classe M, que apresenta um percentual maior
de aditivos incorporadores de ar, conforme o valor observado de teor de
ar incorporado determinado para esta classe de argamassa (Tabela 3.9).
A argamassa M apresentou praticamente o dobro dos valores de teor de
ar incorporado obtidos para as outras duas classes de argamassa.
Para os prismas preenchidos, durante a moldagem do
preenchimento, a barra utilizada no adensamento também pode ter
contribuído para o aumento do teor de ar incorporado da argamassa
classe M. A barra de adensamento possui uma superfície de contato
diferente da superfície da haste utilizada na moldagem dos corpos-deprova cilíndricos e prismáticos, utilizados para a obtenção das
propriedades mecânicas desta argamassa. Esta possível diferença na
energia de adensamento pode ter contribuído para o aumento do teor de
ar incorporado do preenchimento, afetando os valores das suas
propriedades. Isto também justificaria este decréscimo observado para
os valores de resistências obtidos para os prismas preenchidos moldados
com esta argamassa classe M.
Outro fator que deve ser aqui colocado, é que a produção destas
argamassas se deu em um equipamento não recomendado pelo
fabricante. Este fator pode ter afetado o controle de suas propriedades,
também influenciando nos resultados obtidos. Salienta-se que a
163
argamassa da classe M, é comercializada para ser utilizada também para
assentamento de paredes de vedação e para revestimento. Entretanto, as
argamassas das classes 5 e 10, são comercializadas para serem utilizadas
para o assentamento de blocos de alvenaria estrutural.
Para os prismas preenchidos IG6-M, como observado
anteriormente, o valor de resistência à compressão não apresenta o
mesmo comportamento que as demais séries de prismas. Entretanto, o
valor de resistência à compressão dos prismas IG6-M apresenta um
pequeno aumento quando comparado com os valores de resistência dos
prismas IG15-5, moldados com a argamassa da Classe 5, com menor
valor de resistência. Os valores de resistência à compressão destas duas
séries de prismas encontram-se muito próximos, o que pode significar
que não ocorre diferença significa entre estes valores.
164
Tabela 4.24 – Característica mecânicas dos prismas da Etapa com Argamassa
Industrializada.
ETAPARA COM ARGAMASSA INDUSTRIALIZADA
Nº de Exemplares = 5
Bloco B15
Bloco B12
Bloco B6
Prismas
Fp
(kN)
C.V.
fp
(%) (MPa)
Nº de Exemplares = 2
fp liq
(MPa)
C.V.
(%)
Ep
(GPa)
Eficiência
Ep liq C.V. (η) – Área
Bruta
(GPa) (%)
IV6-5
145,5
7,5
3,7
9,4
7,3
2,9
7,2
7,6
0,33
IV6-M
136,3 13,2
3,5
8,9
14,0
2,9
7,4
5,2
0,31
IV6-10
215,7 11,0
5,5
14,0
11,2
3,6
9,8
3,2
0,50
IG6-5
206,5
9,4
5,2
7,4
9,4
3,6
5,1
11,2
0,47
IG6-M
231,8 13,1
5,9
8,3
13,7
4,7
6,5
8,8
0,53
IG6-10
254,8
8,4
6,4
9,1
9,3
3,5
4,9
2,9
0,58
IV12-5
285,8
8,1
7,0
14,0
8,5
5,5
10,8
7,0
0,47
IV12-M
270,0 11,3
6,6
13,3
12,1
3,2
6,1
2,9
0,45
IV12-10
351,1 11,2
8,6
17,3
12,2
4,0
8,2
5,9
0,58
IG12-5
413,0
9,9
10,2
12,9
11,1
4,9
6,0
7,2
0,69
IG12-M
318,6
9,3
7,8
9,9
9,8
5,7
7,5
3,6
0,53
IG12-10
435,0
8,2
10,6
13,5
8,7
4,4
5,6
1,0
0,72
IV15-5
422,5 13,9
10,5
19,4
14,6
4,8
8,9
0,2
0,65
IV15-M
306,1
7,2
7,7
14,2
6,6
5,5
9,9
3,7
0,48
IV15-10
458,2 12,5
11,4
21,1
13,4
6,0
11,1
3,5
0,71
IG15-5
415,6 10,7
10,3
12,6
10,9
5,5
6,6
6,5
0,64
IG15-M
340,1
8,2
8,5
9,8
8,5
7,6
8,8
5,6
0,53
IG15-10
505,4 11,4
12,5
14,6
12,3
5,8
6,8
1,1
0,78
Fonte: Autor (2015).
165
Figura 4.12 – Gráfico da resistência média à compressão dos prismas na área
líquida (fpliq) versus resistência média à compressão das argamassas de
assentamento ou de preenchimento (farg = fg) – Etapa com Arg. Industrializada.
25
Prisma Vazio Bloco B6
Prisma Grauteado Bloco B6
Prisma Vazio Bloco B12
Prisma Grauteado Bloco B12
Prisma Vazio Bloco B15
Prisma Grauteado Bloco B15
23
21
fp liq (MPa)
19
17
15
13
11
9
7
4,0
5,0
6,0
7,0
8,0
9,0
10,0
farg = fg (MPa)
Fonte: Autor (2015).
Para os prismas vazios, observa-se tanto para a Etapa com
Argamassa Mista como a com Argamassa Industrializada, que tanto a
resistência dos prismas como seus respectivos fatores de eficiência
aumentam com o aumento da resistência das argamassas.
Para os prismas preenchidos, os maiores valores de eficiência
encontrados também foram para os prismas das séries preenchidas com
as argamassas de maior rigidez.
Entretanto, para estas séries de prismas isto não significa que
ocorreu aumento em sua eficiência. Para os prismas preenchidos, a
eficiência está ligada ao aumento efetivo da carga de ruptura dos
mesmos. Conforme se observa na Tabela 4.23 e Tabela 4.24, para
algumas séries destes prismas, os valores de carga de ruptura obtidos
encontram-se próximos dos valores de carga de ruptura obtidos para os
prismas vazios, assentados com a mesma classe de argamassa, o que
pode indicar que não houve aumento significativo em suas resistências
e, consequentemente, em seus fatores de eficiência.
Ressalta-se que esse fator de eficiência representa o quanto o
bloco contribui para a resistência da alvenaria, o que fica mais claro
quando se trata de paredes vazias. Entretanto, em se tratando de paredes
166
grauteadas, existe um terceiro componente (graute) e a sua presença
pode levar a conclusões erradas quanto a eficiência dos prismas.
Assim, para aumentar o fator de eficiência de maneira que ocorra
um acréscimo significativo nas resistências à compressão dos prismas
torna-se necessário, porém, aprofundar o estudo das propriedades
mecânicas dos materiais visando a correta compatibilização entre estes,
não se limitando apenas as seus valores de resistência, mas também em
suas propriedades elásticas.
4.5.2.1 Análise da influência dos componentes na resistência à
compressão dos prismas
Com o objetivo de verificar a influência da variação da
argamassa, bloco e o efeito conjunto do bloco e argamassa na resistência
final dos prismas vazios e preenchidos, na área líquida, foi realizada
uma análise fatorial de 2 fatores (ANOVA) para as séries de prismas das
Etapas com Argamassa Mista e Industrializada, com um nível de 95%
de confiança.
Os fatores avaliados foram os valores médios de resistência à
compressão da argamassa de assentamento (e preenchimento) e a
resistência à compressão dos blocos (2 fatores). Cada fator foi variado 3
vezes (3 níveis de variação), ou seja, para os blocos, utilizou-se os
blocos da classe B15 (primeiro nível), B12 (segundo nível) e B6
(terceiro nível) e para a argamassa utilizou-se as argamassas da Classe A
(primeiro nível), Classe B (segundo nível), e Classe C (terceiro nível),
para a Etapa com Argamassa Mista. Para a Etapa com Argamassa
Industrializada, para a argamassa, utilizou-se as argamassas da Classe
10 (primeiro nível), Classe M (segundo nível), e Classe 5 (terceiro
nível). Todos os níveis de variação possuem valores distintos de
resistência à compressão. Os resultados para estas análises encontram-se
na Tabela 4.25.
Assim para a Etapa com Argamassa Mista, com os resultados
encontrados com esta análise para os prismas vazios e preenchidos,
constata-se que as resistências médias à compressão da argamassa, do
bloco e a interação entre estes dois fatores, influenciam
significativamente na resistência média à compressão dos prismas
vazios. Este comportamento observa-se também para os prismas
preenchidos, exceto a interação entre a argamassa e bloco.
167
Tabela 4.25 – Análise de variância para a argamassa e bloco na resistência à
compressão dos prismas.
ETAPA ARGAMASSA MISTA
PRISMAS VAZIOS
Variável
F(calculado) Fα (crítico)
Resultado
Argamassa
37,352
3,28
F > Fα (Há influência)
Bloco
Argamassa x
Bloco
17,589
3,28
F > Fα (Há influência)
2,855
2,65
F > Fα (Há influência)
PRISMAS PREENCHIDOS
Variável
F(calculado) Fα (crítico)
Resultado
Argamassa
25,649
3,28
F > Fα (Há influência)
Bloco
32,736
3,28
F > Fα (Há influência)
Argamassa x
Bloco
2,214
2,65
F < Fα (Não Há influência)
PRISMAS VAZIOS
ETAPA ARGAMASSA
INDUSTRIALIZADA
Variável
F(calculado) Fα (crítico)
Resultado
Argamassa
33,074
3,28
F > Fα (Há influência)
Bloco
Argamassa x
Bloco
63,021
3,28
F > Fα (Há influência)
2,802
2,65
F > Fα (Há influência)
PRISMAS PREENCHIDOS
Variável
F(calculado) Fα (crítico)
Resultado
Argamassa
25,824
3,28
F > Fα (Há influência)
Bloco
Argamassa x
Bloco
59,322
3,28
F > Fα (Há influência)
5,869
2,65
F > Fα (Há influência)
Fonte: Autor (2015).
Conforme os resultados expostos na Tabela 4.25, para os prismas
vazios, a argamassa foi o fator com maior influência na resistência à
compressão dos prismas, seguida pelo bloco e por último, da interação
entre a argamassa e bloco. Este último fator apresenta pequena
influência, em comparação aos demais fatores. Para os prismas
preenchidos, constata-se que o fator com maior influência na resistência
à compressão dos prismas foi o bloco, seguido pela argamassa. Sendo
168
que a interação entre a argamassa e bloco, não influenciam
significativamente na resistência final dos prismas preenchidos.
Para a argamassa, o resultado encontrado diverge dos resultados
obtidos por outros pesquisadores (GARCIA, 2000; ROMAGNA, 2000 e
CUNHA, 2001), na qual a argamassa tem pouca influência na
resistência dos prismas. Entretanto Steil (2003) e Grohmann (2006)
observaram que a resistência da argamassa influencia significativamente
na resistência dos prismas, conforme se observa neste trabalho (Tabela
4.25).
Ainda para os prismas vazios, o aumento de resistência da
argamassa gera um incremento, em média, de 5,8 MPa e o aumento de
resistência dos blocos gera um incremento, em média, de 4,2 MPa,
ambos sobre a resistência dos prismas. O mesmo não se observa com a
interação entre estes dois fatores, ou seja, variando-se a resistência da
argamassa e variando, ao mesmo tempo, a resistência do bloco. Esta
interação gera um decréscimo na resistência dos prismas, em média, de
0,8 MPa. Para os prismas preenchidos, de acordo com a análise, o
aumento de resistência da argamassa de assentamento gera um
incremento, em média, de 2,8 MPa, e o aumento da resistência dos
blocos gera um incremento, em média, de 3,1 MPa, sobre a resistência
dos prismas. O efeito da interação entre os dois fatores, ou seja,
variando-se a resistência da argamassa e variando, ao mesmo tempo, a
resistência do bloco também gera um incremento. Entretanto, este
incremento é, em média, de 0,7 MPa, sobre a resistência do prisma.
Para os prismas da Etapa com Argamassa Industrializada,
conforme os resultados expostos na Tabela 4.25, para os prismas vazios
constata-se que o bloco foi o fator com maior influência na resistência à
compressão dos prismas, seguida pela argamassa e por último, da
interação entre a argamassa e o bloco. Este último fator apresenta
pequena influência, em comparação aos demais fatores. Para os prismas
preenchidos, constata-se que o fator com maior influência na resistência
à compressão dos prismas foi o bloco, seguido pela argamassa.
Entretanto, diferente do observado na Etapa com Argamassa Mista, aqui
se observa que a interação entre a argamassa e o bloco influencia
significativamente na resistência final dos prismas preenchidos.
Novamente, para a argamassa, o resultado encontrado diverge dos
resultados obtidos por outros pesquisadores, na qual este componente
tem pouca influência sobre a resistência dos prismas. Entretanto,
conforme Steil (2003) e Grohmann (2006) observa-se aqui que a
resistência da argamassa influencia significativamente na resistência dos
prismas (Tabela 4.25).
169
Ainda para os prismas vazios da Etapa com Argamassa
Industrializada, o aumento de resistência da argamassa gera um
incremento, em média, de 3,2 MPa e o aumento de resistência dos
blocos gera um incremento, em média, de 7,5 MPa, sobre a resistência
dos prismas. O mesmo não se observa com a interação entre estes dois
fatores, ou seja, variando-se a resistência da argamassa e variando, ao
mesmo tempo, a resistência do bloco gera-se um decréscimo na
resistência dos prismas, em média, de 1,0 MPa. Para os prismas
preenchidos, de acordo com a análise, o aumento de resistência da
argamassa de assentamento gera um incremento, em média, de 1,4 MPa,
o aumento de resistência dos blocos gera um incremento, em média, de
4,1 MPa, sobre a resistência dos prismas. O efeito da interação entre os
dois fatores, ou seja, variando-se a resistência da argamassa e variando,
ao mesmo tempo, a resistência do bloco também gera um incremento.
Entretanto, este incremento é, em média, de 0,1 MPa, sobre a resistência
dos prismas.
Ainda, buscando verificar se o preenchimento influencia
significativamente na resistência dos prismas, realizou-se outra análise
fatorial para as classes de prismas moldados com o mesmo bloco, para
estas duas etapas do programa experimental. O objetivo desta análise
consistiu em separar a influência da argamassa e do preenchimento
tendo em vista que, para estas duas etapas do programa experimental, a
argamassa de assentamento e de preenchimento (quando utilizada), é o
mesmo material.
Aqui os fatores avaliados foram os valores médios de resistência
à compressão da argamassa de assentamento (e preenchimento) e a
utilização de preenchimento ou não (2 fatores). Na Etapa com
Argamassa Mista, para a argamassa utilizou-se as argamassas da Classe
A (primeiro nível), Classe B (segundo nível), e Classe C (terceiro
nível), e para o preenchimento, utilizou-se a condição vazio (primeiro
nível) e com preenchimento (segundo nível). Para a Etapa com
Argamassa Industrializada adotou-se o mesmo procedimento, entretanto
utilizando as três classes de argamassas industrializadas.
Os resultados encontrados com esta análise fatorial, com um nível
de 95% de confiança, apresentam-se na Tabela 4.26.
170
Tabela 4.26 – Análise de variância para a argamassa e preenchimento na
resistência à compressão dos prismas.
ETAPA ARGAMASSA INDUSTRIALIZADA
ETAPA ARGAMASSA MISTA
Variável
Prismas moldados com bloco B6
F(calculado) Fα (crítico)
Resultado
Argamassa
26,345
3,4
F > Fα (Há influência)
Preenchimento
Argamassa x
preenchimento
80,916
4,26
F > Fα (Há influência)
12,034
3,4
F > Fα (Há influência)
Variável
Prismas moldados com bloco B12
F(calculado) Fα (crítico)
Resultado
Argamassa
49,694
3,4
F > Fα (Há influência)
Preenchimento
Argamassa x
preenchimento
143,894
4,26
F > Fα (Há influência)
1,701
3,4
F > Fα (Não Há influência)
Variável
Prismas moldados com bloco B15
F(calculado) Fα (crítico)
Resultado
Argamassa
18,382
3,4
F > Fα (Há influência)
Preenchimento
Argamassa x
preenchimento
73,033
4,26
F > Fα (Há influência)
6,095
3,4
F > Fα (Há influência)
Variável
Prismas moldados com bloco B6
F(calculado) Fα (crítico)
Resultado
Argamassa
27,454
3,4
F > Fα (Há influência)
Preenchimento
Argamassa x
preenchimento
42,086
4,26
F > Fα (Há influência)
10,872
3,4
F > Fα (Há influência)
Variável
Prismas moldados com bloco B12
F(calculado) Fα (crítico)
Resultado
Argamassa
17,213
3,4
F > Fα (Há influência)
Preenchimento
Argamassa x
preenchimento
26,816
4,26
F > Fα (Há influência)
2,372
3,4
F > Fα (Não Há influência)
Variável
Prismas moldados com bloco B15
F(calculado) Fα (crítico)
Resultado
Argamassa
23,777
3,4
F > Fα (Há influência)
Preenchimento
Argamassa x
preenchimento
70,072
4,26
F > Fα (Há influência)
1,244
3,4
F > Fα (Não Há influência)
Fonte: Autor (2015).
171
Para a Etapa com Argamassa Mista, para todas as séries de
prismas, constata-se que a argamassa, o preenchimento e a interação
entre estes dois fatores, influenciam significativamente na resistência
média final dos prismas vazios. Exceto para os prismas moldados com o
bloco B12, onde a interação entre a argamassa e o preenchimento não
influenciam significativamente na resistência à compressão dos prismas
moldados com esta classe de bloco.
Para a Etapa com Argamassa Industrializada, novamente
constata-se para todas as séries de prismas que a argamassa, o
preenchimento e a interação entre estes dois fatores, influenciam
significativamente na resistência média final dos prismas vazios. Exceto
para os prismas moldados com o bloco B12 e B15, onde a interação
entre a argamassa e o preenchimento não influenciam significativamente
na resistência à compressão dos prismas moldados com estas classes de
bloco. Entretanto, como esperado para todas as classes de prismas destas
duas etapas do programa experimental, observa-se que o fator com
maior influência trata-se da utilização ou não do preenchimento.
Prosseguindo com as análises, com o intuito de verificação se
houve aumento significativo nas resistências à compressão dos prismas,
na área líquida, com o aumento de resistência da argamassa, foi
realizada uma análise de variância (ANOVA) com comparação de
múltiplas médias entre as classes de prismas moldados com o mesmo
tipo de bloco. Os resultados desta análise, com um nível de confiança de
95%, para as duas etapas do programa experimental, encontram-se na
Tabela 4.27 e Tabela 4.28.
172
Tabela 4.27 – Análise de múltiplas médias entre a resistência à compressão dos
prismas – Etapa com Argamassa Mista.
Bloco B15
Bloco B12
Bloco B6
Prismas Comparados
MV6-A, MV6-B e
MV6-C
MV6-A e MV6-B
PRISMAS VAZIOS
F
Fα
(calculado) (crítico)
25,360
3,89
F > Fα (Há Diferença)
3,435
2,306
F > Fα (Há Diferença)
MV6-A e MV6-C
8,095
2,306
F > Fα (Há Diferença)
MV6-B e MV6-C
MV12-A, MV12-B e
MV12-C
MV12-A e MV12-B
3,312
2,306
F > Fα (Há Diferença)
10,707
3,89
F > Fα (Há Diferença)
2,444
2,306
F > Fα (Há Diferença)
MV12-A e MV12-C
4,797
2,306
MV12-B e MV12-C
2,098
2,306
F > Fα (Há Diferença)
F < Fα
(Não Há Diferença)
11,222
3,89
F > Fα (Há Diferença)
4,132
2,571
F > Fα (Há Diferença)
MV15-A e MV15-C
2,885
2,306
MV15-B e MV15-C
1,865
2,306
F > Fα (Há Diferença)
F < Fα
(Não Há Diferença)
MV15-A, MV15-B e
MV15-C
MV15-A e MV15-B
B6
Bloco B12
Bloco
PRISMAS PREENCHIDOS
Fα
Prismas Comparados
F(calculado)
(crítico)
Bloco B15
Resultado
Resultado
MG6-A, MG6-B e
MG6-C
3,317
3,89
F < Fα
(Não Há Diferença)
MG12-A, MG12-B e
MG12-C
9,776
3,89
F > Fα (Há Diferença)
MG12-A e MG12-B
1,791
2,306
MG12-A e MG12-C
5,379
2,306
F < Fα
(Não Há Diferença)
F > Fα (Há Diferença)
MG12-B e MG12-C
MG15-A, MG15-B e
MG15-C
2,367
2,306
F > Fα (Há Diferença)
18,444
3,89
F > Fα (Há Diferença)
MG15-A e MG15-B
2,155
2,306
MG15-A e MG15-C
7,303
2,306
F < Fα
(Não Há Diferença)
F > Fα (Há Diferença)
MG15-B e MG15-C
3,818
2,306
F > Fα (Há Diferença)
Fonte: Autor (2015).
173
Para a Etapa com Argamassa Mista, de acordo com os resultados
dispostos na Tabela 4.27, nos prismas vazios moldados com os blocos
B6, o aumento da resistência da argamassa da classe C para a A,
aumenta significativamente as resistências dos prismas. Os prismas
vazios moldados com os blocos B12 e as argamassas das classes C e B
(MV12-C e MV12-B), não apresentam diferença significativa entre suas
resistências à compressão, mesmo apresentando um pequeno aumento
na resistência, conforme pode ser observado no gráfico da Figura 4.11.
Para os prismas moldados com o bloco B12 e a argamassa da classe A,
observa-se um aumento significativo nos valores de resistência quando
comparados com os prismas moldadas com as argamassas das classes C
e B. O mesmo comportamento observado para os prismas moldados
com os blocos B12 ocorre para os prismas vazios moldados com os
blocos B15.
As resistências das argamassas das classes C e B encontram-se
abaixo da faixa entre 70% e 100% do valor de fb do bloco B12 e B15,
valores estes indicados como os mais adequados para prismas vazios
(MOHAMAD, 1998). Valores abaixo desta faixa implicariam na
incompatibilidade entre as propriedades dos materiais do prisma e como
consequência justificariam o comportamento observado para os prismas
MV12-B, MV12-C, MV15-B e MV15-C, cujo aumento na resistência da
argamassa não aumentou significativamente a resistência dos prismas.
Nos prismas preenchidos foi realizada a mesma comparação entre
os prismas de mesmo bloco, ou seja, variando-se as argamassas nas
classes A, B e C, de resistências distintas. Com os prismas moldados
com o bloco B6, o aumento da resistência da argamassa de assentamento
e preenchimento da classe C para a A não gera aumento significativo na
resistência dos prismas.
Para os prismas moldados com os blocos B12, os prismas
assentados e preenchidos com as argamassas A e B (MG12-A e MG12B), não apresentam diferença significativa entre seus valores de
resistência à compressão. Entretanto, os prismas TG12-C assentados e
preenchidos com a argamassa C apresentam valor de resistência
significativamente menor, em comparação às outras duas séries. Para as
séries de prismas moldadas com os blocos B15, ocorre o mesmo
comportamento observado para as séries dos prismas moldados com o
bloco B12.
Para Garcia (2000), Cunha (2001) e Juste (2001), o aumento na
resistência à compressão da argamassa de assentamento contribui muito
pouco para o aumento à compressão da alvenaria, demostrando-se
também um procedimento antieconômico. Neste trabalho é observado
174
que o aumento na resistência da argamassa gera aumento na resistência
dos prismas, exceto para os prismas preenchidos quando moldados com
os blocos B6. Entretanto, observa-se que quando ocorre aumento na
resistência dos prismas este não é proporcional ao aumento da
resistência das argamassas, o que neste aspecto conforme observado
anteriormente, pode representar um procedimento antieconômico.
Ainda, para os prismas preenchidos, percebe-se que com o
aumento da rigidez e resistência das argamassas de assentamento e
consequentemente preenchimento, só ocorre aumento nos valores de
resistências dos prismas quando estes são moldados com blocos de
maior fbk, neste caso os prismas moldados com os blocos B15 e B12.
Esta observação contrasta com os resultados encontrados para os
prismas vazios, na qual o aumento significativo foi mais acentuado nos
blocos com os menores valores de fbk, no caso o bloco B6. Isto se deve
ao fato que a distribuição de tensões e o comportamento na ruptura para
prismas vazios e preenchidos são distintos. Enquanto que para os
prismas vazios o comportamento da argamassa comanda a ruptura dos
prismas, para os prismas preenchidos, as propriedades mecânicas das
argamassas de assentamento e preenchimento, bem como o
comportamento deste último quando confinado dentro dos blocos, tem
grande influencia sobre a ruptura da alvenaria, dificultando assim a
investigação deste fenômeno.
Para a Etapa com Argamassa Industrializada, de acordo com os
resultados dispostos na Tabela 4.28, para os prismas vazios moldados
com os blocos B6 e as argamassas das classes 5 e M (séries IV6-5 e
IV6-M), não apresentam diferença significativa em sua resistência à
compressão, mesmo apresentando uma pequena redução na resistência,
conforme pode ser observado no gráfico da Figura 4.12. Para os prismas
moldados a argamassa da classe 10 (IV6-10), observa-se um aumento
significativo nos valores de resistência quando comparados com os
prismas moldadas com as argamassas das classes 5 e M. O mesmo
comportamento observa-se para os prismas vazios moldados com os
blocos B12.
175
Bloco B15
Bloco B12
Bloco B6
Bloco B15
Bloco B12
Bloco B6
Tabela 4.28 – Análise de múltiplas médias entre a resistência à compressão dos
prismas – Etapa com Argamassa Industrial.
PRISMAS VAZIOS
F
Fα
Prismas Comparados
(calculado) (crítico)
IV6-5, IV6-M e IV6-10
26,839
3,89
Resultado
F > Fα (Há Diferença)
IV6-10 e IV6-M
5,753
2,306
F > Fα (Há Diferença)
IV6-10 e IV6-5
6,004
2,306
F > Fα (Há Diferença)
IV6-M e IV6-5
IV12-5, IV12-M e
IV12-10
IV12-10 e IV12-M
0,854
2,306
F < Fα (Não Há Diferença)
8,003
3,89
F > Fα (Há Diferença)
3,376
2,306
F > Fα (Há Diferença)
IV12-10 e IV12-5
2,987
2,306
F > Fα (Há Diferença)
IV12-M e IV12-5
IV15-10, IV15-M e
IV15-5
IV15-10 e IV15-M
0,854
2,306
F < Fα (Não Há Diferença)
11,630
3,89
F > Fα (Há Diferença)
5,213
2,571
F > Fα (Há Diferença)
IV15-10 e IV15-5
0,989
2,306
F > Fα (Não Há Diferença)
IV15-M e IV15-5
3,904
2,306
F < Fα (Há Diferença)
PRISMAS PREENCHIDOS
F
Fα
Prismas Comparados
(calculado) (crítico)
IG6-5, IG6-M e IG6-10
4,587
3,89
Resultado
F > Fα (Há Diferença)
IG6-10 e IG6-M
1,270
2,306
F < Fα (Não Há Diferença)
IG6-10 e IG6-5
3,582
2,306
F > Fα (Há Diferença)
IG6-M e IG6-5
IG12-5, IG12-M e
IG12-10
IG12-10 e IG12-M
1,567
2,306
F < Fα (Não Há Diferença)
13,479
3,89
F > Fα (Há Diferença)
5,383
2,306
F > Fα (Há Diferença)
IG12-10 e IG12-5
0,770
2,306
F < Fα (Não Há Diferença)
IG12-M e IG12-5
IG15-10, IG15-M e
IG15-5
IG15-10 e IG15-M
3,985
2,306
F > Fα (Há Diferença)
15,195
3,89
F > Fα (Há Diferença)
5,490
2,571
F > Fα (Há Diferença)
IG15-10 e IG15-5
2,020
2,306
F < Fα (Não Há Diferença)
IG15-M e IG15-5
3,842
2,571
F > Fα (Há Diferença)
Fonte: Autor (2015).
As resistências das argamassas das classes 5 e M encontram-se
abaixo da faixa entre 70% e 100% do valor de fb do bloco B6 e B12,
176
valores estes indicados como os mais adequados para prismas vazios
(MOHAMAD, 1998). Valores abaixo desta faixa implicariam na
incompatibilidade entre as propriedades dos materiais dos prismas e
como consequência justificariam o comportamento observado, cujo
aumento na resistência da argamassa não aumentou significativamente a
resistência dos prismas. Outro fato a ser considerado, é que estas duas
classes de argamassas não apresentam diferença significativa entre seus
valores de módulo de elasticidade, o que também justificaria este
comportamento.
Para os prismas vazios moldados com o bloco B15 observa-se um
comportamento distinto. O aumento da resistência da argamassa, não
representou aumento significativo na resistência dos prismas vazios.
Observa-se aqui para os prismas IV15-5 e IV15-10, moldados com as
argamassas classes 5 e 10, não apresentam diferença significativa entre
seus valores de resistência. E para os prismas moldados com a
argamassa classe M (IV15-M), os resultados de resistência obtidos
foram significativamente menores que os valores de resistência das
outras duas séries de prismas. A utilização da argamassa M para
assentamento de prismas vazios, tecnicamente, não se mostra como a
opção mais indicada quando comparada com a utilização das
argamassas das classes 5 e 10, que apresentaram melhores resultados de
resistência média à compressão e eficiência. Para os prismas vazios
moldados com o bloco B15, tendo em vista que não ocorreu aumento
significativo na resistência dos prismas, apenas o aumento da resistência
das argamassas sem a adequada compatibilização entre as propriedades
mecânicas dos materiais dos prismas evidencia que a escolha
inadequada destes componentes pode ser uma opção antieconômica e
não indicada tecnicamente.
Para os prismas preenchidos com a argamassa industrializada,
somente as séries moldados com os blocos B6 apresentam aumento
significativo na resistência à compressão dos prismas com o aumento da
resistência à compressão das argamassas, com a utilização das classes 5
à 10, indicadas para alvenaria estrutural. O prisma preenchido com a
argamassa classe M, em função da variabilidade de seus valores de
resistência, não apresenta diferença significativa entre seu valor de
resistência e as resistências obtidas para as outras duas séries de prismas
moldadas com o mesmo bloco.
Para os prismas moldados com os blocos B12 e B15, não ocorre
aumento significativo em suas resistências à compressão com o aumento
da resistência das argamassas. Entretanto, as séries de prismas moldados
com estas duas classes de blocos e preenchidos com a argamassa da
177
classe M apresentam os menores resultados de resistência à compressão,
em relação as séries moldadas com classes 5 e 10. Novamente, com o
objetivo de aumentar a resistência dos prismas com o aumento da
resistência das argamassas, a argamassa M não se mostra como a opção
mais indicada quando comparada com a utilização das argamassas das
classes 5 e 10, que apresentam melhores resultados de resistência média
à compressão e eficiência, algo esperado pois essas argamassas são
indicadas pelo fabricante para o assentamento de blocos de alvenaria
estrutural.
Como comentado anteriormente, o procedimento de
adensamento utilizado para o preenchimento pode ter aumentado o teor
de ar incorporado para esta classe de argamassa, que durante os
experimentos demonstrou-se mais suscetível à incorporação de ar. Isto
justificaria este decréscimo nos valores de resistência à compressão
obtida para estes prismas. Ressalta-se, que este baixo desempenho dos
prismas utilizando a argamassa M era esperado, pois essas argamassas
não são indicadas pelo fabricante para o assentamento de blocos de
alvenaria estrutural.
Ainda, como Etapa com Argamassa Mista, observa-se que
quando ocorre aumento na resistência dos prismas este não é
proporcional ao aumento da resistência das argamassas, o que neste
aspecto pode representar um procedimento antieconômico.
Por último, visando estimar os valores médios de resistência à
compressão dos prismas (fp), utilizando-se dos resultados experimentais
individuais encontrados de resistência à compressão para cada série de
prisma, construíram-se gráficos da Figura 4.13 e Figura 4.14,
correlacionando às propriedades mecânicas dos materiais constituintes
para cada série de prisma das Etapas com Argamassa Mista. Para a
Etapa com Argamassa Industrializada, os gráficos encontram-se nas
Figuras 4.15 e 4.16.
Para as duas etapas, as equações para a estimativa dos valores de
fpliq, que estabelecem a correspondência entre as relações fpliq/farg e
fbliq/farg, e que apresentaram melhor aproximação (maior valor de R²),
são apresentadas nestes gráficos. Reescrevendo estas equações, foi
possível calcular o erro existente entre os valores médios experimentais
e teóricos de resistência na área líquida, para cada série de prisma,
conforme Tabela 4.29 e Tabela 4.30.
Com estas equações, é possível estimar os valores médios de
resistência dos prismas que se enquadrem dentro dos valores de
resistência de blocos e argamassas utilizados neste trabalho. Observa-se
que para os dados expostos na Tabela 4.29 e Tabela 4.30, para as
178
equações obtidas é possível estimar valores bem próximos dos valores
experimentais médios encontrados.
Para a Etapa com Argamassa Mista, o erro máximo encontrado
para os prismas da classe MG6-B, no valor de 4,9%. Para a Etapa com
Argamassa Industrializada, o erro máximo encontrado para os prismas
da classe IG6-M, no valor de 1,2%.
Entretanto, ressalta-se que estas equações correspondem somente
aos materiais e componentes utilizados nesta pesquisa, podendo estas
serem utilizadas somente como referência de cálculo desde que os
materiais e componentes estudados apresentem propriedades mecânicas
próximas das utilizadas nesta pesquisa.
Figura 4.13 – Gráfico da relação entre fp
vazios – Etapa Arg. Mista.
6,0
liq/farg
e fb
liq/farg,
para os prismas
y = 1,1648e0,1478x
R² = 0,9546
5,5
5,0
4,5
y = 0,7699x0,7664
R² = 0,946
fp liq/farg
4,0
3,5
3,0
y = 0,8766x0,6267
R² = 0,9242
2,5
2,0
1,5
fp Prisma Vazio Bloco B6
1,0
fp Prisma Vazio Bloco B12
0,5
fp Prisma Vazio Bloco B15
0,0
0,0
2,0
4,0
6,0
8,0
10,0
12,0
fb liq/farg
Fonte: Autor (2015).
179
Figura 4.14 – Gráfico da relação entre fp
grauteados – Etapa Arg. Mista.
4,0
e fb
liq/farg,
para os prismas
y = 0,5402x0,7998
R² = 0,9797
fp Prisma Grauteado Bloco B6
fp Prisma Grauteado Bloco B12
fp Prisma Grauteado Bloco b15
3,5
3,0
2,5
fp liq/farg
liq/farg
y = 0,5524x0,7818
R² = 0,9584
2,0
1,5
y = 0,4121x0,905
R² = 0,9663
1,0
0,5
0,0
0,0
2,0
4,0
6,0
8,0
10,0
12,0
fb liq/farg
Fonte: Autor (2015).
180
Tabela 4.29 – Valores experimentais e calculados de resistência média à
compressão, na área líquida.
ETAPA ARGAMASSA MISTA
Bloco B15
Bloco B12
Bloco B6
Prismas
fpliq (MPa) experimental
MV6-A
MV6-B
MV6-C
MG6-A
MG6-B
MG6-C
MV12-A
MV12-B
MV12-C
MG12-A
MG12-B
MG12-C
MV15-A
MV15-B
MV15-C
MG15-A
MG15-B
MG15-C
Fonte: Autor (2015).
17,9
13,9
10,6
10,7
9,2
9,3
19,1
16,3
13,9
13,8
12,1
10,2
22,2
15,5
17,3
14,5
13,1
11,0
Equação
fpliq = 0,8766.fbliq0,6227.
farg0,3733
fpliq = 0,4121.fbliq0,905.
farg0,095
fpliq = 0,7699.fbliq0,7664.
farg0,2336
fpliq = 0,5524.fbliq0,7818.
farg0,2182
fpliq =
1,1648.farg.e0,1478(fbliq/fa
rg)
fpliq = 0,5402.fbliq0,7998.
farg0,2002
fpliq
(MPa) calculado
17,8
13,8
10,6
10,3
9,7
9,1
19,04
16,22
13,75
13,84
11,92
10,22
21,61
15,87
17,06
14,62
12,75
11,07
Erro
(%)
0,3
0,9
0,4
3,2
4,9
2,7
0,4
0,4
0,7
0,1
1,6
0,2
2,6
2,3
1,2
1,0
2,6
1,0
181
Figura 4.15 – Gráfico da relação entre fp
vazios – Etapa Arg. Industrializada.
liq/farg
e fb
liq/arg,
para os prismas
5,5
fp Prisma Vazio Bloco B6
5,0
fp Prisma Vazio Bloco B12
4,5
y = 0,3059x2 - 2,6217x + 7,6181
R² = 0,87
y = 0,1284x2 - 0,8716x + 3,2865
R² = 0,8513
fp Prisma Vazio Bloco B15
fp liq/farg
4,0
3,5
3,0
2,5
2,0
1,5
y = 0,19x2 - 1,4378x + 4,0213
R² = 0,7902
1,0
0,5
2,5
3,0
3,5
4,0
4,5
5,0
5,5
6,0
6,5
7,0
fb liq/farg
Fonte: Autor (2015).
Figura 4.16 – Gráfico da relação entre fp
grauteados – Etapa Arg. Industrializada.
liq/farg
e fb
liq/arg,
para os prismas
5,5
fp Prisma Grauteado Bloco B6
5,0
fp Prisma Grauteado Bloco B12
4,5
fp Prisma Grauteado Bloco B15
fp liq/farg
4,0
y = 0,194x2 - 1,4502x + 4,0705
R² = 0,9202
3,5
3,0
y = 0,1839x2 - 1,5766x + 4,7747
R² = 0,8956
2,5
2,0
1,5
y = 0,459x0,7002
R² = 0,8085
1,0
0,5
2,5
3,0
3,5
4,0
4,5
5,0
5,5
6,0
6,5
7,0
fb liq/farg
Fonte: Autor (2015).
182
Tabela 4.30 – Valores experimentais e calculados de resistência média à
compressão, na área líquida.
ETAPA ARGAMASSA INDUSTRIALIZADA
Bloco B15
Bloco B12
Bloco B6
Prismas
fpliq (MPa) experimental
IV6-5
IV6-M
IV6-10
IG6-5
IG6-M
IG6-10
IV12-5
IV12-M
IV12-10
IG12-5
IG12-M
IG12-10
IV15-5
IV15-M
IV15-10
IG15-5
IG15-M
IG15-10
9,4
8,9
14,0
7,4
8,3
9,1
14,0
13,3
17,3
12,9
9,9
13,5
19,4
14,2
21,1
12,6
9,8
14,6
Equação
fpliq = 0,19.fbliq2. farg-1
– 1,437.fbliq + 4,0213.farg
fpliq = 0,459.fbliq0,7002.
farg0,2998
fpliq = 0,1284.fbliq2. farg-1
– 0,8716.fbliq + 3,2865.farg
fpliq = 0,194.fbliq2. farg-1
– 1,4502.fbliq + 4,0705.farg
fpliq = 0,3059.fbliq2. farg-1
– 2,6217.fbliq + 7,6181.farg
fpliq = 0,1839.fbliq2. farg-1
– 1,5766.fbliq + 4,7747.farg
fpliq
(MPa) calculado
9,4
8,9
14,1
7,36
8,18
9,06
14,04
13,27
17,27
12,91
9,93
13,53
19,38
14,18
21,15
12,56
9,83
14,56
Erro
(%)
0,27
0,27
0,16
0,10
1,20
0,00
0,02
0,02
0,01
0,04
0,04
0,02
0,05
0,04
0,02
0,02
0,02
0,01
Fonte: Autor (2015).
4.5.2.2 Análise da capacidade de carga dos prismas grauteados da Etapa
com Argamassa Mista
Com o objetivo de identificar o aumento efetivo da capacidade de
carga dos prismas quando preenchidos, analisando o gráfico da Figura
4.17, observa-se que com o preenchimento dos prismas com a
argamassa de assentamento, ocorreu um pequeno aumento na carga
resistida pelos prismas até sua ruptura (Fp). Este aumento é mais
evidente com os prismas moldados com os blocos B6, preenchidos com
argamassas com menor resistência e módulo de elasticidade.
183
Figura 4.17 – Carga de ruptura média (Fp) versus resistência média à
compressão das argamassas de assentamento ou de preenchimento (farg = fg) –
Etapa Argamassa Mista.
700
Prisma Vazio Bloco B6
Prisma Vazio Bloco B12
Prisma Vazio Bloco B15
Prisma Grauteado Bloco B6
Prisma Grauteado Bloco B12
Prisma Grauteado Bloco B15
650
600
550
Fp (kN)
500
450
400
350
300
250
200
150
2,0
4,0
6,0
8,0
10,0
12,0
14,0
farg = fg (MPa)
Fonte: Autor (2015).
Assim, com a intenção de verificar a eficácia da utilização das
argamassas como preenchimento para estes prismas, novamente foi
realizada uma análise de variância (ANOVA), utilizando os valores de
resistência média à compressão. Para este procedimento, utilizou-se a
área bruta para manter a mesma área no cálculo da resistência dos
prismas, com o objetivo de verificar se houve ou não aumento efetivo
nos valores da carga resistida pelos prismas preenchidos com a
argamassa de assentamento, até a sua ruptura, quando comparados com
os prismas vazios. Determinou-se também o efeito relativo, ou seja, o
valor percentual de aumento na carga resistida pelos prismas quando
preenchidos com cada classe de argamassa até a sua ruptura. Com um
nível de confiança de 95%, o resultado da análise de comparação de
médias 2x2 obtida entre os valores de resistência média à compressão
dos prismas (fp) na área bruta, bem como o Efeito Relativo (aumento ou
não de fp), encontra-se na Tabela 4.31.
184
Tabela 4.31 – Efeito relativo da capacidade de carga dos prismas preenchidos.
ETAPA ARGAMASSA MISTA
Bloco B15
Bloco B12
Bloco B6
Prismas
F
Fα
(calculado)
(crítico)
MV6-A
MG6-A
1,151
2,306
MV6-B
MG6-B
2,750
2,306
MV6-C
MG6-C
8,299
2,306
MV12-A
MG12-A
2,173
2,306
MV12-B
MG12-B
1,852
2,306
MV12-C
MG12-C
2,300
2,306
MV15-A
MG15-A
0,535
2,306
MV15-B
MG15-B
5,568
2,306
MV15-C
MG15-C
0,110
2,306
Conclusão
F < Fα
(Não Há Diferença)
F > Fα (Há Diferença)
F > Fα (Há Diferença)
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
F > Fα (Há Diferença)
F < Fα
(Não Há Diferença)
Efeito
Relativo
(%)
+ 8,6
+ 22,2
+ 61,0
+ 13,5
+ 17,3
+ 15,9
+ 4,2
+ 34,5
+ 1,1
Fonte: Autor (2015).
Analisando os resultados dispostos na Tabela 4.31, somente os
prismas MG15-B, MG6-B e MG6-C, preenchidos com as argamassas B
e C, apresentam aumento significativo em suas resistências à
compressão. Este aumento nos valores de resistência à compressão na
área bruta (fp), mais especificamente na carga de ruptura, observa-se
para os prismas preenchidos que apresentam fp com valores 22,2%
superior aos valores de fp dos prismas vazios (Efeito relativo > 22,2%).
Como observado na Etapa Referência, esse aumento na resistência para
algumas séries de prismas, com a utilização da argamassa como
preenchimento estrutural, evidencia a viabilidade de utilização desta
técnica de preenchimento dos prismas com a própria argamassa utilizada
no seu assentamento.
Comparando os valores característicos de resistência à
compressão do bloco e da argamassa dos prismas MG15-B, MG6-B e
MG6-C, as argamassas apresentam valores de resistências características
à compressão (fargk) entre 73,4% a 90,7% menores que os valores de
resistência à compressão características do bloco (fbk), na área líquida.
Esta diferença entre os valores de resistência à compressão do
preenchimento e bloco não é recomendado. Conforme Ramalho e
Corrêa (2003) e Parsekian et al (2012) indicam-se valores de resistência
dos grautes próximos aos valores de fbk dos blocos, na área líquida.
185
Como consequência, esta diferença observada para os prismas das séries
MG15-B, MG6-B e MG6-C poderiam ocasionar um decréscimo nos
valores de carga resistente para estes prismas. Entretanto, este
comportamento não se observa para estas séries de prismas.
Conforme Mendes (1998), para argamassas com baixa
resistência, prismas grauteados que apresentam melhor desempenho são
aqueles que são preenchidos com grautes com módulos de elasticidade
próximos ao módulo de elasticidade da argamassa e próximos ao
módulo de elasticidade dos prismas não grauteados. Comportamento
este, também observado por Dhanasekar e Kumar (1994) e Khalifa e
Magzoub (1994). Entretanto, isto não se observa para as séries MG15-B,
MG6-B e MG6-C (Figura 4.18). Para os prismas MG15-A, os valores de
módulos de elasticidade dos prismas vazios MV15-A e da argamassa A
são próximos, com uma diferença de apenas 7,1%, o que não resulta no
aumento significativo na sua capacidade de carga, diferente dos
resultados obtidos por Mendes (1998).
Figura 4.18 – Comparação entre os diagramas tensão-deformação obtidos para
as argamassas e prismas vazios.
15
Argamassa A
Argamassa B
Argamassa C
TV6-A Liq
TV6-B Liq
TV6-C Liq
TV12-A Liq
TV12-B Liq
TV12-C Liq
TV15-A Liq
TV15-B Liq
TV15-C Liq
Tensão Área Líquida (MPa)
12
9
6
3
0
0,0000
0,0005
0,0010
0,0015
0,0020
0,0025
0,0030
Deformação Específica (mm/mm)
Fonte: Autor (2015).
Ainda, segundo este autor, quanto maior o módulo de elasticidade
do graute, maior será a parcela de carregamento total por ele absorvido.
Para os grautes que apresentam pouca diferença entre seus coeficientes
186
de Poisson, o autor afirma que com o aumento da tensão vertical nos
grautes, maior será a tensão lateral gerada nestes e consequentemente
maior será a possibilidade de ocorrer tensões de tração e cisalhamento
no bloco. Contudo, para grautes que apresentam menores módulos de
elasticidade, o conjunto de alvenaria (bloco e argamassa), absorve uma
parcela maior do carregamento total. Deste modo, com o aumento da
carga absorvida pelo bloco e, consequentemente, da tensão de
compressão efetiva nos blocos, há a diminuição de tensões laterais e o
aumento da resistência ao cisalhamento dos blocos, tendo como
consequência, o aumento na resistência à compressão dos prismas.
Desta maneira, visando identificar a parcela de carregamento
suportado pelo preenchimento e pelo prisma, foi adotado o mesmo
procedimento utilizado na Etapa Referência. Os resultados obtidos com
esta análise encontram-se na Tabela 4.32. Novamente ressalta-se, que
esse procedimento analisa a alvenaria dentro do seu regime elástico,
diferente do comportamento que será analisado na análise numérica, ou
seja, considerando a não linearidade dos materiais dos prismas. Ainda,
esta estimativa de carga apresenta limitações em relação a análise
realizada na Etapa Referência. Para esta etapa e a etapa com argamassa
industrializada, a argamassa de assentamento varia juntamente com o
preenchimento, diferente da análise realizada anteriormente. Isto ocorre,
pois o objetivo do estudo é preencher o prisma com a própria argamassa
de assentamento, e utilizar traços diferentes para a argamassa da junta e
para o preenchimento inviabilizaria a utilização da técnica prescrita pela
norma ABNT NBR 15812-2 (2010).
187
Tabela 4.32 – Porcentagem estimada dos carregamentos absorvidos pelos
grautes.
Bloco B6
ETAPA ARGAMASSA MISTA
Área Líquida alvenaria =
Área Graute = 126,4 cm²
158,3 cm²
Prismas
Ep liq prisma
vazio (MPa)
% Carga
Graute
% Carga
Alvenaria
MG6-A
12554,2
7710,7
56,5
43,5
10,7
MG6-B
7120,1
9485,2
37,5
62,5
9,2
MG6-C
2529,6
4890,0
29,2
70,8
9,3
Bloco B12
Área Graute = 116,8 cm²
Área Líquida alvenaria =
204,1 cm²
fp liq
(MPa)
Prismas
Eg
(MPa)
Ep liq prisma
vazio (MPa)
% Carga
Graute
% Carga
Alvenaria
MG12-A
12554,2
10194,5
41,3
58,7
13,8
MG12-B
7120,1
11511,5
26,1
73,9
12,1
MG12-C
2529,6
8941,3
13,9
86,1
10,1
Área Graute = 129,5 cm²
Bloco B15
fp liq
(MPa)
Eg
(MPa)
Área Líquida alvenaria =
221,1 cm²
fp liq
(MPa)
Prismas
Eg
(MPa)
Ep liq prisma
vazio (MPa)
% Carga
Graute
% Carga
Alvenaria
MG15-A
12554,2
11720,6
38,6
61,4
14,5
MG15-B
7120,1
9603,5
30,3
69,7
13,1
MG15-C
2529,6
7662,0
16,2
83,8
11,0
Fonte: Autor (2015).
De acordo com os resultados dispostos na Tabela 4.32 e como
observados na Etapa Referência, para os prismas MG6-C, a diminuição
da rigidez da argamassa de preenchimento da classe A para a classe C,
pode ter contribuído para o aumento da capacidade de carga dos prismas
MG15-B, MG6-B e MG6-C, quando comparadas as respectivas cargas
de ruptura entre prisma vazio e preenchido. Nestas séries de prismas, a
diminuição da parcela de carga absorvida pelo preenchimento, em
virtude de seu baixo valor de módulo de elasticidade, contribui para o
aumento significativo da carga de ruptura dos prismas. Neste caso, a
baixa rigidez dos preenchimentos provocaria o aparecimento de baixas
188
tensões sobre as paredes internas dos blocos, além de absorver parte da
carga total do prisma. Ainda, com o aumento da parcela de carga sob a
alvenaria (bloco-argamassa), aumentam-se as tensões de compressão
sobre o bloco, aumentando sua capacidade de resistência às tensões de
tração impostas pela deformação do preenchimento (MENDES, 1998).
Isto pode ser evidenciado pelo fato de que para a série de prismas MG6A, preenchida com a argamassa da classe A de maior valor de módulo
de elasticidade e maior coeficiente de Poisson, que não apresenta
aumento significativo em sua carga de ruptura quando preenchido com
esta argamassa. Isto fica mais evidente com os gráficos da Figura 4.19 e
Figura 4.20, onde o aumento da rigidez da argamassa e
consequentemente aumento das relações existentes entre os módulos de
elasticidade da argamassa e bloco (Earg/Eb) e as relações entre os
módulos de elasticidade da argamassa e do prisma vazio na área líquida
(Earg/Epvazio liq), não proporcionam o aumento da carga resistida pelos
prismas até sua ruptura (Fp).
Figura 4.19 – Gráfico da carga de ruptura dos prismas (Fp) versus relação entre
os valores médios de módulo de elasticidade da argamassa/módulo de
elasticidade do bloco (Earg/Eb) – Etapa Arg. Mista.
600
Prisma Vazio Bloco B6
Prisma Grauteado Bloco B6
Prisma Vazio Bloco B12
Prisma Grauteado Bloco B12
Prisma Vazio Bloco B15
550
500
Fp (kN)
450
400
350
300
250
200
150
0,0
0,2
Fonte: Autor (2015).
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
Earg/Eb
189
Figura 4.20 – Gráfico da carga de ruptura dos prismas (Fp) versus relação entre
os valores médios de módulo de elasticidade da argamassa/módulo de
elasticidade do prisma vazio na área líquida [Earg/Ep vazio (área líquida)] – Etapa
Argamassa Mista.
600
Prisma Vazio Bloco B6
Prisma Vazio Bloco B12
Prisma Vazio Bloco B15
550
Prisma Grauteado Bloco B6
Prisma Grauteado Bloco B12
Prisma Grauteado Bloco B15
500
Fp(kN)
450
400
350
300
250
200
150
0,0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
Earg/Ep vazio (área líquida)
Fonte: Autor (2015).
Observa-se então que com a diminuição da rigidez da argamassa
aumentam-se os valores dos efeitos relativos encontrados para cada série
de prismas moldados com os blocos B6, e consequentemente,
aumentam-se significativamente os valores das cargas resistidas por
estes prismas, conforme os valores da Tabela 4.23 e Tabela 4.31.
Contudo, os prismas moldados com os blocos B12 não
apresentam aumento em suas resistências quando preenchidos pela
argamassa. O mesmo observa-se com os prismas moldados com os
blocos B15, exceto para os prismas MG15-B, com argamassa de
resistência intermediária. Este diferente comportamento apresentado
para os prismas moldados com os três tipos de blocos, pode ser
explicado pelas diferenças existentes entre os valores de módulos de
elasticidade e, principalmente, pelas geometrias dos blocos. Mesmos
estes blocos apresentando valores de fbk muito próximos, os prismas
moldados apresentam comportamento distintos sob compressão,
indicando que a geometria influencia consideravelmente no
190
comportamento mecânico e distribuição de tensões para estes prismas, o
que já fora comprovado por outros pesquisadores.
Diante do exposto, o aumento na resistência à compressão dos
prismas com a utilização da argamassa como preenchimento estrutural
evidencia a viabilidade de utilização desta técnica, desde que a escolha
entre os componentes dos prismas seja adequada. Isto ocorre,
especificamente, para os prismas moldados com bloco B6 onde se
constata o melhor desempenho dos prismas utilizando argamassas
mistas com valores de resistências média à compressão entre 10% e
23,7% da resistência média à compressão do bloco, na área líquida
(fbliq). E dentro deste contexto, para algumas solicitações de projeto,
além do aumento da capacidade resistente, a técnica proposta eleva
também o peso próprio das paredes, diminuindo-se o nível de
concentração de tensões de tração nestas paredes.
4.5.2.3 Análise da capacidade de carga dos prismas grauteados das
Etapas com Argamassa Industrializada
Com o objetivo de identificar o aumento efetivo da capacidade de
carga dos prismas quando preenchidos, analisando o gráfico da Figura
4.21, observa-se que com o preenchimento dos prismas com a
argamassa de assentamento, ocorreu um pequeno aumento na carga
resistida pelos prismas até sua ruptura. Este aumento é mais evidente
com os prismas moldados com os blocos B6 e B12, com os menores
valores de fbk.
191
Figura 4.21 - Carga de ruptura média (Fp) versus resistência média à
compressão das argamassas de assentamento ou de preenchimento (farg = fg) –
Etapa Argamassa Industrializada.
600
Prisma Vazio Bloco B6
Prisma Vazio Bloco B12
Prisma Vazio Bloco B15
Prisma Grauteado Bloco B6
Prisma Grauteado Bloco B12
Prisma Grauteado Bloco B15
560
520
480
Fp (kN)
440
400
360
320
280
240
200
160
120
4,0
5,0
6,0
7,0
8,0
9,0
10,0
farg = fg (MPa)
Fonte: Autor (2015).
Desta forma, com a intenção de verificar a eficácia da utilização
das argamassas como preenchimento para estes prismas, novamente foi
realizada uma análise de variância (ANOVA), utilizando os valores de
resistência média à compressão dos prismas na área bruta, conforme
procedimento utilizado na Etapa com Argamassa Mista. Determinou-se
também o efeito relativo. Com um nível de confiança de 95%, o
resultado da análise de comparação de médias 2x2 obtida entre os
valores de resistência média à compressão dos prismas (fp) na área bruta,
bem como o Efeito Relativo (aumento ou não de fp), encontra-se na
Tabela 4.33.
Analisando os resultados dispostos na Tabela 4.33, as séries de
prismas moldadas com os blocos B6 e B12, preenchidos com as três
classes de argamassas, apresentam aumento significativo em sua
capacidade de carga. Este aumento nos valores de resistência à
compressão na área bruta (fp), mais especificamente na carga de ruptura,
observa-se para os prismas preenchidos que apresentam fp com valores
16,4% superior aos valores de fp dos prismas vazios (Efeito relativo >
16,4%). Como observado na Etapa Referência e Argamassa Mista, o
aumento na carga de ruptura para algumas séries de prismas, com a
192
utilização da argamassa como preenchimento estrutural, evidencia a
viabilidade de utilização desta técnica de preenchimento dos prismas
com a própria argamassa utilizada no seu assentamento.
Tabela 4.33 – Efeito relativo da capacidade de carga dos prismas preenchidos.
ETAPA ARGAMASSA INDUSTRIALIZADA
IG6-5
6,211
2,306
F > Fα (Há Diferença)
Efeito
Relativo
(%)
+ 40,5
F
Fα
(calculado) (crítico)
Bloco B15
Bloco B12
Bloco B6
Prismas
IV6-5
Conclusão
IV6-M
IG6-M
5,778
2,306
F > Fα (Há Diferença)
+ 68,6
IV6-10
IG6-10
2,488
2,306
F > Fα (Há Diferença)
+ 16,4
IV12-5
IG12-5
5,527
2,306
F > Fα (Há Diferença)
+ 45,7
IV12-M IG12-M
2,365
2,306
F > Fα (Há Diferença)
+ 18,2
IV12-10 IG12-10
3,166
2,306
F > Fα (Há Diferença)
+ 23,3
IV15-5
IG15-5
0,171
2,306
IV15-M IG15-M
2,109
2,306
IV15-10 IG15-10
1,146
2,306
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
F < Fα
(Não Há Diferença)
- 1,9
+ 10,4
+ 9,6
Fonte: Autor (2015).
Comparando os valores característicos de resistência à
compressão do bloco e da argamassa dos prismas IV6-5, IV6-M, IV610, IV12-5, IV12-M e IV12-10, as argamassas apresentam valores de
resistências à compressão (fargk) entre 61,1% a 81,5% menores que os
valores de resistência à compressão do bloco (fbk), na área líquida.
Conforme observado por Ramalho e Corrêa (2003) e Parsekian et al
(2012) esta diferença entre os valores de resistência do preenchimento e
bloco não é indicada, e como consequência ocasionariam um
decréscimo nos valores de carga resistente para estes prismas.
Entretanto, este comportamento não se observa para as séries de prismas
moldadas com os blocos B6 e B12.
Conforme Mendes (1998), para argamassas com baixa
resistência, prismas grauteados que apresentam melhor desempenho são
aqueles que são preenchidos com grautes com módulos de elasticidade
próximos ao módulo de elasticidade da argamassa e próximos ao
módulo de elasticidade dos prismas não grauteados, conforme também
193
observado por Dhanasekar e Kumar (1994) e Khalifa e Magzoub (1994).
Entretanto, isto se observa apenas para a série IG6-5 e IG6-M (Figura
4.22), onde o valor do módulo de elasticidade da argamassa de
preenchimento em relação ao valor de módulo do prisma vazio
presentaram uma diferença de 9,7%. Para os prismas IG15-5 e IG15-10,
a diferença entre os respectivos valores de módulo de elasticidade dos
prismas vazios e das argamassas encontram-se abaixo de 10%, o que
não resulta no aumento significativo na sua capacidade de carga,
novamente contrastando com os resultados obtidos por Mendes (1998),
conforme observado na Etapa com Argamassa Mista.
Figura 4.22 – Comparação entre os diagramas tensão-deformação obtidos para
as argamassas e prismas vazios.
15
ARGAMASSA 10
ARGAMASSA M
Tensão Área Líquida (MPa)
12
ARGAMASSA 5
IV6-M
IV6-5
9
IV6-10
IV12-M
6
IV12-5
IV12-10
IV15-5
3
IV15-M
IV15-10
0
0,0000
0,0005
0,0010
0,0015
0,0020
0,0025
0,0030
Deformação Específica (mm/mm)
Fonte: Autor (2015).
Ainda para esta etapa do programa, com o intuito de investigar se
o enrijecimento da alvenaria com argamassa diminui a resistência dos
prismas, como observado para algumas séries de prismas das Etapas
Referência e Argamassa Mista, novamente calculou-se a parcela de
carregamento suportado pelo preenchimento e pelo prisma. Os
resultados obtidos com esta análise encontram-se na Tabela 4.34.
De acordo com os resultados dispostos na Tabela 4.34 e como
observado nas Etapas Referência e Argamassa Mista, a diminuição da
rigidez da argamassa de preenchimento da classe 5 para a classe 10,
pode ter contribuído para o aumento da resistência das séries de prismas
194
moldados com os blocos B6 e B12, quando comparadas as respectivas
cargas de ruptura entre prisma vazio e preenchido. Diferente da Etapa
Tradicional, nesta etapa utilizando argamassa industrializada, o aumento
na capacidade de carga dos prismas também ocorre para os prismas
moldados com os blocos B12.
Nos prismas moldados com os blocos B6 e B12, como observado
para os prismas moldados com os blocos B6 da Etapa com Argamassa
Mista, a diminuição da parcela de carga absorvida pelo preenchimento,
em virtude de seu baixo valor de módulo de elasticidade, contribui para
o aumento significativo da carga de ruptura dos prismas. Novamente, a
baixa rigidez das argamassas utilizadas como preenchimento provocaria
o aparecimento de baixas tensões sobre as paredes internas dos blocos,
além de absorver parte da carga total do prisma. Ainda, com o aumento
da parcela de carga sob a alvenaria (bloco-argamassa), aumentam-se as
tensões de compressão sobre o bloco, aumentando sua resistência as
tensões de tração impostas pela deformação do preenchimento
(MENDES, 1998).
Bloco B15
Bloco B12
Bloco B6
Tabela 4.34 – Porcentagem estimada dos carregamentos absorvidos pelos
grautes.
ETAPA ARGAMASSA INDUSTRIALIZADA
Área Líquida alvenaria =
Área Graute = 126,4 cm²
158,3 cm²
Eg
Ep liq prisma
% Carga
% Carga
Prismas
(MPa) vazio (MPa)
Graute
Alvenaria
IG6-10 12299,3
9766,8
50,13
49,9
IG6-M
8717,1
7354,1
48,6
51,4
IG6-5
7890,8
7211,1
46,6
53,4
Área Graute = 116,8
Área Líquida alvenaria =
cm²
204,1 cm²
Eg
Ep liq prisma
% Carga
% Carga
Prismas
(MPa) vazio (MPa)
Graute
Alvenaria
IG12-10 12299,3
8237,6
46,1
53,9
IG12-M 8717,1
6057,5
45,2
54,8
IG12-5
7890,8
10802,4
29,5
70,5
Área Líquida alvenaria =
Área Graute = 129,5 cm²
221,1 cm²
Eg
Ep liq prisma
% Carga
% Carga
Prismas
(MPa) vazio (MPa)
Graute
Alvenaria
IG15-10 12299,3 11105,7
39,4
60,6
IG15-M 8717,1
9866,4
34,1
65,9
IG15-5
7890,8
8939,0
34,1
65,9
Fonte: Autor (2015).
fp liq
(MPa)
9,1
8,3
7,4
fp liq
(MPa)
13,5
9,9
12,5
fp liq
(MPa)
14,6
9,8
12,6
195
Isto fica mais evidente com os prismas moldados com os blocos
da classe B6, conforme os gráficos da Figura 4.23 e Figura 4.24. Para
estes prismas e os prismas moldados com os blocos da classe B12 o
aumento da rigidez da argamassa e, consequentemente, o aumento das
relações existentes entre os módulos de elasticidade da argamassa e
bloco (Earg/Eb) e as relações entre os módulos de elasticidade da
argamassa e do prisma vazio na área líquida (Earg/Epvazio liq), não
proporcionam o aumento da carga resistida pelos prismas até sua
ruptura.
Como na Etapa Argamassa Mista, observa-se também com a
diminuição da rigidez da argamassa o aumento nos valores dos efeitos
relativos encontrados para cada família de prismas e consequentemente,
aumentam-se significativamente os valores das cargas de ruptura por
estes prismas moldados com os blocos B6 e B12, conforme os valores
da Tabela 4.34.
Contudo, os prismas moldados com os blocos B15 não
apresentam aumento em suas resistências quando preenchidos pela
argamassa.
Como observado na Etapa com Argamassa Mista, este diferente
comportamento apresentado para os prismas moldados com os três tipos
de blocos, pode ser explicado pelas diferenças existentes entre os
valores de módulos de elasticidade e, principalmente, pelas geometrias
dos blocos, que influenciam consideravelmente no comportamento dos
prismas, o que já fora comprovado por outros pesquisadores.
Diante do exposto, novamente observa-se que o aumento na
resistência à compressão dos prismas com a utilização da argamassa
como preenchimento estrutural evidencia a viabilidade de utilização
desta técnica, desde que a escolha entre os componentes dos prismas
seja adequada. Isto ocorre, especificamente, para os prismas moldados
com os blocos B6 e B12, onde se constata o melhor desempenho dos
prismas utilizando argamassas industrializadas com valores de
resistências média à compressão (farg) entre 17,9 e 35,2% da resistência
média à compressão dos blocos B6, na área líquida (fbliq); e para os
prismas moldados com os blocos B12, argamassas com farg entre 15,8 e
31,4% do fbliq do bloco B12. Dentro deste contexto, para algumas
solicitações de projeto, além do aumento da capacidade resistente, a
técnica proposta eleva também o peso próprio das paredes, diminuindose o nível de concentração de tensões de tração nestas paredes.
196
Figura 4.23 – Gráfico da carga de ruptura dos prismas (Fp) versus relação entre
os valores médios de módulo de elasticidade da argamassa/módulo de
elasticidade do bloco (Earg/Eb) – Etapa Arg. Industrializada.
600
Prisma Vazio Bloco B6
Prisma Grauteado Bloco B6
Prisma Vazio Bloco B12
Prisma Grauteado Bloco B12
Prisma Vazio Bloco B15
Prisma Grauteado Bloco B15
560
520
480
Fp (kN)
440
400
360
320
280
240
200
160
120
0,6
0,8
1,0
1,2
1,4
1,6
Earg/Eb
Fonte: Autor (2015).
Figura 4.24 – Gráfico da carga de ruptura dos prismas (Fp) versus relação entre
os valores médios de módulo de elasticidade da argamassa/módulo de
elasticidade do prisma vazio na área líquida [Earg/Ep vazio (área líquida)] – Etapa
Argamassa Industrializada.
600
Prisma Vazio Bloco B6
Prisma Vazio Bloco B12
Prisma Vazio Bloco B15
560
520
Prisma Grauteado Bloco B12
Prisma Grauteado Bloco B12
Prisma Grauteado Bloco B15
480
440
Fp (kN)
400
360
320
280
240
200
160
120
0,6
Fonte: Autor (2015).
0,8
1,0
1,2
1,4
1,6
Earg/Ep vazio (área líquida)
197
4.5.3. Análise do modo de ruptura dos prismas
Nesta etapa do trabalho caracterizou-se o modo de ruptura
observado para os prismas nas etapas Referência, Argamassa Mista e
Industrializada.
Para os prismas vazios da Etapa com Argamassa Mista, a forma
de ruptura dos prismas ocorreu de forma frágil, sem características
explosivas, para os prismas assentados com as três classes de
argamassas. A ruptura sem características explosivas aqui é designada
pela ruptura de forma lenta, ou seja, o material perde a capacidade
resistente com aviso.
Basicamente, a ruptura ocorreu de forma lenta, iniciando-se com
o surgimento de fissuras e o esmagamento da argamassa em conjunto
com a formação de fissuras e trincas verticais nos blocos, entre 60% e
70% da carga de ruptura. Para as argamassas C e B, observou-se um
esmagamento acentuado das juntas em relação às juntas com a
argamassa A. Na sequência, ocorreu a ruptura localizada dos blocos
próxima à região da interface bloco-argamassa, geradas pela deformação
excessiva junta, levando assim o conjunto ao colapso (Figuras 4.25 a
4.27).
Esta última característica observada, com rupturas localizadas nos
blocos, ocorreu de forma acentuada com todas as séries de prismas
moldados com blocos da classe B15. O mesmo observou-se com os
prismas moldados com os blocos B12 e B6 e assentados com a
argamassa classe A, de maior rigidez. Isto se deve as diferentes
características elásticas existentes entre o bloco e argamassa, onde
quanto maior a diferença de deformação específica entre a unidade e a
argamassa, maior o diferencial de deformação entre os materiais,
ocasionando um aumento das tensões de tração nas unidades
(RIZZATTI, 2003). Ainda, o enrijecimento da alvenaria pode ser
indesejado para as paredes de alvenaria, onde é recomendado o emprego
de argamassas com baixos módulos de elasticidade, com a finalidade de
absorver as deformações da estrutura (ISHIKAWA, 2001).
198
Figura 4.25 – Ruptura característica dos prismas vazios com os blocos B6 Etapa Arg. Mista.
MV6-C
MV6-B
MV6-A
Fonte: Autor (2015).
Figura 4.26 – Ruptura característica dos prismas vazios com os blocos B12 –
Etapa Arg. Mista.
MV12-C
MV12-B
MV12-A
Fonte: Autor (2015).
Figura 4.27 – Ruptura característica dos prismas vazios com os blocos B15 –
Etapa Arg. Mista.
MV15-C
Fonte: Autor (2015).
MV15-B
MV15-A
199
Para os prismas vazios da Etapa com Argamassa Industrializada,
a forma de ruptura dos prismas também ocorreu de forma frágil, sem
características explosivas, para os prismas assentados com as três classes
de argamassas. Basicamente, a ruptura ocorreu de forma similar à
ruptura apresentada pelos prismas vazios da Etapa Tradicional, ou seja,
de forma lenta com formação de fissuras e o esmagamento da argamassa
da junta em conjunto com a formação de fissuras e trincas verticais nos
blocos. Na sequência, ocorreu a ruptura localizada dos blocos próxima à
região da interface bloco-argamassa, levando o conjunto ao colapso
(Figuras 4.28 a 4.30).
Figura 4.28 – Ruptura característica dos prismas vazios moldados com os
blocos B6 – Etapa Arg. Industrial.
IV6-5
IV6-M
IV6-10
Fonte: Autor (2015).
Figura 4.29 – Ruptura característica dos prismas vazios moldados com os
blocos B12 – Etapa Arg. Industrial.
IV12-5
Fonte: Autor (2015).
IV12-M
IV12-10
200
Figura 4.30 – Ruptura característica dos prismas vazios moldados com os
blocos B15 – Etapa Arg. Industrial.
IV15-5
IV15-M
IV15-10
Fonte: Autor (2015).
Para a Etapa Referência, os prismas grauteados moldados com os
blocos B6, grautes G2, G3 e assentados com as argamassas C (séries
RG6-CG2 e RG6-CG3), apresentaram ruptura de forma frágil, sem
características explosivas. Para estes prismas a ruptura ocorreu com
aviso através da formação de fissuras e esmagamento da argamassa,
formação acentuada de trincas verticais e rupturas localizadas nos
blocos próximas a região da junta de argamassa, também entre 60% e
70% da carga de ruptura, até o colapso do conjunto, como mostra a
Figuras 4.31.
Para os prismas da série RG6-CG1, moldados com o grautes G1
de maior rigidez (maiores valores de resistência à compressão e módulo
de elasticidade), a ruptura ocorreu de forma frágil, entretanto com
características explosivas, provocando o fendilhamento lateral das
paredes dos blocos, indicando o aumento na tração das paredes como
consequência da expansão do graute (Figura 4.31). Como o graute
encontra-se confinado dentro do bloco, excedida a resistência à
compressão do graute, a tensão interna gerada contra as paredes do
bloco ocasiona sua ruptura por tração (HAMID e DRYSDALE, 1979;
CHEEMA e KLINGNER, 1986). Como observado no Item 4.5.1.2, o
enrijecimento do graute aumenta o nível de tensão sobre este, e como
consequência, aumenta-se a tensão sobre as paredes do bloco,
justificando este aumento na tração e o fendilhamento de suas paredes.
201
Figura 4.31 – Ruptura característica dos prismas grauteados moldados com os
blocos B6 e argamassa C – Etapa Referência.
RG6-CG1
RG6-CG2
RG6-CG3
Fonte: Autor (2015).
Para as três séries de prismas moldados com os blocos B12, o
comportamento foi similar ao observado para os prismas moldados com
o bloco B6 (Figura 4.32).
Figura 4.32 – Ruptura característica dos prismas grauteados moldados com os
blocos B12 e argamassa B – Etapa Referência.
RG12-CG1
RG12-CG2
RG12-CG3
Fonte: Autor (2015).
Os prismas moldados com os blocos B15, assentados com a
argamassa C e as três classes de grautes, apresentaram ruptura de forma
frágil, sem características explosivas. Para estes prismas a ruptura
ocorreu de forma lenta com a formação de fissuras e o esmagamento da
argamassa, formação de fissuras e trincas verticais e rupturas localizadas
nos blocos próximas a região da junta de argamassa, até o colapso do
conjunto, como mostra a Figuras 4.33.
202
Figura 4.33 – Ruptura característica dos prismas grauteados moldados com os
blocos B15 e argamassa C – Etapa Referência.
RG15-CG1
RG15-CG2
RG15-CG3
Fonte: Autor (2015).
Entretanto, para as séries de prismas moldados com os blocos
B15, assentadas com a argamassa A e preenchidos com os grautes G1 e
G2 (Figura 4.34), a ruptura também ocorreu de forma frágil e com
características explosivas. Novamente, observou-se o fendilhamento
lateral das paredes dos blocos, indicando aumento nas tensões contra as
paredes dos blocos e nas regiões próximas à interface bloco-argamassa.
Para a série RG15-AG3 a ruptura ocorreu de forma lenta, porém com a
formação acentuada de trincas verticais ao longo dos blocos.
Observa-se que o enrijecimento da argamassa de assentamento e
do graute, além de não aumentarem proporcionalmente os valores de
resistências dos prismas (Item 4.5.1.1), provocam rupturas sem
características dúcteis, comportamento este não indicado para a
alvenaria estrutural. Isto é evidenciado quando comparadas as formas de
rupturas das séries de prismas RG15-AG1 e RG15-CG1.
203
Figura 4.34 – Ruptura característica dos prismas grauteados moldados com os
blocos B15 e argamassa A – Etapa Referência.
RG15-AG1
RG15-AG2
RG15-AG3
Fonte: Autor (2015).
Nas Etapas Argamassa Mista e Industrializada, todos os prismas
preenchidos com argamassa apresentaram ruptura de forma frágil, sem
características explosivas. Para estes prismas a ruptura ocorreu de forma
lenta com a formação de fissuras e esmagamento da argamassa,
formação de trincas verticais e o fendilhamento das paredes dos blocos,
indicando aumento nas tensões de tração nas paredes dos blocos e nas
regiões próximas à interface bloco-argamassa, em virtude da expansão
do preenchimento confinado (Figuras 4.35 a 4.40). Entretanto, este
comportamento acentuou-se com os prismas assentados e preenchidos
com as argamassas de maior rigidez, neste caso as argamassas das
classes A e 10. Isto pode ser justificado com o aumento do módulo de
elasticidade dos preenchimentos, e consequentemente com o aumento da
carga por ele absorvida (Tabela 4.32 e Tabela 4.34), aumentando-se
assim o nível de tensão contra as paredes dos blocos.
Ainda, para estas duas séries de prismas, observou uma formação
acentuada de fissuras e diminuição no esmagamento da junta, indicando
aumento de tensões de trações sobre esta região. Observa-se que o
enrijecimento da argamassa de assentamento e preenchimento, além de
não aumentar proporcionalmente os valores de resistências dos prismas
(Item 4.5.2.1), podem aumentar os níveis de tensões de tração próximos
a região da junta de argamassa.
204
Figura 4.35 – Ruptura característica dos prismas grauteados moldados com os
blocos B6 – Etapa Arg. Mista.
MG6-C
MG6-B
MG6-A
Fonte: Autor (2015).
Figura 4.36 – Ruptura característica dos prismas grauteados moldados com os
blocos B12 – Etapa Arg. Mista.
MG12-C
Fonte: Autor (2015).
MG12-B
MG12-A
205
Figura 4.37 – Ruptura característica dos prismas grauteados moldados com os
blocos B15 – Etapa Arg. Mista.
MG15-C
MG15-A
MG15-B
Fonte: Autor (2015).
Figura 4.38 – Ruptura característica dos prismas grauteados moldados com os
blocos B6 – Etapa Arg. Industrial.
IG6-5
Fonte: Autor (2015).
IG6-M
IG6-10
206
Figura 4.39 – Ruptura característica dos prismas grauteados moldados com os
blocos B12 – Etapa Arg. Industrial.
IG12-5
IG12-M
IG12-10
Fonte: Autor (2015).
Figura 4.40 – Ruptura característica dos prismas grauteados moldados com os
blocos B15 – Etapa Arg. Industrial.
IG15-5
Fonte: Autor (2015).
IG15-M
IG15-10
207
5. ANÁLISE NUMÉRICA
A alvenaria é um material composto, formado de unidades
(blocos ou tijolos) cerâmicas ou de concreto, e argamassa. Trata-se,
então, de um material heterogêneo e anisotrópico, apresentando
comportamento estrutural complexo e difícil de prever. Muitos
trabalhos, tentando explicar esse comportamento, foram fundamentados
utilizando-se conjuntamente análises experimentais e análises
numéricas.
Geralmente, os modelos matemáticos utilizados para explicar o
comportamento mecânico da alvenaria são equações simplificadas
obtidas a partir de ajustes estatísticos dos dados experimentais, obtidos
através de ensaios com prismas, mini-paredes e paredes. Entretanto, com
o intuito de correlacionar melhor a interação entre os componentes da
alvenaria e para o melhor entendimento do comportamento mecânico do
conjunto, com o avanço dos recursos computacionais, cada vez mais
vem sendo utilizado métodos numéricos, mais especificamente o
Método dos Elementos Finitos (GONÇALVES JR, 2008). Em virtude
de sua confiabilidade, flexibilidade e relativa facilidade de
implementação computacional, o Método dos Elementos Finitos vem
sendo empregado extensivamente na análise de sólidos, estruturas e a
distribuição de tensões atuante nestes, sendo útil praticamente em todos
os campos da engenharia.
O Método dos Elementos Finitos é um método numérico para
solução de equações diferenciais, largamente utilizados por vários
sistemas informatizados de cálculo para desenvolvimento de produtos,
constituindo-se em uma das mais poderosas ferramentas para analise
estrutural. O método tem como diretriz básica o conceito de que
qualquer corpo pode ser dividido em um conjunto de elementos de
dimensões finitas chamadas de elementos finitos, interligados por um
número reduzido de pontos denominados nós (SORIANO, 2003). A este
conjunto de elementos dá-se o nome de malha de elementos finitos.
Estes elementos podem ter várias formas geométricas, definidas em
função do sistema estrutural que se deseja analisar, onde associados aos
recursos computacionais atuais, permitem uma maior flexibilidade na
solução de problemas de engenharia.
Para que esses elementos possam se relacionar uns com os outros,
é necessário que sejam interconectados por meio de pontos inseridos no
contorno, chamados de pontos nodais, ou simplesmente nós. Assim, o
comportamento estrutural de cada elemento pode ser dado em função
208
apenas dos dados nodais, tais como: coordenadas, deslocamentos e
carregamentos, permitindo a montagem do sistema de equações
governantes do sistema estrutural em estudo.
Na alvenaria estrutural, é de fundamental importância a escolha
apropriada dos modelos matemáticos que representem seu
comportamento estrutural. Estes modelos devem ser selecionados de
acordo com os fenômenos a serem estudados ou do grau de precisão
necessária (PELETEIRO, 2002; DIAZ et al, 2011).
Em geral, para se efetuar uma modelagem numérica são
utilizados dois modelos aproximados: a micromodelagem ou a
macromodelagem. Na micromodelagem os seus componentes são
discretizados individualmente, separando-se unidade e argamassa. A
macromodelagem considera a alvenaria como um compósito, sem
distinção entre argamassa e a unidade. Conforme Lourenço (1996), apud
Peleteiro (2002), dependendo do nível de precisão e da simplicidade
desejada, a alvenaria pode ser modelada numericamente de três formas
distintas, conforme Figura 5.1:
a) Micromodelagem detalhada (Figura 5.1-b): os componentes,
unidades e argamassa nas juntas são representados através de elementos
contínuos, enquanto que a interface unidade-argamassa é representada
através de elementos descontínuos. Cada material é considerado com
suas características físico-mecânicas próprias, como a resistência, o
módulo de elasticidade, coeficiente de Poisson etc.; a interface entre as
unidades e a argamassa é modelada como elementos descontínuos,
representando potenciais planos de fissuração e deslizamento. Este tipo
de modelagem, imprescindível no estudo de detalhes estruturais,
possibilita o estudo da interação entre as unidades e a argamassa,
mostrando-se adequado para a verificação das tensões e deformações
dos materiais.
b) Micromodelagem simplificada (Figura 5.1-c): neste modelo as
unidades expandidas são representadas através de elementos contínuos,
enquanto que o comportamento das juntas de argamassa e a interface
unidade-argamassa são agregados em elementos descontínuos. É dado o
mesmo tratamento às unidades, porém as juntas são representadas por
elementos de contato. A alvenaria é modelada como um conjunto de
unidades, com propriedades elásticas, unidas por elementos de contato
não lineares. Essa modelagem é menos precisa que a detalhada, por
necessitar de ajustes nas dimensões dos blocos em razão da não
consideração da espessura das juntas e por não se considerar o
coeficiente de Poisson da argamassa.
209
c) Macromodelagem (Figura 5.1-d): neste modelo não se tem a
discretização da alvenaria em seus componentes. As unidades, a
argamassa e a interface unidade-argamassa são unidas no contínuo. A
alvenaria é tratada como um compósito, não se fazendo distinção entre
blocos e argamassa (homogeneização). É apropriado para a análise de
estruturas de grande escala, em que as dimensões do painel de alvenaria
são grandes em relação às dimensões das unidades e da espessura das
juntas, que se trabalhe com os parâmetros elásticos da alvenaria como
um conjunto.
Figura 5.1 - Estratégias de modelagem para estruturas de alvenaria: (a)
alvenaria; (b) micromodelagem detalhada; (c) micromodelagem simplificada;
(d) macromodelagem.
Fonte: adaptado de Lourenço (1996).
Peleteiro (2002) em seu estudo agrupou as vantagens e
desvantagens dos diferentes modelos discretos e homogeneizados
utilizados por outros pesquisadores, conforme Tabela 5.1. De acordo
com a autora, não é possível afirmar qual das formas de modelagem é
mais vantajosa em relação às outras, porque cada uma delas apresenta
vantagens e desvantagens para estudos específicos. A escolha deve ser
feita de acordo com o objetivo a ser alcançado. Enquanto que o estudo
da micromodelagem é necessário para fornecer um bom entendimento
sobre o comportamento local das estruturas de alvenaria, a macromodelagem é mais adequada para análises mais gerais de estrutura,
210
como projeto de edifícios, principalmente quando se está estudando
paredes sólidas com dimensões grandes o suficiente para garantir
distribuições de tensões bastante uniformes. Esta característica torna a
macromodelagem mais prática, apresentando um tempo de
processamento reduzido e uma geração de malhas mais simples.
211
Tabela 5.1 – Vantagens
homogeneizados.
Modelo
e desvantagens
Vantagens
dos
modelos
discretos
e
Desvantagens
Modelo discreto com
comportamento linear
isotrópico.
Bons resultados em estruturas
submetidas a baixos níveis de
tensão.
Não adequado para casos em
que as tensões são altas e onde
é necessária uma análise de
redistribuição de tensões.
Modelo
homogeneizado com
comportamento linear
ortotrópico.
Adequado para estudo do
comportamento global da
estrutura. Com vantagem de
uma modelagem mais simples e
um tempo de processamento
menor que o modelo discreto.
O modelo não é capaz de
identificar picos de tensões em
regiões localizadas, sendo que
o modelo discreto consegue
determinar.
Modelo
homogeneizado com
comportamento não
linear do material.
Apresenta bons resultados em
termos de comportamento
global e determinação de carga
de ruptura.
O modelo não é capaz de
representar alguns mecanismos
básicos de ruptura da alvenaria,
como por exemplo, a fissuração
nas juntas e unidades e o
escorregamento das juntas.
Modelo discreto com
comportamento
elástico-linear para
unidades e elemento de
ligação não linear nas
juntas.
Modelagem apropriada com
vantagem de determinação das
características do material
através de ensaios uniaxiais.
Não considera a fissuração e a
não linearidade da unidade.
Não é capaz de determinar a
ruptura da estrutura, quando
fortemente influenciada pela
ruptura das unidades.
Modelo discreto com
características de
deformação não linear
para a argamassa e a
unidade, critério para
ruptura da unidade, da
argamassa e da junta.
A idealização proposta é capaz
de representar o comportamento
nas estruturas em alvenaria,
determinando a carga inicial de
fissuração, a carga última e o
padrão de ruptura com boa
precisão.
São necessários ensaios
complexos de caracterização
das unidades, da argamassa e
de amostras de paredes.
Modelo de fissuras
discretas considerandose as propriedades não
lineares dos materiais.
Mais apropriado para a análise
de painéis submetidos a forças
concentradas.
Apresenta custo computacional
elevado.
Modelo de fissuras
espalhadas
considerando o
comportamento não
linear dos
componentes.
Bons resultados na
determinação da força última de
ruptura e no padrão de ruptura
dos painéis. Tempo de
processamentos mais baixo.
Podem aparecer tensões de
travamento e os resultados
devem ser analisados com
cuidado devido à dependência
da dimensão da malha de
elementos finitos.
Fonte: (PELETEIRO, 2000).
212
5.1. NÃO LINEARIDADE DOS MATERIAIS
Além da escolha adequada da modelagem (micro ou macro), para
a melhor representação do problema que se pretende investigar, outro
parâmetro deve ser considerado com a utilização da análise numérica
por elementos finitos da alvenaria estrutural. Trata-se do regime no qual
se pretende analisar o comportamento da alvenaria, ou seja, regime
elástico-linear ou não linear. Inicialmente, nos trabalhos desenvolvidos,
era feita apenas uma análise elástico-linear, com as propriedades
elásticas dos materiais ajustados pelos resultados experimentais. Era
raro encontrar um modelo matemático não linear aplicado à prismas
e/ou paredes de alvenaria, onde o comportamento mecânico dos
materiais tenha recebido um tratamento matemático mais adequado ao
seu comportamento real (GOMES, 2001).
O modelo elástico-linear era aceito e utilizado universalmente,
em razão da simplicidade de seu equacionamento, porém ele não
representava fielmente o comportamento real da estrutura (SILVA JR et
al, 2010).
Entretanto, após o surgimento e aprimoramento dos
computadores, pesquisadores desenvolveram modelos que possam
melhor representar os sistemas estruturais, bem como os materiais que
os compõem. Assim, a utilização de modelos não lineares tem sido alvo
de muitas pesquisas, porém essa consideração leva a um
equacionamento matemático bastante complexo, mas que, com a
utilização de computadores e métodos numéricos apropriados, tornam a
utilização desses modelos plenamente viáveis. Segundo Gomes (2001),
a análise não linear é extremamente útil para obter a resposta estrutural
completa do comportamento da alvenaria, desde o inicio do processo de
carregamento quando o corpo ainda está no regime elástico-linear até a
ruptura final, passando estágios intermediários em que o corpo está
fissurando e/ou há esmagamentos localizados.
De uma forma geral, conforme exposto por Gomes (2001), é
possível distinguir três tipos de não linearidade: a não linearidade
geométrica, a não linearidade física ou do material e a não linearidade
de estado.
Segundo o pesquisador, a não linearidade geométrica ocorre
sempre que os deslocamentos e/ou deformações sejam suficientemente
significativos para que a configuração inicial não possa mais ser
utilizada para exprimir as condições de equilíbrio e compatibilidade. Os
materiais utilizados na alvenaria apresentam comportamento frágil
(bloco cerâmico, argamassa e graute), deformando-se muito pouco
213
durante o processo de carregamento. Assim, os deslocamentos e/ou
deformações são suficientemente pequenos para que a diferença entre a
configuração inicial e deformada seja desprezível.
Quando as alterações das condições de contorno ou de aplicação
de cargas são suficientes para mudar significativamente o estado de
tensões no corpo analisado, tem-se a não linearidade de estado.
Entretanto este feito é, normalmente, desprezado.
Finalmente, a não linearidade física ou do material é a mais
comum e ocorre quando as leis constitutivas (ou diagramas tensãodeformação) dos materiais são não lineares. Neste tipo de não
linearidade é possível ter muitas subdivisões: a teoria da plasticidade,
onde as leis constitutivas não lineares são levadas em conta; a
viscoplasticidade, onde além das leis constitutivas não lineares, as
propriedades mecânicas dos materiais dependem do tempo; materiais
hiperelásticos, como a borracha, por exemplo, e modelos que
representam a baixa resistência à tração dos materiais frágeis por meio
de rupturas localizadas no corpo (fissuras), como os modelos de
fissuração distribuída e discreta.
Para materiais com baixa resistência à tração, como blocos
cerâmicos, argamassas e concreto, um dos critérios de ruptura mais
adequado para representar o comportamento não linear destes materiais
é o Critério de Mohr-Coulomb, critério este adotado neste trabalho.
O Critério de Ruptura de Mohr-Coulomb, é uma generalização da
equação de ruptura proposta por Coulomb, e definida por:
τ = c - σn tan ϕ
(5.1)
Onde τ é a tensão de cisalhamento, σn a tensão normal, c a coesão
e ϕ o ângulo de atrito interno do material. Os dois parâmetros do
material, c e ϕ, são determinados a partir de ensaios de compressão
triaxial, levando o material até a condição de ruptura.
Graficamente, o critério é representado por uma reta tangente ao
maior círculo formado pelas tensões principais (linha de ruptura),
conforme ilustra a Figura 5.2.
Pela Figura 5.2, quando o par de tensões P(- σn , τ) atuantes em
um ponto qualquer do material situarem-se sobre tal reta (linha de
ruptura), ocorrerá a ruptura do material. Sendo que o domino elástico
para este material, de acordo com o critério de Mohr-Coulomb, é
definido por qualquer círculo de Mohr que não toque (tangencie) a reta
que define o critério de ruptura.
214
Figura 5.2 – Critério de Mohr-Coulomb no plano.
P (- σn
σ3
σ2
,τ)
Linha de Ruptura
σ1
σ1 – σ2
Fonte: adaptado de SOUZA NETO et al (2008).
De acordo com a figura, a equação 5.1 pode ser escrita em função
das tensões principais:
(σ1 – σ3) cosϕ = 2c – [(σ1 – σ3) + (σ1 – σ3) senϕ] tanϕ ϕ
(5.2)
Reescrevendo a equação 5.2, tem-se:
(σ1 – σ3) + (σ1 + σ3) senϕ = 2 c cosϕ
(5.3)
Assim, a equação expressa em função das tensões principais e
definida pelo critério de Mohr-Coulomb pode ser escrita como:
F (σ, c) = (σ1 – σ3) + (σ1 + σ3) senϕ - 2 c cos ϕ
(5.4)
Essa equação indica que há ruptura do material, quando a tensão
de cisalhamento em um determinado plano ultrapassa a resistência a
deslizamento originada de duas parcelas: uma proveniente da referida
coesão do material, outra vinda de uma fração da tensão normal atuante
nesse mesmo plano.
Graficamente, a equação 5.4 representa a superfície de ruptura
dada por uma pirâmide hexagonal irregular (Figura 5.3), no plano das
tensões principais. A seção transversal desta pirâmide denominada plano
215
desviador ou Plano-π, dada quando F (σ, c) = 0 e c constante, é
representada como mostra a Figura 5.4.
Figura 5.3 - Representação gráfica da superfície de ruptura do critério de MohrCoulomb no espaço das tensões principais.
Eixo hidrostático
(σ1 = σ2 = σ3 )
F (σ, c) = 0
Superfície de
Ruptura
Plano Desviador
(Plano-π)
Fonte: adaptado de SOUZA NETO et al (2008).
Figura 5.4 - Representação gráfica da superfície de ruptura no plano desviador.
- σ3
Superfície de
Ruptura
- σ1
Fonte: adaptado de SOUZA NETO et al (2008).
- σ2
216
A equação 5.4 ainda pode ser escrita de uma forma alternativa
(equação 5.5) em função de invariantes de tensões (I1, J2, θ) (Chen e Liu,
1990). Onde I1 representa o primeiro invariante do tensor das tensões e é
definido pela equação 5.6, J2 o segundo invariante do tensor desviador
dado pela equação 5.7, sendo que θ é o ângulo de Lode escrito em
função dos invariantes de tensão J2 e J3, e dado pela equação 5.8.
(5.5)
Onde:
I1 = σ1 + σ2+ σ3
(5.6)
–
(
–
√
)
–
(5.7)
(5.8)
(5.9)
Um modelo plástico é considerado de endurecimento isotrópico
se a evolução da superfície de ruptura é tal que, para um estado de
endurecimento, corresponda a uma expansão uniforme (isotrópica) da
superfície de ruptura inicial. Para um modelo de plasticidade multiaxial
com uma superfície de ruptura de Mohr-Coulomb, o endurecimento
isotrópico corresponde a um aumento da seção transversal indicada na
Figura 5.4. O controle do endurecimento isotrópico é, na prática,
efetuado através da curva tensão-deformação extraída de ensaio de
compressão uniaxial. Para a análise adotada neste trabalho, utilizou-se o
endurecimento isotrópico associado ao critério de Moh-Coulomb
Parabólico, pois era a única opção implementada no programa Marc
Mentat.
Ainda, na aplicação do critério de Mohr-Coulomb para materiais
cerâmicos, o ângulo de atrito interno e a coesão podem ser definidos em
função da resistencia a compressão (fc) e a resistencia à tração do
material (ft), obtidas por meio de ensaio de compressão simples e de
tração simples, respectivamente, conforme as Equações 5.10 e 5.11
(SOUZA NETO et al, 2008).
(5.10)
217
(5.11)
Onde se tem que fc representa a resistência à compressão uniaxial
e ft a resistência à tração uniaxial.
5.2. SIMULAÇÃO NUMÉRICA
A realização desta análise teve por objetivo compreender a
distribuição das tensões desenvolvidas nos prismas e a influência da
argamassa utilizada como preenchimento no desempenho mecânico dos
modelos de prismas avaliados. A adoção de um modelo numérico parte
habitualmente da consideração de que os seus resultados podem ser
determinísticos e não probabilísticos, ou seja, as propriedades mecânicas
são tomadas como médias, sem considerar a variabilidade. Não se
pretende nesta análise a propositura de um modelamento numérico
verificado pelo programa experimental, mas que os resultados da
modelamento numérico utilizando as propriedades mecânicas dos
materiais dos prismas obtidos no programa experimental, forneçam
informações qualitativas e comportamentais da estrutura em análise.
Basicamente, a intenção deste estudo é a obtenção de um modelo capaz
de simular numericamente o ensaio de compressão em prismas, por
meio de um modelo constitutivo usando a teoria de plasticidade. Como o
modelamento numérico é sempre uma representação simplificada de um
fenômeno físico complexo, é necessário simplificar este modelo para
que este forneça resultados dentro de uma precisão considerada
aceitável (GOMES, 2001).
Para este trabalho, desprezaram-se a não linearidade de estado e
de geometria a partir da consideração de que os deslocamentos e/ou
deformações são pequenos o suficiente para que a diferença entre a
configuração inicial e deformada seja desprezível.
A única não linearidade considerada relevante foi a não
linearidade física ou de material, visto que os prismas, composto por
materiais cerâmicos, foram analisados até a sua ruptura.
Para a simulação numérica optou-se pelo uso do aplicativo MarcMentat 2012, pois este aplicativo computacional atende aos requisitos
necessários e está acessível através de um trabalho em conjunto com a
Universidade Federal de Santa Catarina (UFSC) e a Universidade do
Estado de Santa Catarina (UDESC), que possui a licença de uso do
programa.
218
Assim, para esta etapa do trabalho realizou-se a simulação
somente para os prismas MG6-A, MG6-B e MG6-B. A escolha destas
séries de prismas ocorreu em virtude da ocorrência do aumento
significativo da capacidade de carga para os prismas preenchidos com as
argamassas B e C, conforme observado nos resultados da Etapa
Argamassa Mista do programa experimental, em contraste com o
observado para os prismas MG6-A, conforme Tabela 5.2.
Tabela 5.2 – Efeito relativo da capacidade de carga dos prismas preenchidos .
Bloco B6
Prismas
F
(calculado)
Fα
(crítico)
MV6-A
MG6-A
1,151
2,306
MV6-B
MG6-B
2,750
2,306
MV6-C
MG6-C
8,299
2,306
Conclusão
F < Fα
(Não Há Diferença)
F > Fα
(Há Diferença)
F > Fα
(Há Diferença)
Efeito
Relativo
(%)
+ 8,6
+ 22,2
+ 61,0
Fonte: Autor (2015).
O modelo geométrico elaborado consistiu em uma representação
verossímil do corpo de prova, ou seja, com todos os furos e recortes
existentes nas unidades cerâmicas, com a espessura da camada de
argamassa executada entre as unidades e com a geometria assumida
pelos grautes (Figura 5.5), resultando em uma malha de elementos
finitos densa. Em outras palavras, para a realização desta análise foi
adotada a micromodelagem detalhada. Porém, nesses modelos não foi
considerado o comportamento das interfaces bloco-argamassa e blocograute, ou seja, considerou-se a perfeita aderência entre os elementos.
Optou-se por esta simplificação em razão da falta de dados
experimentais e tempo disponível para a sofisticação do modelo.
Considerando-se como modelo o conjunto de dados que o usuário
deve preparar para descrever completamente as características do
problema a ser analisado, as etapas para a geração do modelo foram as
seguintes:
1 – Inicialmente foi definida a seção transversal dos blocos, sendo
utilizado para esse processo o programa AutoCAD 2012.
2 – Em seguida, transformou-se a seção transversal do bloco em
uma única região para a inserção da malha de elementos finitos. Neste
processo foi utilizado o programa GID 11.1.
219
3 – Finalizado esta etapa, na sequência, foi realizada a inserção da
malha de elementos finitos utilizando o programa PATRAN.
Estas etapas iniciais foram realizadas nestes três programas em
consequência da dificuldade encontrada para a geração da malha com o
programa que utilizado para o processamento e análise de resultados,
neste caso o programa Marc Mentat 2012.
4 – Já com a seção transversal do bloco com as malhas definidas,
esta foi inserida no programa Marc Mentat 2012 para a geração do
modelo tridimensional dos prismas. Para isto foi usado um artifício que
o programa dispõe para extrudar elementos de superfície transformandoos em elementos sólidos. Com essa ferramenta foi possível modelar o
bloco o mais próximo da geometria real. Dessa forma, foram
introduzidos os elementos sólidos hexaédricos de oito nós.
5 – Na sequência utilizou-se a ferramenta de cópia dos elementos,
fazendo assim o conjunto de três blocos (unidades) ligados pelas duas
juntas de argamassa, dando a forma geométrica desejada para os prismas
(Figura 5.5).
6 – Com o prisma e componentes todos discretizados, fez-se
necessária a definição das propriedades mecânicas dos elementos
constituintes (bloco cerâmico, argamassa e graute).
Para a cerâmica que compõe o bloco e a argamassa da junta e
preenchimento empregou-se o modelo de material não linear
apresentado pelo programa Marc Mentat 2012, onde as condições limite
de plasticidade utilizada são estabelecidas pelo critério de MohrCoulomb Parabólico (Figura 5.6). Este modelo parabólico apresentado
pelo programa é uma alternativa ao modelo de Mohr-Coulomb Linear e
sua escolha ocorreu por causa dos melhores resultados terem sidos
obtidos com a utilização deste modelo para o problema estudado.
220
137 mm
Figura 5.5 – Características geométricas dos prismas.
190 mm
288 mm
Fonte: Autor (2015).
10 mm
10 mm
190 mm
190 mm
288 mm
221
Figura 5.6 – Critério limite de plasticidade Mohr-Coulomb Parabólico.
σ2
σ1
Fonte: Manual do usuário do Marc Mentat (2012).
A equação que descreve a superfície que representa o critério de
Mohr-Coulomb Parabólico encontra-se abaixo:
F = (3.J2 + √3.β.σ.I1)1/2 – σ = 0
(5.12)
Onde I1 representa o primeiro invariante do tensor das tensões
(equação 5.6), J2 o segundo invariante do tensor desviador (equação
5.7), e σ e β são definidas pelas seguintes equações:
(5.13)
(5.14)
Onde:
(5.15)
Os valores de c (coesão) e de ϕ (ângulo de atrito interno) foram
determinados com as equações 5.10 e 5.11, utilizando os valores de
resistência à compressão unixial dos materiais, obtidos no programa
experimental. Sabe-se que as propriedades não lineares dos materiais
(coesão e ângulo de atrito interno) são determinadas em ensaios de
compressão triaxiais. Entretanto, em virtude da indisponibilidade do
equipamento para este ensaio, as propriedades não lineares dos materiais
222
foram estabelecidas considerando o estado de tensão unixial, ou seja, os
valores obtidos no programa experimental.
Ainda, as características não lineares utilizadas para cada modelo
foram ajustadas de forma a ter uma tensão vertical última próxima ao
valor de ruptura dos prismas do programa experimental. Estas
características também foram ajustadas para a obtenção de diagramas
tensão-deformação, gerados com os modelos numéricos, próximos aos
diagramas obtidos experimentalmente com os prismas. Em síntese, a
calibração do modelo numérico teve como referência o diagrama tensãodeformação obtida experimentalmente e a carga de ruptura dos prismas,
ná área líquida (fpliq).
Assim, as características mecânicas lineares e não lineares dos
materiais empregados na simulação encontram-se nas Tabelas 5.3 e 5.4.
Tabela 5.3 – Características mecânicas lineares dos materiais.
Componente
Bloco B6
Argamassa A
Argamassa B
Argamassa C
Fonte: Autor (2015).
E (MPa)
8243,9
12554,2
7120,1
2529,6
ν
0,05
0,17
0,14
0,14
Tabela 5.4 – Características mecânicas não lineares dos materiais.
Componente
Bloco B6
Argamassa A
Argamassa B
Argamassa C
Fonte: Autor (2015).
ϕ
54,30º
32,12º
29,12º
24,22º
c (MPa)
0,80
1,11
0,60
0,32
7 – A vinculação do prisma foi baseada no equipamento de ensaio
disponível (prensa SHIMADZU) no Laboratório de Materiais de
Construção Civil (LMCC), em que o carregamento é aplicado no topo
do corpo-de-prova (de cima para baixo). Logo, na base do modelo foram
restringidos os deslocamentos em x, y e z. No topo do modelo foram
restringidas as translações somente em x e y deixando a translação em z
livre para a aplicação da carga.
8 – O carregamento imposto no topo do modelo foi definido a
partir da média da resistência à compressão dos prismas rompidos no
223
programa experimental. Neste caso, as resistências médias à
compressão, na área líquida, das séries de prismas analisadas (fpliq).
Logo, a tensão de compressão aplicada nos modelos foi de 20
MPa, valor este aproximadamente igual ao dobro do valor de tensão, na
área líquida, obtida na ruptura dos prismas, conforme constatado nos
ensaios experimentais.
A inserção do carregamento foi feita como carga de superfície
nos elementos situados no topo do modelo. O carregamento foi aplicado
no topo do modelo, em função do tipo de aplicação de carga do
equipamento onde foram realizados os ensaios de ruptura dos prismas
no programa experimental.
5.3. ANÁLISE DOS RESULTADOS DA SIMULAÇÃO
A simulação numérica utiliza elementos sólidos hexaédricos de
oito nós, com uma malha de 41856 elementos, totalizando em 19984
nós.
5.3.1. Resultados para o prisma MG6-C
Abaixo, na Figura 5.7, encontra-se a comparação entre o
diagrama
tensão-deformação
do
prisma
MG6-C,
obtido
experimentalmente e com a simulação numérica. Ressalta-se que a
determinação
do
diagrama
tensão-deformação,
obtido
experimentalmente, foi realizado até a carga referente a 50% da tensão
de ruptura dos prismas, em virtude da capacidade da célula de carga
utilizada, e também assim evitando-se possíveis danos aos equipamentos
utilizados no ensaio. Após a determinação do diagrama tensãodeformação, obtido com o programa, foram extraídas uma série de
informações do prisma simulado, para a melhor compreensão dos
resultados obtidos com o programa experimental.
Assim, nas Figuras 5.8 e 5.9 mostra-se a distribuição de tensões
para o grautes na direção z (σz), para os prismas na direção x (σx),
direção y (σy) e direção z (σz), para os carregamentos incrementais de
4,7 MPa (valor intermediário) e 8,7 MPa. Este último valor corresponde
ao valor aproximado para a resistência à compressão na área líquida, de
9,3 MPa, obtida experimentalmente para o prisma MG6-C.
224
Figura 5.7 – Diagramas tensão-deformação obtidos para o prisma MG6-C.
Experimental
Tensão na área líquida (MPa)
10
Numérico
8
6
4
2
0
0,0000
0,0005
0,0010
0,0015
0,0020
0,0025
0,0030
0,0035
Deformação Específica (mm/mm)
Fonte: Autor (2015).
225
Figura 5.8 – Distribuição de tensão para o prisma MG6-C e o graute para carga
de 4,3 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
226
Figura 5.9 – Distribuição de tensão para o prisma MG6-C e o graute para carga
de 8,7 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
227
5.3.2. Resultados para o prisma MG6-B
Na Figura 5.10, encontra-se a comparação entre o diagrama
tensão-deformação do prisma MG6-B, obtido experimentalmente e com
a simulação numérica. Para esta série de primas, o diagrama tensãodeformação obtido experimentalmente também foi determinado até 50%
da carga de ruptura dos prismas.
Assim, as Figuras 5.11 e 5.12 mostra-se a distribuição de tensões
para o grautes na direção z (σz), para os prismas na direção x (σx),
direção y (σy) e direção z (σz), para os carregamentos incrementais de
4,7 MPa (valor intermediário) e 8,7 MPa. Este último valor corresponde
ao valor aproximado para a resistência à compressão na área líquida, de
9,2 MPa, obtida experimentalmente para o prisma MG6-B.
Figura 5.10 – Diagramas tensão-deformação obtidos para o prisma MG6-B.
Numérico
Experimental
Tensão na área líquida (MPa)
10
8
6
4
2
0
0,0000
0,0005
Fonte: Autor (2015).
0,0010
0,0015
0,0020
0,0025
0,0030
0,0035
Deformação Específica (mm/mm)
228
Figura 5.11 – Distribuição de tensão para o prisma MG6-B e o graute para carga
de 4,3 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
229
Figura 5.12 – Distribuição de tensão para o prisma MG6-B e o graute para carga
de 8,7 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
230
5.3.3. Resultados para o prisma MG6-A
Na Figura 5.13, encontra-se a comparação entre o diagrama
tensão-deformação do prisma MG6-A, obtido experimentalmente e com
a simulação numérica. Com realizado com as séries de prismas
anteriores, o diagrama tensão-deformação obtido experimentalmente
também foi determinado até 50% da carga de ruptura dos prismas.
Assim, as Figuras 5.14 e 5.15 mostra-se a distribuição de tensões
para o grautes na direção z (σz), para os prismas na direção x (σx),
direção y (σy) e direção z (σz), para os carregamentos incrementais de
4,7 MPa, 8,7 MPa e 10,1 MPa; sendo os dois primeiros valores de
tensão, os mesmo analisados para os prismas MG6-B e MG6-C. Este
último valor corresponde ao valor aproximado para a resistência à
compressão na área líquida, de 10,7 MPa, obtido experimentalmente
para o prisma MG6-A.
Figura 5.13 – Diagramas tensão-deformação obtidos para o prisma MG6-A.
Tensão na área líquida (MPa)
10
Numérico
Experimental
8
6
4
2
0
0,0000
0,0010
0,0020
0,0030
Deformação Específica (mm/mm)
Fonte: Autor (2015).
231
Figura 5.14 – Distribuição de tensão para o prisma MG6-A e o graute para carga
de 4,3 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
232
Figura 5.15 – Distribuição de tensão para o prisma MG6-A e o graute para carga
de 8,7 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
233
Figura 5.16 – Distribuição de tensão para o prisma MG6-A e o graute para carga
de 10,1 MPa, extraída do programa Marc Mentat.
σz
σy
Fonte: Autor (2015).
σx
σz
234
5.3.4. Discussão dos resultados
Conforme a análise dos resultados experimentais, o aumento na
resistência à compressão dos prismas com a utilização da argamassa
como preenchimento estrutural evidencia viabilidade de utilização desta
técnica, desde que a escolha entre os materiais seja adequada, como por
exemplo, os prismas das séries MG6-C e MG6-B. Observou-se que com
o aumento da rigidez do preenchimento, aumenta-se a parcela de
carregamento sob estes, aumentando-se assim o nível de tensão sobre a
parede dos blocos. O que a princípio, justificaria o aumento efetivo da
carga de ruptura para os prismas MG6-C e MG6-B, preenchidos com
argamassa de menor rigidez, validando assim a utilização do
preenchimento dos vazios dos blocos com a argamassa.
De acordo com os resultados das análises realizadas com a
simulação numérica (Figuras 5.8, 5.9, 5.11, 5.12, 5.14 à 5.16), como
esperado, para cada série de prismas, com o aumento do carregamento
aumentam as tensões de compressão na direção z para os
preenchimentos (grautes). Entretanto, para o carregamentos de 4,7 MPa,
observa-se praticamente os mesmos valores de tensões de compressão
para os três tipos de preenchimento. A diferença na distribuição de
tensão ocorre próximo da carga da ruptura, acentuando-se
principalmente para os prismas preenchidos com a argamassa de maior
rigidez, neste caso os prismas MG6-A. Para este prisma, quando
analisado as tensões próximas com a carga de ruptura (Figura 5.16),
estes valores acentuam-se. Grautes com maior rigidez absorvem uma
parcela maior do carregamento quando este é aplicado sob o prisma,
então consequentemente, apresentam maiores valores de tensão de
compressão, como visto no item 4.5.2.2 (Tabela 4.29). Isto é
evidenciado nas Figuras 5.9, 5.12 e 5.16, onde ocorre o aumento da
tensão σz no graute com o aumento da rigidez do mesmo e a diminuição
de tensão nos prismas nesta mesma direção.
Com este aumento de tensões de compressão sob os grautes,
aumentam-se também as trações nas direções x e y perpendiculares às
paredes dos blocos (Figuras 5.9, 5.12 e 5.16). Os valores observados
para as tensões de tração no bloco são superiores ao valor de 0,56 MPa,
obtido experimentalmente para o bloco B6. Observa-se também o
aumento nas tensões de tração na direção x e y na região das
argamassas, o que provocariam sua ruptura por tração. Este efeito
combinado (tração no bloco e argamassa) acentua o processo de ruptura
dos prismas, algo observado experimentalmente. Ou seja, com o
aumento do carregamento sob os prismas, aumentam-se as tensões
235
impostas pelo preenchimento sobre as paredes internas dos blocos e
junto com a ruptura da argamassa, iniciar-se-ia o colapso do conjunto.
Entretanto, estes valores de resistência à tração determinados
experimentalmente para o bloco e a argamassa, foram obtidos por meio
de ensaios uniaxiais, o que pode não representar os valores de tração do
material sob um estado triaxial de tensões, como ocorre com a
argamassa confinada. A argamassa em regime de confinamento
apresenta uma mudança significativa no seu comportamento mecânico.
E isto ocorre por causa do estado triaxial de tensões de compressão
surgidas na junta de argamassa e no bloco a um estado biaxial de
tensões de tração (OLIVEIRA, 2001).
Esperava-se com o aumento da resistência das argamassas, que as
tensões verticais de compressão nos preenchimentos, obtidas com a
simulação, apresentassem aumento proporcional ao observado para as
parcelas de cargas absorvidas pelos preenchimentos, calculado com os
dados experimentais (Tabela 4.29). Entretanto, para os resultados da
simulação, esta tendência não foi observada com o aumento da rigidez
do preenchimento. Isto se deve ao fato que esta estimativa de carga foi
realizada com os materiais sob regime linear, diferente do regime de
análise adotado na simulação. Onde o caráter não linear dos materiais do
prisma, evidenciado quando estes são analisados próximos à ruptura,
torna o entendimento deste fenômeno ainda mais complexo do que
apenas a correlação entre
propriedades elásticas definidas em
laboratório para os componentes do prisma.
Ainda, tentando verificar como se comporta a distribuição de
tensão na região da interface entre bloco e a argamassa de
preenchimento (graute) ao longo da altura dos prismas, foram analisados
quatro pontos da seção transversal, neste caso os pontos A, B, C e D
(Figura 7.17). Esta análise fez-se para os carregamentos aplicados de
1,2, 4,7, 8,7 MPa e 10,1 MPa; sendo este último apenas para o prisma
MG6-A, que apresentou maior carga de ruptura. Esta representação da
distribuição de tensões ao longo da altura das três séries de prismas é
apresentada nas Figuras 5.18 à 5.20.
De acordo com os gráficos das Figuras 5.17 e 5.18, para os
prismas MG6-C e MG6-B, com o aumento do carregamento ocorre o
aumento nas tensões de tração impostas pelo preenchimento contra as
paredes dos blocos. A junta de argamassa apresenta valores de tensão
diferentes dos encontrados para os blocos. Este comportamento
observado para estes materiais ocorre por se tratarem de materiais com
diferentes valores de módulo de elasticidade e coeficiente de Poisson,
236
onde com a aplicação do carregamento, apresentam deformações e
tensões distintas.
Figura 5.17 – Pontos da seção transversal para a análise da distribuição de
tensão ao longo da altura.
σy
σx
Fonte: Autor (2015).
Entretanto, conforme os gráficos das figuras 5.16 e 5.18, os
valores de tração observados são inferiores aos valores de resistência à
tração do bloco de 0,56 MPa, o que não implicaria em seu colapso. Isto
pode ser em consequência das seções analisadas ou simplificações do
modelo utilizado, que não apresenta com precisão o comportamento da
região de interface existente entre bloco-argamassa e principalmente
bloco-graute.
Para os prismas MG6-A (Figura 5.20), o comportamento difere
do observado para as outras duas séries de prismas. Nesta série,
preenchida com a argamassa A, observa-se o aumento nos valores de
tração na região da junta de argamassa, com o aumento do
carregamento. Isto pode evidenciar que para essa série de prisma, a
ruptura se deu principalmente pela expansão lateral da argamassa
(tração) do que tração das paredes dos blocos em consequência da
expansão do preenchimento. Durante os ensaios de ruptura dos prismas,
observou-se que o esmagamento da junta de argamassa dos prismas
237
MG6-A foi menor do que o observado para os prismas MG6-B e MG6C, evidenciando o aumento nas tensões de tração sob a junta de
argamassa para os prismas preenchidos com a argamassa A, de maior de
resistência.
Observa-se também que os níveis de tração desenvolvidos contra
as paredes dos blocos do prisma MG6-A, foram menores dos que
encontrado para as outras duas séries de prismas. Isto pode ser explicado
pelo fato que o módulo da argamassa A ser maior, logo se desenvolveria
tensões de tração menores para esse material sobre níveis de
carregamento similares. Esta hipótese pode ser confirmada observando
as Figuras 5.21 a 5.23, onde são apresentadas as tensões principais
máximas para os preenchimento, sob os carregamentos incrementais de
1,2, 4,7 e 8,7 MPa.
De acordo com a distribuição de tensões principais máximas
apresentadas nas figuras, observa-se que com o enrijecimento do
preenchimento, ou seja, aumento da resistência da argamassa de
preenchimento da classe A para a C, os níveis de tensão de tração são
menores para os prismas preenchidos com a argamassa mais rígida,
argamassa A. Para os prismas da série MG6-A, os níveis de tensão de
tração máximos encontram-se na região da junta de argamassa, o que
novamente evidencia que para esta série de prismas o colapso do
conjunto ocorreu com o aumento da tração da junta de argamassa para
depois iniciar-se a ruptura localizada do bloco próximo a interface
bloco-argamassa, em consequência do aumento das tensões de tração da
junta nas direções x e y. Entretanto, esta hipótese difere da observado
com a análise dos dados experimentais, onde com o aumento da rigidez
do preenchimento, aumenta-se a carga sobre este se aumentando as
tensões sobre as paredes dos blocos. Evidencia-se então que a
viabilidade da técnica de preenchimento dos prismas com a argamassa
de assentamento, mesmo que constatada com a análise dos dados
experimentais, demanda modelos numéricos mais sofisticados, com a
inclusão de elementos de interface, para um melhor entendimento do
comportamento dos prismas e maior segurança na sua utilização da
técnica.
238
Figura 5.18 – Distribuição de tensão ao longo da altura para o Prisma MG6-C.
Carga superficial de
1,2 MPa
Carga superficial de
4,3 MPa
Carga superficial de
8,7 MPa
600
550
500
450
400
350
300
250
200
150
100
50
0
PRISMA MG6-C - Distribuição de
Tensão ao longo da altura B
ALtura (mm)
ALtura (mm)
PRISMA MG6-C - Distribuição de
Tensão ao longo da altura A
Carga superficial de
1,2 MPa
Carga superficial de
4,3 MPa
Carga superficial de
8,7 MPa
600
550
500
450
400
350
300
250
200
150
100
50
0
PRISMA MG6-C - Distribuição de
Tensão ao longo da altura C
600
550
500
450
Carga superficial de
400
1,2 MPa
350
Carga superficial de
300
4,3 MPa
250
Carga superficial de
200
8,7 MPa
150
100
50
0
-4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5 0 0,5
Tensão σy (MPa)
PRISMA MG6-C - Distribuição de
Tensão ao longo da altura D
600
550
500
450
Carga superficial de
400
1,2 MPa
350
Carga superficial de
300
4,3 MPa
250
Carga superficial de
200
8,7 MPa
150
100
50
0
-4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5 0 0,5
Tensão σY (MPa)
Fonte: Autor (2015).
ALtura (mm)
-4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5 0 0,5
Tensão σx (MPa)
ALtura (mm)
-4 -3,5 -3 -2,5 -2 -1,5 -1 -0,5 0 0,5
Tensão σx (MPa)
239
Figura 5.19 – Distribuição de tensão ao longo da altura para o Prisma MG6-B.
ALtura (mm)
PRISMA MG6-B - Distribuição de
Tensão ao longo da altura C
600
550
500
450
Carga superficial
400
de 1,2 MPa
350
Carga superficial
300
de 4,6 MPa
250
Carga superficial
200
de 8,7 MPa
150
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σY (MPa)
Fonte: Autor (2015).
ALtura (mm)
PRISMA MG6-B - Distribuição de
Tensão ao longo da altura B 600
550
500
450
Carga superficial
400
de 1,2 MPa
350
Carga superficial
300
de 4,6 MPa
250
Carga superficial
200
de 8,7 MPa
150
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σx (MPa)
PRISMA MG6-B - Distribuição de
Tensão ao longo da altura D
600
550
500
450
Carga superficial
400
de 1,2 MPa
350
Carga superficial
300
de 4,6 MPa
250
Carga superficial
200
de 8,7 MPa
150
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σy (MPa)
ALtura (mm)
ALtura (mm)
PRISMA MG6-B - Distribuição de
Tensão ao longo da A
600
550
500
450
Carga Superficial
400
de 1,2 MPa
350
Carga superficial
300
de 4,6 MPa
250
Carga superficial
200
de 8,7 MPa
150
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σX (MPa)
240
Figura 5.20 – Distribuição de tensão ao longo da altura para o Prisma MG6-A.
ALtura (mm)
PRISMA MG6-A - Distribuição de
Tensão ao longo da altura C 600
550
500
Carga superficial
450
de 1,2 MPa
400
Carga superficial
350
de 4,6 MPa
300
Carga superficial
250
de 8,6 MPa
200
Carga superficial
150
de 10,1 MPa
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σy (MPa)
Fonte: Autor (2015).
ALtura (mm)
PRISMA MG6-A - Distribuição de
Tensão ao longo da altura B
600
550
500
Carga superficial
450
de 1,2 MPa
400
Carga superficial
350
de 4,6 MPa
300
Carga superficial
250
de 8,6 MPa
200
Carga superficial
150
de 10,1 MPa
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σx(MPa)
PRISMA MG6-A - Distribuição de
Tensão ao longo da altura D
ALtura (mm)
ALtura (mm)
PRISMA MG6-A - Distribuição de
Tensão ao longo da altura A 600
550
500
Carga superficial
450
de 1,2 MPa
400
Carga superficial
350
de 4,6 MPa
300
Carga superficial
250
de 8,6 MPa
200
Carga superficial
150
de 10,1 MPa
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σx (MPa)
Carga superficial
de1,2 MPa
Carga superficial
de 4,6 MPa
Carga superficial
de 8,7 MPa
Carga superficial
de10,1 MPa
600
550
500
450
400
350
300
250
200
150
100
50
0
-4,0-3,5-3,0-2,5-2,0-1,5-1,0-0,5 0,0 0,5
Tensão σy (MPa)
241
Figura 5.21 – Distribuição de tensões principais máximas para o graute do
prisma MG6-C, extraída do programa Marc Mentat.
Fonte: Autor (2015).
Figura 5.22 – Distribuição de tensões principais máximas para o graute do
prisma MG6-B, extraída do programa Marc Mentat.
Fonte: Autor (2015).
242
Figura 5.23 – Distribuição de tensões principais máximas para o graute do
prisma MG6-A, extraída do programa Marc Mentat.
Fonte: Autor (2015).
243
6. CONCLUSÕES E RECOMENDAÇÕES FUTURAS
A presente tese teve por objetivo investigar o comportamento
estrutural à compressão da alvenaria de blocos cerâmicos considerando
o preenchimento dos furos com a argamassa de assentamento,
substituindo o graute tradicionalmente utilizado para aumentar a
capacidade resistente das paredes de alvenaria.
Os focos principais dos ensaios experimentais foram os
componentes (blocos, argamassas e grautes) e os prismas, através das
suas propriedades mecânicas e modos de ruptura. Para melhor
entendimento, as conclusões foram subdivididas nos seguintes itens:
ensaios de caracterização mecânica dos prismas e simulação numérica
dos prismas.
6.1
ENSAIO DE
PRISMAS
CARACTERIZAÇÃO
MECÂNICA
DOS
Realizou-se a análise das propriedades mecânicas dos prismas,
correlacionando-as com as propriedades obtidas com a caracterização
dos blocos, argamassas e grautes.
6.1.1 Etapa Referência
6.1.1.1 Influência dos componentes na resistência dos prismas
Com o propósito de verificar a influência da variação da
argamassa, bloco e o efeito conjunto do bloco e argamassa na resistência
dos prismas, foram realizadas análises fatoriais de 2 fatores (ANOVA)
para as séries de prismas grauteados, moldados com os blocos de 6 e 15
MPa e argamassas das classes A (traço 1:1/4:3) e C (traço 1:1:6),
respectivamente, de maior e menor resistência à compressão.
Na primeira análise, para os prismas moldados com os blocos de
6 e 15 MPA e argamassa classe C (de menores resistência e módulo de
elasticidade), com 95% de confiança, constata-se que o graute foi o fator
com maior influência na resistência à compressão dos prismas, seguido
da interação entre o bloco e graute, e por último pelo bloco.
Na segunda análise, para os prismas moldados somente com o
bloco de 15 MPa e as argamassas das classes A e C, com 95% de
confiança, constata-se que a resistência média à compressão do graute,
da argamassa e a interação entre estes dois fatores, influenciam
244
significativamente na resistência média à compressão dos prismas, na
área líquida. Ainda, o graute foi o fator com maior influência na
resistência dos prismas, seguido da argamassa e por último, da interação
entre o graute e argamassa.
Observa-se que em ambas as análises, tanto o bloco, argamassa,
graute e a combinações destes componentes influenciam na resistência
dos prismas. Este comportamento já fora relatado em trabalhos
realizados por outros pesquisadores. Entretanto, o aumento da
resistência da argamassa possui pouca influência no aumento da
resistência à compressão dos prismas. Isto é evidenciado quando
comparados os valores de resistência dos prismas moldados com o bloco
de 15 MPa, preenchidos com a mesma classe de grautes. Enquanto que a
argamassa A possui resistência cinco vezes maior que a da argamassa C,
observa-se que os valores de resistências dos prismas moldados com a
argamassa A não aumentaram proporcionalmente seus valores de
resistência quando comparados com os prismas moldados com a
argamassa C.
6.1.1.2 Análise da capacidade de carga dos prismas grauteados
Nesta análise, com 95% de confiança, somente os prismas RG15CG1 (moldados com bloco de 15 MPa e argamassa do tipo C), prismas
RG12-BG1 (moldados com bloco de 12 MPa e argamassa do tipo B),
prismas RG6-CG1 (moldados com bloco de 6 MPa e argamassa do tipo
C) e prismas RG6-CG2 (moldados com bloco de 6 MPa e argamassa do
tipo C), preenchidos com os grautes G1 (maior resistência à
compressão) ou G2 (resistência à compressão intermediária),
apresentam aumento significativo em suas capacidades de carga, ou
seja, em suas cargas de ruptura. Este aumento, em média, observa-se
para os prismas grauteados que apresentaram Efeito relativo maior do
que 29,3%. Constata-se que o enrijecimento das argamassas e dos
grautes não proporcionam aumento significativo nas cargas de ruptura
dos prismas, exceto para as séries RG15-CG1, RG12-BG1, RG6-CG1 e
RG6-CG2, por serem moldados com as argamassas de menor rigidez,
neste caso a argamassa B (traço 1:1/2:4,5) de resistência à compressão
intermediária e argamassa C (traço 1:1:6), de menor resistência à
compressão.
245
6.1.2
Etapas com Argamassa Mista e Industrializada
6.1.2.1 Influência dos componentes na resistência dos prismas
Para todas as séries de prismas vazios das Etapas com Argamassa
Mista e Industrializada, a resistência média à compressão da argamassa,
do bloco e a interação entre estes dois fatores, influenciaram
significativamente na resistência média à compressão dos prismas
vazios, na área líquida. Este comportamento observa-se também para os
prismas preenchidos, exceto a interação entre a argamassa e bloco, que
para os prismas preenchidos com argamassa mista não influencia
significativamente na resistência dos prismas. Para os prismas
preenchidos, em ambas as etapas, o fator com maior influência na
resistência à compressão dos prismas foi o bloco. Entretanto, para os
prismas vazios da Etapa com Argamassa Mista, a argamassa foi o fator
de maior influência e para a Etapa com Argamassa Industrializada, o
bloco.
Constatou-se que a resistência da argamassa influencia
significativamente na resistência dos prismas, proporcionando o
aumento ou não de sua capacidade de carga, de acordo com a
combinação de materiais utilizada.
Com o aumento da resistência da argamassa, para os prismas da
Etapa com Argamassa Mista, na área líquida, foi observado que:
- para os prismas vazios moldados com os blocos B6, com o
aumento da resistência da argamassa, aumentam-se significativamente
as resistências dos prismas. Os prismas vazios moldados com os blocos
de 12 e 15 MPa e argamassas das classes C e B, não apresentam
diferença significativa entre suas resistências à compressão, sendo que o
aumento significativo nos valores de resistência dos prismas ocorre
quando estes são assentados com a argamassa A, de maior resistência.
Neste caso, para os prismas moldados com os blocos de 12 e 15 MPa,
inicialmente indica-se para assentamento apenas a utilização das
argamassas do tipo C (traço 1:1:6) e tipo A (traço 1:1/4;3), tendo em
vista que não há diferença entre as resistências dos prismas moldados
com as argamassas do tipo B (traço 1:1/2:4,5) e tipo C.
- Para os prismas preenchidos e moldados om o bloco de 6 MPa,
o aumento da resistência da argamassa de assentamento e
preenchimento não gera aumento significativo na resistência dos
prismas, sendo aqui indicada apenas a moldagem dos prismas quando
assentados e preenchidos com a argamassa C, traço com menor
percentual de cimento em sua composição. Para os prismas moldados
246
com os blocos de 12 e 15 MPa, os prismas assentados e preenchidos
com as argamassas A e B, não apresentam diferença significativa entre
seus valores de resistência à compressão. Entretanto, para ambos os
blocos, os prismas assentados e preenchidos com a argamassa C
apresentam valor de resistência significativamente menor. Sendo assim,
indica-se para estes prismas somente a utilização das argamassas C ou
B.
Evidencia-se para esta etapa que a utilização da argamassa do
tipo C (traço 1:1:6), para o assentamento e preenchimento dos prismas,
tecnicamente, se demonstra como a opção mais indicada, por
apresentarem os melhores resultados de resistência média à compressão
e eficiência para os prismas.
Para a Etapa com Argamassa Industrializada, o aumento da
resistência da argamassa não proporciona aumento significativo nas
resistências à compressão dos prismas, na área líquida, para os prismas
vazios moldados com os blocos de 6 MPa com as argamassas das
classes 5 (argamassa de assentamento estrutural de 5 MPa) e M
(argamassa multiplouso). Entretanto, para os prismas vazios moldados
com a argamassa da classe 10 (argamassa de assentamento estrutural de
10 MPa), constata-se o aumento significativo nos valores de resistência
quando comparados com estas duas séries de prismas vazios. O mesmo
comportamento observa-se para os prismas vazios moldados com o
bloco de 12 MPa.
Para os prismas vazios moldados com o bloco de 15 MPa o
comportamento foi outro. O aumento da resistência da argamassa das
classes 5 para 10, não representou aumento significativo na resistência
dos prismas vazios. E para os prismas moldados com a argamassa classe
M, os resultados de resistência obtidos foram significativamente
menores que os valores de resistência das outras duas séries de prismas.
Para os prismas preenchidos com a argamassa industrializada,
somente as séries moldados com os blocos de 6 MPa apresentam
aumento significativo na resistência à compressão com o aumento da
resistência das argamassas, com a utilização das classes de argamassa 5
à 10. O prisma preenchido com a argamassa M, em função da
variabilidade de seus valores de resistência, não apresenta diferença
significativa com os valores de resistências obtidas para as outras duas
séries de prismas moldadas com o mesmo bloco.
Para os prismas preenchidos e moldados com os blocos de 12 e
15 MPa, não ocorre aumento significativo em suas resistências à
compressão com o aumento da resistência das argamassas. Entretanto,
as séries de prismas moldados com estas duas classes de blocos e
247
preenchidos com a argamassa da classe M apresentam os menores
resultados de resistência à compressão, em relação às séries moldadas
com classes 5 e 10.
Assim, nesta etapa, observou-se que a utilização das argamassas
das classes 5 e 10 para o assentamento e preenchimento dos prismas,
aparece como a opção mais indicada, por apresentarem os melhores
resultados de resistência média à compressão e eficiência. Este
comportamento era esperado, pois estas argamassas foram
desenvolvidas para o assentamento de blocos de alvenaria estrutural.
Entretanto, para ambas as Etapas com Argamassa Industrializada
e Mista, quando ocorre aumento na resistência dos prismas este não é
proporcional ao aumento da resistência das argamassas, o que neste
aspecto pode representar um procedimento antieconômico.
6.1.2.2 Aumento efetivo da capacidade de carga dos prismas das
Etapas com argamassa mista e industrializada
De acordo com os resultados obtidos para os prismas da Etapa
com Argamassa Mista, somente os prismas preenchidos moldados com
blocos de 15 MPa e argamassa do tipo B (prismas MG15-B), prismas
preenchidos moldadas com blocos de 6 MPa, assentados e preenchidos
com as argamassas mistas B (traço 1:1/2:4,5) e C (traço 1:1:6),
respectivamente, prismas MG6-B e MG6-C , apresentam aumento
significativo em suas capacidades de carga. Este aumento nos valores da
carga de ruptura observa-se para os prismas preenchidos que apresentam
efeito relativo maior do que 22,2%.
Entretanto, para a Etapa com Argamassa Industrializada, as séries
de prismas moldadas com os blocos de 6 e 12 MPa, preenchidos com as
três classes de argamassas, apresentam aumento significativo em sua
capacidade de carga. Este aumento nos valores da carga de ruptura
observa-se para os prismas preenchidos que apresentam efeito relativo
maior que 16,4%.
Para estas séries de prismas, a diminuição da rigidez da
argamassa de preenchimento proporciona o aumento em sua capacidade
de carga. Nestes prismas, a diminuição da parcela de carga absorvida
pelo preenchimento, em virtude de seu baixo valor de módulo de
elasticidade, contribui para o aumento significativo da carga de ruptura
dos prismas. Neste caso, a baixa rigidez dos preenchimentos (baixos
valores de resistência à compressão e módulo de elasticidade)
provocaria o aparecimento de baixas tensões sobre as paredes internas
dos blocos, além de absorver parte da carga total do prisma. Ainda, com
248
o aumento da parcela de carga sob a alvenaria (bloco-argamassa),
aumentam-se as tensões de compressão sobre o bloco, aumentando sua
capacidade de resistir às tensões de tração impostas pela deformação do
preenchimento.
Isto se evidencia pelo fato que quando comparados os prismas
moldados com os blocos de 6 MPa, assentados e preenchidos com as
argamassas do tipo A (traço 1:1/4:3), do tipo B (traço 1:1/2:4,5) e do
tipo C (traço 1:1:6), os prismas assentados e preenchidos com a
argamassa do tipo A, com os maiores valores de resistência à
compressão, módulo de elasticidade e coeficiente de Poisson, não
apresentam aumento significativo em sua carga de ruptura quando
preenchido pela argamassa.
Ainda, para os prismas moldados com blocos de 6 MPa,
assentados e preenchidos com as argamassa dos tipos B e C, por não
apresentarem diferença significativa entre seus valores de resistências à
compressão, na área líquida, os prismas moldados com a argamassa do
tipo C (traço 1:1:6) demonstra-se o mais indicado para a utilização da
técnica de preenchimento com a argamassa de assentamento, pois
apresenta o maior efeito relativo encontrado para os prismas
preenchidos com argamassa mista, no valor de 60,0%.
Para os prismas preenchidos com argamassa industrializada,
analisando também suas resistências nas áreas liquidas os melhores
resultados obtidos foram para os prismas preenchidos IG6-10 (moldados
com blocos de 6 MPa, assentados e preenchidos com argamassa de
assentamento estrutural de 10 MPa) e prismas preenchidos IG12-5
(moldados com bloco de 12 MPa, assentados e preenchidos com
argamassa de assentamento estrutural de 5 MPa), que apresentam os
maiores efeitos relativos, respectivamente, nos valores de 40,5% e
47,7%.
6.2
MODO DE RUPTURA DOS PRISMAS
Para os prismas vazios da Etapa Argamassa Mista e
Industrializada, a forma de ruptura dos prismas ocorreu de forma frágil,
sem características explosivas, para todos os prismas assentados com as
seis classes de argamassas. Basicamente, a ruptura ocorreu de forma
lenta, iniciando-se com a formação de fissuras o e esmagamento da
argamassa em conjunto com a formação de fissuras e trincas verticais
nos blocos, entre 60% e 70% da carga de ruptura. Na sequência, ocorreu
a ruptura localizada dos blocos próxima à região da interface bloco-
249
argamassa, geradas pela deformação excessiva junta, levando assim o
conjunto ao colapso.
Para a Etapa Referência, os prismas grauteados moldados com os
blocos B6, grautes G2, G3 (de resistência intermediária e menor
resistência à compressão) e assentados com argamassa do tipo C (traço
1:1:6), de menor resistência à compressão, apresentaram ruptura frágil e
lenta, sem características explosivas. Para os prismas da série RG6-CG1,
moldados com blocos de 6 MPa, argamassa do tipo C e o graute G1, de
maior resitencia à compressão, a ruptura ocorreu de forma frágil e
rápida, com características explosivas, provocando o fendilhamento
lateral das paredes dos blocos, evidenciando o aumento na tração das
paredes como consequência da expansão do grautes.
Para as três séries de prismas moldados com os blocos de 12
MPa, o comportamento foi similar ao observado para os prismas
moldados com o bloco de 6 MPa.
Os prismas moldados com os blocos de 15 MPa, assentados com
a argamassa C (de menor resistência) e as três classes de grautes,
apresentaram ruptura frágil e lenta, sem características explosivas.
Entretanto, para as séries de prismas moldados com os blocos de 15
MPa, assentadas com a argamassa A (de maior resistência com traço
1:1/4:3) e preenchidos com os grautes G1 e G2, respectivamente, de
maior resistência e resistência à compressão intermediária (Figura 4.38),
a ruptura ocorreu de forma frágil e rápida, com características
explosivas, com o fendilhamento lateral das paredes dos blocos,
indicando aumento nas tensões contra as paredes dos blocos e nas
regiões próximas à interface bloco-argamassa. Para a série de prismas
RG15-AG3, moldada com blocos de 15 MPa, argamassa do tipo A e
graute G3, de menor resistência à compressão, a ruptura ocorreu de
forma lenta, porém com a formação acentuada de trincas verticais ao
longo dos blocos.
Nesta análise, constata-se que o enrijecimento da argamassa de
assentamento e do graute, além de não aumentarem proporcionalmente
os valores de resistências dos prismas, provocam rupturas sem
características dúcteis, comportamento este não indicado para a
alvenaria estrutural. Isto é evidenciado quando comparadas as formas de
rupturas das séries de prismas RG15-AG1 e RG15-CG1.
Nas Etapas Argamassa Mista e Industrializada, todos os prismas
preenchidos com argamassa apresentaram ruptura de forma frágil e
lenta, sem características explosivas. Para estes prismas a ruptura
ocorreu de forma lenta com a formação de fissuras e o esmagamento da
argamassa, formação de trincas verticais e o fendilhamento das paredes
250
dos blocos, evidenciando também aumento nas tensões de tração nas
paredes dos blocos e nas regiões próximas à interface bloco-argamassa,
em consequência da expansão do preenchimento confinado. Entretanto,
este comportamento acentuou-se com os prismas assentados e
preenchidos com as argamassas de maior rigidez, neste caso as
argamassas das classes A e 10. Isto pode ser justificado com o aumento
do módulo de elasticidade do grautes, e consequentemente com o
aumento da carga por ele absorvida, aumentando-se assim o nível de
tensão contra as paredes dos blocos.
Ainda, para estas duas séries de prismas, observou uma formação
acentuada de fissuras e diminuição no esmagamento da junta, indicando
aumento de tensões de trações sobre esta região. Observa-se que o
enrijecimento da argamassa de assentamento e preenchimento, além de
não aumentar proporcionalmente os valores de resistências dos prismas,
podem aumentar os níveis de tensões de tração próximos a região da
junta de argamassa.
Diante do exposto, o aumento na resistência à compressão dos
prismas com a utilização da argamassa como preenchimento estrutural
evidencia a viabilidade de utilização desta técnica, desde que a escolha
entre os componentes dos prismas seja adequada.
6.3
SIMULAÇÃO DOS PRISMAS
A realização desta análise teve por objetivo compreender a
distribuição das tensões desenvolvidas nos prismas e a influência da
argamassa utilizada como preenchimento no desempenho mecânico dos
modelos de prismas avaliados. Devida as limitações do modelo adotado,
em função da ausência dos elementos de interface e a necessidade de
ajustes nas propriedades não lineares dos materiais, os resultados
obtidos com a simulação pouco contribuíram. Esperava-se com o
aumento da resistência das argamassas, que as tensões verticais de
compressão nos preenchimentos, obtidas com a simulação,
apresentassem aumento proporcional ou próximo dos valores
observados para as parcelas de cargas absorvidas pelos preenchimentos
experimentalmente. Entretanto, para os resultados da simulação, esta
tendência não foi observada com o aumento da rigidez do
preenchimento. Isto se deve ao fato que esta estimativa de carga foi
realizada com os materiais sob regime linear, diferente do regime de
análise adotado na simulação. Onde o caráter não linear dos materiais do
prisma, evidenciado quando estes são analisados próximos à ruptura,
torna o entendimento deste fenômeno ainda mais complexo do que
251
apenas a correlação entre
propriedades elásticas definidas em
laboratório para os componentes do prisma.
Assim, conforme a análise, para os prismas MG6-C e MG6-B,
moldados com as argamassas de menor resistência e o bloco de 6 MPa,
com o aumento do carregamento ocorre o aumento nas tensões de tração
impostas pelo preenchimento contra as paredes dos blocos, aumento este
evidenciado com os dados experimentais.
Entretanto, o comportamento é diferente para os prismas MG6-A,
moldado com a argamassa mais resistente. Nesta série de prismas,
preenchida com a argamassa A, observa-se o aumento nos valores de
tração na região da junta de argamassa, com o aumento do
carregamento. Isto pode evidenciar que para essa série de prisma, a
ruptura se deu principalmente pela expansão lateral da argamassa
(tração) do que tração das paredes dos blocos em consequência da
expansão do preenchimento. O que foi evidenciado com os ensaios de
ruptura dos prismas, onde o esmagamento da junta de argamassa dos
prismas MG6-A foi menor do que o observado para os prismas MG6-B
e MG6-C, evidenciando o aumento nas tensões de tração sob a junta de
argamassa para os prismas preenchidos com a argamassa A, de maior de
resistência.
Observa-se também que os níveis de tração desenvolvidos no
preenchimento para os prismas MG6-A, foram menores dos que
encontrado para as outras duas séries de prismas. Isto pode ser explicado
pelo fato que o módulo de elasticidade da argamassa A ser maior, logo
se desenvolveria tensões de tração menores para esse material sobre
níveis de carregamento similares.
De uma forma geral, a técnica investigada neste trabalho é viável
para prismas moldados com blocos de 6 MPa, quando preenchidos com
argamassas com baixos valores de resistência à compressão e módulo de
elasticidade. Mais especificamente para argamassas com resistência
média à compressão entre 11,5 e 35,2% da resistência média à
compressão (fb) dos blocos de 6 MPa, na área líquida. Em alguns casos,
para os prismas com argamassas dentro desta faixa de resistência, a
utilização da argamassa como preenchimento proporciona forças de
ruptura dos prismas (ou capacidade de carga) com valores superiores aos
encontrados para os prismas preenchidos com os grautes com resistência
de 15 e 25 MPa. Tornando, para estes casos, a utilização da argamassa
como preenchimento mais eficiente que a utilização destes dois tipos de
grautes. O que se demonstra, para estas combinações de argamassabloco, ser mais viável a utilização da argamassa como preenchimento
em substituição ao graute.
252
6.4
RECOMENDAÇÕES PARA TRABALHOS FUTUROS
A seguir são listadas as principais recomendações para os
trabalhos futuros com o objetivo de complementar a compreensão do
comportamento de prismas grauteados e preenchidos com a argamassa
de assentamento:
- Realizar a mesma análise desenvolvida neste trabalho,
entretanto utilizando paredes com as mesmas combinações de blocos e
argamassas.
- Análise da influência do tempo entre o assentamento e
preenchimento com argamassa, na resistência dos prismas.
- Análise da influência do tempo e tipo de equipamento utilizado
no adensamento do preenchimento na resistência dos prismas.
- Estimar fator de eficiência prisma-graute, buscando identificar a
contribuição do graute na resistência dos prismas e paredes.
- Realizar estudo comparativo de custos, para a utilização de
grautes e/ou argamassa como preenchimento.
- Estudos para a verificação da influência da retração das
argamassas, quando utilizadas como preenchimento, na resistência dos
prismas.
- Estudo de metodologias mais adequadas para a obtenção das
propriedades elásticas dos prismas, em função dos materiais que o
constituem.
- Estudos triaxiais em argamassas, para avaliar sua resistência à
compressão, módulo de elasticidade e coeficiente de Poisson confinado
e obtenção de suas propriedades não lineares, utilizadas para o ajuste de
modelos numéricos. O mesmo tipo de ensaio recomenda-se para o
material do bloco, visando fornecer aos modelos numéricos dados
suficientes para a simulação em regime não linear.
- Utilização de modelos numéricos mais sofisticados, que
proporcionem um maior entendimento do comportamento da alvenaria
quando preenchida com argamassa de assentamento.
253
REFERÊNCIAS
ALY, V. L. C. Determinação da capacidade resistente do elemento
parede de alvenaria armada de blocos de concreto, submetido à
esforços de compressão. São Paulo, 1991. 103p. Dissertação
(Mestrado) - Escola Politécnica de São Paulo, Universidade de São
Paulo.
AMERICAN CONCRETE INSTITUTE. ACI 530-92 / ASCE 5-92 /
TMS 402-92. Building code requirements for masonry. Detroit,
Michigan. 1995.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM C
144-84. Aggregate for masonry mortar. American Standard Test
Method. Philadelphia, PA. 1987.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM C
270-86b. Standard Specification for mortar for unit masonry. American
Standard Test Method. Philadelphia, PA. 1987.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM C
476-83. Grout for Masonry. American Standard Test Method.
Philadelphia, PA. 1987.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM C
1006. Standard test method for splitting tensile of masonry units.
American Standard Test Method. Philadelphia, PA. 1984.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM C
1019 – Sampling and testing grout. Philadelphia, PA. 1984.
AMERICAN SOCIETY FOR TESTING AND MATERIALS. ASTM E
447-84. Compressive strenght of prisms. American Standard Test
Method. Philadelphia, 1987.
ANDRADE A. A. Comportamento estrutural de paredes de
alvenaria. São Paulo, 1998. Dissertação (Mestrado) - Escola Politécnica
de São Paulo, Universidade de São Paulo.
254
ARANTES, C. A. Influência do graute na alvenaria estrutural
cerâmica. 2003. 175p.. Dissertação (Mestrado em Engenharia Civil) –
Pós-Graduação em Engenharia Civil, UFSM, Santa Maria-RS.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 5738:
Concreto – Procedimento para moldagem e cura de corpos-de-prova.
Rio de Janeiro. 2003. 6p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 5739:
Concreto – Ensaio de compressão de corpos-de-prova cilíndricos. Rio de
Janeiro. 2007. 9p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118:
Projeto de estruturas de concreto – Procedimento. Rio de Janeiro. 2007.
221p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6467:
Agregados - Determinação do inchamento de agregado miúdo - Método
de ensaio. Rio de Janeiro. 2006. 5p
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7175:
Cal hidratada para argamassas – Requisitos. Rio de Janeiro. 2003. 4p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7211:
Agregados para concreto – Especificação. Rio de Janeiro. 2009. 9p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 7215:
Cimento Portland – Determinação da resistência à compressão. Rio de
Janeiro. 1996. 8p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8215:
Prismas de bloco de concreto para alvenaria estrutural – Preparo e
ensaio à compressão. Rio de Janeiro. 1983. 2p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8522:
Concreto – Determinação dos módulos estáticos de elasticidade e de
deformação e da curva tensão-deformação. Rio de Janeiro. 2008. 9p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 8798:
Execução e controle de obras em alvenaria estrutural de blocos vazados
de concreto. Rio de Janeiro. 1985. 15p.
255
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
10837: Cálculo de alvenaria estrutural de blocos vazados de concreto.
Rio de Janeiro. 1989. 20p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
11578: Cimento Portland composto – Especificação. Rio de Janeiro.
1991. 5p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
13276: Argamassa para assentamento e revestimento de paredes e tetos
– Preparo da mistura e determinação do índice de consistência. Rio de
Janeiro. 2002. 3p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
13277: Argamassa para assentamento e revestimento de paredes e tetos
– Determinação da retenção de água. Rio de Janeiro. 2005. 2p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
13278: Argamassa para assentamento e revestimento de paredes e tetos
– Determinação da densidade de massa e do teor de ar incorporado. Rio
de Janeiro. 2005. 2p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
13279: Argamassa para assentamento e revestimento de paredes e tetos
– Determinação da resistência à tração na flexão e à compressão. Rio de
Janeiro. 2005. 9p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
13281: Argamassa para assentamento e revestimento de paredes e tetos
– Requisitos. Rio de Janeiro. 2001. 3p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
15270: Componentes Cerâmicos – parte 1: Blocos cerâmicos para
alvenaria de vedação - Terminologia e requisitos. Rio de Janeiro. 2005.
11p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
15270: Componentes Cerâmicos – parte 2: Blocos cerâmicos para
alvenaria estrutural - Terminologia e requisitos. Rio de Janeiro. 2005.
11p.
256
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
15270: Componentes Cerâmicos – parte 3: Blocos cerâmicos para
alvenaria estrutural e de vedação – Métodos de ensaio. Rio de Janeiro.
2005. 27p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
15812-1: Alvenaria estrutural – Blocos cerâmicos. Parte 1: Projetos. Rio
de Janeiro. 2010. 41p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR
15812-2: Alvenaria estrutural – Blocos cerâmicos. Parte 2: Execução e
controle de obras. Rio de Janeiro. 2010. 28p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
23: Cimento Portland e outros materiais em pó – Determinação da
massa específica. Rio de Janeiro. 2000. 5p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
45: Agregados - Determinação da massa unitária e do volume de vazios.
Rio de Janeiro. 2006. 8p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
46: Agregados – Determinação do material fino que passa através da
peneira 75 µm, por lavagem. Rio de Janeiro. 2003. 6p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
52: Agregado miúdo – Determinação de massa especifica e massa
especifica aparente. Rio de Janeiro. 2003. 6p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
53: Agregado graúdo – Determinação de massa especifica, massa
especifica aparente e absorção de água. Rio de Janeiro. 2003. 8p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
67: Concreto – Determinação da consistência pelo abatimento de cone.
Rio de Janeiro. 1998. 8p.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR NM
248: Agregados – Determinação da composição granulométrica. Rio de
Janeiro. 2003. 6p.
257
ATKINSON, R. H., e NOLAN, J. L. Investigation into the failure
theory for brick masonry in compression. In: 3rd Canadian Masonry
Symposium, 1985, Edmonton, Canada, Proceedings. 1985, p. 5.1-5.17.
BIGGS, D. T. Grouting Masonry Using Portland Cement-Lime
Mortars. International Building Lime Symposium. March 9 -11, 2005.
Florida, EUA.
BRITISH STANDARD INSTITUTION. BS 1200. Specification for
buildings sand from natural sources. British Standard Institution,
Londres, 1976.
BRITISH STANDARD INSTITUTION. BS 5628-1. Code of practice
for use of masonry - Part 1: Structural use of unreinforced masonry.
British Standard Institution, Londres, 1992.
BRITISH STANDARD INSTITUTION. BS 5628-2. Code of practice
for use of masonry – Part 2: Structural use of unreinforced and
prestressed masonry. British Standard Institution, Londres, 1995.
BRITISH STANDARD INSTITUTION. BS 5628-3. Code of practice
for use of masonry – Part 3: Materials and components, design and
workmanship. British Standard Institution, Londres, 1985.
CALÇADA, L. M. L. Avaliação do comportamento de prismas
grauteados e não grauteados de blocos de concreto. 1998. 167p.
Dissertação (Mestrado em Engenharia Civil) - Pós-Graduação em
Engenharia Civil, UFSC, Florianópolis.
CAMACHO, J. S.; RODRIGUES, R. O. Utilização do graute na
alvenaria estrutural. Anais do 41º Congresso Brasileiro de Concreto,
Salvador, 1999. Artigo técnico. Salvador, BA. 1999. p.142.
CAMARINI, Gladis; ISHIKAWA, Paulo Hidemitsu. Propriedades de
argamassas de assentamento produzidas com areia artificial para
alvenaria estrutural. 10th Encontro nacional de Tecnologia do
Ambiente Construído. São Paulo. 2004.
CARASEK, H.; CASCUDO, O.; SCARTEZINI, L. M.. Importância
dos materiais na aderência dos revestimentos de argamassa. In: 4º
Simpósio Brasileiro de Tecnologia das Argamassas. Brasília, Brasília:
PECC/ANTAC, 2001. p. 43-67.
258
CARVALHO, J. M. Desempenho estrutural de prismas de blocos
cerâmicos com diferentes formas e dimensões. Dissertação (Mestrado
em Engenharia Civil). Universidade Federal de Santa Catarina,
Florianópolis, SC, 2003.
CARVALHO, J. M.; CESAR, C. G.; ROMAN, H. R. Influência da
geometria de blocos cerâmicos no desempenho estrutural de
prismas moldados com diferentes traços de argamassa e espessuras
de juntas. XI Encontro Nacional de Tecnologia do Ambiente
Construído. Florianópolis, SC. 2006.
CASCUDO, O. O controle da corrosão em armaduras em concreto:
inspeção e técnicas eletroquímicas. Goiânia. Editora UFG; Co-edição
São Paulo: Pini, 1997.
CEB-FIP. (1990). CEB-FIP Model Code 1990, Comité EuroInternational du Béton. ACI. (1999). American concrete institute.
Building code requirements for structural concrete with
commentary. ACI-318-99, Detroid.
CESAR, C. G. Desempenho Estrutural de Painéis Pré-Fabricados
Com Blocos Cerâmicos. 2007. Tese (Doutorado em Engenharia Civil)
– Programa de Pós-Graduação em Engenharia Civil, Universidade
Federal de Santa Catarina.
CHEEMA, T. S. e KLINGNER R. E. Compressive strength of
concrete masonry prism. American Concrete Institute Journal, 1986.
January/February, p. 88-97.
CHEN, W.; LIU, X. Limit Analysis in Soil Mechanics. AmsterdamOxford-New York: Elsevier Scientific Publishing Company, 1990.
CINCOTTO, M. A.; SILVA, M. A. C.; CASCUDO, H. C. Argamassa
de revestimento: Características, propriedades e método de ensaio.
São Paulo: Boletim 68, IPT - Instituto de Pesquisas Tecnológicas S/A,
1995. 118 p.
COLVILLE, J. Compressive strenght of grouted concrete masonry.
In: 9th International Brick and Block Masonry Conference, Berlin,
Alemanha, 1991. Proceedings. v.1, p. 149-156.
259
COLVILLE. J. e WOLDE-TINSAE, A. M.. Compressive strength of
hollow concrete masonry. 5th North American Masonry Conference.
1990. June. University of Illinois at Urban-Champaign. p. 663 a 672.
CUNHA, E. H. Análise experimental do comportamento de prismas
grauteados em alvenaria estrutural. Goiânia, 2001. 149p. Dissertação
(Mestrado em Engenharia Civil) – Universidade Federal de Goiás.
DHANASEKAR, M. e KUMAR, M. Parametric studies on the
strength and stiffness of reinforced clay block masonry. In: 10th
Internationa Brick/Block Masonry Conference. Alberta, Canada, 1994.
Proceeding. V1, p 97-106.
DÍAZ, J. J.; NIETO, P.J; RABANAL, F.P; MARTÍNEZ-LUENGAS.
Design and shape optimization of a new type of hollow concrete
masonry block using the finite element method. Engineering
Structures 33, 2011.
DRYSDALE, R.G., HAMID, A.A.; BAKER, L.R. Masonry
structures: behavior and design. Englewood Cliffs, New Jersey.
Prentice-Hall. 1994.
EUROPEAN COMMITEE FOR STANDARDIZATION. Eurocode 6 –
Design of masonry structures - Part 1-1: General rules for
reinforced and unreiforced masonry structures. EN 1996-1-1. 2005.
EUROPEAN COMMITEE FOR STANDARDIZATION. Methods of
test for mortar for masonry – Part 7: Determination of air content
of fresh mortar. EN 1015-7:1999.
FAHMY, E. H.; GHONEIM, T. G. M. Behaviour of concrete block
masonry prisms under axial compression. Canadian Journal of Civil
Engineering. Vol. 22, nº 5. 1995.
FORREST, J. C. M. WILLBOURNE, J. KIPPS, R. M. Some typical
aspects of design and construction (Being as every day story of
masonry folk!) In: Practical Design of Masonry Structures,
Proceedings, p. 71-100. London, 1986.
FRANCO, L. S. Desempenho estrutural do elemento parede de
alvenaria empregado na alvenaria estrutural não armada, quando
submetido a esforços de compressão. São Paulo, 1987. Dissertação
(Mestrado) – Escola Politécnica, Universidade de São Paulo.
260
FRANCO, L. S. Parâmetros utilizados nos Projetos de Alvenaria
Estrutural. Textos Técnicos, Escola Politécnica da USP, São Paulo.
1993.
GALLEGOS, H. Albañileria Estructural. Pontificia Universidad
Católica Del Perú. Lima, Perú. 1989. 367p.
GANESAN, T. P.; RAMAMURTHY, K. Efficient Hollow Block
Geometries for Masonry Under Eccentric Compression. Proceedings
of the 4 th International Seminar on Structural Masonry for Developing
Countries,p.108-115, Madras, India. 1992.
GANESAN T. P. et al. Structurally efficient hollow concrete blocks
in load bearing masonry. Proc. 8 th IBMAC. Elsevier, London, 1988.
GARCIA, P. D. Contribuições ao Estudo da Resistência à
Compressão de Paredes de Alvenaria de Blocos Cerâmicos. São
Carlos, 2000. 255p. Dissertação (Mestrado) em Engenharia de
Estruturas – Escola de Engenharia de São Carlos da Universidade de
São Paulo.
GOMES, I. R. Simulação Numérica do Ensaio de Compressão de
Prismas de Alvenaria pelo Método dos Elementos Finitos com
Comportamento de Interface. 2001. 160p. Tese (Doutorado em
Engenharia de Produção) – Universidade Federal de Santa Catarina.
Florianópolis, SC.
GOMES, N.S. A resistência das paredes de alvenaria. 1983. 190 p.
Dissertação (Mestrado em Engenharia Civil) – Escola Politécnica da
Universidade de São Paulo, São Paulo.
GONÇALVES JR., L.A. Avaliação de Incertezas em Modelo de Dano
com Aplicação a Prismas de Alvenaria Sob Compressão. Dissertação
(Mestrado em Engenharia de Estruturas). Escola de Engenharia de São
Carlos, Universidade de São Paulo. São Carlos, SP, 2008.
GROHMANN, L. Z. Análise do Comportamento de Prismas
Grauteados de Alvenaria Estrutural Cerâmica. 2006. 160p.
Dissertação (Mestrado em Engenharia Civil) - Universidade Federal de
Santa Maria. Santa Maria, RS.
261
GUIMARÃES, J. E. P. A Cal. Fundamentos e aplicações na
engenharia civil. São Paulo. Editora Pini, 2001. 341 p.
HAMID, A. A.; DRYSDALE, R. G. Suggested failure criteria for
grouted masonry under axial compressive. American Concrete
Institute Journal. 1979. p. 1047-1061.
HILSDORF, H.R. Investigation into the failure mechanisms of brick
masonry loaded in axial compression. Designing, Engineering and
Construction with masonry product. Houston, Texas, Gulf Publishing
Co. 1969. p. 34-41.
INTERNATIONAL UNION OF TESTING AND RESERCH
LABORATORIES FOR MATERIALS AND STRUCTURES –
RILEM. MR 3: The complex workability – consistence – plasticity.
France: E & FN Spon. RILEM, 1982.
ISHIKAWA, P. H. Desempenho de argamassa de assentamento de
bloco estrutural utilizando agregado miúdo de pedra britada. IV
Simpósio Brasileiro de Tecnologia das Argamassas. Brasília, DF. 2001.
JUSTE, A. E. Estudo da resistência e da deformabilidade da
alvenaria de blocos de concreto submetida a esforços de
compressão. 2001. 126 p. Dissertação (Mestrado). Escola de
Engenharia de São Carlos, Universidade de São Paulo, São Carlos.
KHALAF, F. M. Factors influencing compressive strength of
concrete masonry prisms. Magazine of Concrete Research. June, 1996,
v48, nº 175, p. 95-101.
KHALAF, F. M.; HENDRY, A. W. and FAIRBAIRN D. R. 1992. The
strength of blockwork prisms tested parallel to the bed face.
Masonry International- Journal of the British Masonry Society. Spring,
vol. 6, nº 1, 29-35.
KHALIFA, M. A. e MAGZOUB, A. E. Compressive strength of
masonry prisms. In: 12th Congress of the structures. EUA, 1994.
Proceeding. p 1100-1005.
LA ROVERE, H.; RODRIGUES, R. M. Análise do Comportamento
Mecânico de Prismas de Alvenaria de Blocos de Concreto Pelo
262
MEF. In: XXVIII Jornadas Sulamericanas de Engenharia Estrutural,
1997, São Carlos. Anais - Estruturas e Fundações, 1997. v.1. p. 179-188.
LEÃO, C. T. Resistência de prismas de blocos estruturais cerâmicos
submetidos a esforços de compressão e tração na flexão. 2008. 188 p.
Dissertação (Mestrado em Engenharia Civil) – Universidade Federal de
Santa Catarina. Florianópolis, SC.
LOURENÇO, P. B. Computacional strategies
structures. Netherlands, Delf University Press. 1996.
for
masonry
MANZANO, R. M.; ROMAN, H. R.; GÓMEZ, L. A. Análise do
comportamento de conexão vertical de painéis estruturais cerâmicos
pré-fabricados. Ambiente Construído, Porto Alegre, v. 13, n. 1, p. 3550, jan./mar. 2013.
MATA, R. C. 2006. 180p. Influência do padrão de argamassamento
na resistência à compressão de prismas e mini-paredes de alvenaria
estrutural de blocos de concreto. Dissertação (Mestrado em
Engenharia Civil) – Universidade Federal de Santa Catarina.
Florianópolis, SC.
MENDES, R. J. K. Resistência à compressão de alvenaria de blocos
cerâmicos estruturais. 1998. 185p. Dissertação (Mestrado em
Engenharia Civil) – Universidade Federal de Santa Catarina.
Florianópolis, SC.
McNARY, W. S.; ABRAMS, D. P. On the modulus of elasticity for
masonry. Structural Engineering Journal. 1985. n 4, v. 111, p. 857-870.
MOHAMAD, G. Comportamento mecânico na ruptura de prismas
de blocos de concreto. 1998. 180 p. Dissertação (Mestrado em
Engenharia Civil) – Universidade Federal de Santa Catarina.
Florianópolis, SC.
MOHAMAD, G. Mecanismo de ruptura da alvenaria de blocos de
concreto à compressão. 2007. 290 p. Tese (Doutorado em Engenharia
Civil) – Universidade do Minho. Portugal.
OLIVEIRA, F. L. Reabilitação de paredes de alvenaria pela
aplicação de revestimentos resistentes de argamassa armada. 2001.
263
Tese (Doutorado em Engenhaeia sw Estruturas). 203p. Escola de
Engenharia de São Carlos da Universidade de São Carlos, São Paulo.
OLIVEIRA, L. A. P. Estudo do desempenho dos grautes com adições
para o enchimento dos blocos de alvenaria estrutural. 1986. 100p.
Dissertação (Mestrado em Engenharia Civil). Escola Politécnica,
Universidade de São Paulo, São Paulo.
PAGE, A.W. A study of the relationship between unit, prism and
wall strenght for hollow masonry loaded in compression. In: 9th
International Brick/Block Masonry Conference, Berlin, Alemanha,
1991. Proceedings. v.1, p. 263-243.
PARSEKIAN, G. A.; FURLAN JUNIOR, S. Compatibilização de
Projetos de Alvenaria Estrutural. III Simpósio Brasileiro de Gestão e
Economia da Construção. São Carlos, SP. 2003.
PARSEKIAN, G. A.; HAMID, A. A.; DRYSDALE, R. G.
Comportamento e Dimensionamento de Alvenaria Estrutural. São
Carlos. Editora EdUFSCAR, 2012.
PAPADAKIS, V. G., VAYENAS, C. G., FARDIS, M. N. Physical and
chemical characteristics affecting the durability of concrete. ACI
Materials Journal. March-April. 1991.
PELETEIRO, S. C. (2002). Contribuições à modelagem numérica de
alvenaria estrutural. 2002. 143p. Tese (Doutorado em Engenharia de
Estruturas) – Escola de Engenharia de São Carlos, Universidade de São
Paulo. São Carlos, SP.
RAGO, F.; CINCOTTO, M. A. A reologia da pasta de cimento e a
influência da cal. In: 1º Simpósio Brasileiro de Tecnologia das
Argamassas. Goiânia: UFG/ANTAC, 1995, p. 25-32.
RAMALHO, M.; CORRÊA, M. R. S. Projeto de Edifícios de
alvenaria estrutural. ed:1. São Paulo. Editora PINI, 2003.
REIS, P. F. O. Análise Numérica da Influência dos Segmentos
Grauteados na Interação entre Paredes de Alvenaria Estrutural de
Blocos de Concreto. 2010. 169p. Dissertação (Mestrado em Geotecnia
264
e Construção Civil) – Escola de Engenharia da Universidade Federal de
Goiás. Goiânia, Goiás.
RILEM-FIP-CEB. Bond test for reinforcing steel – 2. Pull-Out test.
Matériaux et constructions, v.6, n° 32, p.102-105. 1973.
RILEM-CPC 18. Measurement of hardened concrete carbonation
depth. Materials and Structures, vol. 21 nº 126, p. 453-455. 1988
RIZZATTI, E. Influência da Geometria do Bloco Cerâmico no
Desempenho Mecânico da Alvenaria Estrutural sob Compressão.
2003. 176p. Tese (Doutorado em Engenharia Civil) - Universidade
Federal de Santa Catarina. Florianópolis, SC.
ROMAGNA, R. H. Resistência à compressão de prismas de blocos de
concreto grauteados e não grauteados. 2000. 195 p. Dissertação
(Mestrado em Engenharia Civil) – Universidade Federal de Santa
Catarina. Florianópolis, SC.
ROMAN, H. R. Argamassas de assentamento para alvenarias. In: III
Simpósio de Desempenho de Materiais e Componentes de Construção
Civil. Florianópolis: UFSC, 1991. p.111-116.
ROMAN, H. R.; MUTTI, C. N.; ARAÚJO, H. N. Construindo em
alvenaria estrutural. Florianópolis: EdUFSC, 1999. 83p.
SABBATINI, F. H. Agregados miúdos para argamassas de
assentamento. In: 1º Simpósio Nacional de Agregados. São Paulo:
Núcleo de Ligação Industrial – EPUSP,1986, p. 17-25.
SABBATINI, F. H. O processo construtivo de edifícios de alvenaria
estrutural sílico-calcária. 1984. 298p. Dissertação (Mestrado em
Engenharia Civil) – Escola Politécnica da Universidade de São Paulo,
São Paulo.
SÁNCHEZ, E. Histórico sobre pesquisas e elaboração de novas
normas no Brasil sobre alvenaria estrutural. Vol. 29. 5th International
Seminar on Structural Masonry for Developing Countries, 1994.
SANTOS, M. J. F. Análise da Resistência de Prismas e Pequenas
Paredes de Alvenaria Estrutural Cerâmica para Diferentes Tipos de
265
Argamassas. 2008. 136p. Dissertação (Mestrado em Engenharia Civil) Universidade Federal de Santa Maria. Santa Maria, RS.
SHRIVE , N. G. A fundamental approach to the fracture of
masonry. Third Canadian Masonry Symposium. University of Alberta,
Edmonyon. 1983.
SHRIVE, N. G. The failure mechanism of face Shell bedded (ungrouted
an unreinforced) masonry. International Journal of Masonry
Construction, v. 2, nº 3, p. 115-128, London, 1982.
SILVA JR, D. M. Análise Numérica do Comportamento Não-linear
de Prismas de Alvenaria Estrutural Submetidos a Ações Verticais
Utilizando o Elemento Finito Prismático Linear. 2007. 86p.
Dissertação de Mestrado - Universidade Estadual Paulista, SP.
SILVA JR, D. M.; RODRIGUES, M. O.;
Numérico da Influencia da Resistência à
comportamento Não-Linear de Prismas
2010. Revista Mecánica Computacional
Argentina.
CAMACHO, J. S. Estudo
compressão dos blocos no
de Alvenaria Estrutural.
Vol. XXIX. p.1049-1061.
SORIANO, H. L. Método dos elementos finitos em análise de
estruturas. São Paulo: EDUSP, 2003.
STEIL, R. O. Efeito da Geometria do Bloco de Concreto e do Tipo de
Argamassa no Desempenho à Compressão de Prismas de Alvenaria
Não Grauteados. 2003. 162p. Dissertação (Mestrado em Engenharia
Civil) - Universidade Federal de Santa Catarina. Florianópolis, SC.
YOSHIDA, A. T.; BARROS, M. M. S. B. Caracterização de
argamassas no estado fresco: peculiaridade na análise de
argamassas industrializadas. I Simpósio Brasileiro de Tecnologia das
Argamassas, Goiânia, Brasil, 1995, p. 53-62.