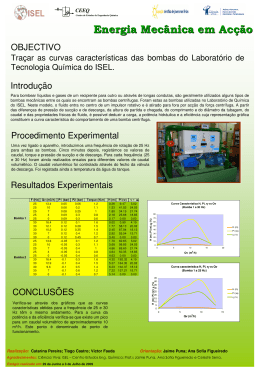
Mecânica dos Fluidos II
Aula VI – Análise Dimensional Aplicada às Turbomáquinas e Modelos Reduzidos
Prof. António Sarmento
Tel. 21 8417405
Email: [email protected]
Exercício
(Adaptado do Exame de 15/06/92)
Considere uma bomba com a qual se pretende transportar água de um rio (nível da superfície
livre z=0 m) para a albufeira de uma barragem sobreelevada (nível zB=100 m). As curvas
características da bomba a 975 rpm estão representadas abaixo, em que Q é o caudal, H a
altura de elevação e η o rendimento. As perdas de carga nas condutas de aspiração e de
compressão (expressas em metros de coluna de água) são, respectivamente, 1,0 Q2 e 15,0 Q2
(Q em m3/s).
a) Qual o caudal debitado e a potência absorvida quando a bomba roda a 975 rpm?
b) Qual o caudal, altura de elevação e potência consumida pela bomba quando roda 1050
rpm?
c) Pretende-se que, alterando a sua velocidade de rotação, a bomba trabalhe em
condições de rendimento máximo na instalação referida. Quais a rotação, o caudal e a
potência consumida nestas condições?
d) A velocidade de rotação calculada na alínea anterior coincide ou não com a velocidade
de rotação para a qual a bomba consome o mínimo de energia por unidade de massa
(ou de volume) de água transportada?
e) Admita que pretendia ter uma bomba geometricamente semelhante à indicada, mas
com outro diâmetro, de tal modo que, na mesma instalação, fornecesse um caudal de
0,6 m3/s em condições de rendimento máximo. Calcule a velocidade de rotação da
nova bomba e a relação entre os diâmetros dos rotores das duas bombas.
N=975 rpm
150
0,9
140
0,8
0,7
H (m)
130
0,6
120
0,5
110
0,4
100
0,3
90
0,2
0
0,5
1
Q (m3/s)
1,5
METODOLOGIA
• Para resolver a alínea a):
o Determine a curva da instalação aplicando a equação de Bernoulli entre as
duas superfícied livres e represente-a no gráfico que contém a curva da altura
de elevação da bomba H=F(Q) (ver Notas 1 e 2);
o Intersecte a curva da instalação com a curva de altura de elevação da bomba de
modo a obter o caudal e a altura de elevação com a bomba funciona na
instalação indicada à rotação de 975 rpm (ver Nota 3);
o Determine o rendimento da bomba e finalmente a potência consumida (ver
Nota 4).
• Para resolver a alínea b):
o Determine a curva de funcionamento da bomba à rotação de 1250 rpm. Para
tanto seleccione diversos pontos sobre a curva de altura de elevação – caudal a
975 rpm, calcule os coeficientes adimensionais de altura de elevação e caudal
desses pontos (ver Nota 5) e calcule os pontos com idênticos coeficientes
(pontos dinamicamente semelhantes) a 1250 rpm (ver Nota 6). Nesta operação
note que o diâmetro da bomba é o mesmo. Marque a curva de H=F(Q) no
gráfico e determine, como na alínea anterior, o caudal e a altura de elevação da
bomba.
o Para determinar o rendimento note que este parâmetro, sendo um grupo
adimensional, tem o mesmo valor para cada par de pontos dinamicamente
semelhantes encontrados. Assim, procure na curva de funcionamento a 975
rpm o ponto dinamicamente semelhante ao ponto de funcionamento
encontrado a 1250 rpm e leia o rendimento desse ponto.
o Está agora em condições de calcular a potência, como na alínea anterior.
• Para resolver a alínea c):
o Escreva a equação dos pontos dinamicamente semelhantes ao ponto de
rendimento máximo (ver Nota 7) e resolva-a conjuntamente com a curva da
instalação para obter a altura de elevação e o caudal correspondentes ao ponto
de rendimento máximo.
o Utilize a igualdade do coeficiente de caudal (ou o de altura de elevação) para
determinar a velocidade de rotação pretendida.
• Para responder à alínea d):
o Comece por verificar que H η é o parâmetro que representa a energia gasta
por unidade de massa peso de fluido transportado (e portanto proporcional ao
gasto de energia por unidade de massa ou de volume).
o Exprima H em função do caudal que passa através da curva da instalação e
conclua sabendo que o rendimento pouco varia na vizinhança do ponto de
rendimento máximo (pois a curva apresenta um máximo)
NOTAS
1. A altura de elevação H representa a energia útil por unidade de peso recebida pelo
fluido quando passa na bomba.
2. A curva da instalação dá o requisito de energia por unidade de peso de fluido H
necessária para fazer circular um caudal Q de fluido na instalação. A curva da
instalação depende apenas da instalação (perda de carga, desníveis ou diferenças de
pressão entre a entrada e saída), mas não da ou das bombas que lá forem instaladas.
A curva da instalação obtém-se aplicando a equação de Bernoulli.
3. O ponto de funcionamento da bomba está na intersecção da sua curva de
funcionamento (H=f(Q)) à velocidade a que a bomba roda, com a curva da
4.
5.
6.
7.
instalação. A primeira curva traduz a energia útil por unidade de peso de fluido
recebida pelo fluido quando um determinado caudal atravessa a bomba, enquanto a
da instalação traduz a absorção de energia pela instalação quando esse caudal
percorre a instalação.
A potência consumida ao veio de uma bomba é P = ρgQ H η .
Nas condições indicadas acima, só há um grupo adimensional independente se
considerarmos a mesma máquina ou máquinas de diferentes diâmetros, mas com a
mesma geometria (ditas da mesma família). Em geral trabalha-se com os grupos
adimensionais de caudal φ = Q ND 3 (normalmente tomado como o grupo
independente), da altura de elevação ψ = gH N 2 D 2 e rendimento η, mas também o
de potência, binário, etc.
Pontos com os mesmos coeficientes adimensionais são designados de pontos
dinamicamente semelhantes (já que todas as grandezas estão na mesma proporção).
Como os coeficientes adimensionais são idênticos em pontos dinamicamente
semelhantes, eles obedecem à equação H=kQ2 se forem obtidos por alteração da
rotação numa mesma turbomáquina, e à equação H=kQ2/3 se forem obtidas à mesma
rotação em máquinas de diferentes diâmetros.
Exercício 5 (Folhas)
A bomba cujas curvas características estão representadas na figura anexa, quando equipada
com um rotor de D=265 mm e montada na instalação de bombagem representada na figura
debita um caudal de 260 m3/h quando a válvula existente na conduta de compressão está
completamente aberta. Admita que pretende reduzir o caudal para 180 m3/h, colocando-se,
então, quatro possibilidades:
a) Fechar parcialmente uma válvula na conduta de compressão;
b) Ajustar a velocidade de rotação;
c) Tornear o rotor de modo a diminuir-lhe o diâmetro (use as curvas indicadas na figura
para diâmetros inferiores a 265 mm);
c) Equipar a bomba com uma derivação (by-pass), isto é uma conduta ligando a saída
da bomba à sua entrada. O caudal que circula na derivação é regulado (através duma
válvula existente na derivação) de modo a fazer circular na conduta principal o
caudal de 180 m3/h.
Admitindo que o escoamento na conduta é completamente turbulento, determine a potência
consumida quando cada um dos processos de regulação indicados é utilizado para conseguir o
caudal de 180 m3/h na conduta principal.
METODOLOGIA
•
•
Para a resposta da alínea a) note que a curva de funcionamento da bomba não se altera,
pois mantém-se a velocidade de rotação da bomba. Por outro lado, ao fechar-se a válvula
na conduta de compressão, altera-se a curva da instalação, visto ocorrerem mais perdas
de carga. Interprete este comentário para encontrar a resposta a esta alínea.
Para a resposta da alínea b):
o Calcule a curva da instalação aplicando a equação de Bernoulli e sabendo o
coeficiente de perda de carga (ver Nota 2) pode ser determinado sabendo que com a
válvula toda aberta (portanto com a mesma instalação) a bomba debita um caudal
de 260 m3/h e uma altura de elevação que pode determinar através da curva de
funcionamento da bomba.
o Determine a altura de elevação que a bomba deve debitar para garantir o caudal de
180 m3/h pretendidos;
o Procure o ponto dinamicamente semelhante a este na curva H=F(Q) conhecida –
esses pontos têm o mesmo rendimento, o que lhe permite calcular a potência (ver
Nota 7 do problema anterior);
•
Para responder à alínea c) siga o raciocínio da alínea anterior e adapte-o para a presente
situação, sabendo que as curvas da bomba são válidas, pois a velocidade de rotação da
bomba é a inicial, bem como a curva da instalação inicial, pois a válvula está
completamente aberta. Leia a Nota 1 para interpretar correctamente a informação contida
no gráfico com as curvas de funcionamento da bomba.
•
Para responder à alínea d):
o Note que a instalação principal continua a mesma (será que se mantém a curva da
instalação?). Conclua sobre a altura de elevação que a instalação requer (e que a
bomba tem que fornecer – ver Notas 3 e 4 do problema anterior). Sabendo que as
curvas da bomba se aplicam nesta situação, pois a bomba roda à rotação inicial,
qual o caudal que circula na bomba e o seu rendimento? Com estes parâmetros
pode calcular a potência fornecida.
•
NOTAS
1. O gráfico apresentado é típico do fornecido pela indústria. Contém as curvas de altura
de elevação H em função do caudal Q para uma determinada velocidade de rotação
(não indicada no caso presente). O gráfico apresenta várias curvas de H para diversos
diâmetros exteriores do rotor, sendo os vários diâmetros obtidos do rotor de 265 mm
por desbaste do rotor através de torneamento. No mesmo gráfico estão sobrepostas as
curvas de igual rendimento, η.
2. Admitindo que o escoamento é completamente turbulento na tubagem, a perda de
carga é proporcional ao quadrado do caudal, h p = k p Q 2 .
Exercício 4 (Folhas)
Dispõe-se de duas bombas A e B cujas curvas características H(Q) e η(Q) são conhecidas
para a velocidade de rotação NA=NB=1500 rpm (ver figura). As duas bombas devem ser
montadas em série de modo a fornecerem um caudal de 0,125 m3/s e uma altura de elevação
total HÁ+HB=49 m. Para isso há a possibilidade de alterar a velocidade de rotação
(inicialmente 1500 rpm) de uma das bombas (mas apenas de uma).
a) Em qual das duas bombas introduziria a variação de velocidade de rotação se, por
razões económicas, pretendesse minimizar a potência total absorvida pelas duas
bombas (admita ausência de cavitação)?
b) Calcule a velocidade de rotação dessa bomba e o respectivo rendimento.
0,9
35
0,8
HA
ηA
HB
0,7
0,6
H (m)
ηB
0,5
0,4
0,3
0,2
0,1
0
0
0
0,125
Q (m3/s)
0,25
METODOLOGIA
•
Para resolver a alínea a) note que:
1. De acordo com as curvas de funcionamento das bombas apresentadas, para o
caudal de 0,125 m3/s a altura de elevação total é inferior aos 49 m pretendidos.
Por este motivo é necessário aumentar a velocidade de rotação de uma das
bombas;
2. A bomba que deverá ver a sua velocidade de rotação aumentada é aquela que
vier a melhorar o seu rendimento em consequência do aumento de velocidade
de rotação.
3. De acordo com as curvas de funcionamento apresentadas, a bomba A está a
trabalhar com um caudal inferior ao de rendimento máximo e a bomba B com
um caudal superior.
4. Assim, a alínea fica resolvida quando esclarecer se o aumento da velocidade de
rotação faz aumentar ou diminuir o caudal para o qual a bomba funciona com
rendimento máximo (chamado caudal nominal ou de projecto) – ver Nota 2.
•
Para resolver a alínea b):
1. Determine a altura de elevação que a bomba que vê a sua velocidade de rotação
alterada deve fornecer – essa altura de elevação e o caudal pretendido (0,125
m3/s) determinam um ponto de funcionamento (ponto 1) que será obtido com a
bomba a rodar à rotação N’;
2. Determine o ponto dinamicamente semelhante ao ponto 1 sobre a curva H,Q à
rotação N=1500 rpm inicial, para a qual conhece as curvas de funcionamento
(ver Nota 7 do problema 1).
3. Determine a nova velocidade de rotação da bomba sabendo que os dois pontos
referidos acima são dinamicamente semelhantes (isto é têm os mesmos
coeficientes adimensionais, nomeadamente o do caudal, ou o da altura de
elevação).
NOTAS
1. Na ausência de influência de número de Reynolds (escoamento completamente
turbulento dentro da bomba) e de ocorrência de caviação (vaporização do líquido
dentro da bomba), só há um grupo adimensional independente se considerarmos a
mesma máquina ou máquinas de diferentes diâmetros, mas com a mesma geometria
(ditas da mesma família). Em geral trabalha-se com os grupos adimensionais de caudal
φ = Q ND 3 (normalmente tomado como o grupo independente), da altura de elevação
ψ = gH N 2 D 2 e rendimento η, mas também o de potência, binário, etc.
2. Pelo exposto atrás, o rendimento máximo de uma dada turbomáquina é sempre o
mesmo qualquer que seja a sua velocidade de rotação e ocorre sempre para o mesmo
valor do coeficiente de caudal (ou de outro qualquer coeficiente adimensional).