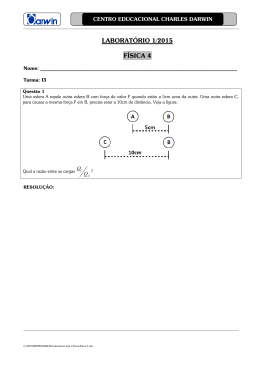
Sociedade Portuguesa de Física
Olimpíadas de Física
Etapa Regional
18 DE ABRIL DE 2015
DURAÇÃO DA PROVA: 1 h 15 min
PROVA TEÓRICA
Escalão A
Problema 1 – NA HORA DO CHÁ
O Pedro e a Maria pararam de estudar para ir tomar um chá ao meio da tarde. A Maria foi
buscar as saquetas de chá e quando a colocou na chávena do Pedro, que já continha a água
quente, ele disse:
- Quando colocas a saqueta de chá na minha chávena, sinto que o peso dela aumentou.
A Maria replicou:
- Impossível, eu ainda seguro a saqueta com o fio esticado, sem que ela toque no fundo!
dinamómetro
O Pedro, que é rapaz de não se deixar ficar, desafiou a Maria para uma experiência.
Colocou uma tina com água sobre uma balança de laboratório e mergulhou na água uma
esfera maciça, suspensa por um fio muito fino, sem que esta tocasse no fundo da tina. O fio
que suspende a esfera foi fixo num dinamómetro.
balança
1
Quando o sistema ficou em equilíbrio, efetuaram as leituras dos valores indicados pelos
aparelhos de medição e reproduzidos na tabela seguinte. A balança foi tarada de modo a
descontar a massa da tina de vidro.
Esfera fora de
água
Esfera dentro
de água
Dinamómetro (N)
2,21±0,03
1,91±0,03
Balança (g)
697,8±0,1
727,8±0,1
Nota: O peso de um corpo com a massa de 1 kg é 9,8 N.
a) Considerando que a densidade da água é 1,0gcm-3 , determina o diâmetro da esfera
utilizada na experiência.
b) Ao mergulhar a esfera, o nível da superfície da água sobe. A pressão exercida por um
líquido, de densidade * e em equilíbrio, no fundo plano da tina é dada pela expressão:
+ , *-.
sendo - , 9,8ms 23 a aceleração da gravidade e . a profundidade.
i) Considera que a área do fundo da tina é 4. Relaciona a variação da intensidade da
força de pressão exercida pela água no fundo da tina com o volume da esfera,
quando se mergulha a esfera sem tocar no fundo.
ii) Calcula o valor da variação de intensidade da força de pressão e compara-a com a
variação da leitura feita na balança.
iii) Compara o valor da impulsão com a variação de força de pressão exercida no fundo
da tina devido à introdução da esfera na água. Explica este resultado com base nas
leis de Newton. Com base nos resultados obtidos, explica o que mede a balança
quando a esfera está dentro de água.
2
Problema 2 – OBSERVANDO O ECLIPSE DO SOL
O eclipse de Sol (eclipse, vem do grego ékleipsis = desaparecimento) que ocorreu no
passado dia 20 de março pôde ser observado em Portugal Continental. Cerca de 70% do Sol
foi tapado pela Lua.
Existem três tipos de eclipse do Sol: eclipse total, quando o Sol fica totalmente encoberto
pela Lua; o eclipse parcial, quando apenas uma parte do Sol fica encoberto pela Lua; e o
eclipse anular, quando a Lua está muito distante da Terra em sua órbita e consegue cobrir
apenas o centro do disco solar.
No pátio da Faculdade de Ciências da Universidade do Porto, pelas 8:00 h da manhã,
juntaram-se diversos alunos e professores para observar o fenómeno. Quase todos
trouxeram os óculos apropriados para observar o eclipse. Contudo, um estudante de Física
trouxe um caixote de papel, o que causou estranheza. No caixote, o aluno de Física recortou
um quadrado de um dos lados e colou uma folha de papel de alumínio onde fez um furo (de
pequeno diâmetro) com a ponta de uma agulha. Ao orientar o furo na direção apropriada,
conseguiu-se observar a imagem do Sol projetada na face do caixote oposta e, assim, várias
pessoas puderam observar o eclipse em total segurança olhando para a imagem na face do
caixote.
A figura seguinte mostra um esquema do caixote feito pelo aluno, com um buraco muito
pequeno, e um objeto, representado por uma seta vertical. A altura da seta é H.
Face onde se
observa a imagem (alvo)
^
buraco de pequeno diametro
H
L
D
a) Utilizando um traçado de raios, construa a imagem da seta no alvo e indica se a imagem
é real ou virtual, direita ou invertida.
b) Determina a altura da imagem da seta no alvo e o fator de ampliação da imagem.
c)
Considerando que o diâmetro do Sol é 1,393 6 107 km, que a distância média Sol-Terra
é 1,496 6 10: km, e que o caixote tem comprimento igual a L = 30 cm, calcula o
diâmetro da imagem do Sol vista no alvo do caixote.
3