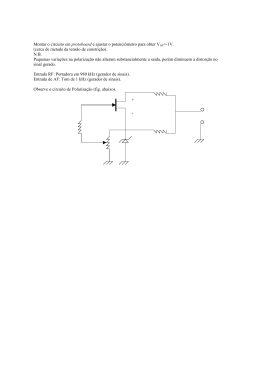
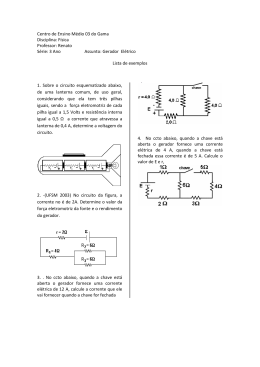
. Laboratório de Eletricidade
S,J.Troise
Exp. 4 -
Estudo dos bipolos geradores
4.1
Fundamentos.
Os bipolos geradores são dispositivos cujo objetivo é elevar o potencial elétrico e assim produzir diferença de
potencial a qual, por sua vez, produz corrente elétrica. Esta elevação de potencial corresponde a um aumento de energia
o que significa que para que o bipolo gerador funcione se faz necessária uma fonte de energia, a qual é utilizada na
realização do trabalho sobre as cargas elétricas que se movem. Esta fonte de energia adicional depende do tipo de
gerador. Nas pilhas convencionais a energia prove de uma reação química irreversível, o que significa que,
gradativamente, os componentes químicos vão sendo consumidos, o que corresponde ao desgaste da pilha. Nas
baterias a reação química é reversível, isto é, a bateria pode ser recarregada através da reversão da reação química.
Existem também geradores eletromagnéticos nos quais a energia elétrica adicional é obtida pela conversão de energia
mecânica em energia elétrica através de processo magnético. Isto é o que ocorre nas grandes usinas geradoras
utilizadas pelas companhias de eletricidade.
Os geradores de energia química fornecem corrente contínua e são representadas pelo símbolo:
Figura 4-1
Os geradores eletromecânicos fornecem corrente alternada e são representados pelo símbolo:
Figura 4-2
É possível também se ter fontes de potencial elétrico pela conversão de corrente alternada em corrente
contínua. Este processo, chamado retificação, exige um circuito elétrico, dotado de vários componentes eletrônicos, os
quais não estudaremos neste texto. A vantagem desse procedimento é a obtenção de fontes de tensão variável, como é
o caso das fontes utilizadas na maioria da experiência de laboratório. Essas fontes são representadas pelo símbolo:
Figura 4-3
4.2
A resistência interna do gerador
Os geradores não são ideais, ou seja, eles mesmos oferecem resistência à passagem da corrente elétrica. Por
esta razão os geradores de corrente contínua devem ser representados pelo símbolo ao lado, onde R I representa a
"resistência interna do gerador". e E representa a tensão nominal da pilha ou seja, a tensão gerada pelo processo que
ocorre no interior do gerador (e indicada pelo fabricante) que é chamada "força eletro motriz" (fem).
Figura 4-4
Observa-se que, quando o gerador está fornecendo uma corrente I , a diferença de potencial V fornecida pelo
gerador não é a tensão nominal E pois ocorre uma queda de potencial na resistência interna, ou seja a tensão oferecida
pelo gerador é:
Página 1 de 6
1
. Laboratório de Eletricidade
S,J.Troise
V = E − R I .I
Equação 4-1
onde R I ⋅ I é a queda de tensão na resistência interna do gerador. A análise esta expressão mostra que a tensão
fornecida pelo gerador só coincide com a tensão nominal do gerador quando a corrente é nula. Mais ainda, que a tensão
fornecida pelo gerador diminui com o aumento da corrente fornecida. Se a resistência interna do gerador for
significativamente elevada, a tensão poderá ser bem menor que sua tensão nominal.
Analisando a expressão obtém-se dois pontos que permitem determinar o gráfico da variação da tensão com a
corrente:
1- quando a corrente é nula obtém-se:
V=E
2- existe uma corrente máxima I CC que o gerador pode fornecer, que é chamada corrente de curto circuito.
Ela é alcançada quando a tensão fornecida pela fonte é nula, ou seja:
V=0
0 = E − R I .I CC
I CC =
E
RI
Equação 4-2
Figura 4-5
Obtemos então graficamente uma reta descendente que mostra a variação da tensão fornecida pelo gerador
em função da corrente.
Existe uma situação prática na qual se pode observar facilmente o efeito da resistência interna de uma pilha.
Quando esta está bastante usada, o que de fato ocorre com a mesma, é que, sua resistência interna está aumentada, e
conseqüentemente, a própria pilha se opõe à passagem a corrente. Quando uma pilha é nova sua resistência interna é
bastante baixa. Isto pode ser experimentalmente verificado com um simples rádio de pilhas. Quando as pilhas estão
gastas, ouvindo-se o rádio em baixo volume (junto ao ouvido) o som tem qualidade. Em alto volume o som tem má
qualidade. Isto ocorre pois a corrente solicitada pelo rádio depende do volume. Em alto volume a corrente consumida
pelo rádio é alta e com isto a tensão fornecida pelo gerador é reduzida fazendo com que o rádio opere fora das suas
especificações, prejudicando assim a qualidade do som produzido.
4.3
Conceito de potência – Potência gerada e potência útil
Dissemos anteriormente que a diferença de potencial ou tensão é o trabalho realizado por unidade de carga, ou
seja
V=
τ
onde τ = Q.V é o trabalho realizado e Q é a carga transportada.
Q
Consideremos então um gerador de tensão E alimentando um circuito que exige uma corrente I tal que a
tensão efetiva aplicada ao mesmo seja V = E − R I .I e seja dQ a quantidade de carga transportada através do gerador
num intervalo de tempo dt . Nesta condição o trabalho realizado sobre o circuito é dτ = dQ.V .
Página 2 de 6
2
. Laboratório de Eletricidade
S,J.Troise
O trabalho por unidade de tempo, isto é, a potência desenvolvida pelo gerador sobre o circuito será
dτ dQ
=
.V . Esta é a potência absorvida pelo sistema que é alimentado pelo gerador (que fornece uma tensão
dt
dt
dQ
nominal E ) e por esta razão é chamada potência útil. Porém,
= I nada mais é do que a corrente fornecida, ou seja,
dt
a potência desenvolvida absorvida pelo circuito que ele alimenta é Pu = V.I ou ainda
Pu =
Pu = (E − R I .I).I = E ⋅ I − R I⋅ .I 2
Equação 4-3
ou seja, a potência desenvolvida é uma função da tensão nominal do gerador E , da resistência interna do gerador R I e
da corrente que está sendo fornecida I . Abaixo é mostrado o comportamento gráfico da variação da potência em função
da corrente.
Figura 4-6
Observamos que a potência útil apresenta um valor máximo, que pode ser calculado.
Derivando a potência na corrente e igualando-se a zero, determinamos que a potência máxima obtemos que
isto ocorre quando
I=
E
o que corresponde a uma potência máxima
2.R I
Pu max =
E2
4.R I
Equação 4-4
Observamos também que a potência se anula para um dado valor de I , o qual pode ser calculado igualandose a zero a potência fornecida obtendo-se
I=
E
R
A potência é medida em Volt.Ampère = Watt = W
Calculemos agora a potência gerada pelo gerador. Ela será dada por Pg = E.I pois E é a tensão nominal do
gerador. Vimos acima que a potência útil é dada por
Pu = E.I − R i .I 2 ou então Pu = Pg − R I .I 2 que estabelece uma
relação entre as potências útil e gerada. Vemos que a potência útil é menor do que a potência gerada ou então, que
2
existe uma potência perdida que é dada por R I .I . Esta potência é dissipada (gasta) na própria resistência interna do
gerador e se manifesta pelo aparecimento de calor. Este resultado pode ser generalizado: sempre que uma resistência
R for percorrida por uma corrente I haverá uma potência dissipada dada por R I .I 2 .
Define-se então rendimento como sendo a relação entre a potência útil e a potência gerada, ou seja
Página 3 de 6
3
. Laboratório de Eletricidade
S,J.Troise
P
E.I − R I .I 2
R
η= u =
= 1 − I .I
Pg
E.I
E
Equação 4-5
4.4
Objetivos da experiência
O objetivo da experiência que se segue é estudar o bipolo gerador, determinando sua resistência interna bem
como determinar, numa condição especial, a corrente de curto circuito e a tensão nominal do gerador, bem como estudar
a potência útil desenvolvida num circuito alimentado por uma fonte de corrente contínua
4.5
4.5.1
Procedimento experimental:
estudo da resistência interna do gerador
4.5.1.1 ( ) Monte o circuito abaixo. Como sempre, monte o circuito com a fonte em seu valor mínimo, bem como, com os
instrumentos de medida em suas escalas máximas.
Atente para as seguintes observações:
Neste circuito utilizaremos um resistor de resistência variável chamada "caixa de resistências" ou "reostato", ou
seja, um conjunto de resistores cuja resistência pode ser alterada girando-se controles rotatórios. O valor desta
resistência pode ser lido nas escalas existentes sob os controles giratórios. Este resistor é representado pelo símbolo:
Figura 4-7
Ao montar o circuito mantenha inicialmente este resistor no seu valor máximo.
Utilizaremos como gerador um conjunto de pilhas. Como as pilhas a serem utilizadas não estão
necessariamente gastas, a resistência interna do conjunto é baixa o que dificulta a sua determinação. Para evitar este
problema usaremos um conjunto de pilhas com o qual associaremos um resistor em série, de baixo valor, que simulará a
resistência interna.
Figura 4-8
4.5.1.2 ( ) Variando a resistência R faça I variar de 5 em 5 mA a partir de zero. Para obter corrente zero abra o circuito em
qualquer ponto. Para cada valor da corrente meça a tensão fornecida pela fonte, preenchendo a tabela abaixo.
I(mA)
V(V)
0,0
5,0
10,0
15,0
20,0
25,0
Página 4 de 6
4
. Laboratório de Eletricidade
S,J.Troise
30,0
35,0
40,0
45,0
50,0
55,0
60,0
65,0
70,0
75,0
80,0
4.5.1.5 ( )
VxI . Trace a reta que melhor se ajusta aos pontos lançados.
E;
Ainda a partir do gráfico determine a corrente e curto circuito I CC .
4.5.2
Estudo da potência útil desenvolvida
4.5.1.3 ( ) Num papel milimetrado faça o gráfico de
4.5.1.4 ( ) A partir da reta obtida determine a tensão nominal do conjunto de pilhas
4.5.2.1 ( ) Transfira para a tabela abaixo os dados da tabela anterior, calculando a potência útil em cada caso. Utilize a tensão
nominal do gerador determinado na primeira parte para calcular a potência útil. Calcule também o rendimento do processo para cada
valor da corrente.
I(mA)
V( V )
PU = V , I (mW) Pg = E. I (mW)
η
0,0
5,0
10,0
15,0
20,0
25,0
30,0
35,0
40,0
45,0
50,0
55,0
60,0
65,0
70,0
75,0
80,0
4.5.2.2 ( ) Faça o gráfico de
Pu xI .
Página 5 de 6
5
. Laboratório de Eletricidade
4.5.2.3 ( ) A partir do gráfico obtido, determine a potência útil máxima.
4.6
S,J.Troise
Relatório:
Siga as instruções contidas no anexo correspondente.
Página 6 de 6
6