Universidade de São Paulo
Escola Superior de Agricultura “Luiz de Queiroz”
Departamento de Ciências Exatas
LCE0212 - Estatística Aplicada às Ciências dos Alimentos
Prof.: Izabela Regina C. de Oliveira
5a Lista de exercícios - Probabilidade
1) Defina o espaço amostral para cada um dos seguintes experimentos aleatórios:
a. Uma moeda é lançada duas vezes e observam-se as faces obtidas.
b. Um dado é lançado duas vezes e a ocorrência de face par ou ímpar é observada.
c. Investigam-se famílias com quatro crianças, anotando-se a configuração segundo o sexo
(M=Masculino, F=Feminino).
d. Lance um dado até que a face 5 apareça pela primeira vez.
e. Mede-se a duração de lâmpadas, deixando-as acesas até que queimem.
f. Uma urna contém 10 bolas azuis e 10 vermelhas com dimensões rigorosamente iguais. Três
bolas são selecionadas ao acaso com reposição e as cores são anotadas.
R: a. Ω = {CC, CR, RC, RR}, para C=Cara e R=Coroa; b. Ω = {P P, P I, IP, P P }, para
P=Par e I=Ímpar; c. Ω = {M M M M, M M M F, M M F M, M F M M, . . . , F F F F }, com o total
de 16 pontos amostrais; d. Ω = {5, F 5, F F 5, F F F 5, F F F F 5, . . .}, em que F=face diferente de
5; e. Ω = {t ∈ R|t ≥ 0}; f. Ω = {AAA, AAV, AV A, V AA, AV V, V AV, V V A, V V V }, A=azul e
V=vermelha.
2) Uma universidade tem 10 mil alunos dos quais 4 mil são considerados esportistas. Temos,
ainda, que 500 alunos são do curso de biologia diurno, 700 da biologia noturno, 100 são esportistas e da biologia diurno e 200 são esportistas e da biologia noturno. Um aluno é escolhido,
ao acaso, e pergunta-se a probabilidade de:
a. Ser esportista. (R : 0, 4)
b. Ser esportista e aluno da biologia noturno. (R : 0, 02)
c. Não ser da biologia. (R : 0, 88)
3) Sejam A e B dois eventos em um dado espaço amostral, tais que P (A) = 0, 2, P (B) = p,
P (A ∪ B) = 0, 5 e P (A ∩ B) = 0, 1. Determine o valor de p. (R : p = 0, 4)
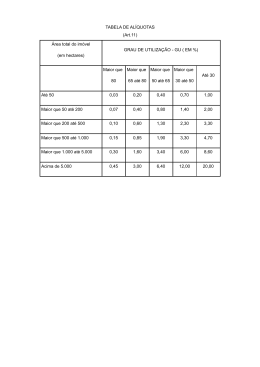
4) Num levantamento em um município sobre a propriedade da terra e o tamanho do estabelecimento agrícola, encontrou-se a seguinte situação:
45 agricultores proprietários com estabelecimentos menores que 50 hectares.
10 agricultores arrendatários com estabelecimentos menores que 50 hectares.
15 agricultores proprietários com estabelecimentos maiores que 50 hectares.
2 agricultores arrendatários com estabelecimentos maiores que 50 hectares.
Ao escolher, ao acaso, algum agricultor do município, qual é a probabilidade de que:
a. o agricultor seja arrendatário e o estabelecimento agrícola menor que 50 hectares?(R :
10/72)
b. o estabelecimento agrícola tenha menos de 50 hectares?(R : 55/72)
5) Se P (A ∪ B) = 0, 8; P (A) = 0, 5 e P (B) = x, determine o valor de x no caso de :
a. A e B serem mutuamente exclusivos. (R : x = 0, 3)
b. A e B serem independentes.(R : x = 0, 6)
6) Em um certo locus podem ocorrer dois alelos: C e D. Admitamos que os possíveis genótipos
têm as seguintes probabilidades:
P(CC) = 0,46; P(CD) = 0,31; P(DD) = 0,23.
Qual é a probabilidade de que um genótipo contenha:
a. o alelo C? (R : 0, 77)
b. o alelo D? (R : 0, 54)
Qual a suposição feita em “a” e “b”?
7) Em um locus de um certo par de cromossomos, podem ocorrer alelos A e a. Os genótipos
AA, Aa, aa tem probabilidades P (AA) = 0, 11, P (Aa) = 0, 37 e P (aa) = 0, 52. Em um locus
de outro par de cromossomos podem ocorrer os alelos B e b. Os genótipos BB, Bb, bb tem
probabilidades P (BB) = 0, 35, P (Bb) = 0, 25 e P (bb) = 0, 40. Encontrar as probabilidades das
combinações genéticas:
a. AA junto com BB, isto é AA e BB. (R : 0, 0385)
b. Aa junto com Bb, isto é Aa e Bb. (R : 0, 0925)
Qual a suposição feita em “a” e “b”?
8) Um enxerto tem a probabilidade duas vezes maior de sobreviver do que não sobreviver.
Plantados três enxertos, qual a probabilidade de exatamente dois sobreviverem? (R : 4/9)
9) Considere uma urna contendo 3 bolas pretas e 5 bolas vermelhas. Retire duas bolas da urna,
sem reposição.
a. Obtenha os resultados possíveis e as respectivas probabilidades.
b. Refaça o item anterior para extrações com reposição.
Calcule as probabilidades dos eventos:
c. bola preta na primeira e segunda extrações. (R : 6/56; 9/64)
d. bola preta na segunda extração. (R : 21/56; 24/64)
e. bola vermelha na primeira extração. (R : 35/56; 40/64)
10) A probabilidade de que A resolva um problema é de 2/3 e a probabilidade de que B resolva é de 3/4. Se ambos tentarem independentemente, qual a probabilidade do problema ser
resolvido? (R : 11/12)
11) As probabilidades de que dois eventos independentes ocorram são p e q, respectivamente.
Qual a probabilidade:
a. de que nenhum destes eventos ocorra? (R : 1 − p − q + pq)
b. de que pelo menos um destes eventos ocorra? (R : p + q − pq)
12) A empresa M&B tem 15.800 empregados, classificados de acordo com a Tabela abaixo:
Tabela 1: Distribuição conjunta das variáveis vacinação e estado de saúde
Sexo
Idade
Homens (H)
Mulheres (F)
TOTAL
< 25 anos (A)
2.000
800
2.800
4.500
2.500
7.000
25 - 40 anos (B)
1.800
4.200
6.000
> 40 anos (C)
TOTAL
8.300
7.500
15.800
Se um empregado é selecionado ao acaso, calcular a probabilidade de ele ser:
a. um empregado com 40 anos de idade ou menos; (R : 0, 62)
b. um empregado com 40 anos de idade ou menos, e mulher; (R : 0, 21)
c. um empregado com mais de 40 anos de idade e que seja homem; (R : 0, 114)
d. uma mulher, dado que é um empregado com menos de 25 anos. (R : 0, 286)
Referências:
ANDRADE, D. F.; OGLIARI, P. J. Estatística para as ciências agrárias e biológicas: com
noções de experimentação. 2 ed. Florianópolis: Editora da UFSC. 2010.
BUSSAB, W. O.; MORETTIN, P. A. Estatística básica. 4 ed. São Paulo: Editora Atual. 1987.
MAGALHÃES, M. N.; LIMA, A. C. P. de Noções de probabilidade e estatística. 7 ed. São
Paulo: Edusp. 2010.