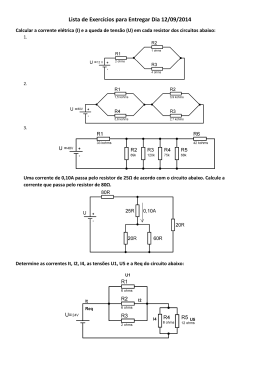
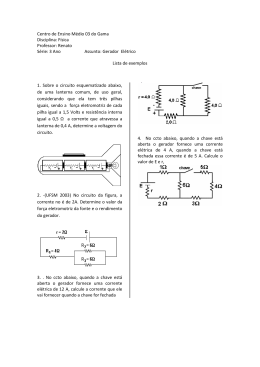
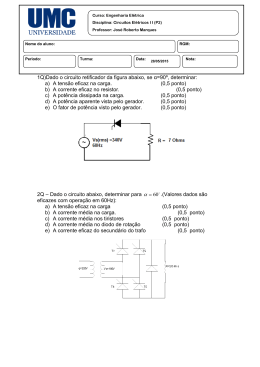
EXPERIÊNCIA 3 – POTÊNCIA ELÉTRICA E GERADORES DE
TENSÃO
1 – INTRODUÇÃO TEÓRICA
A tensão elétrica V é definida como sendo a energia necessária para
mover a carga elétrica Q , entre dois pontos de um meio condutor.
E
Q → E = V .Q
A energia dividida pelo tempo tem a dimensão de potência.
Dividindo ambos os lados da igualdade por ∆t , temos:
E V .Q
=
∆t
∆t
∆Q
E
P=
I=
∆t ( P = potência) e
∆t (corrente elétrica),
Como
V=
substituindo na equação acima, se tem: P = V .I
A unidade de potência no Sistema Internacional de Unidades é watt
(W).
Substituindo V = R.I na equação da potência P = V .I , então:
V2
P
=
P = R.I 2 ou
R
Nos resistores e outros dispositivos utilizados em eletrônica, devido à
passagem da corrente elétrica e da existência de tensão entre seus
terminais, há a dissipação de potência produzindo calor (efeito joule). O
resistor é utilizado em algumas aplicações como dispositivo de
aquecimento, em chuveiros e aquecedores.
Devido à produção de calor, o resistor deve suportar o aquecimento
sem se danificar, dentro de seus limites de operação, sendo a dissipação de
potência uma de suas especificações mais importantes.
O tamanho do resistor é um indicador da potência de um resistor. Em
geral, quanto maior o tamanho do resistor de certo tipo, maior será sua
capacidade de dissipação de potência em watts ( W ).
1.1 – ENERGIA ELÉTRICA
Como
P=
E
∆t então: E = P.∆t . Substituindo P = R.I 2 na equação
2
anterior, tem-se: E = R.I .∆t expressão que permite o cálculo da energia
dissipada numa carga de resistência R , percorrido por uma corrente I ,
durante um intervalo de tempo ∆t . Num resistor, a energia elétrica
dissipada, transforma-se em energia térmica (calor). A transformação de
energia elétrica em calor é conhecida como efeito joule.
A unidade de energia elétrica é W .s (watt.segundo) equivalente a J
(joule), mas, é comum também o uso de kW .h (quilowatt.hora).
1.2 – WATTÍMETRO
Existem instrumentos específicos para medidas de potência,
denominados de wattímetros. A figura a seguir mostra um multímetro com
a função de medidor de potência.
1.3 – GERADORES ELÉTRICOS
Geradores elétricos ou fontes de tensão são dispositivos que
transformam algum tipo de energia em energia elétrica sendo, portanto
considerados elementos ativos dos circuitos elétricos. São os geradores ou
fontes de tensão que produzem a diferença de potencial necessária ao
funcionamento dos circuitos elétricos e eletrônicos. Os geradores podem
ser de diversos tipos de acordo com a transformação da energia realizada. A
seguir, exemplos de geradores.
• bateria - transforma a energia química em energia elétrica.
• dínamo - transforma a energia mecânica em energia elétrica.
1.4 – GERADOR DE TENSÃO IDEAL
Um gerador (fonte) de tensão ideal possui resistência interna nula, e
o resultado disso é que sempre fornece tensão constante ao circuito,
independente da corrente. Essa tensão, denominada força eletromotriz Ε é
constante para qualquer corrente exigida pela carga. O símbolo e a curva
característica do gerador ideal são mostrados na figura a seguir.
1.5 – GERADOR DE TENSÃO REAL
As fontes de tensão reais apresentam uma resistência interna Ri não
nula e a consequência disso é que a tensão de saída depende da resistência
de entrada do circuito. Haverá uma perda interna e, portanto a tensão de
saída não será constante.
Na figura a seguir, R representa a resistência de carga equivalente de
um circuito.
A tensão V entre os pontos A e B é determinada da seguinte forma:
R
V=
.Ε
R + Ri
→ V = Ε − Ri .I
A equação acima é a equação característica ou equação da reta de
carga da fonte de tensão. A representação gráfica é a curva característica
da fonte.
A tensão V diminui com o aumento da corrente. Para V = 0 a
corrente será a de curto circuito denominada I CC .
Na condição de curto circuito com V = 0 , tem se que:
Ε
I CC =
Ri
0 = Ε − Ri .I CC →
A corrente de curto circuito e a resistência interna do gerador
podem ser obtidas experimentalmente a partir da curva característica do
gerador como é mostrado a seguir.
A resistência interna é obtida com a tangente do ângulo α , isto é,
∆V
R =
Ri = tgα sabendo-se que i ∆I . A corrente de curto circuito, portanto
Ε
I CC =
Ri
pode ser determinada:
1.6 – MÁXIMA TRANSFERÊNCIA DE POTÊNCIA
As fontes (geradores) de tensão reais apresentam uma resistência
interna Ri não nula e a consequência disso é que a tensão de saída depende
da resistência de entrada do circuito. Haverá uma perda interna e, portanto
a tensão de saída não será constante. No circuito mostrado a seguir, R
representa a resistência de carga equivalente de um circuito.
A tensão V entre os pontos A e B é determinada da seguinte forma:
V = Ε − Ri .I
A perda de potência interna de um gerador real faz com que a
tensão de saída diminua de valor com o aumento da corrente.
Com uma análise de potência, pode-se dizer que a potência útil
transferida para carga é igual à potência gerada menos a potência perdida
internamente.
PU = PG − PD
onde:
PU = V .I (potência útil)
PG = Ε.I (potência gerada)
PD = Ri .I 2 (potência dissipada)
Substituindo na equação, as potências definidas, temos:
PU = Ε.I − Ri .I 2
A equação da potência útil é uma função do segundo grau, onde Ε
e Ri são parâmetros constantes. A potência e a corrente são variáveis em
função da carga.
A figura a seguir mostra a curva de potência do gerador.
2
Como PU = Ε.I − Ri .I → PU = I .(Ε − Ri .I ) , então:
PU = 0 para I = 0 ou para Ε − Ri .I = 0
Ε
I=
Ri → I = I CC (corrente de curto circuito)
De onde resulta:
A parábola é uma figura simétrica e, portanto a potência será
máxima quando a corrente for igual à metade do valor da corrente de
curto circuito, isto é:
Ε
I
IO =
I O = CC
2.Ri
2 →
Para determinação da potência máxima, substituímos na equação
da potência útil a expressão I O .
2
2
2
2
 Ε 
E
Ε
Ε
Ε

PUmáx = Ε.
− Ri .
PUmáx =
−
PUmáx =
2.Ri
2.Ri 4.Ri →
4.Ri
 2.Ri  →
Substituindo na equação do gerador a expressão da corrente por
I O obtém-se a tensão no ponto de máxima potência,
,
Ε
Ε
VO = Ε − Ri .
V
=
O
2.Ri →
VO = Ε − Ri .I O →
2
Portanto, para o gerador na condição de máxima potência, a tensão
Ε
Ε
IO =
VO =
2.Ri .
2 e a corrente
de saída será
Através desses parâmetros pode-se estabelecer o valor da carga.
Ε
RL = 2
V
Ε
RL = O
IO →
2.Ri → RL = Ri
Para máxima transferência de potência de um gerador, a carga
deve ter um valor igual ao da resistência interna do gerador (fonte).
O rendimento η é a razão entre a potência útil e a potência gerada.
P
V .I
V
η= U
η=
η
=
PG →
Ε.I →
Ε
Para a condição de máxima transferência de potência o rendimento
será:
Ε
V
1
η= 2
η= O
η=
Ε →
Ε →
2
2 – OBJETIVOS
Determinar a potência produzida no circuito através de medidas de
tensão e corrente;
• Verificar o efeito joule;
• Determinar experimentalmente a resistência interna, a força
eletromotriz e a corrente de curto circuito de um gerador;
• Construir a curva característica da potência do gerador de tensão.
•
3 – DESENVOLVIMENTO
3.1 – MATERIAL UTILIZADO
Fonte de tensão ajustável;
2 Multímetros digitais;
Painel de conexões;
Jumpers do painel de conexões;
• 2 Resistores de 100 Ω de potência;
• Resistores de 2.2kΩ , 1kΩ , 820 Ω , 680 Ω , 560 Ω , 470 Ω , 330 Ω ,
270 Ω , 220 Ω , 180 Ω
•
•
•
•
;
•
Resistores de 120 Ω , 82Ω , 68Ω , 56Ω , 47Ω , 33Ω , 22Ω , 10Ω
•
Cabos com pino banana e jacaré.
;
3.2 – PROCEDIMENTO EXPERIMENTAL
3.2.1 – Potência elétrica
1. Monte o circuito mostrado na figura a seguir no painel de conexões.
O resistor deverá ser de 5W potência.
2. Verifique o aquecimento produzido aproximando um termômetro ao
resistor. Obs.: Cuidado, não encoste a mão no resistor!
3. A partir de zero, varie a tensão da fonte de acordo com os passos
indicados na tabela. Para cada valor, meça a corrente e a tensão
utilizando o multímetro como amperímetro e voltímetro,
respectivamente. Anote os valores na tabela.
V (V )
I ( A)
0
1
2
3
4
5
6
7
8
9
V (V )
I ( A)
11
12
13
14
15
16
17
18
19
20
10
4. Com os dados obtidos construa o gráfico da potência em função da
corrente P = f (I ).
3.2.2 – Geradores elétricos
5. Monte o circuito representado na figura a seguir no painel de
conexões. O resistor R = 100 Ω representará a resistência interna da
fonte, que na realidade tem o valor muito baixo e, portanto
comporta-se na prática como ideal em sua faixa de operação.
6. Ajuste a fonte de tensão para fornecer 5V desconectada do circuito.
7. Utilize os resistores fixos de diferentes valores em RV . Para cada
valor indicado na tabela a seguir meça o valor da tensão e da
corrente. Anote os valores:
RV (Ω)
I (mA)
2 .2 k
1k
820
680
560
470
330
270
220
100
8. Ajuste a fonte de tensão para fornecer 10V desconectada do circuito.
9. Repita o procedimento experimental do item 8.
RV (Ω)
2 .2 k
1k
820
680
560
470
330
270
220
100
I (mA)
10. Com os dados obtidos em cada circuito, construa as curvas
características da fonte de tensão respectiva.
11. Determine a resistência interna e a corrente de curto circuito para
cada circuito.
3.2.3 – Máxima transferência de potência
12. Monte o circuito representado na figura a seguir. O resistor
R = 100 Ω representará a resistência interna da fonte, que na
realidade tem o valor muito baixo e, portanto comporta-se na prática
como ideal em sua faixa de operação.
13. Ajuste a fonte de tensão para fornecer 10V desconectada do circuito.
14. Utilize os resistores fixos de diferentes valores em RV . Para cada
valor indicado na tabela a seguir, meça o valor da tensão e da
corrente. Anote os valores na tabela.
2 .2 k
RV (Ω)
V (V )
I (mA)
PU (mW )
η%
1k
120 100
RV (Ω)
V (V )
I (mA)
PU (mW )
η%
820 680 560 470 330 270 220 180
82
68
56
47
33
22
10
0
15. Com os dados obtidos construa a curva característica da fonte de
tensão V = f (I ) .
16. Determine a resistência interna e a corrente de curto circuito da fonte
17. Com os dados obtidos construa a curva da potência útil em função da
corrente PU = f (I ) .
18. Determine, graficamente, a potência útil máxima transferida pelo
gerador e a corrente de curto circuito.
19. Determine o valor da resistência de carga, da tensão do gerador, da
corrente e o rendimento para máxima transferência de potência do
gerador.
20. Organize todo o material fornecido em seu local de trabalho.
21. Realize uma pesquisa com sua equipe de trabalho no laboratório
sobre o assunto do experimento e juntamente com os dados e
informações obtidas, elabore um relatório da aula prática.