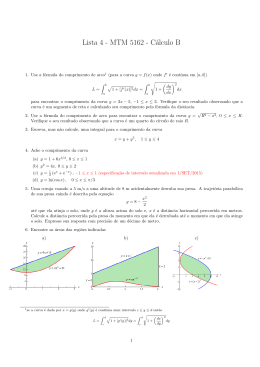
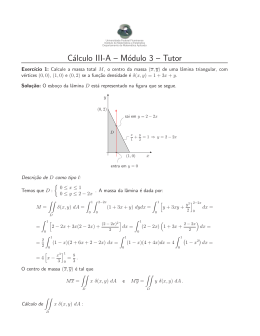
Universidade Federal Fluminense
Instituto de Matemática e Estatı́stica
Departamento de Matemática Aplicada
Cálculo 3A – Lista 2
Exercı́cio 1: Use a mudança u = x+y e v = x−y e calcule a integral de f (x, y) = (x+y)2 sen2 (x−y)
sobre a região D : |x| + |y| ≤ π.
Solução: O esboço da região D está representado na figura que se segue.
y
x − y = −π
π
x+y =π
D
−π
x + y = −π
u+v
π
−π
x
x−y =π
u−v
ey=
. Portanto, o jacobiano da mudança é dado
De u = x + y e v = x − y temos x =
2
2
por:
∂x ∂x 1
1 ∂(x, y)
1
1
−1
2 ∂u ∂v 2
J=
− =− .
=
=
=
4
4
2
1
1
∂(u, v)
∂y ∂y − 2
2
∂u ∂v
1
Como dxdy = |J| dudv então dxdy = dudv. A função f (x, y) = (x+y)2 sen2 (x−y) transforma-se
2
em u2 sen2 v.
Como D é limitada pelas retas x + y = π, x + y = −π, x − y = π e x − y = −π, então Duv é
limitada pelas retas u = π, u = −π, v = π e v = −π.
Cálculo 3A
Lista 2
24
v
π
Duv
−π
u
π
−π
Assim, pela fórmula da mudança de variáveis temos:
ZZ
ZZ
f (x, y) dxdy =
(x + y)2 sen2 (x − y) dxdy =
D
=
D
ZZ
2
1
2
Z
dv =
1
2
1
2
2
(u sen v) dudv =
Duv
=
1
2
Z
π
2
sen v
−π
h
u3
3
iπ
−π
π
2
sen v
−π
·
Z
π
u2 dudv =
−π
2π 3
3
Z
π
sen2 v dv =
−π
h
i
π3 1
π4
sen 2v π
=
· v−
=
.
3
2
2
−π
3
Exercı́cio 2: Use a mudança de variáveis u = xy e v = y/x, e calcule a integral dupla
ZZ
(x2 +
D
2y 2) dA, sendo D a região do plano xy no primeiro quadrante, delimitada pelas curvas xy = 1,
xy = 2, y = x e y = 2x.
u
Solução: Se u = xy e v = y/x vemos que uv = y 2 e
v
outro lado
∂u ∂u ∂x ∂y y
∂(u, v)
1
=
J −1 = =
=
J
∂(x, y)
∂v ∂v −y
x2
∂u
Logo, J =
1
2v
∂y
. Como dA = |J| dudv, então dA =
1
2v
= x2 . Assim, x2 + 2y 2 =
u
v
+ 2uv. Por
x 2y
y y
1 = x + x = x = 2v .
x
dudv .
Como D está limitada por xy = 1, xy = 2, y = x (ou y/x = 1) e y = 2x (ou y/x = 2) então Duv
está limitada por u = 1, u = 2, v = 1 e v = 2.
UFF
IME - GMA
Cálculo 3A
Lista 2
25
v
2
Duv
1
1
u
2
Logo, pela fórmula de mudança de variáveis, temos:
ZZ
ZZ 1
u
2
2
+ 2uv
dudv =
(x + 2y ) dA =
2v
v
D
=
Duv
ZZ 1
2
u
v2
+ 2u dudv =
Duv
=
Z
1
2
1
2
1
v2
+2
h
u2
2
i2
1
1
2
dv =
Z 2Z
1
3
4
1
Z
1
2
2
1
v2
1
v2
+ 2 u dudv =
+ 2 dv =
i2
i
h
h
3
3
15
1
1
=
− + 2v =
− + 4 − (−1 + 2) = .
4
Exercı́cio 3: Calcule
ZZ
v
1
4
2
8
xy 3 dA da região D do primeiro quadrante, limitada por y = x, y = 3x,
D
xy = 1 e xy = 4.
Solução: O esboço da região D está representado na figura que se segue.
y
v
4
y = 3x
Duv
y=x
D
1
xy = 4
1
xy = 1
3
u
x
Com a transformação u = y/x, v = xy, a região D transforma-se na região Duv limitada pelas retas
UFF
IME - GMA
Cálculo 3A
Lista 2
u = 1, u = 3, v = 1 e v = 4. Temos:
∂u ∂u −y
∂x ∂y ∂(u, v)
x2
=
J −1 =
=
∂(x, y)
∂v ∂v y
∂x
∂y
Logo:
26
= − y − y = − 2y = −2u .
x
x
x
x 1
x
∂(x, y)
1
1
1
=− .
= −1 =
J
−2u
2u
∂(u, v)
De u = y/x e v = xy temos que uv = y 2 . Portanto, o integrando xy 3 = xy · y 2 transforma-se em
v · uv = uv 2 . Assim, da fórmula da mudança de variáveis temos:
ZZ
ZZ
ZZ
1 3
2 ∂(x, y) 2
xy dA =
uv dudv
=
uv
−
dudv =
2u
∂(u, v)
D
=
Duv
1
2
ZZ
2
v dudv =
Duv
1
2
Duv
=
1
(64 − 1)
6
Z
1
3
du =
Z 3Z
1
4
2
v dvdu =
1
63 3
u 1
3
=
1
2
21
(3 − 1)
2
Z
1
3
h
v3
3
i4
1
du =
= 21 .
Exercı́cio 4: Use coordenadas polares para calcular as seguintes integrais duplas:
a)
ZZ
b)
ZZ
x2 + y 2
ZZ
ln(x2 + y 2 )
x2 + y 2
p
x2 + y 2 dxdy, sendo D o disco de centro na origem e raio 2.
D
D
c)
2
D
d)
Z
a
Z
√
a2 −x2
dA, onde D é a região dada por x2 + y 2 ≤ 4, com x ≥ 0.
dxdy, sendo D : 1 ≤ x2 + y 2 ≤ e2 , com y ≥ 0.
e−x
2 −y 2
dydx.
−a 0
e)
ZZ
D
f)
ZZ
D
1
p
2
x + y2
dA, sendo D : 1 ≤ x ≤ 3 e 0 ≤ y ≤ x.
(x + y) dA, sendo D : x2 + y 2 − 2y ≤ 0.
Solução:
a) O esboço da região D está representado na figura que se segue.
UFF
IME - GMA
Cálculo 3A
Lista 2
27
y sai em r = 2
2
D
2
x
entra em r = 0
Em coordenadas polares temos
p
x2 + y 2 =
√
r 2 = r e dxdy = rdrdθ.
Descrição de D em coordenadas polares
Efetuando uma “varredura” em D, no sentido anti-horário, a partir do eixo x positivo, vemos que
0 ≤ θ ≤ 2π.
Considerando um ponto P qualquer no interior de D, vemos que a semirreta entra em D na origem
onde r = 0 e sai de D em um ponto da circunferênciaonde r = 2. Então, 0 ≤ r ≤ 2. Assim, a
0≤r≤2
.
região D é transformada na região Drθ dada por Drθ :
0 ≤ θ ≤ 2π
θ
2π
Drθ
2
Logo:
r
ZZ
ZZ
Z 2Z
ZZ p
2
2
2
x + y dxdy =
r · r drdθ =
r drdθ =
Drθ
D
= 2π
Z
2
2
r dr = 2π
0
h 3 i2
r
3
0
Drθ
=
16π
3
0
2π
r 2 dθdr =
0
.
Observação: Notem que em coordenadas polares qualquer disco de centro na origem transforma-se
em um retângulo com os lados paralelos aos eixos coordenados.
b) O esboço da região D está representado na figura que se segue.
UFF
IME - GMA
Cálculo 3A
Lista 2
28
y
2
D
x
2
−2
Descrição de D em coordenadas polares
Efetuando uma “varredura” em D, no sentido anti-horário, a partir do eixo y negativo, onde θ =
−π/2 até o eixo y positivo onde θ = π/2, vemos que −π/2 ≤ θ ≤ π/2.
Considerando um ponto P qualquer no interior de D, vemos que a semirreta OP entra em D na
origem onde r = 0 e sai de D em um ponto da circunferência
onde r = 2. Logo, 0 ≤ r ≤ 2. Assim,
0≤r≤2
.
a região D é transformada na região Drθ dada por Drθ :
−π/2 ≤ θ ≤ π/2
θ
π
2
Drθ
2
r
− π2
Logo:
ZZ
2
2 2
(x + y ) dA =
D
=
ZZ
4
r · r drdθ =
Drθ
Z
0
2
r5
Z
π/2
dθdr = π
−π/2
ZZ
r 5 drdθ =
Drθ
Z
0
2
r 5 dr = π
h 6 i2
r
6
0
=
32π
3
.
c) O esboço da região D está representado na figura que se segue.
UFF
IME - GMA
Cálculo 3A
Lista 2
29
y
e
sai em r = e
1
D
−e
−1
ln(x2 + y 2 )
x2 + y 2
Em coordenadas polares temos
P
=
e
x
entra em r = 1
1
ln(r2 )
2 ln r
= 2
2
r
r
e dxdy = r drdθ.
Descrição de D em coordenadas polares
Efetuando
0 ≤ θ ≤ π.
uma
“varredura”
em
D,
no
sentido
anti-horário,
vemos
que
Considerando um ponto P qualquer no interior de D, vemos que a semirreta OP entra em D em
um ponto da circunferência x2 + y 2 = 1 onde r = 1 e sai de D em um ponto da circunferência
x2 + y 2 =e2 onde r = e. Então, 1 ≤ r ≤ e. Assim, a região D é transformada na região Drθ dada
1≤r≤e
por Drθ :
.
0≤θ≤π
θ
π
Drθ
Logo:
ZZ
ln(x2 + y 2 )
x2 + y 2
dxdy =
D
=2
r
e
1
ZZ
2 ln r
r2
· r drdθ = 2
Drθ
Z
e
1
ln r
r
Z
π
dθdr = 2π
0
ln r
r
drdθ =
Drθ
Z
1
1
ZZ
e
ln r
r
dr .
Fazendo u = ln r temos du =
dr. Por outro lado, para r = 1 temos u = ln 1 =
r
= 0 e para r = e temos u = ln e = 1. Então:
Z 1
Z e
h 2 i1
1
u
ln r
= .
dr =
u du =
0
r
0
2
0
2
Substituindo acima temos:
ZZ
ln(x2 + y 2 )
x2 + y 2
dxdy = 2π ·
1
2
= π.
D
UFF
IME - GMA
Cálculo 3A
Lista 2
d) Temos
I=
Z
a
−a
Z
√
a2 −x2
−x2 −y 2
e
30
dydx =
0
ZZ
e−x
2 −y 2
dxdy
D
−a ≤ x ≤
√a
cujo esboço está represen0 ≤ y ≤ a2 − x2 ⇒ x2 + y 2 = a2 , y ≥ 0
tado na figura que se segue.
onde D é dada por D :
y
a
D
−a
a
2
2
x
2
−(x +y )
Passando para
= e−r e dxdy = r drdθ e a região D transforma coordenadas polares temos e
0≤r≤a
. Logo:
se em Drθ :
0≤θ≤π
ZZ
Z a
Z π
Z a
2
−r 2
−r 2
I=
e r drdθ =
e r
dθdr = π
e−r r dr =
0
Drθ
=
π
−2
Z
a
0
2
0
e−r (−2r)dr = −
π
2
0
h 2 ia
2
π
e−r
= 1 − e−a .
0
2
e) O esboço da região D está representado na figura que se segue.
y
y=x
D
1
Por coordenadas polares temos p
1
x2 + y 2
3
1
dA = √
r2
x
· r drdθ = drdθ.
Descrição de D em coordenadas polares
Efetuando uma “varredura” em D, no sentido anti-horário, a partir do eixo x positivo onde θ = 0
até a reta y = x onde θ = π/4, vemos que 0 ≤ θ ≤ π/4.
Considerando um ponto P qualquer no interior de D, vemos que a semirreta OP entra em D na
1
= sec θ e sai de D na reta vertical x = 3 ou
reta vertical x = 1 ou r cos θ = 1 donde r =
cos θ
UFF
IME - GMA
Cálculo 3A
Lista 2
3
cos θ
= 3 sec θ. Então, sec θ ≤ r ≤ 3 sec θ. Assim, a região D é transformada
sec θ ≤ r ≤ 3 sec θ
. Logo:
dada por Drθ :
0 ≤ θ ≤ π/4
r cos θ = 3 donde r =
na região Drθ
31
ZZ
1
p
x2 + y 2
D
=
Z
0
dA =
ZZ
drdθ =
Z
0
Drθ
π/4
(3 sec θ − sec θ)dθ = 2
Z
π/4 Z 3 sec θ
π/4
0
drdθ =
sec θ
π/4
sec θ dθ = 3 ln(sec θ + tg θ) 0 =
i
h π
π
− ln(sec 0 + tg 0) =
= 3 ln sec + tg
4
4
√
= 3 ln( 2 + 1) − ln(1 + 0) = 3 ln( 2 + 1) .
√
f) De x2 + y 2 − 2y = 0 temos x2 + (y − 1)2 = 1. Assim, o esboço da região D está representado
na figura a seguir.
y
2
D
1
sai em r = 2 sen θ
P
x
entra em r = 0
Temos:
ZZ
(x + y) dA =
D
ZZ
x dA +
D
ZZ
y dA .
D
Como f (x, y) = x é uma função ı́mpar na variável x e a região D tem simetria em relação ao eixo
y, então:
ZZ
ZZ
f (x, y) dA =
x dA = 0 .
D
Assim:
D
ZZ
(x + y) dA =
D
ZZ
y dA .
D
Em coordenadas polares temos ydA = (r sen θ)r drdθ = r 2 sen θ drdθ.
Descrição de D em coordenadas polares
Efetuando uma “varredura” em D, no sentido anti-horário, a partir do eixo x positivo onde θ = 0
até o eixo x negativo onde θ = π, vemos que 0 ≤ θ ≤ π.
UFF
IME - GMA
Cálculo 3A
Lista 2
32
Considerando um ponto P qualquer no interior de D, não situado no eixo y, vemos que a semirreta
OP entra em D na origem onde r = 0 e sai de D em um ponto da circunferência x2 + y 2 = 2y
ou r 2 = 2r sen θ donde r = 2 sen θ, para r6= 0. Então, 0 ≤ r ≤ 2 sen θ. Assim, a região D é
0 ≤ r ≤ 2 sen θ
transformada na região Drθ dada por Drθ :
. Logo:
0≤θ≤π
ZZ
(x + y)dA =
D
=
=
=
y dA =
D
Z
π
8
3
Z
sen θ
0
=
ZZ
Z
2 sen θ
2
r drdθ =
4
sen θ dθ =
0
8
12
Z
π
2
3
1
2
Z
Z
π
0
Z
π
0
1 − cos 2θ
2
h 3 i2 sen θ
r
3
sen θ
2
0
dθ =
dθ =
1 − 2 cos 2θ + cos2 2θ dθ =
0
·
8
3
r 2 sen θ drdθ =
Drθ
0
π
ZZ
π
0
1 − 2 cos 2θ + cos2 2θ d(2θ) =
h
i
1
1
sen 4θ π
1
= (2π + π) = π .
2θ − 2 sen 2θ +
2θ +
=
3
2
2
0
3
Exercı́cio 5: Calcule a área da região no primeiro quadrante, fora da circunferência x2 + y 2 = 4 e
dentro da circunferência x2 + y 2 = 4x.
Solução: O esboço da região D está representado na figura que se segue.
y
sai em r = 4 cos θ
2
√
(1, 3)
√
3
P
θ
1
D
θ
2
4
x
entra em r = 2
Da teoria, temos que:
A(D) =
ZZ
D
dxdy =
ZZ
r drdθ .
Drθ
Descrição de D em coordenadas polares
De x2 + y 2 = 4 e x2 + y 2 = 4x temos 4x = 4 donde x = 1 e, portanto, y =
UFF
√
3 . Assim, a interseção
IME - GMA
Cálculo 3A
Lista 2
33
√
√
√
3
é o ponto (1, 3). No triângulo retângulo acima, temos que tg θ =
= 3 donde θ = π/3.
1
Assim, efetuando uma “varredura” em D, no sentido anti-horário a partir do eixo x positivo, vemos
que 0 ≤ θ ≤ π/3.
Considerando um ponto P qualquer no interior de D vemos que a semirrreta OP entra em D na
circunferência x2 +y 2 = 4 donde r = 2 e sai de D na circunferência x2+y 2 = 4x donde r 2 = 4r cos θ
2 ≤ r ≤ 4 cos θ
. Então:
ou r = 4 cos θ, se r 6= 0. Assim, 2 ≤ r ≤ 4 cos θ. Logo temos Drθ :
0 ≤ θ ≤ π/3
A(D) =
Z
0
Z 4 cos θ
π/3
r drdθ =
2
Z
π/3
0
h 2 i4 cos θ
r
2
2
dθ =
1
2
Z
0
π/3
(16 cos2 θ − 4) dθ =
h
iπ/3
1
1
2π
π
1
sen 2θ
π
=
=
−4·
16 ·
θ+
− 4θ
8 · + 4 sen
=
2
=
1
2
2
4π
3
+
2
√ 4 3
2
=
2
0
2π
3
√
+
3
3
3
3 u.a.
Exercı́cio 6: Seja dada a integral dupla
ZZ
f (x, y) dxdy =
Z 1Z
0
D
x
f (x, y) dydx +
0
Z
1
√Z √
2
2−x2
f (x, y) dydx .
0
a) Esboce a região D.
b) Expresse a soma das integrais do segundo membro como uma só integral na qual a ordem de
integração esteja invertida.
c) Calcule a integral dupla para a função f (x, y) = ln (1 + x2 + y 2 ).
Solução:
a) Temos I =
ZZ
f (x, y) dxdy com D = D1 ∪ D2 , onde D1 = (x, y); 0 ≤ x ≤ 1 , 0 ≤ y ≤ x e
D
√
√
D2 = (x, y); 1 ≤ x ≤ 2 , 0 ≤ y ≤ 2 − x2 . Os esboços de D1 e D2 são:
y
y
1
(1, 1)
y=x
1
(1, 1)
D2
D1
1
x
1
√
2
x
Logo, o esboço de D está representado na figura que se segue.
UFF
IME - GMA
Cálculo 3A
Lista 2
34
y
(1, 1)
1
x=y
x=
D
√
2
1
b) Enquadrando D como tipo II, temos D :
I=
f (x, y) dxdy .
y
c) Expressando D como coordenadas polares, temos D :
I=
ZZ
ln 1 + r
Drθ
=
π
4
Z
0
√
2
x
0 ≤ y ≤ 1p
. Então:
y ≤ x ≤ 2 − y2
Z 1Z √2−y2
0
p
2 − y2
r drdθ =
Z
0
√Z
2 π/4
0
0≤θ≤√
π/4
. Então:
0≤r≤ 2
ln 1 + r 2 r dθdr =
2
ln 1 + r 2 r dr .
dy
Fazendo y = 1 + r 2 , temos dy = 2r dr, donde r dr = . Para r = 0, temos y = 1 e para r =
2
temos y = 3. Então:
Z 3
Z 3
π
dy
π
=
ln y
ln y dy .
I=
4
2
1
8
√
2
1
Aplicando integração por partes, temos:
u = ln y , dv = dy ⇒ du =
Como
Z
u dv = uv −
Z
3 Z
π
y ln y −
I=
8
=
ou
dy , v = y .
v du, então:
"
π
8
1
y
1
1
3 !
3 ln 3 − y 3
y·
1
y
#
dy =
π
8
Z
3 ln 3 − ln 1 −
1
3
dy
=
1
I=
π
8
(3 ln 3 − 2) .
Exercı́cio 7: Passe para coordenadas polares e calcule:
UFF
IME - GMA
Cálculo 3A
Lista 2
a) I =
1−y 2
Z 1Z
1+
Z aZ
√
a2 −x2
0
b) I =
√
0
1−
√
35
xy dxdy
1−y 2
0
p
a2 − x2 − y 2 dydx, a > 0
Solução:
a) A
D:
integral
I está definida sobre a região D descrita pelas desigualdades
0≤y≤1 p
p
. Observe que D está descrita como uma região do tipo
1 − 1 − y2 ≤ x ≤ 1 + 1 − y2
II. Examinemos a fronteira da esquerda de D:
p
p
x = 1 − 1 − y 2 , 0 ≤ y ≤ 1 ⇒ x − 1 = − 1 − y 2 , 0 ≤ y ≤ 1(∴ x ≤ 1) .
Elevando ao quadrado, tem-se:
(x − 1)2 = 1 − y 2, 0 ≤ y ≤ 1 e x ≤ 1
o que implica
(x − 1)2 + y 2 = 1, 0 ≤ y ≤ 1 e x ≤ 1 .
Então a fronteira da esquerda é a parte da circunferência (x − 1)2 + y 2 = 1 com 0 ≤ y ≤ 1 e
x ≤ 1. Examinando a fronteira da direita, temos que consiste da parte da mesma circunferência com
0 ≤ y ≤ 1 e x ≥ 1. Assim, o esboço de D está representado na figura que se segue.
y
r = 2 cos θ
(x, y)
1
r=0
x
2
Portanto D se transforma em:
Drθ = (r, θ); 0 ≤ r ≤ 2 cos θ , 0 ≤ θ ≤ π/2 .
Temos:
I=
ZZ
r cos θr sen θr drdθ =
Drθ
=
Z
=4
0
UFF
3
r cos θ sen θ drdθ =
0
0
r 3 cos θ sen θ drdθ =
Drθ
π/2Z 2 cos θ
Z
ZZ
π/2
cos5 θ sen θ dθ = −4
Z
π/2
cos θ sen θ
0
cos6 θ π/2
6 0
=
2
3
h 4 i2 cos θ
r
4
0
dθ =
.
IME - GMA
Cálculo 3A
b)
Lista 2
36
A
integral I está definida sobre a região D descrita pelas desigualdades
√
0≤x≤√
a
a2 − x2
que
é
do
tipo
I.
A
fronteira
superior
de
D
é
a
curva
y
=
D :
0 ≤ y ≤ a2 − x2
com 0 ≤ x ≤ a e y ≥ 0 que corresponde à parte da circunferência x2 + y 2 = a2 com 0 ≤ x ≤ a e
y ≥ 0.
A fronteira inferior de D é o segmento de reta y = 0 com 0 ≤ x ≤ a. Assim, o esboço de D está
representado na figura que se segue.
y
a
r=a
D
(x, y)
a
x
r=0
O ponto (x, y)
=
(r cos θ, r sen θ)
0 ≤ θ ≤ π/2 e r varia segundo 0 ≤ r ≤ a.
∈
D
é
tal
que
θ
varia
segundo
Portanto D se transforma em:
Drθ = (r, θ); 0 ≤ r ≤ a , 0 ≤ θ ≤ π/2 .
Então:
I=
ZZ √
a2
−
r2
r drdθ =
0
Drθ
=
π
2
Z
a
2
0
a −r
Z aZ
2 1/2
r dr =
π/2
√
0
1
−
2
·
π
2
Z
0
a2 − r 2 r dθdr =
a
a2 − r 2
a
πa3
π 2 2
π
2 3/2 3
=− · a −r
=
−
.
0
−
a
=
4 3
6
6
0
1/2
d a2 − r 2 =
Exercı́cio 8: A base de um sólido é a região do plano xy delimitada pelo disco x2 + y 2 ≤ a2 , com
a > 0. e a parte superior é a superfı́cie do parabolóide az = x2 + y 2. Calcule o volume do sólido.
x2 + y 2
Solução: Seja D o disco x2 + y 2 ≤ a2 e seja z = f (x, y) =
a
que é contı́nua em D.
Então o volume do sólido W de base D
z = f (x, y) =
x2 + y 2
a
V (W ) =
é dado por:
ZZ
D
UFF
≥ 0,
e “teto”
f (x, y) dxdy =
ZZ
D
x2 + y 2
a
dxdy =
1
a
ZZ
(x2 + y 2 ) dxdy .
D
IME - GMA
Cálculo 3A
Lista 2
37
2
2
2
3
Passando para coordenadas
polares, temos (x + y ) dxdy = r r drdθ = r drdθ e o disco D
0≤r≤a
. Logo:
transforma-se em Drθ :
0 ≤ θ ≤ 2π/
V (W ) =
1
a
ZZ
3
r drdθ =
Drθ
=
2π
a
h 4 ia
r
4
0
=
a3 π
2
1
a
Z
a
r
0
3
Z
2π
dθdr =
0
2π
a
Z
a
r 3 dr =
0
u.v.
Exercı́cio 9: Achar o volume do sólido limitado superiormente pela esfera x2 + y 2 + z 2 = 4,
inferiormente pelo plano xy e lateralmente pelo cilindro x2 + y 2 = 1.
Solução: O esboço de W está representado na figura que se segue.
z
2
“teto”
W
x
1
1
y
D (“piso”)
Observemos
que
o
“teto”
do
sólido
W
é
uma
porção
da
esfera
p
x2 + y 2 + z 2 = 4, donde z = 4 − x2 − y 2 = f (x, y). O “piso” de W é o disco D : x2 + y 2 ≤ 1.
Então
ZZ
ZZ p
4 − x2 − y 2 dxdy .
V (W ) =
f (x, y) dxdy =
D
D
Passando para coordenadas polares, temos




x=
y=
dxdy =


 2
x + y2 =
UFF
r cos θ
r sen θ
rdrdθ
r2
IME - GMA
Cálculo 3A
Lista 2
38
O conjunto Drθ é dado por: 0 ≤ r ≤ 1 e 0 ≤ θ ≤ 2π. Então:
ZZ √
Z 1
Z
2 1/2
2
4 − r · r drdθ =
V (W ) =
4−r
r
0
Drθ
= 2π
Z
1
0
4 − r2
1/2
2π
dθdr =
0
r dr .
1
Temos d(4 − r 2 ) = −2r dr, donde r dr = − d(4 − r 2 ). Logo:
2
Z 1
1/2
1
4 − r2
d(4 − r 2 ) =
V (W ) = 2π −
2
0
h
i1
√ 2π
2
2π
2 3/2
= −π · · (4 − r )
=−
33/2 − 43/2 =
8 − 3 3 u.v.
3
0
3
3
Exercı́cio 10: Determine o volume do sólido W limitado pelo parabolóide z = 4 − x2 − y 2 e pelo
plano xy.
Solução: O esboço de W está representado na figura que se segue.
z
4
y
2
D
W
2
2
x
y
2
x
“piso” D : x2 + y 2 ≤ 4
Temos:
V (W ) =
ZZ
f (x, y) dxdy =
D
D
Passando para coordenadas polares temos




UFF
ZZ
x
y
dxdy


 2
x + y2
=
=
=
=
4 − x2 − y 2 dxdy .
r cos θ
r sen θ
r drdθ
r2
IME - GMA
Cálculo 3A
e Drθ :
Lista 2
0 ≤ θ ≤ 2π
. Então:
0≤r≤2
V (W ) =
ZZ
Drθ
= 2π
Z
0
UFF
39
2
4−r
2
r drdθ =
Z
2
4r − r
0
3
Z
2π
dθdr =
0
i
h
r4 2
= 2π(8 − 4) = 8π u.v.
4r − r 3 dr = 2π 2r 2 −
4
0
IME - GMA