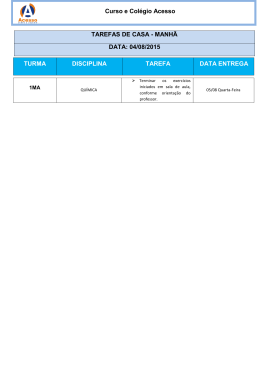
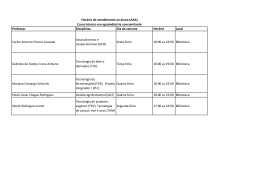
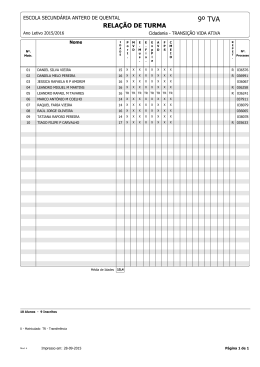
Modelagem Geométrica
Leandro Tonietto
Computação Gráfica
Desenvolvimento Jogos e Entretenimento Digital
[email protected]
http://professor.unisinos.br/ltonietto/jed/cgr/modelGeom.pdf
ago-11
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
Sumário
Introdução
Modelagem
Representação
Polígonos
Exercício
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
2
Introdução
Modelagem:
Descrição de objetos do mundo real
Representação de objetos através de modelos:
Descreve propriedades e implementa regras que representam
um objeto real.
Por exemplo, podemos descrever objetos com atributos, como:
altura, volume, largura, tipo de superfície, ... ou com pontos
que dão a sua forma.
Faz uso de métodos matemáticos para descrição e
representação.
Objetos não reais também podem ser modelados. A
realidade do modelo pode ser fictícia.
Modelar = descrever
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
3
Introdução
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
Como devo modelar? Descrever um objeto com
todas propriedades e detalhes mínimos? Ou usar
uma representação mais simples e funcional?
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Objeto pode ser descrito de diversas formas.
Como devo modelar? Descrever um objeto com
todas propriedades e detalhes mínimos? Ou usar
uma representação mais simples e funcional?
O que e como depende de cada situação.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
4
Introdução
Aspectos a serem considerados quando da escolha
da descrição de um modelo:
Facilidade: para transformar a forma em polígonos.
Não se pode descrever matematicamente qualquer forma
como uma primitiva, mas podemos simplificá-la para um
conjunto de polígonos bem “comportados”.
Tamanho: o bastante para reproduzir o modelo.
Complexidade: gerado manualmente ou
proceduralmente
Interação: permitir alterações e animação
Matemática: representação e uso de ferramentas
matemáticas
Precisão: o quão preciso um modelo deve ser.
Lembre-se: o ótimo é inimigo do bom!!
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
5
Introdução
Aplicações X nível de detalhe:
CAD: precisão matemática
Jogos: precisão visual
Representação em níveis de detalhamento.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
6
Introdução
gCAD3D
Medal Of Honor
Neverwinter Nights
Modelo do Fiat 500
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
7
Introdução
Superfícies X volume
Interessa apenas a superfícies dos objetos
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
8
Introdução
Superfícies X volume
Informações sobre o interior dos objetos
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
9
Modelagem
Como se modela:
Representação poligonal
Curvas e superfícies
Sólidos
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
10
Curvas
Pontos de controle e comprimento
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
11
Superfícies
Área
Apenas uma casca,
ocas
Abertas ou fechadas
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
12
Sólidos
Além das propriedades da casca, o interior
também interessa
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
13
Representação
Formas de representação de objetos:
Funções paramétricas
Pode gerar todos os pontos de um objeto
(sin Ø cos Θ, sin Θ sin Ø, cos Ø)
Definição implícita
Determina se um ponto pertence ou não a um
objeto
x2 + y2 + z2 - 1 = 0
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
14
Representação
É possível ter mais de um tipo de representação
para um objeto:
Exemplo: círculo centrado na origem com raio=1
x2 + y2 = 1 (implícita)
x(Θ)=cos(Θ) e y(Θ)=sin(Θ)(paramétrica)
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
15
Representação
Outra forma de representação dos objetos é
através de pontos (vértices) e faces (um
arranjo de vértices).
Não precisão matemática das representações
paramétrica e implícita, mas tem a facilidade
da modelagem “manual”.
Apenas uma aproximação do modelo real.
Consome mais memória, mas exige menos
processamento para renderização de objetos.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
16
Polígonos
Uso de polígonos para modelar objetos do mundo
real:
Tudo pode ser transformado num polígono (ou quase
tudo)
Podemos renderizar polígonos rapidamente
Várias operações são fáceis de fazer em polígonos
Memória e disco são relativamente baratos
Polígonos são simples
Uma malha de polígonos
representa a superfície de
um objeto.
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
17
Polígonos
Desvantagens ou problemas
São apenas aproximações das superfícies
Mas podem ser tão detalhados quanto necessário
Normais são apenas aproximadas dentro da face.
Ao transformarmos em polígonos perdemos informação e não
há meios de reconstruir a informações original depois
amostrados os polígonos.
A maioria das superfícies reais são curvas (especialmente
estruturas naturais), o que torna a representação aproximada
mais difícil e dispendiciosa.
Falta de estruturação
Alguns cálculos geométricos podem ser altamente
complexos. Exemplo: cálculo de intersecção.
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
18
Polígonos
Malha Convexa/Côncava
Se convexo, várias operações são mais simples: Clipping,
preenchimento, intersecção, detecção de colisão, rendering,
cálculo do volume, etc.
Fechada/Aberta
Malhas fechadas são chamadas de “watertight”
Simples
Faces se encontram apenas nas arestas e vértices
Lados se encontram apenas nos vértices
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
19
Polígonos
Estrutura de dados:
Três componentes
Vértices
Conectividade – quais vértices fazem quais faces
Dados associados: normais, texturas, equação do
plano, etc.
Associados ou ao vértice ou à face, podemos ter
informações nos dois níveis inclusive.
Normalmente, a informação a nível de face é um valor
médio dos seus vértices.
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
20
Polígonos
Vários modelos são apenas lista de polígonos
struct Vertex {
float coords[3];
}
struct Triangle {
struct Vertex verts[3];
}
struct Triangle mesh[n];
glBegin(GL_TRIANGLES)
for ( i = 0 ; i < n ; i++ ){
glVertex3fv(mesh[i].verts[0]);
glVertex3fv(mesh[i].verts[1]);
glVertex3fv(mesh[i].verts[2]);
}
glEnd();
Atenção: Em OpenGL a ordem
dos vértices é importante. O
default é na direção contrária
aos ponteiros do relógio. No
quê isto pode impactar?
Triângulos são compostos por
3 vértices e malha é composta
por n triângulos. Acesso direto
aos vértices dentro do
triângulo.
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
21
Polígonos
Lista de polígonos:
Vantagens:
Simples de ler, gravar, transmitir, desenhar e etc.
Saída comum dos CADs
Formato similar ao desenho na OpenGL
Desvantagens (informação):
Não faz referência aos vizinhos
Não indica se o objeto é aberto/fechado
Sem informações sobre polígono degenerados.
Custo de memória, devido a duplicação de vértices e
informações relativas a estes.
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
22
Polígonos
Acesso indireto:
Não gerar vértices novos para cada polígono, porque:
Wastes memory - each vertex repeated many times
Difícil de encontrar polígonos vizinhos
Difícil de verificar se os polígonos se interseccionam
Solução: acesso indireto
Colocar todos os vértices em uma lista
Cada face armazena os índices dos seus vértices
v0
v4
v1
v2
faces
vértices
v0
0
0
2
1
v1
1
v2 v3
4
1
2
v4
3
1
3
v3
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
23
4
Polígonos
Vantagem:
Fácil de obter informação de conectividade da
superfície
Economiza em armazenamento
O índice pode ter apenas 4 bytes; um vértice 3D tem, em
geral, 12 bytes.
Cada vértice é usado pelo menos 3 vezes (e, em média 4-6
vezes), mas é armazenado apenas uma vez
Normais, coordenadas de textura, cores, etc., podem
ser armazenados da mesma forma
Desvantagens:
Conectividade não é explícita
Acesso ao cache não é otimizado
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
24
Polígonos
OpenGL e Acesso indireto:
struct Vertex {
float coords[3];
}
struct Triangle {
GLuint verts[3];
}
struct Mesh {
struct Vertex vertices[m];
struct Triangle triangles[n];
}
Triângulos são compostos por
3 ponteiros para vértices e
malha é composta por m
vértices e n triângulos. Acesso
indireto aos vértices dentro do
triângulo.
glBegin(GL_TRIANGLES)
for para todos os triangulos
for para todos os vertices
int vi = mesh.triangles[i].verts[j]
glVertex3v(mesh.vertecies[vi]);
glEnd();
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
25
Polígonos
OpenGL e acesso indireto (v1):
glEnableClientState(GL_VERTEX_ARRAY)
glVertexPointer(3, GL_FLOAT, sizeof(struct Vertex),
mesh.vertices);
glBegin(GL_TRIANGLES)
for (int i = 0 ; i < n ; i++ ) {
glArrayElement(mesh.triangles[i].verts[0]);
glArrayElement(mesh.triangles[i].verts[1]);
glArrayElement(mesh.triangles[i].verts[2]);
}
glEnd();
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
26
Polígonos
OpenGL e acesso indireto (v2):
glEnableClientState(GL_VERTEX_ARRAY)
glVertexPointer(3, GL_FLOAT, sizeof(struct Vertex),
mesh.vertices);
for (int i = 0 ; i < n ; i++ )
glDrawElements(GL_TRIANGLES, 3, GL_UNSIGNED_INT,
mesh.triangles[i].verts);
Porém, exige correspondência
entre vértices, normais e
mapeamento de texturas.
Menos chamadas de funções
Em geral é mais rápido
Another variant restricts the range of indices that can be used –
even faster because vertices may be cached
Can even interleave arrays to pack more data in
a smaller space
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
27
Conectividade
Informação de polígonos vizinhos é importante
para vários algoritmos
Cada face armazena ponteiros para seus vizinhos
Ou pode-se gerar uma lista de conectividades,
mapeando cada aresta com os seus polígonos.
Conectividade ajuda em:
Detecção de Colisão
Simplificação de malhas
Subdivisão de superfícies
Recortar e extrair partes do modelo
Etc.
A informação pode ser extraída e armazenada
para futuro uso
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
28
Normais
Normais indicam o formato da superfície
Normais por face:
Uma normal por face
“Flat shading”, toda a face tem a mesma cor de
preenchimento, portanto, sem considerar as variações de
iluminação por região da face.
Normais por vértice:
Uma normal por vértice
“smooth shading”, pontos intermediários são interpolados
pelos pontos dos vértices.
Podemos armazenar vetores de normais (similar a vetores de
vértices)
Índices de vértices e normais podem ser armazenados
separadamente.
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
29
Exemplo de objeto – Cubo
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
30
Calculando os Vetores Normais
Vários modelos não tem normais
Ex.: laser scan
Normais por face são fáceis de calcular:
Produto vetorial de dois vetores normalizados
posicionados nas arestas
Normais por vértice:
Calcular normais das faces
Calcular a médias das faces que cada vértice compõe
(um exemplo de uso da informação de conectividade)
Podemos calcular uma média ponderada considerando a área
dos polígonos
Podemos definir ângulo máximo para considerar a face na
média – evitando suavizar cantos
Não considerar a normal da face na média se o ângulo
entre duas faces é maior do que um ângulo
pré-definido (threshold).
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
31
Definindo a estrutura de dados
Cores, coordenadas de texturas, weights,
etc., podem ser tratados como vértices ou
normais
Coeficientes de iluminação podem ser
definidos por face ou por objeto (raramente
por vértice)
A Idéia é definir subestruturas:
Faces são partes de grupos/objetos
Vértices são parte de faces
...
Slide da apresentação do prof. Christian Hofsetz
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
32
Definindo a estrutura de dados
Diagrama:
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
33
Exercício prático
Implementar as classes do modelo conforme
especificado no slide anterior.
Implementar um programa que renderize objetos a
partir de sua malha poligonal. Esta malha foi
preenchida (vértices, grupos e faces) manualmente,
portanto, o aluno deve especificar dentro do programa
a composição da malha. Não deve carregar de arquivo.
Exemplos de objetos para serem modelados e
desenhados:
Paralelepípedo
Esfera
Toróide
Pirâmide
Ou qualquer objeto aproximado por polígonos.
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
34
Tarefa de programação
Implementar um leitor de arquivo no
formato OBJ (que tem a descrição de
objetos como uma malha poligonal com
vértices, normais, textura e faces).
Copiar arquivos OBJ de exemplo com o
professor.
Armazenar as informações lidas em
estruturas de dados conforme vimos
durante a aula.
Plotar polígonos no OpenGL
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
35
Referências bibliográficas
AGOSTON, Max K. Computer Graphics and Geometric
Modeling: Implementation and Algorithms. Springer.
2005.
WRIGHT Jr., Richard S.; LIPCHAK, Benjamin; HAEMEL,
Nicholas. OpenGL Superbible: Comprehensive Tutorial
and Reference. 4ed.: Addison-Wesley. 2007.
Stephen Chenney: http://www.cs.wisc.edu/~schenney/
courses/cs559-s2002/
Slides sobre CG dos professores: Christian Hofsetz,
Cristiano Franco, Marcelo Walter e Soraia Musse.
Especificação do formato Wavefront OBJ:
http://www.martinreddy.net/gfx/3d/OBJ.spec
02-Mar-11
quarta-feira, 8 de agosto de 12
Leandro Tonietto
36