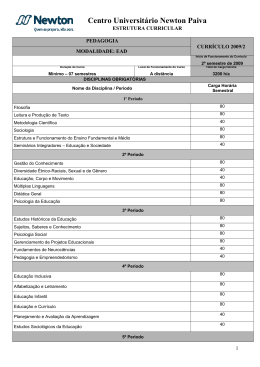
UNIVERSIDADE CRUZEIRO DO SUL
PROGRAMA DE PÓS-GRADUAÇÃO
DOUTORADO EM ENSINO DE CIÊNCIAS E MATEMÁTICA
Formação inicial de pedagogos para ensinar matemática:
constatações, reflexões e desafios do estágio curricular
Júlia de Cássia Pereira do Nascimento
Orientadora: Profª. Dra. Edda Curi
Tese apresentada ao Doutorado em Ensino
de Ciências e Matemática, da Universidade
Cruzeiro do Sul, como parte dos requisitos
para a obtenção do título de Doutora em
Ensino de Ciências e Matemática.
SÃO PAULO
2014
AUTORIZO A REPRODUÇÃO E DIVULGAÇÃO TOTAL OU PARCIAL DESTE
TRABALHO, POR QUALQUER MEIO CONVENCIONAL OU ELETRÔNICO, PARA
FINS DE ESTUDO E PESQUISA, DESDE QUE CITADA A FONTE.
FICHA CATALOGRÁFICA ELABORADA PELA
BIBLIOTECA CENTRAL DA
UNIVERSIDADE CRUZEIRO DO SUL
N195f
Nascimento, Júlia de Cássia Pereira do.
Formação inicial de pedagogos para ensinar matemática:
constatações, reflexões e desafios do estágio curricular / Júlia de
Cássia Pereira do Nascimento. -- São Paulo; SP: [s.n], 2014.
312 p. : il. ; 30 cm.
Orientadora: Edda Curi.
Tese (doutorado) - Programa de Pós-Graduação em Ensino de
Ciências e Matemática, Universidade Cruzeiro do Sul.
1. Ensino de matemática 2. Formação de professores 3. Estágio
curricular supervisionado 4. Pedagogia – Formação inicial do
professor 5. Ensino de matemática – Ensino fundamental. I. Curi,
Edda.
II. Universidade Cruzeiro do Sul. Programa de Pós-Graduação em
Ensino de Ciências e Matemática. III. Título.
CDU: 51:37(043.2)
UNIVERSIDADE CRUZEIRO DO SUL
PROGRAMA DE PÓS-GRADUAÇÃO
Formação inicial de pedagogos para ensinar matemática:
constatações, reflexões e desafios do estágio curricular
Júlia de Cássia Pereira do Nascimento
Tese de doutorado defendida e aprovada
pela Banca Examinadora em 06/06/2014.
BANCA EXAMINADORA:
Profa. Dra. Edda Curi
Universidade Cruzeiro do Sul
Orientadora
Profa. Dra. Cíntia Aparecida Bento dos Santos
Universidade Cruzeiro do Sul
Profª. Dra. Celi Aparecida Espasandin Lopes
Universidade Cruzeiro do Sul
Profa. Dra. Vera Maria Jarcovis Fernandes
Universidade Cidade de São Paulo
Prof. Dr. Rômulo Pereira Nascimento
Secretaria Estadual de Educação
“... mire, veja: o mais importante e bonito do mundo é isto;
que as pessoas não estão sempre iguais, ainda não foram terminadas, mas que elas
vão sempre mudando.
Afinam ou desafinam. Verdade maior. É o que a vida me ensinou.”
João Guimarães Rosa. Grande Sertão: Veredas
AGRADECIMENTOS
Nada disso seria possível se Ele não colocasse Sua mão, sabedoria e proteção em
minha vida e meus caminhos. A Deus, portanto o agradecimento maior por me
sustentar, iluminar e proteger.
Especial agradecimento e carinho à Profª Dra. Edda Curi, por ter abraçado este
trabalho juntamente comigo, sempre com paciência e persistência dosando o rigor e
a amizade, a razão e o coração, me aceitou com todas as minhas limitações,
mostrando enorme competência e segurança, sendo em todos os momentos fonte de
conhecimento, estímulo, incentivo e aprendizado, numa orientação tranquila,
compartilhada e perfeita na conclusão deste trabalho.
Aos professores Dr. Rômulo Pereira Nascimento, Dra.Vera Maria Jarcovis Fernandes,
Dra. Cíntia Aparecida Bento da Silva e Dra. Celi Aparecida Espasandin Lopes,
membros da banca, pelos comentários e sugestões apontadas no momento da
qualificação, que muito contribuíram para a finalização deste trabalho, e por terem
aceito participar também deste momento da defesa, com suas experiências, saberes e
orientações nas análises e reflexões sobre a constituição deste trabalho.
Ao Prof. Dr. Luiz Henrique Amaral, por seu incentivo e acompanhamento no processo
de construção deste trabalho, pelas oportunidades e pela confiança em mim
depositada.
Aos mestres do Programa de Pós-Graduação - Doutorado em Ensino de Ciências e
Matemática da Universidade Cruzeiro do Sul, pelas aulas, conversas e contribuições
para as reflexões sobre minha formação e pesquisas.
À Universidade Cruzeiro do Sul, pela oportunidade de fazer parte de seu corpo
docente, pela confiança e pelo crescimento proporcionado.
Aos alunos do curso de Pedagogia, que se constituíram no principal motivo para
buscar mudanças. Em especial aos meus queridos estagiários, sujeitos desta
pesquisa, “MAO”, “TARS”, “EAM”, “LISE” e “VANGRA”. A colaboração de vocês foi
essencial para que este trabalho pudesse ser realizado.
Aos colegas, professores e alunos que participam do Grupo de Pesquisa CCPPM –
Conhecimentos, Crenças e Práticas de Professores que ensinam Matemática, em
especial àqueles do Programa Observatório da Educação, em cujos encontros
semanais contribuíram com suas discussões, experiências, pesquisas e produções
que foram essenciais para o desenvolvimento desta pesquisa.
Ao meu esposo Joaquim, companheiro inseparável, paciente, atento às minhas
menores necessidades, sempre diligente para que eu tivesse a serenidade
necessária para minhas leituras e reflexões. Obrigada pelos muitos momentos
solitários em frente à TV, pelos cafezinhos na hora certa, por entender quando eu
precisava de silêncio e por me ouvir quando eu precisava conversar. Seu incentivo a
cada pequena conquista e descoberta, trouxe força, alegria, amor e ternura para
meus dias, permitindo a conclusão deste trabalho.
Aos meus filhos Cesar, Felipe e Victor, minhas filhas Lila, Cibele e Cíntia e ao meu
irmão Fábio, que embora privados de minha companhia em muitos momentos, foram
pacientes e presentes, me apoiando, ajudando e incentivando a conclusão deste
trabalho.
O caminho foi longo, muitas pessoas estiveram comigo em minha vida, me
ajudaram, apoiaram, outras infelizmente partiram e deixaram um grande vazio. Sei
que esqueci de várias pessoas, mas a todos que passaram pela minha vida e que
comigo viveram os altos e baixos do caminho percorrido até esta conquista, pela
força, apoio e alegria compartilhada, os quais de alguma forma contribuíram para a
construção de quem sou hoje, o meu muito obrigada.
A todos, o meu carinhoso agradecimento. Que Deus abençoe suas vidas.
NASCIMENTO, J. C. P. Formação inicial de pedagogos para ensinar
matemática: constatações, reflexões e desafios do estágio curricular. 2014. 312 f.
Tese (Doutorado em Ensino de Ciências e Matemática)–Universidade Cruzeiro do
Sul, São Paulo, 2014.
RESUMO
O presente trabalho teve como objetivo analisar os portfólios de cinco estudantes do
curso de Pedagogia de uma Universidade da cidade de São Paulo, com o propósito
de identificar “se” e “como” os estágios podem contribuir para as reflexões destes
alunos sobre o aprender a ensinar Matemática. A questão diretriz desta pesquisa
é “Que mudanças são necessárias à organização e desenvolvimento dos estágios
para melhorar a formação inicial dos pedagogos para ensinar Matemática?”. Por
meio de pesquisa de natureza qualitativa, utilizou-se o método de estudo de caso,
na análise dos relatos dos sujeitos da pesquisa registrados em seus portfólios, com
base em Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011). Nossas
discussões embasaram-se nos aportes teóricos de diferentes autores que tratam da
formação dos professores, do ensino de Matemática e da importância do estágio
nessa formação. Uma pesquisa documental na legislação vigente, nos documentos
norteadores da realização do estágio na Universidade em questão, nas ementas das
disciplinas relativas à formação para ensinar Matemática, além de um mapeamento
sobre as produções existentes sobre o tema, contribuiu para a análise de nossas
questões. As considerações finais mostram que os estágios poderão contribuir
efetivamente para a formação dos professores que vão ensinar Matemática, se
forem realizadas importantes mudanças na organização dos mesmos na
Universidade e em seu desenvolvimento nas escolas de Ensino Fundamental; na
postura dos professores orientadores de estágio na Universidade e dos professores
que acompanham os estagiários nas escolas. As constatações destacadas, os
desafios e as contribuições para superá-los evidenciados em nossas conclusões
mostram que se o estágio for direcionado em sua organização e desenvolvimento,
poderá contribuir para melhorar a formação inicial dos pedagogos para ensinar
Matemática.
Palavras-chave: Formação de professores, Estágio curricular supervisionado,
Ensino de matemática, Educação matemática.
NASCIMENTO, J. C. P. Initial training of teachers to teach mathematics: findings,
reflections and challenges of the traineeship. 2014. 312 f. Tese (Doutorado em
Ensino de Ciências e Matemática)–Universidade Cruzeiro do Sul, São Paulo, 2014.
ABSTRACT
This study aims to analyze the portfolios of five students of pedagogy students of a
University of São Paulo, with the goal of identifying "if" and "how" stages may
contribute to these reflections on the students learn to teach Mathematics. We seek
to answer the guideline question of this research, which is “What changes are
needed to the organization and development stages to enhance the initial training of
teachers to teach mathematics?”. Through qualitative research, we used the method
of case study to analyze the reports of the subjects recorded in their portfolios, based
on Chamoso Sánchez, Caceres Garcia and Azcárate Goded (2011). Our discussions
are based on the theoretical contributions of different authors dealing with the training
of teachers of mathematics teaching and the importance of this training stage.
Documentary research on the current legislation, the guiding documents of the
training course at the University in question, on the menu of courses on training to
teach mathematics, and a mapping of existing productions on the subject,
contributed to the analysis of our questions. The final considerations show that
internships can effectively contribute to the training of teachers who will teach
mathematics, if major changes are made in the same organization at the University
and its development in schools; in the attitude of teachers guiding internship at the
University and teachers who accompany trainees in schools. The findings highlighted
the challenges and contributions to overcome them evidenced in our findings show
that the stage is routed in your organization and development, can contribute to
improving the initial training of teachers to teach Mathematics.
Keywords: Teacher training, Supervised, Teaching of mathematics, Mathematics
education.
LISTA DE ILUSTRAÇÕES
Figura 1 - Gráfico das Observações de Estágio das horas de aulas de
Matemática nos anos iniciais do Ensino Fundamental .................... 28
Figura 2 - Folha de Atividade: A contagem do Seu João ................................. 150
Figura 3 - Folha de Atividade: Xícara Maluca (A e B) ....................................... 151
Figura 4 - Folha de Atividade: Sobe e desce, desce e Sobe (A e B) ............... 152
Figura 5 - Folha de Atividades: Igual e Diferente ............................................. 153
Figura 6 - Folha de Atividades: Sequência Numérica ...................................... 154
Figura 7 - Folha de Atividades: Ordem Crescente ........................................... 155
Figura 8 - Folha de atividades: Quadros Numéricos ........................................ 158
Figura 9 - Folha de Atividades: Bairros e populações ..................................... 159
Figura 10 - Folha de Atividades: Comparando e ordenando ............................. 160
Figura 11 - Folha de atividade: Eu começo, você termina. ................................ 161
Figura 12 - Folha de atividades: Conjunto .......................................................... 162
Figura 13 - Folha de atividades: Sequência numérica e Conjuntos.................. 163
Figura 14 - Folha de atividades: Ditado de números.......................................... 165
Figura 15 - Folha de atividade: Formando dezenas ........................................... 166
Figura 16 - Folha de atividade: Composição ...................................................... 168
Figura 17 - Folha de atividade: Decomposição .................................................. 169
Figura 18 - Folha de atividade: Trabalhando com unidades e dezenas ........... 170
Figura 19 - Folha de atividade: A fruteira da casa de Lívia ................................ 172
Figura 20 - Folha de atividade: Na barraca de frutas ......................................... 173
Figura 21 - Folha de atividade: Outros cálculos de Daniel ................................ 174
Figura 22 - Folha de atividades: Problemas ........................................................ 175
Figura 23 - Folha de atividade: Problemas do campo aditivo ........................... 176
Figura 24 - Folha de atividade: Resolução Grupo A........................................... 177
Figura 25 - Folha de atividade: Resolução Grupo B........................................... 178
Figura 26 - Folha de Atividade: Resolução Grupo C .......................................... 179
Figura 27 - Folha de atividade: Multiplicações ................................................... 181
Figura 28 - Folha de atividade: Formando palavras com resolução de
operações ........................................................................................... 183
Figura 29 - Folha de atividade: Classificação de formas geométricas ............. 185
Figura 30 - Folha de atividade: A forma da melancia ......................................... 186
Figura 31 - Folha de atividade: Geometria e Subtração ..................................... 187
Figura 32 - Folha de atividade: As caixas de presente de Patrícia ................... 189
Figura 33 - Folha de atividade: Hora de ir embora! ............................................ 190
Figura 34 - Folha de atividade: Explicando o caminho ...................................... 191
Figura 35 - Folha de atividade: O quarteirão da escola ..................................... 191
Figura 36 - Folha de atividade: Calendário ......................................................... 193
Figura 37 - Folha de atividade: Dias da semana ................................................. 194
Figura 38- Folha de atividade: Unidade 2 ........................................................... 195
Figura 39 - Folha de atividade: Uma receita muito fácil!.................................... 196
Figura 40 - Folha de atividade: Dúzia .................................................................. 197
Figura 41 - Folha de atividade: É REAL!.............................................................. 198
Figura 42 - Folha de atividade: Calculando......................................................... 199
Figura 43 - Folha de atividade: Arraial Legal ...................................................... 200
Figura 44 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 1º ano do Ensino Fundamental ............................... 262
Figura 45 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 2º ano do Ensino Fundamental ............................... 262
Figura 46 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 3º ano do Ensino Fundamental ............................... 263
Figura 47 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 4º ano do Ensino Fundamental ............................... 263
Figura 48 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 5º ano do Ensino Fundamental ............................... 264
LISTA DE TABELAS E QUADROS
Tabela 1 - Conteúdos trabalhados ..................................................................... 147
Tabela 2 - Número de salas e alunos por escola .............................................. 288
Tabela 3 - Variação do IDEB das escolas pesquisadas nas três últimas
edições ................................................................................................ 289
Quadro 1 - Registro das Observações de Estágio sobre aulas de
Matemática nos anos iniciais do Ensino Fundamental .................. 27
Quadro 2 - Os saberes dos professores ............................................................. 46
Quadro 3 - Trabalhos sobre Ensino de Matemática ........................................... 60
Quadro 4 - Resumo dos trabalhos pesquisados: focos e categorias .............. 63
Quadro 5 - Plano de ensino da disciplina Fundamentos Metodológicos
do Ensino de Matemática I ................................................................ 86
Quadro 6 - Plano de ensino da disciplina Fundamentos Metodológicos
do Ensino de Matemática II ............................................................... 88
Quadro 7 - Plano de ensino da disciplina Prática de Ensino e Orientação
de Estágio Curricular Supervisionado nos anos iniciais do
Ensino Fundamental .......................................................................... 91
Quadro 8 - Conteúdos: Facilidades e dificuldades .......................................... 120
Quadro 9 - Materiais utilizados no planejamento e desenvolvimento das
aulas de Matemática ........................................................................ 124
Quadro 10 - Roteiro para realização do estágio ................................................. 139
Quadro 11 - Parâmetros para análise da dimensão do Conhecimento
segundo Chamoso Sánchez, Cáceres Garcia e Azcárate
Goded (2011) .................................................................................... 143
Quadro 12 - Parâmetros para análise da dimensão da Reflexão segundo
Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011) ..... 144
Quadro 13 - Parâmetros para análise da dimensão da Criatividade
segundo Chamoso Sánchez, Cáceres Garcia e Azcárate
Goded (2011) .................................................................................... 145
Quadro 14 - Categorização dos estagiários: Conhecimento ............................ 222
Quadro 15 - Categorização dos estagiários: Reflexão ...................................... 223
Quadro 16 - Categorização dos estagiários: Criatividade ................................. 223
SUMÁRIO
CAPITULO 1 - O INÍCIO DA JORNADA .................................................................. 17
1.1
Introdução ............................................................................................. 17
1.2
Trajetória enquanto professora do curso de Pedagogia e
professora de Prática de Ensino ......................................................... 17
1.3
Motivação da Pesquisa ........................................................................ 20
1.4
Inserção no Grupo de Pesquisa.......................................................... 21
1.5
Observações empíricas sobre a realização dos estágios pelos
alunos do curso de Pedagogia ........................................................... 24
1.6
Objetivos da Pesquisa ......................................................................... 30
1.6.1
Objetivo Geral ....................................................................................... 30
1.6.2
Objetivos específicos .......................................................................... 30
1.7
Questões de Pesquisa ......................................................................... 31
1.8
Procedimentos da Pesquisa................................................................ 31
1.9
Organização da Pesquisa .................................................................... 36
CAPÍTULO 2 - SOBRE O ESTÁGIO NA FORMAÇÃO DO PROFESSOR .............. 39
2.1
Introdução ............................................................................................. 39
2.2
Procedimentos Metodológicos ........................................................... 39
2.3
Algumas considerações sobre o estágio ........................................... 41
2.4
Discussão teórica sobre a importância do Estágio na formação
do professor ......................................................................................... 43
2.4.1
Contribuições teóricas sobre a formação do professor ................... 43
2.4.2
Contribuições teóricas sobre o estágio na formação do
professor ............................................................................................... 51
2.4.3
Contribuições teóricas sobre o estágio na formação do
professor que vai ensinar Matemática nos anos iniciais do
Ensino Fundamental ............................................................................ 53
2.5
Contribuições de pesquisas sobre o estágio no curso de
Pedagogia e a formação para ensinar Matemática nos anos
iniciais do Ensino Fundamental .......................................................... 59
2.5.1
Análise dos dados ................................................................................ 64
2.6
Considerações sobre o Capítulo ........................................................ 69
CAPÍTULO 3 - CONTEXTUALIZANDO A PESQUISA ............................................. 73
3.1
Introdução ............................................................................................. 73
3.2
Procedimentos Metodológicos ........................................................... 73
3.3
A Legislação Vigente e os Estágios ................................................... 75
3.4
Sobre o estágio no curso de Pedagogia da Universidade
pesquisada............................................................................................ 80
3.5
Análise das ementas das disciplinas relativas à formação para
o ensino de Matemática ....................................................................... 84
3.6
Os estagiários, as escolas e as professoras envolvidas .................. 93
3.6.1
O perfil dos estagiários ....................................................................... 93
3.6.2
O perfil das escolas que recebem os estagiários ........................... 113
3.6.3
O perfil das professoras que recebem os estagiários .................... 116
3.6.3.1
Escolha da carreira ............................................................................ 118
3.6.3.2
Disciplinas ou áreas de maior interesse .......................................... 119
3.6.3.3
Planejamento e a organização das aulas de Matemática ............... 123
3.6.3.4
Contribuições da graduação para o ensino ..................................... 126
3.6.3.5
Orientação pedagógica para o ensino de Matemática .................... 127
3.6.3.6
Formação continuada ........................................................................ 128
3.6.3.7
Acompanhamento de estagiários ..................................................... 129
3.7
Considerações sobre o Capítulo ...................................................... 131
CAPITULO 4 - OS ESTÁGIOS E OS ESTAGIÁRIOS: O ESTUDO DE CASO ...... 135
4.1
Introdução ........................................................................................... 135
4.2
Procedimentos Metodológicos ......................................................... 136
4.2.1
O portfólio ........................................................................................... 138
4.3
A análise dos dados ........................................................................... 146
4.3.1
Conteúdos trabalhados, atividades desenvolvidas e análise
dos estagiários ................................................................................... 146
4.3.1.1
Conteúdos trabalhados ..................................................................... 146
4.3.1.2
Atividades desenvolvidas.................................................................. 149
4.3.1.2.1
Números Naturais e Sistema de Numeração Decimal .................... 149
4.3.1.2.2
Operações ........................................................................................... 171
4.3.1.2.3
Espaço e Forma.................................................................................. 185
4.3.1.2.4
Grandezas e Medidas ......................................................................... 192
4.3.1.2.5
Tratamento da Informação ................................................................ 200
4.3.1.2.6
Outras atividades desenvolvidas ...................................................... 201
4.3.1.3
Algumas
observações
dos
estagiários
com
relação
às
experiências vivenciadas nos estágios ........................................... 203
4.4
A análise das dimensões de aprendizagem reveladas pelos
estagiários .......................................................................................... 214
4.5
Considerações sobre o Capítulo ...................................................... 226
CAPÍTULO 5 – CONSIDERAÇÕES FINAIS ........................................................... 229
5.1
Algumas considerações iniciais ....................................................... 229
5.2
Os gestores e professores da Universidade.................................... 233
5.3
O gestor da escola e o professor que acompanha o estágio ......... 235
5.4
O aluno estagiário .............................................................................. 236
5.5
Considerações e contribuições da pesquisa ................................... 238
REFERÊNCIAS ....................................................................................................... 245
BIBLIOGRAFIA CONSULTADA ............................................................................ 249
APÊNDICES ........................................................................................................... 261
ANEXO ................................................................................................................... 309
17
CAPITULO 1 - O INÍCIO DA JORNADA
Daquilo que eu sei
Nem tudo me deu clareza
Nem tudo foi permitido
Nem tudo me deu certeza...
Daquilo que eu sei...
Nem tudo me foi possível...
Não fechei os olhos,
Não tapei os ouvidos...
(Ivan Lins e Vítor Martins)
1.1
Introdução
Uma pesquisa nasce das inquietações ou curiosidades acerca de um tema
ou na busca de novas ideias ou caminhos para desenvolvermos nosso trabalho.
Fruto de nossa formação e atuação profissional, além de nossas posturas e
concepções sobre as práticas do professor, esta pesquisa pretende discutir a
formação do professor que vai ensinar Matemática nos anos iniciais do Ensino
Fundamental, que se dá nos cursos de Pedagogia e em outros espaços de
formação, aqui por nós ressaltados especialmente o momento da realização do
Estágio Curricular Supervisionado.
Para a realização da pesquisa, iniciamos apresentando os caminhos
percorridos em nossa formação profissional, seja como aprendiz, seja como
orientadora e mediadora da aprendizagem dos alunos do Curso de Pedagogia.
Relataremos as motivações que nos levaram à pesquisa, destacando nossa
preocupação com a formação do professor dos anos iniciais do Ensino
Fundamental,
as
observações
empíricas
realizadas
sobre
os
estágios
e
especialmente sobre os estágios na área de Matemática, considerações relativas
aos objetivos, à questão da pesquisa, aos procedimentos metodológicos e à
organização da pesquisa.
1.2
Trajetória enquanto professora do curso de Pedagogia e professora de
Prática de Ensino
O momento presente nem sempre é parte da primeira escolha que fazemos
18
no início de nossa trajetória profissional. Minha1 primeira graduação foi em Ciências
Contábeis. O gosto e facilidade em cálculos e raciocínio lógico me influenciaram
nesta escolha.
Logo após a conclusão da graduação fui convidada a lecionar em um curso
técnico de Contabilidade. Pensei estar perfeitamente preparada para esta tarefa,
porém o que me esperava em sala de aula não era nem de longe algo que eu fosse
capaz de desenvolver. Rapidamente percebi que gostar de cálculos e conhecer
contabilidade não me conferia competência para ensinar.
Busquei então um curso na Faculdade de Tecnologia de São Paulo FATEC-SP, denominado Esquema-l, hoje extinto, que era um curso de licenciatura
para bacharéis que habilitava à docência no Ensino Médio ou Técnico.
Após esta experiência, identifiquei-me com a área da educação, porém
ainda não reconhecia em mim os conhecimentos e as competências necessárias
para o exercício da docência.
Percebia em muitos de meus alunos falta de conhecimentos matemáticos
básicos que os impedia de desenvolver conceitos e atividades referentes à
Contabilidade. Foi uma época de muitos estudos e descobertas, pois apesar de
perceber a necessidade de ensinar de formas diferentes para que meus alunos
pudessem aprender, eu mesma não possuía a formação pedagógica necessária
para tal. E nas dificuldades que os alunos apresentavam nos conteúdos
matemáticos, também não podia ajudá-los, pois embora conhecesse o conteúdo não
encontrava uma maneira de ensiná-los.
Ingressei então na graduação em Pedagogia na Universidade Cruzeiro do
Sul e paralelamente realizei um curso de Pós-Graduação lato-sensu em Didática, na
Universidade São Luis.
Desde o início de meus estudos trabalhei com jovens ou adultos. A única
experiência que tive diretamente com crianças foi em uma creche da prefeitura, em
que assumi o posto de assistente da direção e paralelamente a esta função auxiliava
nas tarefas da coordenação pedagógica. Foi um período de grandes descobertas. À
1
a
Nesse item utiliza-se a 1 pessoa por se tratar de relatos de experiências e vivências pessoais.
19
época não havia ainda o Ensino Fundamental de nove anos e, portanto as crianças
ficavam na creche até completarem cinco anos, quando eram encaminhadas à
Escola Municipal de Educação Infantil - EMEI. Além disso, ainda tínhamos as
chamadas pajens e a formação das professoras que atendiam às crianças era em
nível médio. Também estávamos em um período de transição, com a
obrigatoriedade do nível superior para os professores de Educação Infantil e dos
anos iniciais do Ensino Fundamental, porém com um período concedido pelo
Ministério da Educação para que os professores procurassem esta formação. Este
fato, aliado ao trabalho realizado na creche chamou minha atenção para a formação
de professores, dando início à pesquisa e formação direcionada a este foco de
trabalho.
Dando continuidade à minha formação e pesquisa, ingressei no Mestrado
em Educação, Arte e História da Cultura da Universidade Presbiteriana Mackenzie e,
antes mesmo de terminá-lo, comecei a lecionar no curso de Pedagogia de uma
faculdade localizada na zona norte da cidade de São Paulo.
O início do trabalho neste curso veio me colocar em um espaço privilegiado
de atuação, pois acreditava que minha colaboração para com a educação seria mais
efetiva se eu atuasse na formação de professores e não diretamente com as
crianças. Assim pensava por entender que a formação do professor é importante, na
medida em que se a mesma não for bem direcionada e mediada, o trabalho com as
crianças torna-se repetitivo e infrutífero.
Após um ano nesta instituição, desliguei-me para ingressar em 2008 em
uma Universidade da zona leste de São Paulo. Já no início de meus trabalhos foi-me
atribuída a orientação na disciplina Prática de Ensino e Estágio Curricular
Supervisionado em Orientação Educacional, no curso de Pedagogia, que desenvolvi
durante um semestre. O foco deste estágio não era a docência, a habilitação dos
alunos visava prepará-los para um trabalho de coordenação pedagógica ou
orientação educacional. Mas as discussões se direcionavam invariavelmente para a
prática do professor, pois o trabalho de coordenação ou orientação pedagógica pode
apresentar problemas para o profissional se o mesmo não conhecer a prática do
professor em sala de aula, as implicações de seu conhecimento e formação para a
docência.
20
A partir do semestre seguinte assumi a orientação da disciplina Prática de
Ensino e Estágio Curricular Supervisionado em Educação Infantil e nos Anos Iniciais
do Ensino Fundamental, voltada à formação de professores, função que desenvolvo
até o presente momento.
Esta disciplina busca propiciar aos alunos a conexão entre teoria e prática,
trazendo para a sala de aula as discussões sobre suas observações confrontadas
com as teorias desenvolvidas nas diferentes disciplinas. Estes momentos fazem com
que as dúvidas dos alunos relacionadas à prática docente se potencializem. Deste
confronto surgiram as questões mais específicas quanto ao ensino de Matemática,
uma vez que na realização do estágio os alunos percebem as dificuldades dos
professores observados em relação a esta disciplina.
Vejo como muito importante a disciplina em questão, que juntamente com
outras que passei a lecionar no curso de Pedagogia, como Didática, Avaliação
Educacional e Gestão Educacional, me permitiram conviver com os medos,
problemas e anseios dos alunos relacionados à prática docente e possibilitaram
reflexões que me trouxeram até a presente pesquisa.
1.3
Motivação da Pesquisa
Sempre entendi que os problemas de aprendizagem tinham que ser antes
encarados como prováveis problemas de ensino. E problemas de ensino, em
qualquer nível, incluem inicialmente os professores do Ensino Fundamental,
formados atualmente nos cursos de Pedagogia, os quais merecem um olhar
diferenciado por desenvolverem um trabalho com as crianças ligado a todas as
disciplinas, talvez por esse motivo conhecidos como professores polivalentes.
Recebemos neste curso alunos com diferentes tipos de formação, com algumas
defasagens cognitivas e conceituais, que invariavelmente vão influenciar em sua
forma de trabalho com as crianças do Ensino Fundamental.
Durante quatro anos consecutivos fui responsável pela maioria das turmas
que deve cumprir Estágio Curricular Supervisionado no curso de Pedagogia. No ano
de 2012 ao encontrar-me novamente nesta tarefa, pude confirmar a importância
desta disciplina como um dos momentos do curso em que temos a possibilidade de
21
propiciar aos alunos a conexão entre teoria e prática, trazendo para a sala de aula
as discussões sobre suas observações confrontadas com as teorias desenvolvidas
nas diferentes disciplinas.
E deste confronto se potencializaram as dúvidas e necessidades dos alunos
com relação à formação para ensinar Matemática. Pesquisa de doutorado anterior,
de nosso grupo de pesquisa defendida por Fernandes (2012) mostra que a teoria
fornecida no curso de formação deixava a desejar e quando na realização do estágio
os alunos percebiam o que ocorria quando o professor adentrava uma sala de
Ensino Fundamental sem o devido conhecimento e formação para o ensino de
Matemática.
1.4
Inserção no Grupo de Pesquisa
O ingresso no curso de Pós-graduação em Ensino de Ciências e
Matemática, para a realização do doutorado, me propiciou a participação no Grupo
de Pesquisa CCPPM - Conhecimentos, Crenças e Práticas de Professores que
ensinam Matemática. Com reuniões quinzenais o grupo discute sobre as situações
de ensino e aprendizagem de Matemática, realiza leituras, apresentação de
seminários, sempre relacionados à prática dos professores e às metodologias do
ensino de Matemática.
Desde o início de 2011, o grupo de pesquisa desenvolve uma significativa
investigação no âmbito do Programa Observatório da Educação, com fomento da
Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Capes,
denominada “Prova Brasil de Matemática: revelações e possibilidades de avanços
nos saberes de alunos de 4ª série / 5º ano e indicativos para formação de
professores”, com o objetivo de promover estudos e pesquisas focados nos estudos
sobre os processos de ensino e aprendizagem de Matemática e na formação de
professores.
Este programa tem a finalidade de, a partir do trabalho colaborativo, avançar
nas pesquisas acadêmicas, analisando o banco de dados de Matemática do Sistema
de Avaliação da Educação Básica - SAEB e da Prova Brasil, relativas à 4a
22
série/5°ano, disponibilizado pelo INEP para o Programa Observatório da Educação
(Edital 2010).
De acordo com Curi (2010), estas ações ampliam os objetivos das
pesquisas, visando estender o diálogo entre a comunidade acadêmica, gestores de
políticas educacionais e os diversos atores envolvidos no processo, subsidiando a
discussão sobre avaliação educacional, ensino-aprendizagem de Matemática e
formação de professores.
Frutos das pesquisas realizadas no grupo colaborativo, percebemos
elementos que contribuem para discussões sobre a avaliação educacional, o
processo de ensino-aprendizagem em Matemática e a formação inicial e continuada
de professores.
O grupo é constituído atualmente de oito alunos do curso de Graduação em
Pedagogia e Matemática da Universidade; sete professoras das redes Municipal e
Estadual de ensino de São Paulo, que atuam com crianças dos anos iniciais do
Ensino Fundamental; cinco mestrandos e um doutorando do Programa de PósGraduação em Ensino de Ciências e Matemática da Universidade, além de mestres
e doutores na qualidade de pesquisadores. Dentre os participantes alguns são
bolsistas da Capes e outros são colaboradores voluntários.
Os dados apresentados e discutidos nas reuniões são coletados no próprio
grupo de pesquisa e nas escolas colaboradoras do Programa Observatório. São seis
escolas envolvidas, distribuídas entre as redes Municipal e Estadual de São Paulo,
as quais se constituem como polos de pesquisa com os alunos do 1º ao 5º ano do
Ensino Fundamental.
Os encontros do grupo ocorrem a cada quinze dias, com reflexões que
partem da tematização da prática, embasando as discussões em estudos teóricos
que contribuam para que se possa avançar também na prática pedagógica. As
ações desenvolvidas permitem que os integrantes do grupo analisem as produções
escritas dos alunos, formulando hipóteses sobre as dificuldades apresentadas, a fim
de que os mesmos avancem nas aprendizagens. Com isto os professores
envolvidos podem incorporar as análises realizadas à sua prática, contribuindo com
o desenvolvimento da aprendizagem matemática de seus alunos.
23
Utilizando os dados quantitativos e qualitativos obtidos nas escolas
participantes, o grupo trabalha coletivamente na elaboração de questões discursivas
que possibilitem a análise das respostas construídas pelos alunos; da forma como
tais questões foram desenvolvidas em sala; dos erros e das dificuldades
apresentados pelos alunos; da reorganização das questões e de sequências de
atividades para o progresso nas aprendizagens dos alunos.
Nos anos de 2011 e 2012 o grupo pesquisou e discutiu alguns temas
matemáticos do currículo dos anos iniciais do Ensino Fundamental, dentre os quais
o Sistema de Numeração Decimal - SND, os problemas do Campo Aditivo e do
Campo Multiplicativo.
O Programa Observatório da Educação é de grande relevância tanto para o
ensino como para a pesquisa, uma vez que promove a integração e o diálogo entre
elementos de várias instâncias educacionais. Observa-se que o grupo abriga
participantes com diferentes experiências e trajetórias profissionais e acadêmicas,
revelando assim diferentes olhares no trabalho coletivo desenvolvido.
As contribuições para a pesquisa se revelam nas participações do grupo em
encontros e congressos ligados à Educação Matemática, além de publicações em
peródicos da área e livros, o que dá visibilidade e credibilidade ao trabalho realizado.
O ingresso neste grupo nos trouxe uma nova visão sobre o ensino de
Matemática no Ensino Fundamental, agregando grande valor à presente pesquisa,
no convívio e discussões com os participantes do grupo, doutores, mestres,
docentes da instituição, doutorandos e mestrandos do programa, professoras das
redes municipal e estadual, e alunos do curso de Pedagogia da Universidade. Os
alunos do curso de Pedagogia que participam do Programa Observatório são
bolsistas e serão colaboradores diretos, na qualidade de sujeitos da presente
pesquisa.
As vivências e observação dos alunos em relação ao estágio, os resultados
da sondagem e minha participação no grupo de pesquisa foram as primeiras
motivações para esta tese de doutorado.
24
1.5
Observações empíricas sobre a realização dos estágios pelos alunos do
curso de Pedagogia
A realização do estágio no curso de Pedagogia na referida Universidade em
que atuo, ocorre a partir do 4° semestre, com foco na Educação Infantil. No 5°
semestre os alunos realizam o estágio de observação nos anos iniciais do Ensino
Fundamental. A partir do 6° semestre o estágio é feito com observações na Gestão
Educacional. Embora em todos os estágios realizados os alunos tragam
questionamentos, dúvidas e sugestões sobre a resolução de certos problemas
observados, é no Ensino Fundamental que se concentram as maiores discussões.
Os alunos trazem questionamentos sobre a prática dos professores
observados, ressaltando a pouca importância dada à Matemática nas aulas do
Ensino Fundamental. Segundo eles durante uma semana de observação nas salas
de aula, têm a oportunidade de acompanhar muitas atividades envolvendo leitura e
escrita, artes, meio ambiente, enquanto a Matemática é pouco trabalhada.
As observações assistemáticas das situações mencionadas nos relatórios de
estágio dos alunos e as conversas informais com os próprios apontavam para a
pouca importância dada à Matemática nas aulas do Ensino Fundamental, pois às
vezes a Matemática era trabalhada uma única vez na semana.
Além disso, os alunos apontavam para a falta de preparo e o aparente
desconhecimento de conceitos matemáticos por parte de certos professores, o que
fazia com que não se esforçassem para trabalhar mais vezes a Matemática. Destas
observações surgiu a discussão sobre os conteúdos, conhecimentos e metodologias
para ensinar Matemática, recebidos pelos alunos, tanto na disciplina Fundamentos e
Metodologia de Ensino de Matemática (FME de Matemática), quanto nos Estágios
Curriculares Supervisionados realizados.
A partir destas considerações surgiram questionamentos sobre o que estes
alunos estavam recebendo no curso de formação para ensinar Matemática, o que
me propiciou a oportunidade de oferecer em 2010 na Universidade em questão, uma
Disciplina Optativa intitulada "Didática da Matemática". Foram abertas 40 vagas,
mas recebi 62 alunos para cursar a disciplina, cujo número não foi maior por falta de
espaço na sala de aula. Muitos me procuraram dizendo-se interessados, pois
25
consideravam que a formação para ensinar Matemática propiciada no curso, por
meio da disciplina FME de Matemática, era muito aquém das necessidades
verificadas nas aulas durante a realização dos estágios, para sua prática docente.
As afirmações dos alunos nos levam a pensar sobre o momento de
realização do Estágio Curricular por parte deles. Segundo Pimenta (2006) o estágio
curricular é o momento da formação em que os alunos desenvolvem atividades nos
futuros campos de atuação profissional, estabelecendo comparações e conhecendo
a realidade. Este é o momento de sintetizar conteúdos, teorias, experiências
pessoais, num processo de reflexão-ação-reflexão.
Neste sentido a opinião da autora vem ao encontro do pensamento de
Schön (2000) ao propor os movimentos de reflexão-na-ação, reflexão-sobre-a-ação
e reflexão-sobre-a-reflexão-na-ação, na formação profissional do professor.
Sendo assim, o aluno deve refletir sobre a ação docente que desenvolverá,
no ensino de Matemática, a partir da teoria, ou seja, do que foi ensinado e aprendido
no curso de formação. Porém, ao cumprir o Estágio Curricular, como parte
obrigatória de sua formação, quando o aluno somente observa, não se apoia na
própria ação de ensinar quando faz suas reflexões. Disso decorre que o aluno acaba
por refletir sobre a ação do outro, o professor observado, o que pode não contribuir
para que ele se torne efetivamente um professor que reflete sobre sua prática no
ensino de Matemática.
Assim, ao observarem a prática do professor os alunos constróem os
saberes necessários à sua própria prática, que no entendimento de Tardif (2002)
são saberes disciplinares, curriculares e experienciais. É preciso refletir e discutir
sobre o papel do Estágio Curricular Supervisionado e da prática do professor
observado na formação do aluno de Pedagogia e em sua reflexão sobre a ação
deste professor.
Os alunos do curso de Pedagogia, via de regra traziam a insatisfação com a
maneira como desenvolviam o Estágio, pois o mesmo não lhes trazia acréscimo de
conhecimento para exercer a docência. Uma das maiores preocupações relatadas
pelos alunos era quanto ao ensino de Matemática. Segundo eles havia poucas aulas
de Matemática nas salas que acompanhavam nos anos iniciais do Ensino
26
Fundamental, e quando tinham a oportunidade de acompanhar esta disciplina
percebiam a falta de interesse, conhecimento e prática específica para trabalhar os
conceitos e conteúdos matemáticos, por parte dos professores observados. Além
disso, os alunos colocavam a questão da formação que recebiam no curso de
Pedagogia para ensinar Matemática nos anos iniciais do Ensino Fundamental.
As queixas e apreensões eram focadas em dois polos: a falta de mais
disciplinas que os preparassem para ensinar Matemática nos anos iniciais do Ensino
Fundamental e a inexistência de uma experiência mais aprofundada sobre este
ensino na realização do estágio nas escolas, junto às professoras deste nível de
ensino. Ainda que estas informações chegassem até nós de forma assistemática e
informal, não era possível ignorar a fala destes alunos, futuros professores, sobre a
prática que estavam acompanhando e especialmente sobre as reflexões que
realizavam a partir da prática do professor observado.
A partir dessas observações empíricas, fiquei motivada para realizar uma
pesquisa mais intencional para identificar a quantidade de aulas de Matemática e de
Língua Portuguesa, em relação ao total de horas observadas em cada sala ou ano
do estágio nos anos iniciais do Ensino Fundamental, o que esperávamos nos
trouxesse maiores subsídios para analisar o problema apontado pelos alunos de que
havia poucas aulas de Matemática.
A escolha da observação somente de Língua Portuguesa e Matemática em
relação ao total de horas acompanhadas deu-se em virtude destas duas disciplinas
serem consideradas prioridade no Ensino Fundamental, até mesmo em virtude das
avaliações externas serem direcionadas para a aprendizagem das crianças nessas
áreas. Ao relacionar com o número total de horas observadas temos uma visão do
tempo destinado à Matemática em relação a tudo que é ministrado nas demais
disciplinas. Assim, solicitamos que os alunos realizassem suas observações no
estágio nos anos iniciais do Ensino Fundamental, coletando dados que
possibilitassem aferir alguns elementos para refletir sobre nossas inquietações.
Neste momento eu era orientadora de estágio nos anos iniciais do Ensino
Fundamental, atendendo aproximadamente 500 alunos. Deste total, inicialmente 124
alunos do 5° semestre do curso de Pedagogia colaboraram nesta pesquisa. Nossa
27
ideia era de que os alunos do curso participassem da coleta de dados para a
elaboração da nossa pesquisa de doutorado. Para cada sala observada, além das
fichas de estágio e relatório exigidos pela Universidade, os alunos preencheriam
quadros que demonstravam as observações realizadas em cada um dos anos do
Ensino Fundamental, de acordo com a proposta de identificar a quantidade de aulas
de Língua Portuguesa e Matemática. Além disso, os estagiários deveriam apontar a
justificativa dos professores sobre o número de horas dispensado a cada disciplina e
para isso foi proposto o instrumento a seguir:
Prof.:
Formação:
Série/Ano:
Total/hs-observadas
Disciplina
N° de aulas
Língua Portuguesa
Matemática
Justificar o porquê desta divisão de horas:
Escola observada:
Aluno estagiário:
Quadro 1 - Registro das Observações de Estágio sobre aulas de Matemática
nos anos iniciais do Ensino Fundamental
Após o retorno dos instrumentos e relatórios de estágio, num primeiro
momento foram tabulados os dados focando na quantidade de aulas de Matemática,
Língua Portuguesa e demais disciplinas. Foram elaborados gráficos sendo um para
cada ano observado, os quais encontram-se nos anexos2 ao final deste trabalho e
um gráfico geral, resumindo as informações sobre o número de aulas de Matemática
observados nos estágios, conforme destacamos a seguir:
2
Apêndice A – Gráficos com quantidade de aulas de Matemática observadas por ano de
escolaridade.
28
Figura 1 - Gráfico das Observações de Estágio das horas de aulas de
Matemática nos anos iniciais do Ensino Fundamental
Estas informações nos levaram a observar a questão do trabalho com
Matemática pelas professoras de cada ano do Ensino Fundamental. Pudemos
apreender que no 1º, 2º e 3º ano do Ensino Fundamental a relação entre as aulas de
Língua Portuguesa e Matemática é em média de 2 para 1. As justificativas das
professoras não mostram incapacidade ou falta de vontade de trabalhar a
Matemática. Declaram que seguem um roteiro planejado pela escola e cumprem o
estabelecido. Outras ainda justificam a necessidade de reforçar a alfabetização nos
primeiros anos do Ensino Fundamental, motivo pelo qual dedicam mais tempo à
Língua Portuguesa do que à Matemática.
Os resultados de nossa análise davam indícios de que, pelo menos no
período em que os alunos realizaram seus estágios, foram observadas menos aulas
de Matemática do que de outras disciplinas.
Esta primeira análise, ao levarmos em conta somente dados quantitativos e
as justificativas das professoras, nos deu indícios de que a contribuição do estágio
para o ensino de Matemática nos anos iniciais do Ensino Fundamental, assim como
relatavam os alunos, pode ser realmente pequena, se levarmos em conta somente o
pequeno número de aulas de Matemática observadas.
29
Porém somente a constatação de que há poucas aulas de Matemática para
os estagiários assistirem, não nos dava subsídios para responder às nossas
questões. A partir deste momento precisávamos de uma observação mais
aprofundada e focada no objeto de estudo desta pesquisa de doutorado. Por este
motivo, foi solicitada a colaboração dos alunos que auxiliaram com suas
observações, para realizar uma pesquisa mais direcionada sobre o ensino de
Matemática, com acompanhamento do 1º ao 5º ano do Ensino Fundamental,
focando na atuação do professor, atividades e conteúdos, relacionando-os com a
aprendizagem proporcionada no curso de Pedagogia, nas disciplinas referentes à
formação do professor para ensinar Matemática nos anos iniciais do Ensino
Fundamental. Queríamos entender quais as aprendizagens para ensinar Matemática
eram propiciadas a estes alunos na realização do estágio.
A disponibilidade para auxiliar em nossa pesquisa foi pouca, em virtude da
mesma focar agora somente no ensino de Matemática. Os alunos relatavam
problemas para realizar o estágio nos dias em que havia aula de Matemática, uma
vez que as professoras justificavam a ausência da disciplina devido à rotina préestabelecida de aulas. Além disso, os alunos justificavam a não participação pela
falta de abertura e disponibilidade das escolas em receber os alunos, compartilhar
materiais e colaborar com a realização do estágio e especialmente da pesquisa.
Diante desta dificuldade e da falta de colaboração dos alunos que
participaram da primeira fase da pesquisa, entendemos que seria interessante
contarmos com a colaboração de alunos que se comprometessem e se
envolvessem com seriedade com este trabalho, escolhendo então cinco alunos do
curso de Pedagogia que por serem bolsistas da Capes e estarem engajados no
Grupo de Pesquisa CCPPM e em especial no Programa Observatório da Educação,
poderiam ter maior disponibilidade para a pesquisa.
Estes alunos, na qualidade de bolsistas tinham o compromisso de realizar
diferentes atividades solicitadas no grupo, entre elas relatórios de observação e
reflexões sobre as discussões desenvolvidas no grupo. Considerou-se que entre
estas tarefas, a observação e colaboração seriam desenvolvidas com mais cuidado
pelos alunos, além do que facilitaria as discussões e reflexões colaborativas entre os
elementos do grupo de pesquisa, uma vez que com o trabalho realizado todos
30
buscamos os mesmos objetivos com relação ao ensino e à aprendizagem de
Matemática.
1.6
Objetivos da Pesquisa
A partir dessa problemática apresentada construimos o objetivo geral e os
objetivos específicos de nossa pesquisa.
1.6.1 Objetivo Geral
Esta investigação tem por objetivo analisar portfólios de cinco estudantes do
curso de Pedagogia, com o propósito de identificar “se” e “como” os estágios podem
contribuir para as reflexões destes alunos sobre o aprender a ensinar Matemática. A
composição do portfólio será explicitada nos procedimentos de pesquisa.
A partir desse objetivo geral, construímos os objetivos específicos.
1.6.2 Objetivos específicos
1. Identificar o perfil dos alunos da graduação, sujeitos da pesquisa, e sua
relação com a Matemática;
2. Identificar o perfil das escolas e dos professores que recebem esses
alunos como estagiários;
3. Identificar “se” e “como” o estágio contribui na formação desses alunos
para ensinar Matemática;
4. Identificar as aprendizagens e dificuldades desses alunos para ensinar
Matemática.
Esta investigação pretende contribuir para a formação de professores para
ensinar Matemática, propiciada nos cursos de Pedagogia por meio do estágio e
disciplinas correlatas.
31
1.7
Questões de Pesquisa
Em função desses objetivos construímos a seguinte questão de pesquisa:
“Que mudanças são necessárias à organização e ao desenvolvimento dos
estágios para melhorar a formação inicial dos pedagogos para ensinar Matemática?”
A partir desta questão, estabelecemos questões diretrizes para o
encaminhamento da pesquisa:
- Qual é a organização da disciplina Estágio Curricular Supervisionado nos
anos iniciais do Ensino Fundamental no curso de Pedagogia pesquisado?
- Qual é o perfil dos estagiários do curso analisado? Quais são as relações
desses estagiários com a Matemática e seu ensino?
- Qual é o perfil das escolas e das professoras que recebem os estagiários
do curso de Pedagogia em questão?
- Que relações com a Matemática e seu ensino têm os professores que
recebem os estagiários?
- O que revelam as aulas de Matemática desses professores, observadas
pelos estagiários?
- Que reflexões fazem os estagiários ao observar as aulas de Matemática
em relação aos conteúdos abordados e metodologias utilizadas?
- Que reflexões fazem os estagiários sobre suas necessidades para ensinar
Matemática?
1.8
Procedimentos da Pesquisa
Segundo Goldenberg (2004) a pesquisa científica exige diferentes atributos
do pesquisador, num constante confronto entre o possível e o impossível, o que é e
o que deveria ser. Portanto, a pesquisa não é reduzida somente a procedimentos
metodológicos, muito embora necessite destes procedimentos para se constituir
como tal.
32
Conforme já abordamos anteriormente, esta investigação contará com a
participação de cinco alunos do curso de Pedagogia, bolsistas da CAPES no
Programa Observatório da Educação, os quais na qualidade de sujeitos desta
pesquisa, colaborarão com suas observações na realização dos estágios e registros
das mesmas em portfólios de aprendizagem, cujos relatos devem envolver suas
colocações sobre o estágio e reflexões sobre a prática do professor e suas
aprendizagens.
Esta pesquisa foi realizada de forma qualitativa pelo método de estudo de
caso. Para Goldenberg (2004) a utilização da pesquisa qualitativa em ciências
sociais dá aos pesquisadores maior liberdade de escolha entre as possibilidades
que podem responder aos objetivos da pesquisa.
Nossa escolha pela pesquisa qualitativa se deu por entendermos que a
mesma é pertinente a este trabalho, uma vez que se pretende observar e
compreender a forma como os alunos, no contexto da realização dos estágios,
pensam, refletem, experienciam, aprendem e agem com relação à sua formação
para ensinar Matemática nos anos iniciais do Ensino Fundamental.
Destaca-se também que a pesquisa qualitativa segundo Lüdke e André
(1986) possui características específicas que nos mostram a sua pertinência para o
desenvolvimento deste trabalho. Uma vez que sua principal fonte de dados é o
ambiente natural e o pesquisador constitui-se em instrumento da pesquisa,
entendemos que as observações dos alunos sujeitos da pesquisa e as análises
realizadas nos colocam no ambiente da pesquisa, no caso as escolas e o momento
das observações do estágios, fazendo com que sejamos em alguns momentos, os
próprios instrumentos da pesquisa.
Além disso, as autoras destacam que na pesquisa qualitativa os dados
coletados são descritos, o que podemos perceber nos registros das atividades
realizadas pelos alunos, permitindo uma análise mais aprofundada e coerente com
as observações, que se estabelecem a partir de um olhar diferenciado que podemos
ter sobre o processo desenvolvido e a percepção das pessoas que estão envolvidas
neste processo, tais sejam a pesquisadora, os alunos e os professores que
acompanham estes alunos na realização dos estágios, buscando as aprendizagens
33
evidenciadas sobre o ensino de Matemática nos anos iniciais do Ensino
Fundamental.
Por se constituir em um método de pesquisa que tem suas bases nas
relações entre os participantes da pesquisa, entre pesquisador e pesquisados,
entendemos que trará maiores contribuições ao presente trabalho.
A partir desta escolha, elegemos o método de Estudo de Caso, na
observação da realização do estágio curricular supervisionado pelos cinco sujeitos
desta pesquisa; delimitado num determinado contexto (o Estágio Curricular
Supervisionado desenvolvido nas escolas); envolvendo tais sujeitos na busca de
respostas e soluções para as questões apresentadas.
O Estudo de Caso tem como característica descrever a realidade de um
determinado
contexto,
estudando
algo
singular
dos
alunos
pesquisados,
representando suas diferenças, utilizando variedades de fontes de informação
através de uma linguagem mais simples. (LÜDCKE; ANDRÉ, 1986).
Apoiamo-nos em Yin (2005) para fundamentar a utilização da estratégia do
estudo de caso, o que permitirá observar cada um dos alunos, assim como todo o
contexto que delineou a realização do estágio, para depois ser feita uma análise dos
pontos coincidentes e discordantes dos relatos de cada sujeito. Segundo o autor
O estudo de caso é a estratégia escolhida ao se examinarem
acontecimentos contemporâneos, mas quando não se podem manipular
comportamentos relevantes. O poder diferenciador do estudo de caso é sua
capacidade de lidar com uma ampla variedade de evidências – documentos,
artefatos, entrevistas e observações – além do que pode estar disponível no
estudo histórico convencional. (YIN, 2005. p. 26-27).
As características do estudo de caso serão apresentadas no capítulo 4.
A fim de levantarmos os dados necessários a esta investigação,
determinamos os instrumentos e técnicas a serem utilizados.
Com a aceitação dos alunos em participar e colaborar com a nossa
pesquisa, com suas observações, solicitamos então que elaborassem portfólios a
partir das observações realizadas nos seus estágios. Entrevistas, narrativas,
atividades e o perfil das escolas e dos professores que recebem estes alunos para a
34
realização do estágio, serão elementos que constituirão a base para a elaboração de
portfólios com dados que após analisados vão incorporar o relatório de nossa
pesquisa. Combinamos que eles assistiriam a pelo menos vinte aulas de
Matemática.
Hernandez (1998) assim define o portfólio:
[...] um continente de diferentes tipos de documentos (anotações pessoais,
experiências de aula, trabalhos pontuais, controles de aprendizagem,
conexões com outros temas fora da escola, representações visuais, etc)
que proporciona evidências do conhecimento que foram sendo construídos,
as estratégias utilizadas para aprender e a disposição de quem o elabora
para continuar aprendendo. (HERNANDEZ, 1998, p. 166).
As características dos portfólios e suas contribuições para o estudo de caso
são apresentadas no capítulo 4, no qual são realizadas as análises dos portfólios
dos alunos.
Embora o instrumento principal de coleta de dados de nossa investigação
seja o portfólio elaborado pelos alunos, utilizamos outras técnicas para embasar
nossa investigação.
A primeira delas é a pesquisa bibliográfica, que nos possibilitou a utilização
das contribuições de autores que permitam aprofundar nossa investigação sobre a
formação do professor para o ensino de Matemática.
Segundo Gil (2008) a pesquisa bibliográfica é desenvolvida com base em
material já elaborado, constituído principalmente de livros e artigos científicos.
Valemo-nos
deste
tipo
de
pesquisa
para
fundamentar
teoricamente
as
considerações sobre a formação do professor, a formação para ensinar Matemática,
conhecimentos e saberes necessários à docência, e o estágio na formação dos
professores.
Utilizamos esta técnica também no capítulo 2, quando discorremos sobre o
estágio na formação do professor e discutimos as contribuições teóricas para esta
formação.
As características desta pesquisa assim como sua utilização neste trabalho
encontram-se no Capítulo 2 e Capítulo 3.
35
Utilizamos ainda no capítulo 3 a pesquisa documental, onde analisamos os
documentos da Universidade pesquisada, como Projeto Pedagógico do Curso de
Pedagogia, documentos institucionais relativos às orientações para a realização dos
estágios e as ementas das disciplinas relativas à formação do professor e ao ensino
de Matemática.
De acordo com Lüdke e Andre (1986) o objetivo da pesquisa documental é
completar as informações obtidas por outras técnicas, ou trazer à tona aspectos
relevantes do trabalho. Para Gil (2008) a pesquisa documental é muito parecida com
a pesquisa bibliográfica, mas a diferença está na natureza das fontes utilizadas, uma
vez que a pesquisa documental utiliza materiais que não receberam ainda um
tratamento analítico, ou que ainda podem ser reelaborados de acordo com os
objetos da pesquisa.
O autor destaca que a análise dos documentos pode ser de “primeira mão”,
ou seja, aqueles que ainda não foram interpretados, ou uma revisão de documentos
que já foram processados, mas podem receber interpretações diferentes do
pesquisador, permitindo o tratamento de documentos que ainda não foram utilizados
para uma pesquisa.
Utilizamos ainda a pesquisa documental na análise das produções
publicadas no site da CAPES, presente no capítulo 2, a fim de encontrarmos
produções que tratassem do mesmo tema e mostrarmos a relevância desta
investigação. Estes documentos foram utilizados para a realização de um
mapeamento, cujos dados foram categorizados sob a perspectiva da análise de
conteúdo proposta por Bardin (2007). Esse processo pode ser dividido em três
fases: pré-análise, exploração dos resultados e interpretação dos mesmos.
As características da pesquisa documental e da análise de conteúdo de
Bardin, assim como sua utilização neste trabalho encontram-se no Capítulo 2.
Os procedimentos de pesquisa utilizados nas ações que darão suporte à
análise serão descritos no início de cada capítulo, contextualizando a utilização do
método em relação às discussões apresentadas no capítulo.
36
1.9
Organização da Pesquisa
Nossa pesquisa está organizada da seguinte forma:
No Capítulo 1 foi apresentada a trajetória percorrida para que se chegasse
ao desenvolvimento da presente pesquisa. Foram relatadas nossas experiências
profissionais e as relações estabelecidas com os alunos do curso de Pedagogia; a
realização do Estágio Curricular Supervisionado nos anos iniciais do Ensino
Fundamental; as observações e os questionamentos oriundos deste estágio e a
participação no Grupo de Pesquisa e Programa Observatório como fatores
determinantes no estabelecimento das questões e objetivos da pesquisa e da
escolha dos sujeitos da pesquisa. Destacamos também os objetivos da investigação,
as questões e procedimentos da pesquisa.
No Capítulo 2 apresentamos uma análise sobre o estágio na formação do
professor. Inicialmente são apresentados os procedimentos metodológicos utilizados
para a realização desta análise. Na sequência, partindo das contribuições teóricas
que apontam para a discussão sobre a importância do estágio na formação dos
professores, discutimos a formação do professor com Shulman (1986), Tardif (2002),
e Pimenta ( 2010); a importância da reflexão nesta formação com Schõn (2000) e
Alarcão (2003); o estágio na formação do professor com Piconez (2000) e Pimenta
(1997, 2006); e a formação de professores que ensinam Matemática sob a
perspectiva de Serrazina (2001), Curi (2005, 2006, 2011) e Ball (2008). Um
mapeamento sobre as investigações nacionais relacionadas ao nosso tema,
demonstra neste capítulo a relevância de nossa pesquisa frente às produções
existentes.
No Capítulo 3 realizamos a contextualização da pesquisa. São apresentados
os procedimentos metodológicos utilizados na apresentação e análise do cenário da
pesquisa. Por meio de análise documental estabeleceu-se um estudo da legislação
de estágio curricular vigente no país, de documentos que embasam a realização do
Estágio na Universidade pesquisada e das ementas das disciplinas oferecidas no
curso em questão relacionadas ao ensino de Matemática e à prática de ensino.
Estabeleceu-se ainda uma análise do estágio no curso de Pedagogia da
Universidade acompanhada com um breve relato da história do estágio neste curso,
37
do percurso e evolução para se alcançar o formato oferecido hoje. Apresentamos
considerações sobre o atual Regulamento de Estágio, a forma de realização,
orientações e contribuições do estágio para a formação dos alunos do curso para
ensinar Matemática e a análise dos planos de ensino das disciplinas FME de
Matemática I, FME de Matemática II e Prática de Ensino e Orientação de Estágio
Curricular Supervisionado nos anos iniciais do Ensino Fundamental. Como parte
importante deste contexto, apresentamos ainda o perfil dos estagiários, das escolas
e dos professores que os receberam na realização do estágio.
No Capítulo 4 apresentamos e analisamos os dados coletados por meio dos
portfólios. São apresentados os procedimentos utilizados para análise, o aporte
teórico para tais análises, assim como os relatos das observações dos cinco
estagiários, com suas contribuições, análise de suas observações e conclusões dos
mesmos sobre o estágio realizado a partir dos portfólios elaborados. Ao final do
capítulo foram feitas as análises interligadas e comparativas dos relatos,
observações e considerações dos cinco sujeitos da pesquisa, com as conclusões e
reflexões propiciadas pelos estudos.
Encerra-se a apresentação da pesquisa no Capítulo 5 em que se encontram
as considerações finais, constatações, contribuições, recomendações e desafios
para que o estágio dos cursos de Pedagogia propicie aprendizagens que melhorem
a formação de professores para ensinar Matemática nos anos iniciais do Ensino
Fundamental.
Destacamos no capítulo a seguir, alguns aportes sobre o estágio na
formação do professor dos anos iniciais do Ensino Fundamental que darão subsídios
à nossa pesquisa.
39
CAPÍTULO
2
-
SOBRE
O
ESTÁGIO
NA
FORMAÇÃO
DO
PROFESSOR
Ninguém começa a ser educador numa certa terça-feira
às quatro horas da tarde. Ninguém nasce educador ou é
marcado para ser educador. A gente se faz educador, a
gente se forma como educador permanente, na prática
e na reflexão sobre a prática.
(Freire, 1986)
2.1
Introdução
Neste capítulo estabelecemos uma discussão sobre o estágio no curso de
formação de professores, especificamente no curso de Pedagogia. Esta ação é
importante para que possamos refletir sobre os aportes teóricos desta pesquisa,
discutindo sobre o estágio, a formação do professor e em especial do professor que
ensina Matemática, assim como verificar a relevância da pesquisa com base nas
produções existentes sobre o tema.
Faremos uma revisão nas contribuições de autores que tratam da formação
do professor, assim como da importância do estágio para esta formação e
especialmente para a formação para o ensino de Matemática. Destacamos também
um levantamento para verificarmos as contribuições das pesquisas existentes sobre
o estágio no curso de Pedagogia e a formação para ensinar Matemática.
2.2
Procedimentos Metodológicos
Conforme já anunciado em capítulo anterior, vamos utilizar a pesquisa
qualitativa no desenvolvimento deste trabalho. Para que possamos entender e
analisar a realização do estágio curricular supervisionado, que em complementação
à formação propiciada na graduação apresenta-se como importante momento de
formação do professor, será feita uma revisão de literatura, valendo-nos da pesquisa
bibliográfica.
Por meio da pesquisa bibliográfica, buscamos autores que nos tragam
fundamentos teóricos que justifiquem ou não nossas colocações sobre as
40
aprendizagens do professor para ensinar Matemática nos anos iniciais e sobre o
estágio e sua importância na formação deste professor.
A pesquisa bibliográfica possibilita conhecermos as diferentes contribuições
científicas disponíveis sobre o tema, nos auxiliando na fundamentação das questões
apresentadas.
Entendemos que este procedimento está de acordo com nossos objetivos
para o presente Capítulo, uma vez que pretendemos discutir a importância do
estágio na formação do professor, levantar as contribuições teóricas sobre esta
formação e especialmente sobre o professor que vai ensinar Matemática nos anos
iniciais do Ensino Fundamental. A pesquisa bibliográfica nos levará, portanto, de
acordo com Cervo, Bervian e Silva (2007) à busca da explicação do problema
apresentado à luz das referências teóricas já produzidas, para conhecer e analisar
as diferentes contribuições sobre o tema.
A procura por produções sobre o foco de nossa pesquisa de doutorado nos
levou ainda à realização de um mapeamento sobre o tema. Para este mapeamento
utilizamos uma pesquisa de caráter documental, nas dissertações e teses
publicadas pela Capes, no período de 2001 a 2012.
Após o levantamento de tais documentos, utilizamos a proposta de análise
de conteúdo de Bardin (2007) para a categorização dos mesmos.
Segundo Bardin (2007, p. 33) a análise de conteúdo é um conjunto de
técnicas de análise das comunicações, que utiliza procedimentos sistemáticos e
objetivos de descrição do conteúdo das mensagens.
A autora assim descreve cada uma das etapas propostas para a
organização da análise de conteúdo:
1. Pré-análise: fase que envolve a preparação do material e a leitura flutuante. Num
primeiro contato com os documentos, é feita uma leitura geral e a escolha dos
documentos a serem analisados de acordo com os objetivos de investigação.
41
2. Exploração do material: fase que envolve a administração sistemática dos rumos
definidos pelo pesquisador, ou seja, momento em que se escolhem a unidade de
registro e as categorias das análises.
3. Tratamento dos resultados obtidos e interpretação: fase em que os dados são
analisados e confrontados com as teorias que sustentam a pesquisa.
Utilizamos os três procedimentos citados por Bardin (2007) para analisar e
categorizar as produções existentes sobre o tema, a fim de evidenciarmos a
relevância da presente investigação.
Para nosso estudo, mostra-se necessário levantar a importância dada ao
ensino de Matemática nos anos iniciais do Ensino Fundamental e especialmente
responder à questão da formação propiciada para este ensino na realização dos
estágios curriculares no curso de Pedagogia.
2.3
Algumas considerações sobre o estágio
Discutir sobre o estágio na formação do professor é importante na medida
em que nesse tipo de atividade os alunos poderão vivenciar situações em seu futuro
local de trabalho, realizando reflexões que permitem aliar a teoria desenvolvida na
Universidade e a prática observada nas unidades escolares.
Porém, resumir o momento do estágio à simples comparação entre teoria e
prática, poderia levar à falsa concepção de que o estágio é um momento de
cumprimento burocrático de uma determinação legal. Esta ideia fragmentada de
alguns alunos, de que na Universidade discute-se a teoria e na escola, no momento
do estágio, se vive a prática tem contribuído para que estes dois momentos não se
articulem, fazendo com que a principal preocupação dos alunos seja o cumprimento
das exigências institucionais, como preenchimento de fichas, tabelas, relatórios, etc.
É preciso vivenciar e entender o estágio como uma oportunidade de agir e
refletir, na constituição da práxis3, que certamente oferecerá ao futuro professor uma
formação mais completa e contextualizada, possibilitando o desenvolvimento de
3
Entendemos “práxis” como Pimenta (2006). Para ela práxis é a atitude (teórico-prática) humana de
transformação da natureza e da sociedade. Não basta conhecer e interpretar o mundo (teórico) é
preciso transformá-lo (práxis). (MARX, 1986, apud PIMENTA, 2006, p.86).
42
competências pedagógicas e sua inserção no mundo do trabalho. Entendemos por
práxis a reflexão e ação dos homens sobre o mundo para transformá-lo,
considerando-a então uma ação com reflexão, com retorno.
O momento da realização do Estágio Supervisionado é portanto muito
importante na constituição da práxis, para que o futuro professor possa adquirir a
prática profissional e a competência pedagógica necessárias à formação de sua
postura e identidade docentes.
Neste sentido Costa (2011) considera que o Estágio é um caminho para que
haja uma integração do futuro professor com seu mundo do trabalho, devendo
promover o aperfeiçoamento e a qualificação profissional deste professor. Desta
forma, a autora entende que o estágio é "um campo significativo de formação, em
que se proporciona a construção de conhecimentos, bem como o aprimoramento
das atividades didático-pedagógicas de formação docente". (IBID., p. 47).
Quando direcionamos o foco de nosso olhar para a formação do futuro
professor dos anos iniciais do Ensino Fundamental, no que se refere ao ensino de
Matemática, acentua-se a fragilidade deste momento. Vejamos o porque desta
fragilidade.
De acordo com o art. 5º, inciso VI, da Resolução CNE/CP 1/2006, que
institui as Diretrizes Curriculares Nacionais para o curso de Graduação em
Pedagogia, licenciatura:
O egresso do curso de Pedagogia deverá estar apto a: [...]- ensinar Língua
Portuguesa, Matemática, Ciências, História, Geografia, Artes, Educação
Física, de forma interdisciplinar e adequada às diferentes fases do
desenvolvimento humano; [...] (CONSELHO NACIONAL DE EDUCAÇÃO
(CNE), 2006).
Se assim deve acontecer, o Estágio Curricular Supervisionado, que é parte
integrante do curso de formação de professores, deve também preparar e formar o
futuro professor para ensinar, entre outras disciplinas, a Matemática.
Para que possamos entender melhor a importância do Estágio na formação
do professor e do professor que vai ensinar Matemática nos anos iniciais do Ensino
Fundamental, nos propusemos a estabelecer uma reflexão embasada em alguns
teóricos que discutem este tema.
43
2.4
Discussão teórica sobre a importância do Estágio na formação do
professor
Entendemos que o estágio é um momento importante da formação em que o
aluno começa a se perceber como professor, pois está no seu futuro ambiente de
trabalho, compartilhando experiências, vivenciando situações que permitem
aprimorar ou não sua formação.
Porém, esta não é a única ou principal fonte de formação. Existem saberes,
conhecimentos e ações que são inerentes à profissão docente e que precisam ser
desenvolvidas pelo futuro professor, numa articulação entre a teoria propiciada no
curso de graduação e a prática vivenciada nos Estágios Supervisionados. Por este
motivo julgamos importante neste momento, antes de focarmos no estágio
propriamente dito como fonte de formação, discutirmos urn pouco sobre as
contribuições de alguns autores que nos mostram caminhos e pontos importantes da
formação do professor.
2.4.1 Contribuições teóricas sobre a formação do professor
Espera-se que o curso de formação de professores, no nosso caso o curso
de Pedagogia, leve o aluno a perceber a importância da articulação entre a teoria e
prática, no sentido de que cada um possa construir, a partir da teoria aprendida e
por meio das experiências práticas, novas teorias que sustentarão seu trabalho
como docente. Esta articulação demanda reflexão sobre os dois momentos, teórico
e prático, no processo de formação do professor.
Os estudos de Schön (2000) nos mostram a importância da reflexão na
formação profissional. Para este autor as discussões sobre a formação profissional,
e especialmente a formação do professor, não podem prescindir de uma reflexão a
partir das ações desenvolvidas na prática. Esta reflexão seria a base da construção
do conhecimento profissional, que segundo ele é tácito e dinâmico. Tácito porque se
mostra na realização da ação, mas nem sempre é passível de ser explicado ou
teorizado pelo profissional. E dinâmico, se levarmos em conta que o profissional
utiliza em sua profissão diferentes conhecimentos, os quais são construídos e
utilizados a partir de seu raciocínio.
44
As ideias centrais do pensamento de Schön (2000) são o conhecimento na
ação, a reflexão-na-ação, reflexão-sobre-a-ação e reflexão-sobre-a-reflexão-naação, assim entendidas:
• Conhecimento na ação, demonstrado na execução da ação, e que se constitui
num saber inteligente, dinâmico, que leva ao aperfeiçoamento da própria
ação.
• A reflexão-na-ação, que refere-se à reflexão realizada no momento em que a
ação é executada, possibilitando intervenção e reformulação da ação no
momento mesmo em que é desenvolvida.
• A reflexão-sobre-a-ação que leva a uma retrospectiva sobre a ação
desenvolvida, para análise e possível reconstrução. Diferentemente da
reflexão-na-ação, que ocorre no momento da ação, esta reflexão pede o
distanciamento da ação para melhor percebê-la e analisá-la.
• A reflexão-sobre-a-reflexão-na-ação que caracteriza-se pela construção pelo
profissional de sua forma pessoal de conhecer. Esta reflexão leva ao
progresso e desenvolvimento profissional.
Levando-se em conta a educação e a formação de professores, as
contribuições de Schön (2000) trouxeram uma modificação na forma de se
conceituar a formação profissional, estabelecendo a necessidade de se pensar nos
professores como profissionais autônomos e capazes de refletir criticamente sobre
suas práticas. Esta formação pode e deve ser propiciada não somente dentro da
Universidade, mas também e principalmente nos momentos de realização dos
Estágios Curriculares Supervisionados.
Sobre a reflexão encontramos os estudos de Alarcão (2003) apoiados nas
ideias de Schön (2000). Esta autora entende que o professor precisa repensar e
ressignificar o seu papel e a reflexão deve ser o ponto chave para si e para a
comunidade escolar, servindo de suporte para as decisões do dia a dia, na sala de
aula e no contexto escolar.
Alarcão (2003) destaca que a noção de professor reflexivo baseia-se na
consciência da capacidade de pensamento e reflexo que caracteriza o ser humano
45
como criativo e não como mero reprodutor de ideias e práticas que lhe são
exteriores. A formação de professores deve objetivar torná-los seres pensantes
intelectuais, capazes de gerir sua ação profissional, contribuindo para mudança e
transformação. Este profissional surge como uma pessoa que, nas situações
profissionais, atua de forma inteligente e flexível, situada e reativa. Isto implica
considerar esta concepção como o produto de uma mistura integrada de ciência,
técnica e arte por meio de uma sensibilidade quase artística. Pressupõe também
uma supervisão que vise o desenvolvimento de processos facilitadores da interação
construtiva entre todos os autores.
A autora destaca então a importância do papel do supervisor (entendido aqui
como o orientador das práticas reflexivas dos alunos), na sua relação com os
professores e os saberes, mostrando que esta supervisão pode contribuir para a
construção do conhecimento pedagógico do professor, com seu trabalho de
acompanhamento do processo de monitoração avaliativa de situações e
desempenho. O acompanhamento resume-se em uma atividade de natureza
psicossocial, de construção intra e interpessoal, com vista à formação, ao
desenvolvimento de capacidades, atitudes e conhecimentos que contribuem para a
competência profissional. Para ela, as estratégias de formação devem levar ao
desenvolvimento e à formação de professores reflexivos, competentes para
analisarem o seu cotidiano, não permanecendo apenas na solução dos seus
problemas imediatos, isolados em suas salas de aula, mas situando-os num
horizonte mais amplo que perspectiva a sua função e a de cada escola na sociedade
em que vivemos.
As informações recebidas no curso de formação são, sem dúvida, muito
importantes. Mas só o conhecimento que resulta de sua compreensão, interpretação
e reflexão, permitirá a visão e a sabedoria necessárias para mudar a qualidade do
ensino e da educação. A formação deste professor na concepção de Alarcão (2003)
pode ser incentivada e propiciada na realização dos estágios, onde há o contato e a
vivência com a escola como um todo e especificamente com a sala de aula, local de
atuação dos futuros professores. Na visão dessa autora o papel do supervisor de
estágio é fundamental para a reflexão.
46
Se por um lado a reflexão é necessária para a formação, por outro lado,
existem saberes necessários para esta formação que devem ser desenvolvidos para
que o professor possa construir sua prática docente.
Ressaltamos aqui os estudos de Tardif (2002, p.36) sobre os saberes
necessários à prática docente. O autor considera o saber do professor "um saber
plural, formado pelo amálgama mais ou menos coerente de saberes oriundos da
formação
profissional
e
de
saberes
disciplinares,
curriculares
e
saberes
experienciais".
O autor busca explicar quais são os saberes que dão suporte ao trabalho
dos professores, mostrando a multiplicidade de saberes necessários à prática
docente, o que demonstra a complexidade desta profissão.
O quadro a seguir traz a categorização dos saberes realizada por Tardif
(2002), com as fontes de aquisição e os modos de integração no trabalho docente.
Saberes dos professores
Fontes sociais de aquisição
Modos de integração no trabalho
docente
História de vida e socialização
primária
Saberes pessoais dos
professores
Família, ambiente de vida,
educação
Saberes provenientes da
formação em escolar
anterior;
A escola primária e secundária,
os estudos pós-secundários não
especializados;
Formação e socialização préprofissionais;
Saberes provenientes da
formação profissional para
o magistério;
Instituição de formação,
estágios, cursos de
capacitação;
Formação e socialização
profissionais nas instituições de
formação;
Saberes provenientes dos
programas e dos livros
didáticos usados no
trabalho;
Utilização de programas, livros
didáticos, cadernos de
exercícios, fichas;
Utilização das “ferramentas” de
trabalho e adaptação às tarefas;
Saberes provenientes de
sua própria experiência na
profissão, na sala de aula
e na escola.
Prática do ofício na escola e na
sala de aula, a experiência dos
pares.
Pela prática do trabalho e pela
socialização profissional.
Quadro 2 - Os saberes dos professores
Fonte: TARDIF, 2002, p.63.
Seus estudos mostram que se por um lado os saberes inerentes à profissão
docente estão categorizados, por outro os mesmos se movimentam numa constante
47
construção de novos conhecimentos, no que o autor chama de mobilização de
saberes.
Para melhor explicitar a categorização de saberes definida por Tardif, nos
valemos de Costa (2011), que destaca os saberes da formação profissional, os
saberes disciplinares, os curriculares e os experienciais, definindo-os como:
• Saber da formação profissional - conjunto de saberes transmitidos pelas
instituições de formação de professores. Não se limitam a produzir
conhecimentos, mas procuram também incorporá-los à prática do professor
[...] esses conhecimentos se transformam em saberes destinados a
formação científica ou erudita dos professores, e, caso sejam incorporados
à prática docente, esta pode transformar-se em prática científica, em
tecnologia de aprendizagem. [...] A articulação entre essas ciências e a
prática docente se estabelece concretamente através da formação inicial ou
contínua dos professores.
• Saber disciplinar - saberes de que dispõe a nossa sociedade, tais como
se encontram hoje integrados nas universidades, sob forma de disciplina
[...]. Os saberes disciplinares (por exemplo, matemática, história, literatura,
etc.) são transmitidos nos cursos e departamentos universitários
independentes das faculdades de educação e dos cursos de formação de
professores.
• Saber curricular - estes saberes correspondem aos discursos, objetivos,
conteúdos e métodos a partir dos quais a instituição escolar categoriza e
apresenta os saberes sociais por ela definidos e selecionados como
modelos da cultura erudita e de formação para a cultura erudita.
Apresentam-se concretamente sob a forma de programas escolares que os
professores devem aprender a aplicar.
• Saber experiencial - Baseados em seu trabalho cotidiano e o
conhecimento de seu meio. Esses saberes brotam da experiência e são por
ela validados. (COSTA, 2011, p. 36-39).
Além da necessidade de considerarmos os saberes necessários ao
professor, há outro ponto importante na constituição do mesmo como profissional: os
conhecimentos necessários à prática docente.
Shulman (1986) nos traz estudos que evidenciam a necessidade de
considerarmos diferentes conhecimentos no trabalho como professores. O autor
deixa explícito em sua categorização que um ensino de qualidade requer um
conhecimento profissional avançado, que vai além de regras simples. Tais
categorias destacam o importante papel do conhecimento do conteúdo e situam-no
como base do conhecimento profissional para o ensino.
48
- Conhecimento pedagógico geral, com especial referência aos amplos
princípios e estratégias de gestão de sala de aula e organização que
parecem transcender o assunto;
- Conhecimento dos alunos e as suas características;
- Conhecimento de contextos educativos, que vão desde trabalhos em
grupo ou em sala de aula, o financiamento do governo e dos distritos
escolares, para o caráter de comunidades e culturas;
- Conhecimento dos fins educacionais, propósitos e valores, e seus
fundamentos filosóficos e históricos;
- Conhecimento do conteúdo;
- Conhecimento do currículo, com compreensão particular dos materiais e
programas que servem como "ferramentas do comércio" para professores;
- Conhecimento pedagógico do conteúdo, que é o amálgama especial de
conteúdo e pedagogia que é exclusivamente da província de professores, a
sua própria forma especial de compreensão profissional. (SHULMAN, 1986,
p. 8).
Dentre os conhecimentos elencados, três deles se destacam, considerados
pelo autor como essenciais ao trabalho do professor: conhecimento do conteúdo da
disciplina (content knowledge), conhecimento pedagógico do conteúdo da disciplina
(pedagogical content knowledge), conhecimento do currículo (curricular knowledge).
O conhecimento do conteúdo da disciplina é entendido pelo autor como o
conjunto de conceitos, propriedades e procedimentos do conteúdo a serem
ensinados aos alunos e dominados pelo professor. Ressalta ainda que este
conhecimento não deve estar preso a regras relativas à aplicação do conteúdo e sim
que o professor conheça a natureza do conteúdo a ser ensinado, seu significado e
as diferentes formas de organizá-lo para ensinar.
Com relação ao conhecimento pedagógico do conteúdo Shulman (1986)
ressalta que é o conhecimento que advém da integração entre o conhecimento do
conteúdo da disciplina e o conhecimento que o professor deve ter de como ensinar
este conteúdo aos alunos de forma que os mesmos possam compreender e
aprender. Este tipo de conhecimento é importante na medida em que o professor
pode usar conhecimentos e recursos utilizados em outro contexto para planejar ou
improvisar uma ação em situação diversa, com o desenvolvimento de novos
conhecimentos e prática.
49
É o desenvolvimento de formas mais úteis de representação das ideias, as
analogias mais poderosas, ilustrações, exemplos, explicações e demonstrações, ou
seja, descobrir e desenvolver formas úteis de representar e formular o assunto para
torná-lo compreensível para os alunos. Este conhecimento deve incluir também uma
compreensão sobre o que torna a aprendizagem de tópicos específicos, fácil ou
difícil: as concepções e preconceitos que os estudantes de diferentes idades e
origens trazem com eles para o aprendizado dos temas mais frequentemente
ensinados nas aulas.
Por fim, ao discorrer sobre o conhecimento do currículo, o autor o apresenta
como a compreensão necessária ao professor sobre os programas e documentos
curriculares, além de suportes e materiais requeridos para o ensino da disciplina.
Além disso, aponta para duas dimensões do conhecimento curricular que são
importantes para o ensino, aspectos denominados de conhecimento curricular
horizontal e conhecimento curricular vertical.
O Conhecimento horizontal refere-se à relação do conhecimento do currículo
que deve ser ensinado na disciplina em questão com o currículo que os alunos estão
aprendendo em outras disciplinas. O conhecimento horizontal permite que o
professor utilize conhecimentos e noções adquiridos em outras disciplinas como
facilitadores do ensino de sua disciplina.
O Conhecimento vertical inclui a familiaridade com os temas e as questões
que foram e serão ministradas na mesma disciplina durante os anos anteriores e,
posteriormente, na escola, assim como os materiais que serão utilizados e
incorporados neste ensino.
A formação do professor está alicerçada nestes conhecimentos, que por sua
vez não se separam, uma vez que se ligam e interligam na constituição da prática
docente.
As considerações e discussões propiciadas pelas leituras nos levam a refletir
sobre o conceito defendido por Pimenta (2002) de formação da identidade docente.
Segundo a autora a formação docente se dá a partir da mobilização de
conhecimentos da teoria da educação e da didática necessários à compreensão do
ensino como realidade social. Além disso, o futuro professor deve ser capaz de
50
investigar a própria atividade para, a partir dela, constituir e transformar os seus
saberes, num processo contínuo de construção de suas identidades como
professores.
Pimenta (2002) destaca que a construção da identidade profissional pelos
professores se estabelece a partir de diferentes ações. Pelo significado social que
cada um dá à profissão e pela revisão constante destes significados; do confronto
constante entre teorias e práticas; da análise sistemática de práticas à luz de teorias
existentes e da construção de novas teorias.
A autora defende que esta identidade é construída também a partir do
significado que o professor, como ator e autor do processo educacional, confere à
atividade docente no seu cotidiano a partir de seus valores, sua história de vida,
suas representações e saberes, suas angústias e anseios, o modo como se situa e
se relaciona com seus pares e especialmente do sentido que tem em sua vida o ser
professor.
Para Pimenta (2002) construir a identidade docente pede o entendimento de
que a docência é um campo de saberes específicos, que incluem várias vertentes,
tais como:
 Conteúdos das diversas áreas do saber e do ensino: das ciências, naturais,
da cultura e das artes;
 Conteúdos didático-pedagógicos: diretamente relacionados ao campo da
prática profissional;
 Conteúdos relacionados a saberes pedagógicos mais amplos (do campo
teórico da prática educacional);
 Conteúdos ligados à explicitação do sentido da existência humana (individual,
sensibilidade pessoal e social).
Entendemos assim como Pimenta (2002) que a docência constitui um
campo específico de intervenção profissional, portanto, não é qualquer um que pode
ser professor. É preciso formação, comprometimento e conhecimento para organizar
51
e desenvolver um trabalho docente que efetivamente contribua para o crescimento
dos alunos, mudanças e transformações na educação e na sociedade.
Esta docência não se constitue pela simples formação universitária, pelo
diploma. Depende do desenvolvimento dos conceitos, posturas e conhecimentos,
ideias que os autores aqui citados trouxeram como contribuições para nossas
reflexões sobre a formação do professor.
Cremos que neste momento, podemos estabelecer uma reflexão sobre a
contribuição do estágio, um dos principais focos de nossa pesquisa, para a formação
do professor.
2.4.2 Contribuições teóricas sobre o estágio na formação do professor
O estágio é um espaço importante na formação do professor, com foco na
aprendizagem, e nos leva a compreender que tudo que é ensinado nas salas de
aula da Universidade é fundamental, porém não suficiente no preparo dos alunos
para exercerem suas profissões. Há a necessidade de inserir o aluno na realidade
profissional que o espera, possibilitando vivenciar as teorias e conhecimentos
adquiridos, e isto se torna possível no momento do estágio.
De acordo com Pimenta (2010, p. 21) o Estágio Supervisionado engloba "as
atividades que os alunos deverão realizar durante o seu curso de formação, junto ao
futuro campo de trabalho".
Já Piconez (2000, p. 16) afirma que "os estágios são vinculados ao
componente curricular Prática de Ensino cujo objetivo é o preparo do licenciamento
para o exercício do magistério em determinada área de ensino ou disciplina de 1° e
2° graus".
Seja qual for a fundamentação teórica dada à elaboração das normas
institucionais para a realização dos Estágios Curriculares Supervisionados, é
importante ressaltar que sempre deverá haver uma práxis reflexiva e atuante, que
forneça ao licenciando subsídios para desenvolver a prática docente com segurança
e competência.
52
Muito embora o estágio seja concebido por muitos profissionais como o
momento em que o aluno vivencia a prática e, portanto no local da formação efetiva
da prática docente, é preciso entender que o estágio é somente uma das
oportunidades em que se reflete sobre a teoria e a prática, reflexão esta fundamental
para a ação docente.
O ensino como prática reflexiva, segundo Pimenta (2006), apresenta-se
como uma tendência nas pesquisas sobre educação, mostrando a importância de se
discutir de que forma o saber docente é produzido a partir da prática reflexiva. Ao
refletir o professor consegue transformar sua prática e ao pensar em suas ações é
capaz de produzir conhecimentos sobre esta prática.
No caso dos alunos, que no contato com a escola nos períodos dos estágios
estarão refletindo e produzindo saberes que os constituirá como professores,
percebemos ainda mais a importância deste momento para esta constituição.
Muitas vezes vemos alunos do curso de Pedagogia negarem a validade da
teoria aprendida na Universidade, pois alegam que a realidade observada nos
estágios ou em seu trabalho é bem diferente de tais teorias, não percebendo a
necessidade da reflexão para mudar conceitos e transformar sua prática.
Segundo Piconez (2000) a necessária ligação entre os conteúdos
aprendidos no curso de formação e o conhecimento da sala de aula deve se dar na
realização do estágio. Ressalta que este estágio não pode se limitar a transferência
de conhecimentos e sim possibilitar a produção de conhecimento, sendo assim
importante instrumento para a formação do professor.
Pimenta (2010) entende que ser professor pede preparação, a qual se inicia
no curso de formação e é desenvolvida a partir do currículo deste curso. Neste
sentido a autora nos mostra de que forma o estágio está inserido na formação do
professor.
O estágio é um dos componentes do currículo do curso de formação de
professores. Currículo que é profissionalizante - isto é, prepara para o
exercício de uma profissão. Essa preparação é uma atividade teórica, ou
seja, atividade cognoscitiva (conhecer) e teleológica (estabelecer
finalidades; antecipar idealmente uma realidade que ainda não existe e que
se quer que exista). Para chegar à antecipação ideal de uma realidade,
requer que se parta do conhecimento (teórico-prático) da realidade que já
53
existe. Essa realidade que já existe (objetiva, prática), no entanto, não se
explica nela mesma, porque enquanto realidade histórico-social, situada,
tem sua explicação no movimento da história, da sociedade. Quer dizer, é
determinada por fatores sociais que a antecedem e por fatores sociais que
lhe são extrínsecos. (PIMENTA, 2010, p. 183, grifo do autor).
Com isso consideramos que o estágio é parte integrante do curso de
formação de professores e como tal deve ser tratado pelos professores formadores,
entendendo que a competência profissional dos futuros professores é estabelecida
nas interações que ocorrem entre professor e aluno no curso e entre professor e
estagiário na escola, cabendo ao professor na Universidade promover discussões,
reflexões e diálogos que permitam aos alunos estabelecerem a necessária ligação
entre a teoria e a prática.
2.4.3 Contribuições teóricas sobre o estágio na formação do professor que
vai ensinar Matemática nos anos iniciais do Ensino Fundamental
Nos
itens
anteriores
discorremos
sobre
saberes
e
conhecimentos
necessários ao professor para o exercício da docência. Alguns autores nos
mostraram também que para cada disciplina existem saberes e conhecimentos
específicos necessários para seu ensino, os quais devem ser desenvolvidos pelo
professor.
Assim, ao pensarmos na formação do profissional que será professor nos
anos iniciais do Ensino Fundamental, egresso do curso de Pedagogia, é necessário
analisar e compreender a complexidade deste trabalho, visto que o professor deverá
atuar no ensino de diferentes disciplinas, sem ser especialista em nenhuma delas.
Esse é um grande ponto para reflexão dos formadores de professores. Se
pretendemos discutir sobre as aprendizagens que o estágio propicia para a
formação do professor que vai ensinar Matemática nos anos iniciais do Ensino
Fundamental, é preciso primeiro pensar sobre esta formação.
Nos propomos a discutir sobre o ensino de Matemática e a formação do
professor dos anos iniciais e elegemos Curi (2005, 2011), Serrazina (1999, 2001) e
Ball (2008) para nos embasar teoricamente no que diz respeito aos conhecimentos
matemáticos necessários aos professores que vão ensinar Matemática e à questão
da contribuição do estágio na constituição destes conhecimentos.
54
A formação do professor que ensina Matemática nos anos iniciais do Ensino
Fundamental, foco de nosso trabalho, se dá nos cursos de graduação em
Pedagogia. Porém segundo Curi (2011) esta formação se inicia antes do aluno
frequentar o curso de graduação.
O professor é o único profissional que vai trabalhar no mesmo ambiente em
que foi formado, por esse motivo carrega marcas de toda sua vivência
naquele ambiente, incluindo de seus professores (bons ou ruins). Muitas
vezes ele se espelha em situações vivenciadas na sua formação anterior ao
curso de Graduação. Cada professor possui uma experiência própria de
situações de aprendizagem ou de dificuldades com a Matemática e esses
aspectos individuais são constitutivos de sua formação, ou seja, os
conhecimentos dos professores são provenientes de várias fontes e
construídos em tempos diferentes. (CURI, 2011, p. 78).
A autora nos mostra que a formação do professor se constitui não somente
das experiências vividas e conhecimentos aprendidos na graduação, mas também
de experiências e conhecimentos vivenciados na própria escola, uma vez que a
formação do professor é constituída em tempos, espaços e fontes diferentes. Este
conhecimento adquirido em diferentes fontes será ensinado pelo professor quando
estiver formado.
Ball (2008) desenvolveu uma pesquisa que nos auxilia nas reflexões sobre a
formação do professor que ensina Matemática, abordando a questão do
conhecimento pedagógico do conteúdo, conceito introduzido por Shulman (1986).
A autora destaca que é preciso discutir e analisar o que os professores
precisam conhecer e ser capazes de fazer, a fim de ensinar Matemática de forma
eficaz, ou seja, o que um ensino eficaz exige em termos de compreensão de
conteúdo? Esta questão coloca a ênfase no uso do conhecimento e no ensino, ao
invés de focar nos próprios professores.
As colocações de Ball (2008) são interessantes, pois nos levam a pensar na
formação do professor que ensina Matemática, mas muito mais que isso, naquilo
que este professor precisa saber sobre Matemática e como e onde os professores
podem usar o conhecimento matemático, na prática.
Destaca ainda que, no passado, o foco naquilo que os professores
precisavam saber conduziu a um conjunto de diferentes posições. Hoje prevalece a
visão de que os professores precisam saber que a Matemática presente no currículo
55
escolar exige um estudo mais aprofundado da Matemática durante a faculdade. A
autora nos mostra que somente a Matemática ensinada e desenvolvida na
graduação, no curso de formação de professores, não é suficiente para que o
professor a ensine no Ensino Fundamental, é preciso aprofundar o conhecimento
com cursos e formação continuada.
Esta proposição de Ball (2008) vem ao encontro das reflexões de Curi
(2011), no que diz respeito à formação para o ensino de Matemática não estar
restrito àquilo que é desenvolvido na Universidade.
Certamente essa gama de conhecimentos requer cuidados especiais dos
formadores e objetivos bem definidos nos cursos de Licenciatura em
Matemática e Pedagogia. Além disso, deve-se ter clareza de que esse
conjunto de conhecimentos é constituído em vários períodos de tempo, por
meio de várias fontes institucionais ou não e apenas nos cursos superiores.
(CURI, 2011, p. 83).
Além disso, a autora entende que é preciso repensar a forma como se
desenvolve a formação do professor para o ensino de Matemática nos cursos de
Licenciatura em Matemática ou em Pedagogia, devido à fragilidade do conhecimento
desse professor destacada por ela.
A fragilidade da relação com o conhecimento para ensinar Matemática na
atividade docente parece constituir um dos mais sérios obstáculos à efetiva
profissionalização dos professores e deve ser uma perspectiva desses
cursos. (CURI, 2011, p. 79).
Muito embora a formação anterior do professor influencie sua formação
atual, é no curso de Pedagogia que se espera o aprofundamento dos conteúdos
matemáticos, para que haja conhecimento dos conteúdos que deverão ser
ensinados nos anos iniciais do Ensino Fundamental. O que se espera é que os
professores formadores propiciem esta possibilidade de desenvolvimento de
conhecimento. No entanto, esse conhecimento tem especificidades próprias
conforme descreve Curi (2011).
Mas não um conhecimento superficial e sim aprofundado, de forma que
compreendam o significado da Matemática, sua estrutura e importância
social, que saibam identificar as dificuldades de seus alunos e que possam
intervir de modo que seus alunos superem os obstáculos do processo de
aprendizagem. (CURI, 2011, p. 83).
Serrazina (1999), pesquisadora portuguesa, também destaca que os
conhecimentos matemáticos dos professores que atuam nos anos iniciais, na
56
maioria das vezes restringem-se aos conhecimentos que trazem de seus estudos na
escola básica. Desta forma sofrem influências de suas crenças e concepções, na
maneira que concebem a Matemática e seu ensino. Assim, a autora entende que
para mudar esta concepção e modificar a forma como os professores ensinam
Matemática é preciso levar o futuro professor a refletir sobre currículos, práticas e
especialmente sobre o significado de ensino e aprendizagem de Matemática.
Segundo ela,
O professor de Matemática pode ser um agente criativo e inovador no
processo de questionamento, característico das práticas reflexivas, mas o
foco desse questionamento deve estar enraizado nos problemas que
afectam o ensino e a aprendizagem. Não há uma única abordagem no
processo de pesquisa ou de questionamento — o professor reflexivo deve
estar atento à variedade de possíveis opções. (SERRAZINA, 1999, p. 39).
Com relação à formação para ensinar Matemática propiciada no curso de
Pedagogia, é preciso que sejam apresentados ao aluno conteúdos que possibilitem
construir um conhecimento da Matemática e sobre o ensino da mesma,
especialmente com relação aos conteúdos que serão ensinados aos alunos dos
anos iniciais do Ensino Fundamental, conforme destaca Curi (2011).
É fundamental ao futuro professor de Matemática o domínio do
conhecimento matemático, não na forma de "estoque" armazenado, mas
como "domínio prático-conceitual", que o torne capaz de levar seus alunos a
serem agentes de sua própria formação, aproveitando o máximo a riqueza
dos espaços de conhecimento propiciados pelas diversas linguagens
(multimídia, Internet, livros, etc). (CURI, 2011, p. 143).
Em pesquisas anteriores Curi (2005) mostra que os cursos de Pedagogia
não propiciam aos futuros professores os conhecimentos de conteúdos matemáticos
que serão necessários em sua atuação como professor dos anos iniciais do Ensino
Fundamental, seja com relação a conceitos, procedimentos ou até mesmo a
linguagem matemática, itens necessários para a prática docente. Segundo a autora,
"parece haver uma concepção dominante de que o professor polivalente não precisa
'saber Matemática' e que basta saber como ensiná-la." (CURI, 2005, p. 62).
Em se tratando de ensino, podemos retornar ao trabalho de Ball (2008) cujo
foco é o ensino e as exigências que este deve enfrentar para a aprendizagem das
crianças. Ela propõe que nos cursos de formação se desenvolvam estudos
relacionados a atividades de ensino, necessários à consecução dos objetivos de
ensino, trabalhos individuais e coletivos.
57
Em vez de começar com o currículo ou com padrões de aprendizagem para
o aluno, estudamos qual o trabalho que está relacionado com a atividade de
ensino. [...] Que atividades fundamentais são exigidas pelos grandes
objetivos de desenvolvimento de uma sala de aula, em que a matemática é
tratada com integridade, as ideias dos alunos são levadas a sério, e
matemática é um trabalho coletivo, bem como um esforço individual?
(BALL, 2008, p. 395).
A autora destaca que entende por "conhecimento matemático para o
ensino", o conhecimento matemático necessário para levar a cabo o trabalho
realizado e desenvolvido para ensinar matemática. Importante notar novamente que
sua definição ressalta o ensino, e não os professores.
Sua preocupação volta-se para as tarefas envolvidas no ensino e nas
demandas matemáticas dessas tarefas. Porque segundo ela, ensinar Matemática
envolve mostrar aos alunos como resolver problemas, responder às suas perguntas,
e conferir os trabalhos destes alunos, o que exige uma compreensão do conteúdo
do currículo escolar.
Se por um lado o trabalho realizado no curso de formação do professor, é
importante e serve de base para sua futura atuação docente, conforme já
discorremos, este trabalho é complementado na realização do estágio curricular, que
deve propiciar a articulação entre teoria e prática. É nos estágios que o aluno do
curso de Pedagogia entra em contato com as tarefas matemáticas desenvolvidas,
observa como as crianças resolvem problemas, que dificuldades apresentam, como
respondem aos professores; o que vai exigir tanto do professor que recebe o
estagiário como do próprio estagiário a compreensão dos conteúdos matemáticos
desenvolvidos na aula observada. É no estágio que o aluno do curso de Pedagogia
constrói o que Ball (2008) denomina de “conhecimento matemático para o ensino”.
Defendemos a formação de professores reflexivos, que contextualizem sua
prática, revejam e construam novas ações para ensinar Matemática. Como propiciar
este desenvolvimento a partir da formação oferecida nos cursos de Pedagogia?
Destaca-se aqui a importância do papel do formador no trabalho com conteúdos que
realmente preparem o aluno para a docência, mas também e especialmente nas
orientações, discussões e reflexões sobre o estágio realizado pelo futuro professor
nas escolas.
58
No que se refere à formação para ensinar Matemática, entendemos que é
constituida a partir das disciplinas específicas para este ensino, mas também
desenvolvida nas observações que o aluno faz do "outro", o professor que
acompanha. Alguns alunos gostariam de uma receita, um roteiro para ensinar
Matemática, porém,
[...] a formação de professores não deve consistir no treino de receitas e
métodos que são diretamente aplicáveis na sala de aula, mas deve, em
primeiro lugar e acima de tudo, ajudar os futuros professores a desenvolver
sua autonomia. Isso implica apoiá-los no sentido de aumentarem o seu
conhecimento sobre a matemática, sobre o aprender e ensinar matemática,
como as crianças aprendem matemática, sobre a qualidade dos materiais
de ensino, etc. (SERRAZINA, 2001, p.12).
As pesquisas de Curi (2005) nos mostram a importância do estágio assim
como da disciplina Prática de Ensino oferecida no curso de formação, no
estabelecimento de um diálogo que fortalece a formação do professor para ensinar
Matemática nos anos iniciais do Ensino Fundamental.
A disciplina Prática de Ensino e Estágio Supervisionado tem como
finalidade que as competências de ordem prática ganhassem destaque,
pois não basta ao professor conhecer teorias, perspectivas e resultados de
investigação como fins em si mesmos - ele deve ser capaz de construir,
com base na relação intrínseca existente entre prática e teoria, soluções
apropriadas para os diversos aspectos de sua ação profissional, o que
requer não só a capacidade de mobilização e articulação de conhecimentos
teóricos, como também a capacidade de lidar com situações concretas,
competências que devem ser desenvolvidas progressivamente ao longo da
sua formação - durante a etapa da formação inicial e ao longo da carreira
profissional. (CURI, 2005, p.143).
A autora destaca não só a questão das aulas referentes às disciplinas
relacionadas ao ensino de Matemática ou ao momento da realização do estágio,
mas principalmente a questão das discussões que devem ocorrer nas aulas de
Prática de Ensino, momento em que o formador tem a oportunidade de ouvir os
alunos com relação à realização do estágio, e encaminhar suas reflexões para
problemas de ensino observados ou desenvolvidos.
Concordamos portanto com a autora no sentido de que as disciplinas
oferecidas no curso de Pedagogia e a realização do estágio pelo aluno, devem ser
responsáveis não só pela consolidação e ampliação dos conhecimentos relativos à
Matemática, mas especialmente pela aquisição de novos conhecimentos que
poderão ser melhor trabalhados e discutidos nas aulas de Prática de Ensino e
Orientação de Estágio Curricular Supervisionado.
59
2.5
Contribuições de pesquisas sobre o estágio no curso de Pedagogia e a
formação para ensinar Matemática nos anos iniciais do Ensino Fundamental
Pensando na questão do ensino de Matemática e a realização dos estágios
nos cursos de Pedagogia, procurou-se aprofundar o conhecimento sobre o tema, na
busca de materiais e produções que servissem de fundamentação e comprovação
às hipóteses construídas acerca da contribuição do estágio curricular no curso de
Pedagogia para a formação dos professores que vão ensinar Matemática nos anos
iniciais do Ensino Fundamental.
A busca de produções acadêmicas esbarra na falta de publicações, que
aliem o estágio realizado no curso de Pedagogia com a formação necessária para
ensinar Matemática, razão pela qual optamos por delinear um levantamento dessa
produção.
Consultamos resumos de dissertações e teses coletadas no banco de teses
da Capes, nos últimos dez anos, cobrindo o período de 2002 a 2011. Para realizar
este mapeamento, a coleta de resumos foi feita a partir das palavras-chave: Estágio,
Estágio
Pedagogia,
Estágio
Matemática.
Neste
primeiro
momento
foram
encontrados 89 resumos de teses e dissertações, sendo 24 teses de Doutorado, 59
dissertações
de
Mestrado
Acadêmico
e
6
dissertações
de
Mestrado
Profissionalizante.
Os resumos foram lidos sob a perspectiva da análise de conteúdo proposta
por Bardin (2007): pré-análise, exploração do material e análise dos dados. A fase
da pré-análise foi realizada com a coleta dos resumos a partir da pesquisa com as
palavras-chave e a leitura dos mesmos, para encontrarmos convergências ou
divergências entre eles, delimitando o foco de nossa pesquisa.
Dos 89 resumos encontrados, ainda na realização da leitura flutuante
proposta por Bardin (2007), foram encontrados resumos que tratam dos estágios
relacionados ao ensino de Matemática, em diferentes cursos de licenciatura,
conforme se pode observar no quadro a seguir:
60
Ano
2002
Nº
total
trabalhos
4
2003
4
2004
8
2005
8
2006
de
1
2
1
3
4
Física
Letras
Pedagogia
Matemática
1
1
2
2
Enfermagem
Letras
Pedagogia
Matemática
1
1
5
4
Letras
Pedagogia
1
7
Licenciaturas
Matemática
1
3
8
Letras/Inglês
Pedagogia
1
4
15
Matemática
Educação Física
Licenciaturas
Pedagogia
2
1
1
7
Matemática
6
Licenciaturas
2
Pedagogia
10
Matemática
3
6
2008
12
2011
Pedagogia
Matemática
Administração
Empresas
Pedagogia
Matemática
Letras
Pedagogia
Matemática
Nº de trabalhos
por foco
1
2
1
1
6
10
2010
Curso foco
Normal Superior
Pedagogia
2007
2009
de
14
Geografia
Total de trabalhos encontrados
1
89
Nível
Mestrado
Mestrado
Mestrado
Mestrado
Mestrado
Mestrado
Mestrado
3 - Mestrado
1 - Doutorado
Mestrado
2 - Mestrado
4 - Doutorado
Doutorado
Mestrado
Mestrado
1-Doutorado
1 – Mestrado
Mestrado
Mestrado
Mestrado
3-Mestrado
1-Doutorado
Doutorado
3-Mestrado
2- Doutorado
2- Profissionalizante
Doutorado
2 –Mestrado
1-Doutorado
Mestrado
3-Mestrado
1-Doutorado
Mestrado
Doutorado
Mestrado
5 – Mestrado
2-Doutorado
3 – Mestrado
1 - Doutorado
2 - Profissionalizante
1 - Mestrado
1 - Doutorado
5- Mestrado
4 – Doutorado
1- Profissionalizante
2 – Mestrado
1 - Doutorado
Mestrado
49 - Mestrado
25 - Doutorado
5 - Profissionalizante
Quadro 3 - Trabalhos sobre Ensino de Matemática
Fonte: Autora
A partir da primeira leitura dos resumos, pudemos destacar pesquisas que
tratavam do foco de nossa investigação, tal seja o estágio no curso de Pedagogia.
61
Esta leitura nos permitiu elencar 46 resumos, sendo 13 de Doutorado, 30 de
Mestrado Acadêmico e 3 de Mestrado Profissionalizante.
Para que pudéssemos passar à fase de exploração do material proposta por
Bardin (2007), foi feita uma leitura dos resumos com vistas à criação de unidades de
registro e de categorias. O quadro a seguir demonstra esta fase, a partir das leituras
dos 46 resumos de trabalhos analisados, sobre a realização de estágios nos cursos
de Pedagogia:
62
Foco principal
(Unidades de Registro)
Formação de professores
Nº de
trabalhos
Temas a partir do foco principal
(Categorias)
17
Significados vivenciados na formação de professores
Contribuições do Estágio na relação teoria e prática
Contribuição das disciplinas da graduação para o estágio e formação do
professor
Estágio como instrumento de integração e treinamento prático
Narrativas das experiências dos licenciandos sobre aprendizagem
Contribuições do estágio na formação do professor reflexivo para o exercício
da docência
Contribuições do estágio na formação do Pedagogo
Papel do estágio em Gestão Escolar na formação do pedagogo
Autores/Ano
Silva (2002)
Campos (2003); Sousa (2004);
Perini (2006); Vincensi (2007);
Barillari (2008); Araújo (2009);
Araújo
(2010);
Peternella
(2011).
Nunes (2005)
Barbosa (2006)
Galvão (2007)
Brasil (2010); Viana (2011)
Santos (2010); Corte (2011)
Mira (2011)
4
Mobilização de saberes: disciplinas e estágio
Papel do estágio na elaboração dos saberes docentes
Conhecimentos necessários para o exercício da docência
Contribuições do estágio na construção e mobilização de saberes
Ponte (2008)
Santos (2008)
Santos (2009)
Soares (2010)
Espaços de formação
3
O estágio na educação formal e não formal
Aprendizagem do ofício de ensinar nos espaços de formação
O estágio no curso de Formação de Professores em Serviço
Pierro (2009)
Martin (2010)
Carvalho (2011)
Formação Profissional
5
Profissionalização docente
Contribuições do estágio na construção da identidade profissional
Lima (2005)
Stivanin (2007); Magalhães
(2009); Neves (2011).
Rosa (2010)
Saberes
necessários
prática docente
à
Contribuições do estágio e da extensão universitária na formação profissional
Continua
Continuação
Foco principal
(Unidades de Registro)
Formação do professor no
contexto
das
políticas
públicas de educação
Nº de
trabalhos
Temas a partir do foco principal
(Categorias)
Autores/Ano
6
O estágio e as políticas públicas na formação de professores
Fonseca(2004)
Reformas curriculares e formação de professores
Contribuições do Programa Bolsa Formação na formação do professor
Novas Diretrizes para formação de professores: papel do estágio e
qualificação da prática pedagógica
O estágio nos projetos e programas públicos de educação e formação de
professores
Aspectos econômicos, políticos, culturais e educacionais do trabalho docente.
Estágio como mediador na formação: pesquisa e produção
O estágio na perspectiva do ensino, pesquisa e extensão.
Hissa (2005)
Lazzarin (2011)
Raymundo (2011)
Sales (2011)
Pilonetto (2007)
Godoy (2005)
Ulhoa (2007)
Estágio e Pesquisa
2
Estágio
e
formadores
professores
4
Relações estagiário e professor em exercício
Importância da supervisão na realização dos estágios curriculares
Interferências do professor em exercício na formação da função docente
O estágio e o professor formador
França (2005)
Silvestre (2008)
Sambugari (2010)
Cruz (2004)
Ensino e Aprendizagem de
Matemática
5
Ensino de Matemática nos anos iniciais do Ensino Fundamental
Contribuição dos estágios na formação de conhecimentos escolares
matemáticos do professor que vai ensinar Matemática
Conhecimentos relacionados à Matemática presentes nas ementas do curso
de formação do professor- Pedagogia
Contribuições do estágio e disciplinas relacionadas à Matemática na formação
de professores dos anos iniciais do Ensino Fundamental
Concepções em relação à Matemática e o processo de ensino e
aprendizagem
Bukowitz (2005)
Mioto (2008)
Total
de
analisados
trabalhos
Mello (2008)
Costa (2011)
Zimer (2008)
46
Quadro 4 - Resumo dos trabalhos pesquisados: focos e categorias
Fonte: Autora
63
64
2.5.1 Análise dos dados
A organização dos trabalhos coletados nos levou a estabelecer os seguintes
focos ou unidades de registro:
1) Formação de professores - 17 trabalhos
2) Saberes necessários à prática docente – 4 trabalhos
3) Espaços de formação – 3 trabalhos
4) Formação Profissional – 5 trabalhos
5) Formação do professor no contexto das Políticas Públicas de
Educação – 6 trabalhos
6) Estágio e Pesquisa – 2 trabalhos
7) Estágio e professores formadores – 4 trabalhos
8) Ensino e Aprendizagem de Matemática – 5 trabalhos
Em virtude do tema de nossa pesquisa: a contribuição dos estágios no curso
de Pedagogia para ensinar Matemática nos anos iniciais do Ensino Fundamental -,
realizamos uma terceira leitura, que nos permitiu selecionar somente os trabalhos
que tratavam do estágio no curso de Pedagogia, no que se refere à formação do
professor que vai ensinar Matemática nos anos iniciais do Ensino Fundamental.
Das leituras realizadas pudemos perceber que a unidade de registro que
atende aos objetivos de nossa pesquisa é a de número 8 - Ensino e a Aprendizagem
de Matemática. Passamos a descrever e analisar os trabalhos pertencentes a este
foco por considerarmos mais relevante neste momento direcionarmos nossas
considerações para os objetivos deste trabalho. Esta unidade de registro é composta
de cinco trabalhos.
O primeiro trabalho desta unidade, alocado na categoria “Ensino de
Matemática nos anos iniciais do Ensino Fundamental”, refere-se ao trabalho de
Bukowitz (2005). É uma tese de doutorado que traz discussões sobre o ensino de
65
Matemática nos anos iniciais do Ensino Fundamental. A pesquisa constitui-se a
partir do desenvolvimento de oficinas aplicadas aos alunos do curso de Pedagogia
de duas instituições privadas do Rio de Janeiro. A autora esperava que as oficinas
trouxessem a articulação entre pesquisa e ensino, para que se pudesse intervir
sobre práticas dos participantes, em relação à abordagem ao ensino da matemática,
nos anos iniciais do ensino fundamental.
As situações de aprendizagem propiciadas nas oficinas e especialmente as
observações
de
situações
de
estágio,
levantaram
algumas
questões
problematizadoras que possibilitaram à autora algumas considerações. Ela ressalta
a influência de significados afetivos que perpassam concepções dos estudantesprofessores sobre a matemática e sobre o ensino e aprendizado dessa ciência.
Demonstra também que é necessário que se mudem as “dinâmicas dos cursos de
formação de professores e as das escolas, tanto como a do reconhecimento da
viabilidade
de
propostas
semelhantes
em
variados
contextos,
visando
à
humanização do ensino da matemática”. (BUKOWITZ, 2005).
O segundo trabalho desta unidade de registro é de Mello (2008), com a
categoria “Conhecimentos relacionados à Matemática presentes em um curso de
formação do professor - Pedagogia”. Refere-se a uma dissertação de Mestrado
Profissionalizante, que num primeiro momento analisou as ementas das disciplinas
de Matemática de um curso de Pedagogia de uma instituição privada de ensino da
zona oeste da cidade de São Paulo. Num segundo momento acompanhou as aulas
de Matemática desse curso, visando perceber de que forma se dá a articulação
entre os conhecimentos presentes nas ementas e o desenvolvimento dos mesmos.
A autora analisou ainda ementas de trinta cursos de Pedagogia.
As considerações finais da autora mostram que os cursos analisados
priorizam as questões metodológicas em detrimento de conteúdo matemático. No
entanto, no curso que acompanhou ressalta como principais resultados os
procedimentos metodológicos adotados pela professora formadora, uma proposta
pedagógica adaptada à realidade das alunas que compõem a turma estudada,
procurando nas aulas aliar a teoria à prática, na busca de contemplar as três
vertentes do conhecimento propostas por Shulman (1986): o conhecimento do
conteúdo, o conhecimento didático do conteúdo e o conhecimento curricular. No
66
resumo não há destaque para as contribuições do estágio na formação do professor,
pois não era o foco do trabalho dessa pesquisadora.
A tese de doutorado de Zimer (2008) é o terceiro trabalho dessa unidade.
Trata-se da categoria “Concepções em relação à Matemática e o processo de
ensino e aprendizagem”. O objetivo de seu trabalho é “conhecer de que maneira o
futuro professor estabelece conexões entre suas concepções e a prática pedagógica
pré-profissional de modo a permitir a compreensão sobre o modo como ele aprende
a ensinar Matemática.” (IBID., 2008).
A obtenção de dados para a pesquisa se deu por meio de questionários
aplicados na disciplina Metodologia do Ensino da Matemática e com entrevistas
reflexivas realizadas durante o período de desenvolvimento do estágio. Embora a
autora destaque os estágios na formação dos professores para o ensino da
Matemática nos anos iniciais do Ensino Fundamental do curso de Pedagogia, seu
foco principal neste trabalho são as concepções que os alunos têm em relação à
Matemática e o processo de ensino e aprendizagem.
A autora destaca alguns resultados que obteve com suas análises: o futuro
professor vincula as próprias experiências com a escolarização como meio de
estabelecer conexões entre suas concepções e a prática pedagógica. Além disso,
percebeu que o estágio em docência é muito importante na aprendizagem da
docência e que o professor formador é elemento mediador entre as concepções
pessoais e a prática pedagógica dos futuros professores. Assim, considera-se que a
análise da evolução conceitual se constitui em um caminho interessante para as
discussões relacionadas à formação de professores que vão ensinar Matemática
nos anos iniciais.
Os dois últimos trabalhos são as dissertações que tratam do tema das
contribuições do Estágio Curricular no curso de Pedagogia, para a formação do
professor que vai ensinar Matemática nos anos iniciais do Ensino Fundamental.
Com o foco “Contribuição dos estágios na formação de conhecimentos
escolares matemáticos do professor que vai ensinar Matemática”, Mioto (2008) nos
apresenta sua dissertação de Mestrado Profissionalizante cujo objetivo é investigar a
formação de conhecimentos escolares matemáticos dos anos iniciais nas atividades
67
de Estágio Supervisionado e Prática como componente curricular. Este trabalho visa
também contribuir para que haja um aperfeiçoamento na formação inicial de
professores dos anos iniciais. Utilizando-se de um estudo de caso, o autor buscou
identificar “as contribuições para a formação de conhecimentos escolares
matemáticos para o futuro professor durante sua formação na universidade, no
curso de Pedagogia, e na escola onde desenvolve seu estágio”. (MIOTO, 2008).
Os dados para análise foram obtidos por meio de análise documental e
entrevistas com professoras de um Curso de Pedagogia, uma aluna que realizou
estágio e a professora regente da escola campo de estágio. Buscou analisar a
investigação, reflexão e crítica sobre o processo de ensino e aprendizagem da
Matemática nas atividades de estágio e prática, assim como a forma como a
professora regente contribuiu para que a futura professora dos anos iniciais pudesse
construir o conhecimento escolar matemático.
O autor conclui que há um distanciamento entre a Universidade e a escola,
uma vez que é de responsabilidade da estagiária a realização do estágio nos termos
dos documentos da instituição, assim como das orientações da professora regente.
O autor entende que nesta questão deveria haver mais diálogo, reflexão e
investigação por parte dos agentes formadores.
Por fim, Costa (2011), com a categoria “Contribuições do estágio e
disciplinas relacionadas à Matemática na formação de professores dos anos iniciais
do Ensino Fundamental”, expõe sua dissertação de Mestrado Profissionalizante,
referente uma pesquisa relacionada à formação inicial de professores dos anos
iniciais do Ensino Fundamental. O objetivo de seu trabalho é destacar quais
contribuições as disciplinas relativas ao ensino de Matemática podem oferecer para
formação dos professores em um curso de Licenciatura em Pedagogia.
Sua pesquisa utilizou-se das disciplinas ligadas à metodologia e ensino de
Matemática, assim como dos relatórios do Estágio Curricular Obrigatório. Os
instrumentos utilizados foram questionários e diários de aula dos alunos do curso de
Pedagogia. A autora analisou especificamente o Estágio e sua influência no
desenvolvimento profissional dos futuros professores que vão ensinar Matemática
nos anos iniciais do Ensino Fundamental.
68
Suas conclusões mostram que as abordagens tradicional e tecnicista,
fizeram parte da escolaridade dos professores pesquisados, influenciando suas
concepções sobre a Matemática e sua prática. Ressalta ainda que,
Identificamos a necessidade de reestruturarmos as propostas de formação
matemática inicial para o professor dos anos iniciais, a partir da imagem
construída da Matemática ao longo da escola básica e das demandas que
emergem da sala de aula, como caminho para estreitar a relação professor
e a Matemática. (COSTA, 2011).
A leitura e análise realizadas nos levaram a duas produções relevantes para
nosso trabalho por tratarem do ensino de Matemática no curso de Pedagogia e
sobre o estágio. São elas:
 O professor que ensina matemática nos anos iniciais do Ensino
Fundamental: limites e possibilidades do curso de licenciatura em
Pedagogia, defendida em 2011 por Shirley Conceição Silva da Costa, na
Universidade Cruzeiro do Sul;
 As inter-relações entre Universidade e escola básica: o estágio e a prática
de futuros professores das séries iniciais na construção de conhecimentos
pedagógicos da matemática, defendida em 2008 por Rodrigo Mioto, na
Pontifícia Universidade Católica de São Paulo.
Por esse motivo aprofundamos as leituras desses trabalhos. Vale ressaltar
que ambas as dissertações que tratam do foco de nossa pesquisa são produções do
Mestrado Profissionalizante e oriundas de Universidades particulares da cidade de
São Paulo.
As conclusões de Mioto (2008) apontam para a necessidade de uma
aproximação entre a escola e a Universidade para que a realização do estágio e
suas contribuições para a formação do conhecimento matemático não seja
responsabilidade única do estagiário. Nesse sentido sugere mais diálogo e reflexão
por parte dos formadores destes estagiários, aqui incluídos os professores da
Universidade, responsáveis pelas disciplinas ligadas à formação matemática e o
professor da escola que acompanha os alunos nas atividades de estágio.
69
Costa (2011) conclui seu trabalho mostrando que a formação matemática
dos professores dos anos iniciais é influenciada pelas abordagens tradicional e
tecnicista, presentes em suas concepções sobre a Matemática e sua prática.
Percebemos que ambos os autores acenam com a necessidade de revisão
da formação matemática e da contribuição dos professores formadores na
Universidade para com os que acompanham os alunos de Pedagogia nas escolas
durante o estágio.
Nenhum dos dois trabalhos aponta o tipo de tarefa realizada pelos alunos do
Ensino Fundamental nem as reflexões dos estagiários sobre essas tarefas.
Com este mapeamento pretendíamos encontrar trabalhos que nos dessem
subsídios para avançar nas considerações sobre a realização dos estágios no curso
de Pedagogia.
Pudemos perceber nas leituras, que os autores consideram que a realização
de estágios no curso de Pedagogia é importante na medida em que a partir desta
atividade os alunos poderão aliar teoria e prática, numa formação mais completa e
contextualizada. Objetiva-se que o aluno observe a prática do professor nas aulas
de Matemática e alie esta prática ao conhecimento adquirido na Universidade. No
entanto, os autores não apresentaram experiências positivas que contribuíssem para
a formação dos professores por meio dos estágios realizados, nem pistas que
permitam melhorar os estágios.
Consideramos que as discussões apresentadas neste levantamento são
importantes na medida em que podemos perceber a carência de produções e
pesquisas no que diz respeito aos estágios curriculares no curso de Pedagogia,
especialmente quanto à formação do professor que vai ensinar Matemática nos anos
iniciais do Ensino Fundamental, o que reforça a relevância desta pesquisa.
2.6
Considerações sobre o Capítulo
Considerando-se nossa preocupação em identificar “se” e “como” os
estágios contribuem para as reflexões dos sujeitos da pesquisa, com relação ao
70
aprender a ensinar de Matemática, este capítulo nos trouxe várias reflexões sobre o
tema.
Podemos perceber como ponto comum nas ideias dos autores que deram
suporte às nossas reflexões sobre o ensino de Matemática, a questão de que os
professores devem conhecer a disciplina que ensinam, sendo fundamental para a
competência deste professor.
As contribuições de Schön (2000) e Alarcão (2003) nos mostraram que a
formação do professor deve passar pela reflexão sobre sua prática, na constituição
do conhecimento profissional e na formação de profissionais autônomos, críticos e
capazes de modificar e transformar suas práticas.
Esta formação profissional deve estar alicerçada na mobilização de saberes,
segundo Tardif (2002) necessários e que não estão somente no curso de formação:
são saberes pessoais, saberes oriundos da formação escolar, dos materiais
utilizados no trabalho e na própria experiência docente.
Os saberes profissionais do professor estão ligados aos conhecimentos
necessários à docência, que na concepção de Shulman (1986) relacionam-se ao
conhecimento do conteúdo, conhecimento pedagógico do conteúdo e conhecimento
do currículo.
As contribuições dos autores sobre a formação do professor culminam com
Pimenta (2002) e a questão da formação da identidade docente. Em nosso
entendimento a autora fecha as discussões dos autores citados anteriormente
quando nos mostra que a identidade docente pede a mobilização de conhecimentos
da teoria e da didática. Entendemos que esta mobilização vai ao encontro das
produções citadas, na questão dos saberes e conhecimentos necessários para a
formação docente, assim como na necessidade de reflexão para que estes saberes
e conhecimentos possam ser ampliados, tratados e modificados conforme a
necessidade dos alunos ou à luz de novas teorias.
Concordamos com Pimenta (2002) no que diz respeito à docência ser um
campo específico de intervenção profissional, sendo que não é qualquer pessoa que
pode ser professor. É preciso formação, comprometimento, escolhas e orientação
71
para ser professor. Esta formação, portanto, não diz respeito somente à parte
pedagógica, mas espera-se que o professor conheça os conteúdos que deverá
ensinar. Entendemos que se o professor não conhece o conteúdo não será capaz de
levar o aluno à aprendizagem deste conteúdo. Porém é também sabido que saber
bem sobre um assunto pode não ser suficiente para seu ensino.
Os autores nos mostram que a Matemática que os professores trabalham
com seus alunos nos anos iniciais do Ensino Fundamental nem sempre tem suporte
na Matemática ensinada e aprendida nas aulas da Universidade.
Além disso, as dificuldades adquiridas na formação básica em Matemática
influenciam a formação para o ensino, conforme ressalta Curi (2011), entendendo
que há fragilidades no conhecimento para o ensino sendo que os conteúdos
trabalhados na formação na Universidade deveriam ser mais aprofundados.
Também Ball (2008) nos mostra que a Matemática aprendida na escola e na
graduação não é suficiente para fazer frente às necessidades de ensino do futuro
professor.
As reflexões que realizamos neste Capítulo nos indicam que a formação do
professor acontece também no momento de realização do estágio. Piconez (2000),
Alarcão (2003) e Pimenta (2010) nos mostram que o estágio é parte integrante do
curso de formação, desenvolvido no futuro local de trabalho dos professores,
permitindo que a formação seja estimulada e propiciada no contato direto com a
escola e com a sala de aula.
Com base nos autores citados nesse Capítulo, apontamos a importância da
formação para ser professor e para ensinar Matemática, e a realização do estágio
como parte integrante desta formação. Destaca-se que deve haver uma integração
entre o aluno estagiário, a Universidade e o professor observado, numa necessária
ligação entre a teoria e a prática.
Estas reflexões nos levarão, no próximo Capítulo, à contextualização da
pesquisa, pensando na forma como o estágio é desenvolvido pelos alunos da
Universidade pesquisada e nas contribuições das disciplinas relativas ao ensino de
Matemática para a formação do professor.
73
CAPÍTULO 3 - CONTEXTUALIZANDO A PESQUISA
Um professor não estará nunca inteiramente
formado, por uma ou outra razão.
(Arnon Andrade).
3.1
Introdução
Neste Capítulo, visando evidenciar o contexto desta pesquisa, vamos
apresentar questões relativas ao Estágio Curricular Supervisionado, no que diz
respeito à Universidade e à sua realização nas escolas de Ensino Fundamental.
Trataremos da legislação que rege o estágio e seu desenvolvimento na
Universidade em questão. Vamos ainda abordar a questão das disciplinas
oferecidas no curso de Pedagogia, no que se refere ao ensino de Matemática e à
prática de ensino.
Além disso, apresentaremos as escolas como cenário de realização do
estágio, completando o contexto com o perfil dos estagiários, das escolas e das
professoras que acompanharam estes estagiários nas referidas escolas.
3.2
Procedimentos Metodológicos
Para pesquisar e discutir a questão da realização dos estágios na
Universidade em questão, optamos pela utilização da Pesquisa Documental.
Segundo Gil (2002, p. 45-47), "a pesquisa documental vale-se de materiais
que não receberam ainda um tratamento analítico, ou que ainda podem ser
reelaborados de acordo com os objetos da pesquisa". Partimos portanto em busca
de documentos e não somente de produções disponíveis nas bibliotecas ou em
outras formas de publicação.
Os documentos analisados foram as leis publicadas e em vigência em
relação à formação de professores no curso de Pedagogia e à realização do Estágio
Curricular; o Projeto Pedagógico do curso de Pedagogia da Universidade em
questão e o Regulamento de Estágio da instituição escolhida para a pesquisa, além
74
dos planos de ensino das disciplinas Fundamentos e Metodologia do Ensino de
Matemática I e II e Prática de Ensino e Estágio Curricular Supervisionado nos anos
iniciais do Ensino Fundamental.
Neste capítulo a pesquisa documental se constituiu no principal caminho
para a obtenção de dados que possam auxiliar o entendimento das bases legais
para a realização do estágio, pois permitiu a compreensão da situação dos estágios
no curso de Pedagogia da Universidade analisada e até mesmo na produção de
novos conhecimentos, além do que os documentos se “constituem fonte rica e
estável de dados". (GIL, 2002, p.46).
Por outro lado a análise dos planos de ensino contribuiu para a verificação
das declarações dos alunos sobre a falta de aprendizagem de Matemática na
graduação, o que segundo eles dificulta o futuro ensino da disciplina.
A pesquisa documental também foi utilizada para a análise e apresentação
de três perfis que a nosso ver se destacam na constituição do contexto da pesquisa:
o perfil dos estagiários, da escola e dos professores que acompanharam esses
estagiários.
Tomando-se por base a individualidade de cada aluno participante, no que
diz respeito aos conhecimentos prévios, formação e expectativas de aprendizagem,
além do fato de realizarem as observações de estágio em escolas e anos de
escolaridade diferentes, fizemos uma análise de cada participante, da escola na qual
estagiou e do professor que o recebeu; a partir dos portfólios elaborados pelos
estagiários.
Conforme já citado quando nos referimos aos procedimentos da pesquisa,
os portfólios serão nosso principal instrumento de coleta de dados, os quais são
definidos por Hernández (1998), como uma coleção seletiva de itens que revelam,
conforme o processo se desenvolve, a reflexão sobre os diferentes aspectos do
crescimento e do desenvolvimento de cada aluno, ou de cada grupo de alunos.
Além disso, nos portfólios elaborados pelos estagiários encontramos várias
fontes de pesquisa, conforme destaca Yin (2005). Cada sujeito da pesquisa elaborou
uma narrativa com sua história de vida, relatando suas experiências, trazendo seu
75
caminho acadêmico desde a educação básica, ressaltando suas experiências com a
Matemática, o ingresso no curso de Pedagogia e suas expectativas profissionais.
Cada um discorreu também sobre a realização do estágio curricular, o ingresso e
participação no grupo de pesquisa do Programa Observatório da Educação, com
destaque para as aprendizagens propiciadas para o ensino de Matemática.
Consideramos que essa narrativa se aproxima do que autores destacam
como História de Vida, pois apresenta uma retrospectiva de experiências pessoais e
profissionais, fatos significativos para sua vivência e constituição de sua identidade
profissional, em consonância com Chizzotti (2006, p. 101): “História de vida é um
relato retrospectivo da experiência pessoal de um indivíduo, oral ou escrito, relativo
a fatos e acontecimentos que foram significativos e constitutivos de sua experiência
vivida”.
As histórias de vida são importantes na medida em que, ao nos mostrarem
os caminhos percorridos pelo narrador em sua trajetória e formação profissional,
permitem analisar e compreender como se deu o processo de formação escolar, em
especial com relação à Matemática, até o momento da escolha em se tornar
professor, evidenciando a escolha pessoal da profissão.
Na realização dos estágios curriculares, solicitamos aos alunos que
aplicassem dois questionários, um para a diretora da escola4 e outro para o
professor5 que os recebeu, que nos trariam informações importantes sobre o perfil
das escolas e dos professores que recebem estes alunos.
3.3
A Legislação Vigente e os Estágios
Pode-se conceituar Estágio Curricular Supervisionado como um conjunto de
atividades de formação, que deverão ser supervisionadas por docentes da
instituição e acompanhadas por profissionais da área, de forma que o aluno possa
vivenciar situações de aprendizado profissional. Esta concepção está amparada pelo
art. 82 da Lei de Diretrizes e Bases da Educação Nacional – LDBEN nº 9.394/96:
4
5
Apêndice B – “Perfil da escola”
Apêndice C – “Perfil do professor”
76
Os sistemas de ensino estabelecerão as normas para a realização de
estágios dos alunos regularmente matriculados no ensino médio ou superior
em sua jurisdição.
Parágrafo único. O estágio realizado nas condições deste artigo não
estabelece vínculo empregatício, podendo o estagiário receber bolsa de
estágio, estar segurado contra acidentes e ter a cobertura previdenciária
prevista na legislação específica. (BRASIL, 1996).
As atividades a serem desenvolvidas no Estágio Curricular Supervisionado
deverão atender às exigências de formação de cada área de conhecimento,
conforme definidas nas respectivas Diretrizes Curriculares Nacionais para os Cursos
de Graduação. Nelas estarão detalhados os Parâmetros Curriculares para o Estágio
Curricular, como por exemplo, o formato, a abrangência e a carga horária mínima,
sem que com isso se contrarie a legislação específica sobre estágio, Lei n° 11.788
de 25 de setembro de 2008, que dispõe sobre o estágio de estudantes:
º
Art 1 Estágio é ato educativo escolar supervisionado, desenvolvido no
ambiente de trabalho, que visa à preparação para o trabalho produtivo de
educandos que estejam frequentando o ensino regular em instituições de
educação superior, de educação profissional, de ensino médio, da
educação especial e dos anos finais do ensino fundamental, na modalidade
profissional da educação de jovens e adultos.
§ 1º O estágio faz parte do projeto pedagógico do curso, além de integrar o
itinerário formativo do educando.
§ 2º O estágio visa ao aprendizado de competências próprias da atividade
profissional e à contextualização curricular, objetivando o desenvolvimento
do educando para a vida cidadã e para o trabalho. (BRASIL, 2008).
Os cursos de licenciatura destinam-se à formação para a docência, porém
como reza a lei, cada curso deverá estabelecer suas próprias normas de realização
dos estágios. Assim sendo, os cursos, de acordo com as especificidades de seu
Projeto Pedagógico, deverá direcionar as atividades exigidas no estágio para a
atividade profissional de seus alunos, pensando em sua inserção futura no mercado
de trabalho e na sociedade. Alguns procedimentos devem seguir determinação
legal, enquanto outros podem ser normatizados por ato institucional, que visa
atender às necessidades específicas de cada curso.
As considerações a seguir baseiam-se na
legislação
educacional,
especificamente focada no Curso de Licenciatura em Pedagogia6.
6
Lei n° 9.394/96 - Lei de Diretrizes e Bases da Educação Nacional
Resolução CNE/CP 1; 2006 – Diretrizes Curriculares Nacionais para o Curso de Graduação em
77
O Parecer CNE/21 de 2001, assim define o Estágio Curricular:
[...] tempo de aprendizagem que, através de um período de permanência,
alguém se demora em algum lugar ou ofício para aprender a prática do
mesmo e depois poder exercer uma profissão ou ofício. Assim o estágio
supõe uma relação pedagógica entre alguém que já é um profissional
reconhecido em um ambiente institucional de trabalho e um aluno estagiário
[...] é o momento de efetivar um processo de ensino/aprendizagem que,
tornar-se-á concreto e autonomo quando da profissionalização deste
estagiário. (CNE, 2001).
Este Parecer nos mostra que a realização do estágio pelos licenciandos de
Pedagogia deve privilegiar a articulação teoria e prática, voltadas para as áreas
específicas de formação docente previstas nesta Resolução, a qual institui as
Diretrizes Curriculares para o Curso de Pedagogia.
Focando no curso de Pedagogia, encontramos na Resolução CNE/CP n° 1,
de 15 de maio de 2006:
Art. 4° O curso de Licenciatura em Pedagogia destina-se à formação de
professores para exercer funções de magistério na Educação Infantil e nos
anos iniciais do Ensino Fundamental, nos cursos de Ensino Médio, na
modalidade Normal, de Educação Profissional na área de serviços e apoio
escolar, bem como em outras áreas nas quais sejam previstos
conhecimentos pedagógicos. (CNE, 2006).
Este artigo remete à diversidade de funções que o futuro professor poderá
exercer e se levarmos em conta o Parecer citado anteriormente, o curso de
Pedagogia deveria proporcionar a seus alunos momentos em que fosse possível
efetivar o processo de ensino e aprendizagem permitindo a profissionalização e a
autonomia do estagiário.
No nosso entender torna-se praticamente impossível ao futuro professor se
profissionalizar em todas essas funções, sendo que, ou os cursos deveriam focar
parte delas, ou os futuros professores deveriam escolher algumas delas.
O artigo 7° das referidas Diretrizes destaca as horas destinadas ao estágio e
reforça que este deve contemplar a Educação Infantil, o Ensino Fundamental e
outras áreas específicas, de acordo com o Projeto Pedagógico da instituição:
Art. 7° O curso de Licenciatura em Pedagogia terá a carga mínima de 3.200
horas de efetivo trabalho académico, assim distribuídas: [...] II - 300 horas
dedicadas ao Estágio Supervisionado prioritariamente em Educação Infantil
e nos Anos Iniciais do Ensino Fundamental, contemplando também outras
Pedagogia, Licenciatura
78
áreas específicas, se for o caso, conforme o projeto pedagógico da
instituição (CNE, 2006).
A Resolução CNE/CP n° 1, dá continuidade às instruções referentes ao
Estágio Supervisionado, reforçando a ideia de que o futuro professor tenha várias
especificidades para exercer diversas funções na escola:
Art. 8° Nos termos do projeto pedagógico da instituição, a integralização de
estudos será efetívada por meio de: IV - estágio curricular a ser realizado,
ao longo do curso, de modo a assegurar aos graduandos experiência de
exercício profissional, em ambientes escolares e não-escolares que
ampliem e fortaleçam atitudes éticas, conhecimentos e competências:
a) na Educação Infantil e nos anos iniciais do Ensino Fundamental,
prioritariamente;
b) nas disciplinas pedagógicas dos cursos de Ensino Médio, na modalidade
Normal;
c) na Educação Profissional na área de serviços e de apoio escolar;
d) na Educação de Jovens e Adultos;
e) na participação em atividades da gestão de processos educativos, no
planejamento, implementação, coordenação, acompanhamento e avaliação
de atividades e projetos educativos;
f) em reuniões de formação pedagógica. (CNE, 2006).
A leitura e análise dos documentos oficiais que subsidiam a formação do
professor para os anos iniciais do Ensino Fundamental, realizadas até aqui, mostram
que a formação que se pretende é de um profissional generalista que pode atuar em
diferentes funções na Educação Infantil, nos anos iniciais do Ensino Fundamental,
no Ensino Médio (na formação de outros professores) e na Educação de Jovens e
Adultos – EJA.
No entanto, ao que parece, não têm a preocupação com os objetos de
ensino, ou seja, com as áreas do conhecimento que serão desenvolvidas na
escolarização das crianças. Em nenhum momento, até aqui, houve indicações de os
estágios serem realizados com foco no ensino das áreas.
Cabe destacar que, no Estado de São Paulo, desde 2002 não existem mais
os cursos de formação de professores de nível médio (as habilitações para o
magistério) e que o curso de Pedagogia é o único que objetiva a formação do
professor que vai atuar na Educação Infantil ou nos anos iniciais do Ensino
Fundamental.
79
Consideramos que não há uma preocupação quanto à formação do
professor que vai ensinar várias disciplinas, o aluno do curso de Pedagogia. O
mesmo pode realizar o Estágio Curricular com foco em diferentes âmbitos, não
havendo determinação de observarem-se os professores atuando com diferentes
disciplinas, mas acaba atuando nos anos iniciais do Ensino Fundamental e precisa
ensinar diferentes disciplinas.
Portanto, muito embora o aluno do curso de Pedagogia será efetivamente
um professor que vai ensinar Matemática, não há nas Diretrizes ou em qualquer
outra legislação que rege a realização dos Estágios Curriculares Supervisionados,
qualquer orientação sobre observações que direcionem para a formação desse
professor para ensinar Matemática nos anos iniciais do Ensino Fundamental.
O que se percebe é que a legislação ressalta a autonomia da instituição
formadora nas orientações e exigências quanto à realização dos estágios pelos
futuros pedagogos, com foco nas práticas docentes em geral e na gestão
educacional, sem especificar as diferentes disciplinas que deverão ser trabalhadas
pelo futuro professor.
As Diretrizes Curriculares Nacionais para o curso de Pedagogia destacam
ainda em seu Art. 8°:
Nos termos do projeto pedagógico da instituição, a integralização de
estudos será efetivada por meio de:
[...] II - práticas de docência e gestão educacional que ensejem aos
licenciandos a observação e acompanhamento, a participação no
planejamento, na execução e na avaliação de aprendizagens, do ensino ou
de projetos pedagógicos, tanto em escolas como em outros ambientes
educativos; [...]. (CNE, 2006).
Interessante ressaltar que, de acordo com as Diretrizes, caso a Instituição
assim determinar, os licenciandos de Pedagogia poderão realizar seus estágios
supervisionados
em
ambientes
não
escolares,
como
empresas,
classes
hospitalares, brinquedotecas, ONGs ou qualquer ambiente em que se necessite de
uma ação educativa, prerrogativa especial dos pedagogos. Esta prerrogativa,
quando assumida, afasta ainda mais o futuro professor do ensino das diferentes
áreas de conhecimento, de suas observações e formação para tal atuação.
80
Os princípios que regem a legislação vigente nos permitem afirmar que a
formação propiciada na graduação é importante, mas não suficiente, sendo
necessário que o estágio proporcione a vivência na sala de aula e a participação no
cotidiano escolar para que os alunos possam se preparar para exercer sua
profissão.
Dessa forma consideramos que o futuro professor pode encontrar no estágio
subsídios que o sustentem na prática docente, no desenvolvimento de um trabalho
polivalente, tendo em vista sua atuação nos anos iniciais do Ensino Fundamental,
nos diferentes campos do conhecimento, e não uma formação ampla e generalista
como a proposta na legislação.
3.4
Sobre o estágio no curso de Pedagogia da Universidade pesquisada
Na Universidade pesquisada o Estágio Curricular Supervisionado de todas
as licenciaturas tem suas orientações ditadas por um Núcleo de Formação e
Estágios. Tais orientações vêm ao encontro do estabelecido em lei, porém
semestralmente são realizadas reuniões com representantes de cada curso, para
que se possam fazer considerações quanto à operacionalização do Estágio
Supervisionado e sobre os procedimentos adotados na sua realização.
Todos os procedimentos e orientações são contemplados no "Regulamento
do Estágio Curricular Supervisionado e da Prática de Ensino e Orientação de
Estágio Curricular Supervisionado das Licenciaturas" da referida instituição, o qual é
atualizado a cada ano.
Em se tratando da disposição na matriz curricular e da denominação da
atividade de estágio, o Regulamento determina que:
Art. 2º - O Estágio Curricular Supervisionado (ECS) obrigatório será tratado
como atividade e, sob o acompanhamento, na universidade, de professororientador de ECS, estará pedagogicamente articulado à Prática de Ensino,
constituindo atividade semestral denominada Prática de Ensino e
Orientação de Estágio Curricular Supervisionado. (CNE, 2006).
Até 2008 as 300 horas de observação do Estágio Curricular Supervisionado
eram assim divididas:
81
a) 100 horas na Educação Infantil, divididas em 50 horas no 3° semestre e 50 horas
no 4° semestre;
b) 140 horas nos anos iniciais do Ensino Fundamental, divididas em 70 horas no 5°
semestre e 70 horas no 6° semestre;
c) 60 horas na Administração Escolar ou Orientação Educacional, cumpridas no 7°
semestre.
Note-se que nesta ocasião o curso tinha a duração de sete semestres.
Os alunos ingressantes em 2008 cumpriam a mesma carga horária dividida
nos semestres, porém no 7° semestre realizavam estágio de observação em Gestão
Escolar.
Neste mesmo período os alunos tinham duas disciplinas distintas, com 40h/a
cada: a Prática de Ensino (em Educação Infantil, anos iniciais do Ensino
Fundamental, Administração Escolar ou Orientação Educacional) e a Orientação de
Estágio Curricular (em Educação Infantil, anos iniciais do Ensino Fundamental,
Administração Escolar ou Orientação Educacional).
A partir de 2009, com a modificação da Matriz Curricular, o curso voltou a ter
a duração de seis semestres e a divisão da carga horária a ser cumprida nos
estágios passou a ser seguinte:
a) 100 horas na Educação Infantil, cumpridas no 4° semestre;
b) 100 horas nos anos iniciais do Ensino Fundamental, desenvolvidas no 5°
semestre;
c) 100 horas na Gestão Educacional, cumpridas no 6° semestre.
Embora continuassem a serem cumpridas 300 horas de estágio, nova
divisão entre os níveis e elementos de observação foi realizada. Além desta
modificação, a alteração da Matriz Curricular trouxe outra novidade para a realização
dos estágios.
Após 2009, foi implantado o sistema web estágio na Universidade, em que
os alunos lançam as atividades em planilhas no sistema, o professor corrige via web
e todas as ações referentes à parte burocrática do estágio são assim desenvolvidas,
82
culminando na autorização de impressão pelo professor e a devida entrega de todos
os documentos pelos alunos.
Com isso, criou-se uma disciplina denominada Prática de Ensino e
Orientação de Estágio Curricular Supervisionado (em Educação Infantil, nos anos
iniciais do Ensino Fundamental e Gestão Educacional) disciplina esta com 40 horasaula. Desta forma o professor responsável deve discutir as concepções sobre a
prática docente relacionada ao estágio realizado naquele semestre e orientar os
alunos na realização do estágio, assinando documentos e tirando dúvidas.
O cumprimento das 300 horas de estágio pelos alunos da Pedagogia,
conforme observado, ocorre a partir do 4° semestre e divide a carga horária
destinada à realização do mesmo igualmente entre três semestres, cada um deles
com foco em um trabalho: Educação Infantil (4º semestre), anos iniciais do Ensino
Fundamental (5° semestre) e Gestão Educacional (6° semestre).
Desta forma, o foco desta pesquisa encontra-se no estágio realizado pelos
alunos do 5° semestre, quando os mesmos desenvolvem diferentes atividades,
acompanhando e observando os professores dos anos iniciais do Ensino
Fundamental.
Cabe destacar que as disciplinas relativas ao ensino de Matemática são
desenvolvidas nos 3º e 4º semestres, o que não permite o diálogo entre a teoria
aprendida na Universidade e a prática observada pelo estudante nos estágios,
conforme pudemos observar na matriz curricular do curso de Pedagogia7, vigente à
época desta pesquisa.
Os professores responsáveis pelas orientações e acompanhamento da
realização dos estágios pelos alunos era chamado até 2009 de "Professor
Supervisor de Estágio". Após discussões realizadas em uma comissão criada pelo
Núcleo de Estágios, chegou-se à conclusão de que os professores não eram
efetivamente Supervisores, uma vez que não acompanhavam os alunos às escolas
na realização dos estágios, somente orientavam na Universidade, conforme as
dúvidas e colocações trazidas pelos próprios alunos. Desta forma, a partir de 2010
7
Anexo – Matriz Curricular do Curso de Pedagogia - 2008
83
passou-se a denominar "Professor Orientador de Estágio Curricular Supervisionado",
o profissional responsável pela disciplina e pelas orientações aos alunos.
Ainda de acordo com a legislação e atendendo determinação do Núcleo de
Estágios, a Universidade entende que caso o aluno exerça atividade regular de
docência, poderá utilizar esta atividade como até 50% da carga total do estágio a ser
cumprido.
A legislação que embasa tal procedimento é a Resolução CNE/CP n° 2, de
19/02/2002 (D.O.U. 04/03/02), que em seu art. 1°, diz: "Parágrafo único. Os alunos
que exerçam atividade docente regular na educação básica poderão ter redução da
carga horária do estágio curricular supervisionado até o máximo de 200 (duzentas)
horas”.
Para esta finalidade, o aluno estagiário do Projeto Ler e Escrever também é
beneficiado. Este programa teve início no ano de 2006 no município de São Paulo,
com foco na qualidade de ensino, contemplando três projetos: "Toda força ao 1°,
Ano - TOF", "Projeto Intensivo no Ciclo l - PIC", e "Ler e escrever em todas as áreas
no Ciclo II". O primeiro deles, cujo foco está no ciclo l, tem como meta criar
condições adequadas para que todos os alunos leiam e escrevam já ao final do 1°
ano do Ciclo I. Para tanto a Secretaria Municipal de Educação (SME) e a Diretoria
de Orientação Técnica (DOT), colocaram um estudante universitário de Pedagogia
ou Letras, como auxiliar de ensino, junto a cada professor do 1° ano, para ajudá-lo
na alfabetização.
Entende-se que, em consonância com o art. 8° das Diretrizes Curriculares
Nacionais para o curso de Pedagogia, este momento de acompanhamento, ensino e
participação em projetos pedagógicos, constitui-se em prática que assegura a
formação para o exercício profissional. Assim, no Regulamento de Estágios da
Universidade, consta no Art. 12 [...]
§ 1°: O aluno-professor (eventual, substituto, regular em regime de
excepcionalidade) e o aluno-pesquisador, do Projeto Ler e Escrever, podem
registrar até 50% da carga-horária do Estágio Curricular Supervisionado,
conforme prevê a legislação vigente. Para efetivar o registro, essas aulas
devem ser alceadas no Grupo de Regência e assinadas pela Coordenação
Pedagógica ou Direção da UE, e, ainda, constar do Relatório Final de ECS.
84
§ 2° - O aluno-professor deve, também, apresentar uma declaração de
docência assinada pela Direção da UE.
Cabe aqui uma ressalva quanto à questão de nossa pesquisa. Se o estágio
é momento importante de observação da prática docente, momento em que o futuro
professor pode analisar a ação do outro, alicerçando assim suas ações, a utilização
de sua própria docência como estágio poderia estar privando este aluno de ricas
experiências, pois quando assim é feito, metade do período de seu estágio estará
sendo cumprido sem as observações que se espera que sejam feitas para sua
formação como professor. No entanto, quando o aluno está em exercício, a reflexão
sobre a prática propagada por Schön (2000) pode ser desenvolvida.
3.5
Análise das ementas das disciplinas relativas à formação para o ensino
de Matemática
O Projeto Pedagógico do Curso – PPC de Pedagogia, da Universidade
pesquisada, traz como finalidade propiciar aos egressos a formação para a docência
na Educação Infantil e nos anos iniciais do Ensino Fundamental, além da
possibilidade de atuação nas atividades ligadas à Gestão escolar.
Esta concepção destacada no PPC visa formar professores, propiciando aos
alunos o desenvolvimento do tripé ensino, pesquisa e extensão. Além disso,
conforme destaca Fernandes (2012)
Almeja-se para a formação do profissional da educação, que tenha domínio
do conteúdo e a compreensão crítica daquilo que ensina e faz; conheça as
novas tecnologias e que as utiliza segundo projetos políticos de
emancipação das classes menos privilegiadas; tenha na sua formação uma
especificidade que contribua para o trabalho coletivo e interdisciplinar na
escola; tenha a compreensão das relações entre a escola e a sociedade.
(FERNANDES, 2012, p. 109).
A autora desenvolveu uma investigação significativa na mesma Universidade
na qual estamos pesquisando, focando no curso de Pedagogia. Realizou análises
comparativas no PPC e nas ementas e bibliografias das disciplinas voltadas ao
ensino de Matemática, nos anos de 2005, 2008 e 2011.
Nos mostra que a Universidade ampliou a perspectiva de formação de
professores de 2005 para 2008, ao determinar a atuação do profissional também na
Educação Infantil, porém o foco do curso continuou amplo, com carga horária
85
pequena nas disciplinas que contemplam os objetos de ensino. Destaca também
que as ementas de 2008 ficaram mais genéricas e a discussão sobre o ensino de
Matemática, antes presente nas ementas de 2005, não aparece nas de 2008, sem
destaque para a abordagem de conteúdos matemáticos presentes nos documentos
curriculares mais recentes e previstos de serem trabalhados com crianças dos anos
iniciais no Ensino Fundamental e da Educação Infantil.
Com a participação dos cinco alunos sujeitos de nossa pesquisa, os dados
referentes às observações de estágio foram colhidos no ano de 2012, quando os
mesmos cursavam o 5º semestre do curso. O PPC em vigor à época ainda era o de
2008.
Quanto às disciplinas voltadas ao ensino de Matemática, os alunos cursaram
Fundamentos e Metodologia do Ensino de Matemática I durante o 3º semestre do
curso, oferecida no 1º semestre de 2011; Fundamentos e Metodologia do Ensino de
Matemática II, no 4º semestre do curso, oferecida no 2º semestre de 2011 e Prática
de Ensino e Orientação de Estágio Curricular Supervisionado nos anos iniciais do
Ensino Fundamental no 5º semestre do curso, oferecida no 1º semestre de 2012.
Apresentamos os planos utilizados no ensino dos alunos sujeitos desta
pesquisa, datados de 2011 e pautados no PPC de 2008, sobre os quais tecemos
algumas considerações.
1º Semestre de 2011
Fundamentos Metodológicos do Ensino de Matemática I
Ementa: Subsídios teórico-metodológicos referentes ao ensino da matemática na pré-escola e nos anos
iniciais. Análise da inter-relação entre o conteúdo da matemática e as demais áreas do conhecimento.
Planejamento e desenvolvimento de atividades e materiais de ensino específicos na área de matemática.
Conteúdos
Ensino e Aprendizagem da Matemática
A História da Matemática - recurso didático; Reconhecimento dos Parâmetros Curriculares Nacionais (PCNs);
Referenciais Curriculares Nacionais para Educação Infantil (RCNEI) de Matemática e Proposta Curricular do
Estado de São Paulo; A Construção da ideia de número na educação infantil; Piaget e o construtivismo em
Matemática
As operações elementares
Processos de resolução de problemas (teoria dos campos conceituais de Vergnaud); Os conceitos de adição,
subtração, multiplicação e divisão ( sem a utilização do algoritmo); Operações com números naturais; Cálculo
mental.
Material concreto nas aulas de Matemática
Blocos lógicos, material dourado, ábaco, disco de frações e cousinaire.
Noções de espacialidade - Educação Infantil
Noções geométricas, constituição da espacialidade, jogos de percurso, orientação e sentido ; Relação entre as
formas tridimensionais e seu uso no cotidiano.
86
Estratégias de Ensino
Aula expositiva e dialogada; Atividades práticas de procedimentos pedagógicos, a serem utilizados no
contexto da sala de aula; Leituras; Grupos de discussão; Utilização da ferramenta black board; Visitação à
sites relacionados com os temas trabalhados nesta disciplina; Utilização de Bibliotecas presenciais e virtuais;
Experimentação de materiais diversos, no ensino de matemática.
Bibliografia Básica:
CARRAHER, T. N. Aprender pensando: contribuições da psicologia cognitiva para a educação. 18ªed.
Petropolis: Vozes, 2005.
CENTURION, M. Conteúdo e Metodologia da Matemática: Números e Operações. 2. Ed. São Paulo:
Scipione, 2002.
DANTE, L. R. Didática da Resolução de Problemas de Matemática. 12ª ed, São Paulo: Ática, 2003.
NUNES, T. B. P. Crianças fazendo Matemática. 2ª ed. Porto Alegre: Artmed, 1997.
Continuação
PARRA, C. Didática da matemática: reflexos psicopedagógicas. Porto Alegre: Artmed, 2001.
Continua
Bibliografia Complementar:
BRASIL. MEC .Referencial Curricular Nacional para a Educação Infantil: formação pessoal e social.
Brasília: MEC, 1998.
BRASIL. SEF. Parâmetros Curriculares Nacionais: (1ª a 4ª série) Matemática: Brasília: Ministério da
Educação, 1997.
CARAÇA, B. J. Conceitos Fundamentais da Matemática. 5ª ed. Lisboa: Gradiva, 2003.
CARRAHER, T. N. O método Clínico: usando os exames de Piaget. 5ª ed. São Paulo: Cortez, 1998.
CARRAHER, T. N. Na vida dez na escola zero. 12ª ed. São Paulo: Cortez, 2001.
Quadro 5 - Plano de ensino da disciplina Fundamentos Metodológicos do
Ensino de Matemática I
A ementa do plano de ensino da disciplina FME de Matemática I está voltada
para o ensino na Educação Infantil e no Ensino Fundamental, buscando a relação
entre teoria e prática na formação do professor, o que está de acordo com as
orientações do PPC do curso.
A análise dos conteúdos propostos na disciplina FME da Matemática I, nos
mostra a indicação de quatro temas: Ensino e Aprendizagem de Matemática; as
operações elementares; material concreto em sala de aula e noções de
especialidade – Educação Infantil.
A indicação no conteúdo em se trabalhar com os blocos lógicos, material
dourado, ábaco, disco de frações e Cousinaire, nos leva a pensar assim como
Fernandes (2012), que antes dos PCN entendia-se que o trabalho com estes
materiais estaria privilegiando o concreto, cuja utilização facilitaria a aprendizagem
da Matemática.
A autora observa que os planos de FME de Matemática I, assim como os da
disciplina de Conteúdo e Metodologia do Ensino de Matemática I (2005) têm o foco
no conhecimento pedagógico mais amplo e genérico e no conhecimento curricular
ao destacar o estudo dos Parâmetros Curriculares Nacionais, embora demonstre o
87
trabalho com os conhecimentos matemáticos e conhecimentos pedagógicos dos
conteúdos matemáticos.
Ao analisarmos as estratégias de ensino propostas para o trabalho dos
conteúdos, podemos perceber que não há um direcionamento ao professor
responsável sobre a forma de trabalhar estes conteúdos. Aulas expositivas
dialogadas, leituras e discussões em grupo e visitas a sites, são orientações muito
amplas e podem servir ao trabalho com qualquer tema e não necessariamente com
a Matemática. Destaca-se somente a “Experimentação de materiais diversos, no
ensino de matemática”, sem porém dar indícios da forma como isso será
desenvolvido, quais experimentações ou quais materiais serão utilizados.
Quanto à bibliografia, o plano apresenta o PCN juntamente com livros que
tratam de conteúdos e também metodologias para o ensino de Matemática. Cabe
destacar que os livros apresentados na bibliografia do curso também mostram
propostas de trabalho com várias concepções. Além disso, notamos que o plano
indica a utilização do RCNEI volume 2 - Formação Pessoal e Social, ao invés do
volume 3 – Conhecimento de Mundo, que é o volume no qual são dadas as
orientações para o trabalho com Matemática.
Apresentamos a seguir o plano de ensino da disciplina FME de Matemática
II com a análise realizada.
2º Semestre de 2011
Fundamentos Metodológicos do Ensino de Matemática II
Ementa: Estudo crítico dos diferentes métodos de ensino de Matemática, no âmbito do Ensino Fundamental,
objetivando a formação docente para atuar nas séries iniciais. Tendências atuais do ensino de Matemática: a
resolução de problemas, aulas investigativas, uso de tecnologias da comunicação e da informação. pesquisas
sobre o ensino de números e operações, de geometria e medidas.
Conteúdos
Grandezas e Medidas
Identificação de grandezas mensuráveis no contexto diário: massa, comprimento, capacidade, superfície, etc.
Utilização de unidades usuais de medida como metro, grama, litro etc. Unidades usuais de tempo e de
temperatura. Reconhecimento dos sistemas de medida que são decimais e conversões usuais, estabelecendo
relações entre unidades usuais de medida de uma medida.
Espaço e Forma
Observação e reconhecimento de formas geométricas presentes na natureza e nos objetos criados pelo ser
humano. Exploração e criação de situações que envolvam formas geométricas. Reconhecimento de
semelhanças e diferenças entre poliedros (como os primas, as pirâmides) e identificação de elementos como
ccomo faces, vécomo faces, vértices e arestas. Exploração das planificações de figuras
Números Racionais
Construção do significado do número racional e de suas representações fracionária e decimal. Estudo de
obstáculos da aprendizagem dos números racionais. Uso da calculadora para interpretar o significado das
representações decimais. Os diferentes significados das frações: parte-todo, quociente, razão. Cálculo de
88
adição e subtração de números racionais.
Operações
Operações Significados das operações e procedimentos de cálculo campo aditivo e multiplicativo Pesquisas e
oficinas
Estratégias de Ensino
Aula expositiva e dialogada.;Oficinas.; Apresentação e realização de pequenas pesquisas; Seminários
temáticos; Leitura e interpretação de textos; Grupos de discussão; Visitação à sites relacionados com os
Continuação
temas trabalhados nesta disciplina.; Utilização de Bibliotecas presenciais, virtuais e do ambiente Blackboard.
Continua
Bibliografia Básica:
CARRAHER, T. N. Aprender pensando: contribuições da psicologia cognitiva para a educação. 18ªed.
Petropolis: Vozes, 2005.
DANTE, L. R. Didática da Resolução de Problemas de Matemática: 1º a 5º Séries. 12. Ed. São Paulo:
Ática, 2003.
NUNES, T. B. P. Crianças fazendo Matemática. 2ª ed. Porto Alegre: Artmed, 1997.
Bibliografia Complementar:
BRASIL. Programa de Formação Continuada de Professores dos Anos/Séries Iniciais do Ensino
Fundamental. Brasília: MEC, 2007.
BRASIL. MEC.. Parâmetros Curriculares Nacionais: (1ª a 4ª série) Matemática: Brasília: MEC, 1997.
PIRES, C. M. E. A. Espaço & Forma: a construção de noções geométricas pelas crianças das quatro séries.
São Paulo: Proem, 2001.
SÂO PAULO (ESTADO) SE. Proposta Curricular de Matemática para o Cefam. São Paulo: Imesp, 1992.
Quadro 6 - Plano de ensino da disciplina Fundamentos Metodológicos do
Ensino de Matemática I
A ementa do plano de ensino está voltada para os métodos de ensino
utilizados nos anos iniciais do Ensino Fundamental, destacando a necessidade de
relacionar teoria e prática na formação do professor. Além disso, acena com a
possibilidade de discussões sobre as tendências atuais no ensino de Matemática,
ressaltando a resolução de problemas, aulas investigativas e o uso de tecnologias
da comunicação e da informação. Encontramos indicação de pesquisas relativas ao
ensino de determinados conteúdos, como números naturais e operações, geometria
e medidas.
O conteúdo a ser trabalhado também é agrupado em quatro temas:
Grandezas e Medidas, Espaço e Forma, Números Racionais e Operações.
Fernandes (2012) mostra que se percebe no plano da disciplina a
apresentação dos conteúdos a serem ensinados, porém no que diz respeito ao
ensino de números baseia-se em concepções anteriores aos Parâmetros
Curriculares Nacionais, ressaltando a classificação, seriação e sequenciação como
fases do desenvolvimento do raciocínio lógico matemático.
89
As ideias de Piaget sobre a construção do número destacavam a
importância de se trabalhar as chamadas atividades pré-numéricas para
possibilitar a construção do conceito de número pela criança. O trabalho
pedagógico com número enfatizava o papel das atividades de seriação,
classificação e correspondência termo a termo para construção desse
conceito. (FERNANDES, 2012, p. 102).
Segundo a autora defendia-se a concepção de que a criança deveria ir além
da associação de um símbolo a determinada quantidade. Para tanto eram
trabalhadas as noções de conjunto, pertinência e inclusão, sendo de grande
importância a distinção que a criança era capaz de fazer entre número e numeral.
Mas ressalta que “os PCN, apoiados em pesquisas de Délia Lerner, Michael Fayol e
outros apontam para outra direção”. (FERNANDES, 2012, p. 103).
Os PCN apontam novas possibilidades para o ensino de Matemática,
levando em conta os avanços alcançados com pesquisas sobre a aprendizagem das
crianças em Matemática, especialmente sobre os números e o sistema de
numeração.
Com relação às estratégias de ensino indicadas no plano, repetem-se as
estratégias utilizadas na disciplina anterior, com a inclusão de oficinas e realização
de pesquisas.
A análise da bibliografia da disciplina FME da Matemática II mostra a
indicação dos PCN além de outras orientações didáticas, como o documento do
MEC do Programa de Formação Continuada de Professores dos anos iniciais do
Ensino Fundamental.
Podemos perceber que embora os conceitos e conteúdos das disciplinas
FME da Matemática I e II sejam diferentes, a bibliografia básica é a mesma. Houve
apenas a exclusão de duas indicações, porém explica-se pelo fato de que neste
semestre houve a indicação institucional de que a bibliografia básica deveria conter
três indicações, enquanto a bibliografia complementar teria cinco indicações.
Se focarmos nas estratégias de ensino, percebemos que as mesmas se
repetem nas duas disciplinas, sem indicação de metodologias específicas para o
ensino de Matemática. Esperava-se que as indicações de estratégias estivessem
diretamente ligadas aos conteúdos a serem trabalhados, mas não foi o que se
observou.
90
Neste plano, em que se destaca o ensino de Espaço e Forma, por exemplo,
o que temos é o conteúdo em si, sem direcionamento para a formação do professor,
sobre como a criança aprende este conteúdo, o que o professor deve saber para
ensiná-lo ou quais estratégias ou atividades seriam facilitadoras do ensino e da
aprendizagem no Ensino Fundamental.
As contribuições de Curi (2005) corroboram com as análises realizadas, ao
nos mostrar que os cursos de Pedagogia, oferecem o ensino de Matemática sem
referenciais teóricos adequados ou sem a tematização da prática. Para a autora há
ainda que se ressaltar o fato de que as referências bibliográficas apontadas nos
planos de ensino dos cursos de Pedagogia favorecem o reforço de concepções e
práticas tradicionais. Por este motivo destaca a importância da pesquisa nesta área,
que possibilitaria novas formas de trabalho e maior atenção ao aluno e à
aprendizagem, tal qual verificamos, por exemplo, no grupo de pesquisa do Programa
Observatório.
Por fim analisamos o plano de ensino da disciplina Prática de Ensino e
Orientação de Estágio Curricular Supervisionado nos anos iniciais do Ensino
Fundamental.
1º semestre de 2012
Prática de Ensino e Orientação de Estágio Curricular Supervisionado nos anos iniciais do Ensino
Fundamental
Ementa: Orientação ao desenvolvimento de estágio curricular supervisionado junto às escolas de Ensino
Fundamental (anos iniciais), com ênfase na observação e intervenção nos ambientes escolares e não
escolares, com destaque no currículo e aprendizagem do aluno.
Conteúdos
O Estágio Supervisionado na Formação do Professor de Ensino Fundamental
Debate sobre a articulação entre a teoria e a prática na formação do profissional da educação; A articulação
entre projetos escolares, consciência política da prática pedagógica e gestão escolar.
Propostas e Projetos de Estágio
Elaboração de propostas e de projetos de estágio; Depoimentos e relatos de estagiários sobre a sua
observação na escola inserida; Colocar em prática algumas intervenções propostas pelos alunos; Sugestões
de aprendizagem e intervenções propostas pelos alunos.
Possibilidades de participação do professor nas atividades escolares
Relatos e depoimentos sobre os educadores escolares e no processo participativo na escola; - Professor
participativo; Criatividade na educação.
A participação da comunidade externa
Relatos e depoimentos sobre os movimentos sociais e a escola; Os condicionantes político-sociais e
ideológicos: os interesses dos diferentes grupos dentro da escola; A participação da comunidade externa na
escola: limites e possibilidades.
Atividade extra-curricular
Pesquisa em sites educacionais sobre os diversos temas debatidos relacionados ao estágio supervisionado;
Leitura de textos sobre a práxis na gestão escolar;
91
Estratégias de Ensino
Aulas expositivas e dialogadas; Debates e discussões sobre o estágio realizado; Elaboração de resenhas de
textos; Apresentação de propostas de intervenção; Atividades individuais; Uso do Ambiente Virtual de
Aprendizagem - Blackboard.
Bibliografia Básica:
GADOTTI, M. Escola Cidada: Uma Aula Sobre a Autonomia da Escola. 10. ed. Sao Paulo: Cortez, 2004
GADOTTI, M. Pedagogia da Praxis. 4. ed. Sao Paulo: Cortez, 2004.
PIMENTA, S. G. O Estagio na Formacao de Professores: Unidade Teoria e Pratica?. 9. ed. Sao Paulo:
Cortez,
2010
Continuação
Bibliografia Complementar:
Continua
CARVALHO, G. T. R. D. Formacao de Professores e Estagios Supervisionados: Algumas Veredas. Sao
Paulo: Andross, 2007.
FREIRE, P. Educacao Como Pratica da Liberdade. 27. ed. Sao Paulo: Paz e Terra, 2003.
FREIRE, P. Professora Sim, Tia Nao: Cartas a Quem Ousa Ensinar. 15. ed. Sao Paulo: Olho D¿agua, 2005.
PIMENTA, S. G. O Estagio na Formacao de Professores: Unidade Teoria e Pratica?. 9. ed. Sao Paulo:
Cortez, 2010.
RIOS, T. A. Compreender e Ensinar: Por Uma Docencia da Melhor Qualidade. 3. ed. Sao Paulo: Cortez,
2002.
Quadro 7 - Prática de Ensino e Orientação de Estágio Curricular
Supervisionado nos anos iniciais do Ensino Fundamental
A ementa do plano ressalta o objetivo de orientar o aluno para a realização
do estágio, destacando a observação do currículo e a aprendizagem do aluno. Além
disso, orienta a observação e intervenção em ambientes não escolares, porém os
alunos não são autorizados a realizar o estágio fora das unidades escolares.
Ao analisarmos os conteúdos que serão trabalhados com os alunos não
encontramos relação com o que determina a ementa. Dividido em cinco temas, “O
Estágio Supervisionado na Formação do Professor de Ensino Fundamental”,
“Propostas e Projetos de Estágio”, “Possibilidades de participação do professor nas
atividades escolares”, “A participação da comunidade externa” e “Atividade extracurricular”, o plano propõe discussões mais amplas e gerais sobre a formação do
professor, a escola, movimentos sociais na escola, participação, política, ideologia.
Assim também as atividades extracurriculares preveêm leituras e visitas a sites
sobre temas relacionados ao estágio.
Não encontramos nos conteúdos, discussões ou orientações para que os
alunos possam discutir a prática do professor observado do ponto de vista do ensino
das diferentes disciplinas, entre elas a Matemática.
Pelo fato da disciplina estar diretamente ligada ao estágio no Ensino
Fundamental para, além de orientar a realização do mesmo estabelecer discussões
que aliem a teoria propiciada no curso e a prática observada no estágio,
92
esperávamos que fosse levada em conta especificamente a prática do professor do
Ensino Fundamental, o professor chamado de polivalente justamente por
desenvolver seu trabalho atuando com diferentes disciplinas.
Não há na ementa ou nos conteúdos orientações para que o professor da
disciplina dirija o olhar dos alunos para as diferentes metodologias, estratégias ou
atividades necessárias para ensinar cada disciplina.
As estratégias indicadas para serem utilizadas, como aulas expositivas
dialogadas, discussões, elaboração de resenhas, apresentação de propostas de
intervenção, não dão ao professor um direcionamento para que se discuta a prática
de ensino do professor dos anos iniciais do Ensino Fundamental.
Privilegia-se a formação geral do professor e sua atuação no contexto global
da escola, sem pensar no espaço da sala de aula ou nas disciplinas dos anos
iniciais do Ensino Fundamental, especialmente a Matemática.
A bibliografia sugerida apresenta dois títulos que discutem o estágio, com
Pimenta (2010) e Carvalho (2007). As demais indicações voltam-se para a formação
de professores.
A disciplina Prática de Ensino, a nosso ver, deveria propiciar maiores
interações e aprendizagens aos alunos sobre a forma de trabalhar tanto na
Educação Infantil como no Ensino Fundamental, nas diferentes disciplinas com
diferentes conteúdos. Porém as orientações e sugestões que observamos no plano
da disciplina não dão os encaminhamentos para tal.
Entendemos assim como Curi (2011) que
[...] a prática de ensino coerente e competente deve ser a viga mestra do
Curso de Licenciatura. Consolidar e ampliar os conhecimentos da
Matemática e levar os alunos a adquirir novos conhecimentos nesse campo,
com base em temas desenvolvidos durante as aulas de Prática de Ensino e
Estágio Supervisionado é, com certeza, o objetivo maior dessa disciplina.
(CURI, 2011, p. 146).
Vemo-nos, portanto, na possibilidade de alcançar o objetivo da disciplina
proposto pela autora, dependendo do professor que assume a disciplina e a
orientação do estágio.
93
3.6
Os estagiários, as escolas e as professoras envolvidas
Neste subitem apresentaremos o perfil dos estagiários, escolas e
professoras como parte do contexto no qual a pesquisa se desenvolveu.
3.6.1 O perfil dos estagiários
As fontes utilizadas para traçarmos o perfil dos estagiários foram os registros
feitos por cada um deles sobre sua história de vida8.
Conforme citado em nossa apresentação, os sujeitos desta pesquisa são
cinco alunos do curso de Pedagogia, que participavam como bolsistas do Programa
Observatório da Educação com fomento da Capes. Eles participavam do Grupo de
Pesquisa coordenado pela Dra. Edda Curi no âmbito desse Programa. A procura
voluntária destes alunos por novos conhecimentos e experiências na área, como a
participação em tal Programa, sugere preocupação e comprometimento com a
própria formação para ensinar Matemática nos anos iniciais do Ensino Fundamental.
Eles percebiam a importância desse Grupo de Pesquisa e sempre manifestavam as
aprendizagens adquiridas nesse grupo.
Dos cinco participantes quatro são do sexo feminino e um do masculino, os
quais identificaremos por “MAO”, “TARS”, “EAM”, “LISE” e “VANGRA” . À época
da realização da pesquisa os estagiários tinham entre 20 e 37 anos. Dois deles
cursavam o 4º Semestre do curso de Pedagogia e três deles estavam no 5º
Semestre do curso. O perfil destes alunos, sua história de formação e relações com
a Matemática baseiam-se nas narrativas de sua vivência registradas em seus
portfólios de aprendizagem.
A relação destes alunos com a Matemática desde sua formação básica, para
alguns era de gosto e facilidade com a disciplina e para outros de dificuldades
extremas.
Para “MAO”, “TARS” e “VANGRA” a relação com a Matemática era difícil
desde o Ensino Fundamental, fazendo com que esta fosse a disciplina da qual
menos gostavam.
8
Apêndices D, E, F, G e H – História de vida do estagiário.
94
"MAO" relata que por esse motivo nunca se preocupou em compreendê-la e
acha que seus professores da época não contribuíram para que gostasse de
Matemática.
Dentre as disciplinas que tive na escola regular, a que eu menos gostava e
me identificava era a Matemática. Por esse motivo nunca me dediquei a
aprender e entender, e alguns professores que tive me ajudaram nisso, pois
não ensinavam de uma maneira que os alunos em geral, se interessassem.
(“MAO”).
Segundo a estagiária, esta dificuldade aliada à postura de seus professores,
fizeram com que não se dedicasse muito à própria aprendizagem.
O comentário de “MAO” demonstra que para ensinar Matemática é preciso
desenvolver saberes específicos para este ensino e também o gosto por essa área
de conhecimento, assim como defende Tardif (2002), ao nos trazer o conceito de
mobilização de saberes, que mostra a necessidade de construção e constante
renovação dos saberes disciplinares, didáticos e pedagógicos, enxergando a
totalidade do ser professor.
A narrativa de "MAO" relaciona a falta de saberes específicos da profissão
de seus professores às suas dificuldades com a Matemática. Para ela, sua
aprendizagem da Matemática no Ensino Fundamental e Médio foi deficitária,
mudando sua postura frente à disciplina somente no final do Ensino Médio, quando
realizou um cursinho pré-vestibular, talvez pela postura dos professores do cursinho
que motivam seus alunos a aprender com vistas a ter sucesso no vestibular.
Durante toda minha vida tive dificuldades com a Matemática, mas quando
entrei em um cursinho pré-vestibular, foi quando mudei minha visão e
comecei a entender a Matemática. (“MAO”).
Os relatos de “TARS” mostram que suas dificuldades com a Matemática
começaram cedo, na educação básica e, com o passar dos anos essas dificuldades
só aumentaram. Isto fez com que desenvolvesse aversão à disciplina, “uma espécie
de raiva”, que fez com que focasse seus estudos em outras disciplinas e deixasse a
Matemática de lado.
Desde muito cedo, durante o estudo regular tive muitas dificuldades com a
Matemática, e com o passar dos anos escolares essa dificuldade ia
somente aumentando. Por isso desenvolvi uma espécie de raiva da
Matemática. Direcionei o foco de meus estudos nas outras disciplinas e
deixei a Matemática de lado. (“TARS”).
95
Embora “TARS” não destaque a influência de seus professores nesta
formação ou no desenvolvimento das dificuldades com a Matemática, podemos
inferir que seus comentários mostram que a formação básica é muito importante na
constituição dos conhecimentos dos alunos. Leva-nos a pensar também no papel do
professor neste nível de ensino, no sentido de propiciar aos alunos, conhecimento e
desenvolvimento nas diferentes áreas do saber.
Também “VANGRA” mostra em seus relatos que não tem uma experiência
muito agradável com a Matemática, ressaltando que boa parte dela foi de grande
desespero e incompreensão.
Segundo “VANGRA”, na 1ª e 2ª séries não teve grandes dificuldades, pois
reproduzia o que era solicitado pelas professoras, como “contas armadas na
casinha”, e não tinha grandes dúvidas. A partir da 4ª série, a relação professor-aluno
começou a influenciar na aprendizagem da estagiária, o que afetou sua forma de
conceber a Matemática.
Tinha uma professora muito ruim que chegou a agredir alguns alunos da
sala. Naquela época me recordo da Matemática como algo muito vago e
sem valor, as atividades eram passadas na lousa, as contas armadas e
nada mais, a professora explicava apenas uma vez e tínhamos que fazer.
Não havia uma explicação, um diálogo entre o professor e aluno, na
verdade não podíamos nem nos comunicar com os outros colegas da sala,
nossas dúvidas eram levadas para casa por que a professora não explicava
novamente. (“VANGRA”).
As recordações de “VANGRA” mostram que os professores que lhe
ensinaram Matemática não se preocupavam com a aprendizagem de seus alunos,
utilizando inclusive a realização de atividades desta área como castigo.
[...] a professora mandava decorar a tabuada que no dia seguinte faria
chamada oral. Quando conversávamos ela mandava os alunos fazerem 10
vezes a tabuada do 2 ao 10. Matemática naquela época era castigo das
professoras, e então começou meu longo caminho de ensino de Matemática
sem compreensão e sem aprendizagem. (“VANGRA”, 2012).
Seus comentários nos levam a refletir que saber ensinar Matemática passa
pelo conhecimento dos conteúdos, mas também pela necessidade de dominar
técnicas e estratégias que possibilitem a qualidade do processo ensinoaprendizagem. Todos os sujeitos revelam que em algum momento de sua formação
tiveram
professores
de
Matemática
que
demonstravam
ter
conhecimento
matemático, porém não sabiam transmitir este conhecimento aos alunos, fato
96
geralmente aliado à falta de paciência dos docentes, que não gostavam quando
eram pedidas explicações ou dúvidas eram expostas.
Para “VANGRA” esta situação provocou desânimo e criou uma defasagem
na aprendizagem, fazendo com que atualmente ela tenha que rever certos
conteúdos matemáticos por não ter aprendido no tempo certo. Suas lembranças
sobre a Matemática eram sempre de dificuldades.
[...] na 5ª série tinha até desânimo ao entrar na sala, minhas notas eram
baixas, [...] eu torcia para que a professora ficasse doente para vir outro
professor no lugar, e percebi que quando a professora faltava e outro
professor a substituía, minha compreensão era melhor, logo, a maneira que
a professora explicava era de fato meu maior desafio, ela fazia as contas
muito rapidamente, e meu raciocínio não conseguia acompanhar.
(“VANGRA”).
A estagiária relata que até pedia explicação para suas dúvidas, mas a
professora não gostava de repetir mais de uma vez a mesma orientação, então não
conseguia acompanhar. Isto fez com que começasse a se questionar, “ou eu sou
muito burra ou ela não está sabendo me ensinar de uma maneira mais fácil de
compreender”. A falta de compreensão e a impaciência da professora fizeram com
que “VANGRA” passasse a detestar a Matemática, afirmando que conseguiu
avançar e não ficar retida graças ao auxílio dos colegas que a ensinavam e
motivavam a continuar.
Mas, nem todos os sujeitos de nossa pesquisa tiveram contatos iniciais
traumatizantes com a Matemática e relacionam estas experiências com a qualidade
de seus professores.
“EAM” nos mostra em seus registros que sempre gostou “da matemática,
cálculos, porcentagem e raciocínio lógico”, desenvolvendo sua vida profissional na
área administrativa de uma empresa, ligada a estes conhecimentos. Assim como
muitos, o estagiário entendia que gostar de Matemática era suficiente para seu
desenvolvimento profissional. Seus relatos sugerem que o mesmo não teve
problemas com a Matemática em sua formação básica.
Por fim, “LISE” nos conta que teve excelentes professores que conseguiram
realmente ensinar e promover a aprendizagem de Matemática, por isso ela e a
97
Matemática sempre foram “amigas”, pois desde a educação básica sempre gostou
desta disciplina.
No período em que cursei o fundamental e o Ensino Médio , tive ótimos
professores de Matemática, outros nem tanto. Lembro que na escola
algumas amigas me apelidaram de "rata" , por estar sempre acompanhando
o raciocínio dos professores. Eu e a Matemática sempre fomos "amigas" ,
nunca a encarei como um bicho de sete cabeças. Creio que tive sorte por
ter aulas com ótimos professores que realmente sabiam ensinar a
Matemática, tinham certeza do que estavam falando, o que aumentava mais
e mais o meu gosto pela Matemática. (“LISE”).
O relato de “LISE” nos mostra que a prática do professor acaba por
influenciar as escolhas profissionais de seus alunos, o que no seu caso reforçou o
gosto pelo ensino e pela Matemática.
A Matemática sempre foi a matéria que eu tive menos dificuldade. É algo
que sempre gostei, sempre fui bem. Confesso que prefiro resolver mil
expressões a interpretar um texto ou fazer alguma resenha. (“LISE”).
Isto, porém não garante uma atuação de qualidade como professora de
Matemática. Gostar de cálculos ou ter facilidade de raciocínio são atributos que
podem facilitar a formação, porém não são suficientes para que o professor cumpra
sua tarefa que é levar o aluno à aprendizagem.
As experiências vividas por esses alunos quanto à aprendizagem em
Matemática, segundo seus relatos, demonstram pouco crescimento ou envolvimento
com a área. Seja pelo ensino desenvolvido pelos professores ou pelo próprio gosto
dos alunos pela disciplina, fato é que esta trajetória influencia as escolhas e
expectativas profissionais de nossos alunos.
O ingresso desses estagiários no curso de Pedagogia à procura de
formação profissional se deu por diferentes motivos.
“MAO” e “LISE” desde pequenas acalentavam o sonho de serem
professoras.
Para “MAO” o sonho de ser professora era acalentado desde pequena, mas
sua decisão pela profissão se deu quando terminou o Ensino Fundamental.
98
Antes de entrar no 2º grau do ensino regular, foi que realmente decidi que
9
queria ser Professora e com isso tive a ideia de entrar no CEFAM , para
estudar o magistério, porém quando entrei na escola do Estado para cursar
o Magistério, eu ainda não tinha a idade mínima para isso, e quando
completei a idade, o governo cancelou esse projeto e não pude fazer o
magistério. (“MAO”).
Este fato, somente adiou o sonho de trabalhar com educação.
Vários autores destacam o sonho dos jovens em se tornarem professores.
Freire (1997, p. 160) nos fala sobre a boniteza do sonho e a boniteza de ser
professor, destacando que “ensinar e aprender não podem dar-se fora da procura,
fora da boniteza e da alegria”.
Gadotti (2003) também nos mostra que os professores perseguem este
sonho, para dar sentido àquilo que realizam, entendendo que sonho e sentido
querem dizer a mesma coisa.
Sentido quer dizer caminho não percorrido mas que se deseja percorrer,
portanto, significa projeto, sonho, utopia. Aprender e ensinar com sentido é
aprender e ensinar com um sonho na mente. A pedagogia serve de guia
para realizar esse sonho. (GADOTTI, 2003, p. 2).
Como “MAO” não conseguiu fazer o curso de Magistério do CEFAM,
terminou o 2º grau e buscou o mercado de trabalho, sem contudo se afastar da área
da educação.
Seu primeiro contato com a educação foi como inspetora de alunos
concursada da Prefeitura da cidade de São Paulo. Nas atividades do dia a dia da
escola teve certeza que era esse o caminho que queria seguir, queria mesmo ser
professora. Esse sonho a levou a entrar na Universidade para cursar Pedagogia.
Embora as experiências vívidas por “MAO” quanto à aprendizagem de
Matemática, segundo seus relatos, demonstram pouco crescimento ou envolvimento
com a área, seja pelo ensino desenvolvido pelos professores ou pelo próprio gosto
da aluna pela disciplina, fato é que esta trajetória influenciou suas escolhas e
expectativas profissionais, buscando uma profissão fora da área das ciências
exatas.
9
CEFAM - Centro Específico de Formação e Aperfeiçoamento do Magistério
99
O comentário de “MAO” em sua narrativa mostra que sua relação com a
Matemática influenciou sua escolha profissional.
No começo do curso planejava atuar apenas na Educação Infantil, porque
tinha um certo preconceito com o Ensino Fundamental, justamente pela
dificuldade que eu tinha com a Matemática. (“MAO”).
Como apresentava dificuldades com a Matemática, pensava em trabalhar
somente com a Educação Infantil, entendendo que neste nível de ensino não
precisaria ensinar Matemática.
Independente desta dificuldade, “MAO” ainda perseguia seu sonho de ser
professora. O ingresso no curso de Pedagogia à procura de formação profissional,
deu-se pela vontade de trabalhar com educação, e para alcançar o sonho de criança
por admirar muito esta profissão. Consideramos este fato muito positivo no início do
século XXI, em que muitos jovens não se interessam pela profissão de professor.
“LISE” assim como “MAO”, também acalentava o sonho de ser professora,
que foi reforçado pelas experiências vividas na Educação Básica, especialmente a
influência de bons professores, levando-a a optar pela docência, no momento da
escolha por uma profissão.
Acredito que o sonho de toda menina, principalmente na infância, é ser
professora. No meu caso não foi diferente, minha brincadeira preferida era
“escolinha”, juntava minhas bonecas e minhas irmãs e passava a tarde toda
brincando. Desde então já havia escolhido o que eu iria ser quando
crescesse. (“LISE”).
Além de correr atrás do sonho de criança, “LISE” relata que teve o exemplo
e a influência dentro de sua família para reforçar esta escolha. “Na minha
adolescência acompanhei minha tia que na época fazia Pedagogia, meu interesse
foi aumentando, comecei a pesquisar na internet o curso, as funções e áreas de
atuação.” A escolha pelo curso de Pedagogia foi, portanto muito natural, mas trouxe
para ela reflexões acerca da posição e reconhecimento da profissão em nosso país,
levando-a a pensar inclusive em mudar sua escolha.
Confesso que me decepcionei um pouco ao ver como o professor não é
valorizado no Brasil, percebendo então as dificuldades e desafios que iria
encontrar, até pensei em mudar minha escolha, mas resolvi apostar e fazer
algo que me interessava. Passei até por preconceito de familiares e amigos
que só criticavam minha opinião, mesmo assim bati o pé, e decidi que era
Pedagogia o caminho a ser seguido. (“LISE”).
100
Os relatos de “LISE” reforçam que ser professor se inicia muitas vezes com
um sonho, assim como nos mostram Freire (2004) e Gadotti (2003), mas é preciso
que o futuro professor saiba que para exercer a profissão não basta sonhar. É
preciso construir uma identidade docente que segundo Pimenta (2002) abrange não
somente posturas mas o conhecimento e desenvolvimento de um campo de saberes
específicos, como conteúdos das diferentes áreas do conhecimento, conteúdos
ligados à prática profissional, conteúdos do campo teórico desta prática e conteúdos
que preparem o professor para trabalhar com seres humanos.
Porém enquanto muitos alunos escolhem a Pedagogia por entenderem que
assim se afastarão da Matemática, a estagiária relata em sua narrativa que
acreditava que poderia se aperfeiçoar nesta área, não só na graduação, mas
também após seu término. “Um dia antes de fazer a matrícula na graduação ainda
não havia me decidido qual curso fazer, optei por Pedagogia para depois me
especializar em Matemática”.
Para “EAM” o ingresso na educação e o gosto pela área surgiram devido a
uma fatalidade. Uma doença aos 30 anos o afastou do trabalho e em casa se propôs
a alfabetizar um sobrinho que cursava a 4ª série do Ensino Fundamental, o que o fez
se encontrar e partilhar das escolhas da esposa e de amigos. “Essa oportunidade foi
muito gratificante e deu um novo sentido a minha vida, uma vez que minha esposa,
formada em Letras, já atuava na área da educação e a maior parte de nossos
amigos também”.
Presta então, aos 33 anos, o ENEM – Exame Nacional do Ensino Médio e
obtém uma bolsa pelo PROUNI - Programa Universidade para Todos, para cursar
Pedagogia na Universidade pesquisada, deixando de lado seus medos e incertezas,
dedicando-se a esta formação.
O estagiário não relata dificuldades com a Matemática em sua trajetória
acadêmica, e sua escolha por Pedagogia se deu pelo gosto que adquiriu ao
alfabetizar o sobrinho e pelas infuências das pessoas com as quais convivia.
Porém para “TARS” as dificuldades com a Matemática influenciaram o
momento da escolha por uma graduação, levando-a a escolher a Pedagogia, pois
101
assim como diversos alunos deste curso, entendia que não precisaria estudar
Matemática para ser professora.
Quando chegou a hora de escolher uma graduação a primeira opção que
me veio em mente foi Letras, mas acabei optando por Pedagogia, por poder
dar aula para crianças e é claro no meu ingênuo pensamento inicial, fugir
um pouco da Matemática, pois pensava que ensinar Matemática para
crianças seria moleza, só dar continhas, adição, subtração, multiplicação e
divisão e pronto! Mas logo que iniciei o curso de Pedagogia percebi que não
seria tão simples assim. (“TARS”).
O pensamento de “TARS” sobre o ensino de Matemática para crianças está
ligado ao desconhecimento que muitos professores apresentam quanto aos
conteúdos de Matemática que devem ser trabalhados nos anos iniciais do Ensino
Fundamental. Além disso, a ideia de que para ser professor basta ter um
conhecimento pedagógico geral relacionado a técnicas, estratégias ou recursos, faz
com que alguns alunos optem pela profissão docente, entendendo que o
conhecimento do conteúdo adquirido em sua formação básica será suficiente para o
ensino.
A esse respeito entendemos, assim como Curi (2006), que há uma
concepção dominante com relação à formação dos professores que vão ensinar
Matemática, de que o professor polivalente não precisa saber Matemática, mas que
basta saber como ensiná-la. Desta concepção surgem diferentes pensamentos tanto
de alunos quanto de professores formadores.
Por fim “VANGRA” relata que escolheu ser professora na busca de maiores
oportunidades de trabalho, especialmente para ela que tinha um bebê pequeno.
Além disso, ressalta que embora não tenha um bom histórico com a Matemática,
sua escolha pela Pedagogia não está ligada ao fato de muitas pessoas entenderem
que este curso é mais fácil por não ter muita Matemática. Seu objetivo era realmente
conhecer um pouco mais da educação e ampliar suas chances de trabalho.
A estagiária relata que esperava que durante o curso pudesse aprender
mais e livrar-se do medo e aversão que tinha pela Matemática. As disciplinas do
curso de Pedagogia, no que se refere à formação do professor que vai ensinar
Matemática, têm o objetivo de subsidiar teoricamente as ações docentes deste
futuro professor. Mas nem sempre é o que ocorre na prática. Para “VANGRA” este
momento deixou a desejar.
102
No curso de Pedagogia a disciplina relacionada ao conhecimento teórico em
Matemática não me deu a visão do olhar do professor. Na verdade é
necessário que o professor tenha uma visão diferenciada da prática para
que seja comparada com o pensamento teórico. Acredito que a disciplina
deveria ser mais bem trabalhada, sobre todas as formas. (“VANGRA”).
Como já foi dito, no curso de Pedagogia da Universidade em questão, os
alunos têm duas disciplinas denominadas Fundamentos e Metodologia do Ensino de
Matemática l e Fundamentos e Metodologia do Ensino de Matemática II, com uma
carga horária de 40 horas cada, oferecidas no 3° e 4° semestre do curso. Estas
disciplinas têm o objetivo de subsidiar teorica e metodologicamente as ações
docentes deste futuro professor para ensinar Matemática. Além destas, há a
disciplina Prática de Ensino e Orientação de Estágio Curricular Supervisionado nos
anos iniciais do Ensino Fundamental, cujo objetivo também é a formação do
professor, porém não especificamente para ensinar Matemática, mas para atuar de
forma polivalente em todas as disciplinas e em qualquer um dos anos iniciais do
Ensino Fundamental
As considerações de “VANGRA” referem-se a tais disciplinas, consideradas
por ela muito teóricas, voltadas somente para os conteúdos matemáticos, quando na
verdade esperava que fossem discutidas questões práticas do ensino, que
pudessem torná-la uma professora diferente daquelas que teve na Educação
Básica, que não encontravam formas de ensino que pudessem levar os alunos à
aprendizagem.
Assim como ela, “LISE” e “MAO” também se manifestam quanto à
formação para ensinar Matemática propiciada no curso de Pedagogia.
Para alguém que sempre gostou da Matemática e pensava até mesmo numa
especialização após a graduação, “LISE” estranhou a importância dada à
Matemática no curso e à postura de seus colegas de classe em relação ao ensino e
aprendizagem nesta área.
Vejo que muitas meninas da minha sala ainda não perderam esse "medo"
da Matemática , escolheram Pedagogia por não ter contas, raciocínio lógico
e rápido e algumas ficaram perdidas nas disciplinas de FME de Matemática
e especialmente de Estatística , com suas fórmulas de tabelas e gráficos.
Esse preconceito com a Matemática já é antigo e é passado de geração à
geração, as pessoas já vêm com um bloqueio o que dificulta ainda mais a
absorção do conhecimento. Não sou nenhuma expert em Matemática
apenas gosto dos exercícios, e a encaro como um desafio a ser cumprido.
(“LISE”).
103
“MAO” também destaca que na busca da formação para realizar o sonho de
ser professora, esbarrou em diversos problemas, entre eles a atuação de alguns
professores, na própria Universidade, que não se preocupavam com sua
aprendizagem e com disciplinas que não lhe trouxeram o conhecimento esperado.
A estagiária esperava que no curso de Pedagogia suas dúvidas fossem
sanadas e sua formação acontecesse de forma que pudesse efetivamente ensinar
Matemática. Porém, segundo ela a contribuição maior deu-se não especificamente
com as aulas na graduação, mas especialmente em um momento de sua formação.
Refere-se ao convite que recebeu para participar do Programa Observatório da
Educação, já descrito na apresentação dessa tese, desenvolvido na Universidade
pesquisada. Relata que no início ficou em dúvida se daria certo, pois sabia de suas
limitações e resistências com a Matemática.
Para participar do Programa Observatório, no começo fiquei em dúvida se
daria certo. Porém a cada encontro que participava, eu ia me identificando e
gostando cada vez mais e percebi que essa era a oportunidade que
precisava para mudar a minha relação com a Matemática. (“MAO”).
A participação neste Programa foi muito importante para todos os sujeitos,
uma vez que todos em seus relatos destacam sua participação e aprendizagem nos
encontros do grupo.
“TARS”, por exemplo, mesmo não gostando de Matemática, começou a
perceber, durante o curso de Pedagogia, que precisaria mais conhecimento do que
somente o domínio das operações para ensinar no Ensino Fundamental. E segundo
ela, a oportunidade de ampliar este conhecimento veio também no convite para
participar do já referido Grupo de Pesquisa.
Fiquei muito feliz quando fui convidada para participar do grupo. A essa
altura eu já sabia que se quisesse realmente ser uma boa professora e
fazer a diferença, não bastaria somente cursar a Pedagogia e parar por aí.
Na verdade eu precisaria de mais base, buscar mais conhecimento,
principalmente na área da Matemática, onde se apresentava minha maior
dificuldade. Se eu não sabia os conteúdos e não gostava de Matemática,
como iria ensinar os alunos e fazer com que se interessassem em
aprender? (“TARS”).
Embora entendesse a necessidade de uma formação que agregasse mais
valor à formação propiciada no curso de Pedagogia, “TARS” sentia-se insegura em
participar do Grupo de Pesquisa, o qual conforme citamos anteriormente, é formado
104
por profissionais de diferentes níveis de ensino, assim como estudantes de
graduação e pós-graduação.
No primeiro encontro do grupo me senti perdida com todos aqueles termos
e nomenclaturas da Matemática. Fiquei ainda mais assustada, achei que
não iria dar conta. Eu, no início da graduação sem saber quase nada,
trabalhando ao lado de doutores, mestres, professores experientes, me
senti fora de contexto. (“TARS”).
A insegurança de “TARS” justifica-se pelo fato da mesma ter tido uma
formação deficitária no que diz respeito à Matemática e também por ter tomado
consciência de que os saberes necessários à docência, conforme nos mostra Tardif
(2002) são múltiplos e devem ser mobilizados e articulados entre si pelo professor,
no que diz respeito ao saber profissional, saber disciplinar, saber curricular e o saber
experiencial, conceitos já discutidos anteriormente. Na busca por estes saberes, a
estagiária relata ter percebido que sua participação no Grupo de Pesquisa traria
grande contribuição para sua formação.
O grupo logo se constituiu como espaço de formação, permitindo que a
estagiária começasse a enxergar a Matemática de forma diferente daquela que a
acompanhou durante toda sua formação até o momento da pesquisa.
Conforme as reuniões iam acontecendo eu ia compreendendo mais do que
se tratava, qual era a proposta, qual era o meu papel e ia também tirando
dúvidas em relação a Matemática que me cercavam há muito tempo, e
também derrubando alguns mitos sobre seu ensino como por exemplo, o da
calculadora. Para mim, trabalhar com calculadora fazia com que não se
usasse o raciocínio e a criança não aprenderia nada dessa forma. Mas
descobri através de experiências no grupo de pesquisa que a calculadora
se bem usada auxilia no processo de desenvolvimento do raciocínio, faz
pensar, encontrar soluções, buscar métodos de resolução.(“TARS”).
“TARS” ressalta ainda que na Universidade, as aulas de FME de
Matemática I e II lhe trouxeram alguns conhecimentos, mas realmente só isso não
foi suficiente.
Participando
do
Programa
Observatório
consegui
aumentar
consideravelmente esse conhecimento, parei de ver a Matemática como
algo ruim e em consequência disso, quando tive que escolher uma matéria
optativa para cursar, ao invés de fugir da Matemática mais uma vez, fui em
busca dela e escolhi Educação Estatística. Era uma aula prática e dinâmica,
aprendi muito, foi uma ótima escolha, pois nessa matéria pude aprender
formas de aplicação da Matemática para crianças de várias formas
diferentes e adaptá-las para diversas idades. (“TARS”).
105
Seu crescimento no que se refere à Matemática e seu ensino é fruto da
participação no Programa Observatório da Educação, assim como das relações que
consegue estabelecer entre sua aprendizagem e seu trabalho no Projeto Ler e
Escrever, da Prefeitura do município de São Paulo, já citado anteriormente.
Paralelamente ao Programa Observatório, também participei do Projeto Ler
e Escrever e auxiliava uma aluna com muita dificuldade de aprendizagem
na alfabetização. Tanto eu quanto a professora da sala achávamos que
devíamos trabalhar com essa menina somente a alfabetização de início,
pois se ela não sabia ler, nem escrever, não conseguiria aprender
matemática. (“TARS”).
Porém segundo a estagiária, em um dos encontros do grupo de pesquisa
este mito foi derrubado, pois aprendeu que uma coisa independe da outra, mesmo
que a criança não seja alfabetizada ela pode fazer cálculos, usar o raciocínio lógico
e resolver problemas.
Assim eu e a professora começamos a trabalhar Matemática com essa
aluna e para nossa surpresa ela se saía muito bem, começou com
contagem com os dedinhos e logo avançou para sobre-contagem e quando
se tratava de problemas, nós líamos para ela e ela resolvia sem grandes
dificuldades, às vezes sendo a primeira da sala a terminar corretamente.
Assim comprovei na prática o que aprendi no Programa Observatório.
(“TARS”).
Em seus relatos “TARS” afirma que as experiências vividas, como fazer
parte do grupo de pesquisa entre outras coisas, certamente enriqueceram sua
prática pedagógica. “Com as mudanças na minha postura diante da Matemática sei
que conseguirei ministrar minhas aulas corretamente sempre buscando me
aprimorar em conhecimentos, sem medo e sem preconceitos com esta área.”
Para “EAM” sua participação no grupo de pesquisas abriu novas
perspectivas e trouxe uma visão diferenciada sobre o ensino e a aprendizagem da
Matemática, permitindo que o professor reflita e se coloque no lugar do aluno,
conforme reforça em seu relato.
O programa não só abre nossos horizontes acadêmicos, como nos traz
meios para ensinar e solucionar as dificuldades que temos com a
Matemática: o quanto é difícil criar e elaborar questões e descobrir se o
aluno vai interpretar aquele enunciado, de que maneira ele resolverá o
problema. (“EAM”).
De fato, conforme citado anteriormente o Grupo de Pesquisa do Programa
Observatório da Educação promove a convivência com profissionais de diferentes
níveis de formação propiciando aos envolvidos no grupo uma experiência e
106
crescimento que não seria possível de outra forma. É esta a opinião de “EAM”
destacada a seguir:
Acredito que este projeto soma muito em minha formação, pois nós
estagiários, sentamos e debatemos com doutores, doutorandos, mestres,
mestrandos, professores, coordenadores pedagógicos, além de outros
estagiários como eu, com foco em aprender como o aluno, nos anos iniciais,
pensa a Matemática. Analisamos e elaboramos atividades e avaliações que
esses alunos farão no decorrer nos anos iniciais. Além de analisar as
avaliações, estudamos as expectativas de aprendizagem do 1° ao 5° ano,
debatemos sobre os descritores do Sistema de Numeração Decimal do
SAEB: a experimentação; a oralidade e a simbologia (escrita). Ao olharmos
as questões podemos ver os erros prováveis que as crianças cometem.
(“EAM”).
Percebemos que a participação no grupo de pesquisa abriu possibilidades
de ampliar seu conhecimento para o ensino de Matemática e sua própria atuação
como docente.
“LISE” se interessou pelo Grupo de Pesquisa quando conheceu a proposta
do Programa Observatório da Educação. Saber sobre as pesquisas que seriam
realizadas, o objetivo do programa e especialmente a relação com a Matemática, foi
decisivo em sua decisão de aceitar o convite. “O maior interesse na participação no
grupo de pesquisa teve relação direta com a Matemática. Acho que a Matemática é
praticada todos os dias e em todos os momentos”.
Embora relate que sempre gostou de Matemática e sentiu-se motivada a
poder aprender mais sobre seu ensino, assim como seus colegas, sentiu certa
apreensão no início de sua participação no Projeto.
Confesso que no início de minha participação no Programa Observatório
fiquei um pouco perdida, pois sou leiga em certos assuntos. No curso de
Pedagogia as disciplinas relacionadas à Matemática deixam um pouco a
desejar, já que são muito teóricas, muitas vezes nem partem para a
realidade. No Programa com o acompanhamento das professoras e demais
participantes, com as apresentações das telas como as de Vergnaud, pude
aprender como trabalhar com as dificuldades dos alunos, sem isso minha
formação seria vaga. (“LISE”).
“LISE” mostra a importância das discussões entre os pares para a
aprendizagem e desenvolvimento de conceitos que facilitem o ensino e a
aprendizagem de Matemática. De fato, no grupo de pesquisa, conforme já citamos
anteriormente, a participação de diferentes profissionais permite troca de
informações e experiências que agregam valor à formação de cada um dos
107
envolvidos. Encontramos respaldo para nossas afirmações nas contribuições de Curi
(2012).
O saber docente construído nas reuniões do grupo de pesquisa, é um saber
situado na ação coletiva e compartilhada em que cada participante exerce
seu papel, conforme sua experiência profissional, mas todos atuam
segundo os objetivos da pesquisa, com a finalidade comum de melhorar a
prática. (CURI, 2012, p. 27).
Notamos que a participação neste grupo nos leva a refletir sobre nossa
formação e nos torna multiplicadores de práticas e informações. É o que nos mostra
“LISE”, no que diz respeito à sua relação com os demais colegas do curso de
Pedagogia.
Discuto com meus colegas de classe sobre minha participação no Programa
Observatório e tudo que tenho aprendido e elas concordam que na
graduação deveríamos ter aulas mais dinâmicas e não fazer apenas uma
pesquisa relacionada a tal assunto ou trabalhos de como ensinar a
Matemática. (“LISE”).
A estagiária entende, assim como nós, que o curso de formação deve
preparar o futuro professor para assumir suas aulas, com o conhecimento
necessário para desenvolver o ensino e possibilitar a aprendizagem. Seu comentário
nos mostra, como afirma Shulman (1986), que para ensinar é necessária a
articulação de diferentes tipos de conhecimento, por ele destacados como
essenciais ao trabalho do professor: conhecimento do conteúdo da disciplina,
conhecimento pedagógico do conteúdo da disciplina, conhecimento do currículo.
Podemos perceber a importância dos conteúdos para o ensino de
Matemática, os quais, segundo a estagiária não foram aprendidos na formação
básica, nem trabalhados nas aulas de FME de Matemática no curso de Pedagogia,
mas sim nos encontros do grupo de pesquisa, os quais a ajudaram a superar alguns
mitos que trazia de sua formação em Matemática.
Acabei com alguns mitos que aprendi na minha formação como a utilização
das casinhas de dezena e unidade, a utilização da palavra “numeral”.
Aprendi algumas estratégias como a utilização de ditados, bingos, cartas
sobrepostas, composição e decomposição de números. São coisas simples
que passam “batidas” no curso de Pedagogia e que pelo que eu presencio
no Programa traz muitos benefícios e faz uma total diferença quando
comparamos as turmas nas quais os professores utilizam esses
procedimentos e aquelas que não usam. (“LISE”).
Porém, mesmo com esta reflexão, “LISE” não destaca em seus comentários
sobre as atividades propostas pela professora, como veremos adiante, a utilização
108
da palavra numeral ao invés de número, conflitante com as orientações curriculares
mais recentes.
É interessante ressaltar as reflexões realizadas por “LISE”, sempre
comparando sua formação básica, as aulas da graduação relativas ao ensino de
Matemática e sua participação no Programa Observatório da Educação.
O trabalho com problemas desenvolvido no Programa também me
impressionou bastante, pois me levou às minhas aulas de Matemática no
Ensino Fundamental, entendendo como alguns problemas se tornam um
problemão quando é utilizada uma palavra desconhecida ou se passa a
ideia de maneira incorreta e acaba se culpando a criança pela dificuldade.
(“LISE”).
Apoiados nas contribuições de Schön (2000) e Alarcão (2003), podemos
entender que a postura de “LISE” ao estabelecer relações entre as aprendizagens
propiciadas nos diferentes níveis de seu ensino, mostra um pensamento e uma
ressignificação de seu papel, pautados em uma reflexão não somente importante
mas necessária para sua atuação no cotidiano escolar e na sala de aula. A
estagiária relata entender que sua prática poderá ser efetivamente desenvolvida nos
estágios.
Após um ano no curso de Pedagogia, “VANGRA” foi convidada para
participar do Programa Observatório da Educação e se interessou muito porque
queria observar se suas concepções sobre a Matemática mudavam e se o medo e a
dificuldade diminuiriam. Porém se perguntava se estava preparada para este
desafio, se conseguiria acompanhar o grupo, porém sabia que precisava desta
oportunidade para ter base para ensinar Matemática aos seus futuros alunos.
“VANGRA” relata considerar o grupo de pesquisa como uma “disciplina” a
mais em sua formação, tendo que estudar, rever e realizar as atividades propostas
no mesmo. As reuniões, discussões e convivência com outros profissionais
propiciadas se constituíram em fonte de aprendizagem e formação para ela.
O grupo é composto por professores que pensam e agem diferente da
forma que estava acostumada a ver. Muitas vezes quando as professoras
do grupo davam exemplos de alunos com dificuldades, eu me via neles, e
através disso, pela minha dificuldade do passado, pelo que presenciei no
Programa, pelo meu novo olhar em relação às dificuldades das crianças,
obtive uma direção bem mais ampla de como ensinar em sala de aula.
(“VANGRA”).
109
A estagiária ressalta sua participação no Programa Observatório como um
marco em sua formação que lhe permitiu enxergar a Matemática de outra forma,
assim como observar a importância da participação e comprometimento dos
professores que a ensinam.
O Programa me permitiu quebrar o mito de que a Matemática é um bicho de
sete cabeças, pois o problema não é a Matemática e sim a forma como os
professores vêm e trabalham a mesma. Pude perceber isso no contato com
os professores do grupo de pesquisa que se comprometem com a
aprendizagem dos alunos e deles mesmos. (“VANGRA”).
Além do curso de Pedagogia e da participação no Grupo de Pesquisa do
Programa Observatório da Educação, os estagiários destacam em seus relatos os
momentos de realização do Estágio Curricular Supervisionado.
Conforme já citado, na Universidade na qual desenvolvemos a pesquisa, a
grade curricular do curso de Pedagogia em vigência prevê a realização de cem
horas de Estágio Curricular, destinadas à observação da prática docente nos anos
iniciais do Ensino Fundamental.
Esta fase do estágio é muito importante por estar ligada ao nível de ensino
no qual a maioria dos alunos egressos do curso atuarão. Constitui-se em um
momento da formação em que o aluno estabelece ligações entre teoria e prática
articulando os conhecimentos adquiridos nas disciplinas do curso e as observações
da prática docente realizadas no estágio.
O saber profissional do professor deve partir das reflexões realizadas sobre
seu conhecimento e ações e sua formação profissional deve ser alicerçada na
reflexão a partir da realidade, para que o professor possa ressignificar e reelaborar
sua prática. Ao chegar às escolas para a realização do estágio, os alunos têm a
expectativa de aprendizagem da prática, do como fazer, com base na atuação do
professor acompanhado. Portanto suas reflexões estão alicerçadas nas ações
destes professores.
Schön (2000) nos mostra a necessidade do aluno refletir sobre a ação
docente que desenvolverá. Entendemos então que esta reflexão deverá subsidiar
novas ações no ensino de matemática, a partir da teoria, da prática e da consciência
da necessidade de mudanças.
110
Quando se trata do professor de Matemática, os alunos presenciam
diferentes situações, que quando analisadas nos mostram que crenças e mitos
quanto a esta disciplina estão muito presentes na ação docente.
Para “MAO” o período de realização do Estágio Curricular Supervisionado
nos anos iniciais do Ensino Fundamental, a ajudou a mudar de ideia em relação ao
preconceito que tinha sobre trabalhar no Ensino Fundamental e os problemas com a
Matemática. Se antes pretendia atuar somente na Educação Infantil devido sua
dificuldade com a Matemática, agora percebe a importância de sua atuação também
no Ensino Fundamental.
No que se refere à formação do professor para ensinar Matemática, a
estagiária nos mostra que as observações realizadas no Estágio Curricular
Supervisionado, trouxeram aprendizagem e crescimento, porém alicerçados mais
em sua participação no Programa Observatório da Educação, embora tenha
percebido que um momento complementava o outro.
Depois que comecei a fazer o estágio, percebi o quanto foi importante estar
participando do Programa Observatório, porque algumas dúvidas que eu
tinha, foram respondidas e alguns mitos que acreditava foram quebrados,
como por exemplo, o uso da calculadora no ensino de Matemática durante o
Ensino Fundamental, pois não acreditava que havia uma forma de usar a
calculadora em sala de aula, fazendo os alunos aprenderem a resolver
problemas e aprender a pensar de maneira lógica. (“MAO”).
Percebemos que “MAO”, embora não tenha vivenciado boas situações de
aprendizagem de Matemática em sua formação, entende a necessidade de
desenvolver competências que a preparem para o ensino de Matemática,
competências estas que em nossa opinião deverão ser desenvolvidas pelo futuro
professor nas aulas do curso de formação, nas observações realizadas nos estágios
curriculares e especialmente nas reflexões e discussões que se estabelecem da
articulação entre ação e teoria.
De fato, encontramos apoio nas contribuições de Pimenta (2002), que
entende que no desenvolvimento destas competências o professor constrói uma
identidade docente própria, com base em seus valores, crenças, sonhos, seu modo
de situar-se no mundo, sua história de vida, seus saberes e sua visão do que é ser
professor. Esta construção se dá em diferentes tempos e espaços, dentre eles a
111
Universidade, o momento de realização do estágio e outros espaços de formação,
como por exemplo o Grupo de Pesquisa.
A afirmação de “MAO” corrobora nossos comentários.
Tenho a certeza que tanto o estágio como o projeto, me ajudarão a tornarme uma profissional melhor, porque tenho a oportunidade de mudar minha
visão para me tornar uma pesquisadora. Com isso estou tirando algumas
dúvidas que me acompanharam durante toda a minha vida escolar e estou
quebrando vários mitos que tinha. (“MAO”).
“EAM” destaca que após seu ingresso no Grupo de Pesquisa do Programa
Observatório da Educação, dois momentos marcaram sua vida acadêmica e
contribuíram para sua formação: sua participação como estagiário no CEFAI –
Centro de Formação e Acompanhamento à Inclusão e a realização do Estágio
Curricular Supervisionado. Porém destaca muito mais o trabalho realizado no
CEFAI, com momentos de grande aprendizado, pois pôde vivenciar em sala de aula
os conhecimentos adquiridos na Universidade, como o trabalho sob uma abordagem
mais construtivista e menos tradicional como um dos caminhos de uma
aprendizagem mais significativa.
“EAM” ressalta então a utilização do construtivismo e da contextualização
não somente na alfabetização mas também no ensino de Matemática.
Passei a entender que com o construtivismo o ensino de Matemática é mais
fácil por relacionarmos o cotidiano com a aprendizagem do aluno. Desta
maneira passei a ver que um aluno não precisa saber de cor uma tabuada,
por exemplo: 3X4=12. Quando eu estudava era fácil para mim entender,
mas hoje a criança precisa e quer a explicação dentro do contexto, com um
problema que traga a realidade para aquela operação. Por exemplo: tenho
três carros com quatro rodas cada. Quantas rodas tenho no total? Desta
forma o aluno consegue trazer o resultado mesmo sem saber a tabuada.
(“EAM”).
Ao acompanhar as aulas de Matemática desenvolvidas pelo professor em
seu estágio no CEFAI, ficou muito clara para ele, a postura de alguns professores
com os quais teve contato. Algumas atividades de Matemática eram utilizadas para
preencher o tempo ou punir alunos.
Muitos professores ao verem que alguns alunos terminavam a lição
passavam a eles números de 1 a 100 e assim por diante. Com isso a
Matemática acabava sendo uma punição para aqueles que terminavam
primeiro suas atividades, acarretando certo desconforto e quando esses
alunos tinham a aula de Matemática já falavam: “De novo números”!
(“EAM”).
112
O estagiário relata que entende que esta postura do professor funcionava
como punição para os alunos, criando já na infância um certo bloqueio, ao invés de
aprender a contextualizar a sua vivência com os números.
Quanto à realização do Estágio Curricular Supervisionado, “EAM” declara
somente que teve a oportunidade de aprender, observando e vivenciando em sala
de aula cada ação do professor que o recebeu na escola.
Já os relatos de “VANGRA” enaltecem as contribuições do grupo de
pesquisa do Programa Observatório da Educação em sua formação, mas não se
refere à realização do estágio curricular. Estranhamos este fato, pois o estágio é
parte obrigatória da grade curricular do curso de Pedagogia e além disso, neste
momento ela realizava uma investigação durante a realização do mesmo que
colaboraria com esta pesquisa. Maior surpresa quanto à falta de comentários neste
ponto, está ligada às características da escola e da professora que a estagiária
acompanhou, conforme veremos a seguir.
Chamou nossa atenção o fato de também as estagiárias, “TARS” e “LISE”
não se manifestarem especificamente sobre a realização do Estágio Curricular
Supervisionado.
Para “LISE” sua aprendizagem no curso de Pedagogia não a prepara para
a prática em sala de aula, pois “a prática só acontece depois, nos estágios ou
quando partimos realmente para a sala de aula”. Porém para haver prática é preciso
partir da teoria, e segundo a estagiária sua prática poderá ser mais bem
desenvolvida a partir dos estágios. Apesar disso não cita a realização do estágio.
Embora afirme a importância do conhecimento matemático para o ensino e
ressalte as contribuições recebidas no Projeto Ler e Escrever e especialmente no
grupo de pesquisa do Programa Observatório da Educação, “TARS” não se
manifesta em seus registros sobre a importância ou não do estágio curricular para
sua formação para ensinar Matemática.
Os relatos das experiências e expectativas de cada sujeito desta pesquisa,
com relação ao ensino e aprendizagem da Matemática, permitiram delinear um perfil
comum a todos, apresentado a seguir.
113
São alunos que tiveram dificuldades com a Matemática na Educação Básica,
especialmente pela postura de seus professores. Os alunos que não tiveram
dificuldades devem este fato nem tanto à boa atuação dos docentes, mas
especialmente à própria competência e habilidade com o raciocínio lógico, o que
facilitou a aprendizagem e não os fez sentir a defasagem no ensino na disciplina.
Seja por um sonho, uma oportunidade de trabalho ou uma descoberta de
vocação, os cinco estagiários escolheram ser docentes. O curso de Pedagogia foi
uma escolha consciente que os levaria a exercer a profissão de professores. Para
tanto, todos colocavam grandes expectativas de aprendizagem e formação no curso
escolhido, principalmente no que diz respeito ao ensino de Matemática. Destacam,
porém que as disciplinas do curso que deviam prepará-los para tal ensino deixaram
a desejar, pois todos esperavam algo mais prático e menos teórico.
Também quanto à decisão de participar do grupo de pesquisa do Programa
Observatório da Educação os alunos mostram o mesmo perfil. Todos vislumbraram
uma oportunidade de aprendizagem e crescimento que somente o curso de
Pedagogia não seria capaz de proporcionar. E são unânimes em ressaltar a
importância de suas participações em tal grupo, estabelecendo relações entre a
aprendizagem propiciada no grupo, o trabalho que realizam e as observações
realizadas no Estágio Curricular.
3.6.2
O perfil das escolas que recebem os estagiários
Entendemos que o local de realização do estágio curricular supervisionado e
a forma como os estagiários são recebidos pela gestão da escola, podem influenciar
na formação dos futuros professores e na concepção de ensino que os mesmos
desenvolverão para sua atuação como professores.
Por este motivo,
parte dos relatos registrados nos portfólios de
aprendizagem dos estagiários incluiu um perfil da escola na qual realizaram suas
observações, traçado a partir de um questionário, já citado anteriormente,
respondido pela direção das escolas. Neste questionário procuramos identificar a
comunidade atendida, número de alunos, o IDEB10 alcançado e a disponibilidade da
10
Índice criado em 2007 pelo INEP – Instituto Nacional de Estudos e Pesquisas Educacionais Anísio
114
direção em realizar parcerias com as Universidades e receber estagiários em sua
escola.
As respostas e colocações das diretoras11, bases de nossa análise para
traçar o perfil das escolas, estão inseridas nos apêndices ao final deste trabalho.
Estes dados nos deram indícios do ambiente em que foram coletados os dados para
esta pesquisa e a contribuição ou não da direção para que tanto o estágio quanto a
coleta de dados pudessem se realizar com vistas à aprendizagem dos estagiários.
As escolas nas quais os alunos realizaram seus estágios e as observações
sobre o foco de nossa pesquisa são escolas públicas municipais, localizadas na
Zona Leste da cidade de São Paulo, as quais identificaremos como “E-MAO”, “ETARS”, “E-EAM”, “E-LISE” e “E-VANGRA”.
Das cinco EMEF - Escola Municipal de Ensino Fundamental - pesquisadas,
três estão organizadas com Ensino Fundamental de nove anos e duas ainda
trabalham com Ensino Fundamental de oito séries.
As escolas “E-TARS”, “E-LISE” e “E-VANGRA” oferecem Ensino
Fundamental de nove anos, e “E-EAM” e “E-MAO” funcionam com Ensino
Fundamental de oito séries, não possuindo portanto salas de 5° ano.
Destacamos que a escola “E-VANGRA” é colaboradora da Universidade em
questão na realização das pesquisas, aplicação de atividades e intervenções do
Programa Observatório da Educação.
O perfil destas escolas, traçado pelas próprias diretoras mostra que as
mesmas se encontram em localidades carentes, evidenciando a importância de sua
atuação para o crescimento da comunidade e dos alunos.
Os relatos das diretoras em seus questionários nos mostram que estas
escolas pesquisadas atendem número médio de 600 alunos nos anos iniciais do
Teixeira, buscando representar a qualidade da educação a partir da observação de dois aspectos:
o fluxo escolar e o desenvolvimento e aprendizado dos alunos. Calculado a partir dos dados sobre
aprovação escolar, obtidos no Censo Escolar, e médias de desempenho nas avaliações do Inep, o
Saeb – para as unidades da federação e para o país, e a Prova Brasil – para os municípios.
11
Apêndices I, J, K, L, M – Respostas das diretoras sobre o “Perfil da Escola”
115
Ensino Fundamental. Uma tabela com estes números por escola e pelo total
encontra-se no final deste trabalho12.
A partir das informações fornecidas pela direção de cada escola,
observamos o IDEB - Índice de Desenvolvimento da Educação Básica, referente às
três últimas avaliações - 2007, 2009 e 2011. Consideramos importante apresentar a
variação do IDEB das escolas em questão, uma vez que este índice é calculado a
partir do aprendizado dos alunos, que se refere à média do desempenho dos alunos
em Português e Matemática na Prova Brasil13. Embora a Prova Brasil seja realizada
somente pelos alunos da 4a série e 5° ano, entendemos que a forma como o ensino
de Matemática é desenvolvido nos anos iniciais do Ensino Fundamental tem reflexos
na avaliação dos alunos e consequentemente no IDEB da escola. Estes índices
encontram-se nos apêndices14 ao final do trabalho.
Observamos que com relação à quantidade de alunos e ao IDEB as escolas
em questão são escolas de médio porte e juntas apresentam uma média de 4,4 no
IDEB.
Interessamo-nos de forma mais específica, com relação ao apoio e
contribuição da direção na realização do estágio e nas aprendizagens dos
estagiários, razão pela qual perguntamos no questionário aplicado se a mesma
gostaria de fazer algum comentário ou sugestão sobre a pesquisa ou sobre o
trabalho realizado pela estagiária.
Somente a diretora da “E-LISE” destacou a postura da estagiária, citando
que “A estagiária mostrou interesse e teve um bom desempenho durante o estágio”.
Quanto a sugestões ou comentários todas as diretoras responderam que
não gostariam de acrescentar nada, somente a responsável pela escola “EVANGRA” afirmou que “A escola tem interesse em dialogar com a Universidade
para melhorar o atendimento aos estagiários e, ainda, apresentar sua disposição em
atender pesquisadores na área da educação”.
12
Apêndice N – Tabela: Número de alunos atendidos
A Prova Brasil faz parte do Sistema Nacional de Avaliação da Educação Básica (SAEB) e avalia duas
competências dos alunos: a de leitura e interpretação de textos (português) e a resolução de
problemas matemáticos (matemática).
14
Apêndice O – Tabela IDEB por escola.
13
116
Conforme citamos anteriormente a escola é colaboradora da Universidade
no desenvolvimento do Programa Observatório da Educação, e as afirmações da
diretora e da estagiária nos mostram a importância do diálogo escola e Universidade
e da participação das escolas nos projetos educacionais, especialmente voltados
para o ensino de Matemática, pois funcionam como formação continuada para os
professores, além de aprimorar a aprendizagem dos alunos.
3.6.3 O perfil das professoras que recebem os estagiários
Os alunos sujeitos desta pesquisa acompanharam cinco professoras15
durante a realização desta pesquisa. Consideramos importante conhecer e delinear
o perfil destas professoras que os receberam, pois suas contribuições extrapolam os
limites da escola ou da sala de aula onde o estágio está sendo realizado, uma vez
que as reflexões propiciadas ao aluno farão com que o mesmo procure rever suas
ações e estabelecer a própria prática alicerçada no modelo que lhe foi passado pelo
professor que o recebeu.
Para conhecer este perfil foi solicitado que as professoras respondessem a
um questionário, já citado anteriormente, com algumas questões relacionadas a
dados pessoais e à sua formação. Foram formuladas questões abertas focando em
dois pontos que consideramos importantes na formação do professor: a identidade
profissional e a prática pedagógica.
Ao focarmos na identidade profissional nos baseamos em Pimenta (2002),
por entendermos assim como a autora que a identidade docente se constrói
[...] pelo significado que cada professor, enquanto ator e autor conferem à
atividade docente no seu cotidiano a partir de seus valores, de seu modo de
situar-se no mundo, de sua história de vida, de suas representações, de
seus saberes, de suas angústias e anseios, do sentido que tem em sua
vida: o ser professor. (PIMENTA, 2002, p. 19).
Por este motivo, tratar da identidade profissional destes professores nos
levou a estabelecer uma linha de pensamento que mostrou de que forma esta
docência foi e continua a ser construída, assim como de que forma esta identidade
15
Para preservar a identidade dos professores acompanhados pelos estagiários, os mesmos serão
aqui chamados de “P-MAO”,” P-TARS”, “P-EAM”,” P-LISE” e “P-VANGRA”.
117
pode contribuir para as reflexões dos alunos estagiários na constituição de sua
própria identidade.
No que se refere à prática pedagógica do professor, pretendíamos ressaltar
a influência do professor observado o estágio, na constituição da prática dos alunos
estagiários e futuros professores.
De acordo com Shulman (1986), a atuação do professor precisa estar
alicerçada no conhecimento do conteúdo da disciplina (o que ensinar), no
conhecimento didático do conteúdo da disciplina (como ensinar) e no conhecimento
do currículo (com o que ensinar). Desta forma, a concepção que as professoras têm
sobre o ensino de Matemática, com seus conteúdos, o desenvolvimento de suas
aulas, os materiais utilizados e até mesmo suas crenças sobre o ensino, são
importantes no delineamento do perfil das mesmas.
Os pontos de análise do perfil das professoras, focando na identidade
profissional e prática docente foram os dados pessoais; a escolha da carreira,
disciplinas ou áreas de maior interesse; planejamento e organização das aulas de
Matemática e os materiais utilizados; contribuições da formação inicial ou graduação
para o ensino de Matemática; orientações pedagógicas para o ensino de
Matemática; formação continuada; e o acompanhamento de estagiários. As
respostas e colocações dos professores16, estão inseridas nos apêndices ao final
deste trabalho, os quais passamos a analisar.
A análise dos dados pessoais mostra que as cinco professoras
acompanhadas têm idade variando entre 35 e 49 anos. Três delas são casadas e
duas são solteiras. Todas são formadas em nível superior, tendo cursado a
graduação em Pedagogia em Universidades particulares. “P-VANGRA” declarou
possuir duas graduações: Pedagogia e Matemática. “P-MAO” declarou possuir
graduação em Matemática e à época da pesquisa cursava Pedagogia.
O tempo de atuação das professoras no Ensino Fundamental varia entre 10
e 27 anos. Quanto ao enquadramento profissional das professoras, todas são
efetivas por concurso no município de São Paulo, sendo que “P-VANGRA” é
também contratada para trabalhar na rede Estadual.
16
Apêndices P, Q, R e S – Respostas das professoras sobre o “Perfil da Professora”
118
3.6.3.1
Escolha da carreira
A escolha da carreira profissional se dá por diferentes motivos: por afinidade,
interesse, influências recebidas ou conhecimento da área. Os relatos das
professoras nos mostram que embora algumas já trouxessem da infância o desejo
de exercer a docência, outras tiveram influências familiares ou até mesmo falta de
opção na hora da escolha.
Para “P-TARS”, “P-EAM” e “P-VANGRA”a escolha pela profissão não foi
aleatória, pois fundamenta-se no início da vida escolar, especialmente no convívio
familiar, assim como nas influências de seus professores “Meu pai era professor.
Sempre fui boa aluna e gostei de ensinar. O curso de graduação me preparou para
trabalhar com crianças, principalmente por meio do estágio” (P-TARS).
Nos relatos sobre sua formação, “P-LISE” nos conta que sua escolha pela
profissão de professora foi determinada pelas alternativas de estudos que se
apresentaram ao sair do Ensino Fundamental. “Como morava em uma cidade do
interior, onde havia apenas os cursos de Magistério e Técnico de Contabilidade, fui
fazer Magistério e logo me interessei pela área.”
A professora “P-MAO” não se posicionou quanto às suas escolhas,
afirmando somente que procurou na graduação uma forma de preparação para a
docência.
Percebemos que as professoras declararam ter escolhido a docência por
motivos diversos, seja pela oportunidade, falta de opções, influência familiar ou o
gosto pela docência. Todas ressaltam porém, que após esta escolha se envolveram
com a área e não trocariam de profissão.
Podemos considerar que os motivos que levaram os sujeitos de nossa
pesquisa a escolherem a carreira de professor se assemelham aos das professoras
que os estão recebendo.
119
3.6.3.2
Disciplinas ou áreas de maior interesse
O conhecimento prático e teórico desenvolvido na graduação, faz com que
os professores tenham preferências quanto à sua atuação, muitas vezes ligadas à
experiência positiva ou negativa propiciada na formação. Um conteúdo que domina
melhor, um ano de escolaridade com o qual se identifica mais ou menos, e
estabelece-se um vínculo que vai determinar suas escolhas ou até mesmo seu
desempenho.
Conforme podemos entender a partir das contribuições de Curi (2006),
somente gostar de ensinar Matemática, ter preferência por determinados conteúdos
ou mesmo achar gratificante trabalhar com crianças de determinado ano não forma
um professor. Existem conhecimentos e competências a serem desenvolvidos, que
são específicos da formação para ensinar Matemática.
Também Serrazina (2001) nos alerta sobre o fato do conhecimento
necessário para o ensino de Matemática estar ligado a diferentes fatores:
[...] o conhecimento da Matemática dos professores do 1° ciclo é difícil de
distinguir do conhecimento da Matemática que ensinam aos seus alunos, e
está muito ligado às suas crenças e concepções sobre a Matemática e seu
ensino. Ela considera como fatores que influenciam a forma como os
professores do 1° ciclo encaram o ensino da Matemática: o conhecimento
da Matemática, o interesse e gosto por ensinar Matemática, as crenças
sobre a importância da Matemática e as expectativas sobre o que os alunos
conseguem fazer [...] (SERRAZINA. 2001, p. 32).
Por este motivo entendemos que conhecer as escolhas e preferências das
professoras com relação ao ensino de Matemática e seus conteúdos, as facilidades
e dificuldades que as mesmas apresentam em suas aulas e especialmente aquilo
que em sua visão é necessário para ensinar Matemática, nos mostrará a forma
como as professoras desenvolvem este ensino, o que pode influenciar a formação
dos estagiários.
Com relação ao ano de escolaridade no qual preferem atuar, quatro
professoras indicam como preferência os 4º e 5º anos. Somente “P-MAO” tem
preferência pelo 1° ano.
Chamou nossa atenção as justificativas das professoras sobre seus
interesses para atuação, uma vez que as mesmas não se referem à suas
120
preferências no que diz respeito aos conteúdos a serem trabalhados, à sua prática
ou à aprendizagem de seus alunos. Parece que se sentem satisfeitas, confortáveis e
aceitas na sala de aula dos alunos mais velhos, pois destacam a "maturidade e
independência dos alunos" , o que nos leva a pensar em falta de preparo para
trabalhar com crianças menores que demandam maior atenção. Somente “PVANGRA” faz alusão às atividades desenvolvidas no 5º ano, mas não explica quais
são elas, a qual área se referem e porque gosta de trabalhar com elas.
Duas professoras, “P-EAM” e “P-LISE” preferem trabalhar com a
alfabetização, e justificam esta preferência devido às suas dificuldades com a
Matemática e o ensino de Matemática. As demais professoras declaram gostar de
trabalhar com a Matemática.
As professoras mostram também em seus relatos as suas preferências no
que se refere ao ensino de Matemática, citando conteúdos que trabalham com mais
facilidade e mais dificuldade, os quais apresentamos no quadro a seguir:
Professora
Mais facilidade
Mais dificuldade
“P-MAO”
Situações problema
Interpretação do texto do
problema
“P-TARS”
Quatro operações
Raciocínio lógico
“P-EAM”
Gráficos e tabelas
Divisão e frações
“P-LISE”
Situações problema
Áreas e perímetros
Cálculo mental
“P-VANGRA”
Tabelas e gráficos
Não especifica
Quadro 8 - Conteúdos: Facilidades e dificuldades
Embora “P-MAO” declare que tem facilidade com o ensino de situações
problema e ressalte em seus relatos a importância da contextualização, como
veremos adiante a professora não contextualiza suas atividades e nem propõe
situações problema, utilizando somente folhas avulsas, sem indícios de que utilize a
Matemática como forma de inserção dos alunos na realidade e na sociedade.
121
Podemos confirmar a preferência de “P-TARS” pelo ensino das quatro
operações, nas atividades apresentadas no portfólio da estagiária “TARS”
envolvendo este conteúdo. Porém encontramos uma contradição em suas
afirmativas, pois ressalta que o mais trabalhoso ou mais difícil para ensinar
Matemática é o raciocínio lógico e depois afirma lhe atrair estimular o raciocínio
lógico.
Isto nos leva a refletir sobre o que seria raciocínio lógico para esta
professora. Ao estudar o raciocínio lógico-matemático, Piaget nos mostra que o
mesmo é muito importante na escola e no ensino da Matemática, mas é algo que
não se ensina, porque depende da estrutura de conhecimento da criança e do
estágio de desenvolvimento no qual a mesma se encontra. Portanto, as dificuldades
da professora em ensinar o raciocínio lógico deveriam ser repensadas para
encontrar atividades que favoreçam este desenvolvimento, de acordo com a idade e
estágio de desenvolvimento de cada criança.
A professora “P-EAM” relata que suas dificuldades estão relacionadas a
"como" ensinar a Matemática, declarando defasagem nessa área. Embora goste de
trabalhar com gráficos e tabelas, considera mais trabalhoso ou mais difícil ensinar
divisão e frações. Entretanto não encontramos nos registros das atividades o
trabalho com nenhum dos conteúdos citados pela professora.
“P-LISE” afirma gostar de ensinar Matemática, principalmente situações
problema e cálculo mental e, com efeito, encontramos nos registros das atividades
várias atividades que envolvem sua preferência por problemas e cálculo mental.
Apesar
de
“P-VANGRA”
relatar
sua
preferência
pelas
atividades
envolvendo tabelas e gráficos, não encontramos registro de seu trabalho com este
tema.
As
professoras
revelam
lacunas
de
sua
formação
referentes
às
metodologias de ensino de Matemática. Não se referem à falta de formação nos
conteúdos matemáticos que devem ensinar, mas apontam o que gostariam de ter
aprendido.
122
“P-EAM” declara que faltou contextualização no ensino de Matemática em
sua formação desde o início no Ensino Fundamental, pois aprendeu somente as
operações descontextualizadas ensinadas mecanicamente, o que hoje reflete em
dificuldades no ensino.
A professora “P-LISE” ressalta a falta de utilização de material “concreto”
em sua formação, conforme seu relato: “Acredito que para ensinar Matemática às
crianças é preciso utilizar material concreto, mas em minha formação inicial houve
esta lacuna, precisaria ter sido trabalhado mais esta utilização em meu curso”.
Sabemos que o uso de material “concreto” no ensino de Matemática hoje
apresenta muitas críticas, no entanto segundo Ponte e Serrazina (2000, p. 116)
"Convenientemente orientada, a manipulação de material pelos alunos pode facilitar
a construção de certos conteúdos".
Mas somente sua utilização pelo professor não garante a construção de
conceitos ou a aprendizagem. Os autores acima discorrem sobre o uso de material
“concreto”:
A primeira regra de ouro é que estes sejam de facto usados pelo aluno. A
segunda regra de ouro é que o aluno saiba realmente qual a tarefa para a
qual é suposto usar o material. É tão ineficaz ser o professor a usar o
material, com o aluno a ver, como ter o aluno a mexer no material sem
saber o que está a fazer. (PONTE; SERRAZINA, 2000, p. 116).
A professora “P-MAO” também destaca a necessidade do “concreto” para a
aprendizagem. Desde sua graduação esperava que aprendesse a ensinar
Matemática focando no uso de materiais, o que nos faz pensar que talvez sua
concepção de “concreto” esteja ligada somente a manipulação de objetos, sem
pensar nas ligações que podemos estabelecer com as crianças na utilização dos
conceitos matemáticos para situações concretas e reais.
Nas questões relacionadas à aprendizagem para o ensino de Matemática,
“P-VANGRA” relata que gosta de ensinar Matemática, muito embora não se recorde
das disciplinas e conteúdos relativos a este ensino desenvolvidas no curso de
formação. Percebemos que embora a professora declare ter formação em
Pedagogia e Matemática, seus relatos se direcionam mais para a Pedagogia e a
formação propiciada neste curso, não se referindo em nenhum momento à sua
123
graduação em Matemática, que a nosso ver poderia contribuir muito para o ensino
que desenvolve com as crianças no Ensino Fundamental, especialmente quando
articulados à formação pedagógica propiciada no curso de Pedagogia.
Os relatos sobre as facilidades e dificuldades das professoras quanto aos
conteúdos matemáticos e seu ensino se confirmam nas demais observações e
análises sobre o perfil destas professoras.
3.6.3.3
Planejamento e a organização das aulas de Matemática
Pretendíamos conhecer a forma como cada professora planeja suas aulas
de Matemática, como organiza e distribui estas aulas em sua rotina, quais materiais
utiliza, incluindo os livros didáticos.
Segundo Haydt (2002) o planejamento é importante e necessário porque
evita improviso e auxilia na prevenção e superação de dificuldades, contribui para
que os objetivos propostos sejam alcançados com eficiência. Além disso, ao planejar
didaticamente suas aulas o professor pode prever quais conteúdos vai trabalhar
para que os alunos adquiram determinados conhecimentos, organizando atividades
que levem o aluno à aprendizagem.
As cinco professoras declaram se organizar e trabalhar com base em um
planejamento que permita apresentar os conteúdos de forma que os alunos se
interessem a aprendam. Embora ressaltem a utilização do planejamento
diariamente, pudemos perceber nos relatos dos estagiários que as mesmas não
apresentam ou discutem o planejamento com os mesmos e nem o consultam
durante as aulas.
Com relação aos materiais previstos no planejamento e utilizados no
desenvolvimento das aulas, destacamos suas declarações no quadro a seguir:
124
Professora
Livro
Caderno de Apoio e
Outros
Didático
Aprendizagem
materiais
“P-MAO”
“P-TARS”
X
X
“P-EAM”
“P-LISE”
X
“P-VANGRA”
X
X
X
X
X
X
Quadro 9 - Materiais utilizados no planejamento e desenvolvimento das aulas
de Matemática
Percebemos que três professoras declararam utilizar o livro didático adotado
pela escola e duas delas não o utilizam. Dentre as três que utilizam, duas delas, “PTARS” e “P-VANGRA”, afirmam complementar o planejamento das atividades com
os Cadernos de Apoio e Aprendizagem17.
Chama nossa atenção o relato de “P-VANGRA” sobre a utilização não só
do Livro Didático adotado na escola em suas aulas. Utiliza vários livros para planejar
suas aulas, dentro da rotina estabelecida e também o Caderno de Apoio e
Aprendizagem, material utilizado por todos os alunos. Não há em seus relatos uma
especificação de quais outros materiais utiliza para as aulas ou de quais livros tira as
atividades.
Temos a hipótese de que a professora “P-VANGRA” provavelmente utiliza
os materiais e atividades que são propostos no Programa Observatório para
desenvolvê-los com as crianças, os quais além de serem objetos de ensino e
aprendizagem são instrumentos de investigação. Mas a professora não cita tais
atividades, nem as relaciona entre os materiais que utiliza na preparação de suas
aulas.
A professora “P-LISE” afirma utilizar o Livro Didático adotado na escola em
suas aulas. Porém ao ser questionado se complementa esta utilização com outros
17
Os Cadernos de Apoio e Aprendizagem, destinados aos estudantes dos nove anos do Ensino
Fundamental, têm como finalidade contribuir para o trabalho docente visando à melhoria das
aprendizagens dos alunos. São distribuídos a alunos e professores da rede municipal de ensino
da cidade de São Paulo.Na área de Matemática, os blocos de conteúdos contemplados são:
espaço e forma, grandezas e medidas, números, operações, tratamento da informação.
Fonte: http://portalsme.prefeitura.sp.gov.br/Projetos/BibliPed/Anonimo/Cadernosdeapoio.aspx
125
materiais de apoio, responde que sim, com tampinhas e palitos. A estagiária “LISE”
também não relata em seus registros o uso do Livro Didático ou dos materiais
citados pela professora.
Cabe destacar que de acordo com Masetto (1996) recursos didáticos ou de
ensino são componentes do plano de ensino e são os materiais à disposição do
professor para a organização do ensino, desde um simples giz até multimeios
complexos e sofisticados. Com relação ao material de apoio, constituem-se em
apoio efetivo ao desenvolvimento do ensino, propiciando informações corretas, que
serão apresentadas pelo professor de forma adequada às necessidades
educacionais dos alunos. Aqui se incluem desde o Livro Didático adotado pela
escola, apostilas, atividades impressas, materiais fornecidos pelo governo, até
consultas a bibliotecas físicas ou digitais e e-books. Portanto, no caso em questão o
Livro Didático e Caderno de Apoio da SME são materiais de apoio e as tampinhas e
palitos são recursos de ensino.
As professoras “P-EAM” e “P-MAO” declararam que não utilizam o Livro
Didático no planejamento de suas aulas.
A professora “P-EAM” usa raramente o Livro Didático e por opção faz
pesquisas de atividades em outros livros e na internet, conforme seu relato:
Raramente uso o Livro Didático utilizado na escola, prefiro pesquisar
atividades, com base nas avaliações externas que os alunos fazem durante
o ano. Utilizo o Caderno de Apoio e Aprendizagem de Matemática, além de
outros livros que pesquiso. (“P-EAM”).
“P-MAO” por sua vez, relata que não utiliza o Livro Didático adotado pela
escola em suas aulas, pois a mesma não recebeu livros e Cadernos de Apoio
suficientes para todos os alunos. Desta forma desenvolve suas aulas e seu trabalho,
retirando atividades do livro didático “Aprender Juntos”, do “Projeto Buriti” e também
da internet. Não esclarece porém se as atividades selecionadas se apoiam nos
conteúdos indicados no Livro Didático da escola, no Caderno de Apoio e
Aprendizagem, no seu próprio planejamento ou se ela mesma seleciona a partir de
outro critério.
126
3.6.3.4
Contribuições da graduação para o ensino
Neste ponto da pesquisa pretendíamos levantar a questão da contribuição
das disciplinas oferecidas no curso de Pedagogia, ligadas ao ensino de Matemática,
na formação dos professores participantes da pesquisa. No entanto as respostas
mostram que esse curso pouco contribuiu para sua formação para ensinar
Matemática.
Todas as professoras declararam que o curso de Pedagogia deixou lacunas
na sua formação para ensinar Matemática.
Quatro professoras consideraram o curso de Magistério mais importante
para sua formação do que o curso de Pedagogia, pois o primeiro estava mais
voltado à prática e o segundo mais à teoria.
Para “P-LISE” houve pouca contribuição do curso de Pedagogia para
trabalhar nas diferentes áreas do conhecimento.
O curso de Magistério foi muito importante para minha formação, já o curso
de Pedagogia pouco contribuiu. Só se aprende a trabalhar com crianças
trabalhando com crianças, e o curso não ajudou nesse sentido, pouco
contribuindo ou preparando nas diferentes áreas do conhecimento, como
Alfabetização, Ciências ou Matemática. (“P-LISE”).
A professora “P-MAO” entende que o Magistério trouxe mais prática que o
curso de Pedagogia, o que a auxilia em suas aulas.
O curso de Magistério me deu suporte para desenvolver minha didática e
com o tempo fui consolidando-a. Este curso me preparou para ensinar as
crianças no Ensino Fundamental porque o 4º ano do curso é voltado para a
prática de ensinar. A faculdade deixou a desejar pois desenvolve uma
didática mais teórica. (“P-MAO”).
No entanto, a professora “P-EAM” comenta que o momento da graduação
foi importante, mas segundo ela o fato de já estar atuando na educação durante o
curso de Pedagogia facilitou sua aprendizagem.
No curso tive aulas teóricas, com vídeo conferência e ótimas referências
bibliográficas que pautam meu trabalho até hoje. Tínhamos aulas práticas
onde vivenciávamos a prática de uma sala de aula com oficinas. No meu
caso foi muito mais fácil, pois eu já estava na rede de ensino e podia aplicar
as oficinas na minha própria sala de aula. (“P-EAM”).
Esses depoimentos mostram deficiências do curso de Pedagogia na
formação do professor para ensinar Matemática. O fato de uma professora não se
127
recordar do que aprendeu revela a pouca contribuição desse curso na sua formação,
pois mesmo afirmando que o curso de Pedagogia lhe trouxe conhecimento, o qual
foi reforçado com sua prática, a professora “P-TARS” assim relata:
Não me recordo das aulas no curso de Pedagogia no que diz respeito ao
ensino de Matemática, seja das estratégias, seja dos assuntos tratados. Por
isso não trabalho em minha prática diária com algo que aprendi na
formação inicial. (“P-TARS”).
Com isso nos perguntamos, se a formação inicial não traz contribuições
efetivas para o ensino de Matemática desenvolvido pelas professoras em suas
aulas, onde as mesmas buscam este conhecimento? De que forma se preparam e
suprem esta defasagem?
3.6.3.5
Orientação pedagógica para o ensino de Matemática
A formação do professor pode ser complementada com a formação
continuada e com a formação em serviço, aqui entendida como a forma que a
Matemática é discutida nas escolas, seja entre os próprios professores, seja no nível
de coordenação. É importante que se saiba das professoras em questão, se o que
ensinar e como ensinar em Matemática é assunto de destaque nas orientações
pedagógicas, se há uma preocupação da escola com este ensino.
Sobre este ponto apenas a professora “P-LISE” declara não ter na escola
um acompanhamento para o ensino de Matemática. “Não tenho orientação
pedagógica para ensinar Matemática aos meus alunos. Não há discussões na
escola, em nenhuma instância sobre o que ensinar e como ensinar”.
Embora as escolas municipais da cidade de São Paulo adotem a JEIF Jornada Especial Integral de Formação, um momento de formação e discussão
sobre a prática pedagógica que envolve não somente como ensinar, mas também o
que ensinar, com orientações pedagógicas e indicação de materiais de apoio, a
professora não se manifesta a este respeito.
Três professoras ressaltam as discussões realizadas nos encontros na
própria escola, como base para suas práticas em sala de aula, conforme podemos
verificar no relato de “P-MAO”:
128
18
No grupo de formação JEIF- Jornada Especial Integral de Formação , é
discutido o ensino de Matemática com outros professores e coordenadores,
e o documento de Orientações Curriculares de Expectativas de
Aprendizagem para o Ensino Fundamental – ciclo I. (“P-MAO”).
A professora “P-EAM” revela sua necessidade de acompanhamento e
formação para o ensino de Matemática, reforçada na resposta dada à última
pergunta do questionário. Quando indagamos se gostaria de fazer algum comentário
ou acrescentar algo que julgasse interessante para o tema discutido, afirma que:
“Gostaria de acrescentar que nós professores necessitamos muito de formação em
Matemática”.
Esta foi a única professora a reconhecer suas limitações na formação para
ensinar Matemática. Entende que os professores precisam de formação específica
para ensinar Matemática, falando inclusive em “Alfabetização Matemática”.
3.6.3.6
Formação continuada
A profissão de professor para muitas pessoas confunde-se com dom ou
vocação, o que não exclui a necessidade de formação constante. Os comentários
das professoras sobre a formação inicial não ter atendido às expectativas quanto às
necessidades do conhecimento para o ensino, nos leva a pensar sobre a
importância de uma formação que ultrapasse a Universidade e que traga ao
professor a possibilidade de discutir com seus pares sobre o ensino e a
aprendizagem, o que é propiciado em encontros de estudo na própria escola; em
grupos de estudo e pesquisa, tal como ocorre no grupo de pesquisas do Programa
Observatório ou na formação continuada.
Embora as professoras que receberam os estagiários reconheçam a
necessidade de aperfeiçoamento na docência, quatro delas acreditam que a
formação inicial e o dia a dia da sala de aula são suficientes para a constituição de
sua prática, não demonstrando necessidade de ir além na busca de cursos ou
atualizações.
18
A JEIF dos professores da Rede Municipal de Ensino da cidade de São Paulo corresponde a 40
h/aulas semanais, sendo 25 h/aulas de regência e 15 h/aulas adicionais, sendo 11 h a serem
cumpridas obrigatoriamente na escola e 4hs em local de livre escolha (Portaria nº 647/2008, Art.
2º, § 4º).
129
Dentre elas ressaltamos a professora “P-VANGRA” que mesmo com as
lacunas observadas na formação inicial e a dificuldade com o conteúdo específico
de Sistema de Medidas, relata que não tem feito cursos de formação continuada
nem está atualmente fazendo algum curso de formação.
Somente a professora “P-EAM” declara que sua formação inicial lhe
proporcionou uma ótima base quanto à alfabetização, mas encontra muita
dificuldade com a Matemática, pois apesar da formação que tem e ainda busca, os
cursos de alfabetização nunca deram muita ênfase para essa área do conhecimento.
Por este motivo percebe a necessidade de continuar estudando para poder ensinar
com maior conhecimento e propriedade aos seus alunos, afirmando que “no
momento não tenho feito curso de formação continuada fora da escola, mas sinto a
necessidade de um curso de alfabetização em Matemática”.
O reconhecimento da professora “P-EAM” acerca de sua limitação no
ensino de Matemática é importante pois mostra uma reflexão sobre a própria prática,
que Schön (2000) denomina de reflexão-sobre-a-ação, uma vez que reflete e
argumenta após suas ações em sala de aula. Não há nos relatos da professora algo
que nos mostre a ampliação desta reflexão conforme o autor defende, para reflexãosobre-a-reflexão-na-ação, o que caracterizaria seu conhecimento pessoal, levando
ao desenvolvimento profissional.
3.6.3.7
Acompanhamento de estagiários
O período do estágio, conforme já citamos, é esperado com ansiedade pelos
alunos da Pedagogia, uma vez que entendem ser este o momento de finalmente
colocar em prática tudo que aprenderam na Universidade. Por este motivo é
extremamente importante que o professor que os recebe tenha uma postura de
mestre, que orienta, encaminha e os ajuda a se constituírem em suas próprias
práticas.
Esses alunos nos relatam que as diretoras ou coordenadoras não têm muita
disponibilidade em abrir as portas da escola para a realização de estágios. Quando
os recebem, o professor muitas vezes os deixa no fundo da sala e os ignora, não
compartilhando conhecimentos importantes para a formação destes alunos. Um
130
programa de orientação dentro da escola, para receber os estagiários seria de
grande
valia,
pois
conforme
já
citamos,
os
professores
aprendem
pelo
compartilhamento de informações e práticas, o que beneficiaria não somente os
estagiários, mas também os professores em questão.
Concordamos com Pimenta e Lima (2004) quando destacam que o professor
é um profissional que ajuda o desenvolvimento pessoal e intersubjetivo do aluno,
sendo um facilitador de seu acesso ao conhecimento.
Dentre as cinco professoras “P-LISE” e “P-VANGRA” mostraram-se
totalmente desinteressadas em formação específica para orientar os estagiários. “PLISE” declara que “recebo estagiários algumas vezes, mas não tenho e não me
interesso em ter uma formação para recebê-los”.
Duas professoras indicam ter orientação para receber os estagiários em sua
sala.
A professora “P-MAO” relata que tem orientações sobre como receber os
estágiários na escola. Nos conta que está acostumada a receber estagiários em sua
sala todos os anos, sendo que isto já tornou-se rotina, mas não nos fala sobre quais
são estas orientações, quem as passa ou de que forma ocorrem. Declara ainda que
“Quando recebo um estagiário, proponho que fique atento a didática e à prática
pedagógica”, mas não esclarece o que entende por tais conceitos. A professora
afirma também que não tem interesse em uma formação mais específica para
receber e acompanhar os estagiários em sua sala, “porque o contato com o estágio
acontece todos os anos”.
Duas professoras declararam que não recebem orientação para a formação
dos estagiários, mas que gostariam de ter orientações mais específicas sobre como
auxiliá-los. Uma delas é “P-TARS”, conforme podemos observar em seu relato.
Estou acostumada a receber estagiários em minha sala, mas não tenho
orientações de como recebê-los. Proponho que observem a aula e às vezes
peço para ajudarem os alunos para adquirirem prática e conhecimento.
Tenho interesse numa formação mais específica para receber e
acompanhar os estagiários em minha sala. (“P-TARS”).
A outra professora é “P-EAM”, que mostra iniciativa e comprometimento,
pois embora não tenha por parte da escola ou da Universidade nenhuma orientação
131
sobre como receber os estagiários, suas ações neste sentido, vêm de sua própria
iniciativa, assim como nos relata.
Quando recebo estagiários em minha sala, proponho que ajudem as
crianças com mais dificuldade. Discutimos sobre as dificuldades que nós
professores temos no ensino e como podemos sanar estas dificuldades,
que materiais podemos utilizar no nosso trabalho. Tenho grande interesse
em uma formação específica para receber e acompanhar os estagiários em
minha sala. (“P-EAM”).
Este relato nos leva a refletir sobre a necessidade, assim como defende
Alarcão (2003), de uma supervisão ao estagiário, em sua formação, no
acompanhamento e contribuição na construção do conhecimento pedagógico do
professor.
Podemos concluir que é preciso reforçar a questão da importância das
orientações do professor na formação dos estagiários que orienta e acompanha.
Entendemos assim como Ponte (2006) que a formação do professor sofre
influências do contexto no qual a mesma se constitui. As reflexões sobre a prática
docente, à falta da própria prática, levam os estagiários a refletirem e se espelharem
na prática do professor que acompanham.
3.7
Considerações sobre o Capítulo
Nas considerações deste Capítulo levantamos, a nosso ver, um importante
questionamento sobre a forma como é desenvolvido o Estágio Curricular
Supervisionado, no que diz respeito a propiciar aos alunos aprendizagens para
ensinar Matemática nos anos iniciais do Ensino Fundamental. Este questionamento
refere-se à forma como a Universidade na qual estamos realizando a pesquisa
orienta a realização dos estágios no curso de Pedagogia.
Percebe-se que não há no regulamento de estágios um direcionamento para
a realização do mesmo. Os alunos devem cumprir determinada carga horária, em
determinado nível de ensino, observando determinadas ações dos professores.
Após organizarem suas planilhas de estágio, com os lançamentos de todas as
atividades realizadas dia a dia, elaboram um Relatório de Estágio onde devem emitir
suas opiniões, críticas e sugestões sobre a prática do professor observado e
eventualmente fundamentar teoricamente suas opiniões.
132
O professor orientador, muitas vezes em virtude da dificuldade enfrentada
pelos alunos para encontrar uma escola que os aceite para realizar o estágio, não
cobra a observação em todas as disciplinas. Vemos alunos que só têm tempo para
realizar o estágio no horário de seu almoço ou no final do dia, o que faz com que
sempre observem o horário do lanche, do intervalo ou atividade de cópia da lição de
casa. Nos questionamos onde fica a observação da ação do professor nestes casos.
Além disso, percebemos na análise dos planos de ensino das disciplinas
FME de Matemática I e II que os mesmos não apresentam contribuições
significativas para que os alunos aprendam a ensinar Matemática.
Os planos não direcionam também as estratégias para trabalhar os
conteúdos, o que se fosse feito daria oportunidade aos alunos de vivenciarem a
prática deste professor e refletir sobre ela na construção de aprendizagens e de
suas próprias práticas.
Por outro lado, como não há espaço disponível para as discussões tão
importantes quanto necessárias em sala de aula, sobre as articulações entre a
disciplina de FME de Matemática I e II e o estágio, as observações ficam restritas à
didática do professor, sua postura, relações pessoais na escola, entre outros
aspectos.
Além disso, na disposição da grade curricular não há sincronia entre as
disciplinas relativas ao ensino de Matemática desenvolvidas nos 3º e 4º semestres e
o estágio no Ensino Fundamental realizado no 5º semestre, o que não possibilita
integração e diálogo, tampouco maiores discussões sobre o estágio nas aulas de
FME de Matemática ou vice-versa.
Estas discussões poderiam ocorrer nas aulas de Prática de Ensino, mas o
plano desta disciplina revela a falta desta articulação, sem preocupação direta com a
prática de ensino das diferentes disciplinas, com maior foco na formação geral do
professor.
Compreendemos que a Universidade analisada, tanto em seu Projeto
Pedagógico quanto no regulamento de estágio obedece à legislação vigente, porém
não propõe o foco no ensino de Matemática nas observações realizadas no estágio.
133
Entretanto, professores que desenvolvem trabalhos ou pesquisas em
determinadas áreas, como Matemática, Ciências ou Língua Portuguesa, por
exemplo, costumam ser orientadores que reforçam com seus estagiários a
necessidade de observações específicas que vão auxiliar em sua formação como
professores chamados de polivalentes. No que diz respeito à alfabetização, por
exemplo, os alunos que participam do Projeto Ler e Escrever têm momentos de
reflexão sobre a prática do professor em seu dia a dia, no desenvolvimento de seu
próprio trabalho. Porém com relação à Matemática, foco de nosso olhar, não temos
estes importantes momentos de trabalho.
É certo que é preciso ter bom senso e análise individual dos problemas que
possam ocorrer, pois cada aluno pode apresentar uma particularidade, um problema
diferenciado na unidade escolar, uma necessidade específica. É preciso que se
cumpram as leis e as normas da instituição, mas nossa preocupação é
especialmente com a aprendizagem destes alunos para o ensino de Matemática e a
contribuição que o estágio supervisionado traz para sua formação.
A pequena contribuição teórica das disciplinas oferecidas no curso de
Pedagogia sobre o ensino de Matemática dificulta a observação e análise no
momento do estágio, o que poderia de alguma forma possibilitar maior
aprendizagem ao futuro professor sobre este tema.
Percebemos que as possibilidades de aprendizagem sobre o ensino de
Matemática no estágio só existem quando o professor orientador de estágios tiver a
preocupação de direcionar as observações e reflexões para este ensino,
vislumbrando aos alunos sua atuação futura, como professores ditos polivalentes.
Mas somente isto não é suficiente, pois ficamos na dependência do
comprometimento desse professor orientador com a formação integral do aluno que
deverá ensinar Matemática nos anos iniciais do Ensino Fundamental.
Quanto ao perfil dos estagiários, percebemos que todos tiveram dificuldades
na formação inicial em Matemática, o que não influenciou a escolha da profissão.
Destacam também a falta de preparo para o ensino de Matemática propiciado no
curso de Pedagogia, no que diz respeito não só aos conteúdos, mas especialmente
134
à prática de ensino. Este perfil, como veremos nas análises de seus portfólios, é
marcante em seus relatos e comentários..
Quanto às escolas, percebemos diretoras que focam mais na dimensão
administrativa de seu trabalho do que na dimensão pedagógica, com destaque para
apenas uma diretora que mostra interesse em parcerias com a Universidade como
forma de elevar o nível do ensino de seus professores. Esta postura também revela
falta de comprometimento com a formação dos professores, em especial dos
estagiários do curso de Pedagogia, que atuarão no Ensino Fundamental.
As contribuições das professoras para a formação e prática docente dos
estagiários que receberam, não aparecem de forma efetiva em seus relatos ou nos
registros dos alunos. Consideramos relevante que cada professor perceba a
importância de sua atenção e colaboração na formação dos estagiários que
acompanham em suas aulas. As experiências e reflexões propiciadas nos estágios,
a partir da prática do professor observado permitem que os estagiários reflitam sobre
a própria prática, apoiando-se na prática e ações deste professor.
Neste Capítulo delineamos o contexto no qual esta pesquisa se realizou: o
curso de Pedagogia e a realização dos estágios. Quanto ao curso, revimos a
legislação pertinente aos estágios, o Projeto Pedagógico do Curso de Pedagogia, as
ementas das disciplinas relativas ao ensino de Matemática, a Prática de Ensino e os
documentos norteadores da Universidade para a realização dos estágios. Quanto à
realização efetiva dos estágios nas escolas de Ensino Fundamental mostramos o
perfil dos estagiários, das escolas e das professoras que os acompanham.
Este contexto nos dará base para as discussões propostas no próximo
Capítulo, onde será apresentado o estudo de caso, a partir das contribuições dos
cinco sujeitos da pesquisa e seus registros nos portfólios de aprendizagem, a
respeito das observações feitas na realização do estágio curricular supervisionado.
135
CAPITULO 4 - OS ESTÁGIOS E OS ESTAGIÁRIOS: O ESTUDO DE
CASO
O conhecimento exige uma presença curiosa do sujeito
em face do mundo. Requer uma ação transformadora
sobre a realidade. Demanda uma busca constante.
Implica em invenção e em reinvenção.
(Paulo Freire)
4.1
Introdução
Neste capítulo apresentaremos a análise das observações dos cinco alunos
sujeitos desta pesquisa, a partir de suas experiências no desenvolvimento do
estágio curricular supervisionado, registradas nos portfólios de aprendizagem. Tais
análises objetivam identificar as reflexões, os dilemas, as interações e as
necessidades dos estagiários com relação ao ensino de Matemática.
Conforme discutimos em capítulo anterior, na Universidade pesquisada o
Estágio Curricular Supervisionado nos anos iniciais do Ensino Fundamental, é
realizado no 5° semestre do curso de Pedagogia. É neste momento que os
estudantes poderão acompanhar a prática do professor observado, estabelecendo
relações entre a teoria aprendida no curso de formação e a prática do professor em
questão, o que permitirá ampliar a própria formação e o conhecimento da
Matemática.
Como parte obrigatória da formação, os alunos se dirigem às escolas para
cumprir a carga horária de estágio estabelecida legalmente, esperando que neste
momento, em seu futuro ambiente de trabalho, vivenciando o dia a dia escolar, no
contato com o professor atuante, possam realizar observações e interações que lhes
tragam conhecimentos, práticas e atividades para ensinar Matemática.
No nosso caso, ressaltamos as observações feitas no capítulo anterior, em
que pudemos perceber nos relatos dos estagiários a necessidade de maior
disponibilidade das escolas em recebê-los ; professoras que se dizem abertas em
receber e orientar estagiários, mas que no entanto apenas uma delas sente a
necessidade de formação ou orientação para recebê-los; falta de articulação entre
136
teoria e prática, sem discussões na Universidade sobre os conteúdos trabalhados e
as observações realizadas no estágio.
É neste contexto que observamos e analisamos a questão proposta nesta
tese de doutorado.
4.2
Procedimentos Metodológicos
Para que pudéssemos obter mais informações sobre cada atividade
desenvolvida pelos sujeitos de nossa pesquisa na realização do estágio,
entendemos que o método a ser adotado para esta pesquisa, que melhor atenderia
às nossas expectativas seria o Estudo de Caso, conforme destaca Ponte:
Um estudo de caso visa conhecer uma entidade bem definida como uma
pessoa, uma instituição, um curso, uma disciplina, um sistema educativo,
uma política ou qualquer outra unidade social. O seu objectivo é
compreender em profundidade o “como” e os “porquês” dessa entidade,
evidenciando a sua identidade e características próprias, nomeadamente
nos aspectos que interessam ao pesquisador. (PONTE, 2006, p. 2).
Com efeito, Yin (2005, p. 28) também ressalta a importância da questão
expressa na investigação, no caso o “como” e o “porque”, que permitem observar
uma vantagem distinta na utilização do estudo de caso. Para o autor esta vantagem
ocorre quando “faz-se uma questão do tipo ‘como’ ou ‘por que’ sobre um conjunto
contemporâneo de acontecimentos, sobre o qual o pesquisador tem pouco ou
nenhum controle” (YIN, 2005, p. 28).
Podemos então identificar a pertinência do método em questão para esta
pesquisa, por entendermos que a contribuição ou não do estágio para a formação do
professor que vai ensinar Matemática nos anos iniciais do Ensino Fundamental é um
caso significativo, que pode levar a análises diferenciadas. Além disso o conjunto de
acontecimentos é delineado no decorrer da pesquisa, durante as observações dos
estagiários
no
estágio
supervisionado,
sem
nosso
controle
sobre
estes
acontecimentos ou resultados apresentados pelos alunos.
As vivências e experiências de cada um dos participantes, assim como o
contexto diferenciado no qual o estágio é realizado, são fatores que interferem na
formação e atuação destes futuros professores. Concordamos com Ponte (2006)
quando o mesmo defende que,
137
Em qualquer das situações, um caso constitui uma entidade bem definida,
necessariamente inserida num certo contexto. O que explica que o caso
seja como é, são sempre as determinantes internas, a sua história, a sua
natureza, as suas propriedades próprias, bem como as influências externas,
próximas e distantes, directas e indirectas que recebe do seu com texto. Por
isso, no estudo de um caso, seja ele qual for, é sempre preciso dar atenção
à sua história (o modo como se desenvolveu) e ao seu contexto (os
elementos exteriores, quer da realidade local, quer de natureza social e
sistémica que mais o influenciaram). (PONTE, 2006, p. 5, grifo do autor).
As contribuições de Yin (2005, p. 32) reforçam nossa escolha, quando o
mesmo descreve que “o estudo de caso é um estudo empírico que investiga um
fenômeno atual dentro do seu contexto de realidade, quando as fronteiras entre o
fenômeno e o contexto não são claramente definidas.” O que podemos acompanhar
durante o trabalho devido aos pontos estudados a partir dos registros dos
estagiários a respeito de suas observações verificadas nos estágios.
Realizamos um estudo de caso, com a colaboração dos cinco alunos
sujeitos desta pesquisa, cada qual focando nas atividades, produções, reflexões e
possíveis aprendizagens para ensinar Matemática relatadas em um portfólio de
aprendizagem, discutido mais à frente, elaborado durante a realização do estágio
curricular supervisionado.
Yin (2005) sugere que sejam utilizadas várias fontes de pesquisa indicando
a análise de documentos, entrevistas abertas e fechadas, análise quantitativa de
dados e observações diretas.
No caso desta investigação foram utilizadas diferentes fontes, tais como
narrativas, questionários, atividades realizadas, dados, todas organizadas no
portfólio de cada estagiário.
Entendemos portanto a pertinência da utilização do método de estudo de
caso, conforme nos mostra Yin (2005), pois nos permitirá compreender de que
maneira se dá a formação do professor para ensinar Matemática nos anos iniciais do
Ensino Fundamental a partir de diferentes momentos desta formação, especialmente
no momento da realização do Estágio Curricular Supervisionado, analisando os
dados obtidos a partir das observações dos cinco estagiários e sujeitos da pesquisa.
A análise do caso nos mostrou a vivência de cada sujeito da pesquisa,
alicerçada nas considerações que tecemos sobre a formação do professor que vai
138
ensinar Matemática nos anos iniciais do Ensino Fundamental. Nossa fundamentação
para as observações dos alunos se apoia portanto na formação do professor, no
conhecimento para ensinar Matemática, na importância da realização do estágio e a
articulação entre teoria e prática na constituição da docência.
4.2.1 O portfólio
Conforme citamos em nossa apresentação, a análise dos dados desta
investigação será feita a partir dos portfólios elaborados pelos sujeitos da pesquisa.
A opção pela utilização do portfólio como instrumento de coleta de dados se
deu em virtude do mesmo possibilitar ao aluno trabalhar num processo denominado
por Hernández (1998) de construção e reconstrução da própria aprendizagem.
A utilização de portfólios vem sendo divulgada nos meios educacionais como
ferramenta de avaliação. Porém Chamoso Sánchez, Cáceres Garcia e Azcárate
Goded (2011) nos alertam que os portfólios vão além de uma avaliação do avanço e
aprendizagem dos alunos pelo professor. Ele se constitui em instrumento de
reflexão, construção de saberes e desenvolvimento dos alunos, permitindo que os
mesmos possam perceber seus próprios avanços.
Hérnandez (1998) descreve ainda os componentes e todos os passos que
devem ser seguidos para a realização de um portfólio, que são: o estabelecimento
do objetivo do portfólio por parte do docente; o estabelecimento das finalidades de
aprendizagem por parte de cada estudante; a integração das evidências e
experiências de aprendizagem; a seleção das fontes que comporão o portfólio e a
reflexão do estudante acerca de seu próprio desenvolvimento.
Estas colocações vêm ao encontro de nossas orientações aos estagiários e
nossos objetivos na utilização deste importante instrumento de coleta de dados.
Além disso, Hérnandez (1998) ressalta que o estudante deve ter um propósito, ou
seja, criar, recolher e organizar todo material que evidencie o seu progresso, de tal
forma que demonstre sua avaliação em relação às finalidades estabelecidas.
139
Durante as aulas, os alunos foram orientados a seguir um roteiro de
observação, que serviria de suporte para os registros de suas atividades e
obvervações. Esse roteiro está apresentado a seguir.
Roteiro de observação de estágio e elaboração de relatório para alunos estagiários
do Programa Observatório da Educação
 Realização do estágio curricular supervisionado nos anos iniciais do Ensino
Fundamental
 Observação de pelo menos 20 horas de Matemática no Grupo 1
 Elaboração de Portfólio contemplando os seguintes itens:
1) História de vida do aluno, suas relações com a Matemática, como concebe
o ensino de matemática, como aprendeu Matemática e sua participação
no grupo de pesquisa.
2) Campo – análise a ser realizada aula por aula
2.a Narrativa da observação da aula, destacando o que observou no
professor, na participação dos alunos, os materiais utilizados. Esta
narrativa deverá enfocar o antes, o durante e o depois da atividade.
2.b Acrescentar cópia das atividades realizadas
2.c Análise da atividade em função dos conteúdos aprendidos na
disciplina FME de Matemática I e II
2.d Análise da reação dos alunos e professores durante a realização da
atividade, na correção da professora, na devolutiva aos alunos.
2.e Se você fosse o professor, que mudanças faria na atividade e na
aplicação e correção da mesma.
3) Conclusão final
Destacar de que forma as observações realizadas no Estágio Curricular Supervisionado
nos anos iniciais do Ensino Fundamental, nas aulas de Matemática, aliadas ao
conhecimento adquirido nas aulas de FME de Matemática, contribuíram para sua
aprendizagem para ensinar Matemática.
Quadro 10 - Roteiro para realização do estágio
Adotamos Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011)
como referencial teórico para a análise dos portfólios elaborados pelos alunos
participantes da pesquisa, em suas observações na realização dos Estágios
Curriculares, focando no ensino e aprendizagem da Matemática. Os autores
discutem a formação de professores de Matemática ressaltando a importância da
reflexão sobre a sua prática como um dos aspectos mais importantes na
140
capacitação profissional. Nesse sentido as ideias dos autores vem ao encontro da
perspectiva da reflexão defendidas por Schön (2000) e Alarcão (2003), discutidas no
Capítulo 2 deste trabalho, que discorreu sobre a formação dos professores.
Chamoso
Sánchez,
Cáceres
Garcia
e
Azcárate
Goded
(2011)
desenvolveram uma pesquisa acompanhando alunos em um curso de formação de
professores e orientaram que os alunos elaborassem portfólios individuais
destacando o conhecimento profissional dos mesmos, a partir de suas reflexões
sobre o processo ensino-aprendizagem que ocorre na aula de formação, como
forma de avaliação. Esta avaliação deveria se relacionar depois, com seu
conhecimento matemático e criatividade.
Entendemos assim como os autores, que os portfólios de aprendizagem são
importantes instrumentos para coletarmos evidências do pensamento reflexivo dos
alunos, por evidenciarem a construção do pensamento e do conhecimento ao longo
da elaboração dos mesmos.
Além disso, Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011)
entendem que os registros dos alunos fornecem indícios sobre seu conhecimento,
habilidades, disponibilidade e reflexão sobre seu trabalho assim como sobre sua
evolução. Assim como os autores entendemos que a utilização de portfólio traz a
possibilidade
de
conhecer
o
progresso
da
aprendizagem
do
aluno,
as
responsabilidades que assume, de que forma participa do processo de diagnóstico e
avaliação, suas atitudes, seus hábitos de independência e de reflexão, e suas
habilidades na resolução de problemas como na comunicação, raciocínio e análises.
Os autores consideram três dimensões da aprendizagem dos alunos, que
podem ser destacadas no portfólio, que julgam necessárias à formação do
professor: Conhecimento, Reflexão e Criatividade.
Na dimensão do “Conhecimento” que os alunos devem possuir, os autores
consideram o Conhecimento do Conteúdo Matemático e Conhecimento Pedagógico
para o ensino de Matemática. Entendem que é preciso que o aluno encare cada
conteúdo específico do programa e se aprofunde nele, tanto do ponto de vista
matemático como de sua aplicação no ensino. No que se refere ao ensino de
Matemática, os autores destacam a reflexão sobre a prática como ponto importante
141
para a superação da carência de qualquer tipo de conhecimento, seja teórico ou
metodológico.
Na pesquisa realizada pelos autores, a questão da “Reflexão” é discutida,
pois perceberam que os alunos não tinham experiência anterior que lhes
possibilitasse refletir sobre sua formação. Segundo eles seu trabalho propiciou o
desenvolvimento da reflexão de duas formas. A primeira delas feita pelos próprios
alunos, em conjunto na sala de aula, com escrita e apresentação posterior de suas
reflexões. A segunda, com sessões de formação que abrangiam a reflexão pessoal
do professor relacionada a diferentes aspectos, complementando as contribuições
dos alunos e discutindo a importância da reflexão para os professores, assim como
de que forma desenvolvê-la. Com isto os autores pretendiam que os alunos
exercitassem a reflexão sobre seus próprios conhecimentos e práticas.
Por fim, a terceira dimensão da aprendizagem descrita pelos autores é a
“Criatividade”, entendida como capacidade de criar em situações imprevistas. Esta
dimensão é importante na medida em que cabe ao professor saber conduzir sua
aula de forma flexível, podendo tomar decisões que facilitarão a aprendizagem dos
alunos, mudando o ritmo ou o rumo da aula conforme as necessidades de
aprendizagem dos mesmos.
Num segundo momento, a partir destas três dimensões: Conhecimento,
Reflexão e Criatividade, os autores estabeleceram uma categorização geral, comum
para todas as dimensões observadas, estabelecendo assim três níveis de
categorização em função do seu aprofundamento, da qualidade no desenvolvimento
do tópico considerado e sua implicação no processo de ensino-aprendizagem. Estes
níveis foram fixados para avaliar a aprendizagem dos alunos levando-se em conta a
profundidade do envolvimento de cada aluno com a própria aprendizagem. Eles são
assim definidos:
Nível 1 - Descrição: Quando o estudante está envolvido no processo, com uma visão
externa.
Nível 2 - Argumentação: Quando o aluno está ativamente envolvido no processo.
142
Nível 3 - Contribuição: Quando o estudante, além de participar e se envolver no
processo, toma suas próprias decisões.
As contribuições de Chamoso Sánchez, Cáceres Garcia e Azcárate Goded
(2011) nos direcionam para nossa própria investigação, pois assim como eles,
pretendemos analisar os portfólios dos estagiários, no que diz respeito à sua
formação para ensinar Matemática, focando nas contribuições que as observações
realizadas no estágio curricular propiciam para esta formação.
Entendemos que os estudos desses autores a partir da análise dos portfólios
de estudantes do curso de formação de professores, são apropriados para esta
pesquisa, uma vez que nos preocupamos com os relatos dos estagiários em seus
portfólios no que se refere ao ensino de Matemática, analisando o nível de reflexão
dos alunos nas suas observações, o conhecimento que eles têm dos conteúdos
matemáticos e do ensino de Matemática, assim como de que forma analisam a
prática dos professores observados e sua própria prática, do ponto de vista da
motivação e criatividade.
Além disso, preocupa-nos a maneira como os alunos se envolvem com a
própria formação, entendendo que os níveis Descrição, Argumentação e
Contribuição descritos pelos autores poderão colaborar sobremaneira com nossas
análises.
Apresentamos a seguir os quadros elaborados por Chamoso Sánchez,
Cáceres Garcia e Azcárate Goded (2011) que sintetizam os parâmetros que serão
utilizados para análise dos portfólios dos cinco estagiários.
Dimensão
Análise
CONHECIMENTO
Analisar a ampliação dos conteúdos
matemáticos
Conhecimento
do
conteúdo
matemático
Níveis
desenvolvidos
1 (Descrição)
Indicadores gerais
Quando o aluno apresenta o conteúdo de
pelos
maneira linear, propõe exemplos e atividades
alunos para sua aplicação na aula dos
que exigem a aplicação direta do conceito
anos iniciais do Ensino Fundamental
explicado sem distinguir a quais níveis do Ensino
Fundamental se destinam.
Conhecimento metodológico para
2 (Argumentação)
o ensino de Matemática
Quando o aluno relaciona conteúdos, usa
exemplos ou atividades motivadoras como uma
introdução que permita a relação entre eles, os
relaciona com outras áreas ou com a vida
cotidiana, segue uma sequência lógica em sua
explicação
ou
distingue
sua
aplicação
a
diferentes níveis do Ensino Fundamental.
3 (Contribuição)
Quando o estudante explica os conteúdos com
seus próprios argumentos, usa exemplos e
atividades
motivadoras
adequadas,
propõe
exemplos e atividades variadas e originais que
facilitam a sua criatividade ou aplica esses
conteúdos em diferentes níveis do Ensino
Fundamental.
Quadro 11 - Parâmetros para análise da dimensão do Conhecimento segundo Chamoso Sánchez, Cáceres Garcia e
Azcárate Goded (2011)
Fonte: Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011, tradução nossa).
143
144
Dimensão
Análise
Níveis
REFLEXÃO
Analisar as reflexões dos alunos sobre
1 (Descrição)
Indicadores gerais
Quando
o
estudante
relacionados
Sobre a formação e como forma
durante
aprendizagem sem envolver-se, ou seja, limita-
de
Curricular Supervisionado, a partir de
se
seus
desenvolvimento de uma atividade.
carência
de
conhecimento
teórico
e
metodológico.
a
realização
registros
aprendizagem.
no
do
Estágio
portfólio
de
2 (Argumentação)
a
rever
numa
análise
pessoal
foi
feito
ensino-
durante
o
sobre
o
processo
de
ensino-
aprendizagem, ou seja, participa do processo
do
compreendendo o sentido da atividade.
19
professor
que
de
Quando o estudante argumenta, justifica ou tira
conclusões
Em conjunto na sala de aula ou
o
processo
aspectos
os diferentes encontros nas aulas,
superar
ao
descreve
3 (Contribuição)
Quando
o
estudante
traz
suas
próprias
contribuições com o objetivo de melhorar o
processo de ensino-aprendizagem, ou seja, além
de
compreender,
se
envolve
com
o
desenvolvimento e aperfeiçoamento de suas
atividades.
Quadro 12 - Parâmetros para análise da dimensão da Reflexão segundo Chamoso Sánchez, Cáceres Garcia e Azcárate
Goded (2011)
Fonte: Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011, tradução nossa).
19
Em nossa pesquisa consideramos as reflexões pessoais realizadas no portfólio.
Dimensão
Análise
CRIATIVIDADE
Analisar a relação dos conteúdos
matemáticos
Capacidade
de
criar
em
situações imprevistas
Flexibilidade,
tomada
decisões
redirecionar
para
de
com
Níveis
o
1 (Descrição)
contexto
Indicadores gerais
Quando
o
aluno
demonstra
conhecer
os
conteúdos, mas não os relaciona entre si. Tanto o
observado no trabalho de cada
desenvolvimento
aluno, adaptando e sugerindo
atividades são os normalmente encontrados no
novas formas de trabalho.
livro didático.
2 (Argumentação)
o
do
conteúdo
quanto
as
Quando o aluno relaciona conceitos e segue uma
sequência lógica que explica o desenvolvimento
ensino e a aprendizagem.
global do trabalho com gráficos e desenhos, ou
seja, adapta as atividades de forma que tenham
relação com o contexto, ainda que não decorram
do mesmo.
3 (Contribuição)
Quando o aluno utiliza seus próprios argumentos e
cria modelos originais para explicar os conteúdos,
o completo desenvolvimento do trabalho com
gráficos e desenhos, ou seja, as atividades
surgem do contexto, sem adaptá-las.
Quadro 13 - Parâmetros para análise da dimensão da Criatividade segundo Chamoso Sánchez, Cáceres Garcia e Azcárate
Goded (2011)
Fonte: Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011, tradução nossa).
145
146
4.3
A análise dos dados
Tomando por base os registros realizados, em que os alunos apresentam o
que pensam, sentem, sabem e produzem, foi feita a análise de cada portfólio,
verificando as contribuições do processo como um todo para a aprendizagem do
ensino de Matemática. Todas as informações que serviram de base para a análise
do caso, encontram-se nos relatos e contribuições registrados nos portfólios de
aprendizagem de cada um dos sujeitos da pesquisa.
Ao realizar as análises constatamos muitas similaridades, com relação aos
relatos dos estagiários com relação às observações, atividades e aprendizagens.
Estas coincidências nos levaram a optar pela comunicação de forma que
pudéssemos interligar os comentários e análises, sem se tornar repetitivo e
cansativo para a leitura, uma vez que neste momento já podemos inclusive
estabelecer relações entre as observações dos cinco estagiários. Assim agiremos a
partir do próximo subítem.
4.3.1 Conteúdos
trabalhados,
atividades
desenvolvidas
e
análise
dos
estagiários
Como já citado em nosso trabalho, as orientações dadas aos sujeitos da
pesquisa para a realização do estágio foram de que suas observações se
direcionassem para o conteúdo e atividade trabalhada pelas professoras, tecendo
seus comentários sobre a postura das mesmas antes, durante e depois da
realização da atividade. Além disso, deveriam procurar estabelecer relações entre as
atividades observadas e os conteúdos aprendidos nas disciplinas relacionadas ao
ensino de Matemática que foram desenvolvidos na Universidade. Com isto os
estagiários deveriam se colocar perante as observações tecendo seus comentários
sobre a prática de professora, os conteúdos trabalhados e sua própria formação.
4.3.1.1
Conteúdos trabalhados
Nos dias em que acompanharam as professoras, os estagiários puderam
observar diferentes atividades envolvendo conteúdos diversificados.
147
Todos os estagiários relatam que algumas atividades eram apresentadas
aos alunos em folhas avulsas, mas a grande maioria encontrava-se nas orientações
do Livro Didático adotado pela escola ou no Caderno de Apoio e Aprendizagem.
Os estagiários ressaltaram o uso dos Cadernos de Apoio e Aprendizagem,
pois o mesmo é distribuído aos alunos da rede e discutido com professores nas
capacitações realizadas pela Secretaria Municipal de Educação.
Somente a professora “P-MAO” declarou que não utiliza estes materiais por
falta de quantidade suficiente para todos os alunos, selecionando as atividades a
serem trabalhadas e entregando-as em folhas avulsas aos alunos.
Apresentamos a seguir uma tabela, elaborada a partir dos registros dos
estagiários em seus portfólios, com os temas e conteúdos trabalhados pelas
professoras, destacando o número de vezes em que tal tema foi trabalhado.
Tabela 1 - Conteúdos trabalhados
Número de atividades observadas por estagiário
Conteúdo
LISE
1º ano
MAO
1ª série/
2º ano
VANGR
A
3º ano
EAM
4ª série/
5º ano
TARS
5º ano
TOTAL
12
8
7
-
4
31
3
1
-
-
-
4
5
6
1
3
7
22
Operações
(Campo multiplicativo)
-
-
2
3
4
9
Espaço e Forma (Formas
geométricas)
2
1
-
-
1
4
Espaço e Forma (Relações
espaciais)
1
-
-
-
1
2
1
1
1
-
3
6
Números Naturais/Sistema
de Numeração Decimal
(Contagem; ordem
crescente e decrescente;
Ditado de números; Valor
posicional; dezena e
unidade; Composição;
Decomposição;
Agrupamento)
Números
Naturais
(Abodagens)
(Conjunto; Função Ordinal)
Operações
(Campo aditivo)
Grandezas
(Calendário;
tempo)
e
Medidas
Medidas de
Continua
148
Continuação
Grandezas
e
Medidas
(Medidas de capacidade;
dúzia; Sistema Monetário)
Tratamento da informação
(Gráficos)
1
1
2
-
1
5
-
1
1
-
-
2
A análise da tabela acima nos mostra que independente do ano observado,
os conteúdos mais trabalhados pelas professoras foram as Operações com
destaque para o campo aditivo e o SND - Sistema de Numeração Decimal.
Observamos ainda que o trabalho com SND se concentra nos três primeiros anos o
que prejudica a sistematização e a ampliação dos conhecimentos das crianças
sobre esse tema.
Chamou nossa atenção a falta de atividades no que se refere ao conteúdo
de Espaço e Forma. Como podemos observar na tabela, no 1º ano “P-LISE”
desenvolveu quatro atividades com os alunos, trabalhando formas geométricas e
relações espaciais. No 2º ano há uma atividade de formas geométricas desenvolvida
por “P-MAO” e depois somente uma atividade de formas geométricas no 5º ano,
trabalhada por “P-TARS”. No 3º e 4º ano as professoras não trabalharam este tema
com os alunos.
Ao analisarmos os temas abordados podemos inferir que os mesmos têm
relação com as preferências das professoras destacadas em seus relatos.
Os conteúdos abordados por “MAO” confirmam a declaração da professora
sobre os temas de Matemática que considera mais importantes para trabalhar em
suas aulas, como o reconhecimento dos números, operações, ditado e escrita de
números.
Com base nos relatos da professora “P-TARS” sobre sua preferência pelo
ensino
das
quatro
operações,
constatamos
essa
opção
nos
conteúdos
desenvolvidos nas aulas observadas pela estagiária.
Com relação às preferências de “P-EAM”, destacam-se as atividades
relacionadas às situações problema e interpretação das mesmas envolvendo
situações concretas vividas pelos alunos. As atividades observadas por “EAM” na
realização do estágio estão relacionadas ao tema que a professora considera mais
149
importante. Porém não foram observados nas atividades apresentadas, gráficos e
tabelas que a professora afirma gostar de trabalhar, assim como divisão e frações –
conteúdos do 5º ano - considerados pela mesma difíceis de ensinar. Por outro lado,
em virtude de “EAM” ter observado somente seis aulas com atividades, esse fato
não nos permite inferir que a professora não trabalhe estes conteúdos ou privilegie
aqueles em que se sente mais confortável.
Nas atividades observadas por “LISE” confirma-se a preferência da
professora no trabalho com atividades ligadas a situações problema e cálculo
mental, pois das 26 atividades apresentadas, 17 referem-se aos conteúdos citados
pela professora. A professora reconhece fragilidades em sua formação com relação
ao ensino de áreas e perímetros e efetivamente não há atividades relacionadas a
este conteúdo, muito embora sua atuação seja no 1º ano, em que este conteúdo
ainda não é trabalhado.
A análise da tabela com os conteúdos trabalhados nas atividades
observadas e descritas por “VANGRA” não permite confirmar as declarações da
professora sobre as atividades nas quais tem mais facilidade de trabalhar com seus
alunos (tabelas e gráficos). Por outro lado também não há atividades com o tema
sistemas de medidas, conteúdo que a professora reconhece ter dificuldades.
Entendemos que talvez, pelo pequeno número de aulas acompanhadas por
“VANGRA” ou pelo período em que o estágio foi realizado, os conteúdos citados
acima não estavam incluídos no planejamento, o que não nos permite afirmar que
não foram trabalhados pela dificuldade da professora em trabalhar tais temas.
4.3.1.2
Atividades desenvolvidas
Realizaremos a seguir nossa análise relativa às atividades trabalhadas pelas
professoras e as respectivas reflexões dos estagiários.
4.3.1.2.1 Números Naturais e Sistema de Numeração Decimal
No que se refere ao trabalho com Números Naturais e Sistema de
Numeração Decimal, foram totalizadas vinte atividades envolvendo contagem e
ordem crescente e decrescente (sequência numérica, maior ou menor, igual e
150
diferente); três com atividades de conjuntos, uma com função ordinal e quatro
atividades com ditado de números, valor posicional e dezena e unidade. Além disso,
sete atividades versavam sobre composição, decomposição e agrupamento.
As atividades de contagem estão mais concentradas no 1º ano, com
contagem por agrupamento, contagem com conjuntos, ordem crescente e
decrescente (sequência numérica, igual e diferente e maior ou menor).
A estagiária “LISE”, que acompanhou o 1º ano, relata que no
desenvolvimento da atividade de contagem por agrupamento, os alunos não
apresentaram dificuldades. Para ela, a atividade está de acordo para o ensino deste
conteúdo às crianças, pois aprendeu nas aulas de FME de Matemática que é
importante trabalharmos a contagem e uso de símbolos para identificar quantidades.
Destacamos uma atividade apresentada pela professora “P-LISE” aos
alunos do 1º ano, extraída do Caderno de Apoio e Aprendizagem.
Figura 2 -
Folha de Atividade: A contagem do Seu João
Fonte: Cadernos de Apoio e Aprendizagem, 2010.
151
Segundo a estagiária a professora lê a atividade e aguarda as crianças
resolverem. Quanto aos alunos, “LISE” entende que “não apresentam dificuldades
na contagem. Notei que algumas crianças usaram como auxílio as próprias mangas
da ilustração”.
A estagiária comenta que o recurso de desenhar ou usar o desenho
oferecido na própria atividade para poder realizar a contagem é muito utilizado pelas
crianças.
Não há registro se a professora desenvolveu a última atividade (oral) da
sequência.
A estagiária observou que a professora “P-LISE” aplica diversas atividades
extraídas do Caderno de Apoio e Aprendizagem de Matemática. Segundo a
estagiária “os Cadernos de Apoio são bem ilustrados, com uma linguagem fácil para
o entendimento das crianças e sempre trabalham com o cotidiano”. Ela afirma que
talvez este seja o motivo de as crianças gostarem bastante da sequência de
atividades a seguir que apresentam como contexto o Parque de Diversões.
A
Figura 3 - Folha de Atividade: Xícara Maluca (A e B)
Fonte: Cadernos de Apoio e Aprendizagem, 2010.
B
152
A
B
Figura 4 - Folha de Atividade: Sobe e desce, desce e sobe (A e B)
Fonte: Cadernos de Apoio e Aprendizagem, 2010.
Os relatos de “LISE” mostram que a professora inicia a atividade pedindo
que alguns alunos que já são alfabetizados leiam o enunciado. Em seguida a própria
professora lê novamente o que deveriam fazer em cada atividade, e solicita o
registro da resolução. Para a estagiária a atividade foi bem entendida e
acompanhada pelos alunos.
A maioria da sala acompanhou e respondeu corretamente. Por ser um
exercício simples e divertido, as crianças não apresentaram dificuldades. A
professora explica o que é para fazer, aguarda uns minutos para que
respondam e então passa para o seguinte. Todos participaram da roda de
contagem, sugerida no último exercício. (“LISE”).
Os comentários da estagiária relacionam a facilidade das crianças ao tipo de
propostas que considera simples e divertidas.
A estagiária relata que pode relacionar a atividade com sua aprendizagem
na disciplina de FME de Matemática, onde viu que a criança precisa utilizar símbolos
numéricos e criar associações. Com relação à postura da professora depois da
atividade, “LISE” relata ainda que “a professora corrigiu com eles contando cada
objeto, acompanhando todos tanto na realização da atividade quanto na correção”.
153
Ainda no 1º ano, a professora “P-LISE” aplicou outras atividades com os
números destacando o trabalho com os sinais e o conceito de igual e diferente. A
atividade foi distribuída em folhinhas avulsas e coladas no caderno de cada aluno.
Figura 5 - Folha de Atividades: Igual e Diferente
Fonte: Portfólio da estagiária.
De acordo com os registros de “LISE”, antes de iniciarem a atividade, a
professora explicou os sinais de igual (=) e diferente (≠), contando com a
participação dos alunos na resolução das propostas.
Alguns entenderam rapidamente o que era para ser feito, mas outros não. A
professora decidiu então resolver junto com eles, iniciando no primeiro
quadrinho como exemplo. Contavam cada elemento do conjunto de bexigas
e depois de petecas. A professora perguntava se o resultado era de igual ou
diferente. (“LISE”).
“LISE” não se recorda de ter aprendido como ensinar este conteúdo nas
aulas da disciplina FME de Matemática. Também não relata como a professora
154
encerrou a atividade, se precisou resolver as duas atividades com os alunos ou se
as crianças resolveram e depois houve correção.
A estagiária não percebeu que a folhinha usada pela professora deveria ser
de material mais antigo, pois usa a palavra Numeral ao invés de Número e se refere
a elementos de conjuntos. Certamente por se tratar de uma abordagem de décadas
anteriores não foi discutida nas aulas de FME de Matemática20. Entretanto, “LISE”
comenta anteriormente sobre sua aprendizagem no grupo de pesquisa a respeito da
utilização das palavras Numeral e Número.
As atividades envolvendo especificamente ordem crescente e decrescente
foram trabalhadas somente pela professora “P-MAO”, que atua no 2º ano.
Destacamos duas atividades relacionadas a este conteúdo para analisarmos
com base nos registros da estagiária.
Figura 6 - Folha de Atividades: Sequência Numérica
Fonte: Portfólio da estagiária
20
Na década de 70, por conta da influência do Movimento Matemática Moderna, havia uma distinção
entre Número (o objeto matemático) e Numeral (a representação do objeto). Nos currículos atuais
não há essa distinção.
155
Figura 7 - Folha de Atividades: Ordem Crescente
Fonte: Portfólio da estagiária
Em ambos os momentos “MAO” percebeu um bom desenvolvimento da
maioria dos alunos, sendo que aqueles com mais dificuldade tiveram auxílio e nova
explicação por parte da professora. Pensa que apesar de algumas dúvidas, este
bom desempenho se deve aos números trabalhados serem baixos e ainda na ordem
das dezenas.
A estagiária ressalta que não faria nenhuma mudança na aplicação das
atividades, pois gostou do desenvolvimento das mesmas pela professora e pelos
alunos. Entende que este tipo de atividade precisa ser aplicado durante o ano todo,
para reforçar o que já foi aprendido e dar oportunidade de desenvolvimento àqueles
que ainda não aprenderam. Destaca ainda que a forma de correção da professora,
passando e dando visto nos cadernos, poderia ser modificada para trazer mais
resultados para os alunos. “MAO” sugere que talvez se a correção fosse coletiva,
com a participação dos alunos na realização na lousa, respondendo e explicando
todos aprenderiam melhor.
156
A estagiária também não percebeu que as folhinhas usadas pela professora
eram de materiais mais antigos que usava Numeral ao invés de Número.
Ainda no trabalho com números, “MAO”, “TARS” e “VANGRA” trazem
relatos em seus portfólios relacionados a atividades de sequência numérica
desenvolvidas pelas professoras.
A professora “P-MAO” trabalhou com sua turma do 2º ano com sequência
numérica em diversas aulas, com diferentes atividades.
Na primeira atividade destacada foi feito um trabalho com um quadro
numérico, no qual os alunos teriam que completar no caderno as lacunas de uma
sequência de números de 100 em 100, no intervalo de 100 a 10000. A estagiária
relata que a explicação dada pela professora para a realização da atividade foi
colocar na lousa, como exemplo, a sequência de 100 a 2000.
Para “MAO” esta atividade tem um ótimo propósito, porém entende que o
quadro numérico entregue aos alunos estava com números muito altos para a
compreensão e idade dos mesmos, e talvez este fator tenha prejudicado o bom
desenvolvimento dos alunos. Segundo ela, trabalharia com outro quadro numérico
até o número 1000, por exemplo, colocando na parede da sala um quadro numérico
grande, para que os alunos pudessem consultar diariamente até aprenderem e não
precisarem mais desse suporte, conforme seu relato.
A atividade desenvolvida tem um ótimo propósito, porém o quadro numérico
estava com números muito altos para a idade dos alunos, acredito que esse
fator tenha prejudicado o bom desenvolvimento da atividade. Precisava ser
feita outro quadro com números até o mil, por exemplo, e ser colocado na
parede da sala um quadro numérico grande, para que os alunos a
consultem diariamente até aprenderem e não precisarem mais desse
suporte. (“MAO”).
Entendemos que esta atividade propiciou uma boa análise de “MAO” pois a
mesma reflete sobre o contexto e o nível de conhecimento dos alunos, sugerindo
inclusive uma nova forma de trabalho que facilitasse o entendimento e
aprendizagem das crianças sobre o conteúdo. No entanto, ela não relata como a
professora fez e se fez a correção e o que foi discutido.
Em outra atividade com sequência numérica, os alunos deveriam escrever
no caderno do número 200 ao número 250. “MAO” relata que não conseguiu
157
perceber o objetivo da realização desta atividade e o que a professora pretendia
com ela, pois além da professora não deixar isto claro, os alunos ainda tinham
dificuldades com sequência numérica, portanto a maioria não conseguiu fazer esta
atividade.
Muitos alunos procuraram sua ajuda, pois não estavam conseguindo
completar a atividade sozinhos. A estagiária relata ter percebido que muitos ainda
não conheciam os números a partir de 200, fazendo com que confundissem , por
exemplo, o duzentos com o doze. Por este motivo, a estagiária sugere que nesta
atividade a professora deveria trabalhar com eles apenas com números até o cem,
reforçando estes números e fazendo a sequência numérica desde o começo,
utilizando para consulta o quadro numérico grande colocado na parede, que indicou
anteriormente para auxiliar a consulta.
Os comentários de “MAO” sobre o trabalho com quadro numérico,
demonstram suas aprendizagens sobre o assunto destacado nos Cadernos de
Apoio e Aprendizagem e nos encontros do grupo do Programa Observatório da
Educação, o que corrobora a afirmação da estagiária de que aprendeu muitos
conteúdos e formas de trabalho no ensino de Matemática em sua participação no
Programa Observatório.
Com o 5º ano a professora P-TARS trabalhou com sequência numérica,
utilizando o quadro numérico disponível no Caderno de Apoio e Aprendizagem.
Segundo a estagiária a atividade foi desenvolvida sem problemas, “os alunos
resolvem sem apresentar dificuldades. A professora faz a correção na lousa, os
alunos vão dando as respostas e ela escrevendo e fazendo intervenções.”
158
Figura 8 - Folha de atividades: Quadros Numéricos
Fonte: Cadernos de Apoio e Aprendizagem, 2010.
A estagiária percebeu que a atividade envolve números na ordem da dezena
de milhar, mas mesmo assim os alunos atendem à solicitação da atividade sem
problemas.
Outra atividade destacada por “TARS” envolvia os números na ordem de
dezena de milhar, em que os alunos deveriam fazer comparações entre os números.
A atividade do Caderno de Apoio contextualiza a utilização dos números mostrando
aos alunos em quais situações são utilizados os números dessa ordem. Além disso,
trabalha a comparação desses números, solicitando que o aluno explique o caminho
percorrido para chegar às suas respostas.
159
Figura 9 - Folha de Atividades: Bairros e populações
Fonte: Cadernos de Apoio e Aprendizagem, 2010.
Segundo a estagiária, “os alunos respondem à atividade com tranquilidade,
mas encontram dificuldade quando é pedido para explicarem como chegaram às
respostas ( alternativa “c” da questão 1 e questão 3).”
E revela que na atividade seguinte a professora tem a mesma postura
quanto às suas explicações: “Nesta atividade a mesma coisa acontece, a professora
lê para a sala e pede para resolverem, dessa vez relembra o significado dos
símbolos > e <.”
160
Figura 10 - Folha de Atividades: Comparando e ordenando
Fonte: Cadernos de Apoio e Aprendizagem, 2010.
Para “TARS”, segundo suas observações o desenvolvimento da atividade
pelos alunos mostra que aparentemente parecem gostar de trabalhar com a
Matemática e com esse material didático.
Por fim, destacamos a atividade registrada por “VANGRA” em seu portfólio,
que acompanhou a professora que atua no 3º ano, envolvendo sequência numérica.
161
Figura 11 - Folha de atividade: Eu começo, você termina.
Fonte: Portfólio da estagiária
Segundo a estagiária, antes de iniciar a atividade a professora segue sua
dinâmica de aulas, explicando e discutindo com os alunos o uso dos números no
cotidiano.
A professora começa discutindo o uso dos números em seu cotidiano, por
exemplo, os números da chamada, número do calçado, número da casa ,
sua idade, dia do calendário etc. Foi feita a sequência numérica nas
folhinhas leram os números e escreveram por extenso no caderno. As
crianças não tiveram dificuldades e efetuaram a atividade com bastante
rapidez. (“VANGRA”, 2012)
A estagiária percebe que a professora demonstra não aplicar a atividade
pela atividade, contextualizando e discutindo o tema e conteúdo matemático
inseridos na atividade para melhor compreensão e aprendizagem de seus alunos.
162
A professora “P-LISE” trabalhou o conteúdo de conjuntos com sua turma do
1º ano e desenvolveu uma atividade tratava especificamente deste conteúdo. Nela a
estagiária notou que as crianças mostraram muito interesse quando a professora
começou a explicar , pois haviam desenhos na atividade.
Figura 12 - Folha de atividades: Conjunto
Fonte: Portfólio da estagiária
“LISE” relata não ter observado nenhuma dificuldade nesta atividade,
citando inclusive que na disciplina de FME de Matemática foi explicada a
necessidade da utilização de símbolos para a representação numérica.
A estagiária não observou que esse tipo de abordagem é conflitante com as
orientações curriculares recentes, que focalizam o número com base na sua função
social e que não utiliza a nomenclatura ligada à Teoria de conjuntos exposta em
currículos da década de 70.
163
Já em outra atividade apresentada pela professora, coletada de materiais de
sua preferência, a estagiária observa a utilizção da Teoria dos Conjuntos.
Figura 13 - Folha de atividades: Sequência numérica e Conjuntos
Fonte: Portfólio da estagiária
Os relatos de “LISE” sugerem que a linguagem proposta na atividade 3
provocou dificuldades nas crianças.
A palavra conjunto e elemento criou o maior reboliço. Os alunos não sabiam
o significado. A professora explicou mas senti um ar de dúvida entre eles e
ela também sentiu. Para ajudá-los desenhou na lousa um exemplo e pediu
apenas para que eles mudassem os desenhos.(LISE).
E continua com comentários.
Como em toda turma sempre tem alunos que participam mais, respondem,
mesmo que seja errado. Mas algumas crianças não estavam colaborando.
A professora explica , espera eles fazerem e recolhe os cadernos. Senti
falta da correção com todos, porque novamente não houve a devolutiva.
Nem a estagiária nem a professora “P-LISE”, percebem a mistura de
concepções de ensino no que se refere aos números e sequências numéricas. A
164
professora usa, ao mesmo tempo, as atividades do Caderno de Apoio, construídas
com base em pesquisas recentes sobre a função social dos números (Delia Lerner,
Michael Fayol e outros) e os procedimentos de contagem (Tall, Curi) com outras
retiradas de livros didáticos da década de 70/80, anteriores às Orientações Didáticas
veiculadas em documentos curriculares. A estagiária não faz nenhum comentário a
esse respeito.
O uso de numerais ao invés de números e de conjuntos, revela a época da
publicação desses livros. Nota-se tnos relatos de “LISE” que a própria professora
não havia percebido que aquela atividade continha noções matemáticas que ela não
havia trabalhado e que não tinha se preparado para desenvolvê-las.
Esse fato vem ao encontro do que os teóricos como Tardif (2002) apontam
sobre a influência do que aprendeu no que vai ensinar, pois provavelmente em seu
tempo de estudante a professora trabalhou com noções de conjunto, elementos,
pertinência e inclusão e não se deu conta que os materiais atuais não trabalham
com esses conteúdos matemáticos.
No que se refere ao trabalho com números por meio de ditado, valor
posicional e dezena e unidade, destacamos os relatos sobre atividades das
professoras “P-MAO” e “P-VANGRA" que atuam no 2º e 3º ano respectivamente.
A professora “P-MAO” apresenta uma atividade de ditado de números, para
colocá-los nas “casinhas” da dezena e da unidade.
165
Figura 14 - Folha de atividades: Ditado de números
Fonte: Portfólio da estagiária
“MAO” relata que percebeu que os alunos não tiveram muita dificuldade, até
porque eram números “baixos”, trabalhando apenas até a casa da dezena. Além
disso, a professora já havia desenvolvido algumas atividades com o mesmo tema, o
que facilitou seu desenvolvimento. A estagiária destaca, o que no seu entender são
os objetivos da atividade.
Esta atividade pode ter duas funções: uma é ajudar os alunos a entenderem
melhor e reforçar a aprendiagem, e outra função é avaliar o que eles já
sabem, para analisar se é preciso trabalhar mais neste conteúdo ou se os
alunos já compreenderam bem. (“MAO”)
O comentário de “MAO” demonstra que a mesma está refletindo sobre a
proposta da atividade e sobre os objetivos de aplicação da mesma, pensando no
ensino e na aprendizagem dos alunos. No entanto, a professora não explicita com
qual objetivo propõe a atividade.
Em outra aula a professora “P-MAO” realizou outro ditado de números,
porém como uma avaliação diagnóstica. A estagiária teve acesso a um certo número
de avaliações e relata que alguns alunos apresentaram dificuldades para
representar os números ditados. Ela comenta que com os números até cem os
alunos não tiveram problemas, porém com os números acima de cem eles já se
atrapalhavam. “MAO” declara que esta avaliação é importante, para analisar o
166
conhecimento das crianças sobre o conteúdo que está sendo trabalhado, assim
como verificar a continuidade deste trabalho ou a necessidade de modificação ou
amplicação do conteúdo.
O trabalho com números focando no valor posicional foi desenvolvido por
“P-VANGRA” em uma atividade desenvolvida destacando a dezena e unidade.
Figura 15 - Folha de atividade: Formando dezenas
Fonte: Portfólio da estagiária
A estagiária “VANGRA” comenta que a “aula foi participativa e prazerosa,
com uns alunos terminando mais rápido do que outros, pedindo inclusive que
tivessem mais atividades desse tipo”.
A estagiária comenta ainda que a professora também ficou satisfeita, e que
ela “observou que a maioria dos alunos obteve sucesso na aplicação da atividade,
mas alguns deles tiveram dificuldade no valor posicional dos números, registrando a
inversão dos valores posicionais”.
No entanto, “VANGRA” apresenta sugestões para melhorar a aplicação da
atividade e aprendizagem dos alunos, em seu portfólio: “A participação e atuação
dos alunos foi bastante produtiva e como gostaram, proporia um gráfico feito por
eles com os aniversariantes da turma que seria uma atividade bastante semelhante”.
167
O comentário da estagiária não deixa claro para nossa análise, sobre a
dinâmica de construção deste gráfico e seus objetivos. Seriam registrados os
aniversariantes de cada mês? Neste caso o gráfico seria elaborado com uma coluna
para cada mês do ano e como resultado uma contagem dos aniversariantes de cada
mês. Se o gráfico devesse retratar os aniversariantes em gráfico de colunas, a
atividade em nada se assemelha ao objetivo daquela proposta pela professora.
A sugestão da estagiária mostra um certo desconhecimento nesta área, uma
vez que o registro dos aniversariantes pressupõe o trabalho com gráficos que não é
semelhante às colunas montadas para que as crianças possam trabalhar o valor
posicional dos números. A mesma não destaca sobre qual a semelhança encontrada
entre as duas atividades.
Para “VANGRA” as aulas de FME de Matemática não lhe prepararam para
trabalhar o conteúdo desta atividade.
Destacamos ainda uma atividade que envolve a composição de números da
ordem das centenas, aplicada pela professora P-VANGRA, com os alunos do 3º
ano.
168
Figura 16 - Folha de atividade: Composição
Fonte: Portfólio da estagiária
169
A estagiária relata que neste trabalho, por se tratar de composição, a
professora resgatou novamente os valores posicionais na realização das operações
de adição. Alguns alunos apresentaram novamente dificuldades no posicionamento
dos números, fazendo com que a professora fizesse a correção individual em sua
mesa, para orientá-los em suas dúvidas. Sua sugestão para a atividade seria
“trabalhar adição com dinheiro de papel”.
Ao que parece a estagiária não observou o objetivo da atividade que
trabalha a composição de um número e o valor posicional. Trabalhar com dinheiro
dificultaria o alcance do objetivo da atividade. No entanto, a estagiária somente
sugere, não explica o que gostaria de fazer.
“VANGRA” destaca que nas aulas de FME de Matemática não aprendeu
como intervir nas dificuldades dos alunos.
A segunda atividade era de decomposição e foi desenvolvida com uma
tabela com palitinhos representando quantidade de centenas, de dezenas e de
unidades.
Figura 17 - Folha de atividade: Decomposição
Fonte: Portfólio da estagiária
A estagiária relata que a maioria dos alunos conseguiu alcançar o objetivo,
determinando a quantidade de unidades, dezenas e centenas que formariam o
170
número. Na mesma atividade, após a primeira etapa a professora trabalhou a
contagem de 10 em 10, 20 em 20, 50 em 50.
Destaca novamente que as aulas na Universidade não lhe ensinaram de que
forma trabalhar este conteúdo com os alunos. “Nas aulas de FME de Matemática
não tive discussões sobre como abordar a matéria através do conhecimento prévio
da criança e como intervir após isso”
Seu comentário é pertinente pois no trabalho do professor que ensina
Matemática não pode ser esquecida a discussão sobre o que a criança já sabe,
quais conhecimentos já traz acumulados e a partir de onde o professor deve iniciar
ou dar continuidade ao ensino. Entretanto, nesta atividade não há registros de que a
professora tenha identificado antes os conhecimentos prévios de seus alunos para
depois iniciar a atividade, o que não nos permite estabelecer uma relação entre a
atividade e o comentário de “VANGRA”.
O último conteúdo envolvendo números naturais refere-se a agrupamentos e
trocas por unidade de ordem superior, desenvolvido pela professora “P-VANGRA”
com uma atividade com unidades e dezenas.
Figura 18 - Folha de atividade: Trabalhando com unidades e dezenas
Fonte: Portfólio da estagiária
171
Para a estagiária esta atividade “valorizou o cálculo mental, as crianças
apresentaram boa produtividade, foi trabalhado o entendimento de quantas dezenas
estão contidas em determinado número”.
“VANGRA” relata que após a atividade, como em todas as anteriores, a
professora explica e corrige, desta vez coletivamente e na lousa.
A sugestão da estagiária para modificar ou melhorar a atividade seria
trabalhar com reagrupamento e sequência numérica de 10 em 10.
Notamos que embora “VANGRA” se preocupe para, conforme solicitado,
sugerir o que faria diferente em cada atividade, é preciso que se leve em conta os
objetivos propostos na aplicação das atividades, pois o professor pode ao trabalhar
diferentes temas ao mesmo tempo, confundir e dificultar a aprendizagem do aluno.
4.3.1.2.2 Operações
Os registros dos estagiários contêm 31 atividades com operações
desenvolvidas pelas professoras que os receberam do 1º ao 5º ano do Ensino
Fundamental. Estas atividades se dividiram em operações relacionadas ao campo
aditivo e ao campo multiplicativo21, com grande predominância do campo aditivo.
No que se refere à subtração, “MAO” detecta as dificuldades apresentadas
pelos alunos do 2º ano, na resolução de operações propostas em uma atividade,
com alguns deles resolvendo os mesmos como se fossem de adição. Comenta que
outros ainda não sabiam “armar” as contas para resolvê-las. Além disso relata que
vários alunos foram até a professora para tirar dúvidas, porque não conseguiam
resolver as contas e a professora tentou explicar até que resolvessem, porém não
descreve se compreenderam a operação.
Em seus registros “MAO” ressalta os conteúdos e a maneira como a
atividade foi apresentada pela professora, sugerindo uma forma diferente de
trabalhar com os alunos.
21
Entendemos por Campo multiplicativo um conjunto de situações que para sua resolução
necessitam de uma multiplicação, uma divisão ou a combinação de ambas.
172
Esta atividade estava com dois temas muito diversos, acredito que se
reformulada, seria melhor desenvolvida pelos alunos, deveria ser abordado
um único tema e focar nele. Se fosse escolhido o tema das contas de
subtração, deveriam ser escolhidos números menores e sem dividir os
números na casa das dezenas, porque isso confundiu muito as crianças.
(“MAO”)
A atividade relatada pela estagiária continha na primeira parte uma
abordagem de formas geométricas e na segunda parte as operações de subtração.
Em sua opinião, baseada na observação da postura dos alunos na resolução da
atividade, a mesma deveria ser reformulada, pois seria melhor desenvolvida por
eles, se os temas fossem separados em folhas distintas: Geometria e Subtração.
Chamou nossa atenção a postura de “LISE”, no que se refere a duas
atividades envolvendo subtração, aplicadas pela professora aos alunos do 1º ano.
No início de seu relato, diz ter sentido falta da operação de subtração. As duas
atividades a seguir trabalham com as noções de subtração, porém a estagiária não
faz menção a este fato, nem registra como foi o desenvolvimento da atividade pelas
crianças.
Figura 19 - Folha de atividade: A fruteira da casa de Lívia
Fonte: Caderno de Apoio e Aprendizagem, 2010.
173
Figura 20 - Folha de atividade: Na barraca de frutas
Fonte: Caderno de Apoio e Aprendizagem, 2010.
Destacamos também a atividade proposta pela professora P-TARS, com os
alunos do 5º ano, sobre cálculos de adição.
A atividade, retirada do Caderno de Apoio e Aprendizagem, propunha aos
alunos formas diferentes de calcular, a partir da decomposição de números.
174
Figura 21 - Folha de atividade: Outros cálculos de Daniel
Fonte: Caderno de Apoio e Aprendizagem, 2010.
Embora preferisse que os alunos pudessem discutir entre si sobre a
resolução das questões, a opinião de “TARS” sobre a atividade e seu
desenvolvimento é favorável.
A atividade foi ótima em minha opinião. Segundo aprendi nas aulas de FME
de Matemática, esse tipo de atividade de decompor e compor desenvolve o
raciocínio do aluno de como se resolve e o que se está fazendo, tirando o
aluno do “automático” arme e efetue. A devolutiva é feita com correção na
lousa. A professora explica várias vezes e tira dúvidas. Aprovei também
essa devolutiva, eu faria da mesma forma. (“TARS”).
A estagiária “VANGRA” relata sobre uma atividade que apresenta
problemas do campo aditivo. Os dois primeiros problemas envolviam adição e o
terceiro tratava da subtração.
175
Figura 22 - Folha de atividades: Problemas
Fonte: Portfólio da estagiária
Para “VANGRA” foi difícil o entendimento e vários alunos apresentaram
dificuldades.
A professora apresentou as atividades de resolução de problemas na lousa
e explicou aos alunos uma das operações. Pela observação os alunos
compreenderam a ideia do problema mas alguns não conseguiram acertar a
operação; outros não compreenderam a ideia mas acertaram a operação e
outros ainda não compreenderam a ideia e também não acertaram a
operação. (“VANGRA”)
Conforme podemos observar na atividade e levando-se em conta o
comentário da estagiária, as crianças muitas vezes confundem a operação de
adição com a de subtração e ambas as operações juntas podem dificultar a
resolução. Não há nos relatos da estagiária a informação de trabalho anterior da
professora com estas operações. Como os alunos estão no 3º ano, podemos inferir
que os problemas do campo aditivo estão sendo trabalhados, o que não exclue a
falta de entendimento e aprendizagem.
176
O estagiário “EAM” relata várias atividades envolvendo problemas do
campo aditivo. Em uma delas a professora forneceu aos alunos algumas “contas
montadas”, pedindo que desenvolvessem um problema que pudesse ser resolvido
com cada uma dessas operações. A ideia era que criassem cada qual do seu jeito e
entendimento o enunciado do problema. A atividade foi desenvolvida novamente em
grupos.
Escreva numa folha de papel um problema que se
resolva com o cálculo abaixo. Depois a troque com a
de outro grupo.
1) 1.345
+ 222
2) 146
- 54
3) 234
+ 212
Figura 23 - Folha de atividade: Problemas do campo aditivo
Fonte: Portfólio do estagiário
Cabe destacar que o enunciado da tarefa está mal formulado, pois para
cada cálculo deviam compor um enunciado de problema e a comanda diz para
escrever “um problema”.
Durante a realização da atividade, o estagiário comenta que percorreu os
grupos para verificar a forma como trabalhavam e faz a seguinte observação.
Observei atentamente circulando entre os grupos de alunos, pois achei
muito interessante a forma com que eles se respeitavam e davam as ideias
para criarem os problemas. Após elaborarem os problemas, chegavam a
votar entre si para decidir qual problema seria colocado na folha a ser
entregue para a professora. (“EAM”).
Ao término da atividade, o estagiário relata que a professora recolheu as
atividades e leu para a classe o que produziram e “todos adoraram a atividade e
principalmente esta leitura da professora, já que eles criaram e puderam colocar eles
ou nós professores na contextualização das situações criadas”.
Esta
forma
de
trabalho,
segundo
“EAM”,
permite
a
criação
e
desenvolvimento da autonomia, pois a professora relata que alguns alunos que eram
177
mais inibidos, haviam mudado muito com esta forma de trabalho e tinham se
desenvolvido acima de suas expectativas.
Após a atividade, o estagiário pode conversar com a professora e teve
acesso a várias produções, dentre as quais destacamos algumas para ilustrar os
comentários.
Resoluções
Grupo A
1) Na doceria existem 1.345 balas. E Seu José comprou mais 222 balas.
Quantas balas tem na doceria?
1.345
+ 222
1.567
R: Tem 1.567 balas na doceria
2) No parquinho existem 146 gangoras o prefeito tirou 54 gangorras.
Quantas gangorras tem o parquinho?
146
- 54
092
R: No parquinho a 92 gangorra.
3) Leonardo foi a feira e comprou 234 bananas. No caminho encontrou
o Diogo que comprou 212 abacaxis. Quantas frutas são juntando as frutas do
Leonardo com as do Diogo?
234
+ 212
446
R: São 446 frutas no total.
Figura 24 - Folha de atividade: Resolução Grupo A
Fonte: Portfólio do estagiário
Os alunos este grupo, embora tentem utilizar situações de seu cotidiano,
elaboram um enunciado distante do mundo real, pois normalmente ninguém vai a
uma feira e compra 212 abacaxis ou 244 bananas; assim como não encontramos
em um parquinho da cidade 146 gangorras.
178
No entanto, o estagiário não faz nenhum comentário sobre o assunto e pela
descrição da aula assistida parece que a professora apenas fez a leitura dos
enunciados sem nenhuma discussão de sua pertinência ou não.
Grupo B:
1) Ana ganhou uma bicicleta nova do tio que custa R$ 1.345 e ela ganhou
outra da mãe que no valor 222,00. Qual foi o total do valor da bicicleta?
1.345
+ 222
1.567
R: O total da bibicleta deu 1.567
2) Patricia foi ao mercado comprou 5 k de arroz que custava 146,00 R$. Ana
comprou 10 k de feijão que custava 54,00 R$. Quanto deu o total?
146
- 54
092
R: As duas juntas deu 92,00.
3) Juan foi para natação no sábado ele nadou 234 quilometros e no
domingo ele nadou 212 quilometros. Quantos quilometros ele nadou?
234
+ 212
446
R: Ele nadou 446 quilometros
Figura 25 - Folha de atividade: Resolução Grupo B
Fonte: Portfólio do estagiário
Os enunciados elaborados por este grupo chamam a atenção pelo fato de
utilizarem unidades de medida nos três problemas. Mas demonstram falta de
conhecimento no que se refere ao contexto nos números e valores utilizados.
Ressaltamos o problema 3, em que Juan nada 234 quilometros no sábado e mais
121 no domingo. Este enunciado sugere desconhecimento da medida de um
quilometro.
Podemos perceber também que a questão do primeiro enunciado não está
de acordo com o texto do problema, pois o algoritmo apresentado não se referia ao
sistema monetário.
179
Também com relação aos enunciados desse grupo, o estagiário não faz
nenhuma análise.
Grupo C:
1) Paulo tem 1.345 cards e Susana tem 222 juntando tudo. Quantas dá ao
total?
1.345
+ 222
1.567
R: Ao total os dois juntos têm 1.567 cards.
2) Bruna tem 146 balas e Lidiane tem 92. Quantas balas faltam para
Lidiane chegar até a mesma quantia de Bruna?
146
- 54
092
R: Elas teve que tirar 92 balas.
2) Vitória tem 234 bombons e Alessandra tem 212. Quantos tem juntando
tudo ao total?
234
+ 212
446
R: Deram ao total 446 bombons.
Figura 26 - Folha de Atividade: Resolução Grupo C
Fonte: Portfólio do estagiário
Este grupo utilizou como contexto para elaboração dos enunciados coisas
de seu dia a dia, brincadeiras, balas e bombons. Mas novamente o contexto é ruim,
na questão dos bombons por exemplo, uma vez que dificilmente alguém tem
consigo 234 ou 212 bombons.
Também nesse grupo de problemas não houve comentários do estagiário.
“EAM” relata que ao analisar esta aula percebeu algo muito interessante, o
fato de que todos os alunos têm o hábito de contextualizar a resposta do problema,
não colocando apenas números para responder. Comentou esse fato com a
professora e relatou o que ela disse sobre isso:
É muito raro ter que pedir a resposta, é um hábito que eles adquiriram,
porque desta maneira eles compreendem melhor. Quando elaboram a
resposta o problema faz mais sentido e trabalho não só a Matemática, mas
melhora também a escrita em todas as matérias.
Além dos pontos já citados por nós em relação à elaboração dos enunciados
dos problemas, as produções dos alunos nos mostram outros pontos que poderiam
180
ter sido discutidos, mas que o estagiário não comenta, voltando sua atenção
somente para o trabalho em grupo e a autonomia dos alunos.
O Grupo B, por exemplo, contextualiza as operações criando problemas que
envolvem o sistema monetário e não quantidade, embora o algoritmo fornecido não
se relacione com valor monetário. Como não observou este ponto, também não há
comentários do estagiário sobre a postura da professora, se comentou este fato, se
corrigiu ou se considerou correta esta abordagem por parte das crianças.
O Grupo C elabora o enunciado do problema 2 invertendo a informação, e já
fornecendo o resultado: “Lidiane tem 92 balas”.
Não há comentários de “EAM” sobre a produção dos alunos, quando
poderia inclusive sugerir outros enunciados utilizando contextos mais adequados.
A falta de envolvimento com o conteúdo e com o ensino de Matemática
propriamente dito por parte de “EAM”, limitando-se a comentar e descrever o
desenvolvimento da aula, sem se ater ao conteúdo ou estabelecendo novas formas
de trabalhar, nos mostra pouco conhecimento, reflexão e criatividade em sua
aprendizagem.
Com relação às operações envolvendo o campo multiplicativo foram
observadas somente pelos estagiários que acompanharam as professoras “PTARS” e “P-EAM”, ambas atuando no 5º ano.
No 5º ano, dentre as quatro atividades em que a professora “P-TARS”
trabalhou a multiplicação, três delas foram de cálculo, cujas operações foram
passadas na lousa para que os alunos copiassem no caderno e as resolvessem.
No primeiro momento do trabalho com a multiplicação “TARS” observou
que a professora distribuiu aos alunos folhinhas com a tabuada do 1 ao 10. Segundo
a estagiária eles resolvem os cálculos sem dificuldade consultando a tabuada.
“TARS” relata que os alunos resolvem e não têm um retorno de seus acertos ou
erros, e faz alguns comentários.
181
Não há correção, nem devolutiva aos alunos. Acho necessária a devolutiva,
se eu fosse a professora mudaria isso, pois pelo que aprendi na disciplina
FME de Matemática e outras disciplinas no curso de Pedagogia, acredito
que nesse momento em que o professor corrige e devolve os trabalhos, os
alunos podem expor suas dúvidas e aprendem mais. (“TARS”).
Dentre as atividades envolvendo multiplicação, “TARS” nos traz vários
exemplos das operações trabalhadas pela professora.
1) 206 x 4 =
2) 186 x 3 =
3) 117 x 5 =
4) 141 x 24 =
5) 121 x 38 =
Figura 27 - Folha de atividade: Multiplicações
Fonte: Portfólio da estagiária
Podemos perceber que a professora trabalhou a multiplicação com
centenas, inicialmente por unidade e depois por dezena.
“TARS” comenta que nesta atividade a professora orientou que utilizassem
a folhinha distribuída anteriormente com as tabuadas.
Em seus relatos a estagiária observa que este tipo de exercício faz com que
os alunos fiquem dispersos, não se concentrem na resolução. Descreve que
enquanto os alunos resolviam as operações, a professora trabalhava com alguns
papéis em sua mesa, sem atender às dúvidas dos alunos, o que os tornou mais
dispersos ainda.
Comenta que alguns alunos estavam sem a folha de apoio da tabuada e se
sentiram perdidos na atividade. Para “TARS”, a postura nesta atividade deveria ser
diferente. Ela descreve:
Penso que não é bom para a aprendizagem essa dependência da tabuada.
Seria melhor se as atividades fossem mais voltadas para que os alunos se
apropriassem da multiplicação. Não decorando, mas aprendendo a calcular
e o significado, sabendo que 2x3 é o mesmo que 3+3, por exemplo. Acho
que a aula deveria estar sendo mais participativa. (“TARS”).
182
O comentário de “TARS” mostra que a mesma está se apropriando de
conteúdos e posturas discutidas nas aulas de FME de Matemática, em que se
ressalta a importância da aprendizagem e não da memorização.
A estagiária descreve que não houve devolutiva por parte da professora.
Para a estagiária este exercício pareceu-lhe mecânico, sem propiciar a utilização do
raciocínio, uma vez que copiavam o resultado na folha da tabuada.
Eu daria devolutiva e ao invés de somente passar as operações, elaboraria
um problema de multiplicação e sem a utilização da folha de apoio da
tabuada. Sei que é importante que o aluno raciocine para chegar ao
resultado. (“TARS”).
O comentário de “TARS” mostra reflexão, pois o relato da professora nas
considerações feitas no questionário ressalta a questão do raciocínio lógico, da
necessidade de desenvolvê-lo e suas dificuldades em trabalhar este conceito com
as crianças. Percebemos que a estagiária também sente falta do trabalho com o
raciocínio, porém nos dá uma alternativa de trabalho, se envolvendo com o processo
de aprendizagem dos alunos com sugestões sobre o ensino de Matemática.
Esta estagiária parece participar mais diretamente do processo durante a
realização do estágio, destacando inclusive uma atividade com multiplicação que
mais chamou sua atenção.
183
Figura 28 - Folha de atividade: Formando palavras com resolução de
operações
Fonte: Portfólio da estagiária
Segundo “TARS” a atividade envolve multiplicação e escrita. A professora
inicia resolvendo a primeira multiplicação como exemplo. Logo após forma duplas
para que os alunos trabalhem juntos na atividade.
A estagiária comentou sobre o interesse dos alunos:
Os alunos se interessaram pela atividade, discutiram os resultados e
encontraram as palavras através da multiplicação. Para mim a atividade foi
bem interessante, pois os alunos achavam divertido, fizeram as
multiplicações com empolgação para alcançar o objetivo de formar as
palavras. Usaram formas diferentes de resolução, tabuada decorada,
cálculo mental, adição e como estavam em duplas podiam trocar idéias.
(“TARS”).
Nas aulas assistidas não há comentários da estagiária sobre a resolução de
problemas do campo multiplicativo e sobre estratégias de cálculos.
Na atividade relatada por “EAM” relativa ao campo multiplicativo foi
entregue em uma folha avulsa aos alunos contendo cinco questões de divisão, que
embora relatada, infelizmente não foi inserida no portfólio pelo estagiário.
184
Os relatos de “EAM” mostram que a professora deixa os alunos resolverem
por si as operações, numa dinâmica que para ele foi novidade:
Observei algo totalmente diferente do que já presenciei em sala de aula os
alunos sentam-se em grupos de quatro ficando todos de lado para a frente.
Soube depois que foram divididos pela professora para que possam ajudar
uns aos outros e vencer os obstáculos, suprindo as lacunas e dúvidas que
surgem em todas atividades. Durante a atividade percebi que nenhum aluno
ia até a mesa da professora e eles tiravam as dúvidas em relação as
atividades entre si, existindo uma democracia rara: um perguntava ao outro
se queria acrescentar algo e se estavam todos de acordo. (“EAM”).
O trabalho em grupos é defendido por muitos autores que entendem que o
mesmo propicia o que denominam de aprendizagem colaborativa, fazendo com que
as discussões que se estabelecem sejam caminhos de reflexão e de novas
construções de conhecimento. Entendemos que, embora “EAM” desconhecesse a
realização de trabalho em grupos na sala de aula do Ensino Fundamental, este se
constitui em momento de troca de experiências e conhecimentos, possibilitando não
a transmissão do conhecimento, mas a construção do mesmo. Talvez por sua
pequena vivência no Ensino Fundamental, o estagiário se surpreendeu com o
trabalho em grupo, embora no curso de Pedagogia esta estratégia fosse
constantemente utilizada, ressaltando-se sua importância na construção de saberes.
“EAM” relata uma atividade onde os alunos deviam resolver uma operação
de multiplicação: 4 x 4 = ?. A maioria deles apresentou a resposta correta efetuando
a multiplicação e resultando em 16. Porém ao efetuar a correção da atividade, o
estagiário relata que a professora convida os alunos a irem a lousa para
apresentarem a resolução e contarem para a turma se alguém tinha resolvido de
forma diferente daquela.
Na quinta questão uma aluna se apresentou e explicou que ela não havia
utilizado a multiplicação como todos: 4X4 =16. Para ela foi mais fácil somar
4+4+4+4 =16 , chegando à resposta do problema proposto, onde para que
cada personagem ficasse com 4 sorvetes precisaria de 16 sorvetes no total.
(“EAM”).
Embora destaque que a aluna resolve a multiplicação aditivamente, o
estagiário não faz reflexões sobre esse fato.
185
4.3.1.2.3 Espaço e Forma
O conteúdo Espaço e Forma apresenta seis atividades, envolvendo Formas
Geométricas e Relações Espaciais.
Somente as professoras “P-LISE”, do 1º ano, “P-MAO”, do 2º ano e “PTARS”, do 5º ano, desenvolveram algum tipo de atividade envolvendo formas
geométricas.
No 1º ano a professora “P-LISE” apresentou duas atividades às crianças
envolvendo o conteúdo em questão.
A primeira delas pedia que as crianças classificassem as formas
geométricas.
Figura 29 - Folha de atividade: Classificação de formas geométricas
Fonte: Portfólio da estagiária
Ao descrever a postura da professora antes, durante e depois da atividade,
“LISE” assim relata:
186
Primeiro a professora foi escolhendo algumas crianças para falarem o nome
da figura geométrica . Depois pediu para que pensassem em algo que
tinham visto em casa , na escola ou na rua que parecesse com aquela
figura. As que tiveram menor dificuldade foram o círculo , triângulo e
quadrado . A professora escreveu o nome na lousa e elas copiaram.
(“LISE”).
O comentário de “LISE” mostra que a professora nomeou as figuras,
escrevendo seus nomes na lousa para que as crianças copiassem. Ao que parece
as crianças tiveram facilidade em encontrar objetos de seu cotidiano cujas formas se
assemelhassem às figuras da atividade.
O relato da estagiária mostra uma conduta interessante da professora e
sugere que a mesma trabalha as formas tridimensionais, no que diz respeito à
aparência de cada uma, relacionando-as com objetos do cotidiano dos alunos e com
suas experiências para que fixem cada uma das formas. Não ficou claro se ao pedir
que as crianças nomeassem as formas geométricas, a professora já havia
trabalhado este tema e, portanto esperava que os alunos pudessem nomeá-las.
Na segunda atividade desenvolvida pela professora “P-LISE”, a estagiária
relata que a professora além de perguntar às crianças quais frutas tinham o mesmo
formato da melancia, perguntou também se havia algo na sala, nas ruas, ou em
casa com a mesma forma. Houve grande participação das crianças.
Figura 30 - Folha de atividade: A forma da melancia
Fonte: Caderno de Apoio e Aprendizagem, 2010.
187
Esta participação reforça a importância da contextualização no ensino de
Matemática, cujo recurso traz mais significado à aprendizagem.
Porém a estagiária não comenta a resposta da criança para a segunda
questão da atividade, atribuída como certa pela professora. Ao ser questionada
sobre o que há de parecido entre a melancia e as frutas desenhadas na questão 1, a
criança responde: “Ela usou balança, xícara e o copo”.
Em virtude de na sequência, o material usado pela professora apresentar
uma atividade com receita de bolo com unidades de medida e algumas questões
para que o aluno respondesse, nos faz pensar que talvez a resposta tenha sido
dada pela professora e o aluno copiou na página errada e colocou como correto.
O trabalho com formas geométricas desenvolvido pela professora “P-MAO”
com as crianças do 2º ano, foi destacado pela estagiária, com comentários pela
atividade apresentar três partes, sendo duas de Geometria e uma de Subtração.
Figura 31 - Folha de atividade: Geometria e Subtração
Fonte: Portfólio da estagiária
Percebemos que não há um título na atividade, que possa confirmar que nas
duas primeiras atividades a professora trabalharia realmente Geometria. Estamos
188
nos baseando no relato da estagiária sobre a realização da atividade, e não há em
seus registros, relatos sobre as explicações dadas pela professora antes da
realização e durante seu desenvolvimento.
“MAO” observou que nos dois primeiros itens da atividade, que segundo ela
se referiam a Geometria, os alunos não tiveram problemas para resolver. Embora
ela não comente, podemos perceber que nesta parte da atividade não há alusão aos
conceitos ou propriedades das figuras, com a atividade limitando-se ao
reconhecimento das formas, com tracejamento e pintura das mesmas. Como a
estagiária não descreveu o que a professora fez antes e depois da atividade, ficanos o entendimento de que não houve efetivamente o trabalho com Geometria.
Inferimos que os poucos comentários da estagiária podem ser atribuídos aos
seus conhecimentos geométricos precários destacados por ela nos instrumentos de
pesquisa.
A análise realizada pela estagiária a respeito da atividade que a professora
desenvolveu com os alunos, destaca que houve a abordagem de diferentes
conteúdos na mesma sequência de atividades, o que segundo ela pode ter se
constituido em um problema para as crianças.
A estagiária “TARS”, ao acompanhar a sala de 5º ano, relata o
desenvolvimento de uma atividade de Geometria.
189
Figura 32 - Folha de atividade: As caixas de presente de Patrícia
Fonte: Caderno de Apoio e Aprendizagem, 2010.
“TARS” registra apenas que “A professora explicou cada forma e fez a
atividade junto com os alunos, explicando como fazer.”
Não temos como saber como a professora explicou estas formas, se
nomeou, discutiu sobre suas propriedades ou se simplesmente se ateve ao que a
atividade mostra e solicita. Por outro lado, a estagiária declara não ter aprendido ou
visto algo sobre Geometria em suas aulas de FME de Matemática no curso de
Pedagogia, o que nos leva a entender que talvez sua falta de comentários sobre a
atividade seja devido à falta de conhecimento desse conteúdo matemático.
Com relação ao trabalho com Relações Espaciais, somente as estagiárias
“LISE”, no 1º ano e “TARS” no 5º ano, acompanharam uma atividade com este
tema.
190
O relato de “LISE” mostra que ao trabalhar com relações espaciais, a
professora aplicou duas atividades do Caderno de Apoio e Aprendizagem de
Matemática. A mesma anunciou o que trabalhariam e indicou no caderno a atividade
a ser realizada. A estagiária relatou que “A professora leu o enunciado e cada
criança descreveu seu caminho, alguns sem sentido, outros na brincadeira,
perdendo totalmente o foco da atividade”.
Figura 33 - Folha de atividade: Hora de ir embora!
Fonte: Caderno de Apoio e Aprendizagem, 2010.
Em várias atividades “LISE” relata a falta de atenção e foco na atividade,
além de brincadeiras que considera que dificultam a aprendizagem, mas não faz
nenhuma reflexão sobre esse fato.
Já a estagiária “TARS” refere-se a este trabalho, relatando que a professora
orientou aos alunos que desenvolvessem duas atividades do Caderno de Apoio e
Aprendizagem.
191
Figura 34 - Folha de atividade: Explicando o caminho
Fonte: Caderno de Apoio e Aprendizagem, 2010.
Figura 35 - Folha de atividade: O quarteirão da escola
Fonte: Caderno de Apoio e Aprendizagem, 2010.
192
A estagiária relatou que a forma como a professora iniciou a atividade
proporcionou muita animação entre os alunos: “A professora explica e a sala fica
animada com a atividade diferente.” Ela observou também que “Os alunos
conversavam e trocavam informações para desenhar e explicar o caminho da escola
e da padaria.”
Embora o início da atividade tenha sido explicado e comentado, “TARS”
relatou que sentiu falta de uma discussão posterior sobre as produções dos alunos,
especialmente para mostrar aos mesmos como os caminhos eram diferentes entre
si, embora partissem do mesmo ponto e levassem ao mesmo destino.
No entanto, a estagiária não identificou o objetivo da atividade nem sua
relaçao com a Matemática, mostrando desconhecer as orientações curriculares
recentes. Ela relata: “A atividade é interessante, mas achei que não tem nada a ver
com o que se estava trabalhando antes. Não vi no que essa atividade pode intervir
em Matemática”.
Percebemos ainda que em seus comentários sobre estas atividades, a
estagiária não nomeia os conteúdos trabalhados pela professora.
Embora no plano de ensino da disciplina FME de Matemática II haja
conteúdos relativos à Geometria e seu ensino e, portanto ligados às relações
espaciais, a estagiária mostra poucos conhecimentos sobre esse tema.
4.3.1.2.4 Grandezas e Medidas
No trabalho com conteúdo Grandezas e Medidas, dividimos as atividades
aplicadas com os temas Calendário e Medidas de Tempo; e Medidas de capacidade,
dúzias e Sistema Monetário.
“LISE” relata o trabalho da professora no 1º ano com o calendário.
193
Figura 36 - Folha de atividade: Calendário
Fonte: Portfólio da estagiária
A estagiária assim relatou suas impressões a respeito da atividade.
A professora entregou um calendário para cada criança colar em seu
caderno. Primeiro ela explicou a diferença entre dia e semana. Explorou
totalmente o calendário contando os sábados, os domingos , o total de dias,
quando começava o mês , quando terminava o mês , os dias das semana. A
cada dia do mês ela voltava no calendário e as crianças localizavam o dia ,
e desenhavam conforme o tempo, frio, chuva ou sol. (“LISE”).
Os relatos de “LISE” sobre esta atividade sugerem que a professora não
aplicou simplesmente a atividade. Neste tema a mesma explica o porque do
calendário, mostra sua utilização e inicia uma discussão sobre as questões do
tempo.
A professora “P-VANGRA”, que atua no 3º ano, desenvolveu uma atividade
com calendário e um gráfico de barras. Antes de realizar a atividade, a estagiária
relata que a professora fez uma leitura sobre a origem do calendário, sua
importância, interpretação e compreensão.
“VANGRA” destaca ter sido bem interessante a preparação da professora
para desenvolver a atividade, tendo trabalhado algumas curiosidades e o contexto
diário dos alunos em relação ao calendário.
194
Mostrou a partir dos punhos e contagens dos meses do ano
correspondentes aos ossos que ligam os dedos como introdução do
calendário. Em seguida foram trabalhados os dias da semana com
questionamentos como : quais são os dias de aula; quais dias da semana
em que os alunos passeiam com seus pais; quantos dias da semana têm
aula de Matemática. Estes questionamentos levaram ao diálogo e
explicação de quais seriam os dias úteis e não. (“VANGRA”).
Somente após estas discussões e explicações “P-VANGRA” entrega a
atividade para os alunos.
Figura 37 - Folha de atividade: Dias da semana
Fonte: Portfólio da estagiária
Nos relatos da estagiária, ela destaca a interação promovida pela professora
e a participação das crianças e considera essa aula bastante produtiva. Comenta
que os alunos tiveram êxito na resolução da atividade, que consistia na leitura de um
gráfico de barras. Destaca que as dificuldades surgidas foram solucionadas quando
a professora fez a correção coletiva na lousa.
195
Ressaltamos que embora a atividade tratasse da leitura de um gráfico, a
criança escreve “esta tabela mostra...”, o que nos faz pensar na forma como a
atividade foi apresentada aos alunos: como gráfico ou como tabela? No entanto a
estagiária não faz reflexões mais elaboradas em seus comentários.
“VANGRA” comenta em seu relatório que as aulas de FME de Matemática
“não lhe deram base para que pudesse ter percepção do que estava ocorrendo na
sala de aula e como poderia intervir nas dificuldades dos alunos”. Ainda assim
sugere que nesta atividade acrescentaria “elaborações de resolução de problemas
com o tema calendário”.
Sua sugestão não veio acompanhada de uma explicação sobre a forma que
seria desenvolvida esta nova atividade.
A estagiária “TARS” relata o trabalho com medidas de tempo realizado com
o 5º ano, pela professora “P-TARS”, que foi iniciado com uma discussão proposta
na atividade inserida no Caderno de Apoio e Aprendizagem.
Figura 38- Folha de atividade: Unidade 2
Fonte: Caderno de Apoio e Aprendizagem, 2010.
196
A estagiária assim relata o início da discussão sobre medida de tempo:
Na atividade há duas perguntas que a professora responde junto com a
sala, fazendo uma espécie de roda de conversa. Vários alunos deram
opiniões, alguns já tinham ido a uma feira de artesanato e aos que nunca
foram foi explicado o que é e como funciona. Fizeram um cálculo de
quantos anos tem a feira de artesanato da Praça da República, chegando
ao resultado correto aprendendo que subtraindo 1956, ano do início da
feira, de 2012, ano em que estamos, obteriam o resultado. (“TARS”).
“TARS” considera o trabalho com medida de tempo foi importante para as
crianças, porque puderam se localizar no espaço e tempo, fazendo cálculos que
levaram a comparações em relação às próprias idades ou idades de seus pais e
avós, quando perceberam que a feira já funcionava há 56 anos.
Já a estagiária “LISE” descreve uma atividade de medidas de capacidade
desenvolvido pela professora “P-LISE” com os alunos do 1º ano. Segundo a
estagiária, “A professora explicou a necessidade de usarmos as medidas,
exemplificou cada uma delas, perguntou onde encontramos medidas e pediu para
cada criança trazer uma receita”.
Figura 39 - Folha de atividade: Uma receita muito fácil!
Fonte: Caderno de Apoio e Aprendizagem, 2010.
A estagiária não faz mais nenhum comentário sobre o desenvolvimento da
atividade. Não há também explicações da estagiária sobre o que será feito com a
receita que a professora pediu que as crianças trouxessem no início das explicações
197
sobre a atividade, nos deixando sem saber se a professora não anunciou o que seria
feito ou se a própria estagiária não se envolveu nesta questão.
“TARS” destaca ainda uma atividade realizada envolvendo resolução de
problemas com o conceito de dúzia.
Figura 40 - Folha de atividade: Dúzia
Fonte: Portfólio da estagiária
A estagiária relata que dessa vez a professora usa uma atividade em
folhinha avulsa. Ela comenta que a professora distribuiu as folhas com a atividade,
explicando como devia ser feita e revendo o conceito de dúzia. Comentou que
mesmo com a revisão, alguns alunos ainda tiveram dificuldade em encontrar o
resultado.
Nesta atividade a estagiária destaca que a postura da professora na
devolutiva da atividade foi diferente daquela normalmente apresentada..
A professora recolhe, corrige e entrega para colarem nos cadernos. Em
seguida faz a correção na lousa, explicando mais detalhadamente. Alguns
não tinham compreendido que uma dúzia é 12 e houve também alguns
erros na multiplicação. Mas a professora retomou as explicações. (“TARS”).
198
Embora relate não se lembrar de ter aprendido como trabalhar com o
conceito de dúzia com os alunos, em suas aulas de FME de Matemática na
graduação, “TARS” considera esta atividade produtiva para a aprendizagem dos
alunos, pois nas referidas aulas foi enfatizada a importância de trabalhar com
problemas para desenvolver o pensamento e o raciocínio.
A estagiária comentou em seus relatos que a professora utiliza sempre o
Caderno de Apoio e Aprendizagem para a realização das atividades. Ela percebeu
que em algumas delas não há uma discussão sobre o conteúdo que será trabalhado
ou uma explicação mais detalhada de como desenvolver as questões, mostrando
uma reflexão sobre suas observações.
Destacamos então o trabalho com Sistema Monetário. Os registros de
“VANGRA” trazem duas atividades envolvendo o sistema monetário.
A primeira atividade foi realizada com a utilização de cédulas brasileiras.
Figura 41 - Folha de atividade: É REAL!
Fonte: Portfólio da estagiária
Os relatos da estagiária destacam que a atividade foi muito interessante e
que as crianças se envolveram bastante, surgindo novas propostas de aplicação
deste conteúdo.
199
Foi apresentado o projeto mercadinho com panfletos trazidos pelos alunos.
Discutiram produtos de sua preferência que iriam comercializar no projeto. A
professora trouxe dinheiro de papel, trabalhando o concreto. Nessa
atividade surgiu a proposta de comparação, diferença e agrupamento das
notas de mesmo valor para fazer a contagem do dinheiro. Os alunos
apresentaram interesse na atividade e gostaram de poder participar com as
escolhas dos produtos e com o manuseio do dinheiro de papel. (“VANGRA”)
A sugestão de “VANGRA” para esta atividade seria “além da atividade de
compra e venda exploraria também a contagem de 2 em 2 , 5 em 5 , 10 em 10 etc.
dos valores”. Ressalta ainda que nas aulas da Universidade, nas disciplinas relativas
ao ensino de Matemática, não houve a abordagem deste tema, nem com exemplos
sobre as cédulas, nem com formas de trabalhá-lo. Consideramos muito interessante
a sugestão da estagiária sobre uma nova forma de desenvolver o trabalho com o
sistema monetário e com cédulas.
Na segunda atividade, a professora reforçou as operações com dinheiro,
desta vez contextualizando com uma visita ao circo.
Figura 42 - Folha de atividade: Calculando
Fonte: Portfólio da estagiária
200
“VANGRA” entende que a professora teve êxito na aplicação desta
atividade, atingindo seus objetivos no sentido de envolver as crianças com
problemas de seu cotidiano, como a utilização de dinheiro, cálculo, troco, etc.
A professora explorou com seus alunos a quantidade de dinheiro necessária
na compra de ingressos e produtos no circo, com a contagem de cédulas,
discriminação dos produtos, preço unitário e valor total. Após a atividade
anterior na aula do mercadinho, pude perceber que a maioria das crianças
teve sucesso na atividade algumas se utiliazaram das figuras contidas na
atividade para que ficasse mais fácil de concluir. (“VANGRA”).
A estagiária relata que ao término da atividade a professora fez a correção
na lousa , fornecendo outros exemplos para explicar e tirar dúvidas sobre o sistema
monetário.
4.3.1.2.5 Tratamento da Informação
O último bloco de conteúdos refere-se ao Tratamento da Informação, com
duas atividades com Gráficos, as quais foram desenvolvidas por “P-MAO”, no 2º
ano e por “P-VANGRA” no 3º ano, na atividade com dias da semana já comentada
por nós.
Destacamos os comentários de “MAO” para esta atividade com gráficos.
Figura 43 - Folha de atividade: Arraial Legal
Fonte: Portfólio da estagiária
201
A estagiária relata que a atividade foi bem elaborada, porque os alunos a
realizaram facilmente. Não há em seus comentários uma descrição sobre como a
professora trabalhou este conteúdo por meio desta atividade.
Cabe destacar que a estagiária não observou um erro dessa atividade, que
apresenta duas variáveis de natureza distina no mesmo eixo (sexo e tipos de
brincadeiras)
Nesta atividade “MAO” relata que pôde perceber que as crianças, embora
entendessem o conceito e a atividade a ser desenvolvida, se dispersavam na
realização, tendo que se concentrar para não errar. Pensando no contexto da sala,
ela sugere uma nova forma de trabalhar estas noções com a criança. “No caso desta
aula, eu acrescentaria uma atividade, fazendo com as crianças um gráfico de barras
tridimensional (com caixas de sapatos, por exemplo) para elas visualizarem melhor.”
Embora analise e dê sugestões de trabalho, a estagiária declara não
conhecer o conteúdo ou a forma de trabalhá-lo com as crianças, afirmando que “não
tenho base para desenvolver este conteúdo com os alunos, pois não tive este
conteúdo durante a disciplina e nem a metodologia.”
Podemos perceber que a estagiária demonstra estar envolvida com esta
atividade, refletindo sobre o trabalho realizado e além disso, procurando o
aperfeiçoamento da atividade. Propõe também a criação de um novo modelo para
explicar o conteúdo, procurando adaptar ao contexto e necessidades da sala.
4.3.1.2.6 Outras atividades desenvolvidas
Os estagiários “VANGRA” no 3º ano e “TARS” e “EAM” no 5º ano,
assistiram e relataram suas observações em outras aulas, em que acompanharam a
aplicação de avaliações de Matemática.
Todas as professoras aplicaram avaliações com base em conteúdos já
trabalhados. “EAM” acompanhou a aplicação da Prova da Cidade.
Os relatos dos estagiários mostram que as três professoras assumem
posturas diferentes no antes e no depois da aplicação das avaliações.
202
Segundo os relatos de “TARS”, durante a aplicação da avaliação, a
professora assume uma postura diferente em relaçõa às aulas. Ela comenta que “PTARS” não se envolve com o desenvolvimento da atividade e não tira dúvidas dos
alunos, justificando que por ser avaliação não pode ajudar. Além disso a estagiária
destaca que não há devolvutiva por parte da professora, não havendo correção ou
informação das notas, o que só ocorre no final do bimestre.
“EAM” relata em seus registros que a professora conversa com os alunos
que a procuram com dúvidas durante a prova, orientando e sugerindo que pensem e
reflitam sobre a resposta correta. Também ressalta que a professora “P-EAM”
corrige individualmente e depois coletivamente para tirar todas as dúvidas sobre os
conteúdos.
A estagiária “P-VANGRA” relata que a professora aplicou a avaliação com
conteúdos que já haviam sido propostos em aula. A professora corrigiu
coletivamente a prova em aula posterior, com os alunos acompanhando a correção
com suas provas em mãos, já corrigidas e devolvidas pela professora.
Entendemos que a avaliação é importante momento do processo de
aprendizagem. A revisão dos conteúdos que serão tratados na avaliação é
importante para que os alunos possam resolver as atividades propostas com mais
segurança e conhecimento.
A devolutiva das provas, com correção e acompanhamento permite não só o
reforço da aprendizagem do aluno mas também um novo direcionamento na prática
do professor, a partir das aprendizagens já desenvolvidas pelos alunos.
As análises e comentários dos estagiários registrados em seus portfólios,
durante toda a realização do estágio supervisionado e acompanhando as
professoras em suas atividades e práticas, nos permitem observar o grau de
envolvimento, conhecimento e reflexão sobre a própria formação, assim como as
aprendizagens manifestadas no desenvolvimento do estágio e da elaboração dos
portfólios.
203
4.3.1.3
Algumas observações dos estagiários com relação às experiências
vivenciadas nos estágios
Os registros dos estagiários em seus portfólios sobre a postura das
professoras que acompanharam seus estágios, mostram alguns pontos importantes
para análise.
Quatro estagiários abordam a postura das professoras. No entanto, “EAM”
foca mais a participação dos alunos e as expectativas dos mesmos com relação ao
desenvolvimento das aulas e menos na postura da professora, não nos mostrando
especificamente como a professora se posiciona nos diferentes momentos da aula.
Embora cada professora tenha uma forma própria de desenvolver seu
trabalho, percebemos nos relatos dos estagiários, nos que se refere à postura antes
da atividade, que todas seguem uma dinâmica parecida em suas aulas: é feita a
correção de alguma atividade que foi passada para os alunos realizarem em casa,
individualmente por meio de visto nos cadernos ou coletivamente na lousa, tirando
as eventuais dúvidas.
Logo após as professoras iniciam as atividades propostas para o dia, sem
nenhum diálogo com os alunos, distribuindo a atividade em folha avulsa ou
reproduzindo a atividade na lousa para que os alunos copiem em seus cadernos. A
maioria das professoras exemplifica o que está sendo solicitado resolvendo a
primeira parte de cada questão proposta para que depois os alunos deêm
continuidade.
Não há nos registros analisados alusão ao que já tinha sido trabalhado com
os alunos em relação aos conteúdos ou às atividades apresentadas, nem sobre o
planejamento da professora e o uso que a mesma faz desse planejamento.
Porém “TARS” destaca que a professora em muitos momentos preocupa-se
com o conteúdo desenvolvido nas atividades, explicando, relembrando os conceitos
e propondo a resolução pelos próprios alunos. Podemos confirmar esta situação em
dois relatos de seus registros.
204
A professora distribui as folhinhas com a atividade que tem como objetivo
trabalhar dúzias. Ela explica a atividade revendo o que é dúzia e explicando
como fazer as atividades da folhinha.
[...]
Lê para a sala e pede para resolverem, lembrando a todos o significado dos
símbolos > e <. (“P-TARS”).
Não há destaque nos relatos dos estagiários para a existência de diálogo da
professora com a classe procurando contextualizar o assunto ou fazer uma
sondagem dos conhecimentos de seus alunos sobre o tema a ser trabalhado, exceto
nos relatos de “VANGRA”, que destaca a preocupação da professora nesta
contextualização. Antes de iniciar a atividade a professora em alguns momentos lê a
atividade para explicar o que será trabalhado; em outras ocasiões traz o conceito
matemático que pretende trabalhar antes de oferecer a atividade para os alunos; em
outros ainda resgata um tema já trabalhado para só depois distribuir as atividades ou
indicar o Caderno de Apoio. Esta postura não foi relatada pelos demais estagiários.
Entendemos que a professora “P-VANGRA” incorporou em sua prática
questões sobre o papel do professor que ensina Matemática, preocupando-se com a
aprendizagem de seus alunos, com seus conhecimentos prévios e com a
importância da contextualização no ensino e aprendizagem da Matemática. Além
disso resgata em suas aulas a importância dos materiais de apoio para o ensino de
Matemática.
Também a estagiária “LISE” destaca na descrição das atividades que a
professora faz com as crianças, a preocupação da mesma com a sondagem,
quando faz ditado de números e a ampliação dos conhecimentos numéricos das
crianças com jogo de bingo, cartelas sobrepostas e quadros numéricos. Todas
essas atividades foram destacadas no grupo de pesquisa e vem sendo discutidas a
partir de pesquisas recentes sobre o ensino de números.
Sobre a postura das professoras durante as atividades, os estagiários
relatam que as mesmas observavam a resolução e atendiam às dúvidas dos alunos
que apresentavam dificuldades.
“MAO” destaca que a professora passava de carteira em carteira para
observar como estavam desenvolvendo a atividade e tirando as dúvidas dos alunos
205
que apresentavam dificuldades. Em algumas atividades, se mesmo com sua
explicação os alunos ainda apresentavam dúvidas, a professora retomava as
orientações para que eles continuassem na resolução.
Tanto “MAO” quanto “LISE” fazem comentários que sugerem que as
professoras demonstram atenção aos alunos, preocupando-se em retomar a
explicação para que continuem a resolução do problema ou atividade. Porém a
forma como desenvolvem as aulas, nos leva a analisar o trabalho de ambas as
professoras pautado em uma abordagem tradicional de ensino, que segundo
Mizukami (1987) se traduz em “dar lição e tomar lição”, entendendo que a
aprendizagem ocorre quando o aluno reproduz de forma correta os conteúdos e
conhecimentos transmitidos pelo professor.
Não há destaque nos relatos para a explicação de um novo conteúdo, o que
parece sugerir que o conteúdo é desenvolvido por meio de atividades que os alunos
desenvolvem a partir das explicações e correções das professoras. Os registros de
“MAO” e “LISE” sugerem que o foco maior é a realização da atividade em si e não
o conteúdo a ser trabalhado na mesma.
Os relatos de “VANGRA” sobre a postura da professora, entretanto, mostra
que a mesma não centra a atenção somente na resolução da atividade e sim nos
conceitos contidos na mesma e nas discussões propiciadas a cada atividade. Ao
que parece a professora não apresenta respostas prontas aos alunos, permitindo
que os mesmos reflitam e raciocinem na resolução dos problemas e atividades
propostas.
“TARS” e “EAM” ressaltam em seus relatos a questão dos trabalhos em
grupos durante a realização das atividades.
Segundo “TARS”, em várias atividades a professora agrupa os alunos em
duplas ou trios, para que possam discutir e resolver as questões propostas. Este
recurso pedagógico é interessante por permitir trocas, discussões e construção
colaborativa de novos conhecimentos.
“EAM” também relata que a professora deixa os alunos resolverem por si as
operações, numa dinâmica que para ele foi novidade.
206
O trabalho em grupos é defendido por muitos autores que entendem que o
mesmo propicia o que denominam de aprendizagem colaborativa, fazendo com que
as discussões que se estabelecem sejam caminhos de reflexão e de novas
construções de conhecimento. Entendemos que, embora “EAM” desconheça o
trabalho em grupos na sala de aula do Ensino Fundamental, este se constitui em
momento de troca de experiências e conhecimentos, possibilitando não a
transmissão do conhecimento, mas a construção do mesmo. Talvez por sua
pequena vivência no Ensino Fundamental, o estagiário se surpreendeu com o
trabalho em grupo, embora no curso de Pedagogia esta estratégia fosse
constantemente utilizada, ressaltando-se sua importância na construção de saberes.
Também após a aplicação das atividades as professoras mantém uma
postura semelhante. Na maioria das vezes os alunos corrigem suas próprias
atividades a partir da correção feita na lousa pela professora.
“TARS” resume a postura da professora após a aplicação da atividade, que
se repete nas observações dos demais estagiários:
A professora recolhe a atividade, corrige e entrega aos alunos para colarem
nos cadernos. Em seguida faz a correção na lousa, explicando mais
detalhadamente. Em várias atividades não há correção, nem devolutiva. (“PTARS”).
A falta de devolutiva por parte da professora também é reforçada por
“LISE”, ao analisar que a prática da professora acompanhada propiciava a
participação e aprendizagem dos alunos, mas podia ser mais bem direcionada.
Nas aulas de Matemática a professora deixa as crianças bem a vontade,
atende as dúvidas, explica uma, duas vezes, ou sempre que necessário.
Porém não tem o hábito de corrigir as atividades junto com os alunos. As
próprias crianças se perguntavam “Será que eu acertei?” “Quantas eu
errei?”
Então acho necessário a correção para uma devolutiva, a criança deve
saber se errou, porque errou. Seria interessante a própria criança também
explicar como chegou a tal resultado, aprendendo assim diferentes
processos de raciocínio e resolução. (“LISE”).
Apenas “VANGRA” nos mostra que a professora acompanhada não
deixava os alunos sem uma correção ou devolutiva da atividade. Relata que após a
atividade, as correções eram desenvolvidas conforme o momento: a professora
corrigia individualmente em sua mesa, coletivamente na lousa, levava para corrigir
207
fora da aula e devolvia posteriormente. Mas na maioria das atividades a correção
era feita na lousa, com explicações e outros exemplos diferentes do exercício
aplicado.
Entendemos que a devolutiva das atividades, seja qual for a forma utilizada
pela professora para a correção, é muito importante para os alunos, no que diz
respeito a situarem-se no processo de aprendizagem, podendo tirar dúvidas e
avançarem neste processo. Por outro lado, a avaliação feita a cada atividade serve
de retorno para o professor verificar se os objetivos propostos em seu planejamento
estão sendo alcançados, se os alunos estão aprendendo, o que deve reforçar, o que
pode ampliar, enfim como deve atuar para que seu ensino propicie realmente a
aprendizagem do aluno.
Ao falarmos sobre avaliação, consideramos importante ressaltar os
comentários “TARS” e “VANGRA” a respeito da participação de ambas em um
momento específico, uma aula em que foi aplicada a avaliação de Matemática.
“TARS” destaca que a postura da professora se modifica durante a
avaliação.
A professora avisa sobre a avaliação e coloca a atividade na lousa. Alguns
alunos reclamam, mas todos copiam e iniciam a prova. Na avaliação é
pedido prova real, as operações são de adição e subtração. Os alunos
dizem ter dificuldade nas “contas de emprestar ”. A professora diz que não
pode explicar porque é prova. Alguns terminam rápido, outros demoram
muito e a prova leva o dia todo. (“TARS”).
Como podemos perceber a professora parece entender a avaliação como
um momento único e individual dos alunos, momento este em que não deve realizar
intervenções que venham a colaborar com o desempenho dos mesmos. Mesmo com
as dificuldades apresentadas pelos alunos nas operações de subtração, a
professora justifica que não explicará por ser o momento da prova. Por outro lado
não estabelece um tempo para a realização da avaliação. Como relata “TARS”, a
prova dura todo o período da aula, o que deixou os alunos cansados e sem
paciência para pensar e resolver as atividades solicitadas.
Segundo a própria professora, ela não corrige a prova nem passa a nota
para os alunos. A devolutiva acontece somente no final do bimestre. Estas ações
podem levar as crianças a construírem o mito de que a avaliação e a Matemática
208
são ruins, o que dificulta a participação e não possibilita a aprendizagem, além de
levá-los a associar a avaliação a castigos. Além disso, conforme já comentamos, a
devolutiva serve de estímulo ao aluno para construir novos conhecimentoe e corrigir
possíveis erros conceituais.
Destacamos as considerações de “VANGRA” sobre a postura da professora
no momento em que é aplicada uma avaliação aos alunos. Esta avaliação é
unificada e aborda conteúdos de todo o primeiro semestre do ano. A estagiária
comenta este momento como se esta fosse uma atividade comum e sem caráter
avaliativo, não nos mostrando como a professora preparou os alunos, de que forma
aplicou a avaliação, se explicou algo, se foi rígida no atendimento às dúvidas
durante a prova, enfim não destaca a postura da professora durante a prova. Seus
comentários dizem respeito aos conteúdos abordados na avaliação e à correção que
a professora realizou na lousa em aula posterior, quando já havia devolvido as
provas corrigidas aos alunos.
Por fim, ao comentar a postura das professoras frente à própria prática e ao
desenvolvimento das aulas, destacam-se as análises de “TARS” sobre um
momento importante por ela relatado, referente à realização de uma atividade que
pedia o uso de calculadora para sua resolução. Como não havia calculadora
disponível os alunos não realizaram a atividade. Este fato se repetiu em outras duas
aulas.
Para a estagiária este momento foi difícil para os alunos que estavam
motivados para utilização da calculadora, um recurso diferente, sendo que segundo
ela a professora deveria ter se programado para esta realização, especialmente na
segunda vez em que a situação se repetiu.
Podemos perceber que “TARS” mostra ter entendido a importância de
planejamento nas aulas de Matemática, assim como na utilização de recursos que
auxiliem o desenvolvimento do raciocínio e conhecimento, como é o caso do uso da
calculadora. Isto denota reflexão sobre a prática da professora na constituição da
própria prática.
Os registros e análises dos estagiários acerca das observações realizadas
durante o estágio curricular supervisionado focando na postura das professoras
209
sugerem que mesmo com práticas e metodologias diferentes entre si, as mesmas se
interessam pela aprendizagem de seus alunos.
Pudemos perceber também que o trabalho destas professoras é
desenvolvido com pouco uso do material institucional ou de livros didáticos,
privilegiando a utilização de folhinhas avulsas para o ensino. Há também pouco
diálogo com os alunos, seja para atender suas dúvidas, antecipar dificuldades com o
conteúdo, ou mesmo para contextualizar novos conteúdos com outros já trabalhados
ou com a vida dos alunos.
As análises dos estagiários relatadas em seus portfólios mostram
observações sem muita participação. Este fato sugere que talvez seja por conta da
falta de diálogo das professoras com os mesmos ou falta de conhecimento tanto
pedagógico quanto matemático para se colocar em uma discussão sobre as formas
de trabalho das professoras observadas. Com isso encontramos mais relatos do que
propriamente análises sobre a postura das professoras.
Sendo assim, pudemos perceber nos relatos registrados nos portifólios,
pouca ampliação das aprendizagens dos estagiários, no que se refere ao ensino de
Matemática, com a análise da postura observada nas professoras.
Entretanto cabe destacar os relatos dos estagiários a respeito das
experiências vividas durante a realização dos estágios, com relação às próprias
aprendizagens propiciadas neste momento.
A estagiária “MAO” cita o estágio como momento integrante de sua
formação. Coloca a formação oferecida na Universidade em segundo plano, pois
segundo ela não houve nas aulas de FME de Matemática I e II ou na disciplina de
Prática de Ensino, a aprendizagem de conceitos ou metodologias que a
preparassem para atuar como professora de Matemática nos anos iniciais do Ensino
Fundamental.
Entretanto, “MAO” não se pronuncia explicitamente a respeito da
contribuição ou não do estágio para sua aprendizagem e formação para o ensino de
Matemática nos anos iniciais do Ensino Fundamental. Porém ressalta a importância
210
deste momento, assim como a participação no Programa Observatório para sua
formação, descobrindo na pesquisa uma forma de crescimento.
Tenho a certeza que tanto o estágio como o projeto, ajudarão a me tornar
uma profissional melhor, porque tenho a oportunidade de mudar minha
visão e me tornar uma pesquisadora. Com isso estou tirando algumas
dúvidas que me acompanharam durante toda a minha vida escolar e estou
quebrando vários mitos que tinha. (MAO).
Por outro lado, um ponto importante de suas reflexões relaciona-se ao
entendimento de que precisa continuar estudando, se atualizando e construindo
sempre novas práticas de ensino.
Espero ter outras oportunidades, como essa que tive com o Projeto, pois
acredito que para me tornar uma ótima professora, não posso parar na
graduação, vou ter que sempre buscar mais fontes de conhecimento, para
conseguir alcançar o meu objetivo que é fazer a diferença em sala de aula e
ser lembrada pelos meus alunos como uma fonte de inspiração, para
futuros professores. (MAO).
Podemos perceber que “TARS” ao término de suas observações, realizadas
na sala de 5º ano, mostra que o estágio colaborou de alguma forma com sua
formação para ensinar Matemática.
Acho que quando se trata de Matemática ainda há muito que aprender, mas
com certeza esse estágio foi uma grande experiência. Aprendi algumas
formas de ensinar observando como a professora explica a atividade. Vi
algumas coisas interessantes e outras que não dão tão certo. Existe muita
coisa que provavelmente eu só vou saber como é, se dá certo ou não na
prática. Mas com certeza muitas coisas eu já pude perceber o resultado
bom ou ruim observando a prática da professora em sua sala. (TARS).
“TARS” considerou o estágio uma experiência muito importante para sua
formação, mostrando nos registros do portfólio que sua participação no estágio não
se limitou às observações, pois reflete sobre a prática da professora estabelecendo
relações com sua futura prática. Neste sentido encontramos nas contribuições de
Schön (2000) o aporte para estas afirmações, quando o mesmo destaca a
importância da reflexão na formação do professor, reflexão esta estabelecida a partir
das ações que são desenvolvidas na prática.
O estagiário “EAM” relata que a realização do estágio foi muito produtiva
para sua formação, especialmente nas reflexões que pode fazer na articulação entre
a teoria aprendida da Universidade e a prática verificada no estágio. Destaca a
participação da professora nesta formação, conforme seu relato a seguir.
211
A convivência e observação do trabalho da professora, durante a realização
do estágio, contribuiu e muito para minha formação ao refletir, pois senti
falta na disciplina FME de Matemática de discussões sobre como e de que
forma ensinar. Ao vivenciar a prática e as técnicas que a professora utiliza
no cotidiano, como levantar a auto- estima do aluno, como vivenciar o
construtivismo em sala de aula com os alunos colaborando buscando
construir o conhecimento sentados agrupados. (EAM).
Ao fazer sua análise a respeito das disciplinas de FME de Matemática I e II,
oferecidas na Universidade com carga de 40 horas/aula em cada semestre, o
estagiário mostra-se frustrado e sem base para o ensino.
Fica uma sensação de frustração pois aprendi somente embasamentos
teóricos que não contemplavam o ensino- aprendizagem. Os professores
frisavam que nós tínhamos obrigação de saber a Matemática, então a
disciplina acabou focando nos Parâmetros Curriculares Nacionais de
Matemática e nas tabelas de competências que os alunos têm que aprender
no decorrer do ano letivo. Mas não levava em conta como ensinar e de que
maneira ensinar. Tivemos somente no campo de ensino aprendizagem
geometria e as nomenclaturas de figuras com bases e vértices diferentes.
(EAM).
Com efeito, conforme comentamos no capítulo em que foi feita a análise dos
planos de ensino das referidas disciplinas, apoiados nas contribuições de Fernandes
(2012), ao privilegiar o conhecimento pedagógico mais amplo, a ênfase volta-se
mais para o conhecimento curricular com destaque para os PCN de Matemática,
sem uma orientação específica para o professor que vai desenvolver estas
disciplinas no sentido de prepará-lo não só na aquisição dos conhecimentos
matemáticos mas também na formação pedagógica para o ensino destes conteúdos,
justamente o que “EAM” relata sentir falta.
A conclusão de “EAM” sobre a realização do estágio é de realização e
agradecimento, especialmente à professora que acompanhou. Destaca novamente a
franqueza da mesma no reconhecimento de suas dificuldades com a Matemática e
seu comprometimento em desenvolver seu trabalho não só com o Livro Didático e
Caderno de Apoio, mas buscando outras fontes para as atividades. Em sua análise
sobre a realização do estágio, o mesmo entende que aprendeu bastante e que
certamente vai utilizar muito do que viu no estágio quando estiver ensinando
Matemática nos anos iniciais.
Podemos perceber nos relatos da estagiária “LISE” uma certa preocupação
com a forma como vai atuar quando estiver à frente de uma sala de aula. Neste
212
sentido, o estágio aparentemente lhe trouxe oportunidade de aprendizagem e
reflexão.
A realização do meu estágio foi diferente de todos os meus colegas de
classe. No curso de Pedagogia, o estágio não é levado a sério por muitos
alunos, alguns fazem por fazer. Em minhas observações diárias com um
olhar crítico, pude ter a noção de como é a rotina de uma classe escolar
com trinta crianças na fase de aifabetização. (LISE).
Seu comentário vem ao encontro de nossa observação e relatos anteriores,
sobre a questão da realização do estágio apenas como o cumprimento burocrático
de um requisito do curso, o que segundo a estagiária não foi o seu caso. Por outro
lado não conseguimos visualizar a postura crítica descrita pela mesma em seu
relato, pois ela não se coloca a cada atividade apresentada.
Segundo a estagiária, a vivência no estágio fez com que percebesse a
fragilidade do conhecimento adquirido para ensinar Matemática, nas aulas da
graduação .
As aulas de FME de Matemática não contribuiram muito para ensinarmos a
Matemática. Primeiro porque a carga horária não é compatível, é pequena e
segundo que tudo é muito teórico. Vi coisas nestas aulas que não são mais
utilizadas em sala como o CAVALU e as "casinhas" de unidade, dezena e
centena. (LISE).
Reconhecendo que precisa se envolver com a própria formação e buscar
alternativas e aprendizagem, “LISE” enfatiza em seus registros a importância do
Programa Observatório da Educação para a formação do professor. Destaca ainda
que as aulas de FME de Matemática poderiam ter seu formato alterado para auxiliar
melhor a formação para o ensino de Matemática, opinião que corrobora nossas
análises feitas no Capítulo 3 sobre a organização e desenvolvimento de tal
disciplina.
Embora entenda que o estágio foi importante para sua formação, a
estagiária não se manifesta a respeito das aprendizagens propiciadas ou não na
realização do estágio, assim como as contribuições da professora que acompanhou
para sua prática como professora que vai ensinar Matemática no Ensino
Fundamental.
Por fim, as conclusões de “VANGRA” sobre a realização do estágio
mostram que, do seu ponto de vista, este período foi produtivo para seu
213
desenvolvimento. Embora não se manifeste explicitamente sobre a contribuição do
estágio em sua formação, ou sobre as aprendizagens propiciadas neste momento,
destaca em seus registros que o olhar pedagógico utilizado para observar e analisar
as atividades e postura da professora, enriqueceram seu conhecimento e seu
trabalho como futura professora.
Com efeito, no momento e ambiente do estágio o aluno pode comparar as
teorias aprendidas com as práticas observadas, desenvolvendo a criticidade e a
reflexão; assim como nos mostra Freire (1998) ao destacar que o professor adquire
sua prática e identidade docentes no cotidiano da escola e da sala de aula, nas
vivências propiciadas por este cotidiano e nas relações interpessoais que se
estabelecem neste ambiente.
Neste sentido “VANGRA” relata que as relações que estabeleceu com
outros professores acrescentaram muito à sua formação, porque nestas relações
“podemos ver os vícios que fomos agregando ao longo de uma educação
autoritária”. A estagiária ainda traz consigo a carga de uma educação tradicional,
com professores que não se preocupavam com sua aprendizagem, o que se reforça
em seu comentário, não especificamente sobre o estágio e a professora que
acompanhou, mas sobre os professores em geral.
Infelizmente muito professor ainda se acha o dono da verdade, agindo como
se fosse o detentor de todo o poder, não considera o conhecimento prévio
que os alunos trazem consigo, tanto que se surpreende quando em nossas
observações nos deparamos com crianças que tem raciocínio lógico e
opinião. (“VANGRA”).
A estagiária destaca em seus comentários a postura da professora
acompanhada, que a seu ver tem uma visão e atenção direcionadas para cada um
de seus alunos, reconhecendo seus conhecimentos prévios e valorizando sua
aprendizagem.
Quanto às aprendizagens propiciadas nas disciplinas FME de Matemática I e
II, “VANGRA” critica em diversos momentos a forma como estas disciplinas são
oferecidas, focando muito nos conteúdos e não trabalhando com os alunos, que
ensinarão Matemática nos anos iniciais do Ensino Fundamental, a questão do
ensino destes conteúdos. O que ensinar é importante, mas segundo a estagiária é
preciso saber como ensinar.
214
Consideramos que, embora em diferentes níveis, os cinco estagiários
mostram em seus relatos que o estágio contribuiu de alguma forma para seu
crescimento e para sua formação como professores que vão ensinar Matemática.
4.4
A análise das dimensões de aprendizagem reveladas pelos estagiários
Levando em conta o foco de nossa pesquisa, que é a contribuição do
estágio para a melhoria da formação pra ensinar Matemática, manifestada no
portfólio, percebemos que no que diz respeito à elaboração do portfólio, todos os
estagiários
demonstraram
comprometimento,
alguns
revelando
inclusive
a
importância deste momento para sua formação.
“TARS” mostrou também que se envolveu com este momento não somente
para realizar o estágio ou nos auxiliar na investigação, mas especialmente
enxergando a importância do estágio na constituição de sua identidade docente,
sendo que em alguns momentos mostra inclusive crescimento e aprendizagem em
seus relatos, no que diz respeito à sua formação e a realização do estágio.
Embora “EAM” tenha mostrado capricho e comprometimento na elaboração
do portfólio, não cumpriu todas as orientações dadas para tal. Conforme já
explicado, o mesmo apresentou treze atividades, sendo somente duas de
acompanhamento de aula com ensino de Matemática, todas as demais se referiam a
avaliações, com revisão e correção. Com isso entendemos que ficou muito limitada
a oportunidade de observações e contribuições por parte do estagiário.
A partir do referencial teórico adotado, nas contribuições de Chamoso
Sánchez, Cáceres Garcia e Azcárate Goded (2011), as análises realizadas nos
direcionam para as três dimensões propostas pelos autores: “Conhecimento”,
“Reflexão” e “Criatividade”. Além disso, levamos em conta os níveis de
desenvolvimento em cada uma destas dimensões, ainda conforme os aportes dos
autores: “Descrição”, quando o aluno se envolve com o processo com uma visão
externa; “Argumentação”, quando o aluno se envolve ativamente no processo e
“Contribuição”, quando o aluno participa, se envolve e toma decisões próprias.
Ao analisar a dimensão do “Conhecimento” pretendíamos observar o
conhecimento do conteúdo matemático e o conhecimento metodológico para o
215
ensino do conteúdo matemático desenvolvido pelos estagiários a partir da realização
do estágio. Além disso, esperávamos observar se, como entendem os autores, os
estagiários encarariam os conteúdos desconhecidos, buscando um aprofundamento
tanto do ponto de vista matemático como de sua aplicação no ensino.
Nesta dimensão os estagiários apresentaram diferentes posturas e níveis de
desenvolvimento.
Em seus registros, em algumas atividades analisadas, “MAO” apresenta os
conteúdos trabalhados, argumenta ou sugere atividades diferenciadas que
possibilitem desenvolver estes conteúdos. Muitos de seus registros são descritivos e
a estagiária não demonstra aprofundamento na questão dos conteúdos matemáticos
a serem trabalhados no Ensino Fundamental ou das metodologias necessárias para
este ensino.
Embora tenha se organizado na questão das atividades, não destaca a
forma como os conteúdos referentes às atividades foram trabalhados. Seus
comentários limitam-se à rotina da professora e não especificamente sobre como a
professora se coloca, para cada atividade, antes, durante e após a aplicação da
mesma. Porém isto nos leva a pensar que a própria ausência deste tipo de
comentário seja um indício de que a professora efetivamente não se posiciona,
limitando-se a distribuir as folhinhas, ler a atividade, dar um exemplo e deixar que as
crianças resolvam. Com isso não temos parâmetros para analisar o que e como a
professora ensina com relação à Matemática e de que forma este ensino propicia a
aprendizagem dos alunos.
Além disso, “MAO” deveria estabelecer relações entre as atividades e os
conteúdos aprendidos nas disciplinas relacionadas ao ensino de Matemática que
foram desenvolvidos na Universidade. Neste quesito também não houve interação
ou esclarecimentos sobre esta aprendizagem, pois na maioria das atividades a
estagiária respondia da mesma forma, ou seja, não havia aprendido o conteúdo ou a
metodologia para seu ensino na Universidade.
Com esta análise entendemos que a estagiária “MAO” encontra-se no nível
1 – Descrição, com relação à dimensão do Conhecimento.
216
“TARS” mostra conhecimento dos conteúdos com exemplos e relacionandoos com o dia-a-dia e com outras áreas. Percebe também o conhecimento adquirido
nas aulas da graduação e sua ampliação na participação no Programa Observatório.
As orientações para a realização do estágio e da investigação foram seguidas e
descritas por “TARS”. Em seus registros faz considerações e análises sobre as
atividades e prática da professora, em alguns momentos mais descritivos, em outros
reflete e faz sugestões. Isto permite afirmar que a mesma encontra-se no nível 2 –
Argumentação na dimensão analisada.
Tomando por referência os estudos de Chamoso Sánchez, Cáceres Garcia e
Azcárate Goded (2011), considerando-se a dimensão Conhecimento, “EAM” mostra
certo desconhecimento dos conteúdos matemáticos que serão trabalhados no
Ensino Fundamental, uma vez que não faz comentários e observações sobre as
atividades
neste
sentido,
embora
estabeleça
algumas
relações
entre
o
conhecimento obtido nas aulas no curso de graduação e o conhecimento que julga
necessário para ensinar Matemática. No que se refere ao conhecimento
metodológico, não aponta relação entre o conteúdo e a metodologia em seus
relatos, pautando suas considerações num caráter mais pessoal nesta dimensão.
Registra desconhecer e se admira com uma estratégia utilizada pela professora, o
trabalho em grupo, sendo que foi ensinada sua utilização na Universidade e no
grupo de pesquisa e, utilizada também como estratégia nos dois espaços.
Consideramos que o estagiário pode ter aprendido como poderia fazer a gestão da
sala de aula, pois a impressão que fica na leitura de seus relatos é que nunca havia
pensado nisso. Com isso entendemos que o estagiário se encontra no nível 1 –
Descrição nesta dimensão.
A estagiária “LISE” não mostra em seus registros e comentários sobre as
atividades acompanhadas no estágio conhecer os conteúdos trabalhados pela
professora, se equivocando em alguns conceitos, numa manifestação de
desconhecimento dos conteúdos matemáticos que serão trabalhados no Ensino
Fundamental. Ao analisarmos o conhecimento metodológico, a estagiária aceita as
atividades propostas pela professora, sem sugerir diferentes intervenções ou
mudanças, o que remete a falta de articulação entre o conteúdo trabalhado e a
metodologia adequada para seu ensino. Com estas considerações, podemos dizer
que “LISE” encontra-se no nível 1 – Descrição nesta dimensão.
217
Por fim “VANGRA” não apresenta registros de domínio ou desenvolvimento
dos conteúdos trabalhados pela professora, confundindo inclusive alguns conceitos,
mostrando desconhecer os conteúdos matemáticos que devem ser trabalhados no
Ensino Fundamental. Quanto ao conhecimento metodológico, suas intervenções
sobre as mudanças que faria em cada atividade proposta pela professora, mostram
que embora apresente exemplos e atividades, ainda não consegue relacionar o
conteúdo com a metodologia adequada. Com isso entendemos que nesta dimensão
a estagiária encontra-se no nível 1 – Descrição, proposto pelos autores.
Podemos perceber que dentre os cinco estagiários, quatro deles encontramse no nível 1 – Descrição, o que significa que nos portfólios por eles elaborados
apresentam os conteúdos trabalhados e algumas atividades desenvolvidas, mas de
forma descritiva, havendo em seus relatos indícios de uma tentativa de
aprofundamento com relação aos conteúdos matemáticos ou metodologias
utilizadas para o ensino dos mesmos, no que se refere ao ensino de Matemática nos
anos iniciais do Ensino Fundamental.
Somente a estagiária “TARS” encontra-se no nível 2 – Argumentação,
apresentando
em
seu
portfólio
os
conteúdos
trabalhados,
as
atividades
desenvolvidas e em muitos momentos argumentações sobre as ações da
professora. Embora seus registros se apresentem descritivos em algumas
atividades, mostra uma tentativa de aprofundamento na questão dos conteúdos
matemáticos e das metodologias necessárias para o ensino de Matemática no
Ensino Fundamental.
Com relação à dimensão da “Reflexão”, os autores levam em conta a
reflexão pessoal sobre a própria formação e a reflexão sobre a prática do professor.
Como os estagiários não têm experiência anterior que lhes possibilite refletir sobre a
própria formação, esperávamos observar se havia reflexão nos relatos dos portfólios
sobre a prática dos professores que os receberam, exercitando a reflexão sobre
seus próprios conhecimentos e práticas.
No que se refere a esta dimensão, “MAO” estabelece comentários nos
quais pudemos perceber que existe reflexão e uma preocupação com o trabalho que
está sendo desenvolvido pela professora que a recebeu e com os conteúdos e
218
atividades trabalhadas. Em suas considerações a estagiária chega a demonstrar a
possibilidade de utilizar a reflexão como instrumento de sua formação ou a
preocupação em desenvolvê-la, mas não destaca a importância da reflexão para a
própria formação como futura professora que vai ensinar Matemática nos anos
iniciais do Ensino Fundamental.
Ressalte-se
que
“MAO”
demonstra
conhecer
a
necessidade
de
complementar sua formação, citando sua participação no Programa Observatório da
Educação como grande oportunidade de aperfeiçoamento na área da Matemática.
Cita também o estágio como momento integrante de sua formação. Coloca a
formação oferecida na Universidade em segundo plano, pois segundo ela não houve
nas aulas de FME de Matemática I e II ou na disciplina de Prática de Ensino, a
aprendizagem de conceitos ou metodologias que a preparassem para atuar como
professora de Matemática nos anos iniciais do Ensino Fundamental.
Isto mostra que “MAO” reflete sobre sua própria formação. A reflexão, de
acordo com Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011) pode
fortalecer a formação e auxiliar na superação de carências do conhecimento tanto
teórico quanto pedagógico, daí nossas expectativas quanto aos comentários
registrados pela estagiária sobre as atividades desenvolvidas, sobre a postura da
professora
acompanhada
e
sobre
a
própria
postura,
aprendizagem
e
desenvolvimento. Sua postura e comentários acerca da prática da professora e sua
futura prática, nos mostra que “MAO” encontra-se no nível 2 – Argumentação, na
dimensão da Reflexão.
Com relação à Reflexão, entendemos que “TARS” se posiciona em vários
momentos questionando a prática da professora e refletindo sobre sua própria
prática, o que nos permite dizer que a mesma está no nível 2 – Argumentação,
também nesta dimensão.
Já “EAM” seja sobre a prática da professora, ou seja, sobre sua própria
prática, fica no campo da descrição de posturas, não se aprofundando ou
questionando as ações observadas. Também com relação às atividades, não analisa
de forma reflexiva, se posicionando em vários momentos de forma superficial em
seus questionamentos. Os comentários que faz sobre a prática da professora são
219
embasados no questionário que a mesma respondeu e não nas observações de
suas aulas. Observa-se que o estagiário registra sua preocupação com a própria
prática, ao argumentar sobre a formação recebida nas aulas de FME de Matemática
oferecidas na Universidade e sua participação no grupo de pesquisa do programa
Observatório da Educação. De certo modo então, se envolve com o processo e
reflete sobre sua formação na tentativa de transpor as dificuldades encontradas no
conhecimento matemático e na metodologia para o ensino do mesmo.
Suas observações estão pautadas em uma prática mais geral da didática,
como por exemplo, do relacionamento da professora com os alunos, da surpresa
com a questão do trabalho em grupo, da cumplicidade entre professoras e alunos.
Embora não relacione especificamente os conteúdos apresentados pela professora
com suas aprendizagens nas aulas do curso de Pedagogia, houve sua reflexão a
respeito das aulas de FME de Matemática, sua formação para o ensino de
Matemática e a participação nas discussões do grupo de pesquisa do Programa
Observatório da Educação.
Por estes motivos, entendemos que “EAM”, na dimensão da Reflexão, está
no nível 1 – Descrição.
A estagiária “LISE” transita entre o nível 1 - Descrição e o nível 2 –
Argumentação na dimensão da Reflexão. Isto porque embora no que diz respeito às
reflexões sobre a prática da professora tenha se manifestado muito pouco, somente
descrevendo as ações desenvolvidas, quando se trata da própria formação a fala da
estagiária denota preocupação, envolvimento e busca pelo crescimento, muito
embora estas considerações não se reflitam nas observações diárias em seu
estágio. Portanto, no que se refere aos registros e relatos acerca das atividades
observadas e à realização do estágio, a estagiária não se envolve, limitando-se a
descrever o que foi desenvolvido e contar sobre a postura da professora e dos
alunos, não realizando uma análise da prática da professora.
Ressaltamos que “LISE” tem consciência da necessidade de aprofundar
sua formação para que possa atuar como professora com conhecimento e prática
adequados. Encontramos em seus registros sobre a realização do estágio e as
contribuições para sua formação, a importância do Programa Observatório e a
220
necessidade das aulas de FME de Matemática trazerem maiores contribuições,
assim como a importância da realização deste estágio. Mas esta postura não
aparece no cotidiano da escola, durante o acompanhamento da professora.
A estagiária “VANGRA” embora não faça reflexões sobre a prática da
professora que acompanhou em seu estágio, reflete e discute a própria formação
para o ensino, estabelecendo relações entre a sua formação matemática na
Educação Básica, a formação matemática propiciada nas aulas de FME de
Matemática oferecidas na Universidade e a formação recebida no grupo de pesquisa
do programa Observatório da Educação, que segundo ela supera e muito as
aprendizagens no curso de Pedagogia. Reflete, portanto, sobre sua formação e
sobre como superar as carências que possui com relação ao conhecimento,
entendendo o Programa Observatório como forma de alcançar esta superação. Por
este motivo, neste ponto de nossa análise permite inferir que a estagiária está no
nível 2 – Argumentação, da dimensão Reflexão. Esta dualidade de análise deve-se
ao fato de que Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011)
destacam dois pontos da Reflexão a serem analisados: reflexão pessoal sobre a
própria formação, na qual a estagiária se destacou e a reflexão sobre a prática do
professor, cujos comentários e reflexões não se revelaram.
No que se refere à dimensão da Reflexão, pudemos perceber que todos os
estagiários trazem em seus relatos ideias e considerações que sugerem a
preocupação com a prática da professora e com a própria prática, muito embora
nem todos mostrem entender a importância desta reflexão para a constituição da
identidade docente e da prática pedagógica para o ensino de Matemática.
Somente o estagiário “EAM” não mostra reflexão em seus registros,
descrevendo as atividades da professora e tecendo suas considerações na
observação da postura dos alunos e não da professora, focando o antes, durante e
depois da atividade em quase todos os encontros nas ações das crianças.
No que se refere à dimensão da “Criatividade”, proposta por Chamoso
Sánchez, Cáceres Garcia e Azcárate Goded (2011), pretendia-se verificar se os
estagiários são capazes de criar diante de situações imprevistas, sua flexibilidade e
a capacidade de tomar decisões que possam redirecionar o processo ensino-
221
aprendizagem para alterar sua prática e melhorar o aproveitamento dos alunos.
Observamos também se os mesmos relacionam os conteúdos matemáticos com o
contexto no qual se inserem suas observações.
Em nossas análises sobre o desenvolvimento de “MAO”, no que se refere à
dimensão da Criatividade, percebemos que na maioria das atividades, a estagiária
demonstra conhecer os conteúdos, mas não estabelece relações entre eles ou
sugere novas formas de trabalhar, o que nos mostra que a mesma não toma
decisões ou faz sugestões que permitam aprimorar seu ensino e melhorar a
aprendizagem de seus alunos. As atividades apresentadas pela professora “PMAO”, disponíveis no livro didático ou na internet, parecem ser adequadas para o
desenvolvimento da prática de “MAO”, no que se refere ao ensino de Matemática
nos anos iniciais do Ensino Fundamental. Porém faz sugestões sobre os materiais
utilizados em algumas atividades ou mesmo sobre a prática da professora.
Mostra ainda que percebe suas carências, mas não reflete sobre formas de
superá-las nem toma decisões sobre sua percepção. Por este motivo entendemos
que MAO encontra-se no nível 1 – Descrição nesta dimensão.
Na análise da dimensão da Criatividade proposta pelos autores, “TARS”
mostra em seus relatos no portfólio que se coloca e dá sugestões alternativas para o
ensino de determinados conteúdos ou desenvolvimento de algumas atividades.
Nesta dimensão entendemos que a estagiária se encontra no nível 3 – Contribuição.
Ao observarmos a capacidade do estagiário “EAM” em criar, inovar ou
propor ações que aproximem o ensino e o conteúdo do contexto, não há nos
registros de seu portfólio sugestões para o ensino da Matemática de forma
diferenciada, assim como propostas de mudanças na prática da professora. Pelo
exposto, entendemos que nesta dimensão o estagiário encontra-se no nível 1 –
Descrição.
Entendemos que “LISE”, na análise da dimensão Criatividade, não
consegue se posicionar para uma mudança naquilo que está sendo trabalhado,
propondo novas atividades. A estagiária não demonstra flexibilidade ou capacidade
de criar em situações imprevistas para contextualizar novas formas de abordar os
222
conteúdos, Com isso entendemos que a mesma se encontra no nível 1 – Descrição,
com relação a esta dimensão.
Por fim, percebemos que “VANGRA” não relaciona os conteúdos entre si,
não adapta e não cria novas atividades a partir do contexto. Suas tentativas de criar
atividades diferenciadas foram equivocadas, o que a coloca no nível 1 – Descrição,
com relação a esta dimensão.
Na dimensão da Criatividade somente a estagiária “TARS” alcançou o nível
3 – Contribuição, ficando os demais alunos no nível 1 – Descrição, uma vez que não
conseguiram sugerir mudanças ou tomar decisões que redirecionassem o ensino e a
aprendizagem de Matemática a partir das observações.
Analisando os portfólios, com todas as questões solicitadas no início do
trabalho, e avaliando os registros realizados pelos estagiários em todas as
atividades, concluímos que cada um deles adotou uma postura diferente na
realização do estágio e na elaboração do portfólio, que nos permite analisar
individualmente os resultados e confrontar com os objetivos propostos.
Nos quadros a seguir é possível observar a categorização de cada um dos
estagiários, de acordo com as dimensões estabelecidas nas contribuições de
Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011).
Dimensão Conhecimento
Estagiário
“MAO”
Nível 1
Nível 2
Nível 3
Descrição
Argumentação
Contribuição
X
“TARS”
X
“EAM”
X
“LISE”
X
“VANGRA”
X
Quadro 14 - Categorização dos estagiários: Conhecimento
223
Dimensão Reflexão
Estagiário
Nível 1
Nível 2
Nível 3
Descrição
Argumentação
Contribuição
“MAO”
X
“TARS”
X
“EAM”
X
“LISE” *
X
“VANGRA”
X
Quadro 15 - Categorização dos estagiários: Reflexão
*Fase de transição do nível I para o nível 2 na dimensão Reflexão.
Dimensão Criatividade
Estagiário
“MAO”
Nível 1
Nível 2
Nível 3
Descrição
Argumentação
Contribuição
X
“TARS”
X
“EAM”
X
“LISE”
X
“VANGRA”
X
Quadro 16 - Categorização dos estagiários: Criatividade
“MAO” mostra um envolvimento e participação que a colocam nos dois
níveis – Descrição e Argumentação, em diferentes momentos, levando em conta as
três dimensões: Conhecimento, Reflexão e Criatividade. A análise do todo,
entretanto nos mostra que a mesma encontra-se no nível 1 – Descrição, nas três
dimensões, uma vez que a mesma se envolveu com o processo, porém com uma
visão externa do mesmo, cujas argumentações ou contribuições estavam pautadas
nos relatos e não no aprofundamento do pensamento da estagiária para o
desenvolvimento de sua prática docente.
A estagiária “TARS” mostra uma tomada de posição com relação à prática
da professora, se envolvendo e comentando, na tentativa de superar suas limitações
para o ensino de Matemática, o que ao levarmos em conta as dimensões
estabelecidas por Chamoso Sánchez, Cáceres Garcia e Azcárate Goded (2011), tais
sejam o Conhecimento, a Reflexão e a Criatividade, nos permite afirmar que,
224
embora as análises individuais de cada dimensão a coloquem nos três níveis, uma
análise geral mostra que “TARS” se encontra no nível 2 - Argumentação, bem
próxima de alcançar o nível 3 - Contribuição.
Embora “EAM” considere que a realização do estágio trouxe a ele muita
aprendizagem, entendendo que vai utilizar esta aprendizagem quando estiver
ensinando Matemática nos anos iniciais. Mas estas considerações não se refletem
nos registros feitos no portfólio ao longo do estágio em relação à Matemática. Assim,
não há em seus registros, relatos que nos permitam afirmar que houve ampliação
dos conhecimentos matemáticos. No entanto, as observações sobre as dinâmicas
das aulas podem contribuir para sua prática pedagógica a partir da realização do
estágio. Com estas análises entendemos que, levando-se em conta as três
dimensões propostas por Chamoso Sánchez, Cáceres Garcia e Azcárate Goded
(2011), “EAM” encontra-se no nível 1 – Descrição, em cada uma das dimensões
analisadas.
A análise do portfólio de “LISE” mostra que a análise do todo nos permite
entender que ela está no nível 1 – Descrição nas três dimensões, uma vez que se
envolveu com o processo, observando, cumprindo as orientações, dando suas
opiniões em vários momentos, mas seus registros são descrições sem
aprofundamento, suas argumentações e contribuições eram relatos descritivos e não
havia aprofundamento que possa contribuir com sua formação e com sua prática
docente.
Por fim, a análise do portfólio de “VANGRA”, levando-se em conta as
dimensões propostas pelos autores, mostra a inserção da mesma nos níveis
Descrição e Argumentação em diferentes momentos. Porém uma análise geral
mostra que a estagiária encontra-se no nível 1 – Descrição nas três dimensões, pois
embora tenha se envolvido com o processo, na observação e elaboração do
portfólio, suas argumentações e contribuições foram relatos descritivos, alguns
comentários equivocados e não havia aprofundamento que permitisse a formação
de sua prática como professora.
Com relação ao nosso objetivo, tal seja verificar as contribuições do estágio
para ensinar Matemática, esperávamos observar um crescimento maior destes
225
alunos no que diz respeito aos conteúdos e práticas que serão utilizadas em sua
futura atuação docente.
Nos relatos dos estagiários “MAO”, “EAM”, “LISE” e “VANGRA” não há
subsídios, a partir da análise realizada, que sugiram a ampliação dos conhecimentos
matemáticos adquiridos na realização do estágio que possam ser utilizados
futuramente, o que certamente será um dificultador na atuação dos mesmos como
professores que ensinam Matemática nos anos iniciais do Ensino Fundamental.
Em virtude de “VANGRA” realizar o estágio em uma escola colaboradora do
Programa Observatório e acompanhando uma professora bolsista participante do
mesmo programa, nossas expectativas com relação às aprendizagens que se
manifestariam a partir da realização do estágio para o ensino de Matemática, seriam
muito grandes. Mas infelizmente não observamos nos relatos da estagiária,
aspectos que pudessem indicar uma interação maior entre estagiária e professora,
que trouxessem maior contribuição na realização do estágio.
Desta forma, consideramos que a realização do Estágio Curricular
Supervisionado, mesmo focando no ensino de Matemática e tendo nossa orientação
direta, como professora orientadora do Estágio Curricular Supervisionado,
possibilitou pouca aprendizagem ou crescimento nesta área para “MAO”, uma vez
que a estagiária revela observações pontuais em seu relatório que permitem detectar
algumas aprendizagens significativas em seu portfólio para o ensino de Matemática, mas
não há sinais de ampliação dos conhecimentos necessários para ensinar Matemática.
Analisamos que “EAM” revela crescimento aparente das reflexões sobre o
gerenciamento da sala de aula e mostra pouca aprendizagem de conteúdos
matemáticos relativos ao ensino de Matemática nos anos iniciais do Ensino
Fundamental.
Consideramos que, em virtude de “LISE”, assim como “VANGRA” pouco
revelarem em seus relatórios, não podemos afirmar que o estágio realizado trouxe
contribuição para as estagiárias ensinarem Matemática, pois pouco revelam sobre
seu crescimento. No entanto “LISE” aponta problemas na prática da professora que
certamente lhe servirão de exemplo do que não deve fazer quando no exercício da
profissão.
226
Os registros de “TARS” trazem relatos que apontam para uma ampliação de
conceitos e adoção de posturas que facilitarão sua atuação como professora, mas
não podemos afirmar se seus conhecimentos matemáticos foram ampliados com a
realização do estágio, ampliação necessária para sua profissão.
Aparentemente houve certo crescimento para “TARS” no que se refere às
reflexões necessárias para o ensino, porém pouca aprendizagem com relação aos
conteúdos matemáticos relativos ao ensino de Matemática nos anos iniciais do
Ensino Fundamental.
Consideramos que as contribuições de Chamoso Sánchez, Cáceres Garcia
e Azcárate Goded (2011) foram valiosas para nossa análise, especialmente no que
diz respeito à necessidade da reflexão na constituição da docência, uma vez que os
autores entendem que se o professor não refletir sobre sua prática não poderá
superar a carência de qualquer tipo de conhecimento, seja teórico ou metodológico.
4.5
Considerações sobre o Capítulo
O estudo de caso envolvendo as observações de cinco estagiários, aqui
descrito e analisado, com base na elaboração dos portfólios de aprendizagem pelos
mesmos nos trouxeram algumas reflexões que julgamos importantes.
Ainda que, de acordo com o referencial teórico por nós adotado para tais
análises, os estagiários mostrem pouco envolvimento, diálogo e reflexão sobre a
prática da professora e sobre a própria prática, nos levando a colocá-los quase
sempre no nível Descrição. Os registros também nos permitem supor que talvez esta
falta de diálogo não deva ser unicamente atribuída aos estagiários.
Em muitos momentos percebemos que, se havia somente a descrição da
ação, esta estava de acordo com a postura que a professora adotava, sem
comprometer-se com a formação deste aluno que estava sob sua orientação.
Quando comentamos sobre as contribuições de Alarcão (2003), a respeito
do papel de um supervisor que acompanhe e dê suporte prático e teórico para a
formação dos estagiários, entendemos que quando na Universidade este
acompanhamento é feito pelo orientador de estágios, porém quando na escola, este
227
papel deve ser atribuído ao professor que acompanha o aluno em seu estágio na
escola.
Talvez por este motivo também, todos os estagiários mostraram pouca
aprendizagem em seus relatos sobre a realização do estágio, pois embora
tivéssemos muitas afirmações sobre a aprendizagem, sobre a importância de terem
realizado o estágio ou sobre a contribuição do mesmo para sua formação como
professor que vai ensinar Matemática nos anos iniciais do Ensino Fundamental,
estas não se refletiam nas análises das atividades ou da postura da professora.
Por outro lado, a pouca aprendizagem no que se refere ao ensino de
Matemática propiciada na Universidade, evidenciada nos comentários dos alunos,
pode ter sido o motivo das reflexões ficarem num nível mais superficial, em virtude
dos estagiários não possuírem conhecimentos matemáticos que lhes possibilitasse
comentar e fazer sugestões a respeito do que estava sendo trabalhado pela
professora.
Estas observações nos dão subsídios para um novo olhar e direcionamento
para nossas considerações finais, numa revisão dos objetivos e das questões
colocadas no início de nosso trabalho, nos fazendo repensar os caminhos da
formação e os fatores que influenciam e proporcionam esta formação.
Pudemos perceber muitas convergências e divergências entre os cinco
portfólios, na postura dos estagiários, na forma dos relatos, na qualidade das
análises e reflexões. A análise destas reflexões e das questões de pesquisa será o
foco do próximo capitulo em que teceremos nossas considerações finais.
229
CAPÍTULO 5 – CONSIDERAÇÕES FINAIS
O inesperado surpreende-nos. É que nos instalamos de
maneira segura em nossas teorias e ideias, e estas não
têm estruturas para acolher o novo. Entretanto, o novo
brota sem parar. Não podemos jamais prever como se
apresentará, mas deve-se esperar sua chegada, ou seja,
esperar o inesperado.
(MORIN, 2000, p.30)
5.1
Algumas considerações iniciais
Os caminhos percorridos na presente investigação levaram a diferentes
momentos de reflexões, constatações e novas indagações.
Ao nos propormos investigar se os estágios curriculares supervisionados
permitiam que os alunos pudessem desenvolver conhecimentos em Matemática que
lhes desse suporte para atuar como professores desta área, nossa visão se
direcionava para as ações do aluno e sua participação ou observação realizada
nestes estágios.
Embora tivéssemos a consciência de que “Daquilo que eu sei, nem tudo me
deu clareza”, embora soubéssemos que não havia certezas e que devíamos estar
de olhos e ouvidos abertos às informações que esta investigação nos traria,
imaginávamos de antemão que o pouco envolvimento dos alunos com os estágios
não permitia que houvesse aprendizagem para o ensino de Matemática.
Nossa veia de pesquisadora, na busca constante pelo novo e por respostas,
nos levou a “Não fechar os olhos e não tapar os ouvidos” às nossas incertezas e
estabelecemos os objetivos e questões que direcionariam esta pesquisa.
Assim, ao estabelecer as questões que pretendíamos responder com esta
procura, chegamos aos estágios e a formação do professor que vai ensinar
Matemática nos anos iniciais do Ensino Fundamental.
É certo que a participação, envolvimento e responsabilidade do aluno
durante a realização do estágio são fatores indispensáveis para sua formação,
porém as pesquisas foram se delineando de modo a nos mostrar outros atores e
230
contextos que, de forma direta ou indireta também têm grande peso na constituição
deste professor.
Ao solicitarmos que os cinco alunos sujeitos desta pesquisa elaborassem
portfólios de aprendizagem, com os registros de suas observações, seus
comentários, possíveis intervenções nas atividades acompanhadas, além das
relações estabelecidas entre o estágio e suas aprendizagens no que se refere ao
ensino de Matemática na Universidade, estabelecemos uma linha de pesquisa e
raciocínio que, como dissemos anteriormente, focava no aluno e sua ação.
Embora Schön (2000) nos dê suporte para entendermos que as reflexões
realizadas por estes alunos durante o estágio se constituem em formação para a
prática, uma vez que refletem sobre a prática do professor acompanhado, ainda
assim nosso entendimento era de que a responsabilidade por esta formação estava
com grande prevalência nas mãos deste aluno.
Porém, “Ninguém nasce educador ou é marcado para ser educador, a gente
se forma como educador na prática e na reflexão sobre a prática”.
As pesquisas bibliográficas iniciais nos trouxeram contribuições de autores
que mostravam o perfil do professor que atua nos anos iniciais do Ensino
Fundamental, nos levando a estabelecer relações entre este perfil e o que os alunos
estagiários mostravam em seus relatos e na realização do estágio.
A leitura de Tardif (2002), que discute os saberes necessários à prática do
docente, estabelecendo a nosso ver, inclusive, os momentos nos quais estes
saberes podem ser desenvolvidos, nos mostrou que ao longo de sua formação estes
estagiários puderam desenvolver e vivenciar cada um destes saberes.
Ao contribuírem com os relatos sobre sua história de vida, destacando a
formação básica e as experiências com a Matemática neste período, os estagiários
nos mostraram que carregam em sua bagagem profissional os diferentes tipos de
saberes destacados pelo autor, os quais se devidamente mobilizados e articulados
trarão uma prática mais eficiente ao professor. Vejamos as relações que
estabelecemos entre os saberes descritos por Tardif (2002) e os relatos dos
estagiários.
231
No que se refere aos “saberes pessoais dos professores” destacados pelo
autor, os estagiários mostram em seus relatos as influências familiares e do
ambiente em que viveram ou vivem na escolha da profissão, na constituição de sua
prática e na educação que desenvolvem.
A seguir sua prática é formada também pelos “saberes provenientes da
formação em escola anterior”, desenvolvido na Educação Básica, cuja influência na
aprendizagem da Matemática e consequentemente em seu ensino, foi fortemente
citada nos relatos dos cinco estagiários. Nesta constituição destacou-se a atuação
dos professores deste nível de ensino, com relação à Matemática, que para uns se
constituiu em facilidade de aprendizagem e escolhas futuras, enquanto que para
outros foi motivo de aversão a esta área, levando a escolhas profissionais que
aparentemente não tinham ligação com a Matemática.
Especial atenção deve ser dada aos “saberes provenientes da formação
profissional para o magistério”. Segundo o autor, estes saberes são adquiridos em
diferentes espaços da formação do professor, tais como a instituição formadora, os
estágios e cursos de capacitação e socialização profissional. Aqui encontramos o
foco desta investigação, o qual já citamos, a princípio voltado para o aluno e sua
aprendizagem.
Podemos entender que o estagiário participante de nossa pesquisa
desenvolve seus saberes para o ensino de Matemática na instituição, em seu curso
de graduação, especialmente nas aulas que se referem a este ensino, onde surge
mais um elemento articulador desta aprendizagem que é o professor que ministra
estas aulas na Universidade. Ao realizar os estágios, observar a prática do professor
acompanhado e estabelecer relações entre a teoria aprendida na Universidade e a
prática desenvolvida nas escolas, novamente não depende mais somente do aluno,
mas da contribuição do professor do Ensino Fundamental, sua prática, seus
conhecimentos
e
disponibilidade
para
auxiliar
este
estagiário
em
seu
desenvolvimento. E por fim, a formação em cursos de capacitação, que podemos
entender como espaços de discussão e revisão de conhecimentos e práticas, o que
certamente em nosso caso podemos relacionar com o grupo de Pesquisa do
Programa Observatório da Educação, do qual os estagiários participavam e podiam
agregar valor à própria formação.
232
Destacamos ainda a importância dos “saberes provenientes dos programas
e dos livros didáticos usados no trabalho”, que se constituem a partir de leituras,
reflexões, sínteses de materiais que podem ser os usados no trabalho ou os
indicados tanto na Universidade quanto no grupo de pesquisa, mas especialmente
aqueles que o próprio aluno busca na complementação do conhecimento.
E por fim, mas muito relevante para nossa investigação, os “saberes
provenientes de sua própria experiência na profissão, na sala de aula e na escola”.
Os alunos que se dirigem às escolas para a realização do estágio esperam aprender
com a prática do professor observado, uma vez que ainda não têm desenvolvidos os
saberes de suas experiências em sala de aula, conforme destaca Tardif (2002).
Conforme já citamos anteriormente Schön (2000) destaca que a formação do
professor se dá pelas reflexões realizadas a partir das ações desenvolvidas em seu
trabalho. Ocorre que este aluno, por ainda não exercer a docência, vai refletir sobre
a ação do outro, do professor observado, se baseando nesta prática para constituir
seu saber proveniente das ações em sala de aula.
Neste ponto de nossas reflexões, entendemos que não há como analisar se
o estágio propicia aprendizagens aos alunos, que os prepare para o ensino de
Matemática no Ensino Fundamental, se não estabelecermos uma relação entre os
diferentes atores que fazem parte desta formação. Atribuir a responsabilidade
unicamente ao aluno não nos deu as respostas que procurávamos com esta
investigação, o que nos levou a pensar e considerar outros fatores.
As contribuições de Tardif (2002) nos ajudaram a considerar que, embora a
formação dos estagiários na Universidade, no estágio ou nos grupos colaborativos,
seja de responsabilidade dos mesmos, não podemos atribuir exclusividade à
mesma. Enxergamos aqui a necessária articulação entre os professores e gestores
da Universidade, o gestor da escola onde o estágio é realizado e o professor que
acompanha o estágio, e finalmente os alunos estagiários, na análise desta
formação.
Este é o caminho que se delineia para nossas considerações finais sobre
este trabalho, apresentando a seguir nossas constatações, contribuições e desafios.
233
5.2
Os gestores e professores da Universidade
Espera-se que no curso de Pedagogia, as disciplinas oferecidas tenham um
foco mais direcionado para os conhecimentos necessários à prática e à formação de
professores.
Porém, entendemos que “Um professor não estará nunca inteiramente
formado, por uma ou outra razão”. Seja pela forma como o ensino é oferecido, seja
pela matriz curricular do curso, pelo comprometimento dos professores formadores,
fato é que a graduação por si, não garante formação adequada para o ensino.
No caso desta investigação pudemos perceber que, embora defendamos,
assim como vários autores citados ao longo deste trabalho, que o estágio é um dos
momentos de formação, em que o aluno vivencia experiências em seu futuro local
de trabalho, observando a prática de outros professores, este também não tem dado
conta das necessidades formativas dos alunos de Pedagogia.
A pesquisa documental realizada nesta investigação nos mostrou que na
Universidade pesquisada os alunos não têm um direcionamento específico na
realização do estágio.
Entendemos que os gestores responsáveis pelo Projeto Pedagógico do
Curso deveriam direcionar esta formação para a atuação do professor polivalente.
Por outro lado os professores que atuam nos cursos de Pedagogia, local de
formação dos professores polivalentes, deveriam orientar os alunos na busca dos
conhecimentos necessários para o ensino, em especial da Matemática.
Talvez a fragilidade apresentada na formação para o ensino de Matemática
durante o estágio pudesse ser superada com uma integração maior da disciplina
FME de Matemática com as demais disciplinas do curso, especificamente com o
estágio, o que pede mudanças no PPC e no trabalho entre os pares dentro da
Universidade.
Ressaltamos que a forma como a Universidade em questão orienta a
realização dos estágios no curso de Pedagogia, embora dentro das exigências
legais, não apresenta um direcionamento aos alunos para a realização dos mesmos,
234
além de não propor que as observações realizadas no estágio tenham seu foco no
ensino de Matemática.
Esta postura abre um leque de possibilidades, inclusive da realização do
estágio apenas como cumprimento burocrático, uma vez que não se cobra do aluno
a observação em todas as disciplinas. Esta questão é muito importante, pois o aluno
da Pedagogia será um professor polivalente e como tal deveria observar a atuação
dos professores em todos os momentos e no trabalho com as diferentes disciplinas.
A análise dos planos de ensino e ementas das disciplinas relacionadas ao
ensino de Matemática mostra que não há formação específica para o ensino,
focando mais nos conteúdos em si. Percebemos na análise dos planos de ensino
das disciplinas FME de Matemática I e II que os mesmos não apresentam
contribuições significativas para que os alunos aprendam a ensinar Matemática.
A disciplina integrada ao estágio, tal seja Prática de Ensino também se
mostra insuficiente na formação para o ensino de Matemática, em virtude de focar
na formação geral do professor, postura e identidade docente. Não há articulação
destas disciplinas com o estágio, as observações ficam restritas à didática do
professor, sua postura, relações pessoais na escola, entre outros aspectos.
E aqui se potencializa a responsabilidade do professor formador na
Universidade, no sentido de reforçar com os alunos a questão do trabalho
polivalente que será desenvolvido por eles e da necessidade de observações
direcionadas para todas as disciplinas que deverão ser trabalhadas.
Nossas observações e conversas informais com os professores do curso
mostram que os mesmos não se sentem responsáveis por este tipo de orientação,
entendendo que isto cabe especificamente ao professor orientador de estágio e nas
discussões estabelecidas na disciplina Prática de Ensino. Neste caso fica totalmente
nas mãos do professor formador o direcionamento dos alunos nas observações ou
reflexões sobre o ensino de Matemática na realização do estágio.
Constatamos na análise das grades e planos das disciplinas oferecidas no
curso de Pedagogia da Universidade em questão, no que se refere à formação do
professor e o ensino de Matemática, e a realização dos estágios, que a forma como
235
são oferecidas não propicia as reflexões esperadas e a necessária articulação entre
teoria e prática.
Esta constatação baseia-se no fato de que as disciplinas Fundamentos e
Metodologia do Ensino de Matemática I e II são oferecidas no 3º e 4º semestre do
curso e o Estágio nos anos iniciais do Ensino Fundamental ocorre somente no 5º
semestre. Desta forma não há como os professores discutirem os conteúdos
matemáticos trabalhados nas disciplinas com base nas observações verificadas nos
estágios ou vice versa, discutirem o que estão observando sobre ensino de
Matemática nas escolas em que realizam o estágio de acordo com o que estão
aprendendo na Universidade.
A nosso ver este é um desafio a ser superado pela própria Universidade,
uma vez que as queixas dos alunos sobre a falta de contribuição teórica das
disciplinas oferecidas no curso de Pedagogia sobre o ensino de Matemática
poderiam ser minimizadas com uma revisão dos planos de ensino e uma maior
interação entre os professores das diferentes disciplinas.
Por outro lado, destacamos a constatação da necessidade de parcerias para
a realização dos estágios que reforcem os objetivos formativos da Universidade e as
necessidades educacionais das escolas. Não encontramos na análise do Projeto do
Curso de Pedagogia ou nos planos de ensino dos Estágios indícios de discussão no
sentido de estabelecer parcerias entre Universidade e Escolas para a realização dos
estágios.
5.3
O gestor da escola e o professor que acompanha o estágio
As informações coletadas a partir das contribuições da direção da escola e
das professoras que acompanharam os estagiários trouxeram diferentes perfis
destes profissionais.
No que diz respeito à direção, somente uma das diretoras se mostrou aberta
à parceria escola-Universidade com o intuito de contribuir com a formação dos
futuros professores assim como propiciar formação em serviço para seus
professores. Destacamos que a escola em questão é parceira da Universidade no
236
Programa Observatório da Educação, o que já demonstra comprometimento com a
educação e formação de professores.
Com relação às professoras que acompanharam os estagiários, pudemos
perceber que em sua maioria não apresentam comprometimento com a formação
dos estagiários que recebem, tampouco com sua própria formação para recebê-los,
conforme já relatado no capítulo anterior.
Uma vez que se espera grande contribuição do estágio na formação dos
alunos de Pedagogia, especialmente no que diz respeito ao ensino de Matemática,
percebemos que não há um trabalho em sala que permita esta formação. Observouse que as professoras não dialogam ou explicam aos estagiários as ações que
direcionam sua prática; não explicam aos alunos os objetivos desta prática e com
relação aos conteúdos muitos deles não são mais bem trabalhados por
desconhecimento, inclusive relatados pelas próprias professoras nos questionários
aplicados.
Consideramos como importante contribuição deste trabalho, a constatação
de que é fundamental o envolvimento dos professores que recebem os estagiários
com o processo de formação dos mesmos, no desenvolvimento de práticas
reflexivas e na construção do conhecimento pedagógico do professor.
Sem isso o estágio torna-se espaço de simples observação, sem reflexão,
sem articulação entre teoria e prática e sem formação para a docência, o que se
delineia como grande desafio para os formadores e professores que acompanham
os estagiários.
5.4
O aluno estagiário
Os cinco estagiários foram unânimes em relatar a importância da formação
para o ensino de Matemática, seja nas aulas de FME de Matemática e na Prática de
Ensino ou nos estágios.
Se no início de nossa investigação tínhamos como certo que cabia ao
estagiário a maior responsabilidade pela formação e aprendizagem durante a
realização do estágio, pudemos perceber ao longo das análises que em muitos
237
momentos a falta de comentários ou posicionamentos era devido à postura das
professoras que os recebiam e o pouco envolvimento dos mesmos com os
estagiários.
Entendemos que “O conhecimento exige uma presença curiosa do sujeito
em face do mundo, [...] demanda uma busca constante”. Nossos estagiários
mostraram em seus relatos, ainda que de forma por vezes superficial, que se
colocam por meio da curiosidade na busca do conhecimento e formação.
Todos os estagiários estabeleceram relações entre os conteúdos vistos nas
aulas de FME de Matemática e as observações no estágio, embora a grande maioria
de forma negativa, destacando que não haviam trabalhado estes conteúdos no
curso de Pedagogia. Isso reforça nossa análise anterior sobre a necessidade de
revisão dos conteúdos presentes nos planos de ensino das disciplinas ligadas ao
ensino de Matemática e a integração Universidade-Escola.
As análises por nós realizadas levam à constatação de que o foco do curso
de Pedagogia não está relacionado à aprendizagem de conhecimentos de áreas
específicos e seu ensino. As disciplinas e metodologias desenvolvidas neste curso
estão voltadas para discussões sobre a educação e textos com reflexões sobre a
formação geral do professor, sua postura e suas escolhas pedagógicas.
Talvez as reflexões mais superficiais dos estagiários em seus relatos, sejam
decorrentes do pouco conhecimento matemático para ensinar essa área, fruto do
próprio foco do curso de Pedagogia que não se preocupa com a formação para as
diferentes áreas com as quais o professor do Ensino Fundamental, por este motivo
chamado de professor polivalente, deverá trabalhar.
Consideramos essencial que a Universidade reveja o foco do curso de
Pedagogia e que o mesmo seja voltado para a formação do professor. Parece-nos
que não está sendo levado em conta que o curso de Pedagogia é atualmente, o
único curso que forma professores para os anos iniciais do Ensino Fundamental, o
que pede uma formação que ultrapasse a formação geral e direcione os
conhecimentos dos alunos para a formação específica.
238
Esta formação a nosso ver, em se tratando do ensino de Matemática, deve
focar nos conhecimentos matemáticos e para o ensino de Matemática discutidos nas
disciplinas FME de Matemática; nos conhecimentos para o ensino desenvolvidos e
nas articulações entre teoria e prática propiciadas nas aulas de Prática de Ensino; e
nas orientações estabelecidas para a realização do Estágio com relação à
Matemática e nas observações feitas a partir destas orientações.
E com relação à realização do estágio, percebemos que a postura do
estagiário depende também da postura do professor que acompanha. Se o
conhecimento “requer uma ação transformadora e implica em invenção e em
reinvenção”, o aluno necessita de supervisão e orientação nesta ação, para que o
momento do estágio propicie aprendizagens significativas para o ensino de
Matemática.
5.5
Considerações e contribuições da pesquisa
Consideramos que o objetivo geral desta investigação, tal seja analisar
portfólios de cinco estudantes do curso de Pedagogia, com o propósito de identificar
“se” e “como” os estágios contribuem para estes alunos ensinarem Matemática, a
partir dos registros nesses portfólios, foi alcançado.
Pudemos perceber que os estágios têm grande potencial formativo,
dependendo de diferentes variantes que influenciam esta formação, conforme
citamos, não somente o próprio estagiário, mas todo o contexto relacionado a este
estágio, como as normas estabelecidas pela instituição formadora, os professores
do curso de Pedagogia, o professor orientador do estágio, a gestão das escolas que
recebem os estagiários e por fim os professores que os acolhem em suas aulas.
Mas o estágio, embora importante, não pode ser o único responsável pela
formação do professor. Há necessidade de a Universidade estabelecer parceria com
as escolas, nas orientações para esta realização tanto nas observações dos
estagiários quanto na postura e contribuições dos professores que os recebem.
A identificação do perfil dos alunos da Pedagogia, sujeitos da pesquisa, e
suas relações com a Matemática nos mostraram que, embora a maioria deles tenha
uma história de dificuldade com esta disciplina, este fato não influencia a busca pelo
239
conhecimento e a consciência da necessidade de aprendizagem para o ensino. No
entanto, constatamos um avanço pequeno e atribuimos este fato à formação
inadequada.
Por outro lado, o perfil das escolas e dos professores que recebem esses
alunos como estagiários indicam que somente uma diretora se mostrou acessível a
parcerias e à abertura da escola para diálogo com a Universidade a fim de colaborar
com a formação dos estagiários e de seus próprios professores. Com relação às
professoras, também somente uma delas admite suas fragilidades no ensino de
Matemática e mostra-se interessada em cursos de formação para aperfeiçoar sua
prática. Esta professora também foi a única que se interessou por uma formação
mais específica para receber os estagiários, citando inclusive que por sua conta
procura orientá-los em sua formação.
Percebemos
que
embora
os
alunos
mostrem
dificuldades
no
acompanhamento e análises das atividades matemáticas apresentadas nas aulas
observadas, houve aprendizagens no estágio, na medida em que procuravam
estabelecer relações entre o que aprenderam no curso de Pedagogia e nos
encontros
do
Programa
Observatório
da
Educação,
com
os
conteúdos
desenvolvidos pelas professoras no estágio. Nesse sentido podemos afirmar que o
estágio contribuiu para a formação desses alunos.
Ao iniciarmos esta investigação, tínhamos estabelecidas sete questões
diretrizes que pretendíamos responder:
- Qual é a organização da disciplina Estágio Curricular Supervisionado nos
anos iniciais do Ensino Fundamental no curso de Pedagogia pesquisado?
- Qual é o perfil dos estagiários do curso analisado? Quais são as relações
desses estagiários com a Matemática e seu ensino?
- Qual é o perfil das escolas e das professoras que recebem os estagiários
do curso de Pedagogia em questão?
- Que relações com a Matemática e seu ensino têm os professores que
recebem os estagiários?
240
- O que revelam as aulas de Matemática desses professores, observadas
pelos estagiários?
- Que reflexões fazem os estagiários ao observar as aulas de Matemática
em relação aos conteúdos abordados e metodologias utilizadas?
- Que reflexões fazem os estagiários sobre suas necessidades para ensinar
Matemática?
Entendemos
que
as
questões
diretrizes
estabelecidas
para
o
encaminhamento da pesquisa foram respondidas ao longo deste trabalho, nas
pesquisas realizadas, nas leituras e análises dos portfólios dos estagiários e em
nossas reflexões finais.
E a partir das respostas a estas questões, encontramos subsídios para
responder nossa questão da pesquisa: “Que mudanças são necessárias à
organização e ao desenvolvimento dos estágios para melhorar a formação inicial
dos pedagogos para ensinar Matemática?”
Entendemos que as mudanças devem ter início nos cursos de Pedagogia, a
partir dos conteúdos trabalhados nas disciplinas ligadas ao ensino de Matemática e
da organização da grade curricular deste curso. Na Universidade em questão, as
disciplinas FME de Matemática I e II devem propiciar aos alunos a oportunidade de
dominar tanto os conteúdos que deverão ensinar às crianças no Ensino
Fundamental como os processos e métodos para o ensino desses conteúdos.
Em suma, é preciso que o desenvolvimento destas disciplinas possibilite que
os alunos se apropriem dos conhecimentos dos conteúdos matemáticos, mas
também do conhecimento para o ensino do conteúdo matemático.
Além disso, ainda na Universidade, é preciso que haja um direcionamento
da realização do estágio para as disciplinas que farão parte da atuação do professor
polivalente, e não só para observações da postura dos professores, focando nos
conteúdos, atividades e prática docente.
Também os planos de ensino da disciplina Prática de Ensino e Estágio
devem ser revistos, a fim de que se privilegie a reflexão como importante
241
componente da formação docente. Além disso, conforme citamos anteriormente, a
localização de tais disciplinas na grade com relação às disciplinas de FME de
Matemática I e II, não favorece a reflexão e articulações entre teoria e prática.
Estas mudanças institucionais devem vir acompanhadas de mudanças na
postura dos professores orientadores, que deveriam na disciplina Prática de Ensino
e nas orientações do Estágio focar na formação do professor polivalente e direcionar
as observações do estágio para esta formação.
No que diz respeito ao professor orientador, ressaltamos as atividades
burocráticas que devem ser cumpridas na aula de Prática de Ensino, as quais
dificultam momentos de maior discussão sobre a formação dos alunos.
Relembramos que são atribuídas 40 horas para a disciplina Prática de
Ensino, as quais devem ser utilizadas também para orientações do estágio,
recebimento e conferência de documentos, e orientações sobre a elaboração do
Relatório de Estágio. Estas orientações, em sua grande maioria não podem ser
generalizadas para todos os alunos, demandando tempo para atendimento
individual, o que especialmente pelo número de alunos alocados em cada sala de
aula, diminui sensivelmente as horas disponíveis para as discussões de Prática de
Ensino.
Entendemos ainda que deve haver também um diálogo entre a Universidade
e as unidades escolares que recebem os estagiários, no estabelecimento de ações e
posturas que transformem o estágio em momento real de formação, conforme já
discutimos sobre a parceria Universidade-Escola.
Neste caso, a necessidade de cursos de formação para receber os
estagiários propostos aos professores, só foi reconhecida por um deles. Este seria
mais um caminho efetivo para a melhoria da formação inicial dos pedagogos, o que
pode ser proposto a partir de uma parceria entre Universidade e escolas no
oferecimento de tais cursos.
Constatamos que os professores que receberam os estagiários não
realizaram cursos de capacitação para ensinar Matemática nos últimos anos e
muitas vezes propõem atividades indicadas em currículos das décadas e 70/80.
242
Entendemos, assim como Freire (2004) que “Ninguém começa a ser
educador numa certa terça-feira às quatro horas da tarde [...] A gente se faz
educador; a gente se forma como educador permanente, na prática e na reflexão
sobre a prática”.
Portanto, ainda que todas as nossas sugestões sejam colocadas em prática,
ainda assim é preciso a reflexão constante dos professores e de cada estagiário,
que não têm data marcada para começar a ser educador, mas devem estar em
constante reflexão sobre sua prática num processo permanente de formação.
As constatações verificadas nesta pesquisa, assim como a busca por
contribuições para superar os desafios apresentados, nos proporcionaram
momentos
de
alegrias,
tristezas,
indignações,
surpresas,
esperanças
e
desesperanças, nas leituras e análises das situações descritas por nossos
estagiários e em nossas próprias reflexões.
Aprendemos muito com este trabalho e esperamos que o mesmo
proporcione a todos que o lerem uma nova perspectiva, reflexões e novas
aprendizagens acerca da realização dos estágios e da formação do professor dos
anos iniciais. Esperamos continuar aprendendo na busca de novos conhecimentos e
desafios na constituição de nossas ações como educadora.
Nossas reflexões nos levam ao trecho (MORIN, 2000) que define nosso
sentimento diante das constatações reveladas nesta investigação.
Somos constantemente surpreendidos pelo inesperado. Surpreendidos
porque “nos instalamos de maneira segura em nossas teorias e ideias, e estas não
têm estruturas para acolher o novo”.
“Não podemos jamais prever como (o novo) se apresentará”, razão pela qual
no decorrer desta pesquisa encontramos novos caminhos que nos levavam a
mudanças de rumos, de focos, de visão. Abrimo-nos às novas ideias, nos
reestruturamos em nossas convicções para acolher as constatações verificadas
neste trabalho.
“Entretanto, o novo brota sem parar... mas deve-se esperar sua chegada, ou
seja, esperar o inesperado”.
243
Desta forma, nosso desafio, como educadora e formadora de professores no
curso de Pedagogia continua ainda mais intenso a partir desta pesquisa, direcionado
agora não só ao fortalecimento de nosso próprio trabalho, mas à socialização com
os demais formadores deste curso e ao diálogo com a Universidade, para que
possamos discutir teorias e renovar ideias e ações que possam acolher o novo no
momento em que este se apresentar, esperar pelo inesperado e melhorar cada vez
mais o conhecimento, a aprendizagem e a formação dos professores que ensinam
Matemática.
245
REFERÊNCIAS
ALARCÃO, Isabel. Professores reflexivos em uma escola reflexiva. São Paulo:
Cortez, 2003.
BALL, Deborah Loewenberg. Content knowledge for teaching: what makes it
special? Journal of Teacher Education, v. 59, n. 5, p. 389-407, Nov./Dec. 2008.
BARDIN, Laurence. Análise de conteúdo. Lisboa: Edições 70, 2007.
BRASIL. Lei n° 9394, de 20 de dezembro de 1996. Fixa as diretrizes e bases da
educação nacional. Disponível em:
<http://www.planalto.gov.br/ccivil_03/leis/l9394.htm>. Acesso em: 15 ago. 2013.
______. Lei nº 11.788, de 25 de setembro de 2008. Dispõe sobre o estágio de
estudantes [...] e dá outras providências. Disponível em:
<http://www.planalto.gov.br/ccivil_03/_ato2007-2010/2008/lei/l11788.htm>. Acesso
em: 15 ago. 2013.
BUKOWITZ, Natercia de Souza Lima. Práticas investigativas em matemática:
uma proposta de trabalho no curso de pedagogia. 2005. 140 f. Tese (Doutorado em
Educação)–Universidade Federal do Rio de Janeiro, Rio de Janeiro, 2005.
Disponível em <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 05
dez. 2012.
CADERNOS de apoio e aprendizagem: matemática: programa de orientações
curriculares, 1º ao 5º ano. São Paulo: Fundação Padre Anchieta; PMSP/SE, 2010. 5
v.
CARVALHO, Gislene Teresinha Rocha Delgado de; UTUARI, Solange dos Santos
(Org.). Formação de professores e estágios supervisionados: algumas veredas.
São Paulo: Andross, 2007.
CERVO, Amado Luiz; BERVIAN, Pedro Alcino; SILVA, Roberto da. Metodologia
científica. 6. ed. São Paulo: Pearson Prentice Hall, 2007.
CHAMOSO SÁNCHEZ, José Maria; CÁCERES GARCIA, Maria José; AZCÁRATE
GODED, Pilar. La reflexión como elemento de formación docente en
matemáticas: análisis e instrumentos. In: ClAEM, 13., 2001, Recife. Disponível em:
<http://www.cimm.ucr.ac.cr/ocs/index.php/xiii_ciaem/xiii_ciaem/paper/viewFile/2735/
1151>. Acesso em: 20 out. 2013.
CHIZZOTTI, Antonio. Pesquisa qualitativa em ciências humanas e sociais.
Petrópolis: Vozes, 2006.
CONSELHO NACIONAL DE EDUCAÇÃO. Conselho Pleno. Parecer CNE/CP nº 21,
6 de agosto de 2001. Duração e carga horária dos cursos de formação de
professores da educação básica, em nível superior, curso de licenciatura, de
graduação plena. Retificado pelo Parecer CNE/CP nº 28/2001. Disponível em:
246
<http://portal.mec.gov.br/dmdocuments/cnecp_212001.pdf>. Acesso em: 20 ago.
2013.
______. Conselho Pleno. Resolução CNE/ CP nº 1, de 15 de maio de 2006. Institui
as diretrizes curriculares nacionais para o curso de graduação de pedagogia,
licenciatura. Diário Oficial da União, Brasília, DF, 16 maio 2006. Seção 1, p. 11.
COSTA, Shirley Conceição Silva da. O professor que ensina matemática nos
anos iniciais: limites e possibilidades de um curso de licenciatura em pedagogia.
2011. 170 f. Dissertação (Mestrado em Ensino de Ciências e Matemática)–
Universidade Cruzeiro do Sul, São Paulo, 2011.
CURI, Edda. A matemática e os professores dos anos iniciais. São Paulo: Musa,
2005. (Biblioteca Aula Musa Educação Matemática; v.2).
______. Prática de ensino e estágio supervisionado nos cursos de licenciatura plena
em matemática. In: CARVALHO, Gislene Teresinha Rocha Delgado de; UTUARI,
Solange dos Santos (Org.). Formação de professores e estágios
supervisionados: relatos, reflexões e percurso. São Paulo: Andross, 2006. p. 139147
______. (Org). Professores que ensinam matemática: conhecimentos, crenças e
práticas. São Paulo: Terracota, 2010.
______. A formação inicial de professores para ensinar matemática: algumas
reflexões, desafios e perspectivas. REMATEC: Revista de Matemática, Ensino e
Cultura, Natal, v. 6, n. 9, p. 75-94, jul. 2011.
______. Contribuições de um grupo colaborativo no desenvolvimento profissional de
seus participantes. In: ______; NASCIMENTO, Julia Cassia P. (Org). Educação
matemática: grupos colaborativos, mitos e práticas. São Paulo: Terracota, 2012.
FERNANDES, Vera Maria Jarcovis. Formação inicial de professores que atuam
nos anos iniciais do ensino fundamental: a matemática em questão. 2012. 222 f.
Tese (Doutorado em Ensino de Ciências e Matemática)–Universidade Cruzeiro do
Sul, São Paulo, 2012.
FREIRE, Paulo. Pedagogia da autonomia. São Paulo: Paz e Terra, 2004.
GADOTTI, Moacir. Boniteza de um sonho: ensinar-e-aprender com sentido. Novo
Hamburgo: Feevale, 2003. 80 p.
GIL, Antonio Carlos. Como elaborar projetos de pesquisa. 4. ed. São Paulo: Atlas,
2008.
GOLDENBERG, Mirian. A arte de pesquisar: como fazer pesquisa qualitativa em
ciências sociais. 8. ed. Rio de Janeiro: Record, 2004.
HAYDT, Regina Célia Cazaux. Curso de didática geral. 7. ed. São Paulo: Ática,
2002. (Série Educação).
247
HERNÁNDEZ, Fernando. Transgressão e mudança na educação: os projetos de
trabalho. Trad. Jussara Haubert Rodrigues. Porto Alegre: Artmed,1998.
LUDKE, Menga; ANDRÉ, Marli Elisa Dalmazo Afonso de. Pesquisa em educação:
abordagens qualitativas. São Paulo: E. P. U., 1986. 99 p. (Temas básicos de
educação e ensino).
MASETTO, Marcos Tarciso. Didática: a aula como centro. 3. ed. São Paulo: FTD,
1996.
MELLO, Beatriz Consuelo Kuroishi. Análise dos conhecimentos matemáticos
desenvolvidos em um curso de pedagogia: um estudo de caso. 2008. 276 f.
Dissertação (Mestrado em Ensino de Ciências e Matemática)–Universidade Cruzeiro
do Sul, São Paulo, 2008.
MIOTO, Rodrigo. As inter-relações entre universidade e escola básica: o estágio
e a prática de futuros professores das séries iniciais na construção de
conhecimentos pedagógicos da matemática. 2008. Dissertação (Mestrado
Profissionalizante)–Pontifícia Universidade Católica de São Paulo, São Paulo, 2008.
MORIN, Edgar. Os sete saberes necessários à educação do futuro. Trad.
Catarina Eleonora F. da Silva e Jeanne Sawaya. 2. ed . São Paulo: Cortez; Brasília,
DF: UNESCO, 2000.
PICONEZ, Stela C. Berhtolo. A prática de ensino e o estágio supervisionado. 5.
ed. Campinas: Papirus, 2000. p. 15-74.
PIMENTA, Selma Garrido (Org.). Saberes pedagógicos e atividade docente. 3.
ed. São Paulo: Cortez, 2002.
______. O estágio na formação de professores: unidade teoria e prática? 9. ed.
São Paulo: Cortez, 2010.
______. Professor reflexivo: construindo uma crítica. In: ______; GHEDIN, Evandro
(Org.). Professor reflexivo no Brasil: gênese e crítica de um conceito. 4. ed. São
Paulo: Cortez, 2006.
______; LIMA, Maria Socorro Lucena. Estagio e docência. São Paulo: Cortez,
2004.
PONTE, João Pedro. Estudos de caso em educação matemática. Bolema, v. 19, n.
25, p. 105-132, 2006.
______; SERRAZINA, Maria de Lurdes. Didáctica da matemática do 1º ciclo.
Lisboa: Universidade Aberta, 2000. 260 p.
SCHÖN, Donald. Educando o profissional reflexivo: um novo design para o
ensino e a aprendizagem. Porto Alegre: Artmed, 2000.
SERRAZINA, Maria de Lurdes. A formação para o ensino de matemática:
perspectivas futuras. Lisboa: Inafop, 2001. p. 9-20.
248
______. Reflexão, conhecimento e práticas lectivas em matemática num contexto de
reforma curricular no 1º ciclo. Quadrante, Lisboa, v. 8, n, 1-2, p.139-167, 1999.
SHULMAN, Lee. Those who understand: knowledge growth in teaching. Educational
Research, v. 15, n. 2, p. 4-14, 1986.
TARDIF, Maurice. Saberes docentes e formação profissional. Petrópolis, RJ:
Vozes, 2002.
YIN, Robert K. Estudo de caso: planejamento e métodos. 3. ed. Porto Alegre:
Bookman, 2005.
ZIMER, Tania Teresinha Bruns. Aprendendo a ensinar matemática nas séries
iniciais do ensino fundamental. 2008. 308 f. Tese (Doutorado em Educação)–
Universidade de São Paulo, São Paulo, 2008.
249
BIBLIOGRAFIA CONSULTADA
ALARCÃO, Isabel (Org.). Professores reflexivos em uma escola reflexiva. Porto:
Porto Editora, LDA, 1996
ANDRADE, Rosana Cássia Rodrigues. Prática de ensino e estágio
supervisionado: um estudo sobre as produções no período 2003-2008. Resumo da
Dissertação de Mestrado. Universidade de Uberaba, 2009. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
ANTUNES, Francieli Cristina Agostinetto. A relação com o saber e o estágio
supervisionado em matemática. Resumo da Dissertação de Mestrado.
Universidade Estadual de Londrina, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
ARAÚJO, Geiza Torres Gonçalves. Estágio supervisionado, espaço e tempo de
formação do pedagogo para a atuação profissional. Resumo da Dissertação de
Mestrado. Universidade Federal de Juiz De Fora, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01 dez. 2012.
ARAÚJO, Raimundo Dutra. O estágio supervisionado no curso de pedagogia da
UESPI: articulação teoria-prática na formação docente. Resumo da Dissertação de
Mestrado. Fundação Universidade Federal do Piauí, 2009. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01 dez. 2012.
ARNONI, Maria Eliza Brefere. A prática do estagiando do magistério na
perspectiva da práxis educativa: uma análise do estágio supervisionado do
CEFAM de Jales. Resumo da Tese de Doutorado. Universidade Estadual de
Campinas, 2001. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
AROEIRA, Kalline Pereira. O estágio como prática dialética e colaborativa: a
produção de saberes por futuros professores. Resumo da Tese de Doutorado.
Universidade de São Paulo, 2009. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
BARBOSA, Aparecida Alice. A formação em pedagogia na Fafi/Unipac: o estágio
curricular em questão. Resumo da Dissertação de Mestrado. Universidade Católica
de Petrópolis, 2006. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
BARILLARI, Cleide Aparecida Martins. A busca da unidade teoria e prática: a
formação de professora no contexto do estágio curricular supervisionado. Resumo
da Dissertação de Mestrado. Universidade de Uberaba, 2008. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
BRASIL. Maria Ghisleny de Paiva. A contribuição do estágio supervisionado
para a formação reflexiva do pedagogo. Resumo da Dissertação de Mestrado.
250
Universidade Federal do Rio Grande do Norte, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
BUENO, Luzia. A construção de representações sobre o trabalho docente: o
papel do estágio. Resumo da Tese de Doutorado. Pontifícia Universidade Católica
de São Paulo, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
CAMPOS, Maria de Lourdes. Estágio supervisionado e formação de
profissionais da educação do curso de Pedagogia do CFP/UFCG. Resumo da
Dissertação de Mestrado. Universidade Federal da Paraíba/João Pessoa, 2003.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
CARDOSO, Bia (Org.). Ensinar: tarefa para profissionais. Rio de Janeiro: Record,
2007.
CARMO, Maria Claudia Silva. Formar docentes e vincular teoria e prática: a
complexidade do possível. Resumo da Dissertação de Mestrado. Universidade do
Vale do Rio dos Sinos, 2001. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
CARVALHO, Gislene Teresinha Rocha Delgado de; ROCHA, Vera Helena Rosa
(Org.). Formação de professores e estágios supervisionados: relatos e
reflexões. São Paulo: Andross, 2004.
______; ATUARI, Solange (Org.). Formação de professores e estágios
supervisionados: relatos, reflexões e percursos. São Paulo: Andross, 2006.
CARVALHO, Maria Lucia Alvarenga. Estágio supervisionado: espaço e tempo de
aprendizagem da docência. Resumo da Dissertação de Mestrado. Pontifícia
Universidade Católica de Campinas, 2004. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
CARVALHO, Mirtes Gonçalves Honório. Estágio supervisionado na formação de
professores em serviço dos anos iniciais do ensino fundamental. Resumo da
Tese de Doutorado. Universidade Federal do Rio Grande do Norte, 2011. Disponível
em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
CASTRO Franciana Carneiro. Aprendendo a ser professor(a) na prática: estudo
de uma experiência em prática de ensino de matemática e estágio supervisionado.
Resumo da Dissertação de Mestrado. Universidade Estadual de Campinas, 2002.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
CONSELHO NACIONAL DE EDUCAÇÃO. Conselho Pleno. Parecer CNE/CP nº 5
de 13 de dezembro de 2005. Diretrizes curriculares nacionais para o curso de
pedagogia. Reexaminado pelo Parecer CNE/CP nº 3/2006, publicado no D.O.U. de
15/05/2006. Disponível em:
<http://portal.mec.gov.br/cne/arquivos/pdf/pcp05_05.pdf>. Acesso em: 16 ago. 2013.
251
CONSELHO NACIONAL DE EDUCAÇÃO. Conselho Pleno. Resolução CNE/CP nº
2, de 19 de fevereiro de 2002. Institui a duração e a carga horária dos cursos de
licenciatura, de graduação plena, de formação de professores da educação básica
em nível superior. Diário Oficial da União, Brasília, DF, 4 mar. 2002. Seção 1, p. 9.
CORTE, Marilene Gabriel Dalla. O estágio curricular e a formação de qualidade
do pedagogo. Resumo da Tese de Doutorado. Pontifícia Universidade Católica do
Rio Grande do Sul, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
CRUZ, Maria Aparecida Silva. Uma proposta metodológica para a realização do
estágio supervisionado em um curso de formação inicial de professores de
matemática: limites e possibilidades. Resumo da Tese de Doutorado. Fundação
Universidade Federal de Mato Grosso do Sul, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
CRUZ, Valdelise Ramon. O estágio na formação do professor: relato de
supervisores de estágio. Resumo da Dissertação de Mestrado. Universidade de
Sorocaba, 2004. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
CUSTODIO, Cândida Maria de Sousa. O papel da escola com a formação inicial
do professor no momento de estágio: limites, desafios e perspectivas. Resumo da
Dissertação de Mestrado. Universidade Federal de Pelotas, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
DINIZ, Marise Soares. A aprendizagem da docência em contextos de formação.
Resumo da Dissertação de Mestrado. Universidade de Uberaba, 2006. Disponível
em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
FELICE, José. Aprender a ser professor: uma contribuição da prática de ensino de
matemática. Resumo da Dissertação de Mestrado. Universidade Federal de São
Carlos, 2002. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
FERREIRA, Cláudia Márcia da Silva. Interações discursivas entre alunos e
estagiários em salas de aula: contribuições ao processo de desenvolvimento
profissional de professores de matemática. Resumo da Dissertação de Mestrado.
Universidade Federal de Minas Gerais, 2009. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
FIGUEIREDO, Jocinete das Graças. A prática de ensino e o estágio
supervisionado no curso de pedagogia da universidade do estado de mato
grosso: uma análise a partir dos estudos culturais. Dissertação de Mestrado.
Universidade Federal do Rio Grande do Sul, 2001. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
FONSECA, Selma Carvalho. Análise de uma proposta de implantação de estágio
na formação de professores - possibilidades e limites. 01/08/2004. Resumo da
Dissertação de Mestrado. Universidade Estadual de Campinas, 2004. Disponível
em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
252
FRANÇA, Dimair de Souza. A constituição da docência: o que se ensina e o que
se aprende sobre o fazer docente na relação entre professoras em exercício e
futuras professoras. Resumo da Tese de Doutorado. Universidade Est. Paulista Júlio
de Mesquita Filho/Araraquara, 2005. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
GALVÃO, Ana Karina de Araújo. Narrativas de aprendizagens no processo
formativo de licenciandos do curso de pedagogia. Resumo da Dissertação de
Mestrado. Universidade Federal de Mato Grosso, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01 dez. 2012.
GODOY, Anterita Cristina de Sousa. Aprendendo a ser formadora, ensinando a
ser professora: a prática de ensino como trabalho e investigação no processo de
formação de professores da educação básica. Resumo da Tese de Doutorado.
Universidade Metodista de Piracicaba, 2005. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
GOLDANI, Andreia. A formação inicial de professores em matemática:
necessidades da prática pedagógica na educação básica. Resumo da Dissertação
de Mestrado. Universidade Federal do Rio Grande do Sul, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
GOSMATTI, Anderson. Prática de ensino na perspectiva de professores de
estágio curricular supervisionado de matemática. Resumo da Dissertação de
Mestrado. Universidade Federal do Paraná, 2010.
GUIDINI, Siane Aparecida. O futuro professor de matemática e o processo de
identificação com a profissão docente: um estudo sobre as contribuições da
prática como componente curricular. Resumo da Dissertação de Mestrado
Profissionalizante. Pontifícia Universidade Católica de São Paulo, 2010. Disponível
em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
GUIMARÃES, Ana Paula de A. Saraiva. A prática reflexiva no estágio
supervisionado dos cursos de formação de professores de matemática da
Universidade Estadual de Goiás (UEG). Resumo da Dissertação de Mestrado.
Universidade Federal de Goiás, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
HAYAMA, Priscila Mayumi. Alunos-professores e professores-alunos: o trabalho
em grupo no estágio supervisionado. Resumo da Dissertação de Mestrado.
Universidade de São Paulo, 2008. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
HISSA, Jeanete Jorge. Os desafios do estágio curricular supervisionado: uma
alternativa no processo de formação de professores da educação básica. Resumo
da Dissertação de Mestrado. Universidade Cidade de São Paulo, 2005. Disponível
em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
LARGO, Vanessa. As dificuldades pedagógicas dos professores de matemática
no desenvolvimento profissional: subsídios para a disciplina de prática de ensino.
Resumo da Dissertação de Mestrado. Universidade Estadual de Londrina, 2004.
253
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
LAZZARIN, Sandra Regina. Estágio: eixo articulador da formação inicial de
professores para os primeiros anos da educação básica. Resumo da Tese de
Doutorado. Pontifícia Universidade Católica de São Paulo, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
LENZI, Giovana da Silva. Prática de ensino em educação matemática: discursos
e regulações da prática pedagógica dos futuros professores de matemática. Resumo
da Dissertação de Mestrado. Universidade Federal do Rio Grande do Sul, 2008.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
LIBANEO, Jose Carlos. Pedagogia e pedagogos, para que? São Paulo: Cortez,
2002.
LIMA, José Ivanildo. Estágio supervisionado na licenciatura em matemática:
possibilidades de colaboração. Resumo da Dissertação de Mestrado. Universidade
Federal do Pará, 2008. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
LIMA, Maria Divina Ferreira. Formação de docentes em serviço: o processo
formativo da experiência de estagio supervisionado. Resumo da Tese de Doutorado.
Universidade Federal do Rio Grande Do Norte, 2005. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
LOPES, Anemari Roesler Luersen Vieira. A aprendizagem docente no estágio
compartilhado. Resumo da Tese de Doutorado. Universidade de São Paulo, 2004.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
LUDWIG, Paula Isabel. Formação inicial de professores de matemática:
situações vivenciadas pelos alunos na realização do estágio. Resumo da
Dissertação de Mestrado. Universidade Luterana do Brasil, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
MAGALHÃES, Elisa Gomes. Estágio supervisionado e aprendizagens da
docência. Resumo da Dissertação de Mestrado. Universidade Federal de São
Carlos, 2009. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
MARTIN, Adriana Ofretorio de Oliveira. Significados e sentidos sobre os
processos formativos de estudantes de pedagogia. Resumo da Dissertação de
Mestrado. Universidade Estadual de Campinas, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
MEDEIROS, Claudete Marques. Estágio supervisionado: uma influência na
constituição dos saberes e do professor de matemática na formação inicial. Resumo
da Dissertação de Mestrado. Universidade Federal do Pará, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
254
MENDES, Bárbara Maria Macedo. A prática de ensino e o estágio
supervisionado na construção de saberes e competências didáticopedagógicas: o caso da UFPI. Resumo da Tese de Doutorado. Universidade
Federal do Ceará, 2005. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
MENEZES, Paulo Henrique Dias. Desenvolvimento profissional de professores:
a influência da vivência em um grupo colaborativo. Resumo da Tese de Doutorado.
Universidade Federal de Minas Gerais, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
MILANESI, Irton. A interdisciplinaridade no cotidiano dos professores: avaliação
de uma proposta curricular de estágio. Resumo da Tese de Doutorado. Universidade
Estadual de Campinas, 2004. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
MIRA, Marilia Marques. O papel do estágio supervisionado para o exercício
profissional dos pedagogos escolares: possibilidades e desafios. Resumo da
Dissertação de Mestrado. Pontifícia Universidade Católica do Paraná – Educação,
2011. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
MOTTA, Josiani Marques. As disciplinas de metodologia de ensino e estágio
supervisionado na formação do professor de matemática: saberes e
dificuldades. Resumo da Dissertação de Mestrado. Universidade Federal de Santa
Catarina, 2006. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
NEVES, Cintia Silva de Vasconcelos. Possíveis contribuições do estágio
curricular supervisionado para a construção da identidade profissional de
professor. Resumo da Dissertação de Mestrado. Universidade Federal de Pelotas,
2011. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
NONATO, Karla Jocelya. Estágio supervisionado em matemática: contribuições
para a formação de professores de matemática. Resumo da Dissertação de
Mestrado. Fundação Universidade Federal de Mato Grosso do Sul, 2011. Disponível
em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
NUNES, Maria Fernanda Villena Castro. Do ensaio à encenação: o estágio
curricular supervisionado na perspectiva dos alunos dos 7° e 8° períodos do curso
de Pedagogia. Resumo da Dissertação de Mestrado. Universidade do Vale do Itajaí,
2005. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
OLIVEIRA, Iracema de Miranda. Formação de professores de matemática: um
olhar sobre o estágio curricular supervisionado. Resumo da Dissertação de
Mestrado Profissionalizante. Pontifícia Universidade Católica de São Paulo, 2008.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
255
OLIVEIRA, Sandra Mara Vieira. Formação da identidade docente: estágio
supervisionado, memórias e representações sociais. Resumo da Dissertação de
Mestrado. Fundação Universidade Federal de Sergipe, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
OLIVEIRA. Raquel Gomes. Estágio supervisionado participativo na licenciatura
em matemática, uma parceria escola-universidade: respostas e questões.
Resumo da Tese de Doutorado. Universidade de São Paulo, 2006. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
PASSERINI, Gislaine Alexandre. O estágio supervisionado na formação inicial
do professor de matemática na ótica de estudantes do curso de licenciatura
em matemática da UEL. Resumo da Dissertação de Mestrado. Universidade
Estadual de Londrina, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
PERINI, Edla Yara Priess. O papel do estágio curricular supervisionado na
formação inicial de professores: um olhar crítico dos egressos e professores do
curso de pedagogia. Resumo da Dissertação de Mestrado. Universidade do Vale do
Itajaí, 2006. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
PETERNELLA, Alessandra. A relação teoria e prática na formação do pedagogo:
contribuições da teoria histórico-cultural. Resumo da Dissertação de Mestrado.
Universidade Estadual de Maringá, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
PIERRO, Gianine Maria de Souza. Arquitetura docente no curso de pedagogia:
dialogando com ciências e arte nas práticas de formação em estágio supervisionado
e museus. Resumo da Tese de Doutorado. Fundação Oswaldo Cruz, 2009.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
PILONETTO, Roseli de Fátima Rech. Mobilizando processos de formação: a
experiência docente com os estágios supervisionados. Resumo da Dissertação de
Mestrado. Universidade Estadual de Campinas, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
PONTE, Adriana Eugênio de Souza. O saber e o fazer de estudantes concluintes
do curso de pedagogia na docência dos anos iniciais do ensino fundamental.
Resumo da Dissertação de Mestrado. Universidade do Estado da Bahia, 2008.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
PONTE, João Pedro da; SERRAZINA, Maria de Lurdes. Professores e formadores
investigam a sua própria prática: o papel da colaboração. Zetetiké, v. 11, n. 20,
jul./ago. 2003. Disponível em: <http://repositorio.ul.pt/bitstream/10451/3992/1/03Ponte-Serrazina%20(Zetetike)pdf>. Acesso em: 7 nov. 2013.
RAYMUNDO, Gislene Miotto Catolino. Prática de ensino e estágio
supervisionado: eixos articuladores da formação inicial dos professores da
256
educação básica. Resumo da Tese de Doutorado. Pontifícia Universidade Católica
de São Paulo, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
RIBEIRO, Flávia Dias. A aprendizagem da docência na prática de ensino e no
estágio: contribuições da teoria da atividade. Resumo da Tese de Doutorado.
Universidade de São Paulo, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
ROCHA, Vera Helena Rosa. Estágios pedagógicos como práxis política
renovadora: um estudo avaliativo desenvolvido na Universidade Cruzeiro do Sul.
Resumo da Dissertação de Mestrado. Pontifícia Universidade Católica de Campinas,
2001. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso
em: 01dez. 2012.
ROSA, Marise Marçalina de Castro Silva. Tecendo uma manhã: o estágio
supervisionado no curso de pedagogia mediado pela extensão universitária. Resumo
da Tese de Doutorado. Universidade Est. Paulista Júlio de Mesquita Filho/Marilia,
2010. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
SACRAMENTO, Weverton Pereira. O estágio supervisionado como eixo central
da formação inicial de professores. Resumo da Dissertação de Mestrado.
Universidade Federal de Minas Gerais, 2003.
SALES. Claudemir Francelino. O estágio e a política de formação do educador:
um estudo a partir de programas e projetos da rede municipal de ensino do Recife.
Resumo da Dissertação de Mestrado. Universidade Federal De Pernambuco. 2011.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
SAMBUGARI, Márcia Regina do Nascimento. Socialização de futuros professores
em situações de estágio curricular. Resumo da Tese de Doutorado. Pontifícia
Universidade Católica de São Paulo, 2010. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SANTANA, Andréia da Cunha Malheiros. Realidade e ficção: o papel do estágio na
formação do educador. Resumo da Dissertação de Mestrado. Universidade Estadual
Paulista Júlio de Mesquita Filho/Araraquara, 2003. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SANTOS, Adriana Alves Pugas. O estágio como espaço de elaboração dos
saberes docente e a formação do professor. Resumo da Dissertação de
Mestrado. Universidade Est. Paulista Júlio de Mesquita Filho/Pr. Prudente, 2008.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
SANTOS, Edlauva Oliveira. A contribuição do estágio na construção dos
conhecimentos necessários ao exercício da docência no curso de pedagogia.
Resumo da Dissertação de Mestrado. Universidade Federal do Amazonas, 2009.
257
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
SANTOS, Helena Maria. O estágio curricular na formação de professores:
diversos olhares. Resumo da Dissertação de Mestrado. Pontifícia Universidade
Católica de São Paulo, 2004. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SANTOS, Lindomar Barros. Estágio supervisionado de educação infantil e anos
iniciais do ensino fundamental do curso de pedagogia – licenciatura: um estudo
de caso. Resumo da Dissertação de Mestrado. Universidade Católica Dom Bosco –
Educação, 2010. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
SANTOS, Maria Aparecida Modesto. Concepção pedagógica do estágio
supervisionado: o olhar dos docentes. Resumo da Dissertação de Mestrado.
Universidade Metodista de São Paulo, 2006. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SCHOLZ, Oswaldir Ehlke. Cubo de dificuldade como modelo referencial para o
estágio supervisionado de estudantes. Resumo da Dissertação de Mestrado.
Universidade Federal de Santa Catarina, 2002. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SHORES, Elizabeth F.; GRACE, Cathy. Manual de Portfólio: um guia passo a
passo para professores. Trad. Ronaldo Cataldo Costa. Porto Alegre: Artmed Editora,
2001.
SILVA, Wilson Rufino. A prática de ensino na formação docente: conversando
com os/as discentes-professores/as. Resumo da Dissertação de Mestrado.
Universidade Federal de Pernambuco, 2005. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SILVA. Amália Fenner. Significado das vivências no estágio em pedagogia:
séries iniciais. Resumo da Dissertação de Mestrado. Pontifícia Universidade Católica
do Rio Grande do Sul, 2002. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SILVEIRA, Denise Nascimento. O estágio curricular supervisionado na escola de
educação básica: diálogo com professores que acolhem estagiários. Resumo da
Tese de Doutorado. Universidade do Vale do Rio dos Sinos, 2008. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
SILVESTRE, Magali Aparecida. Estágios curriculares e práticas de ensino
supervisionadas: sentidos e significados apreendidos por alunas de um curso de
pedagogia. Resumo da Tese de Doutorado. Pontifícia Universidade Católica de São
Paulo, 2008. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
SOARES, Maria do Socorro. O estágio supervisionado na formação de
professores: sobre a prática como lócus da produção dos saberes docentes.
Resumo da Dissertação de Mestrado. Fundação Universidade Federal Do Piauí,
258
2010. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
SOUSA, Valéria de Fátima. A formação de professores e o estágio
supervisionado do curso de pedagogia: o caso da Faculdade do Noroeste de
Minas. Resumo da Dissertação de Mestrado. Universidade Federal de Goiás, 2004.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
STIVANIN, Neridiana Fabia. Estágio curricular: um estudo a partir das
significações sociais construídas pelas estagiárias sobre o curso de
pedagogia/CE/UFSM. Resumo da Dissertação de Mestrado. Univ. Federal de Santa
Maria, 2007. Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>.
Acesso em: 01dez. 2012.
ULHÔA, Andrea Alves. O estágio curricular supervisionado no curso de
pedagogia e a aprendizagem profissional da docência: alguns elementos para
reflexão. Resumo da Dissertação de Mestrado. Univ. Federal de Mato Grosso, 2007.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012.
VIANA, Marta Loula Dourado. A relação teoria e prática na formação do
licenciado em pedagogia: um estudo crítico da formação do professor reflexivopesquisador na proposta do curso de pedagogia da UNEB. Resumo da Dissertação
de Mestrado. Fundação Universidade Federal de Sergipe, 2011. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
VINCENSI, Mônica Felipin. Estágio supervisionado: a teoria e a prática no fazer
docente. Resumo da Dissertação de Mestrado. Univ. Regional do Noroeste do
Estado do Rio Grande do Sul, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
WIELEWICKI, Hamilton de Godoy. Prática de ensino e formação de professores:
um estudo de caso sobre a relação universidade-escola em cursos de licenciatura.
Resumo da Tese de Doutorado. Universidade Federal do Rio Grande do Sul, 2010.
Disponível em: <http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em:
01dez. 2012
WOLFF, Rosane. A formação inicial de professores de matemática: a pesquisa
como possibilidade de articulação entre teoria e prática. Resumo da Tese de
Doutorado. Universidade do Vale do Rio dos Sinos, 2007. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
ZAMARRENHO, Bruno Amalia Maria. As contribuições do estágio
supervisionado em matemática para a constituição de saberes docentes: uma
análise das produções acadêmicas no período de 2002 – 2007. Resumo da
Dissertação de Mestrado. Universidade São Francisco, 2009. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
ZANINI, Alessandra Renata. A relação teoria e prática na visão de professores
de um curso de licenciatura em matemática. Resumo da Dissertação de
259
Mestrado. Pontifícia Universidade Católica de Campinas, 2003. Disponível em:
<http://capesdw.capes.gov.br/capesdw/Teses.do>. Acesso em: 01dez. 2012.
261
APÊNDICES
262
APÊNDICE A - QUANTIDADE DE AULAS DE MATEMÁTICA POR
ANO DE ESCOLARIDADE
Ver pág.24
Figura 44 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 1º ano do Ensino Fundamental
Figura 45 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 2º ano do Ensino Fundamental
263
Figura 46 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 3º ano do Ensino Fundamental
Figura 47 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 4º ano do Ensino Fundamental
264
Figura 48 - Gráfico das Observações de Estágio das horas de aulas de
Matemática no 5º ano do Ensino Fundamental
265
APÊNDICE B – QUESTIONÁRIOS ESCOLA E PROFESSORES:
PERFIL DA ESCOLA
Ver pág. 77
Caro Diretor, venho solicitar sua colaboração para obtenção de dados descritivos de sua
escola, com a finalidade específica de elaboração de pesquisa no programa de Doutorado.
As informações aqui registradas são de suma importância para o desenvolvimento desta
pesquisa.
Escola: _______________________________________________________
Localização: __________________________________________________
Número de alunos atendidos: ________________________________
Organização da escola: 8 séries ou 9 anos
Breve descrição da situação sócio econômica das famílias dos alunos atendidos em sua
escola:
__________________________________________________________________________
__________________________________________________________________________
___________________________________________________________
IDEB da escola
2007: _________________
2009: _________________
2011: _________________
Sobre o número de salas e alunos para o Ensino Fundamental
ANO/SÉRIE Nº DE SALAS
Nº DE ALUNOS
1º
2º
3º
4º
5º
Sobre o número total de professores
ANO/SÉRIE PROFESSORES
PROFESSORES
FORMAÇÃO
FORMAÇÃO
NÍVEL MÉDIO
NÍVEL SUPERIOR
1º
2º
3º
4º
5º
QUANTIDADE POR
ÁREA
PEDAGOGIA
.......................
PEDAGOGIA
.......................
PEDAGOGIA
.......................
PEDAGOGIA
........................
PEDAGOGIA
.......................
266
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
Obrigada por sua atenção e colaboração com minha pesquisa.
267
APÊNDICE C – QUESTIONÁRIOS ESCOLA E PROFESSORES:
PERFIL DO PROFESSOR
Caro professor, venho solicitar sua colaboração para obtenção de dados sobre sua
formação e prática pedagógica, com a finalidade específica de elaboração de pesquisa no
programa de Doutorado. As informações aqui registradas são de suma importância para o
desenvolvimento desta pesquisa.
DADOS DE IDENTIFICAÇÃO
Nome: ______________________________________________Idade_______
Estado Civil __________________________ Nº de Filhos_________________
Formação _______________________________Tempo de atuação ________
Instituição e ano em que se formou ___________________________________
Tempo de atuação no Ensino Fundamental ____________________________
Enquadramento Funcional: ( ) Contratado ( ) Efetivo por concurso
Trabalha quantos períodos? (Especifique série/ano) _____________________
_______________________________________________________________
Série/Ano em que gosta de atuar ____________________________________
Por quê? _______________________________________________________
PARTE A – FORMAÇÃO – IDENTIDADE PROFISSIONAL
1) Conte um pouco da sua história, como foi sua vida escolar, onde você estudou? Enfim,
conte como você chegou ao Magistério e por quê escolheu ser professor(a)?
2)
O que você achou de sua formação? Seu curso lhe formou para trabalhar com
crianças?
3)
Como este curso lhe preparou para ensinar as crianças do Ensino Fundamental?
4)
Em que série/ano você se sente mais à vontade para atuar?
5)
Em relação às áreas do conhecimento, por exemplo, Alfabetização, Ciências,
Matemática entre outros, no que seu curso lhe preparou melhor? Por quê?
6)
Qual área você mais gosta de ensinar? Por quê?
7)
Você gosta de ensinar Matemática? Poderia citar um exemplo do que você mais gosta
na área da Matemática?
8)
Em sua opinião, o que é mais trabalhoso ou mais difícil para ensinar Matemática?
9)
O que você acredita ser preciso para ensinar Matemática para as crianças?
10) Que lacunas você sente em sua formação inicial para ensinar Matemática, ou seja, o
que precisaria ter sido trabalhado mais durante sua formação? Por quê?
11) Você tem feito, ou sente necessidade de fazer algum curso de formação continuada?
Em qual área?
12) O que lhe atrai e o que lhe dificulta em sua profissão?
13) Se tivesse chance mudaria de profissão? O que lhe faz permanecer nela?
268
14) O que lhe atrai e o que dificulta no ensino de Matemática?
15) Você conhece o IDEB de sua escola?
16) Você já viu em que nível de proficiência em Matemática encontram-se os alunos da
escola?
17) Quais são as metas propostas para melhoria da proficiência em Matemática?
PARTE B – PRÁTICA PEDAGÓGICA
1)
Você pode me descrever sua rotina diária, seu trabalho, como organiza as aulas de
Matemática, quantas vezes por semana ensina Matemática, durante quanto tempo?
2)
Como você planeja suas aulas de Matemática, quais materiais utiliza? Tem seu
planejamento em mãos?
3)
Dentre as atividades matemáticas propostas para seus alunos, o que você considera
mais importante? Por quê?
4)
Seus alunos se interessam pelas aulas de Matemática? O que você faz para que eles
se interessem?
5)
Você se recorda de suas aulas no curso de Pedagogia (ou formação inicial), nas
disciplinas ligadas ao ensino de Matemática? Como eram essas aulas? Quais assuntos
eram tratados?
6)
Você trabalha em sua prática com algo que aprendeu na formação inicial? Poderia
exemplificar?
7)
Você tem alguma orientação pedagógica para ensinar Matemática a seus alunos? De
quem? Em alguma instância discute o que ensinar e como ensinar?
De que forma são feitas as orientações pedagógicas para ensinar Matemática? Essas
orientações auxiliam ou não sua prática em sala de aula? Como?
8)
Você usa o Livro Didático adotado na escola em suas aulas? Complementa com outros
materiais de apoio? Quais?
9)
Quais são suas maiores dificuldades para trabalhar Matemática com as crianças?
10) Você gostaria de fazer algum comentário sobre nossa conversa, ou acrescentar algo
que julgue interessante para o tema que discutimos?
11) Você está acostumada(o) a receber estagiários em sua sala?
12) Você recebe alguma orientação sobre como receber os estagiários?
13) O que propõe como atividades aos estagiários? O que é discutido em termos de
formação?
14)
Você tem interesse numa formação específica para receber e acompanhar os
estagiários em sua sala?
269
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
Muito obrigada por sua atenção.
270
APÊNDICE D - HISTÓRIA DE VIDA: “MAO”
Ver pág. 89 - Histórias de vida dos estagiários
Meu nome é “MAO”, tenho 23 anos e estou no 5º semestre de Pedagogia, na
Universidade. Participo como estagiária bolsista do Programa Observatório da Educação PROVA BRASIL DE MATEMÁTICA: REVELAÇÕES E POSSIBILIDADES DE AVANÇOS
NOS SABERES DE ALUNOS DE 4ª SÉRIE/5º ANO E INDICATIVOS PARA FORMAÇÃO
DE PROFESSORES.
Desde criança tinha o sonho de ser professora, por admirar essa profissão. Durante
a minha vida escolar tive vários tipos de professor, alguns foram essenciais para me ajudar
a decidir o caminho que iria trilhar, outros por sua vez, analisando hoje, vão me ajudar a
saber como não agir em sala de aula.
Dentre as disciplinas que tive na escola regular, a que menos eu gostava e me
identificava era a Matemática. Por esse motivo nunca me dediquei a aprender e entender, e
alguns professores que tive me ajudaram nisso, pois não ensinavam de uma maneira que os
alunos em geral, se interessassem.
Antes de entrar no 2º grau do ensino regular, foi que realmente decidi que queria ser
Professora e com isso tive a ideia de entrar no CEFAM, para estudar o magistério, que era
um curso de formação de professores em período integral, com bolsa para os alunos. Porém
quando entrei na escola do Estado para cursar o magistério, eu ainda não tinha a idade
mínima para isso, e quando completei a idade, o governo cancelou esse projeto e não pude
fazer o magistério.
Durante toda minha vida tive dificuldades com a Matemática, então ainda não tinha
certeza se era a carreira de professora mesmo que queria seguir, por causa da dificuldade
com a Matemática. Mas quando entrei em um cursinho pré – vestibular mudei minha visão e
comecei a entender a Matemática. Depois desse cursinho percebi que ainda dava tempo de
aprender e vencer essa dificuldade.
No ano de 2008, passei em um concurso da Prefeitura de São Paulo, para trabalhar
como inspetora de alunos em uma escola. A partir daí, com o dia-a-dia da escola, tive
certeza que era esse o caminho que queria seguir, queria ser professora, foi quando decidi
entrar na Universidade e cursar Pedagogia.
No começo do curso, planejava atuar apenas na Educação Infantil, porque tinha um
certo preconceito com o Ensino Fundamental, justamente com a dificuldade com a
271
Matemática, Foi então que conversando com minha professora Vera, ele me propôs
participar do Projeto Observatório, mas no começo fiquei em dúvida se daria certo.
Porém a cada encontro que participava, eu ia me identificando e gostando cada vez
mais e percebi que essa era a oportunidade que precisava para mudar a minha relação com
a Matemática.
Outro fator que me ajudou muito a mudar de ideia em relação ao preconceito sobre
atuar no Ensino Fundamental e os problemas com a Matemática, foi o estágio no Ensino
Fundamental.
Depois que comecei a fazer esse estágio, percebi o quanto foi importante estar
participando do Projeto Observatório, porque algumas dúvidas que eu tinha, foram
respondidas e alguns mitos que acreditava foram quebrados, como por exemplo, o uso da
calculadora no ensino de Matemática durante o ensino fundamental, pois não acreditava
que não tinha uma forma de usar a calculadora em sala de aula, e fazer os alunos
aprenderem a resolver problemas e aprender a pensar de maneira lógica.
Tenho a certeza que tanto o estágio como o projeto, ajudarão a me tornar uma
profissional melhor, porque tenho a oportunidade de mudar minha visão e me tornar uma
pesquisadora. Com isso estou tirando algumas dúvidas que me acompanharam durante
toda a minha vida escolar e estou quebrando vários mitos que tinha.
Espero ter outras oportunidades, como essa que tive com o Projeto, pois acredito
que para me tornar uma ótima professora, não posso parar na graduação, vou ter que
sempre buscar mais fontes de conhecimento, para conseguir alcançar o meu objetivo que é
fazer a diferença em sala de aula e ser lembrada pelos meus alunos como uma fonte de
inspiração, para futuros professores.
272
APÊNDICE E - HISTÓRIA DE VIDA: “TARS”
Meu nome é “TARS”, tenho 23 anos, sou aluna do 4º semestre do curso de
Pedagogia da Universidade, bolsista e estagiária do grupo de pesquisa do Programa
Observatório da Educação.
Durante o ensino regular tive muitas dificuldades com a Matemática, desde muito
cedo e com o passar dos anos escolares essa dificuldade ia somente aumentando. Por isso
desenvolvi uma espécie de raiva da Matemática. Foquei meus estudos nas outras matérias
e deixei a Matemática de lado.
Quando chegou a hora de escolher uma graduação a primeira opção que me veio
em mente foi Letras, queria dar aula de Língua Portuguesa, então fui verificar os cursos e as
universidades. Mas acabei optando por Pedagogia, por poder dar aula para crianças e é
claro no meu ingênuo pensamento inicial, fugir um pouco da Matemática, pois pensava que
dar aula de Matemática para crianças seria moleza, só dar continhas, adição, subtração,
vezes e dividir e pronto!
Mas logo que iniciei o curso de Pedagogia percebi que não seria tão simples assim.
Foi então que tive a oportunidade de participar do grupo de pesquisa em Matemática do
Programa Observatório da Educação.
Quando fui chamada para o grupo fiquei muito feliz porque a essa altura já sabia que
se quisesse realmente ser uma boa professora e fazer a diferença, não bastaria somente
cursar a Pedagogia e parar por aí. Na verdade eu precisaria de mais base, buscar mais
conhecimento, principalmente na área da Matemática, onde se canalizava minha maior
dificuldade. Se eu não sabia e não gostava desta disciplina, como iria ensinar aos alunos e
fazer com que se interessassem em aprender?
No primeiro encontro do grupo me senti perdida, todos aqueles termos e
nomenclaturas da Matemática. Fiquei ainda mais assustada, achei que não iria dar conta.
Eu ali, no início da graduação sem saber quase nada, trabalhando ao lado de doutores,
mestres, professores experientes, me senti fora de contexto.
À medida que as reuniões iam acontecendo eu ia compreendendo mais do que se
tratava, qual era a proposta, qual era o meu papel e ia também tirando dúvidas em relação a
Matemática que me cercavam há muito tempo, e também derrubando alguns mitos sobre
seu ensino como por exemplo, o da calculadora.
Para mim, trabalhar com calculadora fazia com que não se usasse o raciocínio e a
criança não aprenderia nada dessa forma. Mas descobri através de experiências no grupo
273
que a calculadora, se bem usada, auxilia no processo de desenvolvimento do raciocínio, faz
pensar, encontrar soluções, buscar métodos de resolução.
Outra coisa que descobri é que não adianta tentar fugir da Matemática, pois ela está
presente em todo lugar, é algo necessário no nosso cotidiano e é preciso deixar isso claro
aos alunos.
Na universidade tive aulas de Fundamentos Metodológicos do Ensino de Matemática
em dois semestres e foi possível adquirir alguns conhecimentos a respeito, mas realmente
só isso não seria suficiente.
Participando
do
Programa
consegui
aumentar
consideravelmente
esse
conhecimento, parei de ver a Matemática como algo ruim e em consequência disso, quando
tive que escolher uma disciplina optativa para cursar, ao invés de fugir da Matemática mais
uma vez, fui em busca dela e escolhi Educação Estatística.
Nessa disciplina pude aprender sobre a aplicação da Matemática para crianças de
várias formas diferentes e adaptá-las para diversas idades. Era uma aula prática e dinâmica,
aprendi muito, foi uma ótima escolha. Atualmente tenho na grade do curso de Pedagogia, a
disciplina Estatística Aplicada a Educação, com outro professor e consigo aproveitar ao
máximo essas aulas para melhorar, como professora que já sabe que terá essa grande
responsabilidade nas mãos tenho curiosidade de aprender tanto para meu crescimento
quanto para poder ensinar aos meus alunos.
Paralelamente ao Projeto Observatório no ano passado também participei do Projeto
Ler e Escrever e auxiliava uma aluna com muita dificuldade de aprendizagem na
alfabetização, e tanto eu quanto a professora da sala achávamos que devíamos de início,
trabalhar com essa menina somente a alfabetização, pois se ela não sabia ler, nem escrever
não conseguiria aprender Matemática.
Em um dos encontros do grupo de pesquisa esse mito também foi derrubado,
aprendi que uma coisa independe da outra, mesmo que a criança não seja alfabetizada ela
pode fazer cálculos, usar raciocínio lógico e resolver problemas. Assim começamos a
trabalhar Matemática com essa aluna e para nossa surpresa ela se saía muito bem,
começou com contagem com os dedinhos e logo avançou para sobre-contagem e quando
se tratava de problemas, nós líamos para ela e ela resolvia sem grandes dificuldades, sendo
que às vezes era a primeira da sala a terminar corretamente. Assim comprovei na prática o
que aprendi no Projeto.
Essas experiências, como cursar Pedagogia, fazer parte do Projeto Ler e Escrever, e
participar do grupo de pesquisa entre outras coisas, com certeza enriqueceram minha
prática pedagógica. Com as mudanças na minha postura diante a Matemática sei que
conseguirei ministrar minhas aulas corretamente, sempre buscando novos conhecimentos e
aprimoramentos, sem medo e sem preconceitos com a matéria.
274
APÊNDICE F - HISTÓRIA DE VIDA: “EAM”
Meu nome é “EAM”, tenho 36 anos e sou casado. Estou no 5º semestre do curso de
Pedagogia e participo como estagiário bolsista do PROJETO OBSERVATÓRIO DA
EDUCAÇÃO “Prova Brasil de Matemática: revelações, possibilidades de avanços nos
saberes de alunos de 4ª série/5º ano e indicativos para a formação de professores”,
coordenado pela Profª Drª Edda Curi e financiado pela CAPES.
Venho de família humilde e tenho mais três irmãos. Terminei meus estudos da
educação básica com 17 anos; trabalhei dos 14 aos 34 anos no ramo voltado ao comércio e
ao RH - na parte administrativa. Sempre gostei da Matemática: cálculos, porcentagem e
raciocínio lógico. Aos 30 anos tive um câncer no mediastino (entre pulmão e coração) e
neste período, afastado da empresa, ajudei a alfabetizar um sobrinho com 9 anos, que
estava no 4º ano do Ensino Fundamental. Essa oportunidade foi muito gratificante e deu um
novo sentido a minha vida, uma vez que minha esposa, formada em Letras, já atuava na
área da educação e a maior parte de nossos amigos também.
Prestei o ENEM aos 33 anos (já curado do câncer, após quimioterapia) e consegui
uma bolsa pelo PROUNI para cursar Pedagogia - algo que me enche de orgulho, porque
após 16 anos afastado dos estudos, eu tinha vencido um trauma dentro de mim, já que
tenho um problema de dislexia, um caso raro fonético, cujo entrave é pronunciar palavras
com “r” no meio da palavra. Acreditava que se entrasse na área da educação os alunos
iriam caçoar deste problema (que trouxe traumas na minha infância), mas percebi que venci
este trauma ao conseguir alfabetizar um aluno que acompanho no estagio pelo CEFAI .
Percebi ainda que as crianças não notam este pequeno problema.
Após entrar e cursar o primeiro semestre na Universidade, destaquei-me não só
porque sou representante de uma sala com 114 alunos, mas, acredito que, principalmente
por minhas notas e trabalhos e por conta disto fui convidado por uma professora do curso a
participar de uma entrevista com a professora Dra. Edda Curi, que me selecionou para
ocupar uma das seis vagas, dentre aproximadamente 40 candidatos , disponíveis no Projeto
Observatório da Educação
Ao vivenciar em sala de aula as teorias do construtivismo quebrei meu primeiro mito,
já que eu fui alfabetizado a partir do método tradicional de ensino e acreditava que esse
sistema de educação era o ideal, porque não conhecia amigos analfabetos; porém passei a
acreditar que no construtivismo é mais fácil por relacionarmos o nosso cotidiano à
aprendizagem do aluno, desta maneira passei a ver que um aluno não precisa saber de cor
uma tabuada, por exemplo: 3X4=12. Para mim era fácil entender, mas hoje a criança precisa
275
do contexto. Por exemplo: Tenho três carros com quatro rodas quantas rodas tenho no
total? O aluno consegue trazer o resultado sem saber a tabuada. Primeiro mito derrubado.
O segundo mito surgiu ao estar estagiando e vivenciando em sala de aula cada ação
do professor que ministra as aulas. Muitos professores ao verem que alguns alunos
terminavam a lição passavam a eles numerais de 1 a 100 e assim por diante. Com isso a
Matemática acabava sendo uma punição para aqueles que terminavam primeiro suas
atividades, acarretando um certo desconforto e quando esses alunos tinham a aula de
Matemática eles falavam: “De novo numerais”.
Descobri que isso era uma punição para os alunos, criando já na infância certo
bloqueio, ao invés de aprender a contextualizar a sua vivência com os números.
O projeto não só abre nossos horizontes acadêmicos, como nos traz meios para
ensinar e solucionar os nós que temos na Matemática: o quanto é difícil criar e elaborar
questões e descobrir se o aluno vai interpretar aquele enunciado, de que maneira ele
resolverá o problema.
Acredito que este projeto soma muito em minha formação, pois nós, estagiários,
sentamos e debatemos com doutores, doutorandos, mestres, mestrandos, professores,
coordenadores pedagógicos, com foco em aprender como o aluno, nos anos iniciais, pensa
a Matemática. Analisamos cada avaliação que esses alunos fazem no decorrer dos anos
iniciais.
Além de analisar as avaliações, estudamos as expectativas de aprendizagem do 1º
ao 5º ano, debatemos sobre os descritores do Sistema de Numeração Decimal do SAEB: a
experimentação; a oralidade e a simbologia (escrita). Ao olharmos as questões podemos ver
os erros prováveis que as crianças cometem.
A coordenadora do Projeto nos passou um pouco de seu conhecimento sobre as
orientações didáticas do Sistema de Numeração Decimal, explicando de forma clara e
objetiva esses possíveis erros que os alunos cometem.
Finalizo externando a gratidão por estar vivenciando esta oportunidade.
276
APÊNDICE G - HISTÓRIA DE VIDA: “LISE”
Meu nome é “LISE”, tenho 20 anos e estou no 4º semestre do curso de Pedagogia.
Acredito que o sonho de toda menina, principalmente na infância, é ser professora.
No meu caso não foi diferente, minha brincadeira preferida era “escolinha”, juntava minhas
bonecas e minhas irmãs e passava a tarde toda brincando. Desde então já havia escolhido
o que eu iria ser “quando crescer”. Na minha adolescência acompanhei minha tia que na
época fazia Pedagogia e meu interesse foi aumentando.
Comecei a pesquisar na internet o curso, as funções e confesso que me decepcionei
um pouco em ver como o professor não é valorizado no Brasil, as dificuldades e desafios
que iria encontrar, até pensei em mudar, mas resolvi apostar e fazer algo que me
interessava. Passei até por preconceito de familiares e amigos que só criticavam minha
opinião, mesmo assim bati o pé, e decidi que Pedagogia era o caminho a ser seguido.
Na escola eu e a Matemática sempre fomos “amigas”, tive professores
excelentes que conseguiam realmente passar a Matemática, outros nem tanto. Confesso
que prefiro resolver mil expressões do que interpretar um texto ou fazer alguma resenha.
Lembro que no Ensino Médio meu apelido na sala de aula era de “rata” pois conseguia
acompanhar o raciocínio da professora. A Matemática sempre foi a matéria que eu tive
menos dificuldade.
Minha participação no Projeto Observatório, aconteceu através de uma
professora do curso, que explicou o que seria esse projeto, o objetivo, a relação com a
Matemática, me interessei e participei da seleção.
No início confesso que fiquei um pouco perdida no Projeto, pois sou leiga em
certos assuntos.
No curso de Pedagogia as disciplinas relacionadas a Matemática deixam um
pouco a desejar, já que são muito teóricas, muitas vezes nem partem para a realidade, a
prática só acontece depois, nos estágios ou quando partimos para a sala de aula, se não
fosse o Projeto com o acompanhamento das professoras, as apresentações das telas como
a de Vergnaud, aprender a trabalhar diretamente com as dificuldades dos alunos, minha
formação seria vaga.
Comento com minhas colegas de classe sobre o projeto e elas concordam que
deveríamos ter aulas mais dinâmicas e não fazer apenas uma pesquisa relacionada a tal
assunto ou trabalhos de como ensinar a Matemática.
Acabei com alguns mitos que aprendi na minha formação como a utilização das
casinhas de dezena e unidade, a utilização da palavra numerais. Aprendi algumas
277
estratégias como a utilização de ditados, bingos, cartas sobrepostas, composição e
decomposição de números. São coisas simples que passam batidas no curso de Pedagogia
e que pelo que eu presencio no Projeto traz muitos benefícios e fazem uma total diferença
quando comparamos as turmas que utilizam esses procedimentos e aquelas que não usam.
O trabalho com problemas também me impressionou bastante, pois me levou às
minhas aulas de Matemática no Ensino Fundamental, como alguns problemas se tornam um
problemão quando utilizamos uma palavra ou passamos a ideia de maneira incorreta e
acabamos culpando a criança.
Creio que minha participação no Projeto me auxiliará muito quando estiver
assumindo uma sala de aula, já vejo esse resultado com as professoras que fazem parte do
Projeto. Como já mencionei o curso de Pedagogia não dá a assistência necessária que
realmente precisamos e para isso é necessário mudarmos a base para quando chegarmos à
prática sabermos trabalhar de maneira correta.
278
APÊNDICE H - HISTÓRIA DE VIDA: “VANGRA”
Meu nome é “VANGRA”, tenho 27 anos e estou no 5º semestre do curso de
Pedagogia. Sou estagiária bolsista do Programa Observatório da Educação há 2 anos e
meio.
Minha história na área da Matemática não foi uma experiência agradável, pelo
menos uma boa parte dela, foi de grande desespero e incompreensão.
Não tenho lembranças ruins da 1ª série. A Matemática naquele momento não me
dava dor de cabeça, acredito que conseguia atender os objetivos propostos pela professora.
Na 2ª série me lembro da professora passar contas armadas fazendo aquela
casinha, o que para mim não tinha dificuldade, não tinha problema. Mas a professora tinha,
eu observava que na sala de aula a professora bebia café e comia, não passando muita
coisa na aula.
Da 4ª série em diante me recordo com alguns detalhes. Na 4ª série tinha uma
professora carrasca que não dava moleza, ela chegou a agredir alguns alunos da sala.
Naquela época me recordo da Matemática como algo muito vago e sem valor, as atividades
eram dadas na lousa, as contas armadas e nada mais. A professora explicava apenas uma
vez e tínhamos que fazer, me recordo que não havia uma explicação um diálogo entre o
professor e aluno, na verdade não podíamos nem nos comunicar com os outros colegas da
sala, se tínhamos dúvidas, levávamos para casa por que a professora não explicava
novamente. Ela mandava decorar a tabuada que no dia seguinte faria chamada oral, quando
conversávamos ela mandava os alunos fazerem 10 vezes a tabuada do 2 ao 10 , então
Matemática naquele época era castigo das professoras, e então começou meu longo
caminho de ensino de matemática sem compreensão.
Na 5ª serie me lembro de que já havia um professor para cada aluno, e tive uma
professora que me deu aula na 5ª e 6ª série. A professora podia ter o conhecimento
matemático, porém não sabia transmitir, não conseguia compreender os problemas, para
mim era tudo muito difícil: as regras, ordens, aquelas contas enormes. Pedia explicação,
porém na terceira vez que estava na mesa dela, ela já estava com cara feia, quando
comecei a me questionar: “Meu Deus, ou eu sou muito burra ou ela não está sabendo me
ensinar de uma maneira mais fácil de compreender”. A falta de compreensão e a
impaciência da professora me fizeram detestar a Matemática, tinha até desânimo ao entrar
na sala, minhas notas eram baixas. Minha 5ª série foi um terror de 100% aprendia 30% e
esses trinta agradeço aos colegas que davam uma ajuda.
279
Na 6ª série descobri que a professora seria a mesma, quase chorei , eu torcia para
que ela ficasse doente para vir outro professor no lugar, e percebi que nas vezes que a
professora faltava e outro professor substituía a minha compreensão era melhor, logo, a
maneira que a professora explicava era de fato meu maior desafio. Ela fazia as contas muito
rapidamente, e meu raciocínio não conseguia acompanhar, no mesmo ano a professora
ficou de licença maternidade e foi meu alívio. Aprendi mais dentro desse período, porém
muita coisa ficou defasada, sempre tinha que rever certas regras da Matemática por não ter
compreendido no tempo certo.
Minhas lembranças de Matemática são de que a maior parte do tempo eu estava
sempre com dificuldades.
No ano de 2007 ganhei uma bolsa de estudo de 100% para fazer o curso de
Pedagogia, porém fiz somente três meses e abri mão, pois meu filho tinha 2 meses na
época e estava ficando doente, então tive que parar. Dentro do período que estive na
universidade passei a gostar do curso, e quando houve a oportunidade comecei novamente.
O curso de Pedagogia é um curso que não envolve muita Matemática, por isso
alguns escolhem a Pedagogia e optam por fazer, porém não foi o meu caso, apesar de meu
histórico com a Matemática a escolha pelo curso foi mesmo pelas oportunidades de
conhecer um pouco da Pedagogia e gostar disso. Após um ano de curso a professora Dra.
Edda Curi foi à sala para anunciar o Projeto Observatório da Educação e me interessei
muito, queria fazer para poder ver se minhas concepções sobre a Matemática, o medo e a
dificuldade diminuíssem.
Então após entrar no projeto, no começo fiquei assustada e me perguntei se estava
preparada para aquele desafio, eu pensava se iria conseguir acompanhar o grupo, mas eu
tinha que dar essa oportunidade para mim e para poder mais para frente também ter
subsídios quando estiver ensinando Matemática.
O projeto foi uma disciplina a mais para minha formação. O grupo é composto por
professores que pensam e agem diferente da forma que estava acostumada a ver, muitas
vezes quando as professoras davam exemplos de alunos com dificuldades, me via neles, e
através disso, pela minha dificuldade do passado e pelo que presenciei no projeto meu olhar
em relação as dificuldades das crianças me deu uma direção bem mais ampla de como
ensinar em sala.
No curso de pedagogia a disciplina de conhecimento teórico em Matemática não foi
algo que me deu a visão que tive no projeto, o olhar do professor, na verdade é necessário
que o professor tenha uma visão diferenciada da prática para que seja comparada com o
pensamento teórico, acredito que a disciplina deve ser mais bem trabalhada, sobre todas as
formas.
280
Durante esse período que estou no projeto minha visão com relação a Matemática
mudou, o ensino que tive no passado foi defasado mas superei e aprendi, porém o projeto
me deu chances de compreender e como irei proceder em sala da forma que irei ensinar
Matemática para as crianças.
O projeto me permitiu quebrar o mito de que a Matemática é um bicho de sete
cabeças, pois o problema não é a matemática e sim a forma como os professores vêm e
trabalham a mesma. Pude perceber isso no contato com os professores do projeto que se
comprometem com a aprendizagem dos alunos e deles mesmos.
281
APÊNDICE I - QUESTIONÁRIOS RESPONDIDOS PELAS
DIRETORAS: PERFIL DA ESCOLA “E-MAO”
Ver pág. 110
PERFIL DA ESCOLA “E-MAO”
Escola: “E-MAO”22
Localização: Cidade A.E. Carvalho
Número de alunos atendidos: 1.647
Organização da escola: 8 séries x
ou 9 anos
Breve descrição da situação sócio econômica das famílias dos alunos atendidos em sua
escola:
R: A maioria é de migração nordestina, tem como rendimento menos de um salário mínimo
com apoio do governo de bolsa-família.
IDEB da escola23
2007: 3,9
2009: 4,3
2011: 5,0
Sobre o número de salas e alunos para o Ensino Fundamental
ANO/SÉRIE
Nº DE SALAS
Nº DE ALUNOS
1º
03
30 cada – T= 90
2º
05
32 cada – T= 160
3º
05
35 cada – T= 175
4º
05
158
5º
05
35 cada – T= 175
Sobre o número total de professores
ANO/SÉRIE PROFESSORES
PROFESSORES
FORMAÇÃO
FORMAÇÃO
NÍVEL MÉDIO
SUPERIOR
1º
2º
3º
1
4º
1
5º
-
QUANTIDADE POR
NÍVEL ÁREA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R:
22
Para preservar a identidade da diretora e escola, não reproduzimos o nome e endereço da escola,
optando pelo termo “E-MAO” e somente o bairro no qual se localiza.
23
A diretora não informou os índices do IDEB da escola. À época de nossa pesquisa apuramos nas
fontes oficiais do governo os valores que constam no questionário.
282
APÊNDICE J - QUESTIONÁRIOS RESPONDIDOS PELAS
DIRETORAS: PERFIL DA ESCOLA “E-TARS”
PERFIL DA ESCOLA “E-TARS”
Escola: “E-TARS”24
Localização: Vila Jacuí
Número de alunos atendidos: 1581
Organização da escola:
8 SÉRIES
OU 9 ANOS
X
Breve descrição da situação sócio econômica das famílias dos alunos atendidos em sua
escola:
R: São na maioria famílias de baixa renda
IDEB da escola
2007: 4,3
2009: 4,2
201125:
Sobre o número de salas e alunos para o Ensino Fundamental
ANO/SÉRIE
Nº DE SALAS
Nº DE ALUNOS
1º
6
163
2º
5
147
3º
4
127
4º
6
148
5º
6
199
Sobre o número total de professores
ANO/SÉRIE PROFESSORES
PROFESSORES
FORMAÇÃO
FORMAÇÃO
NÍVEL MÉDIO
SUPERIOR
1º
11
2º
1
3º
24
8
8
QUANTIDADE POR
NÍVEL ÁREA
PEDAGOGIA - 6
Ed.Física – 1
Informática – 1
Leitura – 1
Inglês - 1
PEDAGOGIA - 5
Ed.Física – 1
Informática – 1
Leitura – 1
Inglês - 1
PEDAGOGIA - 4
Para preservar a identidade da diretora e escola, não reproduzimos o nome e endereço da escola,
optando pelo termo “E-TARS” e somente o bairro no qual se localiza.
25
À época desta pesquisa obtivemos a informação de que o valor do IDEB da escola em 2011 foi de
4,8.
283
4º
10
5º
10
Ed.Física – 1
Informática – 1
Leitura – 1
Inglês - 1
PEDAGOGIA - 6
Ed.Física – 1
Informática – 1
Leitura – 1
Inglês - 1
PEDAGOGIA - 6
Ed.Física – 1
Informática – 1
Leitura – 1
Inglês - 1
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R:
284
APÊNDICE K - QUESTIONÁRIOS RESPONDIDOS PELAS
DIRETORAS: PERFIL DA ESCOLA “E-EAM”
PERFIL DA ESCOLA “E-EAM”
Escola: “E-EAM”26
Localização: São Miguel Paulista
Número de alunos atendidos: Aproximadamente 1600
Organização da escola:
8 SÉRIES
X
9 ANOS
Breve descrição da situação sócio econômica das famílias dos alunos atendidos em sua
escola:
R: A grande maioria das famílias encontra-se na faixa média de salários, renda familiar de
01 a 05 mínimos, as crianças em sua maioria encontram-se na faixa de média
vulnerabilidade e alguns casos de grande vulnerabilidade.
IDEB da escola
2007: 4,6
2009: 5,1
2011: ainda não temos o resultado27
Sobre o número de salas e alunos para o Ensino Fundamental
ANO/SÉRIE
Nº DE SALAS
Nº DE ALUNOS
1º Ano
05
150
2º Ano
05
175
3º Ano
04
140
4º Ano
07
245
5º Série
05
175
Sobre o número total de professores
ANO/SÉRIE PROFESSORES
PROFESSORES
FORMAÇÃO
FORMAÇÃO
NÍVEL MÉDIO
SUPERIOR
1º
Todos
2º
Todos
3º
Todos
4º
Todos
5º
Todos
QUANTIDADE POR
NÍVEL ÁREA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA.
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R:
26
Para preservar a identidade da diretora e escola, não reproduzimos o nome e endereço da escola,
optando pelo termo “E-EAM” e somente o bairro no qual se localiza.
27
À época desta pesquisa obtivemos a informação de que o valor do IDEB da escola em 2011 foi de
4,6.
285
APÊNDICE L - QUESTIONÁRIOS RESPONDIDOS PELAS
DIRETORAS: PERFIL DA ESCOLA “E-LISE”
PERFIL DA ESCOLA “E-LISE”
Escola: “E-LISE”28
Localização: Jardim Imperador
Número de alunos atendidos: 822 alunos
Organização da escola:
8 SÉRIES
9 ANOS
X
Breve descrição da situação sócio econômica das famílias dos alunos atendidos em sua
escola:
R: Os alunos são de classe média baixa, muitos dos responsáveis trabalham na
informalidade, poucos trabalham registrados. Na reunião de pais há uma boa frequência.
IDEB da escola
2007: 5,2
2009: 4,9
2011: 5,4
Sobre o número de salas e alunos para o Ensino Fundamental
ANO/SÉRIE
Nº DE SALAS
Nº DE ALUNOS
1º
3
76
2º
3
76
3º
3
87
4º
4
127
5º
3
108
Sobre o número total de professores
ANO/SÉRIE PROFESSORES
PROFESSORES
FORMAÇÃO
FORMAÇÃO
NÍVEL MÉDIO
SUPERIOR
1º
3
2º
3
3º
3
4º
4
5º
10
QUANTIDADE POR
NÍVEL ÁREA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R: A estagiária mostrou interesse e teve um bom desempenho durante o estágio.
28
Para preservar a identidade da diretora e escola, não reproduzimos o nome e endereço da escola,
optando pelo termo “E-LISE” e somente o bairro no qual se localiza.
286
APÊNDICE M - QUESTIONÁRIOS RESPONDIDOS PELAS
DIRETORAS: PERFIL DA ESCOLA “E-VANGRA”
PERFIL DA ESCOLA “E-VANGRA”
Escola: “E-VANGRA”29
Localização: Jardim Matarazzo
Número de alunos atendidos: 840
Organização da escola:
8 SÉRIES
9 ANOS
X
Breve descrição da situação sócio econômica das famílias dos alunos atendidos em sua
escola:
R: A EMEF “E-VANGRA” está situada em um local de baixo IDH, grande parte das pessoas
ocupam moradias legalizadas há pouco tempo em razão da organização das pessoas no
entorno do movimento de moradia. Encontramos um pequeno comércio local organizado, os
meios de transporte mais utilizados são os ônibus e trens da CPTM. No entorno da unidade
existem poucas áreas de lazer e poucos espaços culturais. É perceptível que muitas
mulheres assumem a responsabilidade pela manutenção da família e, ainda, que as avós
possuem uma grande importância para a organização da mesma. Frequentemente são as
mães que acompanham a vida escolar das crianças e adolescentes.
IDEB da escola
2007: *30
2009: 4,1 / 3,831
2011: 4,7 / 3,8
Sobre o número de salas e alunos para o ensino fundamental
ANO/SÉRIE
Nº DE SALAS
Nº DE ALUNOS
1º
3
83
2º
3
92
3º
3
103
4º
4
114
5º
3
102
Sobre o número total de professores
ANO/SÉRIE PROFESSORES
PROFESSORES
FORMAÇÃO
FORMAÇÃO
NÍVEL MÉDIO
SUPERIOR
1º
*
3
2º
*
3
3º
*
3
4º
*
4
5º
*
*
29
QUANTIDADE POR
NÍVEL ÁREA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
PEDAGOGIA
Para preservar a identidade da diretora e escola, não reproduzimos o nome e endereço da escola,
optando pelo termo “E-VANGRA” e somente o bairro no qual se localiza.
30
A escola começou a funcionar em 2008, razão pela qual não foi avaliada em 2007.
31
Os dois valores mencionados pela diretora referem-se ao IDEB alcançado e à meta proposta.
287
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R: A escola tem interesse em dialogar com a Universidade para melhorar o atendimento aos
estagiários e, ainda, apresentar sua disposição em atender pesquisadores na área da
educação.
288
APÊNDICE N - TABELA NÚMERO DE ALUNOS ATENDIDOS
Ver pág. 111
Tabela 2 - Número de salas e alunos por escola
Escola
N° de Salas
N° de Alunos
E-EAM
21
710
E-MAO
18
583
E-TARS
27
784
E-LISE
16
469
E-VANGRA
16
494
Totais
98
2510
289
APÊNDICE O - VARIAÇÃO IDEB POR RESCOLA
Ver pág. 112
Tabela 3 - Variação do IDEB das escolas pesquisadas nas três últimas
edições
Variação IDEB das escolas pesquisadas
Escola
E-EAM
E-MAO
E-TARS
E-LISE
E-VANGRA
2007
4,6
3,9
4,3
5,2
-
2009
5,1
4,3
4,2
4,9
4,1
2011
4,6
5,0
4,8
5,4
4,7
Ano
290
APÊNDICE P - RESPOSTAS PERFIL DAS PROFESSORAS: PERFIL
DA PROFESSORA “P-MAO”
Ver pág. 114
PERFIL DA PROFESSORA “P-MAO”
DADOS DE IDENTIFICAÇÃO
Nome: “P-MAO”32 Idade: 37
Estado Civil : Solteira Nº de Filhos: 01
Formação: Superior Tempo de atuação 15 anos
Instituição e ano em que se formou Universidade C.C.B.33 – 2004
Tempo de atuação no Ensino Fundamental: 15 anos
Enquadramento Funcional: ( ) Contratado ( X ) Efetivo por concurso
Trabalha quantos períodos? (Especifique série/ano) – 1º/2º Ano
Série/Ano em que gosta de atuar: 4º e 5º ano
R: Por quê? Porque os alunos são mais independentes e tem mais maturidade.
PARTE A – FORMAÇÃO – IDENTIDADE PROFISSIONAL
1)
Conte um pouco da sua história, como foi sua vida escolar, onde você estudou?
Enfim, conte como você chegou ao Magistério e por que escolheu ser professor(a)?
R: Estudei no Centro Educacional A.D.34, na Bahia. Escolhi ser professora e após o período
de estágio descobri a minha vocação.
2)
O que você achou de sua formação? Seu curso lhe formou para trabalhar com
crianças?
R: O curso de Magistério me deu suporte para desenvolver minha didática e com o tempo fui
consolidando-a. A faculdade deixou a desejar, pois desenvolve uma didática teórica.
3)
Como este curso lhe preparou para ensinar as crianças do Ensino Fundamental?
R: Magistério, porque o 4º ano é voltado para a prática de ensino.
32
Para preservar a identidade da professora, a mesma será identificada como “P-MAO”
Para preservar a Universidade, utilizamos a sigla C.C.B.
34
Utilizamos a sigla A.D. para preservar a instituição.
33
291
4)
Em que série/ano você se sente mais à vontade para atuar?
R: 4º e 5º ano do Ensino Fundamental.
5)
Em relação às áreas do conhecimento, por exemplo, Alfabetização, Ciências,
Matemática entre outros, no que seu curso lhe preparou melhor? Por quê?
R: Português, porque a alfabetização é o início da aprendizagem.
6)
Qual área você mais gosta de ensinar? Por quê?
R: Todas porque é o início do processo que vai dar condições do crescimento intelectual do
aluno.
7)
Você gosta de ensinar Matemática? Poderia citar um exemplo do que você mais
gosta na área da Matemática?
R: Gosto, pois tenho formação em Matemática. Situações problemas, onde concretiza o
raciocínio e a lógica.
8)
Em sua opinião, o que é mais trabalhoso ou mais difícil para ensinar Matemática?
R: A interpretação.
9)
O que você acredita ser preciso para ensinar Matemática para as crianças?
R: Desenvolver atividades que incorporam a realidade dos alunos.
10)
Que lacunas você sente em sua formação inicial para ensinar Matemática, ou seja, o
que precisaria ter sido trabalhado mais durante sua formação? Por quê?
R: No curso Superior, a didática.
11)
Você tem feito, ou sente necessidade de fazer algum curso de formação continuada?
Em qual área?
R: Estou cursando Pedagogia.
12)
O que lhe atrai e o que lhe dificulta em sua profissão?
R: Depois de 15 anos de prática os desafios que foram surgindo foram superados, surgirão
outros que terei que superá-los.
13)
Se tivesse chance mudaria de profissão? O que lhe faz permanecer nela?
R: Não, eu escolhi ser professora, o que me faz permanecer é a vocação.
292
14)
O que lhe atrai e o que dificulta no ensino de Matemática?
R: Matemática é a realidade de uma construção de sociedade. Mesmo não sendo
alfabetizado o ser humano aprende a lidar com os números.
15)
Você conhece o IDEB de sua escola?
R: Sim
16)
Você já viu em que nível de proficiência em Matemática encontram-se os alunos da
escola?
R: Nos 4ºs anos atinge o índice, nas 8ªs séries o índice está abaixo da média.
17)
Quais são as metas propostas para melhoria da proficiência em Matemática?
R: A escola atende os alunos com a recuperação paralela, procurando assim atingir o nível
ou seja, a meta.
PARTE B – PRÁTICA PEDAGÓGICA
1)
Você pode me descrever sua rotina diária, seu trabalho, como organiza as aulas de
Matemática, quantas vezes por semana ensina Matemática, durante quanto tempo?
R: Leitura do quadro de 1 a 100, ditado de números, escrita dos números, operações e
situações problemas / gráficos. Acontecem 3 vezes na semana ( utilizo duas aulas quando
necessário três).
2)
Como você planeja suas aulas de Matemática, quais materiais utiliza? Tem seu
planejamento em mãos?
R: Sim, jogos lúdicos; cartazes expostos em sala de aula.
3)
Dentre as atividades matemáticas propostas para seus alunos, o que você considera
mais importante? Por quê?
R: Reconhecer os números, realizar operações de adição e subtração.
4)
Seus alunos se interessam pelas aulas de Matemática? O que você faz para que
eles se interessem?
R: Sim, desenvolvo atividades voltadas para a realidade do aluno.
5)
Você se recorda de suas aulas no curso de Pedagogia (ou formação inicial), nas
disciplinas ligadas ao ensino de Matemática? Como eram essas aulas? Quais assuntos
eram tratados?
293
R: Sim. No Magistério confeccionávamos jogos com materiais recicláveis.
6)
Você trabalha em sua prática com algo que aprendeu na formação inicial? Poderia
exemplificar?
R: Confecção de dominós com caixas de fósforos; exposição de tabela de números na sala
de aula.
7)
Você tem alguma orientação pedagógica para ensinar Matemática a seus alunos?
De quem? Em alguma instância discute o que ensinar e como ensinar?
R: Temos. Discutimos no grupo de formação JEIF com o grupo de professores e
coordenadores.
De que forma são feitas as orientações pedagógicas para ensinar Matemática? Essas
orientações auxiliam ou não sua prática em sala de aula? Como?
R: Trabalhamos com o Caderno de Orientações Curriculares de expectativas de
aprendizagem para o Ensino Fundamental – Ciclo I.
8)
Você usa o Livro Didático adotado na escola em suas aulas? Complementa com
outros materiais de apoio? Quais?
R: Não, a escola não recebeu número suficiente de Livro Didático e Caderno de Apoio de
Matemática para todos os alunos. Retiro atividades do Livro Didático Aprender Juntosd,
Projeto Buriti, inernet, etc.
9)
Quais são suas maiores dificuldades para trabalhar Matemática com as crianças?
R: A falta de interpretação dos alunos.
10)
Você gostaria de fazer algum comentário sobre nossa conversa, ou acrescentar algo
que julgue interessante para o tema que discutimos?
R:
11)
Você está acostumada(o) a receber estagiários em sua sala?
R: Sim, todos os anos.
12)
Você recebe alguma orientação sobre como receber os estagiários?
R: Sim, o estagiário na escola tornou-se rotina.
294
13)
O que propõe como atividades aos estagiários? O que é discutido em termos de
formação?
R: Proponho que o estagiário fique atento à Didática e à prática pedagógica.
14)
Você tem interesse numa formação específica para receber e acompanhar os
estagiários em sua sala?
R: Não, porque o contato com o estágio acontece todos os anos.
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R:
295
APÊNDICE Q - RESPOSTAS PERFIL DAS PROFESSORAS: PERFIL
DA PROFESSORA “P-TARS”
PERFIL DA PROFESSORA “P-TARS”
DADOS DE IDENTIFICAÇÃO
Nome: “P-TARS”35 Idade: 45
Estado Civil : Casada Nº de Filhos: 03
Formação: Nível Superior Tempo de atuação 24 anos
Instituição e ano em que se formou: Universidade “U”36
Tempo de atuação no Ensino Fundamental: 20 anos
Enquadramento Funcional: ( ) Contratado ( X ) Efetivo por concurso
Trabalha quantos períodos? (Especifique série/ano) – 1 / 4º série
Série/Ano em que gosta de atuar: 3ª e 4ª séries
Por quê? R: Acho mais gratificante
PARTE A – FORMAÇÃO – IDENTIDADE PROFISSIONAL
1)
Conte um pouco da sua história, como foi sua vida escolar, onde você estudou?
Enfim, conte como você chegou ao Magistério e por quê escolheu ser professor(a)?
R: Sempre fui boa aluna e sempre gostei de ensinar. Meu pai era professor.
2)
O que você achou de sua formação? Seu curso lhe formou para trabalhar com
crianças?
R: Na época sim. O sistema de ensino sofreu modificações que trouxeram algumas
questões que dificultam o processo de ensino aprendizagem de hoje.
3)
Como este curso lhe preparou para ensinar as crianças do Ensino Fundamental?
R: Através do estágio
4)
Em que série/ano você se sente mais à vontade para atuar?
R: 4ª e 3ª
5)
Em relação às áreas do conhecimento, por exemplo, Alfabetização, Ciências,
Matemática entre outros, no que seu curso lhe preparou melhor? Por quê?
35
36
Para preservar a identidade da professora, a mesma será identificada como “P-TARS”
Para preservar a Universidade, utilizamos a sigla “U”.
296
R: A teoria trouxe algum conhecimento, mas somente a prática trouxe o conhecimento.
6)
Qual área você mais gosta de ensinar? Por quê?
R: Português e Matemática. Domino melhor.
7)
Você gosta de ensinar Matemática? Poderia citar um exemplo do que você mais
gosta na área da Matemática?
R: Sim, as quatro operações.
8)
Em sua opinião, o que é mais trabalhoso ou mais difícil para ensinar Matemática?
R: Raciocínio lógico
9)
O que você acredita ser preciso para ensinar Matemática para as crianças?
R: Raciocínio lógico
10)
Que lacunas você sente em sua formação inicial para ensinar Matemática, ou seja, o
que precisaria ter sido trabalhado mais durante sua formação? Por quê?
R: Como ensinar raciocínio lógico
11)
Você tem feito, ou sente necessidade de fazer algum curso de formação continuada?
Em qual área?
R: Não
12)
O que lhe atrai e o que lhe dificulta em sua profissão?
R: O que dificulta é a violência, me atrai poder ensinar.
13)
Se tivesse chance mudaria de profissão? O que lhe faz permanecer nela?
R: Eu gosto de dar aula, mas mudaria porque me sinto impotente perante as dificuldades
que encontro.
14)
O que lhe atrai e o que dificulta no ensino de Matemática?
R: Me atrai estimular o raciocínio lógico, dificulta às vezes não chegar ao aluno, não
conseguir ensinar.
15)
R: Não
Você conhece o IDEB de sua escola?
297
16)
Você já viu em que nível de proficiência em Matemática encontram-se os alunos da
escola?
R: Não
17)
Quais são as metas propostas para melhoria da proficiência em Matemática?
R: Trabalhar o caderno de apoio e ir fazendo algumas intervenções.
PARTE B – PRÁTICA PEDAGÓGICA
1)
Você pode me descrever sua rotina diária, seu trabalho, como organiza as aulas de
Matemática, quantas vezes por semana ensina Matemática, durante quanto tempo?
R: Ensino matemática duas vezes por semana, na terça só matemática e na quarta uma ou
duas aulas. Organizo a rotina na JEIF
2)
Como você planeja suas aulas de Matemática, quais materiais utiliza? Tem seu
planejamento em mãos?
R: Planejo com a turma da série na JEIF, tenho o planejamento na mão.
3)
Dentre as atividades matemáticas propostas para seus alunos, o que você considera
mais importante? Por que?
R: Raciocínio lógico
4)
Seus alunos se interessam pelas aulas de Matemática? O que você faz para que
eles se interessem?
R: Sim, uso assunto que chama atenção deles.
5)
Você se recorda de suas aulas no curso de Pedagogia (ou formação inicial), nas
disciplinas ligadas ao ensino de Matemática? Como eram essas aulas? Quais assuntos
eram tratados?
R: Não
6)
Você trabalha em sua prática com algo que aprendeu na formação inicial? Poderia
exemplificar?
R: Não
7)
Você tem alguma orientação pedagógica para ensinar Matemática a seus alunos?
De quem? Em alguma instância discute o que ensinar e como ensinar? De que forma são
298
feitas as orientações pedagógicas para ensinar Matemática? Essas orientações auxiliam ou
não sua prática em sala de aula? Como?
R: Sim, Prefeitura e JEIF.
8)
Você usa o Livro Didático adotado na escola em suas aulas? Complementa com
outros materiais de apoio? Quais?
R: Sim. Complemento com outras atividades.
9)
Quais são suas maiores dificuldades para trabalhar Matemática com as crianças?
R: Trabalhar raciocínio lógico
10)
Você gostaria de fazer algum comentário sobre nossa conversa, ou acrescentar algo
que julgue interessante para o tema que discutimos?
11)
Você está acostumada(o) a receber estagiários em sua sala?
R: Sim
12)
Você recebe alguma orientação sobre como receber os estagiários?
R: Não
13)
O que propõe como atividades aos estagiários? O que é discutido em termos de
formação?
14)
R: Observar e às vezes ajudar os alunos para adquirir prática e conhecimento
15)
Você tem interesse numa formação específica para receber e acompanhar os
estagiários em sua sala?
R: Sim.
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R:
299
APÊNDICE R - RESPOSTAS PERFIL DAS PROFESSORAS: PERFIL
DA PROFESSORA “P-EAM”
PERFIL DA PROFESSORA “P-EAM”
DADOS DE IDENTIFICAÇÃO
Nome: “P-EAM”37 Idade: 35
Estado Civil : Solteira Nº de Filhos: 0
Formação: Pedagogia Tempo de atuação 13 anos
Instituição e ano em que se formou: “U.A”38
Tempo de atuação no Ensino Fundamental: 10 anos
Enquadramento Funcional: ( ) Contratado ( X ) Efetivo por concurso
Trabalha quantos períodos? (Especifique série/ano) – Trabalho em um período com uma
sala de 5º ano (4ª série)
Série/Ano em que gosta de atuar: 5º ano (4ª série)
Por quê? R: Porque nessa idade já são mais maduros e independentes, gosto dessa faixa
etária.
PARTE A – FORMAÇÃO – IDENTIDADE PROFISSIONAL
1)
Conte um pouco da sua história, como foi sua vida escolar, onde você estudou?
Enfim, conte como você chegou ao Magistério e por quê escolheu ser professor(a)?
R: Minha vida escolar foi tranquila, não tinha dificuldades em assimilar os conteúdos e tive
bons professores que me recordo ainda hoje apesar de ter recebido um ensino
tradicionalíssimo.
Venho de uma família de professores e desde crianças sempre fui encantada com a
profissão, nunca tive dúvidas do que eu gostaria de “ser” quando crescesse.
A minha escolha pelo magistério veio desde criança, adorava brincar de escolinha e claro,
eu sempre era a professora da brincadeira.
Fiz todo o ensino fundamental em escola pública e já me preparava para o vestibulinho para
entrar no tão sonhado Magistério.
Iniciei o Magistério em 1993 em uma escola estadual e terminei em 1997, em outra escola
que oferecia o CEFAM, realizando assim meu grande sonho de ser professora.
37
38
Para preservar a identidade da professora, a mesma será identificada como “P-EAM”
Para preservar a Universidade, utilizamos a sigla “U.A”.
300
2)
O que você achou de sua formação? Seu curso lhe formou para trabalhar com
crianças?
R: Minha formação foi muito boa tanto no magistério quanto na universidade. Tive ótimos
professores, mas aprendi mesmo a trabalhar com as crianças na prática de sala de aula e
nos cursos de formação que faço até hoje, e com os encontros para estudo na EMEF em
que trabalho (JEIf – Jornada especial integrada de formação.
3)
Como este curso lhe preparou para ensinar as crianças do Ensino Fundamental?
R: No curso tive aulas teóricas, vídeo conferencia e com ótimas referências bibliográficas
que pautam meu trabalho até hoje. Tínhamos aulas práticas onde vivenciávamos a prática
de uma sala de aula com oficinas, no meu caso foi muito mais fácil, pois eu já estava na
rede de ensino e podia aplicar as oficinas na mi nha própria sala de aula.
4)
Em que série/ano você se sente mais à vontade para atuar?
R: Adoro atuar no 5º ano do ensino fundamental (4ª serie). Me sinto mais a vontade com
eles porque são mais independentes e mais maduros.
5)
Em relação às áreas do conhecimento, por exemplo, Alfabetização, Ciências,
Matemática entre outros, no que seu curso lhe preparou melhor? Por quê?
R: Creio que tive uma ótima formação quanto à alfabetização, pois além do magistério e da
universidade, fiz cursos de formação como o PROFA, Educação transversal e
multidisciplinar entre outros oferecidos pela SME.
Por outro lado tenho que admitir muita dificuldade com a matemática, pois apesar da
formação que tenho, os cursos de alfabetização nunca deram muita ênfase para essa área
do conhecimento.
6)
Qual área você mais gosta de ensinar? Por quê?
R: Gosto mais da alfabetização, português, ciências, história e geografia relaciono todas
essas áreas entre si com mais facilidade do que com a matemática. Sempre gostei mais da
área de humanas do que de exatas.
7)
Você gosta de ensinar Matemática? Poderia citar um exemplo do que você mais gosta
na área da Matemática?
R: Não gosto muito por conta da minha dificuldade de "como" ensinar a matemática. Tenho
consciência da minha defasagem nessa área. Gosto de trabalhar com gráficos e tabelas.
8)
Em sua opinião, o que é mais trabalhoso ou mais difícil para ensinar Matemática?
301
R: O mais trabalhoso em minha opinião é divisão e frações.
9)
O que você acredita ser preciso para ensinar Matemática para as crianças?
R: Acredito que muito estudo e uma formação específica de alfabetização em matemática
na Universidade e para os professores que já estão em sala de aula.
10)
Que lacunas você sente em sua formação inicial para ensinar Matemática, ou seja, o
que precisaria ter sido trabalhado mais durante sua formação? Por quê?
R: Percebo que faltou contextualização no ensino de matemática na minha formação desde
o inicio no ensino fundamental, aprendi somente as operações descontextualizadas
ensinadas mecanicamente, e hoje tenho dificuldades em ensinar as crianças por conta
dessa falha na minha formação.
11)
Você tem feito, ou sente necessidade de fazer algum curso de formação continuada?
Em qual área?
R: No momento não tenho feito curso de formação continuada fora da escola mas sinto a
necessidade de um curso de alfabetização em matemática.
12)
O que lhe atrai e o que lhe dificulta em sua profissão?
R: Atrai-me o desafio, a magia da troca com os alunos à construção do conhecimento junto
deles o dia a dia e a relação que estabelecemos uns com os outros. O que dificulta é o
pouco tempo que temos com os alunos na sala de aula, a falta de cursos específicos por
área fora do horário de trabalho para nos aperfeiçoar.
13)
Se tivesse chance mudaria de profissão? O que lhe faz permanecer nela?
R: Jamais mudaria de profissão, estar na educação é o que eu quero, permaneço porque
sou cada dia mais apaixonada pelo que faço e busco todos os dias ajudar na formação dos
meus alunos, mesmo com as dificuldades diárias.
14)
O que lhe atrai e o que dificulta no ensino o de Matemática?
R:
15)
Você conhece o IDEB de sua escola? R:
R: Sim
16)
Você já viu em que nível de proficiência em Matemática que se encontra os alunos da
escola?
R:
302
17)
Quais são as metas propostas para melhoria da proficiência em Matemática?
R:
PARTE B – PRÁTICA PEDAGÓGICA
1) Você pode me descrever sua rotina diária, seu trabalho, como organiza as aulas de
Matemática, quantas vezes por semana ensina Matemática, durante quanto tempo?
R: Iniciamos as aulas com a leitura compartilhada, do livro que leio com as crianças em
seguida dou sequência às aulas do dia.
Tenho uma tabela onde dividi as matérias diárias e sigo o horário diário abaixo:
SEGUNDA
TERÇA
QUARTA
QUINTA
SEXTA
Português
Matemática
Português
Ed. Física
Inglês
Português
Matemática
Ed. Física
Ciências
Matemática
Matemática
História
Português
Ciências
Português
Matemática
Informática
Português
Geografia
Sala de leitura
Inglês
Historia
Ciências
Geografia
Artes
2) Como você planeja suas aulas de Matemática, quais materiais utiliza? Tem seu
planejamento em mãos?
R: Planejo as aulas com base no planejamento anual. Faço pesquisas de atividades e de
métodos de ensino, utilizo livros didáticos.
3)
Dentre as atividades matemáticas propostas para seus alunos, o que você considera
mais importante? Por que?
R: Considero mais importante atividades de situações problemas que contextualizam o
raciocínio matemático porque percebo que as crianças tem dificuldade na interpretação dos
problemas mesmo sendo situações concretas vividas por eles.
4)
Seus alunos se interessam pelas aulas de Matemática? O que você faz para que eles
se interessem?
R: Sim eles se interessam pelas aulas, é uma sala que tem facilidade em matemática, como
pude observar em minhas avaliações na prova da Cidade de matemática do primeiro
semestre.
303
5)
Você se recorda de suas aulas no curso de Pedagogia (ou formação inicial), nas
disciplinas ligadas ao ensino de Matemática? Como eram essas aulas? Quais assuntos
eram tratados?
R: Na faculdade, tínhamos oficinas matemáticas e aulas expositivas. Fazíamos seminários
com aulas práticas.
6)
Você trabalha em sua prática com algo que aprendeu na formação inicial? Poderia
exemplificar?
R: Não. Principalmente porque na minha formação inicial tudo era descontextualizado e eu
busco contextualizar a matemática.
7)
Você tem alguma orientação pedagógica para ensinar Matemática a seus alunos? De
quem? Em alguma instância discute o que ensinar e como ensinar?
R: Tenho orientação da Coordenação pedagógica.
De que forma são feitas as orientações pedagógicas para ensinar Matemática? Essas
orientações auxiliam ou não sua prática em sala de aula? Como?
R: Nos estudos de formação dos professores (JEIF) peço orientações a coordenação
pedagógica e a professores da área mas nada sistematizado.
8)
Você usa o Livro Didático adotado na escola em suas aulas? Complementa com
outros materiais de apoio? Quais?
R: Raramente uso o livro didático prefiro pesquisar atividades, com base nas avaliações
externas que os alunos fazem durante o ano, utilizo o caderno de apoio e aprendizagem de
matemática e outros livros que pesquiso.
9)
Quais são suas maiores dificuldades para trabalhar Matemática com as crianças?
R: Como já havia dito anteriormente a minha dificuldade por conta da minha formação
inicial.
10)
Você gostaria de fazer algum comentário sobre nossa conversa, ou acrescentar algo
que julgue interessante para o tema que discutimos?
R: Gostaria de acrescentar que nós professores necessitamos muito de formação em
matemática.
11)
R:
Você está acostumada (o) a receber estagiários em sua sala? R: Sim
304
12)
Você recebe alguma orientação sobre como receber os estagiários? R: Não
R:
13)
O que propõe como atividades aos estagiários? O que é discutido em termos de
formação?
R: Proponho que ajude as crianças com mais dificuldade e discutimos sobre as dificuldades
que temos e como podemos sanar, que materiais podemos utilizar no nosso trabalho.
14)
Você tem interesse numa formação específica para receber e acompanhar os
estagiários em sua sala?
R: Sim
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R: Não
305
APÊNDICE S - RESPOSTAS PERFIL DAS PROFESSORAS: PERFIL
DA PROFESSORA “P-LISE”
PERFIL DA PROFESSORA “P-LISE”
DADOS DE IDENTIFICAÇÃO
Nome: “P-LISE”39 Idade: 49
Estado Civil : Casada Nº de Filhos: Formação: Superior Completo Tempo de atuação 27 anos
Instituição e ano em que se formou: Universidade “U.C”40
Tempo de atuação no Ensino Fundamental: 27 anos
Enquadramento Funcional: ( ) Contratado ( X ) Efetivo por concurso
Trabalha quantos períodos? (Especifique série/ano) – 2 períodos 1º ano em ambos
Série/Ano em que gosta de atuar: 1º ano
Por quê? R: Tenho satisfação em alfabetizar
PARTE A – FORMAÇÃO – IDENTIDADE PROFISSIONAL
1)
Conte um pouco da sua história, como foi sua vida escolar, onde você estudou?
Enfim, conte como você chegou ao Magistério e por quê escolheu ser professor(a)?
R: Como morava em uma cidade do interior, onde havia apenas os cursos de Magistério e
Técnico de Contabilidade, fui fazer Magistério e logo me interessei pela área.
2)
O que você achou de sua formação? Seu curso lhe formou para trabalhar com
crianças?
R: O curso de magistério foi muito importante para minha formação, já o curso de Pedagogia
pouco contribuiu.
3)
Como este curso lhe preparou para ensinar as crianças do Ensino Fundamental?
R: Só se aprende a trabalhar com crianças trabalhando com crianças, e o curso pouco
ajudou nesse sentido.
4)
Em que série/ano você se sente mais à vontade para atuar?
R: No primeiro ano
39
40
Para preservar a identidade da professora, a mesma será identificada como “P-LISE”
Para preservar a Universidade, utilizamos a sigla “U.C”.
306
5)
Em relação às áreas do conhecimento, por exemplo, Alfabetização, Ciências,
Matemática entre outros, no que seu curso lhe preparou melhor? Por quê?
R: Pouco contribuiu
6)
Qual área você mais gosta de ensinar? Por quê?
R: Alfabetização
7)
Você gosta de ensinar Matemática? Poderia citar um exemplo do que você mais
gosta na área da Matemática?
R: Sim. Situações problema, cálculo mental.
8)
Em sua opinião, o que é mais trabalhoso ou mais difícil para ensinar Matemática?
R: Áreas e perímetros
9)
O que você acredita ser preciso para ensinar Matemática para as crianças?
R: Material concreto
10)
Que lacunas você sente em sua formação inicial para ensinar Matemática, ou seja, o
que precisaria ter sido trabalhado mais durante sua formação? Por quê?
R: O uso do material concreto
11)
Você tem feito, ou sente necessidade de fazer algum curso de formação continuada?
Em qual área?
R: Já fiz “A criança de seis anos no Ensino Fundamental”
12)
O que lhe atrai e o que lhe dificulta em sua profissão?
R: O que atrai prazer em ensinar. O que dificulta a falta de compromisso dos pais.
13)
Se tivesse chance mudaria de profissão? O que lhe faz permanecer nela?
R: Não. Gosto do que faço.
14)
O que lhe atrai e o que dificulta no ensino de Matemática?
R: Não tenho dificuldades nessa área.
15)
R: Não
Você conhece o IDEB de sua escola?
307
16)
Você já viu em que nível de proficiência em Matemática encontram-se os alunos da
escola?
R: Não
17)
Quais são as metas propostas para melhoria da proficiência em Matemática?
R: Não sei
PARTE B – PRÁTICA PEDAGÓGICA
1)
Você pode me descrever sua rotina diária, seu trabalho, como organiza as aulas de
Matemática, quantas vezes por semana ensina Matemática, durante quanto tempo?
R: Quatro vezes por semana, durante 1 h/aula
2)
Como você planeja suas aulas de Matemática, quais materiais utiliza? Tem seu
planejamento em mãos?
R: De acordo com o nível dos alunos – palitos, desenhos, livros didáticos. Sim.
3)
Dentre as atividades matemáticas propostas para seus alunos, o que você considera
mais importante? Por que?
R: Situações problema e cálculo mental.
4)
Seus alunos se interessam pelas aulas de Matemática? O que você faz para que
eles se interessem?
R: Acredito que sim. Proponho desafios.
5)
Você se recorda de suas aulas no curso de Pedagogia (ou formação inicial), nas
disciplinas ligadas ao ensino de Matemática? Como eram essas aulas? Quais assuntos
eram tratados?
R: Não havia nada de interessante.
6)
Você trabalha em sua prática com algo que aprendeu na formação inicial? Poderia
exemplificar?
R: Não.
7)
Você tem alguma orientação pedagógica para ensinar Matemática a seus alunos?
De quem? Em alguma instância discute o que ensinar e como ensinar?
308
De que forma são feitas as orientações pedagógicas para ensinar Matemática? Essas
orientações auxiliam ou não sua prática em sala de aula? Como?
R: Não. Não tenho orientações a esse respeito.
8)
Você usa o Livro Didático adotado na escola em suas aulas? Complementa com
outros materiais de apoio? Quais?
R: Sim. Sim, tampinhas e palitos.
9)
Quais são suas maiores dificuldades para trabalhar Matemática com as crianças?
R: Nenhuma
10)
Você gostaria de fazer algum comentário sobre nossa conversa, ou acrescentar algo
que julgue interessante para o tema que discutimos?
R: Não
11)
Você está acostumada(o) a receber estagiários em sua sala?
R: Algumas vezes
12)
Você recebe alguma orientação sobre como receber os estagiários?
R: Não
13)
O que propõe como atividades aos estagiários? O que é discutido em termos de
formação?
R: Não. Nada. Apenas acompanho e proponho atividades para a “aluna pesquisadora”.
14)
Você tem interesse numa formação específica para receber e acompanhar os
estagiários em sua sala?
R: Não.
Gostaria de fazer algum comentário ou acrescentar algo que julgue interessante para o tema
que discutimos?
R:
309
ANEXO
310
ANEXO – MATRIZ CURRICULAR DO CURSO DE PEDAGOGIA
Ver pág. 80
Curso de Pedagogia
Fundamento Legal: LDB n° 9394/96, de 20/12/1996, que estabelece as Diretrizes e Bases
da Educação; Parecer CNE/CP 05/2005, aprovado em 13/12/05; Diretrizes Curriculares
Nacionais para o Curso de Pedagogia; Parecer CNE/CP 3/06, aprovado em 21/02/06 –
Reexame do Parecer CNE/CP 05/2005; Diretrizes Curriculares Nacionais para o Curso de
Pedagogia; Resolução CNE/CP 01/2006, de 15/05/06 - Institui as Diretrizes Curriculares
Nacionais para o Curso de Graduação em Pedagogia, licenciatura.
Ingressantes 2010
C/H
Semanal
1º Semestre
História da Educação e da Pedagogia
Políticas Públicas e Educação Infantil
Legislação da Educação Nacional e Políticas Educacionais (EAD)
Psicologia da Educação
Educação, Jogos e Brincadeiras
C/H/A
Semestral
04
04
04
04
04
C/H/R
Semestral
80
80
80
80
80
-
Estudos Dirigidos
Total
20
320
80
Total em horas-relógio
C/H
Semanal
C/H/A
Semestral
C/H/R
Semestral
2º Semestre
História da Educação no Brasil
Língua Portuguesa (EAD)
Educação Infantil: Currículo
Pensamento, Linguagem e Desenvolvimento Humano
Corpo, Movimento e Psicomotricidade
04
04
04
04
04
80
80
80
80
80
-
Disciplina Optativa
04
80
-
24
400
80
Estudos Dirigidos I
Total
Total em horas-relógio
311
C/H
Semanal
C/H/A
Semestral
C/H/R
Semestral
Organização do Trabalho Docente
Alfabetização e Letramento
Fundamentos Metodológicos do Ensino da Arte e da Música I
Fundamentos Metodológicos do Ensino de Matemática I
Fundamentos Metodológicos do Ensino da História e Geografia I
Fundamentos Metodológicos do Ensino de Ciências
Tecnologias da Informação e da Comunicação na Educação
(EAD)
Disciplina Optativa
Estudos Dirigidos II
04
04
02
02
02
02
80
80
40
40
40
40
-
04
-
80
04
80
-
Total
24
400
80
C/H
Semanal
C/H/A
Semestral
C/H/R
Semestral
Sociologia (EAD)
Filosofia da Educação
LIBRAS
Fundamentos Metodológicos do Ensino da Arte e da Música II
Fundamentos Metodológicos do Ensino da História e Geografia II
Fundamentos Metodológicos do Ensino de Matemática II
Prática de Ensino e Orientação de Estágio Curricular
Supervisionado em Educação Infantil
Estudos Dirigidos III
04
04
02
02
02
02
80
40
40
40
40
80
-
02
40
-
Subtotal
18
280
80
-
-
100
18
280
180
3º Semestre
Total em horas-relógio
4º Semestre
Estágio Curricular Supervisionado em Educação Infantil
Total
Total em horas-relógio
312
C/H
Semanal
C/H/A
Semestral
C/H/R
Semestral
Metodologia de Pesquisa (EAD)
Escola, Currículo e Sociedade
Gestão Educacional e Organização do Trabalho Pedagógico I
Educação de Jovens e Adultos
Avaliação Educacional
Educação e Saúde
Estatística Aplicada à Educação
Prática de Ensino e Orientação de Estágio Curricular
Supervisionado nos Anos Iniciais do Ensino Fundamental
Educação Inclusiva
Estudos Dirigidos IV
Subtotal
Estágio Curricular Supervisionado nos anos iniciais do Ensino
Fundamental
04
02
02
02
02
02
02
40
40
40
40
40
40
80
-
02
40
-
02
40
-
20
320
80
-
-
100
Total
24
320
180
C/H
Semanal
C/H/A
Semestral
C/H/R
Semestral
04
02
02
02
02
04
40
40
40
40
80
80
-
02
40
-
02
40
-
18
-
320
-
80
100
20
320
180
5º Semestre
Total em horas-relógio
6º Semestre
Diversidade Étnico-Cultural (EAD)
Educação, Movimentos Populares e Transformação
Educação não Formal
Gestão Educacional e Organização do Trabalho Pedagógico II
Economia da Educação
Dificuldades de Aprendizagem
Prática de Ensino e Orientação de Estágio Curricular
Supervisionado em Gestão Educacional
Escola, Família e Comunidade
Estudos Dirigidos V
Subtotal
Estágio Curricular Supervisionado em Gestão Educacional
Total
Total em horas-relógio