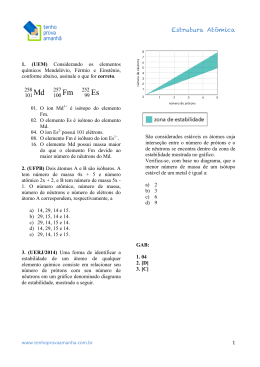
Evolvere Scientia, V. 1, N. 1,p 14-25, 2013
Evolvere Scientia
ARTIGO
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO
NÚCLEOS SUPERPESADOS:
FÓRMULA DE MASSA PARA NÚCLEOS SUPERPESADOS
Cloves dos Santos Miranda, Telio Nobre Leite
Universidade Federal do Vale do São Francisco, 48902-300 Juazeiro, BA, Brasil.
Palavras-chave: Núcleos exóticos, fórmula de massa, energia de ligação, energia de separação,
estabilidade, emissão de partículas.
INTRODUÇÃO
dados experimentais para o valor Q da
reação da emissão de partícula alfa de
A busca por elementos químicos
um bom número de núcleos pesados e
cujos núcleos possuem valor de Z
superpesados. Esta fórmula de massa
grande tem acontecido desde o trabalho
será usada para estimar a existência de
dos Curie que descobriram os primeiros
novos núcleos pesados ligados, pois
elementos radioativos naturais no início
uma das grandes questões que a Física
do
a
Nuclear tenta responder é qual o maior
elementos
número de prótons (chamado de número
atômico
atômico) que um núcleo pode ter e
Z ≥ 110 trouxe muita excitação para
mesmo assim ser ligado (estável). Esta
as comunidades de físicos nucleares e
resposta depende do balanço entre a
atômicos [1] . Estes núcleos, chamados
interação nuclear entre os prótons e
de superpesados, habitam uma região
nêutrons, que é atrativa, mas de curto
bem ao extremo da carta de nuclídeos
alcance, e a interação elétrica entre os
que passou a ser conhecida como ilha
prótons, que é repulsiva e de longo
de estabilidade [2].
alcance, porém menos intensa que a
século
descoberta
químicos
20.
de
com
Recentemente,
novos
número
Neste trabalho buscou-se uma
interação nuclear. À medida que o valor
fórmula de massa que reproduzisse os
de Z vai crescendo (ou seja, o núcleo
14
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
vai ficando mais pesado), o papel da
partículas interagentes) passa a ser um
repulsão elétrica entre os prótons vai se
ponto decisivo na previsão de novos
tornando importante. Desta forma, para
núcleos superpesados estáveis ou de meia-
fazer um núcleo pesado ficar ligado é
vida
necessária a adição de mais nêutrons.
Como se pode observar na carta de
nuclídeo mostrada na Figura 1, a região
dos núcleos estáveis vai se desviando
longa.
analisados
Neste
estes
trabalho
sistemas
foram
nucleares
superpesados a partir de modelos simples
que
buscam
entender
de
forma
fenomenológica as razões da estabilidade
destes sistemas ou que tipo de decaimento
para a direita da linha N = Z à medida
eles devem possuir (decaimento alfa ou
que Z cresce. Aqui N representa o
fissão espontânea).
número de nêutrons existentes no
núcleo.
Metodologia
Para
verificar
os
limites
da
estabilidade nuclear devem-se entender os
mecanismos que fazem um sistema nuclear
constituído de prótons e nêutrons ficar
estável contra a emissão de partícula. Para
isto é observado atentamente a energia de
ligação nuclear. Esta energia, notada por
B (A, Z) , é aquela energia necessária para
d
Figura 1: Carta de Nuclídeo [2].
Uma das grandes dificuldades de
explorar estes limites da estabilidade
nuclear vem do fato que até o momento
não é conhecida completamente a forma
da interação nuclear. Assim a verificação
ligar os constituintes básicos do núcleo, ou
seja, os Z prótons e N nêutrons (temos
que A = N + Z é o número de massa). De
forma mais precisa, a B (A, Z) é definida
como a diferença entre a soma das massas
dos Z prótons e N nêutrons, e a massa
M (A, Z) do núcleo [3] :
de validade, na região de Z grande, de
modelos macroscópicos (onde o núcleo é
B(A,Z ) = Z m
p
+ N m
n
− M (A,Z )
.
tratado como um fluido quântico) e de
Os limites da estabilidade nuclear
modelos microscópicos (onde o núcleo é
são definidos pela energia de separação de
tratado como um sistema quântico de
partícula, ou seja, a partir do ponto em que
15
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
a emissão de partícula nuclear torna-se
, onde os parâmetros desta fórmula foram
espontânea (energia de separação menor
determinados comparando com as medidas
que zero). Estas energias são definidas em
experimentais:
a v = 15.79 MeV ,
a s = 18.34 MeV ,
a c = 0 .71 MeV e
termos da energia de ligação e representa o
quanto de energia precisa ser adicionada ao
sistema para que ele emita partícula. A
a sim = 23.21 MeV . O primeiro termo da
energia de separação de um nêutron é dada
fórmula acima é denominado de termo de
por:
volume, pois se verificou que o volume
ocupado
S
= B ( A , Z ) − B ( A − 1, Z
n
).
pelos
núcleos
estáveis
é
diretamente proporcional ao número de
massa (V ≈ A) . Por esta mesma razão, o
A energia de separação de um próton é
segundo termo é denominado de termo de
dada por:
superfície. O terceiro termo é o termo de
S
p
= B ( A , Z ) − B ( A − 1, Z
− 1)
.
Coulomb, devido à repulsão elétrica entre
os prótons. O penúltimo termo é chamado
A energia de separação de uma
de termo de assimetria nuclear, pois
partícula alfa (núcleo de Hélio) é dada por:
S
α
=
B ( A , Z ) −
B ( A
− 4 , Z
− 2 ) −
B ( 4 ,2 )
A - 2Z = N - Z . Só nos resta mencionar o
.
significado de último termo denotado por
δ . Ele é o termo de energia de
Para verificar a existência de
emparelhamento que assume os seguintes
novos sistemas nucleares estáveis com
δ = a p A −1 / 2 quando N e Z são
valores:
excesso de nêutrons foi realizado a
números
implementação numérica das versões de
pares
(núcleo
par-par),
fórmula de massa que descrevem a
δ = − a p A −1 / 2 quando N e Z são
energia de ligação nuclear: extensões da
números ímpares (núcleo ímpar-ímpar) ou
fórmula de massa de Beth-Weizsäcker
zero quando A é um número ímpar (núcleo
(BW )
( Nos) .
ímpar), onde a p = 12 MeV .
e fórmula do nosso trabalho
No
PIBIC-UNIVASF
desenvolvido de agosto de 2005 a julho de
A curva da fórmula de massa de
Beth-Weizsäcker (BW)
projeto
2006 foi proposta uma extensão da fórmula
é dada pela
de massa de BW considerando o efeito da
expressão [3,4] :
assimetria nuclear nos termos de superfície
B( A, Z ) = av A − a s A
16
2/3
− a c Z ( Z − 1) / A
1/3
2
− a sim ( A − 2 Z ) / A + δ
e de Coulomb:
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
B ( A , Z ) = B BW ( A , Z ) + a S 2 A 2 / 3 I 2 + a C 2
Z ( Z − 1) 2
I
A1 / 3
,
superfície decresce. Com isso a nossa nova
proposta, agora sendo utilizada para núcleos
superpesados, fica da seguinte forma:
onde
I=
N−Z
A
é o parâmetro de
assimetria nuclear, e a S 2
e
a C 2 são
parâmetros a serem ajustados.
B( A, Z) = BBW ( A, Z) + aS2 A2/ 3 I 2 + aC2
Z(Z −1) 2
I + asim2 ( A− 2Z)2 I 2 / A
A1/ 3
Observa-se que esta proposta também
reproduz
com
sucesso
os
dados
foi
experimentais para a energia de ligação [5] .
introduzido mais um parâmetro além dos já
Verifica-se que os parâmetros de assimetria
citados, o parâmetro a Sim 2 no termo de
dos termos de superfície, Coulomb e de
Neste
assimetria,
presente
pelo
fato
trabalho
de
os
núcleos
superpesados serem maiores influenciados
por esse termo em relação aos núcleos mais
leves estudados no projeto passado PIBICUNIVASF 2007/2008. Essa influência pode
ser mais bem interpretada na figura 2.
assimetria nuclear reduzem negativamente a
energia
de
ligação
dos
núcleos
superpesados. Essas reduções de energia de
ligação podem ser interpretadas fisicamente
como influência dos efeitos de deformações
da simetria esférica nos respectivos termos
desses núcleos.
Cerca de 288 núcleos estáveis já
são conhecidos. Aproximadamente seis mil
são previstos possuir algum tipo de
radioatividade (emissão de partículas), mas
somente um terço deles foi encontrado
experimentalmente. Fazendo a comparação
entre as duas fórmulas de massa citadas
com os dados experimentais retirados da
Figura 2: Contribuições à energia de ligação
média por nucleon devido aos termos de
volume, superfície, Coulomb e de assimetria.
compilação feita por Audi, Wapstra e
Thibault [5] , com isso pode-se testar o
sucesso delas em prever a existência de
sistemas nucleares estáveis com excesso de
Na medida em que a massa
aumenta o valor a ser subtraído do termo de
volume é a seguinte: o valor do termo de
assimetria aumenta juntamente com o termo
de Coulomb, enquanto que o termo de
17
nêutrons. Esses sistemas não podem emitir
nenhum tipo de partícula nuclear (nêutron,
próton,
dois
nêutrons,
partícula alfa, etc).
dois
prótons,
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
Para a fórmula proposta pelo
nosso
trabalho
os
parâmetros
de
tabelas com a utilização do programa
computacional
na
assimetria nuclear, a S 2 , a C 2 e a Sim 2
FORTRAN
foram obtidos através de resoluções de
implementadas as equações de massa já
matrizes no software de programação
citadas nesse projeto.
Com
MATLAB.
na
linguagem
ajuda
qual
da
foram
ferramenta
Para testar a estabilidade contra
programa ORIGIN os resultados foram
a emissão de partícula alfa foi calculada
analisados graficamente e interpretados
primeiramente a respectiva energia de
juntamente
ligação B( A, Z ) para uma quantidade
experimentais encontrados na literatura,
de núcleos dos isótopos Ds , Rg , Uub ,
Uut , Uuq , Uup , Uuh e Uus , sendo
seus respectivos números atômicos
Z = 110 , Z = 111 , Z = 112 , Z = 113 ,
Z = 114 ,
Z = 115 ,
Z = 116
e
Z = 117 , respectivamente. Com isso foi
possível
calcular
as
energias
de
separação de um nêutron, dada pela
definição:
S1n = B( A, Z ) − B( A − 1, Z )
de um próton, dada pela definição:
S 1 p = B ( A, Z ) − B ( A − 1, Z − 1)
com
os
valores
compilação feita por Audi, Wapstra e
Thibault [5] .
Os valores dos isótopos para as
demais cadeias foram extrapolados
através da fórmula proposta pelo nosso
projeto a fim de prever a massa atômica
nuclear que seria estável contra emissão
de partícula alfa. Além disso, foi
proposta em estudo uma hipótese a fim
de entender quais os mecanismos que
envolvem os aspectos da interação
nuclear que são responsáveis para
explicar sua estabilidade.
de dois nêutrons, dada pela definição:
S 2 n = B( A, Z ) − B( A − 2, Z )
Resultados e Discussões
de dois prótons, dada pela definição:
S 2 p = B( A, Z ) − B ( A − 2, Z − 2 )
e de partícula alfa, dada pela definição:
Sα = B( A, Z ) − B( A − 4, Z − 2) − B( 4, 2)
Os dados B( A, Z ) , S1n , S1 p ,
S 2 n , S 2 p e Sα
18
foram gerados em
Como já foi dito, a nova fórmula
proposta pelo nosso trabalho é dada por:
B(A, Z) = BBW(A, Z)+aS2A2/ 3I2 +aC2
Z(Z−1) 2
I +asim2(A−2Z)2 I2 / A
1/ 3
A
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
Sendo os parâmetros a S 2 , aC 2 e
Dessa forma na diferença obtida
a sim 2 a serem determinados pelo software
em cada isótopo selecionado da fórmula
MATLAB e posteriormente implementados
de Beth-Weizsäcker em relação aos
valores experimentais, foi considerada
na programação FORTRAN.
como uma correção através dos termos
Foram comparados os valores da
energia de ligação dos isótopos obtidos
pela fórmula de Beth-Weizsäcker com
os valores experimentais, compilação
feita por Audi, Wapstra e Thibault.
adicionais da nossa nova proposta.
Igualando o valor da energia de ligação
obtida experimentalmente com o a
fórmula proposta pelo nosso trabalho,
tem-se que:
Como na nossa fórmula são
utilizados três parâmetros de assimetria
nuclear
aS2 ,
aC 2
e
linear.
Para
isso
foram
escolhidos três isótopos, os de massa
A = 267 , A = 274 e A = 281 , de forma
que abrangesse de forma eqüidistante
toda
a
cadeia
de
Z(Z−1) 2
I +asim2(A−2Z)2 / A
1/3
A
a Sim 2 , foram
necessárias três equações para compor o
sistema
Bexp(A,Z)=BBW(A,Z)+aS2A2/3I2 +aC2
isótopos
do
A
diferença
entre
o
valor
experimental e a dada pela fórmula de
Beth-Weizsäcker é o valor a ser
corrigido pelos termos de assimetria da
nossa fórmula:
aS2A2/3I2 +aC2
Darmstárdio experimentais. Veja na
figura 3.
Z(Z−1) 2
I +asim2(A−2Z)2 / A=Bexp(A,Z)−BBW(A,Z)
A1/3
Como Z = 110 e as respectivas
massas
A = 267 ,
são:
A = 274
e
A = 281 , a matriz ficou da seguinte
forma:
Para A= 267 ⇒ 1,2848
aS2 +57,6973
aC2 +0,2564
asim2 = −7,007

aS2 +71,7005
aC2 +0,4134
asim2 = −9,589
Para A= 274 ⇒ 1,6385

aS2 +86,2642
aC2 +0,6240
asim2 = −12,068
Para A= 281 ⇒ 2,0217
Como já foi dito não só essa
matriz, mas para todas as demais
Figura 3: Comparação da energia de ligação
da fórmula de Beth-Weizsäcker com os
valores experimentais.
19
cadeias de isótopos superpesados foram
calculados
no
MATLAB,
e
foi
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
observado de forma surpreendente que
todos
os
valores
dos
parâmetros
(a)
(b)
poderiam assumir valores únicos e
constantes,
nas
quais
foram
eles
a S 2 = −1 , a C 2 = − 0,1 e a Sim 2 = −1 ,
podendo esses valores ser utilizados em
todos os núcleos superpesados, sendo os
resultados
bem
satisfatórios
em
aos
experimentais.
Os
comparação
valores
desses
implementados
parâmetros
em
foram
programação
FORTRAN para obtenção dos valores
teóricos das fórmulas de massa já
citadas nesse projeto. Na figura 4, as
análises de energia de separação (um
nêutron, um próton, dois nêutrons, dois
prótons
e
representadas.
partícula
alfa)
estão
(c)
(d)
(e)
Figura 4: Comparação dos valores
experimentais da energia de separação, (a) de
um nêutron, (b) de um próton, (c) de dois
nêutrons, (d) de dois prótons e (e) de
partícula alfa, para a cadeia do Darmstádio
com as fórmulas de massa propostas por
20
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
Bethe-Weizsäcker (BW), e pelo
trabalho (Nos), respectivamente.
nosso
diminuir a energia de ligação para tal
equação. Então a assimetria nuclear faz
É interessante ressaltar que os
com que esta redução seja menor. Este
isótopos que estiverem acima da linha
resultado está de acordo com cálculos
da energia de separação igual a zero dos
microscópicos de estrutura nuclear que
respectivos gráficos são ditos estáveis,
indicam que à medida que o excesso de
quando obtidos experimentalmente.
nêutron cresce, os prótons tendem a
As fórmulas responderam bem
ficar mais ligados ao núcleo. Isso
as evidências experimentais, porém em
também pode ser comprovado na figura
algumas ocasiões prevaleceu mais, em
4 nos itens (b) e (d) que mostram a
termos de aproximação, os valores de
energia de separação de um próton e
BW , e em outras situações prevaleceu
dois prótons, respectivamente.
mais a fórmula proposta pelo nosso
Nesta figura mostra que com o
trabalho. Por exemplo, para os gráficos
aumento da massa nuclear (aumento de
de energia de separação de um nêutron,
nêutrons) a energia de separação de
um próton, dois nêutrons, dois prótons e
prótons fica cada fez maior, impedindo
de partícula alfa para os elementos
a emissão de tal partícula, ou seja, o
Z = 110 , Z = 111 e Z = 112 , foram
formato de uma função crescente
melhores
representados
nossa
explica a tendência dos prótons ficarem
fórmula,
porém
Z = 113 ,
mais e mais ligados a medida que o
Z = 114 , Z = 115 , Z = 116 e Z = 117
número de nêutrons aumenta no núcleo
esses valores foram melhores para a
atômico.
para
pela
fórmula de BW exceto para a energia
O objetivo desse trabalho foi
de separação de partícula alfa que foi
verificar a existência de novos sistemas
evidenciado em todos os elementos
nucleares com excesso de nêutrons que
analisados, que foram satisfatoriamente
são estáveis contra a emissão de
bem representados pela nossa fórmula.
partícula.
Como
foi
observado
e
Os valores dos parâmetros a S 2 ,
comentado anteriormente da figura 4,
aC 2 e a Sim 2 foram determinados e esses
em que os prótons tendem a ficar mais
por sua vez obtiveram sinais negativos,
sendo
esses
termos
subtraídos
na
fórmula de BW , ou seja, tendendo a
ligados ao núcleo através da energia de
separação crescente, porém até então
ainda não foi dito que os nêutrons
possuem uma energia de separação
21
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
decrescente, tendendo cada vez mais a
instáveis, as duas primeiras linhas
ficarem menos ligados ao núcleo com o
tracejadas mostram os núcleos que
aumento de sua quantidade. A figura 5
possuem número de massa ímpar
indica uma extrapolação dos valores da
enquanto as duas últimas mostram os
energia de separação de um nêutron
núcleos de número par.
para as fórmulas de Bethe-Weizsäcker e
pela
fórmula
nossa,
mostrada
anteriormente na figura 4(a). Essa
extrapolação é de extrema importância
na previsão de quais isótopos são
instáveis
contra
emissão
de
tais
partículas. Na figura 5 observa-se a
pequena faixa de valores experimentais
para
a
cadeia
dos
isótopos
do
Darmstárdio Z = 110 .
Z
110
111
112
113
114
115
116
117
118
“A” estável
contra emissão
de dois
nêutrons para
fórmula de
BetheWeizsäcker
“A”
“A”
ímpar
par
361
390
393
368
369
396
401
372
377
404
407
380
383
412
415
386
391
418
“A” estável
contra emissão
de dois
nêutrons
proposta pela
nossa fórmula
“A”
ímpar
353
381
361
389
367
397
375
403
381
“A”
par
378
356
386
364
392
370
400
378
408
Tabela 1: Valores previstos de massa para os
núcleos instáveis, emissão de um nêutron
estipulados pela fórmula de BetheWeizsäcker e pela nossa fórmula.
Figura 5: Extrapolação dos valores da
energia de separação de um nêutron da
fórmula Bethe-Weizsäcker (BW) e da nossa
fórmula (Nos) para a cadeia de isótopos do
Darmastádio.
A tabela 1 mostra os valores
previstos de massa para os núcleos com
instabilidade contra emissão de um
nêutron estipulados pela fórmula de
Bethe-Weizsäcker e pela nossa fórmula.
Os núcleos estão previstos em
termos de paridade para os elementos
superpesados estudados.
A
figura
6
indica
uma
extrapolação dos valores da energia de
separação de dois nêutrons para as
fórmulas de Bethe-Weizsäcker e pela
O gráfico da figura 5 mostra
através das linhas tracejadas os núcleos
22
fórmula nossa, mostrada anteriormente
na figura 5(c).
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
para a previsão de núcleos estáveis
contra emissão de partículas alfa para a
cadeia de isótopos do Darmstárdio. Essa
figura é um prolongamento da figura já
vista, a figura 4(e). Os supostos núcleos
estáveis são aqueles que estão acima da
linha “drip line”, na parte positiva do
gráfico.
Figura 6: Extrapolação dos valores da
energia de separação de dois nêutrons da
fórmula Bethe-Weizsäcker (BW) e da nossa
fórmula (Nos) para a cadeia de isótopos do
Darmastádio.
Os valores dos isótopos instáveis
contra emissão de dois nêutrons para os
demais
elementos
superpesados
estudados estão na tabela 2.
“A” estável
“A” estável
contra emissão
contra emissão de
de dois nêutrons
dois nêutrons
para fórmula de
proposta pela
BW
nossa fórmula
375
365
110
379
369
111
382
372
112
386
376
113
389
379
114
393
383
115
397
386
116
400
390
117
404
394
118
Tabela 2: Valores previstos de massa para os
núcleos instáveis, emissão de dois nêutrons
estipulados pela fórmula de BetheWeizsäcker e pela nossa fórmula.
Figura 7: Extrapolação dos valores da
energia de separação de partícula alfa da
fórmula Bethe-Weizsäcker (BW) e da nossa
fórmula (Nos) para a cadeia de isótopos do
Darmastádio.
Z
Observa-se que as extrapolações
dos valores das respectivas fórmulas
estão bem além dos já conhecidos
valores experimentais (pontos pretos do
canto inferior esquerdo do gráfico). No
entanto
os
experimentais
avanços
estão
nas
técnicas
permitindo
a
realização de medidas de massas e
energias de ligação com melhores
precisões, possibilitando a produção de
A
figura
7
mostra
uma
extrapolação dos valores da fórmula de
Bethe-Weizsäcker e da fórmula nossa
23
núcleos com excessos de nêutrons cada
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
vez maiores, estendendo cada vez mais
número de massa atômico que seria
a cadeia de isótopos.
estável contra emissão de partículas alfa
Um exemplo de análise que se
poderia
fazer,
tomando-se
para os demais elementos superpesados.
muita
cautela, é que, para a fórmula proposta
Conclusão
pelo nosso trabalho esperaria que o
primeiro
isótopo
da
cadeia
do
Darmastádio estável contra emissão de
Neste projeto foi implementado
alguns
fórmulas
de
massa
para
Ds , é esperado
descrever tanto a energia de ligação
também que esse núcleo seria estável
como das energias de separação de
contra emissão de nêutron já que seu
prótons, nêutrons e partículas alfa para
valor de massa (A=340) está abaixo do
uma série de cadeias de isótopos
valor estabelecido na tabela 1 para
superpesados.
partícula alfa seria o
340
110
núcleo par, menor que 353 e que
Diante disso, propomos uma
também seria estável contra emissão de
fórmula de massa a partir da antiga
dois neutros já que seu valor de massa
fórmula de Bethe-Weizsäcker com a
está abaixo do valor estabelecido na
adição de três novos termos, o de
tabela 2, menor que 365.
superfície, o de Coulomb e o de
assimetria.
Foi observado que os ajustes
“A” estável
“A” estável
contra emissão de contra emissão de
partícula alfa
alfa proposta pela
para fórmula de
nossa fórmula
BW
301
340
110
305
344
111
309
349
112
313
353
113
318
358
114
322
362
115
326
367
116
331
372
117
335
376
118
Tabela 3: Valores previstos de massa para os
núcleos estáveis contra emissão de partícula
alfa estipulados pela fórmula de BetheWeizsäcker e pela nossa fórmula.
feitos pelo nosso trabalho causaram
Outras previsões poderiam ser
pesados e superpesados, varrendo toda a
Z
feitas analisando a tabela 3 que prever o
24
certo animo e uma boa expectativa em
relação às demais fórmulas. Desta
forma, pretende-se posteriormente fazer
uma unificação da fórmula proposta
pelo
nosso
trabalho
através
da
metodologia proposta na obtenção de
parâmetros, para que possa expressar
satisfatoriamente
os
valores
experimentais tanto para núcleos leves e
intermediários quanto
tabela periódica.
para núcleos
Evolvere Science, V. 1, N. 1,p. 14-25, 2013
Os
avanços
experimentais
estão
nas
técnicas
permitindo
a
[4] K. L. G. Heyde, Basic Ideas and
Concepts
in
Nuclear
Physics.
realização de medidas de massas e
IOP,Bristol, 1999.
energias de ligação com melhores
[5] G.Audi, A.H.Wapstra e C.Thibault,
precisões, possibilitando a produção de
Nuclear Physics A 729, 337 (2003).
núcleos com excessos de nêutrons cada
vez maiores, estendendo cada vez mais
a cadeia de isótopos. Com isso esse tipo
de estudo desenvolvido no presente
trabalho poderia caminhar em paralelo
com esses avanços experimentais a fim
de pelo menos indicar o caminho na
obtenção de núcleos cada vez mais
pesados estáveis contra emissão de
partículas.
É importante lembrar que essas
análises de extrapolação são apenas
previsões com base nos comportamento
histórico dos núcleos já existentes,
porém não são contabilizados quaisquer
comportamentos
anormais
que
por
ventura possam ocorrer nesses novos
núcleos.
Referências
[1] S. Ćwiok, P.–H. Heenen & W.
Nazarewicz, Nature 433, 705 (2005).
[2] W. Zhang et al., Nuclear Physics A
753, 106 (2005).
[3] K. C. Chung, Introdução à Física
Nuclear EdUERJ, Rio de Janeiro, 2001.
25