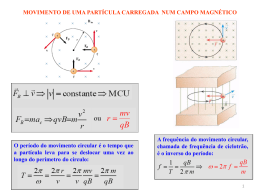
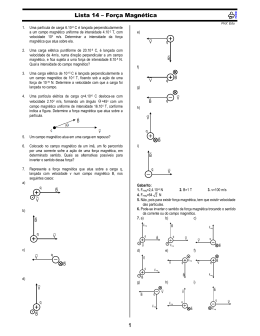
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
1. (Fuvest) Uma partícula, de massa m e com carga elétrica Q, cai
verticalmente com velocidade constante v³. Nessas condições, a força
de resistência do ar pode ser considerada como R(ar)=kv, sendo k uma
constante e v a velocidade. A partícula penetra, então, em uma região
onde atua um campo magnético uniforme e constante B, perpendicular
ao plano do papel e, nele entrando, conforme a figura. A velocidade da
partícula é, então, alterada, adquirindo, após certo intervalo de tempo,
um novo valor v‚, constante.
a) O intervalo de tempo Ðt, em s, que o próton leva para ir de A a P.
b) O raio R, em m, do cilindro que contém a trajetória em hélice do
próton.
c) A intensidade do campo magnético B, em tesla, que provoca esse
movimento.
Uma partícula com carga Q, que se move em um campo B, com
velocidade V, fica sujeita a uma força de intensidade F=Q×VŠ×B,
normal ao plano formado por B e VŠ, sendo VŠ a componente da
velocidade V normal a B.
3. (Ufal) Considere uma região onde existe um campo magnético
uniforme B, perpendicular ao plano do papel e penetrando nele. Um
elétron penetra nessa região, perpendicular às linhas de indução com
velocidade ¬.
(Lembre-se de que a intensidade da força magnética |F(M)|=|q|.|v|.|B|,
em unidades SI, para v perpendicular a B).
a) Expresse o valor da constante k em função de m, g e v³.
b) Esquematize os vetores das forças [Peso, R(ar) e F(M)] que agem
sobre a partícula, em presença do campo B, na situação em que a
velocidade passa a ser a velocidade v‚. Represente, por uma linha
tracejada, direção e sentido de v‚.
c) Expresse o valor da velocidade v‚ da partícula, na região onde atua
o campo B, em função de m, g, k, B e Q.
a) Descreva a trajetória descrita pelo elétron a partir do instante que
penetra na região do campo B.
b) É possível calcular o trabalho realizado pela força magnética que
atua no elétron? Explique.
2. (Fuvest) Um próton de massa M¸1,6×10−£¨kg, com carga elétrica
Q=1,6×10−¢ªC, é lançado em A, com velocidade V³, em uma região
onde atua um campo magnético uniforme B, na direção x. A
velocidade V³, que forma um ângulo š com o eixo x, tem
componentes V³Ö=4,0×10§m/s e V³Ù=3,0×10§m/s. O próton descreve
um movimento em forma de hélice, voltando a cruzar o eixo x, em P,
com a mesma velocidade inicial, a uma distância L³=12m do ponto A.
Desconsiderando a ação do campo gravitacional e utilizando ™¸3,
determine:
4. (Ufc) Duas partículas pontuais PX e P‚, com massas mX e m‚ ,
possuem cargas elétricas qX e q‚, respectivamente. Ambas as partículas
são lançadas através de um tubo em uma região na qual existe um
campo magnético B, perpendicular ao plano da página e apontando
para fora dela, conforme a figura a seguir. Considere mX = 4m, m‚ =
m, qX = 3q e q‚ = q. Desconsidere qualquer efeito da gravidade e
quaisquer atritos que porventura possam existir.
a) Determine a energia mínima necessária de cada partícula para que a
trajetória resultante toque o LADO 2.
b) Determine o tempo gasto pela partícula que primeiro retorna ao
LADO 1, obedecendo à condição do item (a).
1
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
a) na figura 2, represente os vetores força elétrica, ùe, e força
magnética, ùm, que atuam na partícula assim que entra na região de
campos cruzados, indicando suas magnitudes.
b) Determine a velocidade que a partícula deve ter, para não ser
desviada.
5. (Ufg) Uma partícula de massa m e carga q movimenta-se com
velocidade constante v, ao longo de uma determinada direção. Em um
dado instante de tempo, é acionado um campo magnético uniforme B,
em todo o espaço, na direção perpendicular à direção do movimento
da partícula. (Despreze efeitos da força gravitacional).
a) Determine a expressão para o período do movimento da partícula.
b) Qual é a variação do módulo da velocidade da partícula, depois de
decorrido um tempo igual ao período determinado no item a.
6. (Ufg) Um acelerador de partículas é uma instalação na qual
partículas são aceleradas e mantidas em uma trajetória curvilínea
fechada, podendo atingir velocidades próximas à da luz. As colisões
que elas podem ter com outras partículas são extremamente
importantes para o melhor entendimento da estrutura interna da
matéria.
O princípio básico de funcionamento de um acelerador de partículas
consiste na aplicação combinada de campos elétricos e magnéticos, no
interior de um anel no qual as partículas estão confinadas.
A figura a seguir representa duas regiões distintas onde se movimenta
uma carga elétrica positiva q, inicialmente com velocidade v³.
8. (Ufmg) Três partículas - R, S e T -, carregadas com carga de
mesmo módulo, movem-se com velocidades iguais, constantes, até o
momento em que entram em uma região, cujo campo magnético é
constante e uniforme.
A trajetória de cada uma dessas partículas, depois que elas entram em
tal região, está representada nesta figura:
Região I: existe somente campo elétrico E.
Região II: existe somente campo magnético B, entrando no plano da
folha.
a) Represente a trajetória da carga q ao passar pela Região I e,
posteriormente, pela Região II.
b) Considerando que a partícula tenha carga q = 1,6×10−¢ª C, massa m
= 1,6×10−£¨ kg, e que E = 10¤ V/m, v³ = 10¦ m/s e que o tempo gasto
pela partícula na Região I seja t = 10−§ s, calcule a velocidade com que
a partícula entrará na Região II.
c) Se B = 10−¢ T, calcule o raio do arco de circunferência que a
partícula descreve no campo magnético.
Esse campo magnético é perpendicular ao plano da página e atua
apenas na região sombreada. As trajetórias das partículas estão
contidas nesse plano.
Considerando essas informações,
1. EXPLIQUE por que as partículas S e T se curvam em direção
oposta à da partícula R.
Suponha que o raio da trajetória da partícula T mede o dobro do raio
da R.
2. DETERMINE a razão entre as massas dessas duas partículas.
7. (Ufjf) Um filtro de velocidades é um dispositivo que utiliza campo
elétrico uniforme û perpendicular ao campo magnético uniforme B
(campos cruzados), para selecionar partículas carregadas com
determinadas velocidades. A figura a seguir mostra uma região do
espaço em vácuo entre as placas planas e paralelas de um capacitor.
Perpendicular ao campo produzido pelas placas, está o campo
magnético uniforme. Uma partícula positiva de carga q move-se na
direção z com velocidade constante « (conforme a figura 1).
2
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
11. (Ufrrj) Uma partícula de carga positiva q e inicialmente com
velocidade V³ no sentido positivo do eixo Y penetra em uma região
onde existe um campo elétrico E³ constante, no sentido positivo do
eixo X, e um campo magnético B³, também constante.
Em um forno de microondas, a radiação eletromagnética é produzida
por um dispositivo em que elétrons descrevem um movimento circular
em um campo magnético, como o descrito anteriormente. Suponha
que, nesse caso, os elétrons se movem com velocidade de módulo
constante e que a freqüência da radiação produzida é de 2,45 × 10ª Hz
e é igual à freqüência de rotação dos elétrons. Suponha, também, que
o campo magnético é constante e uniforme. Considere que a massa do
elétron é 9,11.10−¤¢kg e a carga elementar vale 1,6.10−¢ªC
3. CALCULE o módulo desse campo magnético.
9. (Ufpe) Uma partícula carregada entra em uma região de campo
magnético uniforme, B vetorial, com a trajetória perpendicular ao
campo. Quando a energia cinética da partícula é 4,0 × 10−¢£ J, o raio
de sua órbita circular vale 60 cm. Qual seria o valor, em centímetros,
do raio de sua órbita circular, se esta mesma partícula tivesse uma
energia cinética igual a 2,56 × 10−¢£ J?
Sabendo-se que a velocidade da partícula não se altera, mesmo depois
que ela passa a sofrer a ação dos campos, determine em função de V³
e E³:
(Desconsidere qualquer efeito gravitacional)
a) a componente X do campo magnético;
b) a componente Z do campo magnético;
12. (Ufu) Uma partícula de massa desconhecida e carga elétrica q =
5,0 × 10−¢§ C é acelerada a partir do repouso por uma diferença de
potencial ÐV = 1,6V, indo do ponto PX até o ponto P‚, distantes 2 m
um do outro, conforme figura a seguir.
10. (Ufpe) Uma partícula de massa m = 20 mg e carga q = +400 ˜C
em movimento circular uniforme, na presença de um campo
magnético uniforme B = 1,0 T, tem velocidade escalar v = 5,0 m/s.
Considere que o movimento ocorre no vácuo e que a ação da força
peso é desprezível em relação à força magnética que atua na partícula.
Calcule o raio, da trajetória circular, em centímetros.
O tempo gasto pela partícula no percurso PXP‚ é de 2 × 10−¥ s. Após
atingir o ponto P‚, a partícula penetra em uma região que contém um
campo magnético orientado perpendicularmente à sua trajetória, como
mostra figura. Nessa região, a partícula descreve uma trajetória
circular de raio R = 8 × 10−£ m.
Com base nessas informações, determine:
a) o trabalho realizado pelo campo elétrico sobre a partícula no trecho
PXP‚.
b) a intensidade da força magnética sobre a partícula durante a sua
trajetória circular.
c) a massa da partícula.
3
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
13. (Unesp) Uma partícula eletrizada com carga q e massa m descreve
uma trajetória circular com velocidade escalar constante v, sob a ação
exclusiva de um campo magnético uniforme de intensidade B, cuja
direção é perpendicular ao plano do movimento da partícula.
Para responder, utilize somente as variáveis necessárias, dentre
aquelas fornecidas no enunciado (q, m, v, B).
a) Qual é a expressão que fornece o módulo da força magnética Fm
que age sobre a partícula?
b) Obtenha a expressão que fornece o raio R da trajetória e a que
fornece o período T do movimento circular.
Desprezando-se a ação do campo gravitacional sobre o feixe de
partículas, é correto afirmar:
(01) A força elétrica que atua nas partículas de carga negativa é
perpendicular ao campo magnético.
(02) As partículas de carga negativa não sofrem a ação da força
magnética.
(04) Quando as partículas de carga positiva entram na região, a força
magnética que atua sobre elas aponta no sentido contrário ao do
campo elétrico.
(08) A força elétrica atuante em cada partícula se mantém constante.
(16) As partículas de carga positiva passarão pela fenda f, qualquer
que seja a velocidade do lançamento.
(32) As partículas de carga negativa serão aceleradas, ao atravessar a
região entre as placas, qualquer que seja a velocidade do lançamento.
14. (Unesp) Um feixe é constituído de dois tipos de partículas com
cargas elétricas iguais, mas massas mX e m‚ (mX · m‚). Ao
adentrarem, com velocidades iguais, uma região onde existe um
campo magnético uniforme, as partículas de massa mX e m‚
descrevem, num mesmo plano, trajetórias semicirculares diferentes,
com raios RX e R‚, respectivamente, como ilustradas na figura.
Soma (
)
16. (Fuvest) Um feixe de elétrons, todos com mesma velocidade,
penetra em uma região do espaço onde há um campo elétrico uniforme
entre duas placas condutoras, planas e paralelas, uma delas carregada
positivamente e a outra, negativamente. Durante todo o percurso, na
região entre as placas, os elétrons têm trajetória retilínea,
perpendicular ao campo elétrico. Ignorando efeitos gravitacionais,
esse movimento é possível se entre as placas houver, além do campo
elétrico, também um campo magnético, com intensidade adequada e
a) perpendicular ao campo elétrico e à trajetória dos elétrons.
b) paralelo e de sentido oposto ao do campo elétrico.
c) paralelo e de mesmo sentido que o do campo elétrico.
d) paralelo e de sentido oposto ao da velocidade dos elétrons.
e) paralelo e de mesmo sentido que o da velocidade dos elétrons.
Expresse a razão entre as massas mX e m‚, em termos de RX e R‚.
TEXTO PARA A PRÓXIMA QUESTÃO
(Ufba) Na(s) questão(ões) a seguir escreva nos parênteses a soma dos
itens corretos.
15. Um feixe de partículas eletricamente carregadas é lançado
horizontalmente numa região, entre duas placas planas e paralelas, que
contém campo elétrico e campo magnético uniformes, dispostos
conforme a figura a seguir.
17. (Mackenzie) Partículas de carga q e massa m são aceleradas, a
partir do repouso, por uma diferença de potencial U e penetram numa
região de indução magnética B, perpendicular à velocidade « das
partículas. Sendo o raio das órbitas circulares igual a R e desprezando
as perdas, assinale a alternativa correta:
a) m/q = U/R£B
b) q/m = R£B£/2U
c) q/m = 4U/RB£
d) q/m = 2U/R£B£
e) m/q = 3U/R£B
4
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
18. (Mackenzie) Um pósitron (q/m = +1,75 . 10¢¢ C/kg) e um elétron
(q/m = -1,75 . 10¢¢ C/kg) penetram simultaneamente pelos pontos m e
n, numa região onde existe um campo de indução magnética uniforme
e de intensidade 4,0 . 10−£ T.
A penetração das partículas ocorre perpendicularmente às linhas de
indução, conforme a ilustração a seguir, e se chocam no ponto P.
Desprezando os efeitos relativísticos, a velocidade relativa do pósitron
em relação ao elétron, no instante do choque é:
a) 5,6 . 10¨ m/s.
d) 2,8 . 10¨ m/s.
b) 4,2 . 10¨ m/s.
e) 1,4 . 10¨ m/s.
21. (Mackenzie) Uma partícula eletrizada movimenta-se com
velocidade «, numa região onde existe um campo magnético de vetor
indução û, ficando sujeita, por isso, à ação da força ù. Com relação a
esse fato, considere as afirmações abaixo:
I. « é sempre perpendicular a û
II. ù é sempre perpendicular a û
III. ù é sempre perpendicular a «
c) 3,5 . 10¨ m/s.
Assinale:
a) se todas as afirmações estão corretas.
b) se somente as afirmações I e II estão corretas.
c) se somente as afirmações II e III estão corretas.
d) se somente as afirmações I e III estão corretas.
e) se todas as afirmações estão incorretas.
19. (Mackenzie) O condutor AB da figura a seguir está imerso numa
região onde atua um campo de indução magnética B de intensidade
0,5 T, perpendicular ao plano desta folha e orientado para o leitor. O
condutor situado no plano desta folha é percorrido por uma corrente i
= 2A. A intensidade da força magnética que atua sobre o condutor é:
22. (Pucmg) Uma partícula de carga q, com velocidade « e massa m
dentro de um campo magnético B, fica sujeita a uma força ù pela ação
desse campo. Sobre a situação, foram feitas três afirmações.
I. A intensidade da força depende do valor de q.
II. O sentido da força ù depende do sinal de q.
III. A intensidade da força depende da velocidade v e da massa m da
partícula.
A afirmativa está CORRETA em:
a) I e III apenas. b) I e II apenas.
a) 5 N.
b) 4 N.
c) 2 N.
d) 1 N.
c) II e III apenas.
d) I, II e III.
23. (Pucpr) Quando uma partícula carregada positivamente se desloca
com velocidade v perpendicular a um campo magnético uniforme, ela
sofre a ação de uma força que:
a) é coincidente com as linhas de campo, causando uma redução na
velocidade da partícula.
b) é coincidente com as linhas de campo, causando um aumento na
velocidade da partícula.
c) é perpendicular à velocidade, causando um desvio na trajetória da
partícula.
d) é perpendicular à velocidade, causando um aumento na velocidade
da partícula.
e) é perpendicular à velocidade, causando uma redução na velocidade
e) zero.
20. (Mackenzie) Um elétron atravessa uma região do espaço, na qual
atuam um campo elétrico uniforme û e um campo magnético vetorial,
de indução B, também uniforme, sem sofrer qualquer deflexão. A
figura que melhor representa a situação descrita é:
5
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
da partícula.
24. (Pucpr) Um próton de massa m e carga q percorre uma
circunferência num plano perpendicular a um campo magnético de
indução B, com velocidade de módulo v.
Podemos fazer as seguintes afirmações:
I. A força magnética que atua no próton tem intensidade F = qvB.
II. O período do movimento do próton é T = (2™m)/(qB).
III. A freqüência do movimento do próton depende de sua velocidade.
São corretas:
a) I e III somente.
b) II e III somente.
c) I e II somente.
d) somente I.
e) I, II e III.
28. (Ufc) Duas partículas, PX e P‚, com massas mX e m‚, possuem
cargas elétricas qX e q‚, respectivamente.
Ambas as partículas são lançadas, simultaneamente, com a mesma
velocidade inicial, de módulo v, em uma região na qual existe um
campo magnético B, perpendicular ao plano da página e apontando
para fora dela, de acordo com a figura a seguir. Uma possível
trajetória das partículas é mostrada na figura. Considere que os raios
das trajetórias de ambas as partículas são maiores que a distância L
que separa o LADO 1 do LADO 2, conforme a figura.
25. (Pucsp) Lança-se um elétron nas proximidades de um fio
comprido percorrido por uma corrente elétrica i e ligado a uma
bateria. O vetor velocidade « do elétron tem direção paralela ao fio e
sentido indicado na figura a seguir.
Sobre o elétron, atuará uma força magnética
ù, cuja direção e sentido serão melhor representados pelo diagrama
Sendo mX = 2m, m‚ = m, qX = q/4 e q‚ = q, determine a partícula que
atinge primeiro o LADO 2 e o raio R da trajetória descrita por essa
partícula. (Desconsidere qualquer efeito da gravidade.)
a) partícula PX; R = 8 mv / qB
b) partícula P‚; R = mv / qB
c) partícula PX; R = mv / qB
d) partícula P‚; R = 8 mv / qB
e) PX e P‚ chegam juntas; R = mv / qB
26. (Uece) A maior força de origem magnética (medida em newton)
que pode atuar sobre um elétron (carga e = 1,6 × 10−¢ª C) em um tubo
de TV, onde existe um campo magnético de módulo B = 83,0 mT,
quando sua velocidade é de 7,0 × 10§ m/s, vale aproximadamente
a) 9,3 × 10−¢¥
b) 4,7 × 10−¢§
c) 13,3 × 10−¢¡
d) 8,1 ×
10−¢¡
27. (Ufc) Num hipotético detetor de partículas, baseado na interação
delas com um campo magnético, aparecem os traços deixados por três
partículas: um próton, um elétron e um pósitron. Suponho que as
partículas cheguem ao detetor com valores de velocidade não muito
diferentes entre si, os traços representados na figura ao lado seriam,
respectivamente:
a) I, II e III b) I, III e II
c) II, III e I d) II, I e III
e) III, II e I
6
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
29. (Ufg) O vetor campo magnético B, produzido por imãs naturais ou
por correntes circulando em fios, possui inúmeras aplicações de
interesse acadêmico, prático, industrial e tecnológico. Em relação a
algumas dessas aplicações, pode-se afirmar que
( ) o princípio de funcionamento de um motor elétrico é baseado no
fato de que uma espira, conduzindo uma corrente elétrica i, quando
colocada em uma região onde B · 0, com seu plano paralelo as linhas
de B, gira devido ao torque produzido pelo campo magnético sobre a
espira.
(
) em um espectrômetro de massa, partículas de mesma carga e
massas diferentes podem ser separadas e identificadas de acordo com
o raio da trajetória circular que elas descrevem, quando lançadas
perpendicularmente em direção a uma região onde B · 0, uma vez que
o raio da trajetória e inversamente proporcional a massa da partícula.
( ) em um gerador de eletricidade, a rotação de uma espira, colocada
numa região onde B · 0, faz variar o fluxo magnético através dela,
induzindo uma corrente elétrica na espira.
( ) campos magnéticos transversais ao movimento de elétrons, num
tubo de TV, são responsáveis pelo direcionamento desses elétrons
para diferentes pontos na tela do televisor, gerando a imagem vista
pelo telespectador.
31. (Ufmg) Na figura, estão representadas duas placas metálicas
paralelas, carregadas com cargas de mesmo valor absoluto e de sinais
contrários. Entre essas placas, existe um campo magnético uniforme
de módulo B, perpendicular ao plano da página e dirigido para dentro
desta.
Uma partícula com carga elétrica POSITIVA é colocada no ponto P,
situado entre as placas.
Considerando essas informações, assinale a alternativa em que
MELHOR está representada a trajetória da partícula após ser solta no
ponto P.
30. (Ufjf) Você está sentado numa sala em que existe um campo
magnético vertical apontando para baixo. Um emissor de elétrons
(carga elétrica negativa), localizado na parede atrás de você, emite
elétrons com velocidade horizontal dirigida para a parede que está à
sua frente. A força gravitacional é desprezível em comparação com a
força magnética. Se você continuar olhando para a frente, você verá:
a) o feixe desviar-se para baixo.
b) o feixe desviar-se para a sua direita.
c) o feixe seguir em frente sem desviar-se.
d) o feixe desviar-se para cima.
e) o feixe desviar-se para a sua esquerda.
32. (Ufmg) Uma bateria, ligada a uma placa metálica, cria, nesta, um
campo elétrico E, como mostrado na figura I. Esse campo causa
movimento de elétrons na placa.
Se essa placa for colocada em uma região onde existe um determinado
campo magnético B, observa-se que elétrons se concentram em um
dos lados dela, como mostrado na figura II.
Com base nessas informações, assinale a alternativa em que
MELHOR estão representados a direção e o sentido do campo
magnético existente nessa região.
7
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
36. (Ufrrj) Uma partícula de carga q entra com velocidade V³ numa
região onde existe um campo magnético uniforme B.
33. (Ufmg) Um feixe de elétrons entra em uma região onde existe um
campo magnético, cuja direção coincide com a direção da velocidade
dos elétrons.
Com base nessas informações, é CORRETO afirmar que, ao entrar no
campo magnético, os elétrons desse feixe
a) são desviados e sua energia cinética não se altera.
b) não são desviados e sua energia cinética aumenta.
c) são desviados e sua energia cinética aumenta.
d) não são desviados e sua energia cinética não se altera.
34. (Ufpi) "O vento solar, um plasma fino de alta velocidade, sopra
constantemente do Sol a uma velocidade média de 400 km/s. Se a
Terra não tivesse um campo magnético global, ou magnetosfera, o
vento solar teria um impacto direto em nossa atmosfera e a desgastaria
gradualmente. Mas o vento solar bate na magnetosfera da Terra e é
desviado ao redor do planeta...."
.http://www.uol.com.br/inovacao/ultimas/ult762u212.shl
Para que ocorra o desvio acima mencionado é absolutamente
necessário que as partículas do vento solar tenham:
a) carga positiva e alta velocidade.
b) carga negativa e baixa velocidade.
c) carga diferente de zero e velocidade alta.
d) carga diferente de zero e velocidade diferente de zero.
e) carga positiva e baixa velocidade.
No caso em que V³ e B possuem a mesma direção, podemos afirmar
que a partícula
a) sofrerá um desvio para sua direita.
b) sofrerá um desvio para sua esquerda.
c) será acelerada na direção do campo magnético uniforme B.
d) não sentirá a ação do campo magnético uniforme B.
e) será desacelerada na direção do campo magnético uniforme B.
35. (Ufrrj) Um próton é lançado com velocidade constante ¬ numa
região onde existe apenas um campo magnético uniforme B, conforme
a figura abaixo:
A velocidade ¬ e o campo magnético B têm mesma direção e mesmo
sentido. Sendo V=1,0×10¦m/s e B=5,0×10−£ Tesla, podemos afirmar
que o módulo da força magnética atuando no próton é
a) 8 × 10−§ N. b) 0N. c) 18 × 10−¢§ N. d) 16 × 10−¢§ N . e) 12 × 10−¢§
N.
8
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
38. (Ufu) Conforme representado na figura abaixo, em uma região do
espaço há um campo elétrico uniforme, û, de 1,0.10§V/m na direção
+x; nesta região também há um campo magnético uniforme, B, na
direção +y. Um feixe de partículas eletricamente carregadas,
conhecidas como mésons, desloca-se com velocidade c/3 (c é a
velocidade da luz no vácuo, cujo valor é 3,0.10©m/s), e passa nesta
região em linha reta na direção +z.
37. (Ufsc) A figura representa um espectrômetro de massa, dispositivo
usado para a determinação da massa de íons. Na fonte F, são
produzidos íons, praticamente em repouso. Os íons são acelerados por
uma diferença de potencial VÛ½, adquirindo uma velocidade « sendo
lançados em uma região onde existe um campo magnético uniforme
B. Cada íon descreve uma trajetória semicircular, atingindo uma
chapa fotográfica em um ponto que fica registrado, podendo ser
determinado o raio R da trajetória.
Considerando as informações acima, analise as seguintes afirmativas e
responda de acordo com o código.
I - O campo magnético tem módulo 1,0.10−£T.
II - Com esse experimento pode-se dizer que a carga do méson é
positiva.
III - Se desligarmos o campo elétrico (E=0) o feixe descreverá um
trajetória circular contida no plano xz
a) Apenas I é correta.
b) I e III são corretas.
c) I e II são corretas.
d) Apenas II é correta.
Considerando a situação descrita, assinale a(s) proposição(ões)
CORRETA(S):
(01) A carga dos íons, cujas trajetórias são representadas na figura, é
positiva.
(02) A energia cinética EÝ que o íon adquire, ao ser acelerado pela
diferença de potencial elétrico VÛ½, é igual ao trabalho realizado sobre
ele e pode ser expressa por EÝ = qVÛ½, onde q é a carga do íon.
(04) A carga dos íons, cujas trajetórias são representadas na figura,
tanto pode ser positiva como negativa.
(08) O raio da trajetória depende da massa do íon, e é exatamente por
isso que é possível distinguir íons de mesma carga elétrica e massas
diferentes.
(16) Mesmo que o íon não apresente carga elétrica, sofrerá a ação do
campo magnético que atuará com uma força de direção perpendicular
à sua velocidade «.
39. (Unesp) Uma partícula eletricamente neutra está em repouso no
ponto P de uma região com campo magnético uniforme. Ela se
desintegra em duas outras partículas com massas iguais, porém com
cargas de sinais opostos. Logo após a desintegração, elas são
impulsionadas para lados opostos, com velocidades constantes
perpendiculares ao campo magnético. Desprezando a força de atração
entre as cargas e considerando o sentido do campo magnético
entrando perpendicularmente a esta página, da frente para o verso,
podemos concluir que a figura que melhor representa as trajetórias
dessas partículas é
9
ELETROMAGNETISMO – MOVIMENTO DE CARGAS
circular, no sentido anti-horário.
b) 2.10¦m/s
c) 0,02 m
7. a)
40. (Unesp) Uma mistura de substâncias radiativas encontra-se
confinada em um recipiente de chumbo, com uma pequena abertura
por onde pode sair um feixe paralelo de partículas emitidas. Ao
saírem, três tipos de partícula, 1, 2 e 3, adentram uma região de campo
magnético uniforme B com velocidades perpendiculares às linhas de
campo magnético e descrevem trajetórias conforme ilustradas na
figura.
b) v = E/B
8. 1. Por que possuem carga elétrica de sinal diferente.
2. razão = 2
3. 0,088 T
9. 48 cm
10. 25 cm.
11. Se a velocidade da carga permanece constante, então as forças
elétrica e magnética que atuam sobre ela se cancelam, ou seja, a força
magnética deve estar dirigida ao longo de X, no sentido negativo.
a) Se houvesse uma componente X para o campo magnético, a força
magnética teria uma componente Z, o que está excluído pela
consideração anterior. Assim sendo, temos Bx = 0.
b) Como os módulos da força elétrica e da força magnética devem ser
iguais, devemos ter qE³ = qV³ | Bz |, de forma que | Bz | = E³/V³. Pela
regra da mão direita, para que o sentido da força magnético seja
contrário ao da força elétrica, a componente Bz deve ser negativa.
Considerando a ação de forças magnéticas sobre cargas elétricas em
movimento uniforme, e as trajetórias de cada partícula ilustradas na
figura, pode-se concluir com certeza que
a)as partículas 1 e 2, independentemente de suas massas e
velocidades, possuem necessariamente cargas com sinais contrários e
a partícula 3 é eletricamente neutra (carga zero).
b) as partículas 1 e 2, independentemente de suas massas e
velocidades, possuem necessariamente cargas com sinais contrários e
a partícula 3 tem massa zero.
c) as partículas 1 e 2, independentemente de suas massas e
velocidades, possuem necessariamente cargas de mesmo sinal e a
partícula 3 tem carga e massa zero.
d) as partículas 1 e 2 saíram do recipiente com a mesma velocidade.
e) as partículas 1 e 2 possuem massas iguais, e a partícula 3 não possui
massa.
12. a) 8 × 10−¢§J ou 5keV b) 2 × 10−¢¥N
c) 4 × 10−£¥kg
13. a) Fm = | q | . v . B.
b) R = mv/| q | B
T = 2™m/| q | B
14. A força magnética é a resultante centrípeta, então, F mag = F centr
ë qvB = mv£/R, de onde vem que m = RqB/v. Para os dois tipos de
partícula tanto q, B e v são constantes, de modo que, mX/m‚ = RX/R‚.
15. 01 + 04 + 08 + 32 = 45
16. [A]
17. [D]
18. [D]
19. [A]
20. [A]
21. [C]
22. [B]
23. [C]
24. [C]
25. [B]
26. [A]
27. [D]
28. [A]
29. V F V V
30. [B]
31. [C]
32. [A]
33. [D]
34. [D]
35. [B]
36. [D]
37. 01+02+08=11
38. [B]
39. [E]
40. [A]
GABARITO
1. a) k = mg/v³
b) Observe a figura a seguir
c) v‚ = mg/Ë(Q£ B£ + k£)
2. a) Ðt = 3 . 10−§s
b) R = 1,5 m
c) B = 2 . 10−£ T
3. a) o elétron passará a realizar, dentro do campo magnético, uma
trajetória circular, com sentido horário.
b) como a força magnética e o deslocamento sofrido pelo elétron são
perpendiculares o trabalho da força magnética será nulo.
4. a) kX = 1/2mXvX£ = 9/8 (q£B£L£)/m k‚ = 1/2m‚v‚£ = 1/2 (q£B£L£)/m
b) t = T/2 = (™m)/(qB)
5. a) T = (2™m)/(qB)
b) zero
6. a) na região I a carga permanece na mesma direção e sentido que
originalmente, enquanto que, na região II ela irá realizar uma trajetória
10