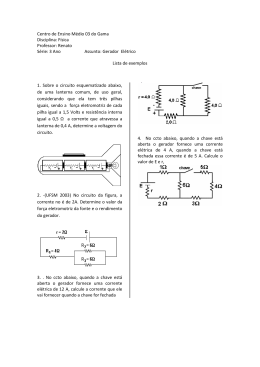
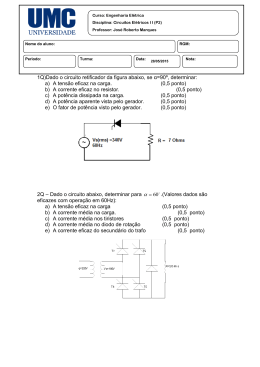
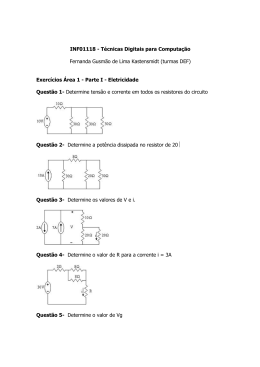
Lista de Exercícios de Recuperação de FÍSICA [2º Bimestre 2012] 3o Ano/EM
Resistores
1] Calcule a resistência do resistor equivalente entre os pontos A e B das associações a seguir
a)
b)
c)
d)
2] Os terminais A e B da associação da figura estão sob uma ddp de 360 V. Determine: a) a corrente elétrica no
resistor de 30 Ω b) potência dissipada pelo resistor de 20 Ω.
Capítulo 5: Associação de resistores e medidas elétricas
Resolvidos = 1 a 9; 30 e 31;
Propostos: 11, 15, 16, 27, 29; 34 a 36; 38; 41;
Capacitores
1] Na associação a seguir considere C1 = C4 = 2 µF, C2 = C3 =1 µF e Va – Vb = 60 V
Determine:
a) a capacitância equivalente e a carga total na associação. b) a carga nos capacitores 2 e 3, em µC.
c) a ddp nos terminais do capacitor 4.
2] (Unifor – CE adaptada) Na associação a seguir VA – VB = 200 V e considere C1 = 4,0 x 10-8F,
C2 = 12,0 x 10-8F e C3 = 3,0 x 10-8F.
Determine:
a) a carga total na associação (em µC) e a energia armazenada na associação, em J.
b) a carga nos capacitores, em µC.
c) a ddp nos terminais dos capacitores, em volts.
Capítulo 7: Capacitores
Resolvidos = 2; 12 e 13;
Propostos: 3, 9, 10; 15 a 18;
Circuitos Elétricos
1] (Mogi-SP) O gráfico representa a curva característica de um gerador. Liga-se aos seus terminais um resistor
de resistência igual a 10Ω.
Determine:
a) a intensidade de corrente elétrica que se estabelece no circuito; b) o rendimento do gerador.
2] As curvas características de um gerador e de um resistor são mostradas na figura abaixo.
Conectando-se o resistor aos terminais do gerador, determine:
a) a potência gerada pelo gerador; b) a potência fornecida pelo gerador ao circuito externo; c) a potência
dissipada internamente no gerador; d) o rendimento do gerador nesse circuito elétrico.
3] (UFSCar – SP) No circuito da figura, os potenciais nos pontos A e C valem, respectivamente:
A. (
)
2 V e –1 V.
B. (
)
4 V e 6 V.
C. (
)
12 V e –8 V.
D. (
)
8 V e –4 V.
E. (
)
nenhum destes valores.
4] (PUC – SP) A figura esquematiza o circuito elétrico de uma enceradeira em funcionamento.
A potência elétrica dissipada por ela é de 20 W e sua fcem é de 110 V. Calcule a sua resistência interna.
5] Um receptor tem f.c.e.m. de 100 V e resistência interna 2 Ω. Sabendo que esse motor é atravessado por uma
corrente de intensidade 5 A. calcule: a) a potência consumida pelo receptor; b) a potência dissipada por efeito
Joule; c) o rendimento elétrico do motor.
6] No circuito a seguir, calcule:
a) a corrente no circuito; b) a carga armazenada no capacitor.
7] No circuito elétrico mostrado abaixo, determine:
a) a intensidade da corrente elétrica no circuito; b) A ddp VB – VD, entre os pontos B e D desse circuito.
Capítulo 6: Circuitos elétricos
Resolvidos = 1 a 7 e 26 a 29;
Propostos: 9, 10, 14, 17, 30 a 33; 42, 45, 58;
Influência do Campo Magnético sobre cargas elétricas
1] Uma carga elétrica q = 5µ C de massa m = 4x10-8 kg penetra num campo de indução magnética de
intensidade 2T, conforme indica a figura.
Sendo v = 200 m/s o módulo da velocidade com que a partícula penetra no campo, calcule:
a) a intensidade da força magnética que age na partícula durante seu movimento no interior do campo
magnético;
b) o raio da trajetória descrita pela carga (esboce a trajetória da partícula na figura).
c) a que distância do ponto O a carga atinge o anteparo.
d) o intervalo de tempo decorrido entre a entrada da partícula pelo ponto O e o choque contra o anteparo.
2] Um próton ( carga +e e massa = mp) e uma partícula alfa (carga +2e e mα = 4 mp) movem-se em órbitas
circulares em um campo magnético. Os raios das órbitas são iguais.
a) Calcule a razão entre as velocidades das partículas,
b) Calcule a razão entre os períodos das partículas,
Tp
Tα
vp
vα
.
.
Revisão – Livro Texto
Capítulo 8: Campo magnético e sua influência sobre cargas elétricas
Resolvidos = 1 a 3, 16 e 17;
Propostos: 11, 14, 18, 21 e 22;