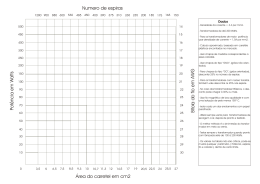
MANUTENÇÃO ELÉTRICA
INDUSTRIAL
* TRANSFORMADORES 1Ø DE PEQUENA POTÊNCIA:
PROJETO E CONSTRUÇÃO *
Vitória – ES
2006
10. TRANSFORMADORES
Transformadores são máquinas responsáveis pela transferência de energia em
circuitos,
dependendo
da
ação
indireta
da
indutância
mútua
entre
os
enrolamentos. Utilizados para diversas aplicações, entre elas:
ƒ
Modificar níveis de tensão e corrente;
ƒ
Propiciar isolamento elétrico;
ƒ
Efetuar casamento de impedância.
Existem basicamente 3 tipos de núcleos de transformadores: núcleo aberto,
núcleo envolvido e núcleo envolvente. Daremos ênfase, na abordagem de projeto
para pequenos transformadores, ao núcleo envolvente por proporcionar maior
rendimento e padronização de chapas magnéticas para pequenas potências.
O fluxo gerado na coluna central do núcleo envolvente, divide-se em duas partes
iguais, percorrendo as colunas laterais onde se concentra a metade do fluxo
principal. Por esta razão as colunas laterais possuem a metade da seção da
coluna central.
A montagem das lâminas é feita de forma alternada a fim de proporcionar maior
resistência mecânica e diminuir a relutância magnética.
1
O transformador apresenta perdas no cobre devidas ao efeito Joule (ocasionada
pela resistência dos enrolamentos) e perdas no núcleo, caracterizadas pelas
correntes de Foucault e pela histerese magnética.
Os diversos elementos físicos, elétricos e magnéticos de um transformador são
mostrados na figura a seguir.
Ao iniciarmos o projeto de um transformador monofásico de pequena potência, a
partir de um núcleo pré-existente, precisamos determinar qual a potência
máxima que poderá ser considerada.
A utilização de lâminas tipo E,I padronizadas, permite a utilização de uma
equação empírica que relaciona a potência fornecida em função da seção
geométrica da perna central, conforme podemos constatar pela expressão:
P = Sg2 x 0,7
onde
P = potência máxima fornecida, em watts.
Sg = seção do núcleo (a x b) elevado ao quadrado.
2
A partir daí, podemos definir os valores de tensão e corrente exigidos pela carga,
a qual seja alimentada pelo transformador. Em seguida definimos a tensão de
alimentação do transformador e, por conseqüência, a corrente fornecida pela
fonte de energia que alimenta o mesmo.
Consideremos, para efeito de exemplo, as seguintes dimensões do núcleo:
a = 4 cm
b = 3 cm
Sg = 4 x 3 = 12 cm2
Suponhamos que a carga exija uma tensão de 24 volts e que o transformador
seja ligado a uma rede de 120 volts.
Pela equação empírica inicial, podemos oferecer a suposta carga uma potência
máxima de:
P = (12)2 x 0,73 = 105 watts
O próximo passo será calcular o número de espiras específicas, ou seja, o
número de espiras por volt para a confecção dos enrolamentos primário e
secundário.
Determinação do número de espiras/volt:
Ne =
10 8
4,44.B. f .Sm
onde
B = indução magnética (Gauss)
f = freqüência da fonte de alimentação (Hertz)
Sm = seção magnética da perna central (cm2)
3
A seção magnética corresponde apenas a seção do ferro que constitui a perna
central do núcleo. Como as lâminas possuem isolamento (verniz, etc.) e podem
apresentar deformações, para efeitos práticos é feita uma redução em torno de
10% na área total da perna central para conhecermos a área efetiva da
ferragem.
Logo, Sm = Sg . 0,9
Sm = 12 . 0,9 = 10,8 cm2
Como não temos informações precisas sobre a indução magnética das chapas
magnéticas, usaremos as referências fornecidas pela literatura técnica, que
indica uma variação entre 6500 a 14000 Gauss para chapas de transformadores
de pequena potência. A escolha de um valor médio, em torno de 10000 Gauss
nos parece uma opção sensata.
A freqüência da rede de alimentação do transformador é de 60 Hertz, padrão em
todo o território nacional.
Portanto, já podemos calcular o valor da quantidade de espiras por volt.
Ne =
10 8
4,44.10 4.60.10,8
Ne = 3,47 espiras/volt
Assim, o enrolamento primário conterá:
Np = 3,47 x 120 = 416 espiras
e o enrolamento secundário conterá:
Ns = 3,47 x 24 x 1,1* = 92 espiras
O fator 1,1 corresponde ao acréscimo de 10% sobre o total de espiras do
secundário para compensar a queda de tensão durante o funcionamento da
carga (sugestão prática). Dessa forma esperamos que, a vazio, o trafo apresente
um valor de tensão em torno de 24,6 volts.
Considerando que as perdas envolvidas neste transformador de baixa potência
nominal são reduzidas, consideraremos a potência de entrada será igual a
potência de saída. Logo, para uma tensão de 24 volts, o transformador poderá
fornecer no máximo:
4
P = VI,
I = P/V
logo
I = 105/24 = 4,37 A
Portanto, a corrente no enrolamento primário, para essa situação poderá
alcançar o valor de:
I = 105/120 = 0,87 A
Observe que estamos considerando a potência total estimada pela equação
empírica. Porém podemos trabalhar com qualquer valor de potência abaixo do
valor estimado.
Para calcular a seção transversal dos condutores, é necessário definir a
densidade de corrente para o transformador em questão.
Resultados práticos satisfatórios alcançados por projetistas nos orientam a seguir
a tabela abaixo na escolha da densidade de corrente, em função da potência
projetada:
Potência
(watts)
Até 500
> 500 até 1000
>1000 até 3000
Densidade de Corrente
(A/mm2)
3
2,5
2
Fonte: Martignoni, Alfonso. Transformadores. Ed. Globo.
A densidade de corrente é a quantidade de ampéres que circula por uma seção
de 1mm2 de um condutor. Em geral aumentando-se o volume do transformador,
aumenta-se a dificuldade de irradiação do calor gerado internamente (pelos
enrolamentos e pelo núcleo); por isso, na medida que a potência do trafo
aumenta é preciso diminuir a densidade de corrente.
Valores maiores de densidade podem ser usados, contudo poderá haver a
necessidade da utilização de dispositivos auxiliares de refrigeração para melhorar
a dissipação de calor e/ou o uso de materiais isolantes que suportam
temperaturas mais elevadas.
A seção do enrolamento primário será calculada pela divisão da respectiva
corrente pela densidade, que no presente caso é igual a 3.
Sp = 0,87/3 = 0,29 mm2
Repetindo o mesmo procedimento para o fio do enrolamento secundário, temos:
Ss = 4,37/3 = 1,45 mm2
5
Fazendo uso da tabela de fios esmaltados, constante no final desse material,
encontraremos os respectivos condutores a serem utilizados, tanto em mm2
quanto em AWG (American Wire Gauge), padrão americano para medir o
diâmetro de um fio. Quanto maior o AWG, menor é o diâmetro do fio.
Ao consultar a tabela, caso não seja encontrado o valor exato da seção
calculada, deverá ser escolhido o valor imediatamente superior, o que representa
um menor aquecimento, menos perda e menor queda de tensão para o
enrolamento.
Considerando os resultados, os fios escolhidos são os seguintes:
Enrolamento primário: 22 AWG com seção de 0,322 mm2
Enrolamento secundário: 15 AWG com seção de 1,65 mm2
Às vezes o fio escolhido apresenta uma seção elevada o que dificulta a sua
aquisição e a confecção do enrolamento em carretéis pré-fabricados. Uma saída
seria a sua substituição por dois ou mais fios cuja somatória das seções seja no
mínimo igual ao fio original. A execução dos enrolamentos poderá ser feita em
carretel de plástico pré-fabricado ou pode ser necessária a confecção de um
carretel com fibra isolante de consistência e classe de isolamento compatíveis.
O último procedimento a ser efetuado antes da execução dos enrolamentos será
o de confirmar a ocupação dos mesmos no espaço existente, que corresponde as
medidas da janela da lâmina. Para isso é necessário saber a distância interna
entre as duas abas laterais do futuro carretel. Para efeitos práticos podemos
considerar que cada aba lateral do carretel possui 2mm de espessura.
Logo, o comprimento útil será de:
Cútil = 1,5 a – 4mm = 1,5 x 40mm – 4mm = 56 mm
O primeiro enrolamento a ser colocado deverá ser o primário (120 V) pois este
possui o fio mais fino que o secundário, acomodando-se melhor nos cantos
(quinas) do carretel e também, por estar mais próximo do núcleo, terá um
comprimento médio menor, diminuindo seu custo (o fio mais fino é mais caro
que o grosso, por quilo de peso).
6
Podemos estimar o número de espiras que poderão ser colocadas em cada
camada do enrolamento, dividindo o comprimento interno pelo diâmetro do fio
em questão.
Espiras
primário = 56 mm / 0,69 mm = 81 espiras
camada
Como o enrolamento primário possui 416 espiras, serão necessárias:
No de camadas = 416 / 81 = 5,13 camadas.
Isto significa que serão necessárias 6 camadas para receber as 416 espiras do
enrolamento primário (5 camadas completas com 81 espiras cada + 1 camada
com 11 espiras).
O mesmo procedimento é realizado para o enrolamento secundário.
Espiras
sec undário = 56 mm / 1,5 mm = 37 espiras
camada
Como o enrolamento secundário possui 92 espiras, serão necessárias:
No de camadas = 92 / 37 = 2,48 camadas.
Isto significa que serão necessárias 3 camadas para receber as 92 espiras do
enrolamento secundário (2 camadas completas com 37 espiras cada + 1 camada
com 18 espiras).
20mm
Enrolamento
secundário
Enrolamento
primário
7
Como a altura da janela vale a/2 = 20mm, precisamos calcular a altura ocupada
por cada enrolamento e verificar se a altura total dos dois enrolamentos não
ultrapassa o espaço disponível. Deverá ser levado em conta o espaço ocupado
pelo material isolante usado (fundo do carretel + isolamento entre enrolamento
primário e secundário + isolamento final para proteção do carretel). Em termos
práticos, considera-se um percentual de 30 a 40% da altura total para o
isolamento, sendo o restante destinado aos enrolamentos.
No exemplo desenvolvido temos a seguinte situação:
Altura do enrolamento primário = 6 x 0,69mm (diâmetro do fio 22 AWG) = 4,14mm
Altura do enrolamento secundário = 3 x 1,5mm (diâmetro do fio 15 AWG) = 4,5mm
Altura total = 4,14 + 4,5 = 8,54mm.
A altura total ocupada pelos enrolamentos sendo de 8,54mm corresponde a
42,7% da altura disponível na janela. Portanto estamos dentro da faixa prevista,
o que implica numa reserva de potência que pode ser utilizada pelo projetista,
fazendo novo dimensionamento, com alterações na corrente de carga, nas
tensões utilizadas, ou em ambas.
Após a viabilidade do projeto adotado, iniciamos a confecção do carretel, se
assim for necessário, ou a execução dos enrolamentos.
A seguir algumas orientações sobre a confecção de um carretel de fibra simples e
de uma fôrma de madeira que simula o núcleo do trafo, para fixação numa
bobinadeira manual que pode ser construída com poucos recursos.
Caso seja construído um carretel para receber os enrolamentos, deverá ser feito
um molde de madeira para servir de base de sustentação.
As medidas do molde de madeira devem ser ligeiramente alteradas em relação
ao corpo do núcleo central (a, 1,5a, b). Não existe um padrão definido em
relação às medidas; o que realmente acontece é que o projetista, com sua
experiência, define essas medidas.
8
Porém, de uma maneira geral, podemos considerar as medidas do molde do
núcleo para transformadores que utilizam chapas tipo E.
a’ = a x 1,05
e
b’ = b x 1,1
Estamos na realidade adicionando uma folga em torno de 5% na largura da
perna central (para que as lâminas não entrem de forma justa, raspando nas
laterais do carretel, podendo danificá-lo) e de 10% na altura total do núcleo para
que haja facilidade na colocação das lâminas, principalmente as últimas.
As medidas da lâmina do núcleo devem ser verificadas usando um paquímetro; a
confirmação do diâmetro dos fios esmaltados deverá ser efetuada com o uso do
micrômetro.
Escolha uma fibra para confecção do carretel com uma consistência suficiente
que pode ser em torno de 1mm. Para a confecção do fundo do carretel faça
algumas incisões nas arestas para facilitar as dobras e o acabamento, sem
porém cortar totalmente a mesma. A junção dos dois extremos da fibra será de
topo e na posição perpendicular a entrada das lâminas, para evitar a possível
penetração de alguma lâmina no carretel.
A seguir passa-se a construção das abas laterais, cujas medidas são tomadas a
partir das medidas da fôrma de madeira acrescida da espessura da fibra que a
envolve.
9
A execução dos enrolamentos não necessita de grandes detalhes, porém
daremos algumas orientações básicas para melhoria da qualidade do trabalho:
a) Ao iniciar o enrolamento, faça um orifício na aba lateral, rente ao fundo do
carretel, verificando o lado que permanece fora do núcleo (os terminais não
podem coincidir com a parte interna da janela);
b) As espiras devem ficar unidas, tanto quanto possível, uma das outras para
otimizar do espaço existente;
c) Caso tenha optado por um isolamento entre camadas, utilize uma fibra de
papel impermeável de baixa espessura;
d) É válida a inserção de uma fibra isolante entre o final do enrolamento primário
e o início do enrolamento secundário, devido a maior diferença de potencial
existente;
e) Procure usar uma tensão mecânica adequada nos condutores, durante a
colocação dos enrolamentos. Esforços maiores poderão romper o fio, ou em caso
contrário, as espiras ficarão frouxas dificultando a sua acomodação;
f) A saída do terminal do enrolamento deve ser feita ao lado da extremidade
onde ocorreu a entrada do enrolamento. Coloque uma fibra isolante ou um tubo
isolante (espaguete fino) para isolar o condutor da camada inferior (observe a
classe de isolamento compatível);
10
g) O restante da última camada, quando não tiver o total
das espiras, poderá ser preenchida por uma fibra isolante
cuja espessura deverá ser a mais próxima possível do
diâmetro do fio. Desta forma a camada ficará bem
nivelada, permitindo um melhor acabamento;
h) O enrolamento secundário deverá ter seus terminais,
de preferência, no lado oposto ao do enrolamento primário;
i) Use uma fibra isolante final para o encerramento dos enrolamentos e proteção
do conjunto;
Caso possua recursos para tal, efetue a secagem em estufa com temperatura
controlada para retirar a umidade e providencie a impregnação com verniz
apropriado a fim de aumentar o poder de isolação, evitando a penetração de
umidade e reduzindo os efeitos da vibração entre espiras e das chapas do
núcleo.
Faça uma avaliação da performace do transformador construído efetuando
alguns testes, tais como: resistência do isolamento, continuidade dos circuitos,
corrente a vazio, etc.
11
TABELA DE FIOS ESMALTADOS
12
11. INSTRUMENTOS DE MEDIÇÃO DIMENSIONAL
11.1 PAQUÍMETRO
É um instrumento finamente acabado, com as superfícies polidas e planas. O
cursor é ajustado à régua, de modo que permite sua livre movimentação com um
mínimo de folga. Geralmente é construído em aço carbono ou inoxidável,
temperado, e suas graduações referem-se a 20oC. A escala é graduada em
milímetros e polegadas, podendo a polegada ser fracionária ou milesimal. O
cursor é provido de uma escala, chamada nônio ou vernier, que se desloca em
frente às escalas da régua e indica o valor da dimensão medida.
Por ser essencialmente um instrumento de medição, o paquímetro permite obter
medidas lineares das faces de uma determinada peça. Estas faces podem ser:
externas, internas e ainda, de profundidade.
13
Modo correto de segurar a peça e o instrumento.
Condições para que a medida seja bem tomada
ƒ
O contato dos encostos com a superfície da peça deve ser suave. Não se deve
fazer pressão exagerada;
ƒ
Mantenha a posição bem alinhada. Qualquer inclinação do instrumento
alterará a medida;
ƒ
Antes da medição, limpe bem as superfícies de onde serão tiradas as
medidas;
ƒ
A peça a ser medida deve estar na temperatura ambiente. O calor dilata o
material e altera a medida.
14
Conservação do Paquímetro
ƒ
Mantenha sempre o paquímetro fechado quando não estiver um uso (mesmo
que logo depois haja necessidade de novas medidas);
ƒ
Evite as quedas;
ƒ
O paquímetro não deve ficar em contato com ferramentas usuais de trabalho
mecânico. Mantenha-o, sempre que possível, em estojo próprio;
ƒ
Evite arranhões ou entalhes que prejudiquem a graduação;
ƒ
Após o uso, limpe e lubrifique com óleo fino.
GRADUAÇÃO DA ESCALA – SISTEMA MÉTRICO DECIMAL
1 METRO = 100 CENTÍMETROS
1 m = 100 cm
1 CENTÍMETRO = 10 MILÍMETROS
1 cm = 10 mm
0
1cm
0
1cm
Como 1 cm = 10 mm, a distância entre traços vale 1 mm.
PROCESSO PARA LEITURA DE MEDIDAS
Exemplo: Leitura da medida na figura a seguir.
0
1
0 1
2 3 4
5 6
2
7 8 9 0
15
Para efetuar a leitura conte os milímetros inteiros da escala fixa que estão antes
do zero do nônio. Depois conte os traços do nônio até aquele que estiver
coincidindo com um traço da escala fixa para obter os décimos de milímetros. É
preciso passar por 6 traços até encontrar um traço do nônio que coincida com
um traço da escala fixa. Portanto a medida do nônio é de 6/20 ou seja, 0,3 mm.
A medida final será a soma dos milímetros encontrados somados a medida do
nônio, ou seja, 2mm + 0,3mm = 2,3 mm.
PROCESSO PARA COLOCAÇÃO DE MEDIDAS
Exemplo: Colocação da medida 8,5 mm no paquímetro.
Conte o número de milímetros pelo zero do nônio até chegar a 8. A seguir
movimente lentamente o cursor procurando coincidir o traço de valor 6 do nônio
com um traço da escala fixa.
0
1
0 1
2 3 4
2
5 6
7 8 9 0
Assim será encontrada a medida de 8,5 mm que estará representada por
qualquer das 3 formas de medição possíveis no paquímetro (medida externa,
interna e de profundidade).
16
11.2 MICRÔMETRO
A precisão de medição que se obtém com o paquímetro, às vezes, não é
suficiente. Para medidas mais rigorosas como espessuras de fibras, chapas,
diâmetro de fios esmaltados, utiliza-se o micrômetro, que assegura uma
exatidão de 0,01mm.
O micrômetro é um instrumento de dimensão variável que permite medir, por
leitura direta, as dimensões reais com uma resolução de até 0,001 mm.
O
princípio
usado
é
o
sistema parafuso e porca.
Assim, se numa porca fixa,
um parafuso der um giro de
uma
avanço
volta,
de
haverá
uma
um
distância
igual ao seu passo.
As figuras a seguir mostram alguns exemplos de uso do micrômetro.
17
Medição do diâmetro de um fio
Condições para que a medida seja bem tomada
ƒ
A peça a ser medida deve estar desempenada;
ƒ
A faces da haste de encosto devem ser ajustadas quando juntas;
ƒ
A peça a ser medida deve estar isenta de poeira, graxa, etc.;
ƒ
A peça a ser medida deve estar na temperatura normal.
Conservação do micrômetro
ƒ
As faces do encosto e da haste devem ficar separadas quando o aparelho não
estiver em uso;
ƒ
Deve ser manejado com todo o cuidado evitando as pancadas e quedas;
18
ƒ
O micrômetro não deve ficar em contato com as ferramentas usuais de
trabalho mecânico;
ƒ
Use a catraca para o contato na medição da peça. NUNCA dê um aperto para
fazer a medição usando o tambor;
ƒ
Após o uso, limpe e lubrifique com óleo fino;
ƒ
O instrumento deve ser guardado em estojo próprio.
SISTEMA MÉTRICO DECIMAL
Inicialmente observaremos as divisões da escala da bainha. Sabendo-se que nos
micrômetros do sistema métrico o comprimento da escala mede 25 mm, se
dividirmos o comprimento da escala pelo número de divisões existentes no
tambor, encontraremos o valor da distância entre as divisões (0,50 mm), que é
igual ao passo do parafuso micrométrico.
Estando o micrômetro fechado e dando uma volta completa no tambor rotativo,
no sentido anti-horário, teremos um deslocamento do parafuso micrométrico
igual ao seu passo (0,50mm), aparecendo o primeiro traço na escala da bainha.
A leitura da medida será de 0,50mm. Dando-se duas voltas completas aparecerá
o segundo traço e a leitura será de 1mm, e assim sucessivamente.
Sabendo-se que uma volta no tambor equivale a 0,50mm e tendo o tambor 50
divisões, concluímos que cada divisão equivale a 0,01mm.
19
Conhecendo-se a leitura da escala da bainha e do tambor, poderemos ler
qualquer medida registrada no micrômetro.
1o Exemplo:
Leitura na escala da bainha = 7mm
Leitura no tambor = 0,37mm
Para efetuarmos a leitura da medida, somamos a leitura da escala da bainha com
a do tambor:
7 + 0,37 = 7,37mm
2o Exemplo:
Leitura na escala da bainha = 15,5mm
Leitura no tambor = 0,08mm
Resultado final = 15,58mm
Antes de efetuarmos qualquer medição devemos verificar o micrômetro: quando
as faces da ponta fixa e móvel estiverem juntas, a borda do tambor deve
coincidir com o traço “zero” da graduação da bainha. Ao mesmo tempo, a reta
longitudinal gravada na bainha, entre as escalas de milímetros e meio
milímetros, coincidem com o “zero” da graduação circular do tambor.
20
Procedimento básico para efetuar uma medida:
ƒ
Pegue o micrômetro pelo arco, com a mão esquerda, bem firme;
ƒ
Abra o micrômetro, com a mão direita, girando o tambor no sentido antihorário até que as pontas apresentem uma abertura maior que a dimensão a
medir;
ƒ
Limpe a peça ou parte que vai ser medida, bem como as pontas de medição
do micrômetro;
21
ƒ
Posicione o micrômetro, encostando a ponta fixa em um dos lados da parte
da peça a ser medida;
ƒ
Feche o micrômetro, girando a catraca até que a ponta móvel toque no lado
oposto da peça;
ƒ
Após as pontas encostarem as faces da peça a ser medida, gire a catraca
duas ou três voltas para ajustar bem as superfícies de medição do
micrômetro com a peça.
ƒ
Faça a leitura cuidadosamente.
22