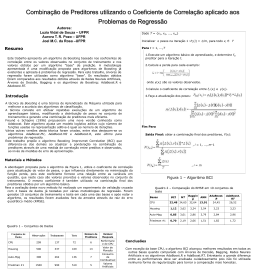
Adaboost
A decision theoretic generalization of on-line learning and an
application to boosting
Journal of Computer and System Sciences, no. 55. 1997
Yoav Freund & Robert Schapire
Irineu Júnior Pinheiro dos Santos
Mirela Ferreira César
Roberto Ribeiro Castro Menezes
Sumário

Introdução



Boosting
Adaboost


Ensemble Methods
Exemplos
Conclusões
2
Introdução - Ensemble Methods



Reúne a predição de múltiplos
classificadores em um único classificador;
Constrói um conjunto de classificadores base
a partir de um conjunto de treinamento;
Realiza a classificação a partir de um
sistema de votação, constituído a partir do
resultado de classificação de cada algoritmo
base.
3
Introdução - Ensemble Methods
Dados originais de
treinamento
Passo 1:
Criar múltiplos
conjuntos de
dados
Passo 2:
Construir
múltiplos
classificadores
D
D1
D2
D3
...
Dt
h1
h2
h3
...
ht
Passo 3:
Combinar
classificadores
H*
4
Ensemble Methods

Como um Ensemble method pode melhorar a
performance em comparação a um único
classificador?

1 classificador Base → Error rate = 0,35
25 classificadores Base → Error rate = 0,06

5
Ensemble Methods

Considerando 25 classificadores base:




iguais
Com taxa de erro de cada c. base ε = 0.35
Tx erro ensemble ε = 0.35
Ensemble vai classificar incorretamente se o
base classificar incorretamente
6
Ensemble Methods

Considerando 25 classificadores base:



Diferentes
Ensemble classifica erroneamente somente se
mais da metade dos classificadores base
predizem erroneamente.
Tx Erro ensemble:


25


25

i
i


1

0
.
06


ensemble
i

i

13
25
7
Ensemble Methods
8
Ensemble Methods

Métodos para construção de um classificador
Ensemble:

Manipulação de Conjunto de testes


Manipulação das características de entrada



Bagging e Boosting
Random Forest
Manipulação do rótulo de classes
Manipulação do algoritmo de aprendizado
9
Ensemble Methods

Métodos para construção de um classificador
Ensemble:

Manipulação de Conjunto de testes


Manipulação das características de entrada



Bagging e Boosting
Random Forest
Manipulação do rótulo de classes
Manipulação do algoritmo de aprendizado
10
Ensemble Methods

Algoritmo geral do E.M.

Sendo:
D o conjunto de dados de treinamento originais
K o número de classificadores base
T os dados de teste
for i = 1 to k do
crie conjunto de treino Di a partir de D
Construa um classificador hi a partir de D
End for
para cada registro de teste x Є T
C*(x) = Voto(h1(x),h2(x),...,hk(x))
fim para
11
Ensemble Methods

Considerações:

O tamanho dos dados de treino é igual entre os algoritmos
Base, mas a distribuição destes dados não necessariamente;

E.M. funcionam melhor em classificadores base instáveis:

Classificadores sensíveis a pequenas perturbações no
conjunto de treinamento:
Arvores de decisão;
 Redes Neurais;
 Classificadores baseado em regras;
Agregando muitos classificadores podem ajudar a reduzir tais
erros.


12
Boosting

Boosting é um procedimento iterativo
utilizado adaptativamente para alterar a
distribuição de exemplos de treinamento tal
que os classificadores base foquem nos
exemplos que são difíceis de classificar.
13
Boosting

Atribui peso para cada exemplo de
treinamento e pode adaptativamente alterar o
peso no final de cada iteração do boosting.
14
Boosting
O peso atribuído para o exemplo de treinamento
pode ser usado das seguintes formas:



Pode ser usado como distribuição de amostragem para
traçar uma faixa inicial (bootstrap) do conjunto de
amostras dos dados originais.
Pode ser usado pelo classificador base para aprender
um modelo que atribui alto peso nos exemplos de difícil
classificação.
15
Boosting
Inicialmente são distribuídos pesos iguais (1/N) e possuem
as mesmas chances de serem escolhidos para o
treinamento.
Iterativamente:






Gera um classificador usando a atual distribuição dos
exemplos.
A distribuição é dada pelos pesos.
Os pesos do exemplo de treinamento são atualizados no final
de cada iteração.
Exemplos que são classificados incorretamente terão seus
pesos aumentados e os que são classificados corretamente
terão seus pesos diminuídos.
16
Boosting
Dados originais de
treinamento
D1
D
D2
ω1
h1
α1
ω = peso dos exemplos
α = importância do class.
h2
...
D3
ω2
h3
α2
α3
Dt
ω3
ht
αt
H*
17
Boosting - Exemplo

Supondo que o exemplo 4 seja difícil de classificar.

O peso para este exemplo será aumentado nas futuras
iterações e é classificado de forma errada repetidamente.
Boosting (Iteração 1)
7
3
2
8
7
9
4
10
6
3
Boosting (Iteração 2)
5
4
9
4
2
5
1
7
4
2
Boosting (Iteração 3)
4
4
8
10
4
5
4
6
3
4
18
Boosting - Exemplo

Exemplos que não foram escolhidos na iteração anterior
tem mais chances de serem selecionados na próxima
iteração (1 e 5).

À medida que as iterações avançam, os exemplos mais
difíceis de classificar tendem a tornar-se mais prevalentes.
Boosting (Iteração 1)
7
3
2
8
7
9
4
10
6
3
Boosting (Iteração 2)
5
4
9
4
2
5
1
7
4
2
Boosting (Iteração 3)
4
4
8
10
4
5
4
6
3
4
19
Boosting

O ensemble final é obtido através da
agregação de classificadores a partir de
cada iteração do boosting.
20
Boosting
Várias implementações do algoritmo de boosting
tem sido desenvolvidas e diferem entre si em
termos de:



Como os pesos do exemplo de treinamento são
atualizados no final de cada iteração e;
Como as previsões feitas por cada classificador são
combinadas.
21
AdaBoost


AdaBoost (Adaptative Boost) é um algoritmo
que utiliza Boosting como método de
aprendizagem;
A partir da combinação de vários
classificadores com acurácia baixa
(hipóteses fracas), uma regra de predição
para um classificador com acurácia mais alta
(hipótese forte) é produzida;
22
AdaBoost

Seja {(xi,yi) | i = 1,2,...,N} um conjunto de N
exemplos de treinamento, onde yi é o rótulo de
classe associado com a instância xi;

xi ϵ R
yi ϵ {natural,plastic} ou yi ϵ {+1,-1}

23
AdaBoost – Taxa de Erro


Dado um classificador aplicado ao conjunto de
treinamento, é necessário estimar a taxa de erro da
classificação realizada;
A a taxa de erro de uma hipótese (classificador) hf
(fraco) é dada por:
  Pri ~ D h f xi   yi 
24
AdaBoost – Importância de ht

A importância de um classificador fraco ht, onde t é
o índice de iteração, é dado pelo seguinte
parâmetro:
1 1 t 

 t  ln
2  t 
25
AdaBoost – ε x α
Com isso é possível
observar que quanto
menor a taxa de erro,
maior é a importância
atribuída ao
classificador.
5
4
Importância do Classificador

3
2
1
0
-1
-2
-3
-4
-5
0
0,2
0,4
0,6
0,8
1
Taxa de Erro
1 1 t
 t  ln
2  t



26
AdaBoost – Cálculo de ε e α





Taxa de erro (ε):
2/11 = 0,18
Importância (α):
½*LN(1-0,18/0,18)
0,75
27
AdaBoost - Pesos


Usa-se o parâmetro αt para atualizar os pesos dos
exemplos de treinamento.
Considerando ωi(t) o peso atribuído ao exemplo
(xi,yi) na iteração t, temos:
t 1
i


it   exp if ht xi   yi
t

Z t  exp t if ht xi   yi
Onde Zt é o fator de normalização usado para
assegurar que o somatório dos pesos seja 1.
28
AdaBoost - Pesos
t 1
i


it   exp if ht xi   yi
t

Z t  exp t if ht xi   yi
A partir dessa fórmula então é realizado a
atualização dos pesos:


Registros classificados corretamente: peso diminui;
Registros classificados erroneamente: peso aumenta;
29
AdaBoost – Pesos em (t=1)

ωi(t=0) = 1/11 = 0,091

Corretos (ht(xi)=yi):



ωi(t=1) = 0,091*exp-0,75
0,091*0,047 = 0,043
Incorretos (ht(xi)≠yi):


ωi(t=1) = 0,091*exp0,75
0,091*2,117 = 0,193
30
AdaBoost - Normalização

Após o cálculo dos pesos, é necessário
normalizá-los para que sua soma seja
exatamente 1;

(0,043 * 9) + (0,193 * 2) = 0,387 + 0,386 = 0,773

Corretos: 0,043/0,773 = 0,056
Incorretos: 0,193/0,773 = 0,248

31
AdaBoost – Ensemble

O resultado final do algoritmo se baseia na junção
dos resultados obtidos pelos classificadores fracos,
ponderada pelo peso calculado de cada um deles;


H f x   sign  t ht x 
 t

32
AdaBoost - Algoritmo
Inicializa o peso para todos os N exemplos
Seja t o número de iterações
Para i = 1 a t faça:
1.
2.
3.
Criar conjunto de treinamento Di pela amostragem de D de acordo com o
peso;
Treinar um classificador base ht sobre Di;
Aplicar ht para todos os exemplos no conjunto de treinamento original D;
Calcular a taxa de erro de ht (ε);
Se a taxa de erro for maior que 50% então:
1.
2.
3.
4.
5.
1.
2.
6.
7.
4.
Reinicializa os pesos para todos os N exemplos;
Vai para o passo 3.1;
Calcular a importância do classificador (α);
Calcular o novo peso para cada exemplo (ω);
Constrói o classificador final (forte) ponderando as importâncias (α)
de cada classificador fraco;
33
AdaBoost – Exemplo 1

Conjunto de
Treinamento:


10 pontos
(representados por sinais
de mais e menos)
Status original:

Peso igual para todas as
amostras de treinamento
(1/10)
34
AdaBoost – Exemplo 1

Iteração 1:


Três sinais de mais são classificados incorretamente;
Os pesos para esses três sinais são aumentados
(boosted);
35
AdaBoost – Exemplo 1

Iteração 2:


Três sinais de menos são classificados incorretamente;
Os pesos para esses três sinais são aumentados (boosted);
36
AdaBoost – Exemplo 1

Iteração 3:


Um sinal de menos e três de mais são classificados
incorretamente;
Os pesos para esses três sinais são aumentados (boosted);
37
AdaBoost – Exemplo 1

Classificador final:

Integra os três classificadores fracos e obtém um classificar final
forte.
38
AdaBoost – Exemplo 2
Maçãs naturais
x
Maçãs de Plástico

Como classificar?
39
AdaBoost – Exemplo 2

1ª hipótese:


Classificador fraco;
Corta no eixo X;
40
AdaBoost – Exemplo 2

Recalcula os pesos
para os elementos de
treinamento.
41
AdaBoost – Exemplo 2

2ª hipótese:

Corta no eixo Y.
42
AdaBoost – Exemplo 2

Recalcula os pesos
43
AdaBoost – Exemplo 2

3ª hipótese.
44
AdaBoost – Exemplo 2

Recalcula os pesos;

4ª hipótese
45
AdaBoost – Exemplo 2

Combinação das
hipóteses.
46
AdaBoost – Comparação
47
AdaBoost – Conclusões

Vantagens:



Algoritmo simples e fácil de implementar;
Flexível para se combinar com os vários
algoritmos base de aprendizagem disponíveis;
Como o algoritmo se foca nos exemplos difíceis
de classificar, a identificação correta de ruídos é
bem tratada;
48
AdaBoost – Conclusões

Desvantagens:


Dependente da boa escolha do algoritmos base
de aprendizagem (Weak Learners), pois se esses
tiverem má performance no geral, o classificador
resultante do AdaBoost tende a ser pior, de forma
exponencial;
Quando a quantidade de ruído é alta, a
performance do algoritmo tende-se a degradar,
devido aos classificadores base terem altas taxa
de erro.
49