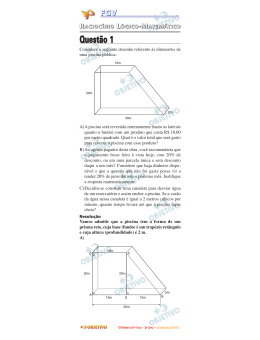
VESTIBULAR 2011
1ª Fase
RACIOCÍNIO LÓGICO-MATEMÁTICO
GRADE DE CORREÇÃO
A prova de Raciocínio Lógico-Matemático é composta por três questões e vale 10
pontos no total, assim distribuídos:
Questão 1 – 3 pontos (sendo 1 ponto para o subitem A, 1 ponto para o subitem B e 1
ponto para o subitem C)
Questão 2 – 3,5 pontos (sendo 1 ponto para o subitem A, 1 ponto para o subitem B e
1,5 ponto para o subitem C)
Questão 3 – 3,5 pontos (sendo 1 ponto para o subitem A, 1 ponto para o subitem B e
1,5 ponto para o subitem C)
As respostas deverão apresentar a resolução completa das questões. Não basta
escrever apenas o resultado final, é necessário mostrar o raciocínio utilizado e os
cálculos, quando for o caso.
Questão 1
Considere o seguinte desenho referente às dimensões de uma piscina pública:
A A piscina será revestida internamente (tanto as laterais quanto o fundo) com um produto que
custa R$ 18,00 por metro quadrado. Qual é o valor total que será gasto para revestir a piscina com
esse produto?
B
Ao agente pagador desta obra, você recomendaria que o pagamento fosse feito à vista hoje, com
20% de desconto, ou em uma parcela única e sem desconto daqui a um mês? Considere que haja
dinheiro disponível e que a quantia que não foi gasta possa vir a render 20% de juros durante o
próximo mês. Justifique a resposta matematicamente.
C
Decidiu-se construir uma canaleta para desviar água de um reservatório e assim encher a piscina.
Se a vazão da água nessa canaleta é igual a 2 metros cúbicos por minuto, quanto tempo levará
até que a piscina fique cheia?
Respostas:
A Área para revestimento:
Laterais:
2 x 15 + 2 x 20 + 2 x 30 + 2 x 25 = 180m2
Fundo:
20 x 15 +
20 x 15
= 450m2
2
Valor total gasto = 630 m² * R$ 18,00/m² = R$ 11.340,00.
B A cada R$ 100,00 pagos:
Caso o pagamento seja à vista, gasta-se R$ 100,00 x(1-0,05) = R$ 95,00 e aplica-se R$ 5,00. Depois de um
mês, sobram R$ 5,00 x (1+0,05) = R$ 5,25.
Caso o pagamento seja sem desconto daqui a um mês, obtém-se R$ 100,00 x(1+0,05) = R$ 105,00 depois
de um mês. Depois do pagamento de R$ 100,00, sobram R$ 5,00.
Logo, a melhor opção é pagar à vista com 5% de desconto.
1
Alternativamente: o valor do pagamento à vista é R$ 9.072,00 (R$ 11.340,00 x 0,80). Se, em vez de efetuar
o pagamento, esse dinheiro fosse aplicado, resultaria em 1,20 * 9.072,00 = R$ 10.886,40 ao final do mês,
valor insuficiente para pagar o custo de R$ 11.340,00.
C Volume da piscina:
20 x 15 x 2 +
20 x 15 x 2
= 900m3
2
Tempo para encher a piscina:
=
900 m 3
= 450 min
m3
2
min
Levará 450 minutos, ou 7h30min, para que a piscina fique cheia.
Grade de pontuação:
Questão
Categoria
de acerto
0%
25%
01.A
50%
75%
100%
0%
25%
01.B
50%
75%
100%
0%
25%
01.C
50%
75%
100%
Padrão utilizado para correção
Em branco OU questão totalmente errada.
Indicação de procedimento para obter a resposta e montagem
do raciocínio.
Cálculo correto da área do fundo da piscina OU cálculo correto
da área das laterais da piscina, devidamente indicado.
Cálculo correto da área total de revestimento (fundo e lateral).
Cálculo correto do valor de R$ 11.340,00.
Em branco OU totalmente errada OU indicação simples da
resposta (mesmo que pagamento à vista), sem qualquer cálculo
ou justificativa.
Acerto na indicação de pagamento à vista com justificativa
tímida / insuficiente.
Estruturação correta do problema e imprecisão na
argumentação OU estruturação correta e boa argumentação
com erro de conta que comprometa a resposta (valor absurdo).
Estruturação correta do problema e argumentação correta com
(pequeno) erro de conta.
Justificativa matemática correta de que a melhor opção é o
pagamento à vista.
Em branco OU questão totalmente errada.
Indicação correta de procedimentos, mas erro na execução.
Estruturação correta da resolução incluindo regra de três para
obtenção do tempo de enchimento e erro no procedimento de
cálculo do volume OU Estruturação correta da resolução
incluindo regra de três para obtenção do tempo de enchimento
e erro no procedimento de cálculo da regra de três.
Estruturação correta da resolução incluindo regra de três para
obtenção do tempo de enchimento e (pequeno) erro de conta.
Cálculo correto do valor de 450 minutos ou 7h30min.
2
Questão 2
João é um investidor do mercado financeiro. Após cuidadosa análise, optou por investir todo o seu
dinheiro em ações das empresas A e B. A evolução do preço dessas duas ações entre janeiro e junho
de 2009 está representada no gráfico abaixo. (Considere que seja possível adquirir frações de uma
ação).
90
80
80
70
R$/ação
60
50
50
45
50
45
40
Ação A
40
Ação B
30
20
10
11
12
Jan.
Fev.
Mar.
14
16
18
Abr.
Maio
Jun.
10
0
A Considere que João gastou todo o seu dinheiro apenas em ações da Empresa B em janeiro.
Vendeu todas essas ações em março e, imediatamente, com todo o dinheiro obtido desta venda,
comprou ações da Empresa A. Em junho, vendeu as ações da Empresa A. Qual foi seu lucro
porcentual total, entre janeiro e junho?
B Se João tivesse gasto metade do seu dinheiro em ações da Empresa A e a outra metade em ações
da Empresa B em janeiro e vendido todas as ações em maio, qual teria sido seu lucro porcentual
total?
C João comprou ações das empresas A e B em janeiro. Vendeu todas as ações em junho e obteve
um lucro de 74%. Qual a proporção de ações da Empresa A e da Empresa B que ele adquiriu em
janeiro?
Respostas:
A Sendo x o número de ações compradas em janeiro, João gastou R$ 10x em janeiro. Em março,
recebeu R$ 12x por essas ações e comprou 12x/40 ações da empresa A. Em junho, vendeu estas
ações obtendo (12x/40)*80 = R$ 24x. O investimento inicial foi de R$ 10x; portanto, o lucro foi de
(24-10)/10 = 140%.
B Seja 2x reais o valor total investido por João em ações, em janeiro. Com x reais, João comprou
x/50 ações de A e y/10 ações de B. Em maio, obteve 50*(y/50) reais com a venda de ações da
empresa B e 16*(y/10) reais com a venda de ações da empresa A, em um total de (y + 8y/5) =
13y/5. Portanto, teve um lucro de (13y/5)/2y = 30%.
3
C Sejam x e y as quantidades compradas, em janeiro, de ações das empresas A e B, respectivamente.
No mês de janeiro, João tinha (50x + 10y) reais. Em junho, sua receita com a venda das ações foi
80a + 18b.
Para um lucro de 74%, tem-se que 80x+18y = 1,74*(50x + 10y) => x/y = 3/35.
Note-se que 30% do capital de João foi empregado para adquirir ações da Empresa A e 70% do
capital de João foi empregado para adquirir ações da Empresa B.
Grade de pontuação:
Questão
Categoria
de acerto
0%
25%
02.A
50%
100%
02.B
0%
50%
100%
0%
50%
02.C
75%
100%
Padrão utilizado para correção
Em branco OU questão totalmente errada.
Indicação de que o capital em março é (12/10)*C (sendo C o
capital em R$ de João em janeiro).
Indicação de que ao final de junho terá (80/40)*(12/10)*C =
2,40C.
Resposta correta de lucro porcentual total de 140% entre janeiro
e junho.
Em branco OU questão totalmente errada.
Indicação de que ao final de junho terá 1,30C.
Resposta correta de lucro porcentual total de 30% entre janeiro
e maio.
Em branco OU questão totalmente errada.
Correta montagem do problema (média ponderada da
proporção do capital aplicado em cada ação pelo retorno de
cada ação igual a 74%).
Identificação de que o investidor aplicou, em janeiro, 30% de
seu capital em ações da Empresa A e 70% de seu capital em
ações da Empresa B.
Indicação de que a proporção de ações da Empresa A e da
Empresa B que o investidor adquiriu em janeiro é 3/35.
4
Questão 3
Uma empresa vende dois tipos de computadores (desktops e notebooks), que são fabricados no Rio
Grande do Sul e depois transportados para clientes no Rio Grande do Norte. Para transportar os
computadores, há dois tipos de caminhão, cujas capacidades de carga encontram-se na tabela
abaixo.
Computador
Caminhão A
Caminhão B
Desktop
400
300
Notebook
200
100
Para que o caminhão possa iniciar a viagem, ele deve estar cheio. Assim, um caminhão do tipo A, por
exemplo, só poderá partir se estiver carregado exatamente com 400 desktops e 200 notebooks.
A Se a empresa deve entregar d desktops e n notebooks, expresse o número necessário de
caminhões do tipo A (x) e do tipo B (y), para efetivar a entrega.
B Indique o número necessário de caminhões do tipo A e do tipo B, se a empresa entregar 15 mil
desktops e 7 mil notebooks.
C Os preços unitários de venda dos desktops e dos notebooks são, respectivamente, R$ 300,00 e
R$ 200,00, e a frota de veículos é de 5 caminhões do tipo A e 5 do tipo B. Nessas condições, seria
possível à empresa auferir a receita mínima de R$ 4,3 milhões?
Respostas:
A Seja d o número de desktops entregues, n o número de notebooks entregues, x o número de
caminhões do tipo A e y o número de caminhões do tipo B.
d = 400x + 300y
n = 200x + 100y
x = (3n – d)/200
=>
y = (d - 2n)/100
B Sendo d = 15.000 e n = 7.000, tem-se que:
15.000 = 400x + 300y e 7.000 = 200x + 100y
Resolvendo o sistema de equações: x = 30 e y = 10
C Sendo R a receita obtida, R = (400x + 300y)*300 + (200x + 100y)*200
Para x=y=5, R = (400*5 + 300*5)*300 + (200*5 + 100*5)*200= R$ 1.350.000.
Assim, com cinco caminhões de cada tipo, em uma única viagem a receita mínima não seria
atingida.
5
Grade de pontuação:
Questão
03.A
03.B
Categoria
de acerto
0%
75%
100%
0%
75%
100%
0%
25%
03.C
75%
100%
Padrão utilizado para correção
Em branco OU questão totalmente errada.
Montagem das equações sem isolar x e y.
Montagem correta das equações isolando x e y.
Em branco OU questão totalmente errada.
Resolução correta por tentativa e erro mesmo tendo errado a
montagem das equações no item 03.A.
Apresentação do sistema de equações e correta resolução da
questão.
Em branco OU questão totalmente errada.
Indicação do raciocínio a ser utilizado e início da estruturação da
resposta.
Correta resolução do problema com (pequeno) erro de conta.
Indicação de que, em uma viagem, a empresa atingiria a receita
de R$ 1.350.000,00 (inferior aos R$ 4.300.000,00).
6