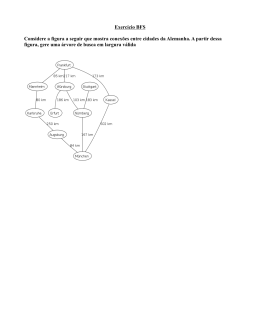
Busca em Largura
BFS(G)
1 for every vertex s of G not explored yet
2
do Enqueue(S,s)
3
mark vertex s as visited
while S is not empty do
4
5
Running time: O(n + m)
u ← Dequeue(S);
6
For each v in Adj[u] then
if v is unexplored then
7
8
mark edge (v,u) as tree edge
9
10
mark vertex v as visited
Enqueue(S,v)
Notação
• Adj [u ] : lista dos vértices adjacentes a u em alguma ordem
• Dequeue(S): Remove o primeiro elemento da fila S
• Enqueue (S,v) : Adiciona o nó v na fila S
Exemplo
S
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
1
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
4
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
45
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
452
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
52
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
52
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
52
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
2
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
6
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
3
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
3
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Exemplo
S
3
4
1
BFS(G)
2
1 for every vertex s of G not explored yet
2
do Enqueue(S,s);
3
4
5
6
7
8
9
10
mark vertex s as visited
while S is not empty do
7
5
6
u ← Dequeue(S);
For each v in Adj[u] then
if v is unexplored then
mark edge (v,u) as tree edge
mark vertex v as visited
Enqueue(S,v)
Busca em Profundidade
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Busca em Profundidade : Exemplo
DFS(G)
1
Para todo v em G
2
Se v não visitado então
3
DFS-Visit(G, v)
DFS-Visit(G, v)
1
Marque v como visitado
2
Para todo w em Adj(v)
3
Se w não visitado então
4
Insira aresta (v, w) na árvore
5
DFS-Visit(G, w)
3
4
1
2
7
5
6
Topological Ordering Algorithm: Example
v2
v6
v3
v5
v7
v4
v1
Topological order:
27
Topological Ordering Algorithm: Example
v2
v6
v3
v5
v4
v7
Topological order: v1
28
Topological Ordering Algorithm: Example
v3
v6
v5
v4
v7
Topological order: v1, v2
29
Topological Ordering Algorithm: Example
v6
v5
v4
v7
Topological order: v1, v2, v3
30
Topological Ordering Algorithm: Example
v6
v5
v7
Topological order: v1, v2, v3, v4
31
Topological Ordering Algorithm: Example
v6
v7
Topological order: v1, v2, v3, v4, v5
32
Topological Ordering Algorithm: Example
v7
Topological order: v1, v2, v3, v4, v5, v6
33
Topological Ordering Algorithm: Example
v2
v6
v3
v5
v7
v4
v1
v2
v3
v4
v5
v6
v7
v1
Topological order: v1, v2, v3, v4, v5, v6, v7.
34