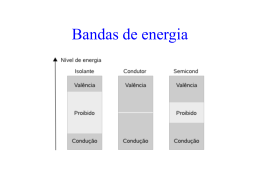
Conceitos Básicos
de Electrónica
Capítulos 1 a 4
Versão 1.0
Isabel Maria Cacho Teixeira
João Paulo Cacho Teixeira
IST
Novembro de 2003
Índice
1.
1.1
1.2
Conceitos Básicos de Electrónica ......................................... 4
Funções Básicas dos Sistemas Electrónicos ................................................ 4
Dispositivos Electrónicos ........................................................................... 5
2.
Análise de Circuitos Electrónicos ......................................... 5
2.1
Leis Fundamentais da Análise de Circuitos ................................................ 6
2.1.1
Leis Topológicas ................................................................................ 6
2.1.2
Leis Características............................................................................. 6
2.1.2.1 Leis Características de Dispositivos Passivos.................................. 6
2.1.2.2 Fontes Ideais e Reais ...................................................................... 7
3.
Modelação de Dispositivos Electrónicos................................ 8
3.1
Conceitos Básicos de Modelação................................................................ 8
3.1.1
Modelos Formais................................................................................ 9
3.1.2
Modelos de Circuito ........................................................................... 9
3.1.3
Componentes de Modelos de Circuito................................................. 9
3.1.4
Desenvolvimento de Modelos de Circuito........................................... 9
3.1.5
Efeitos Capacitivos........................................................................... 13
3.1.6
Análise de Circuitos Electrónicos com Modelos de Dispositivos....... 14
3.2
Introdução à Física de Semicondutores..................................................... 17
3.2.1
Condutores, Semicondutores e Isolantes ........................................... 18
3.2.2
Condução em Metais. Condutividade. Resistência. ........................... 19
3.2.3
Condução em Semicondutores. Electrões e Buracos ......................... 21
3.2.3.1 Condução por Deriva .................................................................... 25
3.2.3.2 Condução por Difusão .................................................................. 25
3.2.4
Semicondutores Extrínsecos (Tipo N e Tipo P)................................. 26
3.2.5
Junção P-N ....................................................................................... 29
4.
Díodo de Junção................................................................. 35
4.1
Equação Característica do Díodo.............................................................. 35
4.1.1
Região de Corte................................................................................ 37
4.1.2
Região de Condução......................................................................... 37
4.1.3
Modelo Linear por Troços ................................................................ 39
4.2
Mecanismos de Disrupção. Díodo Zener .................................................. 40
4.3
Exemplos de Circuitos com Díodos .......................................................... 43
2
Lista de figuras
Figura 2-1 – Dispositivos passivos............................................................................. 6
Figura 2-2 – Símbolos de fontes de corrente e de tensão ideais .................................. 7
Figura 2-3 – Símbolos de fontes de corrente e de tensão reais .................................... 7
Figura 3-1 – Circuito genérico.............................................................................. 9
Figura 3-2 – Modelo de circuito............................................................................... 10
Figura 3-3 - Símbolo de uma fonte de tensão controlada por corrente ...................... 11
Figura 3-4 - Símbolo de uma fonte de corrente controlada por corrente.................... 12
Figura 3-5 - Símbolo de uma fonte de corrente controlada por tensão ...................... 12
Figura 3-6 - Símbolo de uma fonte de tensão controlada por tensão ......................... 12
Figura 3-7– Técnica de análise de circuitos electrónicos proposta ............................ 14
Figura 3-8 – Tipos de modelos de dispositivos electrónicos ..................................... 16
Figura 3-9– Resistividade de diversos materiais condutores metálicos ..................... 20
Figura 3-10 – Resistência de um material condutor de resistividade ρ. ..................... 21
Figura 3-11 – Tabela de classificação periódica de elementos químicos, de
Mendeleiev. ..................................................................................................... 22
Figura 3-12 – Modelo de bandas de energia para semicondutores e para isolantes.... 23
Figura 3-13 – Geração de pares electrão-buraco....................................................... 24
Figura 3-14 – Gradiante de concentração de portadores de carga (electrões) na
direcção x......................................................................................................... 26
Figura 3-15 - Mobilidade de deriva de portadores maioritários no Si em função da
concentração total de impurezas. ...................................................................... 29
Figura 3-16 - Estrutura básica de uma junção P-N.................................................... 30
Figura 3-17 – Campo eléctrico associado a duas cargas ........................................... 31
Figura 3-18 – Região de carga especial (RCE) e regiões neutras num díodo de junção.
........................................................................................................................ 32
Figura 3-19 – Distribuição de carga, campo eléctrico e função potencial numa junção
P-N. ................................................................................................................. 33
Figura 3-20 – Dependência da capacidade de junção, Cj, com a tensão de polarização
do díodo, vD. .................................................................................................... 34
Figura 4-1 - Característica de um díodo de junção: .................................................. 36
Figura 4-2 – Circuito equivalente do díodo quando vD < 0 e | vD| >> VT ............. 37
Figura 4-3 – Curvas características do díodo com IS = 10e-15 A e com IS = 10e-16 A.
........................................................................................................................ 38
Figura 4-4 - Aproximação linear por troços da característica iD(vD) do díodo........... 39
Figura 4-5 – Modelo do díodo para vD < 700mV e vD ≥ 700mV..................... 40
Figura 4-6 – Símbolo e característica do díodo ideal ............................................... 40
Figura 4-7 – Modelo de circuito, equivalente de um díodo (aproximação linear por
troços).............................................................................................................. 40
Figura 4-8 – Símbolo de um díodo Zener................................................................. 42
Figura 4-9 – Modelo de circuito (completo) de um díodo de Zener. ......................... 43
Figura 4-10 – Circuito com um único dispositivo não linear. ................................... 43
Figura 4-11 – Circuito limitador de tensão. .............................................................. 44
3
1.Conceitos Básicos de Electrónica
A Electrónica é a ciência que estuda o comportamento de dispositivos,
circuitos e sistemas electrónicos e a forma de os utilizar para realizar
determinadas funções.
Circuitos e sistemas electrónicos podem ser olhados numa perspectiva de
análise ou de síntese.
A análise refere-se ao estudo do comportamento de circuitos, com vista a
determinar as leis de variação das grandezas (por exemplo, correntes e
tensões) que os caracterizam.
A síntese de circuitos refere-se à realização de circuitos que realizem uma
dada função, a partir, por exemplo, da descrição formal dessa função.
A fim de realizar funções em suporte físico (hardware), dispõe-se de um
conjunto de componentes básicos, designados dispositivos electrónicos.
A interligação de dispositivos permite concretizar a função (ou funções)
pretendidas.
A descrição do comportamento dos dispositivos, incorporados nos circuitos e
activados por estímulos exteriores ao circuito, torna necessário a definição
de modelos.
Um modelo é uma representação concisa de uma realidade, o
comportamento do dispositivo, descrito por um conjunto de características
valorizadas num dado domínio.
1.1 Funções Básicas dos Sistemas Electrónicos
Circuitos e sistemas electrónicos realizam funções. O termo circuito aplicase normalmente, quando a função realizada é relativamente simples. Caso
contrário, quando a função realizada é complexa, aplica-se o termo sistema
electrónico. Não esquecendo esta distinção (de âmbito) entre circuito e
sistema electrónico, utilizar-se-á neste texto, indiscriminadamente, o termo
circuito. Os circuitos electrónicos processam sinais digitais e analógicos.
O processamento de sinais digitais refere-se à propagação de informação,
conforme é associada a determinados valores de uma grandeza eléctrica
(usualmente uma tensão) (por exemplo o ‘1’ lógico pode corresponder a 5Volt
e o ‘0’ lógico a 0 Volt) através de determinados caminhos, que permitam a
realização de determinada função lógica. Este processamento é realizado em
electrónica por associação de fontes de tensão e dispositivos, alguns dos
quais devem comportar-se como interruptores.
O processamento de sinais analógicos corresponde a amplificação ou
alteração de forma de sinais contínuos no tempo de acordo com uma dada
lei. No primeiro caso, amplificação, pretende-se amplificar a amplitude de
um sinal, sem alterar a forma do mesmo. Neste caso, a lei de controlo do
4
processamento analógico é uma lei linear. No segundo caso, o
processamento é realizado segundo uma lei não linear. Em qualquer dos
casos, este processamento é realizado por associação de fontes de energia e
de sinal e por dispositivos, alguns dos quais devem ser capazes de usar
energia para transformar quer a amplitude de sinais quer a sua forma.
1.2 Dispositivos Electrónicos
Dispositivos são os componentes com os quais se constróem circuitos e
sistemas electrónicos. Distinguem-se dois grandes grupos de dispositivos:
passivos e activos. O dispositivo diz-se (passivo) activo se (não) é capaz de
converter energia estática em energia dinâmica, alterando a amplitude e a
forma dos sinais eléctricos. Resistências, condensadores, bobinas e díodos
são exemplos de dispositivos passivos. O dispositivo activo básico é o
transistor.
De entre os componentes utilizados em circuitos electrónicos, o díodo é o
elemento de um acesso mais simples que realiza a função de interruptor,
embora não opere como um interruptor ideal. Como se verá em capítulo
seguinte, embora o díodo se comporte, numa região de funcionamento, como
uma resistência praticamente infinita, na outra região de funcionamento,
comporta-se como uma resistência de valor muito reduzido, mas apresenta
aos seus terminais uma tensão elevada (700 mV nos díodos de silício que
são os habitualmente utilizados), patamar incompatível com os níveis de
tensão de alimentação com que actualmente se trabalha.
Um outro dispositivo que pode realizar a função de interruptor electrónico,
muito mais próximo do ideal que o díodo, é o transistor. Por outro lado,
tratando-se de um dispositivo activo, o transistor permite igualmente
amplificar sinais bem como modulá-los (alterar a sua forma). Assim, o
transistor é o dispositivo que, pelas suas características, está na base da
realização de quase todos os circuitos e sistemas electrónicos.
2. Análise de Circuitos Electrónicos
A análise de circuitos é realizada com base em leis que permitem descrever
formalmente o comportamento do circuito. Utilizam-se leis de dois tipos,
nomeadamente, leis topológicas e leis características. As leis topológicas,
designadas por leis de Kirchhoff, descrevem as restrições que os diferentes
componentes, interligados num circuito, estabelecem entre si. As leis
características, ou simplesmente, características, descrevem as relações
entre correntes e tensões num dispositivo.
A descrição formal das características de alguns dispositivos é complexa. Por
exemplo, um díodo operando em regime estático é descrito aproximadamente
por uma relação exponencial entre a corrente que o percorre e a tensão aos
seus terminais. Assim, o sistema de equações resultante da aplicação dos
dois tipos de leis a um circuito pode ser transcendente, e consequentemente
de difícil resolução analítica, manual. Nessa situação procura-se substituir
a descrição formal geral das características por descrições mais simples,
válidas em domínios mais restritos de tensões e correntes.
5
2.1 Leis Fundamentais da Análise de Circuitos
Como foi referido anteriormente, na análise de circuitos utilizam-se as leis
topológicas e as leis características dos dispositivos ou componentes.
2.1.1 Leis Topológicas
As leis topológicas, designadas por leis de Kirchhoff, descrevem as restrições
que os diferentes componentes, interligados num circuito, estabelecem entre
si. As leis de Kirchhoff são as seguintes:
Lei de equilíbrio de correntes (lei dos nós):
Σ ij = o
Lei de equilíbrio de tensões (lei das malhas):
Σ vj = o
2.1.2 Leis Características
A lei característica, ou simplesmente, a característica, descreve a relação
entre correntes e tensões num componente. Como se referiu, circuitos e
sistemas electrónicos são construídos com base em componentes passivos
e/ou activos.
2.1.2.1 Leis Características de Dispositivos Passivos
i
R
+ v -
V = Ri
Resistência
i C
i
L
+ vL -
+ vc -
i = C dvC/dt
vL = Ldi/dt
Condensador
Bobina
i
D
+ vD -
i = Is (e vD/ηvT - 1)
Díodo
i
v
Figura 2-1 – Dispositivos passivos
Na Figura 2-1 ilustram-se diversos dispositivos passivos de um só acesso
(dois terminais), que exibem relações lineares ou não lineares na sua
característica tensão/corrente. Uma vez que só possuem um acesso, são
descritos por uma só lei característica. Assim, a resistência, o condensador e
6
a bobina, quando descritos por parâmetros constantes R, C e L,
respectivamente, são dispositivos lineares. O díodo (realizado com material
semicondutor e designado usualmente por díodo de junção) é um dispositivo
passivo não linear, descrito por uma relação tensão/corrente como a que se
indica na Figura 2-1, na qual i=ID é a corrente no díodo, vD é a tensão aos
terminais do díodo, Is é a corrente de saturação, VT é a tensão térmica e η
é um parâmetro dependente da tecnologia de fabricação, e que varia entre 1
e 2. Assume-se η = 1 em circuitos integrados e η = 2 em circuitos discretos.
Is, a corrente inversa, é tipicamente uma corrente muito reduzida, da ordem
de grandeza de 10-10 - 10-16 A. Em díodos de junção, IS é proporcional à área
da junção. A tensão térmica é dada por
VT = kT/q
em que k é a constante de Boltzmann, T é a temperatura absoluta e q a
carga do electrão. À temperatura ambiente (27oC), a tensão térmica vale
aproximadamente VT ≈ 25mV.
Is e vD variam com a temperatura de acordo com as seguintes leis de
variação aproximadas:
Is duplica em cada 10º C
∆vD / ∆T = - 2mV / oC.
2.1.2.2 Fontes Ideais e Reais
Além dos componentes passivos, são elementos fundamentais dos circuitos
electrónicos as fontes de energia, de tensão ou de corrente. Idealmente,
pretende-se que uma fonte de tensão (corrente) forneça a mesma tensão
(corrente), qualquer que seja a carga a ela ligada. Uma fonte que satisfaça
este requisito, diz-se ideal. A tensão (corrente) fornecida por uma fonte de
tensão (corrente) real depende da carga a ela ligada. Os símbolos são os que
se representam nas Figura 2-2 e Figura 2-3.
vS
IS
Fonte de corrente
+
_
Fonte de tensão
Figura 2-2 – Símbolos de fontes de corrente e de tensão ideais
RS
IS
vS
RS
Fonte de corrente
+
_
Fonte de tensão
Figura 2-3 – Símbolos de fontes de corrente e de tensão reais
7
Qualquer das representações dos componentes é um modelo do
componente. Com efeito, o recurso a modelos é crucial na Electrónica. Os
modelos permitem simplificar o que é complexo, retendo os aspectos que,
para um dado domínio de aplicação, são os relevantes, e desconsiderando
todos os outros. Analisam-se na secção seguinte os aspectos fundamentais
da modelação em Electrónica.
3. Modelação de Dispositivos Electrónicos
3.1 Conceitos Básicos de Modelação
Como foi referido, um conceito fundamental na análise de circuitos é o
conceito de modelo. Modelo é uma representação concisa da realidade. É
preciso e consequentemente válido dentro de um dado conjunto de
pressupostos que definem o domínio de validade do modelo. O modelo,
dentro do seu domínio de validade, considera aspectos do funcionamento do
dispositivo que modela, relevantes nesse domínio, desprezando os outros
aspectos. Como se conhece, exactamente, o que se está a desprezar e a
considerar, pode dizer-se que, no contexto do domínio de validade, o modelo
e a análise que permite são precisos, dado que se podem conhecer os
resultados e os erros ou aproximações cometidos na análise. Modelo e
domínio de validade do modelo são, pois, indissociáveis.
No âmbito da Electrónica, os objectivos a atingir, nomeadamente, o tipo de
análise que se pretende realizar, condicionam as características de um
dispositivo que devem ser consideradas no desenvolvimento do modelo que o
representa. Por exemplo, se a análise a realizar é para determinar o
comportamento do dispositivo quando submetido a fontes de energia (tensão
ou corrente) constantes no tempo, análise estática, então o modelo só deve
contemplar os aspectos que reagem a este tipo de estímulo. Se se pretende
conhecer o comportamento do circuito quando submetido a estímulos
variáveis no tempo e/ou na frequência, são os parâmetros dos dispositivos
que reagem a estes estímulos que devem ser considerados.
Um aspecto adicional a considerar é a precisão que se pretende alcançar
com a análise, isto é, qual a gama de erros aceitável. Este requisito reflectese a vários níveis. De facto, condiciona a precisão dos componentes que se
utilizam no circuito, e os aspectos de comportamento dos dispositivos que
devem ser tomados em consideração.
Por exemplo, uma resistência, RL, cuja lei de variação entre a tensão aos seus
terminais, vL, e a corrente que a percorre, iL, é expressa pela lei de Ohm, vL =
RL iL,, pode deixar de ser correctamente descrita por aquela lei. Por exemplo,
em frequências muito elevadas, determinado tipo de resistências podem
passar a comportar-se como uma bobina em série com uma resistência. Este
exemplo muito simples destina-se a realçar o carácter limitado do domínio
de validade dos modelos, enquanto representações de uma dada realidade.
Em Electrónica recorre-se fundamentalmente a dois tipos de modelos,
nomeadamente, modelos formais e modelos de circuito.
8
3.1.1 Modelos Formais
Os modelos formais descrevem o comportamento de um dispositivo ou de
um circuito ou sistema através de um conjunto de equações matemáticas.
Estas podem ser derivadas com base em considerações físicas, reflectidas
nos parâmetros que caracterizam os modelos (designados por este motivo
como modelos físicos), ou por exemplo, por aproximação polinomial de
curvas laboratoriais, designando-se os modelos por modelos numéricos.
Exemplo de um modelo formal, físico, é a equação que representa a
característica estática de um díodo de junção, já referida na Figura 2-1.
i = Is (e
vD/ηVT
- 1)
Este modelo é caracterizado por três parâmetros, IS, η e VT.
3.1.2 Modelos de Circuito
Os modelos de circuito representam o comportamento do dispositivo
através de circuitos eléctricos, equivalentes, que descrevem esse
comportamento dentro do domínio de validade do modelo.
3.1.3 Componentes de Modelos de Circuito
Resistências, condensadores e bobinas são componentes físicos reais. Podem
comprar-se em qualquer loja de componentes. Também as fontes de energia
são componentes físicos reais. Contudo, os correspondentes elementos de
circuito idealizados (R, L, C, V e I) são utilizados por vezes para representar
ou modelar efeitos físicos cuja relação entre as grandezas corrente e tensão
que os caracterizam seja coincidentes com as relações características de tais
componentes.
3.1.4 Desenvolvimento de Modelos de Circuito
A fim de compreender como é que se desenvolve um modelo de circuito,
considere-se o circuito genérico da Figura 3-1.
a
v1
i2
i1
X1
X2
b
c
v2
d
Figura 3-1 – Circuito genérico
9
O circuito da Figura 3-1 representa quaisquer 4 nós de um circuito, dois dos
quais são comuns, e comuns ao terminal de referência do circuito, b=d.
Representa, pois, uma rede eléctrica de dois acessos. Ligar dois dos
terminais ao nó de referência não altera em nada a generalidade do que vai
ser exposto. Simplifica somente o raciocínio, na medida em que, em vez de
referir diferenças de potencial entre o nó a e o nó b e o nó c e o nó d, se
consideram as tensões v1 e v2 respectivamente. Não se conhece à partida a
natureza de X1 e de X2. Assim, suponhamos que
V1 = X1 i1
equação 3-1
X1 tem, neste caso, a dimensão de uma resistência, em que a corrente que o
percorre é proporcional à tensão aos seus terminais. Assim, X1 comporta-se
como um elemento resistivo, e pode por isso ser modelado por uma
resistência R1=X1.
Suponhamos agora que
i1 = X1 dv1/dt
equação 3-2
Neste caso, X1 descreve um efeito capacitivo e pode ser modelado por uma
capacidade C1=X1.
Se se admitir que
i1 = X’1/v1 + X’’1 dv1/dt
Equação 3-3
neste caso, X1 é uma admitância que representa o paralelo entre a
resistência 1/X’1 e a capacidade X’’1 .
X’’1
X’1
X1
Figura 3-2 – Modelo de circuito
10
Suponhamos, contudo, que :
V1 = X1 i2
Também neste caso, X1 tem a dimensão de uma resistência. Contudo, a
tensão aos seus terminais não é proporcional à corrente que a percorre. Ou
seja, embora tenha a dimensão física de uma resistência (Ω), não se
comporta como tal, nem pode ser modelada dessa maneira. Com efeito, a
tensão V1 permanece constante qualquer que seja a corrente i1. Mas o
elemento que tem uma tensão constante aos seus terminais,
independentemente da corrente que o percorre, é uma fonte de tensão ideal.
Só que, neste caso, o valor da tensão é imposto por uma corrente noutro
ramo do circuito. Diz-se que X1 se comporta como uma fonte de tensão
controlada por corrente. O símbolo que a representa é indicado na
Figura 3-3.
+
_
vS
vs= v2 = Rtr i2
Figura 3-3 - Símbolo de uma fonte de tensão controlada por corrente
Dado que vs= Rtr i2. Rtr diz-se uma trans-resistência, porque relaciona a
forma como uma corrente actua sobre um outro ramo do circuito.
Se se admitir que
i2 = X2 i1
X2 é adimensional e exprime a relação que existe entre a corrente i1 e a
corrente i2. Isto é, representa um ‘ganho’ de corrente, Gi. A corrente i2 é
independente de v2, e x2 comporta-se como uma fonte de corrente
controlada por outra corrente. O símbolo que representa a fonte de
corrente controlada por corrente é que se representa na
Figura 3-4.
11
iS
is = i2 = Gi i1
Figura 3-4 - Símbolo de uma fonte de corrente controlada por corrente
Se a relação entre as grandezas for:
i2 = X2 v1
X2 tem dimensão de condutância mas não pode ser representado por uma
resistência porque a corrente que a percorre é independente da tensão aos
seus terminais. Ou seja, comporta-se como uma fonte de corrente
controlada por tensão. X2 é designada por transcondutância, Gtr. O
símbolo é o representado na Figura 3-5.
iS
is = i2 = Gtr v1
Figura 3-5 - Símbolo de uma fonte de corrente controlada por tensão
Suponhamos que
v2 = X2 v1.
Neste caso, X2 é adimensional e representa a relação entre a tensão em dois
nós, ou seja o ganho de tensão entre eles, Gv, neste caso, entre v2 e v1. O
símbolo é representado na
Figura 3-6.
+
_
vS
vs= v2 = Gv v1
Figura 3-6 - Símbolo de uma fonte de tensão controlada por tensão
12
Os modelos de circuito são pois constituídos, genericamente, por elementos
passivos, resistências, por elementos armazenadores de energia,
condensadores e/ou bobinas e por fontes de tensão ou de corrente
controladas por tensão ou por corrente.
Genericamente, numa fonte de corrente controlada por corrente ou por
tensão is é dado por:
is = gm vk ou por is = β ij sendo ij uma corrente
noutro ramo do circuito e vk uma tensão entre dois nós do circuito distintos
dos nós de entrada e de saída da fonte de corrente.
Do mesmo modo, numa fonte de tensão controlada por corrente ou por
tensão vs é dado por :
vs = rm ik ou por vs = α vj sendo ik uma corrente
noutro ramo do circuito e vj uma tensão entre dois nós do circuito distintos
dos nós de entrada e de saída da fonte de corrente.
Com estas primitivas de modelação, isto é, resistências, condensadores,
bobinas e fontes controladas de tensão e de corrente pode modelar-se o
comportamento de qualquer dispositivo electrónico cujas relações entre
tensões e correntes aos terminais são descritas por equações mais ou menos
complexas.
Os modelos de circuito correspondem, necessariamente, a somas de tensões
ou/e de correntes, na medida em que qualquer circuito, como se viu, pode ser
descrito, do ponto de vista topológico, pelas leis de Kirchhoff.
3.1.5 Efeitos Capacitivos
O símbolo do condensador é utilizado para modelar efeitos capacitivos, isto
é, efeitos associados a variação de carga eléctrica num dispositivo.
Num condensador, a relação entre a corrente, i, e a carga, Q, é dada por:
i = dQ / dt
equação 3-4
Se Q puder ser descrita por
Q=Cv
equação 3-5
em que o termo de proporcionalidade, C, se supõe constante (capacidade
linear), então
i = C dv / dt
equação 3-6
Nos dispositivos semicondutores, as variações de carga associadas a
variações de tensão são modeladas por capacidades, usualmente não
lineares.
13
3.1.6 Análise de Circuitos Electrónicos com Modelos de
Dispositivos
Os circuitos electrónicos reais são constituídos por uma interligação de
elementos de circuito lineares e dispositivos não lineares. Os dispositivos,
por imposição do circuito exterior, são conduzidos a operar em determinado
regime de funcionamento. Qual? E como deve ser conduzida a análise do
circuito electrónico, real?
Na Figura 3-7 ilustra-se, de forma resumida, um método eficaz de conduzir
tal análise, por forma a utilizar modelos de dispositivos tão simples quanto
possível.
Dispositivos
HIP. (operação)
Modelos
Análise do Circ.
Analíticos
Analíticos
Simulação
Simulação
Experimentação
Experimentação
Função (operação)
N
Modelos: OK?
S
fim
.
Figura 3-7– Técnica de análise de circuitos electrónicos proposta
Como ponto de partida do raciocínio, há que ter em mente que um
dispositivo é inserido num circuito, a fim de realizar uma função. Se essa
função for conhecida à partida, é trivial a definição da sua região de
operação. Em princípio, uma região de funcionamento específica permite a
caracterização de um modelo regional mais simples.
Designa-se por modelo regional um modelo de dispositivo cujo domínio de
validade se restringe a uma região de operação específica. A região de
operação pode corresponder a um sub-domínio de tensões e correntes no
dispositivo (por exemplo, a região de saturação de um transistor bipolar),
e/ou a um sub-domínio da variação dos estímulos a ele aplicado (por
exemplo, funcionamento estático, ou de variação lenta no tempo).
Modelos regionais são modelos mais simples que modelos aplicáveis a
diversas regiões de operação. A título ilustrativo, o modelo exponencial para
um díodo de junção é válido para a região de corte e para a região de
condução, no regime estático ou no regime de variação lenta no tempo. Se,
de início, se souber que o díodo (inserido no circuito em análise) está em
14
condução, e a ordem de grandeza da corrente que o percorre, pode definirse, à partida um modelo linear por troços.
Modelos lineares por troços (PWL, Piecewise Linear) são modelos
aproximados (isto é, com menor precisão) que descrevem, para cada região
de operação, o comportamento do dispositivo através de um comportamento
regional linear. Assim, para o díodo, é possível identificar um modelo linear
correspondente ao troço de condução. Tal modelo, como se verá no Capítulo
4, é caracterizado por dois parâmetros, Vγ e Rγ. Tal modelo simplificado
permite uma análise de um circuito não linear através de uma rede eléctrica
linear.
Se a função do circuito não for conhecida a priori, ainda assim torna-se
recompensador fazer uma hipótese quanto à região de operação do
dispositivo. O conhecimento aprofundado do comportamento do dispositivo e
uma análise preliminar do efeito restritivo do circuito exterior sobre o
dispositivo permitem guiar a escolha do região de operação mais provável em
que o dispositivo, no circuito em análise, deve operar. Assim, a definição da
hipótese de operação não é aleatória, nem equi-provável, mas antes pode ser
guiada, de modo inteligente, por forma a que, tanto quanto possível, se
realize uma escolha right first time – isto é, a escolha acertada na sua
primeira tentativa.
Uma vez feita uma escolha (baseada na hipótese de operação mais provável),
o modelo mais adequado à técnica de análise pode ser seleccionado. Se a
análise for manual, a fim de se identificar a função realizada e as
características essenciais do circuito, o modelo deve ser tão simples quanto
a precisão da análise o consinta. Se a análise for realizada por simulação
em computador, usualmente os programas de simulação possuem em
biblioteca modelos elaborados, que permitem uma análise de grande
precisão.
Naturalmente, a complexidade do circuito pode condicionar a complexidade
dos modelos utilizados, e o nível de abstracção em que o circuito (e os seus
elementos constituintes) é descrito. Finalmente, as representações
abstractas do dispositivo e do circuito electrónico podem ser confrontadas
com a realidade que modelam, através da experimentação laboratorial.
Tendo realizado a análise do circuito real, através de um circuito
equivalente, que utiliza os modelos dos dispositivos, há que demonstrar que
a solução encontrada é consistente com a hipótese feita, no início, quanto à
região de operação do dispositivo. É a fase de verificação. Por exemplo, um
circuito com um transistor MOS de canal N, de reforço, e para o qual se
admitiu que operava na região de saturação, há que verificar (de acordo com
o modelo de primeira ordem que iremos utilizar, descrito no Capítulo 5) que
vDS > vGS –Vt. Em caso afirmativo, os resultados obtidos são válidos. Em caso
contrário, há que estabelecer uma hipótese diferente quanto à região de
operação do dispositivo, e repetir a análise do circuito (agora um circuito
equivalente diverso).
Neste ponto, pode resumir-se o conjunto de modelos de dispositivos
electrónicos que servem como “ferramentas” na identificação da função
realizada pelo circuito real que os contém. Tal resumo é ilustrado na Figura
3-8.
15
Lineares
Lineares(R,
(R,
PWL
PWL
Não
Lineares
(D,
T,
AMPOP)
Não Lineares (D, T, AMPOP)
equações
equações
Modelos
Modelos
Analíticos
Analíticos
L,C)
L,C)
Estáticos
Estáticos(DC)
(DC)
Análise no tempo (dig.)
ou na frequência (analog.)
Dinâmicos
Dinâmicos
Circuitos
Circuitos
equivalentes
equivalentes Não
NãoLineares
Lineares(sinais
(sinaisfortes)
fortes)
Lineares
Lineares(sinais
(sinaisfracos)
fracos)
PWL
PWL
Quasi-estáticos
Quasi-estáticos
Variação
VariaçãoRápida
Rápida
Figura 3-8 – Tipos de modelos de dispositivos electrónicos
Assim, caracterizam-se modelos estáticos (DC) e modelos dinâmicos. Os
modelos estáticos descrevem o comportamento de dispositivos quando
actuados por grandezas eléctricas (tensões ou correntes) de valor constante
no tempo.
Quando essas grandezas variam no tempo, duas situações de interesse
podem ocorrer:
as variações são suficientemente lentas no tempo, para que o dispositivo
se comporte aproximadamente como se fosse actuado, instante a
instante, por estímulos constantes no tempo, cujo valor iguala o valor
instantâneo desses estímulos. Neste caso, o comportamento dinâmico
pode ser descrito como uma sucessão, no tempo, de estados
estacionários. Podem assim estender-se o domínio de validade dos
modelos estáticos a regimes de variação lenta no tempo, designando-se
tais modelos por modelos quasi-estáticos. Naturalmente, o ritmo de
variação temporal dos sinais (estímulos) consentâneo com os modelos
quasi-estáticos depende das características tecnológicas dos dispositivos.
As variações são rápidas no tempo, dando origem a que efeitos dinâmicos
do comportamento do dispositivo se tornem relevantes, alterando de
forma significativa o comportamento dos dispositivos, relativamente ao
comportamento previsto pelos modelos quasi-estáticos. É necessário,
neste caso, recorrer a modelos de variação rápida, para uma descrição
precisa do comportamento dos dispositivos. A título ilustrativo, num
modelo quasi-estatico de um transistor MOS, admite-se (ver Capítulo 5)
que a corrente de porta (gate) é nula. Todavia, a presença do óxido fino
da porta (SiO2) entre o terminal de porta e o canal do transistor, junto
com regiões condutoras acima e abaixo do isolante, configuram uma
capacidade distribuída porta-canal. Na presença de sinais de variação
rápida no tempo, esse efeito pode ser descrito pela representação de duas
capacidades concentradas nos extremos do canal (Cgs e Cgd), sendo que
correntes capacitivas originam correntes de porta (iG) não nulas.
Do ponto de vista da facilidade de análise, é um facto bem conhecido que
circuitos lineares são objecto de uma análise muito mais simples que os
circuitos não lineares. Assim, uma vez que os principais dispositivos
16
electrónicos são dispositivos não lineares, importa identificar sub-domínios
para os quais o comportamento do dispositivo seja linearizável.
Deste modo, para modelos estáticos, a forte não linearidade das suas leis
características permite, usualmente, definir modelos lineares por troços
(PWL). Tais modelos descrevem, para cada região de operação, o
comportamento do dispositivo através de um comportamento regional linear.
No caso de regimes dinâmicos de operação, que obrigam à utilização de
modelos dinâmicos, duas situações podem ocorrer:
Quando a amplitude dos sinais é elevada (sinais fortes), os dispositivos,
ao longo do tempo, percorrem mais do que uma região de operação. Dado
o carácter fortemente não linear das suas leis características, essa
circunstância inviabiliza a definição de modelos lineares; quando muito,
permite uma descrição aproximada em que modelos PWL percorrem mais
de um troço linear. Este é o caso de circuitos digitais, em que as variáveis
Booleanas são descritas por tensões eléctricas, próximas de dois valores
extremos de tensão – usualmente as tensão de alimentação.
Quando a amplitude dos sinais é reduzida (sinais fracos), os dispositivos
operam sempre na mesma região, observando-se apenas variações
limitadas das tensões e correntes em torno de valores fixados pelas
tensões de alimentação estática. Nestas circunstâncias, os valores
instantâneos totais das grandezas eléctricas podem ser calculados
através da sobreposição linear de duas componentes, uma estática
(normalmente calculada a partir de modelos estáticos não lineares) e
outra dinâmica, com sinais de amplitude reduzida. Para as componentes
dinâmicas das tensões e correntes no dispositivo (componentes
incrementais), é de novo possível definir modelos lineares – o que facilita
em muito a análise dos circuitos equivalentes incrementais.
Se as variações forem lentas, a partir dos modelos quasi-estáticos podem
derivar-se (ver Capítulo 6) modelos incrementais (isto é, modelos que
descrevem as relações entre os incrementos das tensões e correntes).
Estes são modelos lineares resistivos, descritos por sistemas de equações
algébricas nas componentes dinâmicas das tensões e correntes.
Se as variações forem rápidas, os modelos incrementais dos dispositivos
são lineares reactivos, contendo elementos de circuitos capazes de
armazenar energia (condensadores, bobinas) e são descritos por sistemas
de equações diferenciais. Como se verá adiante, a análise no domínio da
frequência e o recurso à variável complexa permite transformar os
sistemas de equações diferenciais, no domínio do tempo, em sistemas de
equações algébricas, no domínio da frequência, o que novamente
simplifica muito a análise dos circuitos equivalentes.
3.2 Introdução à Física de Semicondutores
Nesta secção pretende-se tão só introduzir o leitor nos conceitos básicos da
física de semicondutores, que lhe permita compreender o comportamento
(aos seus terminais) de dispositivos electrónicos que utilizam esta tecnologia
como suporte físico. Diversas equações fundamentais são introduzidas sem
demonstração. A linguagem utilizada, de carácter frequentemente qualitativa
17
e coloquial, visa explicar, a traços largos, os fenómenos de condução em
semicondutores e o seu impacto sobre o comportamento terminal.
Recomenda-se ao leitor que deseje aprofundar estes tópicos a consulta a
uma obra de referência neste domínio.
3.2.1 Condutores, Semicondutores e Isolantes
Relativamente às suas propriedades eléctricas, os materiais que constituem
o suporte físico dos dispositivos electrónicos apresentam diversas
capacidades de condução de corrente eléctrica.
A corrente é assegurada pelo movimento de cargas eléctricas móveis
(electrões). A ligação (ou não) de electrões aos átomos dos elementos
químicos modifica radicalmente a capacidade do material em conduzir (ou
não) corrente eléctrica.
Os materiais utilizados na indústria semicondutora para a fabricação de
dispositivos, circuitos e sistemas integrados incluem:
condutores (predominantemente, metais, em particular alumínio (Al) e
cobre (Cu)),
semicondutores (silício (Si), Germânio (Ge) e Arsenieto de Gálio (GaAs),
entre os mais usados) e
isolantes (óxido de silício (SiO2), entre outros).
O Si, sendo o segundo elemento químico mais abundante à superfície da
Terra, é o material semicondutor mais utilizado.
Electricamente, o que os distingue no essencial? Macroscopicamente,
quando se aplica uma diferença de potencial estática aos terminais de uma
porção destes materiais, de que resulta um campo eléctrico interno, os
materiais isolantes não conduzem (corrente nula), os semicondutores
conduzem pouco (corrente reduzida) e os metais conduzem muito (corrente
elevada). A capacidade de condução varia com a temperatura do material.
Contudo, para os isolantes quase não varia, para os semicondutores pode
variar muito e para os condutores diminui ligeiramente com o aumento de
temperatura.
Uma vez que a condutividade de um material depende, entre outros factores,
da população de portadores de carga disponíveis para a condução, isto
significa que, nos isolantes (também designados materiais dieléctricos),
praticamente não existem electrões livres (isto é, sem ligação de valência
aos átomos do material); nos semicondutores existe uma população reduzida
e, nos metais, uma população elevada.
A densidade de cargas móveis, disponíveis para a condução, depende da
quantidade de energia que tem de ser fornecida a um electrão de valência
(ou electrão ligado) para quebrar a sua ligação de valência e assim tornarse um electrão livre.
A energia necessária para libertar um electrão pode provir da energia
cinética recebida de outra carga móvel, por colisão inelástica1, da
1
Cargas eléctricas do mesmo sinal repelem-se; assim, no seu movimento no material, quando dois
electrões se aproximam a sua força de repulsão fá-los trocar energia (perder ou ganhar) e mudar de
direcção. Designa-se usualmente este acidente de percurso como “colisão inelástica”.
18
temperatura (energia de agitação térmica) e do campo eléctrico aplicado ao
material.
Para os metais, basta uma energia reduzida para quebrar a ligação de
valência dos electrões da última camada. Para os isolantes, é necessário
fornecer uma energia muito elevada. É o que acontece quando, na presença
de campos eléctricos muito elevados, se produz um fenómeno de disrupção
do dieléctrico, originando uma corrente eléctrica.
Para os semicondutores observa-se uma situação intermédia: é preciso
fornecer uma energia considerável, mas não comparável à necessária para
os isolantes. Este aspecto será explicado mais em detalhe na descrição da
condução nos materiais semicondutores, em que se recorre-se a um modelo
de bandas de energia.
3.2.2 Condução em Metais. Condutividade. Resistência.
O que caracteriza a condução nos metais é que, à temperatura ambiente, os
electrões da última camada (ou “órbita”) já quebraram a sua ligação aos
átomos (que ficam, assim, ionizados com carga positiva, fixa). Cargas
iónicas, fixas, não contribuem para a corrente eléctrica.
Nestas circunstâncias, existe uma enorme população de cargas móveis
(electrões livres), que se deslocam no material segundo um movimento de
agitação térmica e que podem, quando solicitadas por um campo eléctrico,
constituir uma corrente coerente segundo o campo, originando uma corrente
eléctrica aos terminais. Tal população de electrões livres é designada por
“nuvem electrónica”.
O movimento de agitação térmica é um movimento aleatório de cargas
móveis, que possuem uma energia cinética cujo valor é proporcional à
temperatura (daí a designação “de agitação térmica”). Nesse movimento,
electrões livres aproximam-se (ou afastam-se) de outros electrões. Cargas
eléctricas do mesmo sinal repelem-se. Assim, quando dois electrões se
aproximam, a sua força de repulsão fá-los trocar energia (perder ou ganhar)
e mudar de direcção. Como se referiu, esta modificação no movimento
dessas cargas é designada por “colisão inelástica”.
Uma vez que, sem tensão aplicada, não há corrente, o saldo deste
movimento de electrões livres é macroscopicamente nulo. Todavia, ao aplicar
uma tensão estática (de que resulta um campo eléctrico, E, constante, no
interior do metal), esse campo aplica ao electrão uma força f = - q.E (q, carga
do electrão) que induz neste um movimento uniformemente acelerado, entre
duas colisões. Deste modo, ao longo do tempo, observa-se uma sobreposição
de dois efeitos, a agitação térmica e a movimentação coerente com o campo.
Designa-se o movimento coerente segundo o campo eléctrico como
movimento de deriva.
Embora a movimentação segundo o campo eléctrico tenha uma velocidade
variável entre colisões, macroscopicamente pode definir-se um valor médio
dessa velocidade segundo o campo, v. Uma vez que v é proporcional ao
campo eléctrico, E, define-se uma constante de proporcionalidade, µ, como
19
v=µ.E
e designa-se essa constante de proporcionalidade como mobilidade de
deriva2. Quanto maior for o percurso médio entre colisões, maior a velocidade
de deriva imprimida à carga móvel, ou maior a sua “mobilidade”.
A densidade de corrente de deriva, J, pode obter-se como o produto da carga
móvel por unidade de volume pela sua velocidade de deriva, v. A carga será
(q.N), se N for a densidade de portadores de carga móvel. Pode então
escrever-se
J = (q.N).v = (q.µ.N).E = σ . E
em que se introduz o conceito de condutividade do material, σ, definido por
σ=q.µ.N
A natureza do material (neste caso, o metal) determina o valor da
condutividade. A condutividade expressa a facilidade (ou dificuldade) de, por
acção do campo E, obter uma corrente, I = J.A (em que A é a secção
transversal do material ao qual se aplica o campo). No caso dos metais, N é
muito elevado, o que ocasiona condutividades elevadas. Também é usual
definir o inverso da condutividade, ρ, designada como resistividade, através
de
ρ=1/σ=1/ q.µ.N
Na Figura 3-9 indicam-se os valores de resistividade de diversos condutores.
Material condutor
Alumínio
Cobre
Ferro
Chumbo
Prata
Ouro
Ω.cm)
Resistividade a 300oK (Ω
-6
2.9x10
1.7x10-6
9.8x10-6
2.1x10-5
1.8x10-6
2.4x10-6
Figura 3-9– Resistividade de diversos materiais condutores metálicos
Tipicamente, N não varia com a temperatura, T. Todavia, a mobilidade de
deriva, µ, diminui com T, dado que o aumento da agitação térmica reduz o
percurso médio entre colisões. Assim, a resistividade de metais aumenta
ligeiramente com a temperatura.
Considerando uma porção de material condutor, de comprimento L
(Length) e de secção transversal rectangular, A, tal como se ilustra na
2
Para valores elevados do campo eléctrico, a proporcionalidade entre a velocidade e o campo deixa de
ser constante e observa-se um fenómeno de saturação da velocidade de deriva. Essa saturação traduzse por uma redução efectiva da mobilidade, µ, e pode ser modelada como um efeito de modulação da
mobilidade.
20
Figura 3-10, o valor da corrente eléctrica que resulta da aplicação de uma
tensão eléctrica V aos seus terminais pode, finalmente escrever-se
I = J.A = σ.E . A = σ.A . E = σ.A . V/L
Donde se obtém
I=V/R
em que R, a resistência do material condutor, é avaliada por
ρ/t). (L/W)
R = L / σ.A = ρ . L/A = (ρ
Nesta última relação, discrimina-se a secção transversal A = t.W, suposta
rectangular, em que t (thickness) é a espessura da camada condutora e W
(Width) a sua largura. Obtém-se assim a bem conhecida lei de Ohm, que
descreve a lei característica de uma resistência linear, de valor R.
ρ
I
→
L
t
W
A
A = W.t
R = ρ. (L/W.t)
Figura 3-10 – Resistência de um material condutor de resistividade ρ.
Note-se que a expressão da resistência depende da característica eléctrica
intrínseca do material (através da resistividade) e das características
geométricas do condutor físico (secção transversal e comprimento). Como se
verá adiante, no projecto de circuitos integrados com condutores,
semicondutores e isolantes, o fabricante fixa, por construção, o primeiro
factor (ρ/t) das camadas disponíveis para construir o circuito. O projectista
tem a liberdade de definir as dimensões geométricas (W, L) dos seus
dispositivos, de acordo com a função pretendida. Por este motivo, é comum
designar o primeiro factor da resistência como resistência da camada, RS
(sheet resistance), isto é,
ρ/t)
RS = (ρ
3.2.3 Condução em Semicondutores. Electrões e Buracos
O semicondutor é um material que deve o seu nome ao facto de, à
temperatura ambiente, nem conduzir como os metais, nem isolar como os
dieléctricos. Como se observa na tabela de classificação periódica de
elementos químicos (Figura 3-11),
os materiais semicondutores
21
homogéneos3 estão alistados na coluna IV, que se caracteriza por os seus
elementos terem quatros electrões na última camada, ou órbita.
Num semicondutor cristalino, a estrutura regular em que se dispõem os
átomos (em forma de tetraedro com um átomo adicional, no centro do
tetraedro) faz com que os 4 electrões da última camada, quando ainda
ligados aos átomos, partilhem cada um a sua ligação de valência com um
átomo vizinho, naquilo que se designa por “ligação de co-valência”.
Figura 3-11 – Tabela de classificação periódica de elementos químicos, de Mendeleiev.
Nos materiais condutores (metais), à temperatura ambiente, praticamente
todos os electrões da última camada já se libertaram da sua ligação de
valência e, portanto, deslocam-se livremente.
Contudo, num semicondutor intrínseco, por exemplo, Silício puro, apenas
uma fracção muito reduzida de electrões da última camada quebraram a sua
ligação de co-valência tornando-se electrões livres. De facto, existe um
acréscimo considerável de energia que tem de ser fornecida ao electrão para
quebrar essa ligação.
Num diagrama de energia, En, tudo se passa como se os estados de energia
possíveis de ser preenchidos pelos electrões possam assumir valores até um
valor máximo na situação de electrões ligados (valência), EV, e de um novo
valor, superior, EC > EV, na situação de electrões livres, como se ilustra na
Figura 3-12.
Este modelo, de bandas de energia, define assim um hiato (gap) de valores
de energia que não são possíveis para os electrões nesse semicondutor. Fala3
Designa-se por material homogéneo aquele que é constituído por apenas um elemento químico.
Assim, semicondutores de Si ou Ge são semicondutores homogéneos. Também existem
semicondutores heterogéneos, constituídos por átomos de elementos nas colunas III e V (tal como o
GaAs) ou da mesma coluna (caso recente do SiGe).
22
se assim de uma banda de valência (E < EV), uma banda de condução (E >
EC) e de uma banda proibida, de “altura”
EG = EC - EV.
Para o Si, EG = 1.11 e.V (electrão.Volt). O Germânio exibe uma altura da
banda proibida menor: EG = 0.67 e.V. Materiais isolantes apresentam valores
de energia, para a banda proibida, muito mais elevados: por exemplo, para o
óxido de silício (SiO2), EG = 8.5 e.V (ver Figura 3-12).
Banda de Condução
EC
EC
Banda de
Condução
EG
EV
EG
Banda de Valência
semicondutor
EV
isolante
Banda de
Valência
Figura 3-12 – Modelo de bandas de energia para semicondutores e para isolantes
A existência desta “banda proibida” torna compreensível que, à temperatura
ambiente, a energia térmica seja insuficiente para libertar uma fracção
significativa dos electrões da última camada. Justifica ainda a forte
dependência da concentração intrínseca de portadores de carga, ni, com a
temperatura, dada por
ni2 (T) = A. T3 . e- EG/KT
em que T é a temperatura absoluta (Kelvin), A é uma constante do material,
EG é o valor da banda proibida, K a constante de Boltzmann (K = 1.62x10-5
e.V/ºK). Para o Silício, A = 5.06x1043 m-6.ºK-3.
À temperatura ambiente, no silício, ni (300ºK) = 1.45x1010 cm-3. O que indica
este valor? Recordando que, na rede cristalina de Si, a concentração de
átomos é de 5x1022 cm-3, isto significa que a concentração de electrões livres,
à temperatura ambiente, é aproximadamente 1012 vezes menor que a dos
átomos. Este valor tão reduzido justifica que o Si intrínseco, à temperatura
ambiente, apresente uma resistividade muito elevada.
Todavia, na condução em semicondutores, existe outro fenómeno relevante.
Com efeito, cada electrão que, recebendo um acréscimo de energia EG, rompe
a sua ligação de co-valência e torna-se um electrão livre, deixa atrás de si
uma ligação de co-valência por preencher, literalmente, – um buraco.
Que importância tem isso? Significativa. Com efeito, enquanto que, à
temperatura ambiente, poucos electrões recebem acréscimos de energia EG,
muitos podem receber incrementos bem menores. Contudo, a energia
23
necessária para um electrão ligado passar de uma ligação de co-valência, em
torno de um átomo, para outra ligação de co-valência de um átomo vizinho,
é bem menor que EG. Assim, se se aplicar um campo eléctrico que forneça
alguma energia, é possível produzir um movimento de deriva de electrões
livres, e um movimento de deriva de electrões ligados, de ligação de covalência em ligação de co-valência, ou, dito de outro modo, de buraco em
buraco.
Nestas condições, diz-se que cada electrão que recebe energia para quebrar
a sua ligação de co-valência gera um par electrão-buraco (
Figura 3-13). Na realidade, haverá electrões a deslocarem-se livremente na
banda de condução e electrões a deslocarem-se entre ligações de co-valência
na banda de valência. Assim, para um semicondutor intrínseco, a
concentração de electrões livres, n, e a concentração de buracos, p, são
iguais, isto é,
n = p = ni(T)
Banda de Condução
-
EC
EG
EV
+
Banda de Valência
semicondutor
Figura 3-13 – Geração de pares electrão-buraco.
Por outro lado, o movimento de agitação térmica, com as correspondentes
trocas de energia entre cargas, origina que, aleatoriamente, se produza uma
geração de pares electrão-buraco e uma recombinação pares electrãoburaco, quando electrões livres perdem energia e retomam uma ligação de
co-valência.
Em equilíbrio, as taxas de geração e de recombinação são iguais (g = R) e
proporcionais à concentração intrínseca, através de
g = R = r.n. p = r. ni
2
É fácil de perceber que a velocidade dos electrões livres, na banda de
condução é superior à velocidade dos buracos (entre ligações na banda de
valência). Consequentemente, a mobilidade de deriva de electrões livres (µn)
excede a de buracos (µp).
De um ponto de vista macroscópico fala-se, por simplicidade de linguagem,
em dois tipos de portadores de carga, cargas negativas, os electrões livres
na banda de condução, e cargas positivas, os buracos na banda de
valência. O movimento aparente de buracos é em direcção oposta ao
24
movimento de electrões ligados, de ligação de co-valência em ligação de covalência. Na realidade, os portadores de carga - quem se desloca - são
sempre electrões. Todavia, as duas correntes (a de cargas móveis “positivas”
e negativas) somam-se. Surge assim, no semicondutor, o conceito de
condução bipolar (de cargas “positivas” e negativas). Por contraste, a
condução em metais é uma condução unipolar.
3.2.3.1Condução por Deriva
Na presença de dois tipos de portadores de carga – electrões e buracos -,
pode derivar-se a expressão da condutividade de um material semicondutor.
Dado que a corrente de deriva é composta de duas componentes – corrente
de electrões e corrente de buracos – a condutividade do semicondutor pode
escrever-se
σ = q . (µ
µn . n + µp . p)
Analogamente pode definir-se a resistividade. No Si intrínseco, as
mobilidades de deriva são aproximadamente µn = 1330 cm2/V.s e µp = 495
cm2/V.s. Como se referiu, no semicondutor intrínseco a condutividade, à
temperatura ambiente, é muito reduzida (n = p = ni = 1.45x1010 cm-3). A sua
resistividade vale, então, cerca de 2.36x105 Ω.cm, isto é, muitas ordens de
grandeza superior à resistividade dos condutores (ver Figura 3-9).
Importa, pois, procurar formas de fazer variar (aumentar) a condutividade,
em particular por modular a população de portadores de carga, electrões
e/ou buracos. Como se verá adiante, a introdução selectiva de impurezas
permite variar de ordens de grandeza n e p. Adicionalmente, é possível variar
electronicamente a condutividade de uma porção de material, sendo este
fenómeno a base do funcionamento dos dispositivos activos que se estudam
adiante no capítulo 5.
Antes de analisar como a condutividade pode ser influenciada pela
introdução de impurezas, observe-se que a condução num semicondutor
pode ser originada por um fenómeno diverso da condução por deriva.
Referimo-nos à condução por difusão.
3.2.3.2 Condução por Difusão
Por razões que se tornarão evidentes mais adiante, pode suceder que a
concentração de portadores de carga móveis não seja homogénea – isto é,
que possa variar no volume do semicondutor.
Considere-se um modelo uni-dimensional (dimensão espacial x), como se
ilustra na Figura 3-14, para o caso de uma concentração de electrões livres,
n, variável com x.
25
n
θ
x
Figura 3-14 – Gradiante de concentração de portadores de carga (electrões) na direcção x.
A ocorrência de um gradiente de concentração produz um movimento
coerente de electrões da região onde existem em maior concentração para a
região onde escasseiam. A corrente eléctrica resultante é tanto maior,
quanto maior for o gradiente de concentração. Este é um fenómeno de
difusão de portadores, que tende a uniformizar a sua concentração. Assim,
a densidade de corrente de electrões, Jn, pode escrever-se
dn
Jn = q Dn
dx
em que se define a constante de proporcionalidade entre a densidade de
corrente e o gradiente da concentração, Dn, designando-a como coeficiente
de difusão de electrões, ou difusibilidade de electrões.
Analogamente, se existir um gradiente de concentração de buracos, a
densidade de corrente de buracos pode escrever-se como
dp
J p = −q D p
dx
em que o coeficiente de difusão de buracos, Dp, exprime essa
proporcionalidade. Os coeficientes de difusão e as mobilidades de deriva
estão relacionados entre si pela relação de Einstein,
D n = D p = KT =
VT
µn
µp
q
Este processo de condução por difusão desempenha um papel crucial em
dispositivos semicondutores que contém concentrações de impurezas, que
variam bruscamente no interior do dispositivo.
3.2.4 Semicondutores Extrínsecos (Tipo N e Tipo P)
Quando se adicionam átomos de impureza à rede cristalina de um
semicondutor intrínseco, obtém-se um semicondutor extrínseco. Designamse impurezas porque são átomos, não de silício, mas de outro elemento
químico. A sua introdução numa rede cristalina de silício, adulterando a sua
pureza, é usualmente designada dopagem.
O processo de introdução de impurezas (por implantação iónica, ou por um
processo de difusão de estado sólido, facilitada por temperaturas elevadas)
traduz-se na substituição, em alguns (poucos) nós da rede cristalina, do
átomo original (Si, por exemplo), por um átomo de um elemento químico
26
diverso. Como se referiu, na rede cristalina de Si, a concentração de átomos
é de 5x1022 cm-3. Os valores típicos de concentrações de impureza em
semicondutores extrínsecos variam entre 1015-1016 cm-3 (dopagem fraca) até
1020 cm-3 (dopagem forte). Deste modo, a substituição de átomos na rede
cristalina é efectuada de tal forma que a rede seja perturbada de forma
ligeira – 1 em cada 107 a 103 átomos de Si são substituídos. A estrutura da
rede cristalina é mantida praticamente intacta.
O silício é um material do grupo 4 da tabela de classificação periódica de
elementos químicos, de Mendeleiev, como se mostra na Figura 3-11. Tem 4
electrões na última órbita.
Impurezas aceitadoras são elementos do grupo 3 da tabela, que possuem 3
electrões na última órbita. O Boro (B) é a impureza aceitadora mais comum.
Quanto se adaptam à estrutura cristalina do silício, fica uma ligação de covalência da última camada vazia, originando um buraco. Ou seja, a sua
introdução na rede cristalina aumenta a concentração de buracos, ou
ligações de co-valência não preenchidas, originando um excesso de buracos,
relativamente à situação observada no semicondutor intrínseco. Este
aumento da concentração de buracos desequilibra a igualdade (que se
observa no semicondutor intrínseco) n=p. Com efeito, uma densidade de
buracos muito elevada facilita a recombinação de pares electrão-buraco, o
que reduz a concentração de electrões, n, a valores inferiores aos que exibe
no semicondutor intrínseco, à mesma temperatura. Neste caso, os buracos
tornam-se portadores de carga maioritários (pcM) e os electrões,
portadores de carga minoritários (pcm).
Se a impureza for um elemento do grupo 5, com 5 electrões na última órbita,
então, quando se adapta à estrutura cristalina do silício, liberta o seu quinto
electrão, sem lhe corresponder nenhum buraco na zona de valência. Uma
vez que “dão” portadores de carga (electrões na banda de condução), são
designadas como impurezas dadoras. Impurezas dadoras comuns são o
fósforo (P) e o arsénio (As). Adicionar a um semicondutor intrínseco
impurezas dadoras origina um excesso de electrões (na banda de condução),
relativamente à situação observada no semicondutor intrínseco. Novamente
se desequilibra a igualdade (que se observa no semicondutor intrínseco) n=p.
Agora, a densidade elevada de electrões livres facilita a recombinação de
pares electrão-buraco, o que reduz a concentração de buracos a valores
muito limitados. Neste caso, os electrões tornam-se portadores de carga
maioritários (pcM) e os electrões, portadores de carga minoritários (pcm).
À temperatura ambiente, tanto impurezas dadoras como aceitadoras já
adicionaram portadores de carga ao semicondutor (respectivamente,
electrões e buracos), um portador por átomo de impureza.
Seja NA (ND) a concentração de átomos aceitadores (dadores) que são
adicionados ao semicondutor. Uma vez que NA (ND) << 5x1022 cm-3, a taxa de
geração de pares electrão-buraco mantém-se aproximadamente e, assim,
num semicondutor extrínseco pode estimar-se que o produto n.p se mantém
constante,
n.p ≈ ni2 (T)
Com concentrações NA (ND) muito superiores a ni (1.45x1010 cm-3), e
“gerando” cada átomo de impureza aceitadora (dadora) um portador de carga
móvel (buraco (electrão)), tem-se que:
27
num semicondutor ao qual se adicionam impurezas aceitadoras, a
concentração de buracos é, à temperatura ambiente,
p ≈ NA
n ≈ ni2(T) / NA
num semicondutor ao qual se adicionam impurezas dadoras, a
concentração de electrões é, à temperatura ambiente,
n ≈ ND
p ≈ ni2(T) / ND
Num semicondutor, particularmente numa dada região desse semicondutor,
podem adicionar-se impurezas dos dois tipos, aceitadoras e dadoras. Uma
vez que produzem efeitos contrários sobre a concentração de electrões e de
buracos, o que importa é o saldo, ND - NA, positivo ou negativo.
Se o saldo é positivo, numa dada região do semicondutor, a concentração de
electrões (cargas negativas) torna-se maioritária, e essa região diz-se do tipo
N. Se o saldo for negativo, os buracos (cargas positivas) tornam-se
maioritários, e essa região diz-se do tipo P.
Pode então concluir-se que, num semicondutor extrínseco, a mobilidade de
deriva é dominada pela população de portadores de carga maioritária (pcM).
Para uma região de semicondutor tipo P, tem-se
σ = q . µp . NA
enquanto que, para uma região semicondutora do tipo N, pode escrever-se
σ = q . µn . ND
Até que ponto varia a condutividade de um semicondutor extrínseco,
relativamente ao intrínseco? Um factor dominante é a concentração dos
portadores de carga maioriários, quando comparada com a concentração
intrínseca, à mesma temperatura. Sendo, para 300ºK, ni da ordem de 1010
cm-3 e de 1015-1016 cm-3 (dopagem fraca) até 1020 cm-3 (dopagem forte), pode
compreender-se que, mesmo para dopagem fraca, a concentração de pcM é
cerca de 105 vezes maior que ni.
A variação da concentração de impurezas introduzidas numa região de
semicondutor permite, assim, variar de muitas ordens de grandeza a
condutividade do material, nessa região.
O segundo factor que influencia a condutividade é a mobilidade de deriva
dos pcM. A existência de uma população de portadores de carga muito
diversa da que se observa no semicondutor intrínseco altera
substancialmente a velocidade de deriva dessas portadores e, assim, a sua
mobilidade. Com efeito, quanto maior a concentração de portadores de
carga, menor será o percurso médio entre colisões e, deste modo, a sua
mobilidade de deriva. Esse efeito pode observar-se na Figura 3-15.
28
Figura 3-15 - Mobilidade de deriva de portadores maioritários no Si em função da concentração
total de impurezas.
Assim, embora a redução da mobilidade de deriva contrarie o aumento da
concentração de pcM. Este último efeito é muito superior, e a condutividade
(ou resistividade) variam de ordens de grandeza, consoante o valor de NA ou
ND.
O que sucede, se introduzirmos, em regiões adjacente de semicondutor,
impurezas aceitadoras e dadoras? Esse processamento do semicondutor leva
à fabricação do que se designa por uma junção P-N.
3.2.5 Junção P-N
Quando se introduzem impurezas aceitadoras, de concentração NA, numa
região de semicondutor, e impurezas dadoras, de concentração ND, numa
região adjacente, cria-se uma zona de variação muito acentuada do saldo de
impurezas, NA – ND. Cria-se assim uma junção P-N. O dispositivo que contém
uma junção P-N e terminais metálicos designa-se por díodo de junção.
Consideremos um modelo uni-dimensional, como se ilustra na Figura 3-16.
Em torno de um plano (caracterizado pela abcissa x=0 e designado por
junção metalúrgica), no qual o saldo de impurezas varia bruscamente,
existem duas regiões com populações de portadores de carga muito diversa,
e que interagem. Com efeito, na região tipo P, os buracos são pcM e os
electrões, pcm. Todavia, do outro lado da junção metalúrgica, os buracos são
pcm e os electrões, pcM.
29
p
+
+
+
n
_
+
+
+
+
+
+ + + + + +
+
+
+ +
+
+
+
+
+
+
+
+ + + +
_
_
+
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
Figura 3-16 - Estrutura básica de uma junção P-N
A existência de um forte gradiente de concentração de portadores de carga
móvel, na vizinhança da junção metalúrgica, origina uma forte condução por
difusão. Esta tende a deslocar os portadores de carga maioritários para o
lado onde são minoritários – isto é, tende a deslocar buracos da região P
para a região N, e electrões da região N para a região P. É o poderíamos
designar como principio de Robin Hood. Tirar aos ricos para dar aos pobres!
Neste contexto. deveria haver uma corrente positiva segundo x. Contudo, em
equilíbrio, com uma tensão nula aos terminais do díodo, não existe corrente
eléctrica. Então, outro fenómeno de condução, igualmente forte, deve existir
no semicondutor.
De facto, há que tomar em consideração o princípio da neutralidade eléctrica
– isto é, a existência de cargas móveis (positivas e negativas) é equilibrado
pela existência de cargas fixas (negativas e positivas), as cargas dos átomos
de Si ou de impurezas que ficam ionizados quando “contribuem” para a
população de portadores de carga móvel.
Por exemplo, do lado P, um átomo aceitador, ao receber um electrão a mais
(em relação aos 3 electrões que possui, na última camada, quando está
electricamente neutro) fica carregado electricamente com uma carga (-q),
transformando-se num ião. No volume da zona P, haverá assim uma
densidade de iões NA-.
De igual forma, do lado N, um átomo dador, ao libertar um electrão de
condução, fica carregado electricamente com uma carga (+q). No volume da
zona N, haverá assim uma densidade de iões ND+. Aonde prevalecer a
neutralidade eléctrica, ter-se-á que o saldo de carga positiva igual o salde de
carga negativa, isto é,
(ND+) + p = (NA-) + n
O movimento de buracos, do lado P para o lado N deplecciona muito a
concentração de cargas móveis do lado P, na vizinhança imediata da junção
metalúrgica, deixando “a descoberto” a carga iónica, fixa, NA-. A corrente de
difusão de electrões, do lado N para o lado P, reduz significativamente a
30
concentração de cargas móveis do lado N, na vizinhança imediata da junção
metalúrgica, deixando “a descoberto” a carga iónica, fixa, ND+.
Surgem assim, na zona da junção, duas cargas iónicas fixas de sinais
contrários, não compensadas electricamente pelas populações de carga
móvel. E associado a essas cargas iónicas, fixas, está um campo eléctrico,
conforme se representa na Figura 3-17. Este campo eléctrico, em torno da
junção metalúrgica, estabelece uma estreita região de transição entre duas
regiões electricamente neutras, o volume das regiões P e N. Devido à
presença da carga iónica, fixa, esta região é também designada por região
de carga espacial (RCE).
-
E
+
Figura 3-17 – Campo eléctrico associado a duas cargas
Que efeito produz este campo eléctrico interno, na RCE? Naturalmente, deve
actuar os portadores de carga móveis que se desloquem na sua zona de
influência, produzindo um processo de condução por deriva.
De facto, na junção, o campo eléctrico, E, tende a arrastar as cargas em
sentido contrário ao da difusão, isto é, arrasta os electrões e os buracos do
lado em que são minoritários para o lado em que são maioritários. Tira
assim dos pobres para dar aos ricos. É a lógica do Sheriff de Nottingham!
Uma vez que, sem tensão aplicada, isto é, em equilíbrio, o saldo de corrente
que atravessa a junção P-N é nulo, a forte corrente de difusão é exactamente
contrabalançada pela forte corrente de deriva, na RCE. Por tal motivo,
qualquer portador de carga móvel, nessa região, é actuado pelo campo e
retirado dessa região pelo mesmo.
Desta forma, a RCE caracteriza-se também por ser uma região esvaziada de
cargas móveis, razão porque esta região é também designada região de
deplecção (Figura 3-18). A igualdade de correntes de difusão e de deriva fixa
a intensidade do campo eléctrico, E, e desse modo a quantidade de carga a
descoberto, a um e outro lado da junção. Supondo que a junção é abrupta,
isto é, em x=0 saldo, ND - NA de concentração de impurezas (suposta
constante em cada lado da junção), varia de - NA para +ND Com este
pressuposto, a igualdade de correntes fixa a largura da região de carga
espacial, já que o total da carga iónica, que contribui para o campo, será
q . NA . xP = q . ND xN
em que xP (xN) são a penetração da RCE no lado P(N). Nestas condições, a
largura da RCE, W, será
W = x P + xN
31
Em função das concentrações de impurezas, a um e outro lado da junção, a
largura da RCE pode escrever-se
W = [ (2 εSi / q) . (1 / NA + 1 / ND) . ψo ]1/2
em que εSi representa a constante dieléctrica do Si e ψo a barreira de
potencial na junção. Isto significa que, quanto mais forte for a dopagem de
impurezas a um e outro lado da junção, mais estreita é a RCE. Por outro
lado, junções assimétricas (isto é, junções em que a concentração de
impurezas de um e outro lado da junção diferem muito – por exemplo, NA >>
ND) caracterizam-se pelo facto que a RCE invade predominantemente o lado
mais fracamente dopado.
E
P
NA
-
+
+
+
+
+
iões
negativos
N
ND
iões
positivos
Figura 3-18 – Região de carga especial (RCE) e regiões neutras num díodo de junção.
O campo eléctrico está ainda associado a uma diferença de potencial de
contacto, característico da junção, ψo, dado por
ψo = VT . ln [ (NA. ND) / ni2 ]
Tipicamente, ψo é cerca de 0.7 V para díodos de Si. Ao longo de x, o campo
E, é dado por
1 ρ
E =
∫ dx
ε
em que ρ representa aqui a densidade volumétrica de carga. E campo E é
ainda o gradiante da função potencial que, no modelo uni-dimensional, se
escreve
Ψ = − ∫ Edx
Assim, a uma distribuição rectangular de carga iónica, fixa, não
compensada com carga móvel, na RCE, corresponde uma distribuição
triangular do campo eléctrico (máximo para x=0) e uma distribuição da
função potencial, como integral da distribuição triangular (ver Figura 3-19).
32
(saldo de carga eléctrica)
ρ
→←
- xp
-
- q.NA
+ q.ND
+
+ xn
x
E
Emax.
x
Ψ
ψo
x
RCE (Região de Carga Espacial)
Figura 3-19 – Distribuição de carga, campo eléctrico e função potencial numa junção P-N.
Poder-se-ia perguntar: então, com ψo ≠ 0, como é que não existe corrente? A
razão prende-se com o facto de os terminais do díodo serem de material
diferente do Si. Com efeito, junções metal-semicondutor (Al/Si) também
apresentam potenciais de contacto. A soma total (ψ
ψo da junção de
semicondutor e as duas junções metal-semicondutor) dos potenciais de
contacto é zero.
O que acontece quando se aplica uma tensão entre os dois terminais do
díodo? Basicamente, altera-se o equilíbrio entre a difusão e a deriva. A
condução por difusão pode ser assegurada por uma larga população de
portadores de carga (pcM em cada lado da junção). Pelo contrário, a
condução por deriva é assegurada por uma população de portadores de
carga muito reduzida (pcm em cada lado da junção). Essa circunstância irá
originar correntes muito diferentes em sentido directo e inverso.
Com efeito, quando se aplica uma tensão eléctrica, vD, negativa, de P para N
(o sentido convencional), a tensão favorece o campo eléctrico interno,
positivo de N para P. Contudo, não consegue mais do que uma corrente
muito reduzida, correspondente a arrastar os portadores minoritários para o
lado em que estão em maioria. Os pobres fornecem a corrente. Mas os
pobres têm pouco para dar. A corrente é sempre muito diminuta.
Corresponde, no modelo exponencial definido anteriormente, a corrente
inversa de saturação, IS. Uma tensão vD negativa corresponde ao que se
convenciona chamar um regime de polarização inversa.
Se se enfraquecer o campo eléctrico, aplicando agora uma tensão positiva de
P para N, nesse caso favorece-se o processo de difusão dos portadores de
carga, isto é, o movimento dos portadores maioritários para o lado onde são
33
minoritários. Neste caso, obtêm-se correntes elevadas e uma pequena
variação de tensão provoca uma variação considerável de corrente
(exponencial com a tensão aos terminais do díodo). Uma tensão vD positiva
corresponde ao que se designa por um regime de polarização directa.
A variação do campo eléctrico na RCE, por efeito da tensão exterior aplicada,
origina uma variação da carga iónica, fixa, posta a descoberto e, desse modo,
a uma variação da largura da RCE. Se a lei de variação de vD for rápida no
tempo, a variação de carga, dQ/dt põe em evidência um efeito capacitivo,
especialmente notório quando o díodo está operando com polarização
inversa. Designa-se essa capacidade parasita como capacidade de junção,
Cj. O seu valor corresponde essencialmente ao valor da capacidade
electrostática de um condensador plano, cujo dieléctrico é o Si, cujas placas
estão distanciadas de W (a largura da RCE) e cuja área é a área da junção:
Cj = A . εSi / W
Para uma junção plana, à qual se aplica uma tensão vD, a largura da sua
região de carga espacial pode escrever-se
ψo - vD)]1/2
W (vD) = [ (2 εSi / q) . (1 / NA + 1 / ND) (ψ
Assim, se se designar por Cj0 a capacidade de junção para vD = 0, pode
escrever-se
Cj = Cj0 . W (vD = 0) / W (vD) = Cj0 . [(1 + vD / ψo)] -1/2
Deste modo, a capacidade de junção varia com a tensão de polarização
inversa, (-vD), da forma como se ilustra qualitativamente na Figura 3-20.
Num regime de polarização directa, a injecção de pcM no lado onde são
minoritários causa um armazenamento de carga (pcm) nas regiões neutras,
a um e outro lado da RCE. Quando vD varia rapidamente no tempo, a
variação dessa carga, dq/dt, produz uma corrente que descreve um efeito
capacitivo que limita a resposta dinâmica do dispositivo. Designa-se essa
capacidade com capacidade de difusão, Cd.
Cjo
Cj (fF)
VD < 0
VD (V)
0
ψo
Figura 3-20 – Dependência da capacidade de junção, Cj, com a tensão de polarização do díodo,
vD.
34
4. Díodo de Junção
O díodo de junção é um dispositivo semicondutor. As densidades de
portadores de carga aumentam com a temperatura. É possível realizar
funções electrónicas num semicondutor intrínseco? Tantas como com um fio
de metal. Nenhumas. Então?
As funções electrónicas construem-se com dispositivos que apresentam
características especiais, por exemplo comportam-se como interruptores, ou
têm um comportamento linear permitindo amplificar sinais eléctricos.
Consegue-se? Sim.
Como? Criando no semicondutor intrínseco regiões dos diferentes tipos, P e
N. Por exemplo, um díodo, ou mais correctamente, uma junção P-N. A
relação entre a tensão eléctrica aplicada aos seus terminais e a corrente que
o percorre é descrita pela lei característica do díodo.
4.1 Equação Característica do Díodo
Um elemento de dois terminais que pode constituir um exemplo interessante
de dispositivo não linear a ser modelado em termos de elementos de circuito
é o díodo. Como foi referido, a relação entre a corrente e a tensão no díodo é
expressa por
i = Is (e
vD/ηVT
- 1)
onde vD é a tensão aos terminais do díodo, VT é a tensão térmica, descrita
por VT = KT/q, com K- constante de Boltzmann, T a temperatura absoluta
(grau Kelvin) e q é a carga do electrão (q = 1.6x10-19 C).
A corrente IS é designada a corrente inversa de saturação. A designação
inversa decorre do facto de se tratar da corrente que percorre o díodo
quando este está polarizado inversamente, isto é, quando tem aplicada aos
seus terminais uma diferença de potencial positiva de n para p. A
designação de saturação decorre do facto desta corrente ser praticamente
constante para uma gama considerável de valores da tensão aplicada.
De facto, quando se aplica uma tensão de polarização inversa, como se
referiu, favorece-se a deriva de portadores de carga em comparação com a
difusão dos mesmos. Nestas circunstâncias, os portadores de carga
minoritários, nas regiões neutras em um e outro lado da região de carga
espacial, são transportados por efeito do campo eléctrico (mecanismo de
deriva) para o lado onde são maioritários. Mais ainda, a partir de valores
muito reduzidos da tensão inversa, o campo eléctrico correspondente é
suficiente para arrastar “todos” os portadores minoritários em cada lado da
junção para o outro lado. Assim, a corrente é praticamente constante para
uma gama considerável de valores da tensão inversa. Daí chamar-se
corrente “de saturação”.
35
Electrões são transportados de P para N e buracos de N para P. Uma vez que
as corrente de deriva dependem directamente das concentrações dos
portadores de carga, portadores de carga minoritários só asseguram
correntes de carga residuais (tipicamente, da ordem de 10-10 A para díodos
discretos e de 10-15 A para díodos integrados). A corrente IS é obtida por:
IS = q A ni2 (Dp/LpND + Dn/LnNA)
em que A é a área da secção transversal da junção, q é a carga do electrão,
ni é a concentração intrínseca de portadores de carga do semicondutor, Dp e
Dn são os coeficientes de difusão de buracos e de electrões, Lp e Ln são os
comprimentos de difusão de buracos e de electrões, e NA e ND são as
densidades de impurezas aceitadoras e dadoras, respectivamente.
Representa-se na Figura 4-1 a característica exponencial do díodo para as
duas regiões de funcionamento, associadas à polarização directa e inversa.
Destacam-se, deste modo, os valores das correntes no díodo nas duas
situações.
iD
(mA)
iD
(fA)
10
1
0
0
vD(V)
vD(V)
(a)
(b)
Figura 4-1 - Característica de um díodo de junção:
(a) polarização directa; (b) polarização inversa
Tratando-se de uma relação exponencial, não é imediato estabelecer o
modelo de circuito em termos de somas de tensões ou de correntes, que
correspondem, genericamente a relações lineares entre tensões e correntes.
Assim, um modelo de circuito para um díodo terá representações diferentes
em diferentes domínios de validade. Uma vez que, na equação característica
do díodo a que se está a recorrer, neste exemplo, a tensão no díodo aparece
como a variável independente, os domínios de validade em que serão
definidos as diferentes representações do modelo do díodo são definidos a
partir dos valores de vD. Mais ainda, como vD aparece no expoente da
exponencial, é vantajoso considerar valores negativos e positivos de vD, e
para cada caso, os valores relativos entre vD e VT (admitindo-se por
simplicidade (matemática, visto que de um ponto de vista semântico nada se
altera) η=1, isto é, considerando-se um díodo integrado).
Assim, considere-se em primeiro lugar, os dois domínios :
vD < 0 e vD > 0 e que à temperatura de trabalho (temperatura ambiente
de 27 0C), VT ≈ 25mV.
36
4.1.1 Região de Corte
Quando vD
< 0 e | vD| >> VT , e
vD/VT
<< 1 e iD ≈ - IS.
Isto é, a partir de valores muito reduzidos de tensão (por exemplo, para | vD|
é = 4VT = 100mV, e vD/VT = 0,018...) a corrente no díodo é praticamente
nula. Nesta situação, o díodo comporta-se como um circuito aberto, podendo
ser representado, do ponto de vista estático (tensões e correntes constantes),
como uma resistência infinita. Assim, para vD < 0 e | vD| >> VT o modelo de
circuito do díodo é o representado na Figura 4-2 (circuito aberto).
Figura 4-2 – Circuito equivalente do díodo quando vD < 0 e | vD| >> VT
4.1.2 Região de Condução
Quando vD > 0 e | vD| >> VT (por exemplo, para | vD| é = 4VT = 100mV,
donde resulta e vD/VT = 54,598...) ou e vD/VT >> 1 e
iD ≈ I S e
vD/VT
Para realçar a base de raciocínio que se segue neste procedimento, é
vantajoso traçar as curvas características iD (vD) atribuindo valores a vD (por
exemplo, múltiplos de VT), para, por exemplo, dois valores de IS (distintos
entre si de uma ordem de grandeza). Os resultados numéricos estão
indicados na. Na Figura 4-3 apresentam-se as curvas características obtidas
nestes dois casos (cada uma delas em duas escalas diferentes).
IS=10e-15
vD (mV)
100
200
300
400
500
600
650
680
700
720
750
800
IS=10e-16
iD(mA)
5,5E-11
3,0E-09
1,6E-07
8,9E-06
4,9E-04
2,6E-02
2,0E-01
6,5E-01
1,4E+00
3,2E+00
1,1E+01
7,9E+01
vD (mV)
100
200
300
400
500
600
650
680
700
720
750
800
iD(mA)
5,5E-12
3,0E-10
1,6E-08
8,9E-07
4,9E-05
2,6E-03
2,0E-02
6,5E-02
1,4E-01
3,2E-01
1,1E+00
7,9E+00
Tabela 4-1 – Característica do díodo com IS = 10e-15 A e com IS = 10e-16 A.
37
IS=10e-15
1,2E+01
iD(mV)
1,0E+01
8,0E+00
6,0E+00
Series2
4,0E+00
2,0E+00
0,0E+00
0
200
400
600
800
vD(mV)
IS=10e-16
1,0E+01
iD(mA)
8,0E+00
6,0E+00
4,0E+00
Series1
2,0E+00
0,0E+00
-2,0E+00 0
200
400
600
800
1000
vD(mV)
Figura 4-3 – Curvas características do díodo com IS = 10e-15 A e com IS = 10e-16 A.
Observando as características iD(vD) obtidas com os dois valores de IS, pode
notar-se que, em qualquer dos casos e dum ponto de vista macroscópico,
isto é, para correntes da ordem de grandeza dos mili Ampere e para
correntes da ordem de grandeza dos micro Ampere existem, nitidamente,
duas rectas que aproximam a exponencial.
Podem então identificar-se dois domínios de tensão vD, disjuntos, vD ≤
600mV e vD ≥ 600 mV. Para vD ≤ 600mV, a corrente ID < 2,6E-2mA para IS
= 10E-15 A e ID < 2,6E-3mA para IS = 10E-16 A. Assim, dum ponto de vista
macroscópico, isto é, se as correntes que interessam considerar no circuito
são da ordem de grandeza de mA, a corrente no díodo torna-se desprezável.
Como primeira aproximação, pode admitir-se que é nula.
38
4.1.3 Modelo Linear por Troços
Considerando, a título de exemplo, a característica do díodo de junção para
IS = 10E-15, (ver Figura 4-4), a característica exponencial do díodo pode
então ser aproximada por duas rectas que se intersectam em vD ≈ 700mV.
IS=10e-15
1,2E+01
iD(mV)
1,0E+01
8,0E+00
6,0E+00
Series2
4,0E+00
2,0E+00
0,0E+00
0
200
400
600
800
vD(mV)
Figura 4-4 - Aproximação linear por troços da característica iD(vD) do díodo.
Assim, de acordo com esta análise, o comportamento do díodo pode ser
descrito pelas equações:
vD
< 0 iD = IS ≈ 0
para
vD > 0
vD < 700mV
vD ≥ 700mV
0 iD ≈ 0
0 iD = (VD –700 mV)/RD
Ou seja, o díodo comporta-se como uma resistência de valor ∞ para
vD<700mV e como uma resistência de valor muito reduzido (no gráfico da
Figura 4-4 , RDON ≈ 50mV / (11-1.4)mA = 5.2 Ω) para vD ≥ 700mV. Assim,
de acordo com este modelo, o díodo, comporta-se quase como um
interruptor em torno da tensão de 700 mV aos seus terminais.
Em termos de componentes de circuito, o modelo do díodo é pois descrito
por:
vD < 700mV
RDOFF = ∞
39
vD ≥ 700mV
ID = [vD – 700(mV)]/ RDON
O modelo de circuito que corresponde a esta descrição é o da Figura 4-5.
vD < 700mV
VDON
vD
RDON
≥ 700mV
Figura 4-5 – Modelo do díodo para vD < 700mV e vD ≥ 700mV
Introduzindo o conceito de díodo ideal, (símbolo na
Figura 4-6) como o interruptor perfeito, isto é, o circuito que se comporta
como uma resistência infinita (RDOFF = ∞) para vD < 0V e como curto
circuito (RDON = 0) para vD ≥ 0V, o modelo de circuito equivalente do díodo
(na aproximação linear por troços) é o que se representa na Figura 4-7.
iD
+
vD
−
vD
Figura 4-6 – Símbolo e característica do díodo ideal
iD
→
+
vD
−
iD
iD
→
+
vD
−
±
V
γ
Rγ
V
γ
vD
Figura 4-7 – Modelo de circuito, equivalente de um díodo (aproximação linear por troços)
4.2 Mecanismos de Disrupção. Díodo Zener
40
O modelo exponencial, utilizado para descrever o comportamento de um
díodo de junção (isto é, a sua relação iD(vD)), em regime estático ou de
variação lenta no tempo é uma excelente aproximação da realidade,
enquanto o fenómeno físico do desequilíbrio entre os processos de condução
por difusão e por deriva (desequilíbrio causado pelo aplicar de uma tensão vD
aos terminais) é dominante. Todavia, no regime de operação com polarização
inversa, outro fenómeno pode tornar-se activo, e dominar a dependência
corrente-tensão. Referimo-nos ao mecanismo de disrupção na junção.
Que mecanismo se trata? Bom, até aqui observou-se que a região de carga
espacial (RCE), em torno da junção metalúrgica, é uma região depleccionada
de portadores de carga móveis, uma vez que a presença do campo eléctrico
interno obriga a movimentar tais cargas para fora da região onde o campo
exerce a sua influência. Tal campo eléctrico, na RCE, é, como se viu,
associado a uma diferença de potencial (ψ
ψo - vD). Por efeito da tensão exterior
aplicada, a carga iónica, fixa, posta a “descoberto” na RCE varia, a RCE
alarga com vD < 0 e o valor máximo do campo eléctrico, Emax., aumenta. A
largura da RCE de uma junção abrupta, W, varia com a diferença de
potencial e com as concentrações de impurezas a um e outro lado da junção,
através da equação
W (vD) = [ (2 εSi / q) . (1 / NA + 1 / ND) (ψ
ψo - vD)]1/2
que se repete aqui por conveniência. Desta equação se nota que, quanto
mais forte for a dopagem de impurezas, NA e ND, mais estreita é a largura da
RCE. Quanto mais estreita for a RCE, mais elevado é o valor do campo
eléctrico interno.
Na presença de uma polarização inversa, um fluxo reduzido de portadores de
carga atravessa a RCE. O seu ritmo de passagem corresponde ao valor da
corrente inversa de saturação. Quanto mais forte for o campo eléctrico, e
mais larga a RCE, maior a energia cinética que esses portadores de carga
adquirem, ao atravessar a junção. Adicionalmente, há que considerar que,
na RCE, existem átomos ionizados, em cuja última camada ainda existem
electrões na banda de energia de valência (electrões ligados). Deste modo,
existe o potencial de formação local de pares electrão-buraco. Esse potencial
é reforçado, para valores da tensão de polarização inversa, pela possibilidade
de transferência de energia (para os electrões ligados) oriunda, quer do
campo eléctrico, quer dos portadores de carga que atravessam a junção. Se
se formarem pares electrão buraco na RCE, esses novos portadores móveis
vão engrossar a corrente eléctrica que percorre o díodo. Designa-se este
efeito por efeito de disrupção.
Quando se utiliza a palavra “disrupção”, isto causa usualmente
consternação, já que mentalmente se cria a ideia de destruição previsível e
eminente do dispositivo. Contudo, esta ideia pode ser uma conclusão
apressada. Com efeito, a corrente que circula num dispositivo electrónico é
limitada pelo circuito exterior. Assim, o efeito de disrupção influencia a lei
característica do dispositivo, mas o seu ponto de funcionamento é
determinado pela verificação simultânea das leis características e das leis
topológicas. A eventual destruição do dispositivo está normalmente
associada ao ultrapassar dos limites de corrente, tensão e/ou potência que o
mesmo pode, por construção, suportar. Se o circuito exterior impedir que tal
41
suceda, então o efeito de disrupção não tem carácter destrutivo, antes é
reversível, quando a tensão aos terminais do díodo assumir outros valores.
Como se altera a lei característica de variação, iD(vD), de um díodo de junção,
sujeito ao efeito de disrupção? Certamente, a corrente inversa no díodo,
aumentará para valores superiores (em módulo) ao valor de IS. Todavia, o
andamento da característica, na zona inversa, depende dos seus perfis de
impureza, que condicionam o mecanismo predominante de transferência de
energia para os electrões ligados.
Com efeito, se a concentração de impurezas for moderada, a um e outro lado
da junção, o campo eléctrico máximo não é muito elevado, mas a largura da
RCE é elevada. Nestas circunstâncias, os portadores de carga que
atravessam a RCE adquirem muita energia cinética e, por colisões
inelásticas, podem gerar pares electrões-buraco. Estes, por sua vez, sendo
acelerados pelo campo eléctrico, podem gerar outros pares electrão-buraco.
Este fenómeno de “bola-de-neve” é designado de efeito de multiplicação por
avalanche. Quando este efeito domina, o aumento da corrente inversa com a
tensão é gradual. A fim de aproveitar as propriedades do díodo (descritas
pela lei exponencial) na realização de funções, o projectista de circuitos
usualmente limita o valor da tensão inversa no díodo, a fim de que o díodo
nunca opere nesta região de funcionamento.
No entanto, se o díodo, por construção, tiver elevadas concentrações de
impurezas, NA e ND, a RCE é muito estreita e o campo eléctrico máximo,
muito elevado. Nestas condições, existe um valor do campo máximo (e, deste
modo, da tensão vD) para o qual o campo pode fornecer a electrões ligados
uma energia correspondente à altura da banda proibida, EG. Desse modo,
para um valor da tensão de polarização (vD = - VZ), a corrente inversa na
junção aumenta bruscamente com a tensão. Quando este fenómeno é
dominante, o efeito é designado como efeito de Zener. Os díodos em que
esse efeito predomina, designam-se abreviadamente díodos de Zener. O
símbolo correspondente é representado na .
Figura 4-8 – Símbolo de um díodo Zener.
Que vantagem têm os díodos de Zener, relativamente aos díodos “normais”,
isto é, aos díodos em que predomina a multiplicação por avalanche?. A
existência de um valor específico de tensão, para o qual a característica é
abrupta, permite dispor de uma tensão de referência, que pode ser muito útil
em diversas aplicações, como se verá adiante.
Como se pode representar, através de um modelo de circuito, um díodo
Zener? Admitindo que a característica pode ser aproximada por um modelo
linear por troços, a lei característica exibe agora três troços, dois
correspondentes à descrição da lei exponencial, e um troço adicional (válido
para vD < - VZ) correspondente ao que pode ser chamado zona de Zener. O
correspondente modelo de circuito está ilustrado na Figura 4-9.
42
iD
→
R
V
Z
v
± Vγ
Rγ
D
Z
Figura 4-9 – Modelo de circuito (completo) de um díodo de Zener.
Este modelo é, naturalmente, mais complexo, tornando a análise de circuito
mais complexa. Contudo, é possível usualmente definir sub-modelos
regionais, isto é, sub-modelos cujo domínio de validade abranja não os três,
mas dois troços. Por exemplo, se se pretender utilizar o díodo na região de
Zener, a interligação do circuito exterior permite verificar que o díodo irá
operar, ou nessa zona, ou na zona de corte. Neste caso, o modelo de circuito
simplifica-se para se reduzir aos ramos correspondentes à série de RZ. VZ e o
díodo ideal (ver Figura 4-9).
4.3 Exemplos de Circuitos com Díodos
Nesta versão do documento, apenas se inserem duas figuras,
correspondentes a um circuito com um único díodo, e a um circuito
limitador de tensão. Os circuitos são considerados na Colectânea de
Problemas de Electrónica I.
R1
VI
R
+
+
−
iD
→
R2
vD
−
→
rede linear
não
linear
Figura 4-10 – Circuito com um único dispositivo não linear.
43
R
+
vI
−
v D1
+
−
D1
+
V1
−
v D2
−
+
D2
−
V2
+
+
vo
−
Figura 4-11 – Circuito limitador de tensão.
44
Vγ =0
Rγ = 0
(Díodo ideal)