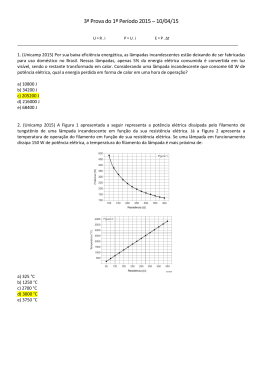
Laboratório de Eletricidade
Exp. 3 -
S.J.Troise
ESTUDO DA ASSOCIAÇÃO DE BIPOLOS
3.1
FUNDAMENTOS:
Em muitas aplicações práticas os bipolos são ligados entre si. Dizemos neste caso que os bipolos estão
associados. Esta associação pode ser de dois tipos: paralelo e série. As figuras abaixo mostram essas duas
associações de dois bipolos B1 eB 2 .
Figura 3-1
Quando isto ocorre há interesse em saber qual a curva característica resultante da associação, conhecidas
as curvas características dos bipolos associados. Essa curva resultante é a curva resultante de um bipolo equivalente
à associação. Mostraremos a seguir como obter essa curva.
3.2
ESTUDO TEÓRICO DA ASSOCIAÇÃO EM PARALELO:
A figura abaixo mostra dois bipolos, denominados B1 e B 2 , associados em paralelo.
Figura 3-2
É fácil observar-se que nesta associação os bipolos estão submetidos as um mesmo potencial V e que a
corrente através da associação é a soma das correntes que atravessam cada um do bipolos. Ou seja:
V1 = V2 = V
I1 + I 2 = I
A análise destas duas equações nos permite estabelecer um método gráfico para o estudo da associação, o
qual nos permitirá determinar a curva característica de uma associação paralela a partir das curvas características de
cada um dos bipolos associados. Para isto observe a figura abaixo . Nela são mostradas as curvas do bipolos B1
linear e B 2 não linear.
Figura 3-3
Observe nesta figura que, para um mesmo potencial V , a medida do segmento AB representa a corrente
I1 do bipolo B1 e a medida do segmento AC representa a medida da corrente I 2 no bipolo B 2 . Se as medidas
desses dois segmentos forem somadas obtemos o segmento AD que é, portanto, um ponto da associação paralelo.
Se este processo for repetido para diferentes valores do potencial obteremos um sucessão de pontos D, os quais,
unidos determinarão a curva característica da associação. Isto significa que, para obter a curva característica de uma
associação paralela, basta conhecer as curvas características dos bipolos associados.
11/10/2005
Página 1 de 4
Laboratório de Eletricidade
3.3
S.J.Troise
ESTUDO TEÓRICO DA ASSOCIAÇÃO EM SÉRIE:
A figura abaixo dois bipolos, denominados B1 e B 2 , associados em série. É fácil observar-se que nesta
associação os bipolos são percorridos pela mesma corrente
tensão aplicada sobre a associação. Ou seja:
I e que os potenciais neles aplicados se soma dando a
Figura 3-4
V1 + V2 = V
I1 = I 2 = I
A análise destas duas equações nos permite estabelecer um método gráfico para o estudo da associação, o
qual nos permitirá determinar a curva característica de uma associação série a partir das curvas características de
cada um dos bipolos associados.
Para isto observe a figura abaixo. Nela são mostradas as curvas dos bipolos B1 linear e B 2 não linear.
Observe nesta figura que, para uma mesma corrente I , a medida do segmento AC representa a tensão V1 sobre o
bipolo B1 e a medida do segmento AB representa a medida da tensão V2 sobre o bipolo B 2 Se as medidas desses
dois segmentos forem somadas obtemos o segmento AD que é, portanto, a tensão V sobre a associação. Assim, o
ponto D é portanto um ponto da curva característica da associação série.
Figura 3-5
Se este processo for repetido para diferentes valores da corrente obteremos uma sucessão de pontos D, os
quais, unidos, determinarão a curva característica da associação. Isto significa que, para obter a curva característica
de uma associação série, basta conhecer as curvas características dos bipolos associados.
3.3.1
PROCEDIMENTO EXPERIMENTAL:
Para estudarmos experimentalmente a associação de bipolos é necessário que as curvas características
dos bipolos que serão associados sejam conhecidas.
3.3.1.1 ( ) Monte o circuito abaixo utilizando como bipolo um resistor. Utilizando os procedimentos da experiência anterior
levante a curva característica desse resistor, anotando os resultados experimentais na tabela abaixo. Este resistor será o bipolo
B1 que será associado em paralelo com outro
bipolo para a verificação do método.
11/10/2005
Página 2 de 4
Laboratório de Eletricidade
S.J.Troise
Figura 3-6
V (V)
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
I (mA)
3.3.1.2 ( ) Utilizando o mesmo circuito acima e os mesmos procedimentos, faça o levantamento da curva característica da
lâmpada, anotando os resultados na tabela abaixo. (substitua o resistor pela lâmpada). Cuide para que a tensão sobre a lâmpada
não ultrapasse 12V. A lâmpada será a bipolo B 2
V (V)
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
3.4
I (mA)
ESTUDO EXPERIMENTAL DA ASSOCIAÇÃO EM PARALELO
3.4.1.1 ( ) Utilizando o mesmo circuito acima e os mesmos procedimentos, faça o levantamento da curva característica da
associação do resistor e da lâmpada paralelo. Utilize obrigatoriamente o mesmo resistor e a mesma lâmpada para que haja
compatibilidade de dados. Anote os resultados na tabela abaixo
V (V)
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
I (mA)
3.4.1.2 ( ) Num papel milimetrado trace as curvas características (utilize diferentes representações para os pontos para que
as curvas sejam distinguíveis):
a)
do resistor (+)
b)
da lâmpada (∗)
c)
da associação da resistor com a lâmpada em paralelo (•)
3.4.1.3 ( ) No mesmo papel milimetrado trace a curva da associação pelo método da soma das correntes para um mesmo
potencial, conforme mostrado acima (:)
3.4.1.4 ( ) Compare as curvas da associação obtidas nos itens 3.4.1.2 ( ) e 3.5.1.2 ( ) 0. Elas devem ser coincidentes a
menos dos erros experimentais normais em qualquer experiência.
3.5
ESTUDO EXPERIMENTAL DA ASSOCIAÇÃO EM SÉRIE:
3.5.1.1 ( ) Monte o mesmo circuito anterior, utilizando como bipolo a associação em série do resistor e da lâmpada
anteriormente utilizados. Utilize os mesmos procedimentos anteriores. Cuide para que sejam utilizados o mesmo resistor e a
mesma lâmpada anteriormente utilizados para que haja compatibilidade de dados.
11/10/2005
Página 3 de 4
Laboratório de Eletricidade
S.J.Troise
V (V)
1,0
2,0
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
11,0
12,0
I (mA)
3.5.1.2 ( ) Num papel milimetrado trace as curvas características:
a)
do resistor (+)
b)
da lâmpada (∗)
c)
da associação da resistor com a lâmpada em série (•)
3.5.1.3 ( ) No mesmo papel milimetrado trace a curva da associação pelo método da soma das correntes para um mesmo
potencial, conforme mostrado acima.(:)
3.5.1.4 ( ) Compare as curvas da associação obtidas no item 4 e no item 5. Elas devem ser coincidentes a menos dos erros
experimentais normais em qualquer experiência.
3.6
RELATÓRIO:
Siga as instruções contidas no anexo correspondente.REL03
11/10/2005
Página 4 de 4