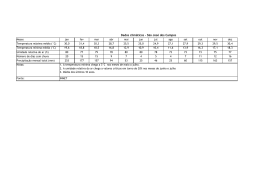
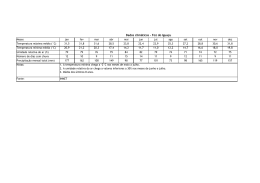
Manejo de irrigação
Parâmetros solo-planta-clima
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Relações água e solo
• Fases do solo
– Sólida
– Líquida (Água/Solução)
– Ar
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Fase sólida
Densidades do solo e de partícula
• Densidade de partícula (real)
– Relação entre a massa de uma amostra de solo e o
volume ocupado pelas suas partículas sólidas.
ms
p 
Vs
– Desconsidera a porosidade presente no volume;
– Valores variam entre 2,3 a 2,9 g cm-3 (média de 2,65)
– Valor é determinado pela mineralogia do solo.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Densidades do solo e de partícula
• Densidade do solo (aparente)
– relação entre a massa de uma amostra de solo seca a
110°C e a soma dos volumes ocupados pelas partículas
e pelos poros.
ms
ms
s 

Vt Vs  Va  Vw
– Valor varia entre 1,1 a 1,6 g cm-3;
– Quanto maior o valor da densidade do solo:
• Maior é a compactação e restrição para o crescimento e
desenvolvimento das raízes e das plantas
• Menor a estruturação do solo e porosidade total
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Fase líquida - Umidade ou teor de água
• Umidade (base massa)
– relação entre a massa de água de uma amostra
de solo e a massa das partículas.
mw

ms
• Umidade (base volume)
– relação entre o volume de água de solo e o
volume total de uma amostra .
Vw
Vw
θ

Vt Vs  Va  Vw
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Fase ar - Porosidade
• Porosidade: relação entre o volume de poros
e o volume total da amostra.
Va  Vw


Vt Vs  Va  Vw
Vp
– Valores médios da porosidade do solo:
• Arenosos: 35 – 50%
• Argilosos: 40 – 60%
• Orgânicos: 60 – 80%.
– Solo saturado: água ocupa todo espaço poroso
– Solo seco: poros estão ocupados pelo ar
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Relações entre parâmetros
• Porosidade e densidades
s
  1
p
• Umidades e densidade do solo
θ  ω.ρ s
– Para se obter a umidade do solo na base
volume é preciso determinar a sua densidade.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Lâmina de Água
• Quantidade de água fornecida por irrigação ou utilizada
pela planta e armazenada pelo solo é medida em mm:
Volume (Litros)
h(mm) 
Área (m 2 )
• Se aplicarmos 1 Litro de água sobre uma superfície
plana e impermeável de 1 m2, obteremos uma lâmina
líquida de 1 mm
• Para uso de lâmina é preciso conhecer a umidade do
solo base volume.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Lâmina de Água
1 cm
θ  20%  0,20
Volume da amostra de solo = 1 x 1 x 1= 1 cm3
1 cm
Volume de água na amostra = 0,20 x 1 = 0,2 cm3
Como a área da amostra tem 1 cm2 esse volume
de água representaria uma altura de:
2 mm
h(mm) 
Volume 0,20cm3

 0,2cm  2mm
1cm2
Área
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Prática – água e solos
1. Coletou-se uma amostra de solo na camada de 0-10cm, com
anel volumétrico de diâmetro de 7,5cm e 7,5cm de altura. O peso
úmido da amostra do solo foi 560g e após 48 horas em estufa à
105 oC, seu peso permaneceu constante e igual a 458g. Determine:
– a densidade do solo, a umidade base massa, a umidade base
volume, porosidade.
– a densidade das partículas do solo, sabendo que a amostra
após a secagem foi colocada em uma proveta contendo
100cm3 de água, lendo-se então, um volume de 269cm3.
– lâmina armazenada nessa camada.
2. Calcular a lâmina de água em mm que deve ser adicionada pela
irrigação para trazer a umidade volumétrica do solo ao valor de
0, 34 na camada de 0-10 cm. Qual o tempo de irrigação se o
sistema de aspersão aplica 10 mm/h a uma eficiência de 75%?
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Armazenamento de Água no Solo
A água armazenada em um perfil de solo é a somatória das
alturas de água (h= ) para cada incremento de profundidade.
AL =  i
ou
Z
AL    .dz
0
onde z é a profundidade do solo
Obs.: as variações de umidade no perfil do solo são reflexos
das taxas de evapotranspiração, chuva, irrigação e
movimentos de água no perfil de solo.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Armazenamento de Água no Solo
3. Determinou-se em campo os valores de umidade
volumétrica em função da profundidade nos dias 22/07 e
30/07, num determinado solo. Calcular a variação de
armazenagem até a profundidade de 0,40 m no período.
Camada (cm)
22/07
30/07
0 – 10
0,33
0,25
0 – 20
0,30
0,21
0 – 30
0,27
0,18
0 - 40
0,24
0,20
4. Um agricultor precisa irrigar sua plantação de feijão que
tem os seguintes valores da umidade do solo (base volume):
(0-20) 20% e (20-40) 24%. Se o agricultor deseja elevar a
umidade até a capacidade de campo (30%), qual a lâmina
total que ele deve aplicar?.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Armazenamento de água no solo
• Processo de retenção de água no solo.
– Resultante de forças capilares (adesão) e de adsorção
que surgem devido a interação entre a água e as
partículas sólidas do solo, isto é, a matriz do solo;
– Essas forças atraem e fixam a água no solo;
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Energia da água no sistema Solo-Planta
• O estado de energia da água determina se ela está
em equilíbrio ou se movendo no perfil do solo.
• O potencial total da água ( ), em dada posição,
determinar seu movimento no sistema solo-plantaatmosfera.
 t   g  m  p  o
Ψt = Potencial total da água
Ψg = Potencial gravitacional
Ψm = Potencial matricial
Ψp = Potencial de pressão
Ψo = Potencial osmótico
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Tensão de água no solo
• É medido no campo com uso de tensiômetros
Vacuômetro
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Tensímetro
Curva característica de umidade do solo
• Gráfico do Potencial Matricial (Ψm)em função de θ (bv)
• Para um determinado valor de potencial matricial
corresponde a um valor característico de umidade.
• Determinada em laboratório com uso de panelas de
pressão (Placa de Richards)
– Panela de pressão, placa cerâmica porosa e equipamentos de produção e
controle de pressão e balança de precisão;
– Possível utilizar amostras indeformadas como deformadas.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Curva característica de umidade do solo
10000
0 - 20 cm
POTENCIAL MATRICIAL (kPa))
20 - 40 cm
1000
100
10
1
0
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
UMIDADE (m3/m3)
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
52
54
56
58
60
Constantes de umidade do solo
o Capacidade de Campo
cc = umidade para  (-0,1 a -0,3)
Valor recomendado de 0,1 bar
o Ponto de Murcha Permanente
pmp = umidade para  (-15 bar)
o Disponibilidade Total de Água
DTA (mm/cm) = CC – PMP
o Capacidade de Água Disponível
CAD (mm) = DTA . Z
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Constantes de umidade do solo
Saturação
Capacidade de Campo Ponto de murcha permanente
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Constantes de Umidade (Exemplo)
10000
0 - 20 cm
POTENCIAL MATRICIAL (kPa))
20 - 40 cm
1000
100
10
1
0
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
UMIDADE (m3/m3)
5. Calcular o valor da DTA para cada profundidade e de CAD
para a profundidade de 40 cm
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Constantes de Umidade (Aplicação)
6. Planejou-se um experimento de campo para verificar o
efeito da irrigação na cultura do milho, profundidade de
raiz de 40 cm, utilizando-se dois tratamentos
T1= esgotamento de 20% da CAD (capacidade de água
disponível) e
T2= esgotamento de 50% da CAD.
Utilizando a mesma curva do exercício anterior,
calcule o valor da lâmina de irrigação que deve ser
aplicado em cada tratamento se a eficiência de 80%.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Curva característica de retenção de água
• Modelo de Van Genutchen (1980)
– Mais utilizado para representar o ajuste
dos dados de umidade volumétrica com
potencial matricial.
  r 
s  r
1  ( . ) 
n m
m
– Sendo
• Θr = umidade residual
• α, n e m = parâmetros do solo
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Disponibilidade Total de Água
Textura do solo
Textura do Solo
DTA
(mm de água/cm de solo)
Grossa
0,4 a 0,8
Média
0,8 a 1,6
Fina
1,2 a 2,4
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Infiltração da água no solo
• Processo de entrada de água no solo através
de sua superfície.
– Taxa de infiltração é a quantidade de água que
atravessa a unidade de área da superfície do solo
por unidade de tempo
– Importante para evitar a ocorrência de
escoamento superficial e erosão nas áreas
irrigadas.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Infiltração da água no solo
• Equação de Kostiakov (1932)
z  k.t
a
– onde z = lamina infiltrada acumulada (mm), t =
tempo de infiltração (h) e k, a = parâmetros da
equação, sendo a taxa de infiltração i (mm/h) igual
a:
dz
( a 1)
i
 (ka).t
dt
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Infiltração – tipo de solo
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Infiltração – Aplicação
7. Sabendo que a equação de infiltração de um
solo é igual a:
𝑍 = 4,5 𝑡 0,61
• sendo Z = lâmina infiltrada em mm e t = tempo
de infiltração em minutos,
determine o valor da velocidade de infiltração
básica deste solo em mm/hora.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Capacidade de infiltração
• Potencial do solo em absorver água pela
superfície.
• Diferente da taxa real de infiltração que
acontece quando há disponibilidade de água
para penetrar no solo.
– A curva de infiltração da água no solo só coincide
com a curva de capacidade de infiltração quando
ocorre precipitação na superfície com intensidade
igual ou superior à capacidade de infiltração.
FEAGRI/UNICAMP - Prof. Roberto Testezlaf
Infiltração – Aplicação
8. Em um projeto de irrigação por aspersão
selecionou-se um aspersor que opera a 2,5
kgf/cm2, fornecendo uma vazão de 2,5 m3/h para
o espaçamento de 12 m por 12 m. Determine se
ocorrerá escoamento superficial para um tempo
de irrigação de 3 horas, sabendo que o solo da
área irrigada possui a seguinte equação de
infiltração:
0,13
𝑍 = 60 𝑡
• sendo: Z = lâmina infiltrada acumulada (mm) e
t = tempo acumulado (horas)
FEAGRI/UNICAMP - Prof. Roberto Testezlaf