VII Workshop de Visão Computacional – WVC 2011
Capítulo
2
A Morfologia Matemática e suas Aplicações em
Processamento de Imagens
Jacques Facon
Resumo
A Morfologia Matemática surgiu, a primeira vez, em 1964 das pesquisas conjuntas dos
pesquisadores Franceses Georges Matheron e Jean Serra. Entre 1964 e 1968 foram
estabelecidas as primeiras noções teóricas (Operação Hit-Miss, abertura, fechamento).
Neste mesmo período foi criado o Centre de Morphologie Mathématique na École des
Mines de Paris localizada em Fontainebleau (França).
A força da Morfologia Matemática reside no fato de quantificar a intuição do pesquisador, analisando a estrutura geométrica das imagens a partir de um conjunto perfeitamente definido e conhecido pelo usuário chamado de Elemento Estruturante. Este vai
interagir com cada entidade contida na imagem, modificando a sua aparência, a sua
forma, o seu tamanho permitindo assim tirar algumas conclusões necessárias. A eficiência e também a dificuldade da morfologia matemática reside na escolha da deformação
certa para transformar a intuição intelectual em aplicação prática.
Outra grande vantagem da Morfologia Matemática é a sua simplicidade de implementação. Além do Elemento Estruturante, os dois outros pilares da Morfologia Matemática são as duas operações básicas, a erosão e a dilatação, a partir das quais, por
composição, é possível realizar muitos outros operadores poderosos. O que faz que a
Morfologia Matemática se destaca muito de outras técnicas de processamento de imagens onde, na maioria dos casos, as implementações não aproveitam das ferramentas já
existentes.
Por todas estas razões, a área da Morfologia Matemática foi e ainda é o centro de
muitas atenções, de numerosas pesquisas que originaram descobertas sensacionais que
revolucionaram a área de Processamento de Imagens. Pesquisadores do mundo inteiro
usam e estudam novos rumos da Morfologia Matemática, principalmente da Morfologia
Matemática para imagens coloridas. O que explica que emergeram várias “escolas”
desta além da linha tradicional da École de Mines de Paris. Como por exemplo as esco-
61
VII Workshop de Visão Computacional – WVC 2011
las Americana e Holandesa, já estabelecidas faz já alguns anos. Mas também a escola
Brasileira em plena expansão.
As conseqüências destas diversas influências é a aparição de notações, de regras
às vezes um pouco diferentes para cada escola. O que pode às vezes confundir o leitor.
Para evitar ao máximo este tipo de confusões, o autor tentou seguir de forma mais fiel
possível a linha tradicional da École de Mines de Paris. As notações adotadas seguem
portando o formalismo de G. Matheron e de J. Serra.
Com este capítulo, o autor pretende apresentar as definições das ferramentas básicas da Morfologia Matemática Binária e em Níveis de cinza, demonstrar como compor
ferramentas mais complexas a partir destes operadores básicos e ilustrar suas aplicações
através de exemplos didáticos, teóricos e práticos.
2.1. INTRODUÇÃO
2.1.1. Preâmbulo
Composta das palavras gregas morphê (forma) e logos (ciência), a morfologia trata das
formas que a matéria pode tomar. Por exemplo, a morfologia vegetal refere-se ao estudo
da estrutura dos organismos vegetais. Da mesma maneira, a morfologia social é o estudo
das estruturas da vida social.
O que é morfologia matemática? De fato, seguindo esses exemplos, a morfologia
matemática, inicialmente elaborada por Georges Matheron e Jean Serra, concentra seu esforço no estudo de estruturas geométricas presentes numa imagem através de ferramentas
matemáticas.
O princípio básico da morfologia matemática consiste em extrair informações relativas à geometria e à topologia de conjuntos desconhecidos de uma imagem a partir
do elemento estruturante. O que é um elemento estruturante ? É um conjunto, completamente definido e conhecido pelo computador em forma e tamanho, que é comparado,
a partir de uma transformação, aos conjuntos desconhecidos da imagem. O formato e
o tamanho do elemento estruturante possibilitam testar e quantificar de que maneira o
elemento estruturante “está ou não está contido” na imagem. O resultado dessa transformação permite avaliar estes conjuntos.
2.1.2. Elemento estruturante
Para facilitar a interpretação do conteúdo das imagens, os elementos estruturantes devem ser os mais simples possíveis. Na maioria dos casos, os elementos estruturantes
são escolhidos em função das propriedades de convexidade, não-convexidade, isotropia e
anisotropia.
Do ponto de vista digital, um elemento estruturante é definido pelos pixels que o
formam. Na notação que será usada a seguir, os pixels que formam um elemento estruturante serão representados por “.” e por “•”. Um pixel marcado “.” será um pixel do
fundo, inativo ou neutro, que não interagirá com a imagem f . Este tipo de pixel simplesmente aparecerá no elemento estruturante para visualizar o seu aspecto geométrico. Um
pixel marcado “•” significará um pixel ativo que tem um papel a desenvolver na interação
com a imagem f . Os pixels ativos “•” do elemento estruturante criam um sub-conjunto
62
VII Workshop de Visão Computacional – WVC 2011
que vai agir com a imagem f . O resultado dessa interação será colocado numa posição
específica, a do ponto central PC do elemento estruturante, na imagem no momento da
ação. O símbolo
“( )” representará este ponto central PC no elemento estruturante. Por
• • •
exemplo, •• (•)• •• . Na maioria dos exemplos apresentados, o ponto central do elemento
estruturante correspondará a seu centro físico.
caso,
. num
objetivo de simplificação,
. Neste
• .
• .
o símbolo “( )” será omitido. Por exemplo, •. •. •. = •. (.)• •.
Freqüentemente será necessário introduzir o elemento estruturante transposto B̃
que representa o elemento estruturante obtido por
central deB. pela
origem {o }
. simetria
• .
. .
do sistema de referência. Por exemplo, Se B = .. (.). •. então B̃ = •. (.)• ..
Nas diferentes transformações que serão abordadas, Bx representará o elemento
estruturante B centrado no pixel x. Em função do contexto e por necessidade de simplificação, Bx será simplesmente notado B.
Os elementos
na morfologia
são o ho . . . estruturantes maisutilizados
. • matemática
. • .
.
•
•
•
.
•
.
•
•
•
rizontal BH = . . . , o vertical BV = . • . , o cruz BC = . • . , o quadrado BQ =
⎧. . . . . . .⎫
⎪
⎬
⎨ .. •. •• •• •• •. .. ⎪
• • •
• • •
.
•
•
•
•
•
.
e o Rhombus BR = . • • • • • .
• • •
⎪
⎩. . • • • . .⎪
⎭
. .
.
. .
. .
Da mesma maneira, no caso de imagens binárias, a imagem digital f contêm dois
tipos de informação, o fundo (representado por “.”) e os pixels relevantes (representados
por “•”). Na forma digital, a imagem f será representada entre “[ ]” da seguinte forma:
Exemplo 2.1 : Representação da imagens binária f
. . . . .
f=
.
.
.
.
•
•
.
.
•
•
•
.
.
•
•
.
.
.
.
.
2.1.3. Operadores Elementares
Um conceito fundamental em Morfologia Matemática é o de relação de ordem. Seja E
um conjunto não vazio. A relação habitualmente usada no caso de sub-conjuntos de E é
a de inclusão que permite comparar certos sub-conjuntos entre si. Seja P(E ) a coleção
de todos os sub-conjuntos de E associada à relação de inclusão ⊂. P(E ) representa um
conjunto parcialmente ordenado anotado (P(E ), ⊂). [BB94] mostraram que o conjunto
(P(E ), ⊂), provido das operações de união e interseção estendidas às famílias em P(E ),
forma um reticulado completo. Sejam ψ um operador sobre P e X uma subcoleção
de P . [BB94] demonstraram que qualquer operador pode ser decomposto a partir de
quatro classes fundamentais de operadores, chamados de operadores elementares, que
são a erosão , a anti-erosão , a dilatação e a anti-dilatação .
Definição 2.1
Um operador ψ é uma:
• dilatação se e somente se, para todo X ⊂ P, ψ (supX ) = sup(ψ (X ))
63
VII Workshop de Visão Computacional – WVC 2011
• erosão se e somente se, para todo X ⊂ P, ψ (in f X ) = in f (ψ (X ))
• anti-dilatação se e somente se, para todo X ⊂ P, ψ (supX ) = in f (ψ (X ))
• anti-erosão se e somente se, para todo X ⊂ P, ψ (in f X ) = sup(ψ (X ))
2.2. OPERADORES DA MORFOLOGIA MATEMÁTICA BINÁRIA
2.2.1. Erosão e Dilatação Binárias
Serão apresentados aqui os dois operadores básicos que constituem os pilares da Morfologia Matemática binária, a erosão e a dilatação,
2.2.1.1. Erosão binária
[Ser82] define a operação de erosão binária ε da seguinte maneira:
A erosão de uma imagem f pelo elemento estruturante B é:
Definição 2.2
ε B ( f ) = {x ∈ E : Bx ⊂ f }
onde Bx representa o elemento estruturante B transladado na posição x.
Segunda a definição 2.2, deve-se deslizar o elemento estruturante B sobre a imagem f
e para cada pixel x verificar a configuração de sua vizinhança em relação à estrutura do
elemento estruturante B. Por ser binários, a imagem f e o elemento estruturante B contém
dois tipos de informação, o fundo e os pixels relevantes. O significado da definição 2.2 é
que o elemento estruturante Bx , posicionado e centrado no pixel x de f , tenta aparelhar-se
com a vizinhança de x. Entende-se que cada pixel relevante de Bx deve encontrar-se na
mesma posição na vizinhança de x. Caso seja verificado, o pixel x na imagem erodida será
considerado um pixel relevante e será preservado. Caso contrário, ele será considerado
como irrelevante e será apagado.
[Ser82] e [BB94] demonstraram que a primeira definição 2.2 da erosão pode ser
relacionada com a subtração de Minkowski [Min03]. Sejam dois conjuntos P e Q, a
subtração de Minkowski do conjunto P em relação a Q, denotada P Q, é definida como
sendo:
(1)
P Q = {x ∈ E : ∀b ∈ Q, ∃a ∈ P : x = a − b} = ∩(b∈Q) Pb
Seguindo o formalismo de [Ser82], tem-se uma segunda formulação da erosão:
A erosão da imagem f pelo elemento estruturante B é:
Definição 2.3
ε B( f )
=
∩(b∈B̃) fb = ∩(b∈B) f−b
onde B̃ representa o elemento estruturante obtido por simetria central de B
pela origem {o} do sistema de referência, e é chamado de B transposto
64
VII Workshop de Visão Computacional – WVC 2011
Nesta nova definição, pode-se constatar que o elemento estruturante B não desliza mais
na imagem f , mas que, ao contrário, é a imagem f que vai se deslocar em função das posições permitidas pelo elemento estruturante B. Entende-se que, na diferença da definição
2.2, tem-se que transladar f e não mais B. Os deslocamentos são realizados em relação
ao ponto central de B̃.
Qualquer que seja a definição de erosão, fica fácil adivinhar o que este operador
faz . Veja na figura 2.1 um exemplo simples de uma imagem poluída por um leve ruído
preto regular. Aplicando a erosão
• • • nos conjuntos pretos da imagem, usando o elemento
estruturante quadrado BQ = •• •• •• , percebe-se o que o ruído preto desaparece.
a)
(b)
Figura 2.1. Limpeza de uma imagem ruidosa: (a) Image Original, (b) Erosão dos
conjuntos pretos.
A figura 2.2 ilustra um exemplo mais complexo de uma imagem cujo fundo é
poluída por um ruído preto e que contêm alguns conjuntos furados, outros conectados e
ainda alguns prejudicados internamente por um ruído branco irregular. Aplicando a erosão nos conjuntos pretos da imagem, usando o mesmo elemento estruturante quadrado
BQ , percebe-se o que o ruído preto quase desaparece na sua totalidade. Mas que o ruído
branco regular se expande, prejudicando o conjunto circular. Aplicando a erosão com o
elemento estruturante ainda maior 3 × BQ , fica evidente que todo o ruído preto desaparece, que o ruído branco se expande, fazendo desparecer quase por completo o conjunto
circular. Percebe-se portanto que, a medida que o elemento estruturante cresce, todos
os conjuntos se modificam diminuindo de tamanho e sofrem desgastes maiores. Não
somente a aparência externa muda, mas em caso de conjuntos apresentando cavidades
internas, as mesmas aumentam de tamanho.
2.2.1.2. Dilatação Binária
[Ser82] define a operação de dilatação binária δ da seguinte maneira:
Definição 2.4
A dilatação de uma imagem f pelo elemento estruturante B é:
δ B ( f ) = {x ∈ f : Bx ∩ f = 0}
onde Bx representa o elemento estruturante B transladado na posição x.
65
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.2. Erosões de conjuntos pretos: (a) Image Original, (b) Com o elemento
estruturante BQ , (c) Com o elemento estruturante 3 × B Q .
Segundo a definição 2.4, o elemento estruturante Bx , posicionado e centrado em
cada pixel x de f desliza na imagem f e verifica uma possível interseção com a vizinhança de x. Caso seja verdadeiro, o ponto central na imagem resultado será considerado
um pixel relevante e será marcado como tal. Caso contrário, ele será considerado como
irrelevante e será apagado.
[Ser82] e [BB94] demonstraram que a primeira definição 2.4 da dilatação pode
ser relacionada com a adição de Minkowski [Had50] [Had57]). Sejam dois conjuntos P
e Q, a adição de Minkowski do conjunto P em relação a Q, denotada P ⊕ Q, é definida
como sendo:
P ⊕ Q = {x ∈ E : ∃a ∈ P e ∃b ∈ Q : x = a + b} = ∪b∈Q Pb
(2)
Seguindo o formalismo de [Ser82], temos a seguinte formulação:
A dilatação de uma imagem f pelo elemento estruturante B é:
Definição 2.5
δ B( f )
=
f ⊕ B̃ = ∪(b∈B̃) fb = ∪(b∈B) f−b
onde B̃ representa o elemento estruturante obtido por simetria central de B
pela origem {o} do sistema de referência, e é chamado de B transposto
Na definição 2.5, é possível constatar que a imagem f a ser dilatada é deslocada
em função das posições permitidas pelo elemento estruturante B̃. Entende-se que, na
diferença da definição 2.4, não é mais B̃ que translada-se mas f . Os deslocamentos são
realizados em relação ao ponto central de B̃.
Novamente, qualquer que seja a definição, é fácil prever o que dilatar significa.
Veja na figura 2.3 um exemplo simples de uma imagem com conjuntos prejudicados
internamente por um leve ruído branco regular. Aplicando a dilatação nos conjuntos
66
VII Workshop de Visão Computacional – WVC 2011
a)
(b)
Figura 2.3. Limpeza de uma imagem ruidosa: (a) Image Original, (b) Dilatação
dos conjuntos pretos.
•
pretos da imagem, usando o elemento estruturante quadrado B Q = ••
o que o ruído branco desaparece e que os conjuntos são preenchidos.
• •
• •
• •
, percebe-se
A figura 2.4 ilustra um exemplo mais complexo de uma imagem apresentando um
fundo poluída por um ruído preto e que contêm alguns conjuntos furados, outros conectados e ainda alguns prejudicados internamente por um ruído branco irregular. Aplicando
a dilatação nos conjuntos pretos da imagem, usando o elemento estruturante quadrado
BQ , percebe-se o que o ruído branco quase desaparece na sua totalidade, que os conjuntos
prejudicados internamente recuperam o aspecto original. Mas que o ruído preto regular
se expande. Aplicando a dilatação com o elemento estruturante ainda maior 3 × B Q , fica
evidente que todo o ruído branco desaparece, que o ruído preto regular se expande mais,
chegando a grudar em alguns conjuntos, criando deformações. Percebe-se portanto que, a
medida que o elemento estruturante cresce, todos os conjuntos aumentam gradativamente
de tamanho e todas as cavidades internas diminuem. Não somente as aparências interna e
externa mudam, mas em caso de conjuntos próximos, os mesmos podem ficar conectados.
(a)
(b)
(c)
Figura 2.4. Dilatações de conjuntos pretos: (a) Image Original, (b) Com o elemento estruturante BQ , (c) Com o elemento estruturante 3 × B Q .
67
VII Workshop de Visão Computacional – WVC 2011
2.2.1.3. Implementação avançada da Erosão e da Dilatação binárias
As erosão e dilatação binárias podem ser programadas de duas maneiras, seguindo as
definições 2.2 ou 2.3, e as definições 2.4 ou 2.5, respectivamente. Qual é a forma
mais eficiente de programar erosão e dilatação binárias rápidas? Uma primeira diferença
importante se situa na ausência de verificação quando são aplicadas as definições empregando a subtração e adição de Minkowski (definições 2.3 e 2.5). Enquanto nas definições
baseadas no deslocamento do elemento estruturante B em cada pixel da imagem, se deve
verificar o resultado da interação de B com a imagem f (o que consome tempo), nas
definições pelos operadores de Minkowski, as operações são simplesmente realizadas.
Uma segunda grande diferença se situa no fato que as definições baseadas nos operadores de Minkowski podem ser implementadas usando a instrução BIT BLT da linguagem
C, C + + ou ainda Del phi. Também existe uma instrução parecida no Linux. A grande
vantagem de utilizar este tipo de instrução é que ela emprega a memória do monitor do
computador para agilizar a erosão e e dilatação em tempo real. Portanto uma forma de
erodir e dilatar de forma veloz imagens binárias é empregar tal instrução para agilizar a
subtração e adição de Minkowski.
2.2.1.4. Efeitos do elemento estruturante, da Erosão e da Dilatação binárias
A figura 2.5 ilustra o impacto de vários elementos estruturantes (ver parágrafo 2.1.2)
Cruz BC (em azul), Quadrado BQ (em verde) e Rhombus BR (em vermelho) em conjuntos
de geometrias diversas. É óbvio que maior for o elemento estruturante, mais agressivas
serão a erosão e a dilatação. Mas os elementos estruturantes não imprimem a sua marca
somente na quantidade de pixels removidos ou adicionados, mas também no formato que
os conjuntos atingem. Um conjunto circular erodido pelo Cruz BC (em azul) ou Quadrado
BQ (em verde) perde progressivamente o seu aspecto redondo a medida que o tamanho do
elemento estruturante aumenta. Um conjunto quadrado dilatado pelo Cruz BC (em azul)
ou Rhombus BR (em vermelho) perde progressivamente o seu aspecto quadrado a medida
que o tamanho do elemento estruturante cresce. O que significa que a geometria pode
variar e se deformar com uso de um elemento estruturante inapropriado.
Pelos exemplos anteriores (figuras 2.1, 2.2, 2.3, 2.4), pode ser constatado que a
erosão e dilatação modificam todos os conjuntos. Em todos os casos, enquanto que esses
ficam menores após a erosão, os mesmos ficam maiores após a dilatação. Agrupando
os resultados apresentados nesses exemplos, pode-se concluir que, por erosão, os efeitos
obtidos são:
• Diminuir conjuntos, desconectá-los e eventualmente eliminá-los caso o tamanho do
elemento estruturante for maior;
• Aumentar e abrir cavidades.
Enquanto que, por dilatação, os efeitos obtidos são:
• Aumentar conjuntos e eventualmente conectá-los caso o tamanho do elemento estruturante for maior que o espaço entre eles;
68
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.5. Influência dos elementos estruturantes Cruz, Quadrado e Rhombus:
(a) Imagem Original (b) Na erosão (c) Na dilatação.
• Diminuir e preencher cavidades.
2.2.1.5. Propriedades da Erosão e da Dilatação binárias
Vale a pena esclarecer que as operações de erosão e de dilatação são ditas duais e que a
interpretação da dilatação é complementar da interpretação da erosão. O complemento da
proposição “Bx está incluído em f ” é a proposta “a interseção de B x e f não é vazia”.
Propriedade 2.1 Enquanto a erosão é uma transformação não comutativa, a dilatação
é comutativa:
ε B( f ) =
ε f (B)
δ B ( f ) = δ f (B)
(3)
Propriedade 2.2 A erosão e a dilatação por um ponto reduzem-se a uma translação.
Como conseqüência, a dilatação e a erosão são invariantes por translação.
ε x ( f ) = δ x ( f ) = fx
(4)
Propriedade 2.3 A erosão e a dilatação tem comportamentos interessantes em relação à
interseção e à união.
69
VII Workshop de Visão Computacional – WVC 2011
δ B∪B ( f ) = δ B ( f ) ∪ δ B ( f )
(5)
Pelo uso da dualidade que existe entre a erosão e a dilatação, tem-se:
ε B∪B ( f ) = ε B ( f ) ∩ ε B ( f )
(6)
ε B ( f ∩ g) = ε B ( f ) ∩ ε B (g)
(7)
e
Propriedade 2.4 A erosão e a dilatação têm duas propriedades interessantes relativas à
repetição.
B (B̃)
B (B̃)
A primeira é:
ε B (ε B ( f )) = ε δ
A segunda é:
δ B (δ B ( f )) = δ δ
(f)
(8)
(f)
(9)
Essas propriedades são fundamentais porque mostram que:
• Erosões e dilatações com elementos estruturantes grandes podem ser decompostas
em seqüências de erosões e dilatações com elementos estruturantes menores. Essa
propriedade é particularmente interessante para elementos estruturantes convexos.
O que explica que, novamente, os elementos estruturantes mais usados são simples,
como BH , BV , BC .
⎧. . . . . . .⎫
⎪
⎨ .. •. •• •• •• •. .. ⎪
⎬
Veja o exemplo 2.2 da erosão da imagem f = .. •• •• •• •• •• .. pelo elemento es⎪
⎩. . • • • . .⎪
⎭
. . .
.
. . .
truturante BR . A erosão de f pode ser realizada diretamente ou ainda por duas
erosões sucessivas, a primeira pelo elemento estruturante BC seguida da segunda
pelo elemento estruturante BQ . Ou ainda o inverso.
Exemplo 2.2
⎧
.
⎪
⎪
⎪
⎨ ..
.
ε
⎪
.
⎪
⎪
⎩.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
⎡.
⎢
(⎣
.
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
⎤
⎥
⎦) = ε
⎡.
⎢
= ⎣
70
.
.
.
.
.
.
• • •
• • •
• • •
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
(ε
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎦
. • .
• • •
. • .
⎡.
⎢
(⎣
.
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
⎤
⎥
⎦))
VII Workshop de Visão Computacional – WVC 2011
• Elementos estruturantes grandes podem ser decompostos em elementos estruturantes menores. O que explica que os elementos estruturantes mais usados são simples,
como BH , BV , BC (ver parágrafo 2.1.2). O exemplo a seguir 2.3 mostra o significado dessa propriedade. O elemento estruturante Rhombus B R (que simula o menor
elemento estruturante circular) pode ser decomposto a partir do elemento estruturante cruz BC dilatado pelo elemento estruturante quadrado transposto B˜Q , ou ainda
o inverso. Onde B̃ representa o transposto de B obtido por simetria central pela
origem do sistema de referência. Como ambos BC e BQ são simétricos, B˜C = BC e
B˜Q = BQ . Seja portanto:
Exemplo 2.3
BR = δ BQ (B˜C )
= δ BC (B˜Q ) =
⎧.
⎪
⎨ ..
⎪
⎩
.
.
•
•
•
.
.
.
.
.
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
•
•
•
•
•
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
⎫
⎪
⎬
⎪
⎭
=δ
. • .
• • •
. • .
(
•
•
• •
• •
•
•
)=δ
•
• • •
• • •
• • •
(
.
• .
• • •
. • .
)
Ou ainda no exemplo 2.4 do grande elemento estruturante
a seguir que
. •convexo
.
•
•
•
pode ser composto a partir de outro bem menor BC = . • . por 7 dilatações
sucessivas da seguinte maneira:
Exemplo 2.4
⎧. . . . . .
. . . . . .
⎪
⎪
. . . . . .
⎪
⎪
. . . . . •
⎪
⎪
.
⎪
⎪ . .. .. •. •• ••
⎪
⎪
⎨ .. •. •• •• •• ••
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
•
.
.
.
.
.
.
.
.
•
•
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
•
•
•
•
.
.
.
.
.
•
•
•
•
•
.
.
.
.
•
•
•
•
•
•
.
.
.
.
.
•
•
•
•
•
•
•
•
•
•
•
•
•
.
.
.
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
.
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
.
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
.
.
.
•
•
•
•
•
•
•
•
•
•
•
•
•
.
.
.
.
.
•
•
•
•
•
•
•
•
•
•
•
.
.
.
.
.
.
.
•
•
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
=δ
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎭
. • .
• • •
. • .
(δ
. • .
• • •
. • .
(... δ
. • .
• • •
. • .
(
.
• .
• • •
. • .
)))
vezes
7
Propriedade 2.5 A erosão e a dilatação são operações crescentes.
f ⊂ f =⇒ ε B ( f ) ⊂ ε B ( f )
=⇒ δ B ( f ) ⊂ δ B ( f )
(10)
E pela dualidade:
B ⊂ B =⇒ ε B ( f ) ⊂ ε B ( f )
=⇒ δ B ( f ) ⊂ δ B ( f )
71
(11)
VII Workshop de Visão Computacional – WVC 2011
Propriedade 2.6 Enquanto que a erosão é uma operação anti-extensiva, a dilatação é
uma operação extensiva.
ε B( f ) ⊂ f ⊂ δ B( f )
(12)
Propriedade 2.7 As erosão e dilatação são transformações contínuas.
2.2.2. Detecção de bordas
O contorno é um dos conceitos mais importantes da área de Processamento de Imagens. A
obtenção morfológica do contorno de conjuntos em imagens binárias é uma tarefa muito
fácil. Uma maneira simples consiste em comparar imagem original com a versão erodida
ou dilatada, como segue:
Contorno por erosão: =⇒ f − ε B ( f )
Contorno por dilatação: =⇒ δ B ( f ) − f
(13)
(14)
Foi comprovado que o melhor elemento
estruturante para obter contornos de um
. • .
•
•
•
pixel de espessura e sem falha é BC = . • .
A figura 2.6 exemplifica a obtenção do contorno de conjuntos pretos numa imagem por erosão com o elemento estruturante BC
(a)
(b)
Figura 2.6. Obtenção do contorno: (a) Imagem original (b) Contorno por erosão.
2.2.3. Abertura e Fechamento Binários
Foi visto anteriormente que a erosão e a dilatação podem corrigir defeitos numa imagem
com desconectar e eliminar conjuntos ou ainda preencher cavidades etc... Porém, nenhum
conjunto retocado por essas operações mantém o tamanho original. A erosão reduz enquanto que a dilatação engorda. A partir das propriedades de iteratividade e de dualidade
da erosão e dilatação, é possível filtrar reduzindo o impacto às características geométricas
dos conjuntos processados.
72
VII Workshop de Visão Computacional – WVC 2011
2.2.3.1. Abertura binária
Como eliminar as partículas indesejáveis sem modificar o tamanho dos outros conjuntos?
Intituivamente, pode-se prever que esta operação consiste em erodir e depois dilatar o
resultado da erosão. Define-se assim uma nova operação morfológica chamada de “abertura binária” e o novo conjunto processado pelo elemento estruturante B chamar-se-á de
conjunto aberto por B
Definida por [Ser82], a abertura binária γ escreve-se como sendo:
A abertura γ de uma imagem f pelo elemento estruturante B
Definição 2.6
é:
γ B ( f ) = δ B (ε B̃ ( f ))
onde B̃ representa o transposto de B obtido por simetria central
pela origem {o} do sistema de referência
Veja novamente o exemplo da figura 2.1. Por erosão
conjuntos pretos da
• • •dos
imagem, usando o elemento estruturante quadrado B Q = •• •• •• , foi possível remover
o ruído preto. Mas, como já explicado anteriormente, o tamanho original do conjunto
filtrado não foi mantido. Aplicando em seguida uma dilatação com o mesmo elemento
estruturante, tem-se o re-estabelecimento do tamanho original. A figura 2.7 ilustra tal
resultado.
a)
(b)
(c)
Figura 2.7. Limpeza de uma imagem pouco ruidosa: (a) Image Original, (b) Erosão dos conjuntos pretos seguida de (c) Dilatação dos conjuntos pretos.
A figura 2.8 exemplifica a limpeza de uma imagem pesadamente contaminada
por partículas pretas indesejáveis usando o processo de abertura com os elementos estruturantes 5 × BQ e 4 × BR . Percebe-se que a escolha do elemento estruturante modifica o
resultado final. Conforme explicado no parágrafo 2.2.1.4, os elementos estruturantes imprimem o seu formato. Na figura 2.8-(b), onde é usado o elemento estruturante quadrado
5 × BQ , o formato do conjunto quadrado é mantido enquanto o conjunto circular fica imperfeito. Na figura 2.8-(c), onde é usado o elemento estruturante arredondado 4 × BR , o
formato do conjunto circular é mantido enquanto o conjunto quadrado perde os cantos.
73
VII Workshop de Visão Computacional – WVC 2011
a)
(b)
(c)
Figura 2.8. Limpeza de uma imagem muito ruidosa: (a) Image Original, (b) Abertura com BQ , (b) Abertura com BR .
A figura 2.9 exemplifica a limpeza de uma imagem poluída por um ruído preto
e que contêm conjuntos furados, conjuntos conectados e conjuntos prejudicados internamente por um ruído branco irregular. Usando o processo de abertura com o elemento
estruturante 2 × BQ , percebe-se que o ruído preto desaparece, que o ruído branco permanece e se expande prejudicando os conjuntos contaminados por tal ruído.
a)
(b)
(c)
Figura 2.9. Limpeza de uma imagem ruidosa: (a) Image Original, (b) Erosão dos
conjuntos pretos seguida de (c) Dilatação dos conjuntos pretos.
2.2.3.2. Fechamento binário
Como preencher cavidades sem modificar o tamanho dos outros conjuntos? Intituivamente,
pode-se prever que esta operação consiste em dilatar e depois erodir o resultado da dilatação. Define-se assim uma nova operação morfológica chamada de “fechamento binário”
e o novo conjunto processado pelo elemento estruturante B chamar-se-á de conjunto fechado por B Definido por [Ser82], o fechamento binário φ escreve-se como sendo:
O fechamento φ de uma imagem f pelo elemento estruturante
Definição 2.7
B é:
φ B( f )
=
ε B (δ B̃ ( f ))
74
VII Workshop de Visão Computacional – WVC 2011
onde B̃ representa o transposto de B obtido por simetria central
pela origem {o} do sistema de referência
Veja novamente o exemplo da figura 2.3. Por dilatação
• • • dos conjuntos pretos da
imagem, usando o elemento estruturante quadrado B Q = •• •• •• , foi possível eliminar o
ruído branco, resultando no preenchimento dos conjuntos pretos. Mas, como já explicado
anteriormente, o tamanho original do conjunto filtrado não foi mantido. Aplicando em
seguida uma erosão com o mesmo elemento estruturante, tem-se o re-estabelecimento do
tamanho original. A figura 2.10 ilustra tal resultado.
a)
(b)
(c)
Figura 2.10. Limpeza de uma imagem pouco ruidosa: (a) Image Original, (b)
Dilatação dos conjuntos pretos seguida de (b) Erosão dos conjuntos pretos.
A figura 2.11 ilustra um exemplo mais complexo de uma imagem poluída por
um ruído preto que contém conjuntos furados, conjuntos conectados e conjuntos prejudicados internamente por um ruído branco irregular. Usando o processo de fechamento
com o elemento estruturante 2 × BQ , percebe-se que o ruído preto permanece cuja partes
ficaram grudadas a conjuntos e que os conjuntos contaminados por partículas brancas são
corrigidos.
a)
(b)
(c)
Figura 2.11. Limpeza de uma imagem ruidosa: (a) Image Original, (b) Dilatação
dos conjuntos pretos seguida de cb) Erosão dos conjuntos pretos.
75
VII Workshop de Visão Computacional – WVC 2011
2.2.3.3. Efeitos da Abertura e do Fechamento binários
Agrupando os resultados apresentados nos exemplos anteriores (figuras 2.7, 2.8, 2.9,
2.10, 2.11 ), pode-se concluir que, a abertura:
• Pode separar conjuntos conectados. Para isto, é preciso usar elementos estruturantes
de tamanho maior que a conexão:
• Pode eliminar conjuntos. Para isto, faz-se necessário usar elementos estruturantes
de tamanho maior que os conjuntos:
• Nivela os contornos pelo interior;
• Devolve conjuntos abertos mais regulares que os conjuntos originais;
• Gera imagens menos ricas em detalhes que as imagens originais.
Enquanto que o fechamento:
• Pode conectar conjuntos separadas. Para isto, é preciso usar elementos estruturantes
de tamanho maior que o intervalo que os separa:
• Pode preencher buracos e cavidades. Para isto, faz-se necessário usar elementos
estruturantes de tamanho maior que os buracos e cavidades:
• Nivela os contornos pelo exterior;
• Devolve conjuntos fechados mais regulares que os conjuntos originais;
• Gera imagens menos ricas em detalhes que as imagens originais.
A figura 2.12 exemplifica o exemplo de filtragem de uma imagem contaminada
por um ruído preto e branco intenso ( ruído sal pimenta). Percebe-se que a filtragem do
fundo pelo processo de abertura permite limpá-lo, mas danificando ainda mais os conjuntos. Pelo processo dual de fechamento, percebe-se que a integridade desses conjuntos
é restaurada. A seqüência abertura-fechamento permite uma filtragem quase perfeita da
imagem. Aqui a abertura é realizada com o elemento estruturante BQ . O fechamento é
realizado com dois elementos estruturantes diferentes, os 4 × B Q e 3 × BR . É possível notar que o elemento estruturante 4 × BQ restaura melhor a geometria do conjunto quadrado
enquanto que o elemento estruturante 3 × BR restaura melhor a geometria do conjunto
arredondado.
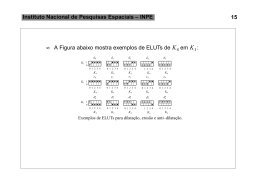
A figura 2.13 exemplifica o exemplo real de filtragem de uma imagem contendo
a letra R danificada por partículas pretas e brancas. A seqüência usada para restaurar a
letra R é um fechamento com o elemento estruturante 2 × BC seguido de uma abertura
com o elemento estruturante 4 × BC por fim seguido de um fechamento com o elemento
estruturante 4 × BC .
76
VII Workshop de Visão Computacional – WVC 2011
a)
(b)
(c)
(d)
Figura 2.12. Limpeza de uma imagem ruidosa: (a) Image Original, (b) Limpeza do
fundo com BQ , (c) Filtragem dos conjuntos com B Q ,(d) Filtragem dos conjuntos
com BR .
a)
(b)
(c)
(d)
Figura 2.13. Exemplo complexo de filtragem: (a) Image Original, (b) Limpeza
parcial do fundo, (c) Filtragem do "R",(d) Unificação do fundo.
2.2.3.4. Propriedades da Abertura e do Fechamento binários
Propriedade 2.8 A abertura e o fechamento são transformações crescentes:
f ⊂ g =⇒ γ B ( f ) ⊂ γ B (g)
f ⊂ g =⇒ φ B ( f ) ⊂ φ B (g)
(15)
Propriedade 2.9 Enquanto a abertura é uma transformação anti-extensiva, o fechamento é uma transformação extensiva:
γ B( f ) ⊂ f
f ⊂ φ B( f )
(16)
Propriedade 2.10 A abertura e o fechamento apresentam a importante propriedade de
idempotência.
γ B (γ B ( f )) = γ B ( f )
φ B (φ B ( f )) = φ B ( f )
77
(17)
VII Workshop de Visão Computacional – WVC 2011
A abertura e o fechamento diferem da erosão e da dilatação pela propriedade
da idempotência. Esta propriedade é crucial nos processos de filtragem. Imagine
que durante um certo tratamento, o processo de abertura ou fechamento com um certo
elemento estruturante dado B não resolveu o problema. Um modo de pensar seria reiterar
o processo com o mesmo elemento estruturante B. No caso da abertura e do fechamento,
a propriedade da idempotência faz com que o resultado seja idêntico. O que significa
que a obtenção de novos resultados será somente possível com o uso de outros elementos
estruturantes que o empregado na experiência anterior.
2.2.4. Afinamento e Espessamento Binários
2.2.4.1. Transformação Hit − miss
Testar ao mesmo tempo as partes internas e externas de conjuntos de uma imagem, pode
ser realizado pela transformação Hit − miss que consiste em testar o conteúdo de uma
imagem f e seu conteúdo complementário f c a partir de dois elementos estruturantes
diferentes disjuntos. Para realizar isso, é preciso de dois elementos estruturantes Bi e Be
que formam um par V = (Bi , Be ), um para testar o interior e o outro o exterior da imagem.
Definição 2.8
Aplicar uma transformação Hit − miss hom em uma imagem
f a partir de um par de elementos estruturantes V = (B i , Be ) é:
homV ( f ) = {x : Bix ⊂ f ; Bex ⊂ f c }
Pode-se dizer que um ponto da imagem f pertence à imagem transformada por Hit − miss
se e somente se Bi “cabe“ em f e se Be “cabe“ em f c . Isso supõe obrigatoriamente que
Bi e Be sejam disjuntos, senão é impossível definir o operador Hit − miss. Na prática, a
transformação Hit − miss pode ser expressa a partir da definição da erosão da seguinte
maneira:
Definição 2.9
Aplicar uma transformação Hit-miss hom sobre a imagem f
a partir de um par de elementos estruturantes V = (B i , Be ) é:
i
e
homV ( f ) = ε B ( f ) ∩ ε B ( f c )
2.2.4.2. Afinamento
Uma transformação homotópica é uma transformação que não modifica o número de conectividade. Isso quer dizer que a imagem inicial e a transformada têm o mesmo número
de partes.
Uma primeira transformação homotópica é a operação de afinamento “afi” de uma
imagem f que consiste em reduzir a espessura dos componentes conexos de f até um
valor infinitamente pequeno sem mudar o número nem o tipo. Ela opera retirando de f
pontos que correspondem a uma configuração dada.
78
VII Workshop de Visão Computacional – WVC 2011
Afinar uma imagem f é:
Definição 2.10
i
e
afiV ( f ) = f /(homV ( f )) = f /(ε B ( f ) ∩ ε B ( f c ))
Onde a expressão C1 /C2 exprime a diferença pixel a pixel entre os conjuntos C1 e C2 ,
definida, em termos de operações entre conjuntos da seguinte maneira C1 /C2 = C1 ∩C2c .
2.2.4.3. Espessamento
Uma transformação homotópica dual do afinamento é a operação de espessamento “esp”
de uma imagem f que consiste em adicionar a f pontos que correspondem a uma configuração dada.
Definição 2.11
Espessar uma imagem f é:
i
e
espV ( f ) = f ∪ (homV ( f )) = f ∪ (ε B ( f ) ∩ ε B ( f c ))
2.2.4.4. Afinar e Espessar até convergência
Afinar e espessar representam processos homotópicos e portanto não destrõem as propriedades da conectividade e preservam a propriedade da homotopia. Os processos afinamento e de espessamento podem ser iterados até atingir a convergência. Nesse nível, as
transformações morfológicas de afinamento e de espessamento tornam-se idempotentes.
A escolha do par de elementos estruturantes V = (Bi , Be ) é crucial. Nesse par de
elementos estruturantes, nenhum ponto válido deve pertencer aos dois elementos estruturantes ao mesmo tempo. Por exemplo, este par Bi e Be descrito como segue:
. . .
• • •
Be = .. .. ..
Bi = •. •• •.
Na literatura, existe uma outra maneira de representação do par de elementos estruturantes V = (Bi , Be ) de forma matricial, onde Bi é representado com pixels pretos
“•”, Be com pixels brancos . Os pixels que não interagem, chamados de ”don’t care”
são representados com o símbolo“×”. O precedente exemplo de V = (B i , Be ) é portanto
representado assim:
V = (Bi , Be ) = X• •• X•
No lugar de afinar uma imagem através de um par de dois elementos estruturantes,
as operações podem ser efetuadas de forma simétrica a partir de famílias de pares de
elementos estruturantes, permitindo assim um processo simétrico. É descrita a seguir
uma família de pares de elementos estruturantes M permitindo um processo simétrico:
M = (M1 , M2, M3 , M4 , M5, M6 , M7 , M8)
X • X • • •
X • X
• •
• •
• • X
X
=
• • X
• X
X
• • •
79
• •
• X
X
• •
• •
X
X •
• •
X •
X
• •
X • •
VII Workshop de Visão Computacional – WVC 2011
Da mesma maneira, espessar uma imagem pode ser efetuado de forma simétrica a
partir da família de pares de elementos estruturantes L abaixo representada:
L = (L1 , L2 , L3 , L4 , L5 , L6 , L7 , L8 )
• • X X • • X X • X • X
X • X
• •
=
X
X
X X
X
X X
• •
X •
X
X • X
X • •
X
X • X
• • X
X
X
• •
• X X
•
X X
• •
X X
A figura 2.14 exemplifica o afinamento e o espessamento de conjuntos.
(a)
b)
(c)
Figura 2.14. Afinamento e espessamento: (a) Image Original, (b) Afinamento, (c)
Espessamento.
2.2.5. Pruning
Freqüentemente os processos de afinamento fazem aparecer nas imagens finais as linhas
genéricas procuradas para permitir uma futura pesquisa mas também segmentos de tamanho reduzido chamados de “rebarbas” ou ainda “pés de galinha” que são o resultado do
processo sobre extremidades. Quando essas rebarbas são relativamente espessas, é possível tirá-las com um processo de abertura a partir de um elemento estruturante adequado
do tipo quadrado BQ . Caso as rebarbas sejam finas demais, um processo de abertura não
pode ser usado sob pena de destruição excessiva. É possível utilizar nesse caso uma variante do afinamento, o pruning. O objetivo desse processo é tirar, a partir de uma imagem
já afinada, os pontos extremos. Para isso, é possível empregar uma das duas seguintes
famílias de elementos estruturantes:
X X X X X X X X X •
X X X
ou
X •
X X
X •
X
•
•
•
•
• •
X •
•
•
•
•
•
• X
•
•
• X
X X
• X
X
• •
•
•
A grande diferença com o processo de afinamento reside no número de ciclos de
supressão de pontos extremos (figura 2.15). Ao contrário do afinamento, o pruning não é
um processo idempotente e o fato de continuar o processo pode resultar em uma redução
ou grande diminuição ou até destruição parcial da imagem afinada (figuras 2.15-(b) e (c)).
Por isso, o número de ciclos no processo de pruning deve ser predeterminado.
80
VII Workshop de Visão Computacional – WVC 2011
Figura 2.15. Exemplos de pruning
2.2.6. Pontos Extremos e Pontos Múltiplos
As entidades afinadas têm uma espessura de um pixel na imagem. Cada pixel possui, em
geral, dois vizinhos exceto para alguns pixels particulares que são:
• Os pixels isolados e as extremidades do conjunto afinado que são os pixels extremos. Duas famílias permitindo extrair os pixels extremos são ilustradas a seguir:
X
X X
X • X
X • X
ou
X
X X
X • X
• X X
X
X X
• • X
X X X
X
X
•
X X X
•
X X
X • X
X X X
X
X • X
X X
X
• X
X • X
X X X
X
X
X •
X
X
X
X •
X • X
X X X
X
X
X • X
X
X
X X
X • •
X X X
X
X X
•
X
X
X
X X
X • X
X X •
• As ligações que representam os pixels múltiplos. O número de ligações pode variar
entre 3 e 8 (qualquer configuração ao redor do ponto central, tendo pelo menos
três pontos brancos, pode representar estes pontos múltiplos), o que corresponde
a 56 possibilidades em configurações de vizinhança. Uma forma mais simples de
detectar os pontos múltiplos consiste em definir uma função de vizinhança cujo
centro seja 1 e onde haja no mínimo mais de dois vizinhos a 1. Dois exemplos de
configuração seguem abaixo:
X • X • X X • X • X X • X • X
• X •
ou
X
• X
X • •
• X X
X • •
• X X
•
X
X
X X
• •
• X
X
X
X
em uma
81
• X
• X
X •
• • X
X • X
• • X
X X •
X
• X
• • X
X X •
VII Workshop de Visão Computacional – WVC 2011
2.2.7. Esqueletização
Um problema comum quando se processa uma imagem binária é determinar uma réplica
“estruturada” dessa imagem que seja fiel à imagem original. Uma réplica que reflete todas
as características da imagem, porém mais econômica em termos de memória, consiste em
esqueletizar essa imagem. O interesse desse processo reside na compressão dos dados
para permitir análises mais rápidas.
2.2.7.1. Definições da Esqueletização
Uma primeira definição ( 2.12) do esqueleto da imagem f leva em consideração a fronteira
de f .
Definição 2.12
Sejam um conjunto f e sua fronteira Δ f , um ponto de f
pertence ao esqueleto esq( f ) se a distância euclidiana de f até Δ f for atingida no mínimo
em dois pontos distintos de f .
x ∈ esq( f ) =⇒ ∃y1, y2 ∈ Δ f , y1 = y2
d(x, Δ f ) = d(x, y1) = d(x, y2)
A noção de esqueleto pode ser ilustrada pela idéia da propagação do fogo no
campo: o fogo aceso em todos os pontos do contorno de um campo propaga-se de uma
forma isotrópica. Quando duas propagações de fogo encontram-se, esse acaba pela falta
de combustível. Os pontos de extinção constituem então o esqueleto.
O esqueleto pode ser igualmente definido a partir do conceito de discos máximos
contidos em f . Para um ponto pertencente à figura da imagem, existem vários discos
centrados nesse ponto completamente contidos na figura. Entretanto, existe um único
disco de raio máximo contido na figura e centrado nesse ponto. Qualquer disco que
satisfaça essa condição é chamado de disco máximo. O conjunto dos centros de todos os
discos máximos constituem o esqueleto da figura da imagem (figura 2.16). Uma segunda
definição permite expressar o esqueleto em termos de erosão e de dilatação (figura 2.17):
esq(λ B,μ B) ( f ) = ∪λ >0 ∩μ >0 [δ λ B ( f )/γ μ B (δ λ B ( f ))]
(18)
O esqueleto é a união, segundo todos os λ positivos, da interseção, segundo todos
os μ positivos, da diferença da imagem f erodida por λ B com o resultado da abertura
pelo elemento estruturante μ B da imagem f erodida por λ B.
O termo x ∈ ∩μ >0 [δ λ B ( f )/γ μ B (δ λ B ( f ))] na definição 18, traduz a idéia que x
representa o centro de um disco máximo de raio λ . Onde a expressão C1 /C2 exprime a
diferença pixel a pixel entre os conjuntos C1 e C2 , definida, em termos de operações entre
conjuntos da seguinte maneira C1 /C2 = C1 ∩C2c .
Os discos de tamanho superior a λ podem ser eliminados manipulando a operação
interseção do termo γ μ B (δ λ B ( f )). Uma terceira definição 2.13, mais acessível em termos
82
VII Workshop de Visão Computacional – WVC 2011
Figura 2.16. Esqueleto pela noção de disco máximo.
Figura 2.17. Erosão e abertura de um conjunto X: geração de um esqueleto.
83
VII Workshop de Visão Computacional – WVC 2011
de implementação, preconiza a decomposição do esqueleto morfológico em sub-esqueletos da seguinte forma ([Dou92]): cada sub-esqueleto sesqB ( f , n) é associado a um disco
máximo nB (n ≥ 0) e representa o conjunto de todos os centros de f do disco máximo nB
contido em f . Desta maneira, pode afirmar que o esqueleto esq( f ) representa a união dos
sub-esqueletos sesq( f , n) (n ≥ 0).
esqB ( f ) = ∪n sesqB ( f , n)
O sub-esqueleto sesqB ( f , n) pode ser definido da seguinte maneira:
sesqB ( f , n) = δ nB ( f )/γ B (δ nB ( f ))
Onde a expressão C1 /C2 exprime a diferença pixel a pixel entre os conjuntos C1 e C2 ,
definida, em termos de operações entre conjuntos da seguinte maneira C1 /C2 = C1 ∩C2c .
Definição 2.13
truturante B é:
O esqueleto esqB ( f ) da imagem f a partir do elemento esesqB ( f ) = ∪n sesqB ( f , n) = ∪n [δ nB ( f )/γ B (δ nB ( f ))]
A figura 2.18 ilustra o resultado da obtenção do esqueleto pelo processo de
esqueletização dos conjuntos pretos da imagem original com o elemento estruturante B Q .
(a)
(b)
Figura 2.18. Esqueleto por esqueletização: (a) Image Original, (b) Esqueleto.
A figura 2.19 ilustra as diferenças entre o esqueleto por afinamento e por esqueletização. No segundo, as estruturas obtidas ficam mais descontínuas e compactadas que no
primeiro onde não há presença de descontinuidades nas estruturas geradas. Isto constitui a
grande diferença entre os processos de afinamento e de esqueletização. No primeiro caso,
as estruturas obtidas são contínuas e refletem a geometria dos conjuntos. No segundo
caso, as estruturas obtidas são quase sempre descontínuas e podem apresentar geometrias
muito diferentes dos conjuntos. Essas diferenças nos resultados de afinamento e esqueletização têm na realidade aplicações diferentes.
84
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
Figura 2.19. (a) Esqueleto por afinamento versus (b) Esqueleto por esqueletização.
2.2.7.2. Reconstrução do conjunto inicial a partir do seu Esqueleto
O conhecimento do esqueleto esqB ( f ) permite a geração ou a reconstrução da imagem
inicial f . Uma primeira definição formula este conceito:
X = ∪ρ >0 (δ ρ B̃ (esqB ( f )))
(19)
onde ρ representa o raio máximo associado a cada ponto do esqueleto esq B ( f ).
O esqueleto obtido pelo método acima, no caso de imagens digitais não tem obrigatoriamente as propriedades do esqueleto não digital por causa dos valores discretos de
λ ou de μ .
Uma segunda definição formula uma reconstrução implementável da imagem inicial f a partir do esqueleto esqB ( f ), [Dou92].
Definição 2.14
A reconstrução da imagem inicial f a partir de seu esqueleto
B
esq ( f ) com o elemento estruturante B é:
f = ∪n [δ nB̃ (sesqB ( f , n))]
(20)
Essa propriedade de reconstrução a imagem f é muito interessante sabendo que
pode-se “reduzir” a imagem f sabendo retornar a ela e que a memorização do esqueleto do conjunto requer menos espaço. Essa técnica constitui então uma ferramenta de
compressão.
2.2.7.3. Propriedades da Esqueletização
A esqueletização tem as seguintes propriedades:
85
VII Workshop de Visão Computacional – WVC 2011
Propriedade 2.11 A esqueletização não é uma transformação crescente:
f ⊂ g =⇒ esqB ( f ) ⊂ esqB (g)
(21)
Propriedade 2.12 A esqueletização é uma transformação anti-extensiva:
esqB ( f ) ⊂ f
(22)
2.2.8. Esqueletização (SKIZ) por regiões de influência
Outra tarefa comum quando se processa uma imagem binária contendo vários conjuntos
consiste em determinar a região de influência de cada um deles para, futuramente, ter um
meio de separá-los. Um processo comumente usado consiste em definir o esqueleto por
regiões de influência (SKIZ) da imagem ([CC89], [Pré93]).
Seja uma imagem f constituída de f 1 , f2 , . ., fn , n conjuntos individuais conexos.
Para cada conjunto fi pode ser associada uma região de influência IZ( f i ) que representa
o conjunto de todos os pontos do plano que estão mais próximos de f i que de qualquer
outro f j , j = i [Vin91]. Tem-se então:
IZ( fi ) = ∪[y ∈: d(y, xi ) < d(y, x j ), j = i]
(23)
Definição 2.15
O esqueleto por regiões de influência SKIZ da imagem f ,
anotado SKIZ( f ), é por definição o complementário da união de todos os IZ( f i ):
SKIZ( f ) = [∪i IZ( fi )]c
Esse esqueleto por regiões de influência divide a imagem f no mesmo número
de regiões que o número de conjuntos fi . O SKIZ constitui um sub-conjunto do esqueleto do complementário f c . Portanto, esse esqueleto pode ser obtido por espessamentos
homotóticos de f (ver a equação 24). Um primeiro passo consiste em empregar a família
de elementos estruturantes L anteriormente apresentada.
O esqueleto por regiões de influência SKIZ não deve conter nenhum ponto extremo, enquanto o esqueleto do complementário f c obtido por espessamento homotótico
de f pela precedente família de elementos estruturantes, (espL ( f ))c , tem ramos apresentando pontos extremos. Para eliminar esses ramos que constitui o segundo passo, basta
efetuar um espessamento com a família E de elementos estruturantes abaixo ilustrada:
X X X X X X • X
•
•
X •
•
• X
X •
•
E=
X X
X
X
X X
Um maneira de definir o esqueleto por regiões de influência logo é:
SKIZ( f ) = (espE (espL ( f )))c
(24)
A figura 2.20 ilustra o resultado da esqueletização por regiões de influência SKIZ
sobreposto à imagem original. Percebe-se claramente o assentamento de cada conjunto
em relação aos conjuntos vizinhos.
86
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
Figura 2.20. Esqueleto por regiões de influência: (a) Image Original, (b) Esqueleto SKIZ.
2.2.9. Reconstrução binária
2.2.9.1. Introdução
Os operadores apresentados anteriormente consideram as imagens como sendo conjuntos
indivisíveis. Porém, pode surgir a necessidade de restringir os processos em regiões específicas de uma imagem. A seguir será mostrado que as transformações morfológicas
podem ser modificadas de maneira a trabalhar somente em subconjuntos da imagem. Serão apresentados aqui operadores morfológicos condicionais que, iterados, poderão atingir a idempotência, propriedade normalmente válida somente para abertura e fechamento
euclidianos.
2.2.9.2. Erosão e Dilatação condicionais binárias
Uma primeira possibilidade de processar parcialmente uma imagem consiste em definir um subconjunto da imagem onde as operações são válidas, por exemplo, tratar um
conjunto particular de uma imagem. Operadores erosão e dilatação ditos condicionais
permitem realizar esse tipo de processamento.
Definição 2.16
A erosão condicional do subconjunto z da imagem f , pelo
elemento estruturante B, condicionada à imagem f , sendo que z ⊂ f , é definida por ε cBf :
εcBf (z) = ε B (z) ∩ f
De maneira equivalente:
Definição 2.17
A dilatação condicional do subconjunto z da imagem f , pelo
elemento estruturante B condicionada à imagem f , sendo que z ⊂ f , é definida por δ cBf :
87
VII Workshop de Visão Computacional – WVC 2011
δcBf (z) = δ B (z) ∩ f
A figura 2.21 ilustra as possibilidades que oferece a dilatação condicional comparada à dilatação tradicional. A imagem da figura 2.21-(a) representa o subconjunto z
citado na definição 2.17. Dilatando iterativamente 40 vezes o subconjunto z pela dilatação tradicional com o elemento estruturante quadrado B Q , obtêm-se a imagem de um
simples quadrado maior (figura 2.21-(d)). Agora, aplicando a dilatação condicional no
subconjunto z iterativamente 40 vezes com o mesmo elemento estruturante condicionada
à imagem f do gato da figura 2.21-(b), percebe-se que o resultado obtido é uma parte da
imagem do gato (figura 2.21-(e)). Aplicando a dilatação condicional no subconjunto z
nas mesmas condições, mas agora condicionada à imagem f da máscara (figura 2.21-(c)),
percebe-se que o resultado obtido é uma parte da imagem da máscara (figura 2.21-(f)). O
que demonstra que o processo de dilatação no caso condicional não mais é dominado pela
geometria do elemento estruturante, mas pela geometria da imagem f . O que também se
verifica no caso da erosão condicional.
(a)
(b)
(c)
(d)
(e)
(f)
Figura 2.21. Dilatação condicional versus dilatação tradicional: (a) Subconjunto
z, (b) Imagem f do gato, (c) Imagem f da máscara, (e) Dilatação tradicional, (b)
Dilatação condicionada à imagem do gato, (c) Dilatação condicionada à imagem
da máscara.
Percebe-se claramente as novas perspectivas oferecidas pelas dilatação e erosão
condicionais detalhadas no parágrafo 2.2.9.3.
2.2.9.3. Definição da reconstrução binária
Os conceitos e operadores apresentados anteriormente mostraram que é possível, através
de transformações condicionais, processar somente alguns conjuntos S de uma imagem
f . Essa característica abre novos horizontes na área de reconstrução.
88
VII Workshop de Visão Computacional – WVC 2011
Sejam uma imagem binária f contendo um conjunto S e outra imagem binária
Z contendo z um subconjunto de S, z ⊂ S. Pode-se dizer que o conjunto S é marcado
pelo subconjunto z. A dilatação condicional permite recuperar o conjunto S a partir do
subconjunto z. Esse processo chama-se reconstrução onde a imagem binária Z chamase imagem marcadora ou simplesmente marcador e a imagem binária f de imagem
máscara ou simplesmente máscara.
Sob algumas restrições, [LM84] mostram que a reconstrução binária pode expressarse a partir da dilatação condicional por um elemento estruturante disco unidade da seguinte maneira:
Definição 2.18
A reconstrução binária ρ f (Z) de f a partir do marcador Z,
Z ⊆ f usando o elemento estruturante unidade B é:
ρ f (z) = limn→+∞ δcBf (...δcBf (z))
n
A figura 2.22 ilustra um exemplo de potencialidade da reconstrução binária. A
imagem da figura 2.22-(a) representa a imagem “Page 5” corrompida por ruído intenso. A
eliminação desse ruído exige uma filtragem agressiva ilustrada na figura 2.22-(b), onde
permanecem “resíduos” das letras “Page” e do número “5”. A tentativa de recuperar
“Page 5” por dilatação tradicional só permite obter uma versão aproximada (figura 2.22(c)), onde as letras “Page” e o número “5” aparecem danificados. Empregando a imagem
resultante da filtragem agressiva (figura 2.22-(b)) como marcador e a imagem original
ruidosa (figura 2.22-(a)) como máscara, o processo de reconstrução permite regenerar
perfeitamente “Page 5” conforme aparece na figura 2.22-(d), sem nenhuma distorção.
(a)
(b)
(c)
(d)
Figura 2.22. Filtragem por reconstrução binária: (a) Imagem ruidosa, (b) Eliminação do ruído, (c) Tentativa de recuperação por dilatação tradicional, (d) Reconstrução.
A figura 2.23 ilustra outro exemplo das potencialidades da reconstrução binária. A imagem da figura 2.23-(a) representa a imagem das letras“Sbf” circundadas por
uma margem ruidosa e irregular. Por uma filtragem agressiva, elimina-se as letras“Sbf”e
desgasta-se a margem (figura 2.23-(b)). Por reconstrução dessa margem desgastada empregando a imagem original como máscara, gera-se uma imagem da margem completa
ruidosa e irregular (figura 2.23-(c)). Basta subtraí-la da imagem original para obter as
letras “Sbf” conforme aparecem na (figura 2.23-(d)), sem nenhuma distorção.
89
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(d)
Figura 2.23. Filtragem por reconstrução binária: (a) Imagem com margem ruidosa e irregular, (b) Filtragem inicial, (c) Reconstrução da margem, (d) Obtenção
das letras“Sbf”.
Estes dois exemplos da figura mostram a importância da reconstrução. Enquanto
que filtragens clássicas permitem eliminar padrões indesejáveis porém, deformando os
padrões remanescentes, por reconstrução, é possível eliminar esse problema e recuperar
os padrões exatos.
2.2.10. Última Erosão binária
Seja f uma imagem constituída de subconjuntos conectados. Por erosão de f pelo elemento estruturante nB, na medida que n aumenta, os subconjuntos vão gradativamente diminuir de tamanho, alguns deles vão separar-se dos outros e/ou desaparecer. Guardando
o que resta de cada subconjunto antes da sua remoção definitiva, é possível provar que o
conjunto constituído dos resíduos de cada subconjunto constitue a Última Erosão Últ( f )
de f . Guardar as ”sementes” dos subconjuntos que formam a imagem f pode constituir
um processo interessante quando se quer numerar, reconstruir e identificar as partículas
existentes. Esse processo pode ser realizado a partir da operação de Última Erosão binária, constituída de etapas, umas euclidianas, outras condicionais. Vincent [Vin94] fornece
uma definição da Última Erosão (definição 2.19) levando em consideração o processo de
reconstrução binária ρ introduzido anteriormente.
A reconstrução do subconjunto A1 pelo subconjunto A2 ρA1 (A2 ), onde A2 ⊂ A1 ,
representa a união dos subconjuntos de A1 que tem uma interseção não nula com A2 .
n
Tendo na mente essa abordagem, o conjunto Últ ( f ) da Última Erosão de f , em
relação à nB, expressa-se, em função da reconstrução, da seguinte maneira:
n
Últ (X ) = ε nB ( f )/ρε nB( f ) (ε (n+1)B ( f ))
Definição 2.19
O conjunto Últ(X ) constituído de todas as últimas erosões
do conjunto binário X é definido pela seguinte equação:
n
Últ(X ) = ∪n∈ℵ Últ (X )
= ∪n∈ℵ [ε nB ( f )/ρε nB ( f ) (ε (n+1)B ( f ))]
90
VII Workshop de Visão Computacional – WVC 2011
Figura 2.24. Última Erosão por erosões sucessivas
A figura 2.24 ilustra os resíduos de cada subconjunto para cada etapa da erosão e
o resultado final da Última Erosão com as ”sementes” em vermelho.
Para “descobrir” os resíduos da erosão na iteração n + 1, efetua-se a comparação
entre o resultado da reconstrução da erosão ε (n+1)B e o resultado da erosão ε nB . Caso o resultado dessa comparação for nulo, isto significa que nenhum subconjunto foi descoberto.
Caso contrário, um novo subconjunto é portanto descoberto através de sua semente. Essa
descoberta pode não ser sempre prevista pela análise puramente visual, devido à própria
geometria dos conjuntos. A figura 2.25⎧ilustra o resultado
do processo de Última Ero⎫
. . . . . . .
⎪
⎨ .. •. •• •• •• •. .. ⎪
⎬
são com o elemento estruturantes BR = .. •• •• •• •• •• .. . Pode constatar que as sementes
⎪
⎩. . • • • . .⎪
⎭
. .
. .
. . .
obtidas se encontram bem centralizadas.
Figura 2.25. Última Erosão: exemplo
2.2.11. Granulometria Binária
2.2.11.1. Introdução
A análise de imagens por medição de estruturas (de células, de grãos) é uma tarefa importante. Quando um “tamanho médio” de estrutura existe, uma análise global pode ser
91
VII Workshop de Visão Computacional – WVC 2011
realizada e os processos podem ser facilmente automatizáveis. Porém, o “tamanho médio” de uma estrutura pode não ser suficiente para descrever o conjunto a ser analisado.
Poder estabelecer a distribuição de tamanhos é um meio mais preciso de atingir esse objetivo.
Quando se fala de grandezas a serem medidas, um paralelo pode ser estabelecido
com o processo de peneiramento. Peneirar consiste em separar substâncias reduzidas ao
estado de fragmento, que apresentam vários tamanhos. Efetuar um bom peneiramento depende do tamanho da malha da peneira usada. Após peneirar são obtidos dois conteúdos:
o primeiro com os objetos menores que a malha da peneira deixou passar, o segundo com
o que sobrou do peneiramento, o refugo, de tamanho maior que a malha da peneira não
deixou passar.
Pode se pensar em peneirar várias vezes, com peneiras cujo tamanho da malha
varia. O estudo da distribuição de tamanho em análise de imagens obedece aos mesmos princípios, e o termo usado para descrever essa distribuição é granulometria. A
figura 2.26 ilustra um tipo clássico de imagem que pode ser analisada por processo granulométrico.
Figura 2.26. Exemplo de imagem podendo ser submetida ao processo granulométrico
2.2.11.2. Princípios básicos da granulometria
A análise granulométrica existe e é usada desde tempos antigos, o que explica que a literatura nesse assunto é ampla. Do ponto de visto morfológico, por exemplo [Mat75] propôs
um conjunto de regras que, se forem verificadas, permitem obter uma boa granulometria.
Para isto, existem três axiomas:
Sejam a imagem f a ser analisada e T (λ ) ( f ) a transformação que permite realizar uma análise granulométrica. T (λ ) ( f ) representa exatamente o refugo da peneira de
tamanho λ .
1. A transformação morfológica deve ser anti-extensiva; isso significa que o conjunto
transformado deve ser menor que o de origem ou seja:
∀λ > 0,
T (λ ) ( f ) ⊂ f , ∀ f
92
(25)
VII Workshop de Visão Computacional – WVC 2011
2. A transformação morfológica deve ser crescente, ou seja:
∀λ > 0,
Y ⊂ f =⇒ T (λ ) (Y ) ⊂ T (λ ) ( f ) , ∀ f
(26)
3. O resultado final deve ser idêntico qualquer que seja a seqüência de transformações
empregada. Além disso, o resultado deve idêntico ao obtido pela transformação de
maior parâmetro λ :
∀λ1 , λ2 > 0,
T (λ1 ) (T (λ2 ) ( f )) = T (λ2 ) (T (λ1 ) ( f ))
= T sup(λ1 ,λ2 ) ( f ) , ∀ f
Pode-se verificar que o processo de peneiramento obedece a esses três axiomas.
• No primeiro, porque qualquer conjunto de substâncias peneirado fica menor que o
conjunto inicial;
• No segundo, porque a quantidade de matéria depositada é proporcional à quantidade
analisada;
• No terceiro, porque usar uma peneira grossa e depois uma fina ou uma fina e depois
uma grossa resulta no mesmo peneiramento e porque o resultado fica idêntico a
peneirar com peneira grossa.
É possível constatar que a conseqüência do terceiro axioma é a propriedade de
idempotência:
∀λ > 0, T (λ ) (T (λ ) ( f )) = T (λ ) ( f ) , ∀ f
2.2.11.3. Diferentes tipos de granulometria
Diferentes tipos de granulometria existem da mesma maneira que os diversos parâmetros
granulométricos que os caracterizam.
Granulometrias em número e em medida : Qualquer granulometria pode ser representada:
Em número : consiste em numerar o conteúdo de cada peneiramento e representar
o resultado em função do tamanho da peneira.
Em medida : consiste numa tomada de peso (medida da massa) do conteúdo de
cada peneiramento. Essa massa é representada em função do tamanho da
peneira;
Esses dois tipos de granulometria não têm o mesmo significado. No caso da granulometria em número, a cada partícula é atribuído o mesmo valor qualquer que
seja a sua massa ou o seu tamanho. No caso da granulometria em medida, a cada
partícula é atribuído o valor proporcional a sua massa ou ao seu tamanho. Enquanto
a primeira granulometria faz somente sentido no caso da imagem constituída de
subconjuntos disjuntos, a granulometria em medida não requer esse tipo de restrição
e é mais geral.
93
VII Workshop de Visão Computacional – WVC 2011
Definições do tamanho : O parâmetro λ que é usado nas granulometrias representa sempre um parâmetro de tamanho (comprimento, largura, área, volume). Podem ser
realizadas granulometrias lineares ou bidimensionais. No primeiro caso, qualquer
que seja a imagem f , a sua análise faz-se por interseção com retas e define conjuntos disjuntos. O único parâmetro de tamanho possível é portanto o comprimento da
reta. Esse parâmetro pode ser usado para os conjuntos constituídos de grãos como
para os conjuntos interconectados. Essa reta constitui portanto o elemento estruturante que permite realizar granulometrias lineares pela morfologia matemática.
Em relação às granulometrias bidimensionais, deve ser separado o caso dos conjuntos interconectados do caso dos conjuntos indivisualisáveis. No primeiro caso,
somente a morfologia matemática permite fornecer uma solução. O parâmetro usado é o tamanho do elemento estruturante convexo B. No caso de B ser um disco,
λ representa o raio do maior disco inscrito na partícula. No caso dos conjuntos
indivisualisáveis, uma granulometria no sentido de Matheron [Mat75] envolvendo
um parâmetro relativo a uma componente conexa pode ser definido. Por exemplo o
diâmetro do disco inscrito, a sua área, o seu diâmetro de Féret.
Representação de uma granulometria :
A evolução do número e/ou da massa das partículas é representada por uma função.
Para permitir comparar as granulometrias de dois materiais, por exemplo, é necessário usar funções normalizadas [CC89]. Levando em consideração os axiomas
de Matheron [Mat75], podemos definir uma função de distribuição em número,
Fn ( f , λ ) ou ainda Fn (λ ):
Fn ( λ ) =
N(T (λ ) ( f ))
N( f ) − N(T (λ ) ( f ))
= 1−
N( f )
N( f )
(27)
onde N( f ) representa o número de partículas da população inicial e N(T (λ ) ( f )) o
número de partículas da população que sobrou na peneira.
A partir de Fn (λ ), pode ser definida a densidade de distribuição em número fn (λ ):
d(Fn (λ ))
ou Fn (λ ) =
fn (λ ) =
d(λ )
λ
0
fn (λ )d(λ )
(28)
Da mesma maneira, para a granulometria em medida, pode ser definida uma função
de distribuição em medida, Fm ( f , λ ) ou ainda Fm (λ ):
Fm ( λ ) =
Leb(T (λ ) ( f ))
Leb( f ) − Leb(T (λ ) ( f ))
= 1−
Leb( f )
Leb( f )
(29)
onde Leb() representa a medida de Lebesgue, seja o volume em ℜ3 , a área em ℜ2
e o comprimento em ℜ1 .
94
VII Workshop de Visão Computacional – WVC 2011
A densidade de distribuição em medida fm (λ ) é:
d(Fm (λ ))
ou Fm (λ ) =
fm (λ ) =
d(λ )
λ
0
fm (λ )d(λ )
(30)
Na prática, as imagens usadas são digitais, portanto é preciso adaptar os métodos
empregando granulometrias. Infelizmente, por causa de uma noção apropriada de
convexidade e da impossibilidade de multiplicação por um valor escalar arbitrário,
isso não pode ser feito diretamente. Os seguintes resultados apresentados são aplicáveis no caso de imagens euclidianas e digitais. Representando as distribuições
em medida Fm (λ ) e em número Fn (λ ) pela função Ω(λ ), é possível escrever a sua
derivada discreta, d(Ω(λ ))/ d λ , respectivamente a função densidade em número
fn (λ ) ou a função densidade em medida fm (λ ), da seguinte forma:
d(Ω(λ ))
= Ω(λ + 1) − Ω(λ )
d(λ )
(31)
2.2.11.4. Granulometria por abertura
Por verificar ao mesmo tempo as propriedades de anti-extensividade, crescência e idempotência, a abertura faz parte do conjunto das transformações introduzidas anteriormente
que verifica os três axiomas de [Mat75]. Se desejar usar a abertura como processo granulométrico, tem-se ainda que definir as condições que o elemento estruturante deve verificar e o elemento estruturante deve verificar principalmente o axioma número 27 de
[Mat75] que escreve-se no caso da abertura:
∀λ1 > λ2 > 0
γ (λ1 B) (γ (λ2 B) ( f )) = γ (λ2 B) (γ (λ1 B) ( f )) = γ sup(λ1 B,λ2 B) ( f )
[Ser82] demonstra que essa relação verifica-se somente no caso do elemento estruturante ser convexo.
Definição 2.20 Um conjunto compacto B é convexo se e somente se ∀r > s > 0, rB é
sB-abertura, seja γ sB (rB) = rB.
No espaço ℜ1 , o único elemento estruturante convexo é o segmento de reta. Em ℜ 2 ,
existe uma escolha mais diversificada como por exemplo o círculo, o hexágono, etc..
2.2.11.5. Granulometria por abertura bidimensional
Considerando uma seqüência de elementos estruturantes de tamanho crescente {B i } =
(B1 , B2 , ..., Bk, .., Bi ), onde Bk+1 é Bk -abertura ∀k > 0, aplica-se a abertura da imagem
binária f por Bk . Pela propriedade de anti-extensividade da abertura, pode ser escrito
que:
...γ Bk+1 ( f ) ⊂ γ Bk ( f )... ⊂ γ B2 ( f ) ⊂ γ B1 ( f )
95
VII Workshop de Visão Computacional – WVC 2011
Dessa maneira cria-se uma granulometria por abertura bidimensional onde o parâmetro λ é o raio ou o fator k de crescimento do elemento estruturante. Uma maneira exata
de criar uma seqüência de elementos estruturantes {Bi } é criar a seqüência Bk+1 = δ B (Bk ),
onde Bk+1 é Bk -abertura ∀k > 0. O elemento estruturante B1 é o elemento estruturante
unidade constituído de um pixel B 1 = { • }.
A lei de distribuição usada no caso da granulometria por abertura bidimensional
é geralmente a distribuição em medida (definições 29 e 30), a distribuição em número
é pouco usada nesse caso (equações 27 e 28). A função de distribuição em medida é
portanto:
Fm (k) = 1 −
Á(γ Bk ( f )
(32)
Á( f )
onde Á(I) representa a medida de Lebesgue de I em ℜ2 , seja a área de I. A densidade em
medida fica idêntica (equação 30) e calcula-se segundo a equação 31.
O exemplo teórico 2.5 ilustra um estudo granulométrico por abertura a partir da
seqüência
de elementos estruturantes de tamanho crescente {Bi = i × BQ }, onde BQ =
• • •
• • •
• • •
, lembrando que B1 = { • }. . Na imagem f foram dispersados de forma aleatória
conjuntos de três tamanhos diferentes.
⎡.
⎢
⎢
⎢
⎢
⎢
f =⎢
⎢
⎢
⎢
⎢
⎣
Exemplo 2.5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
•
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
•
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
Por aberturas sucessivas com {Bi }, tem-se os seguintes resultados:
⎡.
⎢
⎢
⎢
⎢
⎢
B1
γ (f) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
•
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
•
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎡.
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ B
⎥ γ 2( f ) = ⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
96
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
VII Workshop de Visão Computacional – WVC 2011
⎡.
⎢
⎢
⎢
⎢
⎢
B3
B4
γ (f) = γ (f) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎡.
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ B
⎥ γ 5( f ) = ⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
É possível constatar que, à medida que
estruturante B k cresce, a ima o elemento
gem f é peneirada pelo processo de abertura γ Bk ( f ) e são geradas imagens onde sobram
os conjuntos ≥ Bk . As respectivas áreas Á() acumuladas dos conjuntos de γ Bk ( f ) são:
• Á(γ B1 ( f )) = 74;
• Á(γ B2 ( f )) = 67;
• Á(γ B3 ( f )) = 49;
• Á(γ B4 ( f )) = 49;
• (∀Bk ≥ B5 ) Á(γ Bk ( f )) = 0.
A partir desses diferentes resultados, são definidas a função de distribuição em
medida, a função de distribuição em medida normalizada e a densidade de distribuição
em medida (figura 2.27) em função do tamanho k do elemento estruturante.
a)
b)
(c)
Figura 2.27. Distribuições em medida do exemplo teórico 2.5 : (a) Distribuição,
(b) Distribuição normalizada Fm (λ ), (c) Densidade normalizada fm (λ ).
É possível interpretar a densidade de distribuição em medida como sendo uma
maneira de descobrir o padrão que foi isolado pelo peneiramento na etapa k, seja ainda
a classificação desse padrão segundo o critério de abertura em função do elemento estruturante escolhido [Vin94]. Essa interpretação é ilustrada a seguir a partir do exemplo
97
VII Workshop de Visão Computacional – WVC 2011
anterior:
⎡.
⎢
⎢
⎢
⎢
⎢
fm (0) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎡.
⎢
⎢
⎢
⎢
⎢
fm (2) = ⎢
⎢
⎢
⎢
⎢
⎣
⎡.
⎢
⎢
⎢
⎢
⎢
fm (4) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎡.
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎥ e fm (1) = ⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎡.
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎥ e fm (3) = ⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎡.
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎥ e ∀k ≥ 5 fm (k) = ⎢
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
A figura 2.28 exemplifica o processo granulométrico por abertura a partir da
seqüência de elementos estruturantes idêntica à do exemplo 2.5. A imagem f foi criada de forma artificial onde os conjuntos tem uma forma quadrada e foram distribuídos
de forma aleatória e de maneira a não sobreporem-se. O processo de peneiramento começa a ser operacional a partir da abertura com B3 (figura 2.28-(b)). Uma segunda classe
de conjunto é peneirada com a abertura usando B4 (figura 2.28-(c)), uma terceira classe
com a abertura usando B7 (figura 2.28-(d)) e finalmente a última classe com a abertura
usando B10 . Donde as distribuições granulométricas, a função de distribuição, a função
de distribuição normalizada e a densidade de distribuição da figura 2.29.
2.2.11.6. Granulometria por abertura e reconstrução
Na realidade, raras são as imagens onde os conjuntos tem formas idênticas e não se sobrepõem. O fato de que conjuntos poderem ter diversas formas, ou seja, a imagem conter
vários padrões e/ou ruído, dificulta o processo de peneiramento. Peneirar, por exemplo,
estruturas redondas e alongadas a partir de uma única seqüência de elementos estruturantes pode resultar em resultados duvidosos. Conjuntos sobrepostos criam o mesmo
98
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(d)
Figura 2.28. Peneiramento por abertura binária: a) imagem original b) Abertura
B3 c) Abertura B4 d) Abertura B7
efeito. Acontece que peneirar pelo processo de abertura da maneira como foi descrito
anteriormente resulta na deformação dos conjuntos restantes. O que resulta em função
e densidade de distribuição incorretas dificultando portanto a interpretação. Várias soluções são possíveis. Uma delas é modificar o processo de peneiramento por abertura
introduzindo o processo de reconstrução binária a partir de marcadores binários. Sabe-se
que após abertura, o conjunto que “sobrevive” existe realmente na peneira. Somente a
sua forma e as suas dimensões foram alteradas. A idéia consiste, portanto, em extrair o
marcador de cada conjunto restante (por exemplo pelo processo de Última Erosão) para
depois reconstruir o verdadeiro conjunto que normalmente deveria aparecer.
Veja o exemplo teórico 2.6, simplesmente uma versão deteriorada do exemplo
teórico 2.5 onde foi adicionado ruído, que vai ilustrar o estudo granulométrico por abertura com inclusão do processo de reconstrução binária. Foi usada a mesmaseqüência
• • •
•
•
•
de elementos estruturantes de tamanho crescente {Bi = i × BQ }, onde BQ = • • • do
exemplo teórico 2.5.
⎡.
Exemplo 2.6
⎢
⎢
⎢
⎢
⎢
X =⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
•
•
•
•
.
.
.
.
.
•
•
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
•
.
.
.
•
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
•
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
•
•
.
.
•
•
.
.
.
.
.
.
•
.
•
.
.
•
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
A primeira abertura fornece um resultado sem nenhuma ambigüidade, e a sua área
é Á(γ B1 ( f )) = 83:
⎡. . . . . . . . . . . . . .⎤
. .
•
.
.
.
.
.
.
.
.
.
•
•
. •
. •
. .
⎢ ..
⎢.
⎢.
⎢.
⎢.
B1
γ (f) = ⎢
⎢ ..
⎢.
⎢.
⎢.
⎣.
.
.
.
•
•
.
.
.
.
.
.
.
•
•
•
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
•
•
•
•
•
•
•
.
•
.
.
.
•
.
.
99
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
•
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
.
.
•
•
.
.
.
.
.
•
.
•
.
.
•
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.29. Distribuições em medida do exemplo 2.28 : (a) Distribuição, (b)
Distribuição normalizada Fm (λ ), (c) Densidade normalizada fm (λ ).
100
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(d)
(e)
(f)
Figura 2.30. Etapas de peneiramento por abertura binária com reconstrução
Já a segunda abertura fornece um resultado distorcido:
⎡.
⎢
⎢
⎢
⎢
⎢
B2
γ (f) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
Os conjuntos peneirados não têm a mesma forma que os conjuntos correspondentes
na imagem original. O que gera como conseqüência a modificação das distribuições.
Como já visto anteriormente, uma maneira de restituir os conjuntos iniciais consiste em
efetuar uma reconstrução de f . Uma primeira idéia excelente é reconstruir a partir da
extração de marcadores de (γ B2 ( f )) gerados pelo processo de Última Erosão. Porém é
possível acelerar o processo usando (γ B2 ( f )) como sendo a própria imagem de marcadores. Isso é possível pela propriedade de anti-extensividade da abertura ((γ B2 ( f )) ⊂ f ).
101
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.31. Distribuições em medida do exemplo 2.28 : (a) Distribuição, (b)
Distribuição normalizada Fm (λ ), (c) Densidade normalizada fm (λ ).
102
VII Workshop de Visão Computacional – WVC 2011
Portanto, a reconstrução de f a partir de (γ B2 ( f )) é:
⎡. . . . . .
⎢
⎢
⎢
⎢
⎢
B2
ρ f (Últ(γ ( f )) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
.
.
.
.
•
•
.
.
.
.
.
.
.
•
•
•
.
.
•
•
•
•
•
•
•
.
.
.
.
•
•
•
.
.
•
•
•
•
•
•
•
.
.
.
.
.
•
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
•
•
•
•
•
•
•
.
•
•
•
.
.
.
.
.
.
.
.
.
.
.
•
•
.
.
•
•
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
Pelo processo de reconstrução, é possível corrigir as deformações introduzidas
pela abertura. O algoritmo de peneiramento é portanto perfeito. No caso do peneiramento
perfeito de f por B2 , a área é Á(ρX (Últ(γ B2 ( f ))) = 76. Reiterando esse processo para
cada etapa de abertura, tem-se:
⎡. . . . . . . . . . . . . .⎤
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
. .
.
.
.
•
•
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎢ ..
⎢.
⎢.
⎢.
⎢.
B3
B4
ρ f (Últ(γ ( f )) = ρ f (Últ(γ ( f )) = ⎢
⎢ ..
⎢.
⎢.
⎢.
⎣.
⎡.
⎢
⎢
⎢
⎢
⎢
B5
ρ f (Últ(γ ( f )) = ⎢
⎢
⎢
⎢
⎢
⎣
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
⎤
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
•
•
•
•
•
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
•
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
As respectivas áreas Á() acumuladas, que permitem definir as distribuições em
medida ilustradas na figura 2.32, são:
• Á(γ B1 ( f )) = 83;
• Á(ρX (Últ(γ B2 ( f ))) = 76;
• Á(ρ f (Últ(γ B3 ( f ))) = 54;
• Á(ρ f (Últ(γ B4 ( f ))) = 54;
• (∀Bk ≥ B5 ) Á(ρ f (Últ(γ Bk ( f ))) = 0.
A figura 2.30 ilustra um exemplo real de processo granulométrico por abertura
com reconstrução binária, e a figura 2.31, as funções de distribuição e a densidade de
distribuição decorrentes.
103
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.32. Distribuições em medida do exemplo teórico 2.6 : (a) Distribuição,
(b) Distribuição normalizada Fm (λ ), (c) Densidade normalizada fm (λ ).
104
VII Workshop de Visão Computacional – WVC 2011
2.2.11.7. Granulometria por fechamento ou anti-granulometria
Da mesma maneira que foi definida uma granulometria, é possível definir uma granulometria por fechamento ou anti-granulometria T (λ ) ( f ) a transformação que verifica os
dois últimos axiomas de [Mat75] e verifica a propriedade de extensividade:
∀λ1 ≥ λ2 > 0, T (λ1 ) ( f ) ≥ T (λ2 ) ( f )) ∀ f
(33)
Uma transformação verificando essas três axiomas é o fechamento. Uma granulometria por fechamento analisa uma imagem f em relação a uma família de fechamento
e é estritamente equivalente por, dualidade, a uma análise granulométrica por abertura do
complementário de f , seja f c . Uma tal granulometria pode ser usada por exemplo para
analisar conjuntos contendo furos.
2.3. OPERADORES DA MORFOLOGIA MATEMÁTICA EM NIVEIS DE
CINZA
2.3.1. Considerações matemáticas
Seja E um conjunto qualquer e P(E) o conjunto dos subconjuntos de P. Um sinal euclidiano é uma função f (x) definida num certo domínio D[ f (x)] que pode ser real ou inteiro
por exemplo. Considerando uma função de uma variável f (x) positiva, o que é o caso de
imagens em níveis de cinza, é possível definir operações de translação. Uma translação
horizontal à direita de valor z, ou “shift”, do sinal f (x) pode ser definida como:
fz (x) = f (x − z)
(34)
Da mesma maneira, uma translação vertical do sinal f (x) de valor y, chamada
também de “offset”, pode ser definida como:
( f + y)(x) = f (x) + y
(35)
Aplicando as duas operações, obtém-se uma translação morfológica, como:
( f + y)z (x) = f (x − z) + y
(36)
Precisa-se também definir uma noção de ordem entre as imagens. Sejam f (x)
e g(x) dois sinais com domínios respectivos D[ f ] e D[g], g(x) é declarado como sendo
abaixo de f (x), escrito como g << f , se:
• o domínio D[g] é um sub-conjunto do domínio D[ f ],
• ∀x ∈ D[g], g(x) < f (x).
Como em morfologia binária, onde a intersecção e a união têm um papel importante, da mesma forma, em morfologia em níveis de cinza, duas funções equivalentes, o
máximo e o mínimo (figura 2.33) têm um papel fundamental.
105
VII Workshop de Visão Computacional – WVC 2011
Figura 2.33. Exemplo de operações Máximo e Mínimo
O mínimo de duas funções f (x) e g(x), notado f ∧ g, pode ser definido da seguinte
forma:
Definição 2.21
Se x pertence à intersecção de f (x) e de g(x), x pertence
então à D[ f ] ∩ D[g], portanto:
( f ∧ g)(x) = Min{ f (x), g(x)}
(37)
Da mesma maneira, o máximo de duas funções f (x) e g(x), notado f ∨ g, pode ser
definido em termos de união da seguinte forma:
Definição 2.22
D[g], então:
Se x pertence à união de f (x) e de g(x), x pertence à D[ f ] ∪
( f ∨ g)(x) = Max{ f (x), g(x)}
(38)
Em morfologia em níveis de cinza, existe mais uma operação básica de reflexo que
corresponde à rotação de um conjunto em relação à origem. Se f (x) é um sinal definido
no seu domínio D[ f ], o transposto de f (x) em relação à origem é:
f˜(x) = − f (−x)
(39)
2.3.2. Erosão e Dilatação em níveis de cinza
Serão apresentados aqui os dois operadores básicos que constituem os pilares da Morfologia Matemática em níveis de cinza, a erosão e a dilatação.
2.3.2.1. Erosão em níveis de cinza com elementos estruturantes 3D
[Ser82] (página 443) mostrou que é possível relacionar a erosão com a extensão da subtração de Minkowski extendida para funções:
106
VII Workshop de Visão Computacional – WVC 2011
A erosão de um sinal f por um elemento estruturante 3D g
Definição 2.23
é:
ε g ( f )(x) = ∧{ f (y) − g(x − y) : y ∈ E}
onde a erosão não é definida num ponto onde o elemento estruturante não está abaixo do
sinal f . No caso de imagens digitais, os sinais são definidos sobre inteiros e tomam os
valores de nível de cinza, na maioria dos casos entre 0 e 255 (8 bits).
A figura 2.34 ilustra o princípio da interação do elemento estruturante g em níveis
de cinza sobre o sinal f (rampa) no caso de uma erosão em níveis de cinza. O ponto
escolhido para a exemplificação é x = 2. Nesse ponto, são efetuadas todas as operações
f (y) − g(x − y) para os pontos relevantes y do elemento estruturante g. É possível constatar que o elemento estruturante g é centrado no ponto 2 em estudo (2 − y = 0 para y = 2)
(figura 2.34-b)). O cálculo f (y) + g(2 − y) deve ser efetuado três vezes para os pontos
relevantes de g que são y = 1, y = 2 e y = 3. Os resultados são respectivamente 1 − 1 = 0,
2 − 1 = 1 e 3 − 1 = 2. Portanto o resultado da erosão no ponto 2 é Min{0, 1, 2} = 0.
Os resultados da erosão de f por g são (figura 2.34-c)): ε g ( f (0)) < 0, ε g ( f (1)) < 0,
ε g ( f (2)) = 0, ε g ( f (3)) = 1, ε g ( f (4)) = 2, ε g ( f (5)) = 1, ε g ( f (6)) = 0, ε g ( f (7)) < 0,
ε g ( f (8)) < 0.
Figura 2.34. Exemplo teórico de erosão em níveis de cinza
Uma imagem, de forma geral, apresenta um fundo que pode ser ou não é uniforme
e onde sobrepõem-se padrões mais claros e/ou escuros. É possível comparar este imagem
a um relevo topográfico onde os padrões claros são picos e os padrões escuros são vales. Tendo esta analogia em mente, é possível estabelecer padrões de comportamento da
erosão.
Os efeitos da erosão em níveis de cinza são:
• Escurecer a imagem
107
VII Workshop de Visão Computacional – WVC 2011
• Alargar e engordar os vales (padrões mais escuros)
• Conectar vales próximos
• Reduzir e as vezes eliminar picos (padrões mais claros)
• Separar picos próximos.
2.3.2.2. Erosão em níveis de cinza com elementos estruturantes 2D
A definição anterior leva em consideração elementos estruturantes 3D em níveis de cinza.
Muitas vezes esses elementos estruturantes são funções analiticamente bem definidas
como um disco, uma meia-esfera etc.. O uso desses tipos de elementos estruturantes
permite processos poderosos mas que dependem muito da escolha analítica da função de
representação.
Outra definição mais simples e muito empregada consiste em não mais usar elementos estruturantes 3D mas sim 2D ou planares. Esta nova definição usando elementos
estruturantes 2D é:
Definição 2.24
planar g é:
A erosão de um sinal f por um elemento estruturante 2D
ε g ( f )(x) = ∧{ f (y) : y ∈ D[g]}
Nos exemplos que servirão para ilustrar os processos morfológicas en níveis de
cinza, serão usados elementos estruturantes 2D.
A figura 2.35 ilustra efeitos da erosão em uma imagem poluída por ruído. A
erosão com o elemento estruturante BC tem como efeito de remover o ruído mais claro
mas tem com inconveniente de reforçar o ruído mais escuro.
A figura 2.36 ilustra os efeitos acima citados a partir de uma imagem erodida
pelos elementos estruturantes nBQ com n = 1 e n = 3. Percebe-se que, na medida que n
aumenta, gradativamente a imagem vem escurecendo, os vales aumentam, as partes claras
diminuem. O que resulta na disparição das letras e detalhes mais claros e no reforço das
letras e detalhes mais escuros.
2.3.2.3. Dilatação em níveis de cinza com elementos estruturantes 3D
A dilatação de um sinal f por um elemento estruturante g pode ser definida, como no caso
da morfologia binária, como a operação dual da erosão em níveis de cinza. Na prática, a
dilatação em níveis de cinza de f por g consiste em verificar se o elemento estruturante
centrado em x está acima da função f . [Ser82] (página 443) mostrou que é possível
relacionar a dilatação com a extensão da adição de Minkowski extendida para funções:
108
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
Figura 2.35. Exemplo de erosão de uma imagem ruidosa: (a) Image Original, (b)
Com o elemento estruturante BC .
(a)
(b)
(c)
Figura 2.36. Exemplos de erosão: (a) Image Original, (b) Com o elemento estruturante BQ , (c) Com o elemento estruturante 3 × B Q .
109
VII Workshop de Visão Computacional – WVC 2011
A dilatação de um sinal f por um elemento estruturante 3D
Definição 2.25
g é:
δ g ( f (x)) = ∨{ f (y) + g(x − y) : y ∈ E}
A figura 2.37 ilustra o princípio da interação do elemento estruturante g em níveis de cinza sobre o sinal f no caso de uma dilatação em níveis de cinza. O ponto
escolhido para a exemplificação no sinal f é x = 2. Nesse ponto, são efetuadas todas as
operações f (y) + g(x − y) para os pontos relevantes y do elemento estruturante g (figura
2.37-b)). É possível constatar que o elemento estruturante g é centrado no ponto 2 em
estudo (2 − y = 0 para y = 2). O cálculo f (y) + g(2 − y) deve ser efetuado três vezes,
para y = 1, y = 2 e y = 3. Os resultados são respectivamente 1 + 1 = 2, 2 + 1 = 3 e
3 + 1 = 4. Portanto o resultado da dilatação no ponto 2 é Max{2, 3, 4} = 4. Os resultados
da dilatação de f por g são (figura 2.37-c)): δ g ( f (0)) = 2, δ g ( f (1)) = 3, δ g ( f (2)) = 4,
δ g ( f (3)) = 5, δ g ( f (4)) = 5, δ g ( f (5)) = 5, δ g ( f (6)) = 4, δ g ( f (7)) = 3, δ g ( f (8)) = 2.
Figura 2.37. Exemplo teórico de dilatação em níveis de cinza
Tendo ainda em mente a analogia da imagem em níveis de cinza com o relevo
topográfico onde os padrões claros são picos e os padrões escuros são vales, é possível
determinar padrões de comportamento da dilatação. Os efeitos da dilatação em níveis
de cinza são:
• Clarear a imagem
• Alargar e engordar os picos (padrões mais claros)
• Conectar picos próximos
• Reduzir e as vezes eliminar vales (padrões mais escuros)
• Separar vales próximos.
110
VII Workshop de Visão Computacional – WVC 2011
2.3.2.4. Dilatação em níveis de cinza com elementos estruturantes 2D
Outra definição mais simples e muito empregada usando elementos 2D ou planares é:
A dilatação de um sinal f por um elemento estruturante 2D
Definição 2.26
planar g é:
δ g ( f (x)) = ∨{ f (y) : y ∈ D[g]}
Nos exemplos que servirão para ilustrar os processos morfológicas en níveis de
cinza, serão usados elementos estruturantes 2D.
A figura 2.38 ilustra efeitos da dilatação em uma imagem poluída por ruído. A
dilatação com o elemento estruturante BC tem como efeito de remover o ruído mais escuro
mas tem com inconveniente de reforçar o ruído mais claro.
(a)
(b)
Figura 2.38. Exemplo de dilatação de uma imagem ruidosa: (a) Image Original,
(b) Com o elemento estruturante BC .
A figura 2.39 ilustra os efeitos acima citados a partir de uma imagem dilatada
pelos elementos estruturantes nBQ com n = 1 e n = 3. É possível perceber que, na medida
que n aumenta, gradativamente a imagem vem clareando, os vales diminuem, as partes
claras aumentam. O que resulta na disparição das letras e detalhes mais escuros e no
reforço das letras e detalhes mais claros.
2.3.2.5. Propriedades da Erosão e da Dilatação em níveis de cinza
Vale a pena esclarecer que a erosão e a dilatação são duais.
Propriedade 2.13 Enquanto a erosão é uma transformação não comutativa, a dilatação
é comutativa:
111
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.39. Exemplos de dilatação: (a) Image Original, (b) Com o elemento estruturante BQ , (c) Com o elemento estruturante 3 × B Q.
112
VII Workshop de Visão Computacional – WVC 2011
ε g( f ) =
ε f (g)
δ g ( f ) = δ f (g)
(40)
Propriedade 2.14 A erosão e a dilatação em níveis de cinza por um ponto reduzem-se a
uma translação. Portanto a dilatação e a erosão são invariantes pela translação.
ε x ( f ) = δ x ( f ) = fx
(41)
Propriedade 2.15 A erosão e a dilatação em níveis de cinza têm propriedades interessantes em relação às operações de mínimo e de máximo:
δ g∨g ( f ) = δ g ( f ) ∨ δ g ( f )
(42)
Pelo uso da dualidade que existe entre a erosão e a dilatação, tem-se:
ε g∨g ( f ) = ε g ( f ) ∧ ε g ( f )
(43)
ε g ( f ∧ h) = ε g ( f ) ∧ ε g (h)
(44)
e
Propriedade 2.16 A erosão e a dilatação em níveis de cinza têm duas propriedades relativas à repetição que são interessantes.
A primeira é:
A segunda é:
g (g̃)
δ g (g̃)
ε g (ε g ( f )) = ε δ
δ g (δ g ( f )) = δ
(f)
(f)
(45)
(46)
Essas propriedades são fundamentais porque mostram que erosões e dilatações com elementos estruturantes grandes podem ser decompostas em seqüências de erosões e dilatações com elementos estruturantes menores. Essa propriedade é particularmente interessante para elementos estruturantes convexos. O que explica que, novamente, os elementos
estruturantes mais usados são simples, como B H , BV , BC .
Propriedade 2.17 A erosão e a dilatação em níveis de cinza são operações crescentes.
f ≤ f =⇒ ε g ( f ) ≤ ε g ( f )
=⇒ δ g ( f ) ≤ δ g ( f )
(47)
E pela dualidade:
g ≤ g =⇒ ε g ( f ) ≤ ε g ( f )
=⇒ δ g ( f ) ≤ δ g ( f )
113
(48)
VII Workshop de Visão Computacional – WVC 2011
Propriedade 2.18 Enquanto que a erosão é uma operação anti-extensiva, a dilatação é
uma operação extensiva.
ε g( f ) ≤ f ≤ δ g( f )
(49)
Propriedade 2.19 As erosão e dilatação são transformações contínuas.
2.3.3. Deteção de bordas em níveis de cinza: Gradiente Morfológico
A informação do gradiente é muito usada no processamento de imagens para detectar
bordas. De forma geral, a informação gradiente é uma versão digital da informação diferencial. Supondo o sinal f diferenciável no seu domínio, é possível mostrar [Sch67] que
a derivada de f segundo a coordenada h na direção α na Borda é:
δf
δf
(50)
(x) = ( )(x) + σ cos Θ − αδx (Borda)
δh
δh
onde a função (δ f /δ h) representa a derivada do termo contínuo, σ o salto no ponto
x ∈ Borda, o angulo θ representa a reta perpendicular à Borda no ponto x orientada no
sentido positivo do salto, e δ x (Borda) é o pulso de Dirac no ponto x.
A definição do gradiente de f no ponto x é o vetor (δ f /δ x), (δ f /δ y) associada à
função diferencial d f :
δf
δf
dx +
dy
(51)
df =
δx
δy
[Beu77] propôs uma avaliação do gradiente morfológico a partir de erosões e dilatações em níveis de cinza efetuadas com disco de raio unitário (ver figura 2.40):
Grad(x) = limλ →0
δ λ g( f ) − ε λ g( f )
2λ
(52)
Na morfologia matemática, existem várias implementações digitais do gradiente
e três delas serão aqui apresentadas.
• Gradiente Morfológico por erosão em níveis de cinza:
Definição 2.27
O gradiente morfológico Grad gε de uma imagem f por
um elemento estruturante g a partir da erosão é:
g
Gradε ( f ) = f − ε g ( f )
O processo de Gradiente por erosão em níveis de cinza detecta bordas nas
posições dos níveis de cinza mais elevados das bordas.
• Gradiente Morfológico por dilatação em níveis de cinza:
114
VII Workshop de Visão Computacional – WVC 2011
Figura 2.40. Exemplo teórico do gradiente morfológico
g
Definição 2.28
O gradiente morfológico Grad δ de uma imagem f
pelo elemento estruturante g a partir da dilatação é:
g
Gradδ ( f ) = δ g ( f ) − f
O Gradiente por dilatação em níveis de cinza detecta bordas nas posições dos
níveis de cinza mais baixos das bordas.
• Gradiente Morfológico por dilatação e erosão em níveis de cinza
Definição 2.29
O gradiente morfológico Grad gεδ de uma imagem f
pelo elemento estruturante g a partir da erosão e da dilatação é:
Gradgεδ ( f ) = δ g ( f ) − ε g ( f )
A figura 2.41 exemplifica o processo de gradiente morfológico por dilatação e
erosão em níveis de cinza Gradiente a partir do elemento estruturante BC .
2.3.4. Abertura e fechamento em níveis de cinza
As propriedades de iteratividade da erosão e da dilatação em níveis de cinza permitem
novas operações.
115
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
Figura 2.41. Exemplo de gradiente morfológico por dilatação e erosão: (a) Image
Original, (b) Com o elemento estruturante BC .
2.3.4.1. Abertura em níveis de cinza
Uma dessas, chamada de “abertura em níveis de cinza” consiste em erodir uma imagem
f por um elemento estruturante g e depois dilatar essa imagem erodida pelo mesmo elemento estruturante g. Como em morfologia binária, a operação morfológica de abertura
em níveis de cinza é definida, inicialmente a partir das operações de Minkowski estendidas para funções ([Ser82] página 444), da seguinte maneira:
Definição 2.30
por definição
A abertura de uma imagem f pelo elemento estruturante g é
γ g ( f ) = δ g (ε g̃ ( f ))
onde g̃ representa o transposto de g obtido por simetria central
pela origem {o} do sistema de referência
Depois da aplicação de uma abertura em níveis de cinza, de forma geral, a
preservação dos conjuntos iniciais é muito rara. Seguindo a analogia da imagem em
níveis de cinza com o relevo topográfico, o comportamento da abertura é:
• Separar picos próximos;
• Eliminar picos inferiores em tamanho ao elemento estruturante;
• Conservar vales afastados;
• Juntar vales próximos;
• Deixar a imagem resultante mais regular que a imagem original;
• Deixar a imagem resultante menos rica em detalhes que a imagem original.
116
VII Workshop de Visão Computacional – WVC 2011
2.3.4.2. Fechamento em níveis de cinza
Outro novo operador dual da operação de abertura em níveis de cinza, chamada de “fechamento em níveis de cinza” , φ , pode ser definida como segue ([Ser82] página 444):
Definição 2.31
g é:
O fechamento φ de um sinal f por um elemento estruturante
φ g ( f ) = ε g (δ g̃ ( f ))
onde B̃ representa o transposto de B obtido por simetria central
pela origem {o} do sistema de referência
Depois de aplicar um fechamento em níveis de cinza, de forma geral, a preservação dos conjuntos iniciais é muito rara. Seguindo a analogia da imagem em níveis de
cinza com o relevo topográfico, o comportamento do fechamento é:
• Juntar picos próximos;
• Eliminar vales inferiores em tamanho ao elemento estruturante;
• Conservar picos afastados;
• Separar vales próximos;
• Deixar a imagem resultante mais regular que a imagem original;
• Deixar a imagem resultante menos rica em detalhes que a imagem original.
A partir das propriedades de iteratividade e de dualidade das erosão e dilatação, é
possível filtrar reduzindo o impacto às características geométricas dos conjuntos processados. Veja a figura 2.42 ilustrando tais propriedades retomando os exemplos das figuras
2.35 e 2.38. Na figura 2.35, foi visto que a erosão permite remover o ruído mais claro
porém reforçando o ruído mais escuro (ver na figura 2.42-(b)). E que, conforme ilustrado
na figura 2.38, a dilatação permite remover o ruído mais escuro porém reforçando o ruído
mais claro (ver na figura 2.42-(e)). Em cada caso, pelas propriedades de iteratividade e
de dualidade respectivas das dilatação e erosão, é possível, por abertura e fechamento,
reestabelecer a geometria dos conjuntos filtrados. O que é ilustrado nas figuras 2.42-(c)
e 2.42-(f). Mas percebe-se que o ruído que tinha sido reforçado anteriormente permanece. E que só pode ser completamente eliminado pelos processos duais com elementos
estruturantes maiores que os usados anteriormente. A figura 2.42-(d) ilustra os efeitos de
aplicar um fechamento com elemento estruturante 2 × BC após ter aplicado uma abertura
com elemento estruturante BC . E de forma análoga, a figura 2.42-(g) ilustra os efeitos de
aplicar uma abertura com elemento estruturante 2 × BC após ter aplicado um fechamento
com elemento estruturante BC . Permitindo a remoção completa do ruído com menos impactos nos conjuntos filtrados.
117
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Figura 2.42. Benefícios da abertura e do fechamento: (a) Imagem Original ruidosa, (b) Erosão com BC , (c) Abertura com BC , (d) Abertura com BC seguida de
Fechamento com 2 × BC , (e) Dilatação com BC , (f) Fechamento com BC , (g) Fechamento com BC seguida de Abertura com 2 × BC .
118
VII Workshop de Visão Computacional – WVC 2011
2.3.5. Filtros produtos e alternados seqüenciais
Pelas propriedades de crescência, de idempotência, de extensividade e de anti-extensividade, a abertura e o fechamento constituem filtros de grande importância. Estes filtros
não representam os únicos filtros com estas propriedades mas constituem uma boa base.
É possível pensar em associar a busca do máximo e do mínimo entre uma imagem, a imagem aberta ou fechada e combinar de forma seqüencial a abertura e o fechamento. E ver
até que ponto a combinação desses dois operadores conservem essas quatro propriedades.
2.3.5.1. Produto de aberturas e de fechamentos
Definição 2.32
A partir da abertura γ e do fechamento φ , podem ser definidos quatro operadores, γφ , φ γ , φ γφ e γφ γ :
γφ g ( f )
φ γ g( f )
φ γφ g ( f )
γφ γ g ( f )
=
=
=
=
γ g (φ g ( f ))
φ g (γ g ( f ))
φ g (γ g ((φ g ( f )))
γ g (φ g (γ g ( f )))
Esses operadores, que são essencialmente filtros, ordenam-se como segue:
φ ≥ φ γφ ≥
γφ
≥ γφ γ ≥ φ γ ≥ γ
φγ
É possível constatar que os filtros produtos γφ e φ γ não são ordenados entre eles.
É possível também constatar que, devida à propriedade de idempotência (φ γφ γ = φ γ e
γφ γφ = γφ ) esses filtros são os únicos a poderem ser realizados desta maneira. É possível
ainda acrescentar que, caso o usuário não for satisfeito com os resultados desses produtos
de aberturas ou de fechamentos, a única possibilidade consiste em mudar o tamanho ou a
forma do elemento estruturante empregado.
Esses filtros compostos são muito usados, particularmente antes de qualquer operação que aumenta o ruído da imagem, como por exemplo o gradiente. A figura 2.43
ilustra o efeito dos filtros produtos φ γφ e γφ γ , a partir do elemento estruturante g = B Q
sobre uma mesma imagem. O uso do produto γφ γ g teve como conseqüência de reduzir as
regiões claras para reforçar as regiões escuras (figura 2.43-(b)). Enquanto que empregar
o produto φ γφ g teve com efeito limpar o fundo reforçando de certa maneira o contraste
entre o fundo e as regiões escuras (figura 2.43-(c)). Ambos os filtros produtos φ γφ e γφ γ
homogeneizaram as partes internas dos objetos.
2.3.5.2. Filtros alternados seqüenciais
A partir de uma abertura, é possível definir uma família de aberturas de parâmetro λ da
seguinte maneira:
γ (λ ) ( f ) = γ (λ g) ( f ) = γ (λ )g (γ (λ −1)g (...γ g( f )))
119
(53)
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
Figura 2.43. Exemplos de filtros produtos: (a) Imagem original, (b) Filtro γφ γ , (c)
Filtro φ γφ .
Uma tal família tem a seguinte propriedade:
∀ f , λ ≥ μ =⇒ γ (λ ) ( f ) ≤ γ (μ ) ( f )
Da mesma maneira, é possível definir uma família de fechamentos de parâmetro
λ da seguinte maneira:
φ (λ ) ( f ) = φ (λ g) ( f ) = φ (λ )g (φ (λ −1)g (...φ g( f )))
(54)
É possível verificar que uma família de fechamento verifica a seguinte propriedade:
γφ (i)
∀ f , λ ≤ μ =⇒ φ (λ ) ( f ) ≥ φ (μ ) ( f )
A geração dessas duas famílias permite definir dois filtros alternados seqüenciais
e φ γ (i) .
Definição 2.33
O filtro alternado seqüencial γφ (i) é:
γφ (i) ( f ) = γ (i) (φ (i) [γ (i−1) (φ (i−1) [.. ..γ (1) (φ (1) ( f )).. ..])])
e
Definição 2.34
O filtro alternado seqüencial φ γ (i) é:
φ γ (i) ( f ) = φ (i) (γ (i) [φ (i−1) (γ (i−1) [.. ..φ (1) (γ (1) ( f )).. ..])])
O mecanismo de filtragem é aqui mais complexo e também mais poderoso. A
primeira iteração com o elemento estruturante unidade φ (1) no filtro alternado seqüencial
120
VII Workshop de Visão Computacional – WVC 2011
γφ (i) (respectivamente γ (1) no filtro alternado seqüencial φ γ (i) ) consiste em eliminar o
ruído pequeno. Usar imediatamente o processo dual γ (1) (respectivamente φ (1) no filtro
alternado seqüencial φ γ (i) ) deve permitir recuperar a informação prejudicada pelo primeiro processo. Caso for necessário, pode eliminar mais ruído usar portanto um elemento
estruturante maior. Donde as outras etapas γ (i) e φ (i) .
A figura 2.44 ilustra o efeito dos filtros alternados seqüenciais φ γ (2) e γφ (2) , a
partir do elemento estruturante g = BC sobre a mesma imagem da figura 2.43-(a). No
caso do filtro alternado seqüencial φ γ (2) , o ruído claro no fundo e nos objetos é eliminado
e conjuntos pequenos escuros integram-se nas regiões escuras (figura 2.44-(b)). Tudo isto
realçando o contraste entre estas regiões e dando mais importância às regiões escuras. O
filtro alternado seqüencial γφ (2) , como é de se esperar, tem o efeito dual (figura 2.44-(c)).
Elimina o ruído escuro no fundo e nos objetos e integra conjuntos pequenos claros nas
regiões claras. Tudo isto realçando novamente o contraste entre estas regiões e dando
mais importância às regiões claras.
(a)
(b)
(c)
Figura 2.44. Exemplos de filtros alternados seqüenciais: (a) Imagem original, (b)
Filtro φ γ (2) , (c) Filtro γφ (2) .
Constata-se, através dos exemplos anteriores que esses filtros tem como particularidade suavizar a imagem. Os filtros produtos e alternados seqüenciais têm a fama de
constituir os melhores "limpadores de ruído"dentro dos filtros morfológicos existentes.
Uma maneira de ilustrar esse fato é aplicar um filtro passa-alta de tipo operador de gradiente. A figura 2.45 ilustra os efeitos do gradiente morfológico por dilatação e erosão
(página 55) respectivamente sobre a imagem da figura 2.45-(a) e sobre a imagem filtrada
pelos filtros produto φ γφ (figura 2.45-(c)) e alternado seqüencial φ γ (figura 2.45-(d)),
respectivamente. Percebe-se a aparição de menos altas freqüências (menos bordas) indesejáveis.
Empregar filtros alternados seqüenciais supõe uma certa estacionaridade espacial
das imagens a serem tratadas, o que não é sempre verificado. Na prática, o uso de tais
filtros faz-se por uso heurístico dos elementos estruturantes sobre as imagens. [Net95]
propôs uma versão adaptativa desses filtros onde o elemento estruturante é definido em
função do aspecto local das imagens, que [Net95] chamou de filtros alternados seqüenciais adaptativos.
121
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(c)
Figura 2.45. Gradiente da imagem original versus Gradiente das imagens filtradas: a) Imagem original, (b) Gradiente da imagem original, (c) Gradiente após o
filtro produto φ γφ , (d) Gradiente após o filtro alternado seqüencial φ γ .
122
VII Workshop de Visão Computacional – WVC 2011
2.3.6. Transformação TOPHAT
É comum na área de Processamento e Análise de imagens ter que extrair conjuntos de
geometria complexa num universo ruidoso e/ou em imagens com fundos heterogêneos.
Técnicas tradicionais de segmentação como a detecção de bordas ou a limiarização, de
forma geral, têm dificuldades para recuperar a informação relevante e ao mesmo tempo
eliminar a heterogeneidade do fundo e o ruído. Veja o exemplo da figura 2.46 onde
nenhuma técnica de limiarização é capaz de lidar com a heterogeneidade do fundo para
obter uma imagem satisfatória dos caracteres manuscritos.
Como lidar com a heterogeneidade do fundo e a presença de ruído? Serão apresentadas a seguir ferramentas que respondem muito bem a essa necessidade.
(a)
(b)
Figura 2.46. Exemplo de imagem com fundo heterogêneo: (a) Imagem Original,
(b) Segmentação por limiarização.
2.3.6.1. Tophat por abertura
No caso de detecção de estruturas mais claras que o fundo (picos), um modo de pensar
consiste em usar uma combinação entre uma imagem original e a imagem correspondente
g
aberta. A transformação Tophat por abertura Tophat γ segue esse princípio.
Definição 2.35
mento estruturante g é:
g
O Tophat por abertura Tophat γ de uma imagem f pelo ele-
g
Tophatγ = f − γ g ( f )
Como a abertura é um processo anti-extensivo, o seu resultado fica abaixo do sinal
original, portanto a transformação Tophatγg é sempre positiva. A figura 2.47 ilustra os
aspectos teóricos deste processo.
O exemplo da figura 2.48 ilustra a extração do brilho em gotas em uma imagem
apresentando um fundo heterogêneo por Tophat por abertura. Com o uso de um elemento
123
VII Workshop de Visão Computacional – WVC 2011
Figura 2.47. Exemplo teórico da transformação Tophat por abertura
estruturante adequado (figura 2.48-(c)), o processo de abertura permite a eliminação de
estruturas mais claras que o fundo (picos) preservando o fundo heterogêneo. Realizar
a diferença entre as imagens original e aberta permite tirar o ruído e eliminar o fundo
heterogêneo, assim ressaltando as estruturas mais claras que tinham sido eliminadas após
a abertura. O exemplo da figura 2.48-(e)) ilustra bem a extração de caracteres manuscritos
após limiarização do Tophat.
2.3.6.2. Tophat por fechamento
De forma análoga, a detecção de estruturas mais escuras que o fundo (vales) consiste em
usar uma combinação entre uma imagem original e a imagem correspondente fechada. A
g
transformação Tophat por fechamento Tophatφ segue esse princípio.
Definição 2.36
elemento estruturante g é:
O Tophat por fechamento Tophatφg de uma imagem f pelo
g
Tophatφ = φ g ( f ) − f
Como o fechamento é um processo extensivo, o seu resultado da transformação
g
Tophatφ é sempre positiva. A figura 2.49 ilustra os aspectos teóricos deste processo.
O exemplo da figura 2.50 ilustra a extração de caracteres manuscritos em uma
imagem apresentando um fundo heterogêneo com uso do Tophat por fechamento. O
processo de fechamento permite, com o uso de um elemento estruturante adequado (figura 2.50-(c)), a eliminação de estruturas mais escuras que o fundo (vales) preservando o
124
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(d)
(e)
Figura 2.48. Exemplo de segmentação por Tophat: (a) Imagem Original, (b) Imagem erodida, (c) Imagem abertura, (d) Tophat por abertura, (e) Extração do brilho
em gotas após limiarização do Tophat.
125
VII Workshop de Visão Computacional – WVC 2011
Figura 2.49. Exemplo teórico da transformação Tophat por fechamento
fundo heterogêneo. Realizar a diferença entre as imagens original e fechada permite tirar
o ruído e eliminar o fundo heterogêneo, assim ressaltando as estruturas mais escuras que
tinham sido eliminadas após o fechamento. O exemplo da figura 2.50-(e) ilustra bem a
extração de caracteres manuscritos após limiarização do Tophat.
126
VII Workshop de Visão Computacional – WVC 2011
(a)
(b)
(c)
(d)
(e)
Figura 2.50. Exemplo de segmentação por Tophat: (a) Imagem Original, (b) Imagem dilatada, (c) Imagem fechada, (d) Tophat por fechamento, (e) Extração dos
caracteres manuscritos após limiarização do Tophat.
127
VII Workshop de Visão Computacional – WVC 2011
Referências
[BB94] G.J.F Banon and J. Barrera. Bases da Morfologia Matemática para a Análise
de Imagens Binárias. IX Escola de Computação, Recife, 1994.
[Beu77] S. Beucher. Random process simulation on the texture analyser. Lecture Notes
in Biomathematics, 23, 1977.
[CC89] M. Coster and J.L Chermant. Précis D’ Analyse D’ Images. Presses du CNRS,
1989.
[Dou92] E. R. Dougherty. An Introduction to Morphological Image Processing, volume
TT9. SPIE Press, 1992.
[Had50] H. Hadwiger. Minkowskische addition und subtraktion beleibiger punktmengen
und die theoreme von erhard schmidt. Math.Zeitschrift, 53(3):210–218, 1950.
[Had57] H. Hadwiger. Vorlesungen uber inhalt, oberfläche und isoperimetrie. Springer
Verlag, Berlin, 1957.
[LM84] C. Lantuéjoul and F. Maisonneuve. Geodesic methods in quantitative image
analysis. Pattern Recognition, 17:177–187, 1984.
[Mat75] G. Matheron. Random Sets and Integral Geometry. J. Wiley, New York, 1975.
[Min03] H. Minkowski. Volumem und oberflache. Math. Annalen, 57:447–495, 1903.
[Net95] U.D.M.B. Neto. Adaptative alternating sequencial filters. SIGRAPI-95, VIII
Simpósio Brasileiro de Computação Gráfica e Processamento de Imagens, pages 35–42, Outubro 1995.
[Pré93] F. Préteux. Mathematical Morphology in Image Processing, chapter On a Distance Function Approach for Gray-Level Mathematical Morphology. E. Dougerthy, Rochester Institute of Technology, New York, 1993.
[Sch67] L. Schwartz. Mathematics for Physical Sciences. Hermann, Paris, 1967.
[Ser82] J. Serra. Image Analysis and Mathematical Morphology. Academic Press, London, 1982.
[Vin91] L. Vincent. Exact euclidean distance function by chain propagation. Proc.
Computer Vision and Pattern Recognition Conf. Hawaii, pages 520–525, Junho
1991.
[Vin94] L. Vincent. Digital Image Processing Methods, chapter Morphological Segmentation. E. Dougerthy, Rochester Institute of Technology, New York, 1994.
128