ESTUDO DA EVOLUÇÃO TERMOMECÂNICA DA BACIA DO PARNAÍBA
Regina Freitas Fernandes
Dissertação
de
Mestrado
apresentada
ao
Programa de Pós-graduação em Engenharia
Civil, COPPE, da Universidade Federal do Rio
de
Janeiro,
como
parte
dos
requisitos
necessários à obtenção do título de Mestre em
Engenharia Civil.
Orientador: Luiz Landau
Rio de Janeiro
Outubro de 2011
ESTUDO DA EVOLUÇÃO TERMOMECÂNICA DA BACIA DO PARNAÍBA
Regina Freitas Fernandes
DISSERTAÇÃO SUBMETIDA AO CORPO DOCENTE DO INSTITUTO ALBERTO
LUIZ COIMBRA DE PÓS-GRADUAÇÃO E PESQUISA DE ENGENHARIA (COPPE)
DA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO COMO PARTE DOS
REQUISITOS NECESSÁRIOS PARA A OBTENÇÃO DO GRAU DE MESTRE EM
CIÊNCIAS EM ENGENHARIA CIVIL.
Examinada por:
________________________________________________
Prof. Luiz Landau, D.Sc.
________________________________________________
Prof. Fernando Pellon de Miranda, D.Sc.
________________________________________________
Dr. Luiz Felipe Carvalho Coutinho, D.Sc.
RIO DE JANEIRO, RJ - BRASIL
OUTUBRO DE 2011
ii
Fernandes, Regina Freitas
Estudo da evolução termomecânica da Bacia do
Parnaíba/ Regina Freitas Fernandes. – Rio de Janeiro:
UFRJ/COPPE, 2011.
XIV, 102 p.: il.; 29,7 cm.
Orientador: Luiz Landau
Dissertação (mestrado) – UFRJ/ COPPE/ Programa de
Engenharia Civil, 2011.
Referências Bibliográficas: p. 96-102.
1. Bacia do Parnaíba. 2. Avaliação termomecânica. 3.
Maturação térmica. I. Landau, Luiz. II. Universidade Federal
do Rio de Janeiro, COPPE, Programa de Engenharia Civil.
III. Título.
iii
"...E não há melhor resposta
que o espetáculo da vida:
vê-la desfiar seu fio,
que também se chama vida,
ver a fábrica que ela mesma,
teimosamente, se fabrica,
vê-la brotar como há pouco
em nova vida explodida;
mesmo quando é assim pequena
a explosão, como a ocorrida;
mesmo quando é uma explosão
como a de há pouco, franzina;
mesmo quando é a explosão
de uma vida severina.”
(Morte e Vida Severina,
João Cabral de Melo Neto)
iv
Para meu querido Eduardo
v
Agradecimentos
Agradeço ao professor Luiz Landau e aos professores do Programa pela oportunidade
e aprendizado a mim oferecidos.
À professora Jaci Maria Bernardo da Silva Guigon, que me acompanhou neste
trabalho com competência e dedicação. Agradeço-a também pelo apoio em todos os
momentos, inclusive na difícil e necessária decisão de mudar de área. E, pela
paciência com que lidou com minha falta de tempo.
À EPE – Empresa de Pesquisa Energética, por permitir e liberar para a realização
deste trabalho, mais especificamente, agradeço, ao Diretor Elson Ronaldo Nunes e ao
Reneu Rodrigues Silva, além de toda a equipe de E&P da qual me orgulho de fazer
parte.
Aos geólogos Norival Brisola e Sergio Martins de Souza pelo companheirismo, pelos
ensinamentos, e pelo incentivo para a realização (e conclusão!) deste trabalho, e
claro, por nossos prazerosos almoços. Ao Sergio, agradeço também pela revisão do
meu texto.
Aos colegas da equipe de E&P da EPE, pelas contribuições para esta dissertação.
Ao meu querido Eduardo, pela paciência e companhia nos finais de semana que estive
na Universidade.
À minha querida irmã Raquel, com quem pude compartilhar tudo, em todo momento,
pelo seu incentivo e positivismo (“...ela me faz tão bem, que eu também quero fazer
isso por ela...”).
As minhas amigas da EPE, Angela de Oliveira Costa, Rachel Martins Henriques e
Adriana Queiroz Ramos, com quem sempre pude contar. Elas que me receberam com
tanta prontidão nesta cidade, que agora, também é minha. À Rachel agradeço também
pela ajuda com o índice.
Aos meus amigos: Alessandra Brito, Cleide Rejane A. dos Santos, Daniele Abdiel,
Débora F. Pereira, Janaina Trindade, Jefferson Acioli, Kelly Stanicch, Rodrigo Teixeira,
Wanderley Oliveira, de quem tenho sentido muita falta nestes tempos, pelos passos
que deram comigo, sempre avançando junto, cada um a seu modo e a seu tempo.
Muito obrigada a todos!
vi
Resumo da Dissertação apresentada à COPPE/UFRJ como parte dos requisitos
necessários para a obtenção do grau de Mestre em Ciências (M.Sc.)
ESTUDO DA EVOLUÇÃO TERMOMECÂNICA DA BACIA DO PARNAÍBA
Regina Freitas Fernandes
Outubro/2011
Orientadores: Luiz Landau
Programa: Engenharia Civil
A Bacia do Parnaíba situada na região nordeste brasileira, possui uma área de
aproximadamente 675.000 km² e, apesar do fomento exploratório ocorrido nos últimos
anos, é considerada pouco explorada. Possui características inerentes a uma bacia
paleozoica, com uma longa história evolutiva, marcada por discordâncias expressivas
e com uma cunha sedimentar relativamente rasa se comparada às bacias cretáceas
brasileiras, o que levanta controvérsia a respeito da suficiência do soterramento para
a eficiência de geração.
Contudo, ocorrem na bacia rochas vulcânicas básicas
intrusivas e extrusivas, eotriássicas e eocretáceas, que representam um aspecto
importante na evolução térmica. O efeito térmico destas intrusões seria responsável
pelo acréscimo de calor necessário à maturação da matéria orgânica e consequente
geração de hidrocarbonetos. Este trabalho contribui com a reconstrução da história
térmica desta bacia a partir da modelagem das variáveis termais e da história de
soterramento. Para isso, foram utilizados modelos consagrados na literatura, que
permitem, de forma simples, a estimativa do fluxo térmico do embasamento.
Na
análise da influência de intrusões ígneas na estrutura térmica da bacia, o modelo
bidimensional desenvolvido pelo método de diferenças finitas se mostrou apropriado.
Utilizou-se o fluxo térmico basal calculado nas condições de contorno da modelagem
da influência térmica das ígneas. Como resultado obteve-se a estruturação térmica da
bacia e a maturação de suas rochas geradoras.
vii
Abstract of Dissertation presented to COPPE/UFRJ as a partial fulfillment of the
requirements for the degree of Master of Science (M.Sc.)
STUDY OF THE PARNAÍBA BASIN THERMOMECHANICAL EVOLUTION
Regina Freitas Fernandes
October/2011
Advisors: Luiz Landau
Department: Civil Engineering
The Parnaiba Basin located in the Northeast of Brazil has an area nearly to 675.000
km² and despite of the intense exploring activities in the latest years, it is considered an
exploration frontier. It has inherent features to a Paleozoic basin, with a long evolution
history marked by significant unconformities and a sedimentary wedge that is relatively
shallow if it is compared to the Brazilian Cretacics basins. This raises controversy
regarding to the burial sufficiency for its hydrocarbon generation. However, there are
intrusive and extrusive basic volcanic rocks in the eotriassics and eocretaceous basin,
what represent an important factor in the thermal evolution. The thermal effect of these
intrusions would be responsible for the heating increase required for organic matter
maturation and following hydrocarbons generation. This study contributes to the
Parnaiba Basin thermal history reconstruction from the thermal variables modeling and
burial history. For this were used models established in the literature. They allow a
heat flow estimation from the basement. In the analysis of igneous intrusions influence
on the basin thermal structure the two-dimensional model using finite difference
method was proved to be suitable. The basal heat flow calculated was used in the
boundary conditions of the igneous rocks thermal effects modeling. As outcome, were
obtained the basin thermal structure and the source rocks maturation.
viii
Sumário
1.
2.
Introdução.............................................................................................................. 1
1.1
Motivação e objetivos ..................................................................................... 2
1.2
Desenvolvimento do trabalho ......................................................................... 3
Caracterização da Bacia do Parnaíba.................................................................... 5
2.1
Localização..................................................................................................... 5
2.2
Geologia Regional .......................................................................................... 7
2.2.1
Arcabouço estratigráfico .......................................................................... 7
2.2.2
Rochas magmáticas .............................................................................. 12
2.2.3
Arcabouço Estrutural ............................................................................. 13
2.3
Evolução tectônica da Bacia do Parnaíba ..................................................... 15
2.4
Sistemas Petrolíferos.................................................................................... 16
2.5
Histórico exploratório .................................................................................... 20
3.
Intrusões ígneas em rochas sedimentares: um problema físico-geológico........... 24
4.
Fundamentos físicos envolvidos na transferência de calor em bacias ................. 28
4.1
Mecanismos de condução de calor............................................................... 28
4.2
Lei de Fourier e a equação de difusão de calor ............................................ 29
4.3
Parâmetros físicos usados em modelagem térmica ...................................... 33
5. Modelos termomecânicos que descrevem a estruturação térmica de bacias
sedimentares .............................................................................................................. 37
5.1
Modelos de extensão litosférica .................................................................... 37
5.1.1
Modelo de extensão uniforme................................................................ 38
5.1.2
Modelo de extensão não-uniforme......................................................... 42
5.1.3
Modelo de reconstrução geológica da profundidade do embasamento:
técnica de backstripping ...................................................................................... 45
6.
Metodologia Aplicada .......................................................................................... 47
6.1
Introdução .................................................................................................... 47
ix
6.2
Base de dados e informações ...................................................................... 48
6.2.1
Construção do bloco 3D para extração das seções geológicas ............. 48
6.2.2
Estratigrafia ........................................................................................... 55
6.2.3
Unidades litológicas, composição litológica, porosidade e constante de
decaimento .......................................................................................................... 55
6.2.4
Massa específica e propriedades termais .............................................. 60
6.2.5
Dados geotérmicos ................................................................................ 60
6.2.6
Dados de Maturação ............................................................................. 62
6.3
Modelagem térmica por contato intrusivo ..................................................... 63
6.3.1
Modelo bidimensional para análise da influência de intrusões ígneas ... 63
6.3.2
Ambiente de desenvolvimento ............................................................... 65
6.4
Reconstrução do embasamento (história térmica da bacia).......................... 66
6.5
Modelagem da maturação da matéria orgânica ............................................ 66
6.5.1
7.
Método Easy%Ro .................................................................................. 67
Modelagem da estrutura térmica da Bacia do Parnaíba ....................................... 70
7.1
Calibração do modelo ................................................................................... 70
7.2
Modelagem termomecânica .......................................................................... 76
7.2.1
Reconstrução sedimentar ...................................................................... 78
7.3
Subsidência termal ....................................................................................... 82
7.4
Fluxo térmico ................................................................................................ 86
7.5
Estruturação térmica da Bacia do Parnaíba considerando fluxo térmico basal
e de intrusões ígneas .............................................................................................. 87
7.6
Maturação térmica ........................................................................................ 90
8.
Conclusões .......................................................................................................... 94
9.
Referências Bibliográficas ................................................................................... 96
x
Lista de Figuras
Figura 2-1: Localização da Bacia do Parnaíba. ............................................................. 5
Figura 2-2: Divisão da Bacia Parnaíba em quatro sítios deposicionais distintos ........... 6
Figura 2-3: Carta estratigráfica da Bacia do Parnaíba (veja próxima página). ............. 10
Figura 2-4: Mapa com os principais lineamentos e feições estruturais da Bacia do
Parnaíba. .................................................................................................................... 14
Figura 2-5: Principais ocorrências de hidrocarbonetos na Bacia do Parnaíba. ............ 17
Figura 2-6: Carta de eventos do sistema Tianguá-Ipu (.). ........................................... 18
Figura 2-7: Carta de eventos do sistema Pimenteiras-Cabeças (!). ............................ 19
Figura 2-8: Seção sísmica que passa pelo poço 2-CP-1-MA, localizado na região de
Capinzal...................................................................................................................... 22
Figura 2-9: Esforço exploratório na Bacia do Parnaíba. .............................................. 23
Figura 3-1: Diagrama de ilustração do mecanismo de intrusão de uma soleira de
diabásio. ..................................................................................................................... 25
Figura 3-2: Modelos de intrusão de soleiras. .............................................................. 26
Figura 4-1: Mecanismos de transferência de calor. ..................................................... 29
Figura 4-2: Volume de controle infinitesimal, para a análise da condução de calor ..... 31
Figura 5-1: Modelo de Extensão Uniforme de MCKENZIE (1978)............................... 40
Figura 5-2: Modelo de duas camadas de ROYDEN & KEEN (1980) ........................... 43
Figura 6-1: Resumo da metodologia aplicada. ............................................................ 48
Figura 6-2: Domínio do bloco 3D ................................................................................ 49
Figura 6-3: Bloco 3D da Bacia do Parnaíba ................................................................ 51
Figura 6-4: Bloco 3D e os poços, em corte. ................................................................ 52
Figura 6-5: Comparação entre seção sísmica que passa pelo poço 2-CP-1-MA com a
seção extraída do bloco 3D da Bacia do Parnaíba. .................................................... 53
Figura 6-6: Seções, em planta, sobre o bloco 3D da Bacia do Parnaíba..................... 54
Figura 6-7: Seção N-CP-SW. ...................................................................................... 56
Figura 6-8: Seção W-CP-E. ........................................................................................ 57
xi
Figura 6-9: Seção NE-CP-SE. .................................................................................... 58
Figura 6-10: Gráfico de porosidade versus permeabilidade vertical ............................ 59
Figura 6-11: Gradientes geotérmicos da Bacia do Parnaíba. ...................................... 62
Figura 6-12: Dados de carbono orgânico e reflectância de vitrinita do poço 2-CP-1-MA
................................................................................................................................... 63
Figura 6-13: Exemplificação da malha aplicada na seção N-CP-SW .......................... 65
Figura 6-14: Diagrama com a evolução térmica da matéria orgânica.......................... 67
Figura 7-1: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas
nas camadas da seção N-CP-SW............................................................................... 71
Figura 7-2: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas
nas camadas da seção W-CP-E. ................................................................................ 72
Figura 7-3: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas
nas camadas da seção NE-CP-SE. ............................................................................ 73
Figura 7-4: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas
no poço 2-CP-1-MA. ................................................................................................... 73
Figura 7-5: Efeito da maturação térmica através do modelo Easy%Ro após o evento
de intrusão ígnea. ....................................................................................................... 74
Figura 7-6: Comparação dos índices de reflectância da vitrinita com dados reais
obtidos de RODRIGUES (1995). ................................................................................ 75
Figura 7-7: Localização dos sete poços utilizados na determinação da história
termomecânica da Bacia do Parnaíba. ....................................................................... 77
Figura 7-8: Curvas de subsidência tectônica e total do embasamento do poço 2-CP-1MA que corta as seções N-CP-SW, W-CP-E e NE-CP-SE. ........................................ 79
Figura 7-9: Curvas de subsidência tectônica e total do embasamento do poço 9-PAF3-MA ........................................................................................................................... 79
Figura 7-10: Curvas de subsidência tectônica e total do embasamento do poço 1-TM1-MA que corta as seções N-CP-SW. ......................................................................... 80
Figura 7-11: Curvas de subsidência tectônica e total do embasamento do poço 1-IZ-2MA que corta a seção W-CP-E. .................................................................................. 80
Figura 7-12: Curvas de subsidência tectônica e total do embasamento do poço 1-MA1-PI que corta as seções W-CP-E. ............................................................................. 81
Figura 7-13: Curvas de subsidência tectônica e total do embasamento do poço 2BGST-1-MAque corta a seção NE-CP-SE. ................................................................. 81
xii
Figura 7-14: Curvas de subsidência tectônica e total do embasamento do poço 2VGST-1-MA que corta a seção NE-CP-SE. ................................................................ 82
Figura 7-15: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 2-CP-1-MA. ................................................ 83
Figura 7-16: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 9-PAF-3-MA. .............................................. 84
Figura 7-17: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 1-TM-1-MA. ................................................ 84
Figura 7-18: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 1-IZ-2-MA. .................................................. 84
Figura 7-19: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 1-MA-1-PI................................................... 85
Figura 7-20: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 2-VGST-1-MA. ........................................... 85
Figura 7-21: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 2-BGST-1-MA. ........................................... 85
Figura 7-22: Variação temporal do fluxo térmico nos poços que cortam as seções .... 86
Figura 7-23: Efeito térmico das intrusões ígneas e maturação térmica na seção N-CPSW.............................................................................................................................. 89
Figura 7-24: Efeito térmico das intrusões ígneas e maturação térmica na seção W-CPE. ................................................................................................................................ 89
Figura 7-25: Efeito térmico das intrusões ígneas e maturação térmica na seção NECP-SE. ....................................................................................................................... 90
Figura 7-26: Perfil de maturação térmica para o poço 2-CP-1-MA na seção N-CP-SW.
................................................................................................................................... 91
Figura 7-27: Perfil de maturação térmica para o poço 2-CP-1-MA na seção W-CP-E. 92
Figura 7-28: Perfil de maturação térmica para o poço 2-CP-1-MA na seção NE-CP-SE.
................................................................................................................................... 92
Figura 7-29: Comparação dos índices de reflectância da vitrinita com dados reais
obtidos de RODRIGUES (1995). ................................................................................ 93
xiii
Lista de Tabelas
Tabela 6-1 – Poços da Bacia do Parnaíba utilizados na construção do Bloco 3D ....... 50
Tabela 6-2: Unidades litológicas e idades geocronológicas das seções modeladas.
Tempo em milhões de anos (M.a.).............................................................................. 55
Tabela 6-3: Composição litológica, porosidade (Φ), e constante de decaimento (c) para
cada unidade litoestratigráfica. ................................................................................... 60
Tabela 6-4: Parâmetros físicos usados no modelo, aplicados à Bacia do Parnaíba por
unidade litológica. ....................................................................................................... 61
Tabela 6-5: Malha utilizada nas seções geológicas. ................................................... 64
Tabela 7-1: Valores dos parâmetros utilizados na aplicação dos modelos.................. 77
Tabela 7-2: Valores dos graus de estiramento para δ e β ........................................... 83
Tabela 7-3: Fluxo térmico calculado para os sete poços ............................................. 88
Tabela 7-4: Temperatura no embasamento para os poços que cortam as seções. .... 88
xiv
1. Introdução
Alguns estudos foram realizados na Bacia do Parnaíba acerca da maturação térmica
das potenciais rochas geradoras. De fato, estas rochas apresentam diferentes níveis
de maturação térmica (Rodrigues, 1995). Entretanto, poucos estudos abordam de
forma contundente a história da evolução térmica desta bacia. Desta forma, a
evolução termomecânica e as implicações na estruturação térmica ainda carecem de
estudos mais conclusivos.
A Bacia do Parnaíba, por características inerentes a uma bacia paleozoica, com uma
longa história evolutiva, marcada por discordâncias expressivas e com uma cunha
sedimentar relativamente rasa se comparada às cretáceas brasileiras, apresenta
controvérsia a respeito da suficiência do soterramento para a geração de
hidrocarbonetos.
Contudo, ocorrem na bacia rochas vulcânicas básicas intrusivas
(diques e soleiras) e extrusivas, associadas à eventos magmáticos do Eotriássico e
Eocretáceo, que representam um aspecto importante na sua evolução térmica. O
efeito térmico destas intrusões seria responsável pelo acréscimo de calor necessário à
maturação da matéria orgânica e consequente potencial de geração de petróleo.
Vários autores avaliaram o efeito termal que as intrusões ígneas básicas produzem
nas bacias paleozoicas brasileiras (RODRIGUES, 1995, ALVES & RODRIGUES 1985,
BENDER, 2001). Conforme sugerido por THOMAS FILHO et al. (2007), considerando
que nestas bacias ocorrem boas rochas geradoras de hidrocarbonetos no Devoniano e
no Permiano, pode-se prognosticar que quantidades de petróleo podem ter sido
geradas pela ação dos corpos ígneos intrusivos.
O exemplo de sucesso nas bacias paleozoicas brasileiras que consolida a eficácia de
sistemas petrolíferos não convencionais, cuja maturação se dá pelo efeito térmico de
intrusões, é o da Bacia do Solimões. Além da expressiva produção de 34,8 mil barris
de petróleo por dia (em junho de 2011), tal bacia possui a terceira maior produção de
gás natural do país, com cerca de 11,8 milhões de metros cúbicos diários (ANP,
2011).
Na década de oitenta, quando o mecanismo de geração não-convencional de petróleo
pela ação direta do calor dos corpos intrusivos ainda não era adequadamente
equacionado, as atividades exploratórias da bacia foram estagnadas. Hoje, técnicas e
1
ferramentas modernas de aquisição e interpretação de dados aliadas ao estudo de
sistemas petrolíferos, incluindo os não convencionais, abrem novas oportunidades
exploratórias.
Segundo GÓES & FEIJÓ (1994), os efeitos térmicos devido ao calor gerado pelas
intrusões, somados aos efeitos naturais de soterramento causaram a maturação dos
principais níveis geradores na Bacia do Parnaíba. Baseado nessa assertiva, este
trabalho propõe um estudo que contribua com a reconstrução da história térmica desta
bacia a partir da modelagem das variáveis termais associadas ao magmatismo e à
história de soterramento.
Desde a década de 1970, diversos modelos foram formulados objetivando quantificar
os processos de subsidência e fluxo térmico em bacias sedimentares. Os modelos
termomecânicos de MCKENZIE (1978) e ROYDEN & KEEN (1980) são amplamente
usados e resultam, de forma simples, em uma estimativa aproximada do fluxo térmico
ao nível do embasamento. Já para a análise da influência de intrusões ígneas na
estrutura térmica da bacia, o modelo de VASCONCELOS (2010) mostra-se
apropriado, uma vez que foi elaborado e aplicado em função de uma bacia similar.
Soma-se a isto o fato dos inputs necessários não serem influenciados pela baixa
disponibilidade de dados, viabilizando a modelagem.
1.1
Motivação e objetivos
A analogia com as outras bacias paleozoicas brasileiras, produtoras ou portadoras de
acumulações importantes, o esforço exploratório atualmente realizado nos blocos
exploratórios com descobertas potenciais e a convicção de que sistemas petrolíferos
não convencionais contribuem com novas oportunidades exploratórias na Bacia do
Parnaíba constituem o conjunto de fatores motivacionais que sustentam o tema desta
dissertação.
Com isso, a motivação principal deste trabalho é contribuir com a reconstrução da
evolução térmica da Bacia do Parnaíba através da modelagem da história térmica
devido ao afinamento da litosfera e ao efeito térmico devido às intrusões ígneas. E a
partir
da resultante deste estudo,
avaliar
a possibilidade de
geração de
hidrocarbonetos, através dos resultados dos indicadores de maturação.
2
Os dados disponíveis ainda são restritos para as dimensões da Bacia do Parnaíba
dificultando o desenvolvimento de modelos que busquem entender a sua estruturação
térmica regional. Contudo, procurou-se aplicar uma metodologia que se adaptasse aos
dados públicos disponíveis na literatura.
Com base nas motivações acima, foram listados os principais objetivos desta
dissertação:
1) elaborar seções geológicas da Bacia do Parnaíba para a aplicação da
modelagem térmica e da reconstrução sedimentar;
2) calcular a estrutura térmica da bacia:
a. com base na história térmica do soterramento; utilizando a técnica de
backstripping, bem como os modelos de extensão litosférica de
MCKENZIE (1978) e ROYDEN & KEEN (1980);
b. com base no efeito térmico das intrusões ígneas: empregando o modelo
numérico bidimensional de VASCONCELOS (2010).
3) avaliar a geração de petróleo na bacia, utilizando o modelo Easy%Ro para a
determinação teórica dos índices de reflectância da vitrinita e consequente
delimitação das janelas de geração de óleo e gás.
1.2
Desenvolvimento do trabalho
Primeiramente, foi feita uma caracterização geológica da Bacia do Parnaíba. Intrusões
ígneas ocorridas nesta bacia podem ter contribuído com a evolução térmica e ter
estabelecido uma influência importante na maturação da matéria orgânica,
consequentemente, na geração de hidrocarbonetos, similar ao que ocorre nas bacias
paleozoicas amazônicas. Para entendimento do efeito térmico de intrusões ígneas
sobre as rochas geradoras da Bacia do Parnaíba, buscou-se encadear atividades que
integrassem uma sequência metodológica. Essa sequência é composta por três
etapas principais: construção das seções geológicas; cálculo da estrutura térmica da
bacia; e avaliação da maturação da matéria orgânica.
A primeira etapa foi destinada à construção de seções geológicas mais próximas da
realidade, que suportassem a modelagem do efeito térmico devido às intrusões.
Foram correlacionados dados de 31 poços perfurados na bacia pela Petrobras até
1986 (CUNHA,
1986, GÓES et
al.,
1994). Os
dados
dos poços foram
georreferenciados e integrados no Temis, um software convencional para modelagem
3
de sistemas petrolíferos desenvolvido pelo Instituto Francês do Petróleo (IFP). No
Temis foi gerado um bloco 3D, a partir do qual foram extraídas as seções utilizadas na
modelagem.
A segunda etapa tratou da modelagem térmica em 2D, relacionando a estrutura
térmica ao fluxo térmico basal e ao efeito térmico devido a intrusões ígneas comuns na
bacia. Na modelagem do fluxo térmico basal e da história térmica devido ao
estiramento litosférico foram utilizados os modelos de MCKENZIE (1978) e ROYDEN
& KEEN (1980) e a técnica de backstripping (STECKLER & WATTS, 1978). Na
modelagem para avaliação do efeito térmico devido às intrusões, foi utilizado o modelo
numérico bidimensional implementado por VASCONCELOS (2010). Neste modelo, o
tratamento físico da condução de calor, em uma bacia sedimentar influenciada por
intrusões ígneas, é resolvido pelo Método das Diferenças Finitas (MDF), mais
especificamente a classe de Método de Direções Alternadas (ADI).
A terceira etapa, uma vez conhecida a estrutura térmica, refere-se à determinação dos
índices de maturação do querogênio e consecutiva determinação das janelas de
geração de óleo e gás. Neste trabalho, a modelagem da maturidade térmica foi
baseada no modelo Easy%Ro desenvolvido por SWEENEY & BURNHAM (1990).
4
2. Caracterização da Bacia do Parnaíba
2.1
Localização
A Bacia do Parnaíba ocupa uma área de 675.000 km², no nordeste brasileiro,
recobrindo os estados do Piauí, Maranhão, Tocantins, Pará, Ceará e Bahia. Está
situada geograficamente entre os paralelos 2º00” e 12º00”S e meridianos 41º00” e
50º00”W (Figura 2-1). Encontra-se posicionada entre as faixas de dobramentos que
bordejam os crátons do Guaporé, São Luís e São Francisco (GÓES et al., 1990). Está
limitada geologicamente a norte pelo arco Ferrer–Urbano Santos, que a separa das
bacias de São Luís e Barreirinhas na margem continental; a sul, pelo arco do Médio
São Francisco, separando-a da bacia Sanfranciscana; a noroeste, pelo arco de
Tocantins, que a separa da bacia de Marajó (SILVA et al., 2003).
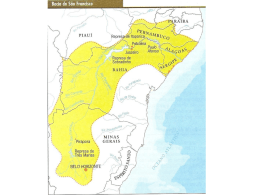
Figura 2-1: Localização da Bacia do Parnaíba.
Fonte: Elaboração própria, a partir de dados da ANP/BDEP (2011).
5
A espessura sedimentar alcança cerca de 3.000 m, com uma coluna sedimentar
constituída, em sua maior parte, por rochas de idade ordoviciana a cretácea, com
delgada cobertura terciária e quaternária (ZEMBRUSCKI & CAMPOS, 1988).
A Bacia do Parnaíba, em sua extensa área de ocorrência apresenta uma evolução
tectono-sedimentar complexa. Por conseguinte, é subdividida por alguns autores em
sub-bacias com as características geológicas e tectônicas de determinados sítios
deposicionais. SILVA et al. (2003) denominaram a região de Província Parnaíba, que
segundo
esses
autores,
é
caracterizada
por
uma
evolução
policíclica,
compartimentada em bacias com gêneses, estilos tectônicos, preenchimento
sedimentar e idades distintas, o que corroborou a divisão em quatro sub-bacias: Bacia
do Parnaíba propriamente dita, Bacia das Alpercatas, Bacia do Grajaú e Bacia do
Espigão-Mestre (Figura 2-2).
Figura 2-2: Divisão da Bacia Parnaíba em quatro sítios deposicionais distintos: Bacia do
Parnaíba, Bacia das Alpercatas, Bacia do Grajaú e Bacia do Espigão-Mestre.
Fonte: SILVA et al. (2003).
6
Neste trabalho, com perspectivas regionais, a Província é tratada como uma única
entidade sedimentar.
2.2
Geologia Regional
2.2.1 Arcabouço estratigráfico
O embasamento da Bacia do Parnaíba é constituído de rochas metamórficas, ígneas e
sedimentares, cujas idades abrangem um longo intervalo do Arqueano ao Ordoviciano,
Contudo,
possivelmente,
há
predominância
de
rochas
neoproterozóicas
e
eopaleozoicas, que correspondem ao tempo de consolidação da Plataforma SulAmericana (VAZ et al., 2007). As unidades que compõem o embasamento são a
Formação Riachão e o Grupo Jaibaras constituídas por rochas sedimentares
continentais que preenchem estruturas grabenformes.
Para VAZ et al. (2007), movimentos eustáticos do nível do mar são os principais
responsáveis pelas discordâncias entre as sequências, uma vez que a eustasia
controla os ciclos transgressivos-regressivos. A proposta estratigráfica destes autores
sugere uma relação de cinco supersequências deposicionais que seguem do período
Siluriano até o Cretáceo (Figura 2-3):
1. Sequência
completo.
Siluriana
Está
–
compreende
depositada
sobre
um
ciclo
rochas
transgressivo-regressivo
proterozóicas.
A
unidade
litoestratigráfica correlaciona-se ao Grupo Serra Grande (formações Ipu,
Tianguá, Jaicós). A Formação Ipu é composta por arenitos com seixos e
conglomerados com matriz argilosa, que caracterizam grande variedade de
ambientes deposicionais de glacial a fluvial e leques deltaicos (CAPUTO, 1984
in VAZ et al., 2007). Na Formação Tianguá prevalecem os folhelhos cinza
escuros bioturbados depositados em ambiente de plataforma rasa (GÓES, et
al., 1990). Esta unidade representa a superfície de inundação máxima,
enquanto que a Formação Jaicós é o intervalo regressivo dessa sequência. Na
Formação Jaicós predominam os arenitos grossos, mal selecionados, com
pelitos subordinados, depositados em sistema fluvial entrelaçado. Para GÓES
et al. (1990), o término da sedimentação do Serra Grande é marcada pela
Orogenia Caledoniana;
7
2. Sequência Mesodevoniana-Eocarbonífera – a unidade litoestratigráfica
correspondente
é
composta
pelo
Grupo
Canindé
(formações
Itaim,
Pimenteiras, Cabeças, Longá e Poti). A Formação Itaim é constituída por
arenitos finos a médios, com intercalações de folhelhos bioturbados
depositados em ambientes deltaicos e plataformais. Nesta sequência se
destaca a Formação Pimenteiras, composta por folhelhos escuros ricos em
matéria orgânica, que representam a transgressão marinha mais importante
da bacia (VAZ et al., 2007). Na Formação Cabeças predominam os arenitos
depositados em ambiente plataformal sob influência de correntes decorrentes
de processos de marés. Esses arenitos são considerados reservatórios
potenciais da Bacia do Parnaíba. A Formação Longá consiste de folhelhos
escuros, por vezes laminados e bioturbados, de ambiente plataformal
dominado por tempestade (GÓES & FEIJÓ, 1994). Segundo estes autores a
Formação Poti é composta por arenitos esbranquiçados, com lâminas de siltito
subordinadas, associados a deltas e a planícies de maré. O encerramento do
ciclo deposicional do Grupo Canindé é marcado por uma notável discordância
regional associada por GÓES et al. (1990), GÓES & FEIJÓ, (1994) e VAZ et
al. (2007) à Orogenia EoHerciniana. Após a deposição dos sedimentos do
Grupo Canindé, a Bacia do Parnaíba teria entrado em um processo erosivo
conduzido por movimentos epirogênicos ascendentes e uma regressão de
âmbito global (VAZ et al., 2007).
3. Sequência Neocarbonífera-Eotriássica – a unidade estratigráfica é composta
pelo Grupo Balsas (formações Piauí, Pedra de Fogo, Motuca e Sambaíba). Na
Formação Piauí, predominam arenitos intercalados com folhelhos. GÓES &
FEIJÓ (1994) atribuem à deposição um ambiente continental e litorâneo, sob
um clima extremamente árido. Entretanto, há outras interpretações que
associam a um ambiente fluvial, com contribuição eólica e breves incursões
marinhas. A Formação Pedra do Fogo é caracterizada por uma grande
variedade de rochas, com presença de sílex, calcário oolítico e psolítico,
eventualmente estromatolítico, intercalado com arenito fino a médio, folhelho,
siltito, anidrita e por vezes dolomito. As rochas desta formação são associadas
por GÓES & FEIJÓ (1994) a um ambiente marinho raso a litorâneo, com
planícies de sabkha. A Formação Motuca é composta predominantemente por
siltitos, arenitos e folhelhos. Ocorrem subordinadamente anidrita e raros
calcários depositados em um sistema desértico. Na Formação Sambaíba
predominam arenitos bem selecionados associados a um sistema eólico em
ambiente desértico (GÓES & FEIJÓ, 1994). Essa sequência marca mudanças
8
ambientais e tectônicas profundas na região, que levaram à mudança dos
eixos deposicionais com direção NE-NW para o centro da Bacia e restringiram
a circulação dos mares abertos (GÓES et al., 1990). Segundo tais autores,
essa sequência também compõe um ciclo transgressivo-regressivo, porém sob
condições marinhas rasas e restritas, em clima quente e árido, propiciando a
deposição de evaporitos e a desertificação progressiva da área. Rochas
basálticas recobrem a Formação Sambaíba (VAZ et al., 2007).
4. Sequência Jurássica – constituída pela Formação Pastos Bons, que é
composta por arenitos nas porções basal e superior. A porção intermediária é
constituída por siltitos e folhelhos por vezes intercalados com arenito (VAZ et
al., 2007). A deposição dessa sequência seria relacionada à subsidência
causada pela soma dos pesos da carga de derrames basálticos e da carga
sedimentar existente (GÓES et al., 1990). O fim dessa fase sedimentar seria
consequência de processos tectônicos associados à abertura do Atlântico
Equatorial (VAZ et al., 2007).
5. Sequência Cretácea – essa unidade litoestratigáfica é composta pelas
formações: Codó, Corda, Grajaú e Itapecuru. A formação Corda é composta
essencialmente por arenitos com estratificação cruzada de grande porte e
outras estruturas que sugerem a deposição em sistema desértico (VAZ et al.,
2007). Na Formação Grajaú, predominam arenitos esbranquiçados, finos a
conglomeráticos. A Formação Codó é composta por folhelhos, calcários,
siltitos, gipsita/anidrita e por arenito com níveis de sílex e estromatólitos. A
Formação Itapecuru se constitui predominantemente de arenitos, com
ocorrência subordinada de pelitos e arenitos conglomeráticos. A tectônica que
atuou na abertura do Atlântico Equatorial refletiu na estrutura interna da bacia
durante o Cretáceo, acarretando o deslocamento dos depocentros, que se
mantinham até então na região central, para norte e nordeste (VAZ et al.,
2007).
9
Figura 2-3: Carta estratigráfica da Bacia do Parnaíba (veja próxima página).
Fonte: VAZ et al. (2007).
10
(continuação) Carta estratigráfica da Bacia do Parnaíba.
Fonte: VAZ et al. (2007).
11
2.2.2 Rochas magmáticas
Um magmatismo jurocretáceo, de caráter básico a alcalino, relacionado à ruptura do
Supercontinente Gondwana, ocorreu por toda a extensão que corresponde hoje ao
território do Brasil. O magmatismo básico pronunciado, sob a forma de diques, soleiras
e derrames, concentrou-se nas bacias intracontinentais (MIZUSAKI & THOMAZ
FILHO, 2004).
Na Bacia do Parnaíba, ocorrem rochas ígneas intrusivas (diques e soleiras) e
extrusivas de composição básica, que estratigraficamente foram divididas em duas
unidades: Formação Sardinha e Formação Mosquito (VAZ et al., 2007). Estes autores
atribuem uma idade média de 124 milhões de anos (Ma), Eocretáceo, para a
Formação Sardinha e de 178 Ma (Eojurássico) para a Formação Mosquito. Essas
duas unidades diferem também com relação à sua natureza química e isotópica, à
forma de ocorrência em superfície (Sardinha em grandes diques e pequenas soleiras;
Mosquito em grandes derrames e pequenas soleiras) e à sua localização na bacia
(VAZ et al., 2007).
Para MIZUSAKI & THOMAZ FILHO (2004) e ZALÀN (2004), a Formação Mosquito tem
correlação com as soleiras de diabásio relacionadas ao magmatismo Penatecaua das
bacias do Solimões e Amazonas, cuja idade gira entre 210 e 201 Ma. As rochas
básicas da Formação Sardinha seriam correlatas aos derrames da Formação Serra
Geral, na Bacia do Paraná, com idade entre 137 a 127 Ma.
MIZUSAKI & THOMAZ FILHO (2004) sugerem que as manifestações magmáticas com
idade em torno de 130 Ma podem estar relacionadas com o processo de rifteamento e
consequente formação do Oceano Atlântico Sul. Dentro de um contexto evolutivo de
extensão crustal, o rifte precursor do Atlântico Sul teria se propagado de SW para NE
induzindo às manifestações magmáticas que hoje podem ser reconhecidas na Bacia
do Parnaíba (MIZUSAKI & THOMAZ FILHO, 2004). Essas manifestações seriam
referentes às rochas ígneas da Formação Sardinha. Já o magmatismo que originou a
Formação Mosquito estaria relacionado ao rifteamento e posterior abertura do
Atlântico Central (MILANI & THOMAZ FILHO, 2000 in VAZ et al., 2007).
Segundo VAZ et al., (2007), a partir de interpretação sísmica, é possível verificar
soleiras em uma grande extensão da Bacia do Parnaíba, sem, no entanto, estarem
classificadas como Formação Mosquito ou Sardinha. Entretanto, esses autores
admitem possível predominância da Formação Mosquito (magmatismo Penatecaua),
12
por correlação com as bacias do Solimões e Amazonas.
Com relação à ocorrência nas sequências estratigráficas, os diques e soleiras estão
presentes em maior quantidade na Sequência Mesodevoniana-Eocarbonífera e na
Siluriana, contudo são raros na Sequência Neocarbonífera-Eotriássica (VAZ et al.,
2007).
2.2.3 Arcabouço Estrutural
A Bacia do Parnaíba é classificada como intracratônica, possui forma circular e
depocentro levemente elíptico com orientação NW-SE. Desenvolveu-se sobre um
embasamento continental durante a fase de estabilização da Plataforma SulAmericana (ALMEIDA & CARNEIRO, 2004).
A sedimentação pós-ordoviciana da Bacia do Parnaíba foi fortemente influenciada pelo
período terminal do Ciclo Brasiliano, cujos pulsos propiciaram a formação de grabens
distribuídos por toda a bacia (GÓES et al., 1990, VAZ et al., 2007). Esses autores
corroboram que estruturas grabenformes interpretadas no substrato da Bacia do
Parnaíba teriam controlado o depocentro inicial desta bacia. Esses sítios
deposicionais, ou riftes precursores da Bacia do Parnaíba, seriam correlacionáveis ao
Graben Jaibaras e a outros grabens, situados na Província Borborema, que foram
gerados em um sistema de riftes do final do Proterozóico e início do Paleozóico (VAZ
et al., 2007), conforme Figura 2-4.
O Lineamento Picos-Santa Inês e a Zona de Falha Transbrasiliana constituem fraturas
e falhas herdadas do embasamento, com relevante importância desde a fase inicial da
bacia e por toda a sua evolução, pois controlaram as direções dos eixos deposicionais
até o Eocarbonífero (VAZ et al., 2007). Esses lineamentos destacam-se entre as
principais feições estruturais da Bacia do Parnaíba.
A Zona de Falha Transbrasiliana, também chamada de Lineamento Transbrasiliano,
constitui uma faixa altamente estruturada no sentido NE-SW, que abrange um
complexo de falhas normais e transcorrentes, altos estruturais e grabens com eixos
paralelos às falhas. Apresenta uma feição alongada com cerca de 2.700 km, que cruza
o território brasileiro do Ceará ao Mato Grosso do Sul.
No interior da Bacia do
Parnaíba, o Lineamento Transbrasiliano é demarcado por falhas orientadas no sentido
NE-SW que cortam seções paleozoicas e mesozoicas, bem como por diques de
diabásio orientados no mesmo sentido (CUNHA, 1986).
13
As evidências do Lineamento Picos-Santa Inês não são tão explícitas quanto às do
Transbrasiliano; entretanto, se refletem em uma série de alinhamentos orientados para
noroeste que possivelmente interagiram com o desenvolvimento da bacia, controlando
um expressivo eixo deposicional NW-SE (CUNHA, 1986). As principais feições
estruturais da Bacia do Parnaíba estão representadas na Figura 2-4.
Acompanhando os efeitos da separação dos continentes sul-americano e africano com
consequente abertura do Oceano Atlântico Equatorial, ocorreu um significativo
processo magmático intrusivo e extrusivo (GÓES et al., 1990), que foi responsável por
falhamentos de pequeno rejeito, dobras e outras estruturas (VAZ et al., 2007).
Figura 2-4: Mapa com os principais lineamentos e feições estruturais da Bacia do
Parnaíba.
Fonte: Elaboração própria a partir de informações obtidas de CUNHA (1986), GÓES et al.
(1990), SILVA et al. (2003).
14
2.3
Evolução tectônica da Bacia do Parnaíba
As sedimentações paleozoicas desenvolveram-se em extensas sinéclises, que tiveram
como base uma plataforma consolidada a partir de colagens de placas tectônicas
isoladas, cuja união aconteceu no Ciclo Brasiliano, acompanhada de todos os eventos
deformacionais, metamórficos, ígneos, sedimentares e geomorfológicos típicos de
orogêneses (ZALÁN, 2004). Um estágio de estabilização, ocorrido do Siluriano ao
Jurássico, marcado por calmaria tectônica e mudança no padrão de sedimentação, foi
essencial para o desenvolvimento das sinéclises paleozoicas. As sinéclises formaramse independentemente das estruturas subjacentes locais e passaram a sofrer
extensas transgressões e regressões marinhas regionais. Em resposta à subsidência,
arcos regionais ergueram-se e circundaram as sinéclises, terminando por separá-las.
Entre o Jurássico e o Triássico, sob extrema calma tectônica, toda a plataforma sofreu
ascensão, limitando a sedimentação e ocasionando o fim das ingressões marinhas.
Entretanto, a origem da subsidência inicial, que localiza geograficamente as sinéclises
e
os
mecanismos
de
subsidências
adicionais
que
vão
aprisionando
as
supersequências superiores, refletem aspectos ainda considerados controversos
(ZALÁN, 2004).
Estudos recentes levantam a hipótese de que a subsidência inicial das bacias
paleozoicas seria originada em um processo semelhante a de um rifte ativo,
caracterizado pela presença de vulcanismo na base de algumas delas, evidenciando
prenúncio de esforços distensionais (ZALÁN, 2004).
Na Bacia do Parnaíba, no fim do evento do Ciclo Brasiliano, durante a transição do
Cambriano para o Ordoviciano, o resfriamento e a contração da litosfera favoreceram
a formação de falhas normais e a ativação de antigas estruturas lineares. Deste modo,
surgiu um quadro tectônico e estrutural dominado por extensos falhamentos normais e
fossas desenvolvidas ao longo de zonas de fraqueza crustal anteriormente instaladas.
De acordo com CUNHA (1986), estas zonas são bem representadas na Bacia do
Parnaíba por expressivos lineamentos, destacando-se o Transbrasiliano e Picos-Santa
Inês.
As fossas assim instaladas foram sincronicamente preenchidas por clásticos cambroordovicianos, que chegam a atingir milhares de metros de espessura e que em
conjunto, constituem a estruturação precursora da Bacia do Parnaíba, demarcando no
tempo e no espaço o início de sua subsidência (CUNHA, 1986).
15
Como resultado da evolução termomecânica da área, estabeleceu-se a grande
depressão ordoviciana, sobre a qual se depositou a Sequência Siluriana, composta
pelos sedimentos flúvio-deltaicos a marinhos rasos do Grupo Serra Grande.
Posteriormente, com o prosseguimento dos processos termais, já com efeitos
flexurais, foi depositada a Sequência Mesodevoniana-Eocarbonífera, constituída
principalmente pelos sedimentos devonianos do Grupo Canindé (GÓES et al., 1990).
Do Neocarbonífero até o Jurássico, os depocentros deslocaram-se para a parte central
da bacia (GÓES et al., 1990; VAZ et al., 2007), a sedimentação passou a ter um
padrão concêntrico e a forma externa da região deprimida tornou-se ovalada, típica de
uma sinéclise interior (VAZ et al., 2007).
2.4
Sistemas Petrolíferos
Um sistema petrolífero é definido por MAGOON & DOW (1994) como um sistema
natural que relaciona uma rocha geradora a um determinado tipo de óleo ou gás em
uma bacia sedimentar e que inclui todos os processos que são essenciais para a
existência e acumulação de hidrocarbonetos. Constitui uma combinação de elementos
e processos que, sob condições adequadas propiciam a geração, acumulação e
armazenamento de petróleo. Dentro de um sistema petrolífero a rocha geradora
matura expulsa os hidrocarbonetos gerados, que migram por falhas ou carrier beds até
rochas porosas que servem de reservatórios, onde são armazenados e aprisionados
por estruturas ou descontinuidades de diferentes tipos litológicos. Uma capa selante,
formada por rocha de baixa permeabilidade, garante que o hidrocarboneto mantenhase acumulado. Para que acumulações ocorram, todo o processo deve ocorrer de
maneira contínua e simultânea.
O sistema petrolífero pode ser classificado de acordo com o nível de incerteza em:
conhecido (!), hipotético (.) e especulativo (?). Em um sistema conhecido existe
correlação geoquímica entre a rocha geradora e os hidrocarbonetos da acumulação.
Em um sistema hipotético a geradora é identificada, mas não há correlação com
acumulação de hidrocarbonetos. No especulativo, a existência da rocha geradora ou
de hidrocarbonetos é postulada com base em evidências geológicas e geofísicas
(MAGOON & DOW, 1994). A nomenclatura para sistemas petrolíferos, proposta por
tais autores, consiste no nome da rocha geradora, seguido pelo nome da rocha
reservatório e do nível de incerteza.
16
MAGOON & DOW (1994) classificaram ainda os sistemas petrolíferos em típicos e
atípicos. Nos sistemas típicos a rocha geradora sofre maturação por soterramento
devido ao aumento das temperaturas em profundidade. Já nos sistemas atípicos a
geração de hidrocarbonetos ocorre de outro modo que não por soterramento. Inclui-se
nesta categoria a maturação da rocha geradora por condução do fluxo térmico
proveniente de intrusões ígneas.
Os sistemas petrolíferos comumente mencionados para a Bacia do Parnaíba, na
literatura disponível (GÓES et al., 1990; RODRIGUES, 1995; MENDONÇA et al.,
2004; ANP, 2007), são o Tianguá-Ipu (.) e o Pimenteiras-Cabeças (!). Corroboram a
existência de pelo menos um desses sistemas as ocorrências de hidrocarbonetos em
Teste de Formação (TF), poços com indícios em amostras de calha, exsudações de
gás, além de anomalias geoquímicas de superfície verificadas na bacia (ANP, 2007),
como observado na Figura 2-5. A acumulação, até então tida como subcomercial, do
poço 2-CP-1-MA confirma especificamente o sistema Pimenteiras-Cabeças (!),
conforme Figura 2-7.
Figura 2-5: Principais ocorrências de hidrocarbonetos na Bacia do Parnaíba.
Fonte ANP/Nona Rodada (2007).
17
O sistema petrolífero Tianguá-Ipu (.) foi postulado por GÓES et al. (1990),
relacionando como rocha geradora os folhelhos da Formação Tianguá e como
reservatórios, os conglomerados e arenitos da Formação Ipu. Neste sistema, a rocha
selante seria também os folhelhos da Formação Tianguá (Figura 2-6). Caracterizada
como a rocha geradora siluriana na Bacia do Parnaíba, os folhelhos marinhos da
Formação Tianguá possuem teor de carbono orgânico (COT) normalmente inferiores a
1%, mas em raros níveis podem atingir 1,2%. A matéria orgânica é do tipo III,
originada de vegetais superiores e suscetível a oxidação. Segundo RODRIGUES
(1995), a maturação estaria associada ao efeito térmico das intrusões juro-triássicas.
Figura 2-6: Carta de eventos do sistema Tianguá-Ipu (.).
Fonte: Elaboração própria a partir de informações obtidas de GÓES et al. (1990), CUNHA
(1986), RODRIGUES (1995), VAZ et al. (2007), ANP/Nona Rodada (2007).
O sistema Pimenteiras-Cabeças (!) é aqui classificado como conhecido com base no
trabalho de RODRIGUES (1995), que associou os melhores indícios de óleo (no poço
1-TB-2-MA) e gás (no poço 2-CP-1-MA) aos folhelhos geradores devonianos da
Formação Pimenteiras, considerando suas características geoquímicas. O estudo
mostrou ainda que estes folhelhos apresentam COT entre 2% e 5%, com a influência
de intrusões ígneas, em vista de sua elevada maturação, incompatível com a evolução
térmica por soterramento da bacia. O tipo de matéria orgânica associada aos folhelhos
devonianos da Formação Pimenteiras constitui uma mistura em diferentes proporções
dos tipos II e III (RODRIGUES, 1995). Segundo GÓES et al. (1990), a Formação
Pimenteiras é considerada a principal unidade potencialmente geradora de petróleo na
Bacia do Parnaíba, distribuindo-se amplamente e alcançando espessuras superiores a
18
500 m. A relativa riqueza orgânica nesta formação é restrita a níveis de radiação
elevada, atingindo valores de carbono orgânico total residual de até 6 % e isólitas
máximas em torno de 60 m (GÓES et al., 1990). Os reservatórios são os arenitos da
Formação Cabeças, enquanto que os selos são representados por folhelhos, tanto da
Formação Cabeças, quanto da Formação Longá (RODRIGUES, 1995). A carta de
eventos do sistema Pimenteiras-Cabeças (!) pode ser verificada na Figura 2-7.
Figura 2-7: Carta de eventos do sistema Pimenteiras-Cabeças (!).
Fonte: Elaboração própria a partir de informações obtidas de GÓES et al. (1990), CUNHA
(1986), RODRIGUES (1995), VAZ et al. (2007), ANP/Nona Rodada (2007).
Diversos autores (GÓES et al., 1990; YOUNG, 2003; SANTOS et al., 2007) sugerem
ainda a possibilidade da existência do sistema petrolífero Pimenteiras-Pimenteiras (?).
YOUNG (2006) analisou os corpos arenosos situados dentro da Formação
Pimenteiras, constatando valores elevados de porosidade e permeabilidade, além de
fornecer uma nova interpretação geológica para o posicionamento destes corpos
dentro desta formação. Um novo modelo estratigráfico baseado em regressões
forçadas, obtido através da análise estratigráfica de alta resolução em testemunhos de
sondagem na borda Leste da Bacia do Parnaíba (YOUNG & BORGHI, 2003; YOUNG,
2006), propõe a deposição de arenitos em corpos isolados intercalados com os
folhelhos da Formação Pimenteiras. Embora o estudo não permita a compreensão das
heterogeneidades macro e mesoscópicas relacionadas às potenciais rochas
reservatório, abre novas perspectivas para um sistema petrolífero PimenteirasPimenteiras (?).
19
2.5
Histórico exploratório
A evolução exploratória das bacias paleozoicas brasileiras teve seu ápice entre os
anos de 1954 a 1968, durante o período de monopólio da Petrobras. Durante esses
anos de atuação, a Petrobras buscou manter duas estratégias principais: descobrir
novas reservas petrolíferas com eficiência e rentabilidade; incluir no esforço
exploratório as bacias que então pareciam menos atraentes. Contudo, investimentos
relativamente baixos foram destinados às bacias de novas fronteiras, pelo menos até
1997 (BACOCCOLI, et al., 2003).
Além disso, a falta de sucesso nas bacias paleozoicas, aliada, em parte, às
dificuldades logísticas da época e à baixa qualidade dos dados, direcionaram os
esforços exploratórios para as bacias cretáceas (BACOCCOLI, et al., 2003).
As bacias paleozoicas foram então privadas de uma evolução tecnológica que poderia
dar outro rumo à suas histórias exploratórias, bem como ao conhecimento de seus
potenciais petrolíferos. Nesse contexto, um exemplo que pode ser evidenciado é a
presença de rochas ígneas nestas bacias, então consideradas como um problema que
dificultaria a obtenção de dados sísmicos confiáveis, assim como a interpretação
gravimétrica, magnetométrica e de geologia de superfície (BACOCCOLI, et al., 2003).
Hoje, alguns autores defendem que as rochas ígneas, em alguns casos, são, em
alguns casos, essenciais para a maturação térmica da matéria orgânica em sistemas
petrolíferos não convencionais (LUTHI & O’BRIEN, 1993; RODRIGUES, 1995;
BENDER, 2001; WANDERLEY FILHO et al. 2006). A Bacia do Solimões é um
exemplo clássico do efeito magmático no processo de geração de óleo e gás.
O encerramento das atividades exploratórias nas bacias terrestres paleozoicas
propiciou um círculo vicioso, onde a ausência de dados exploratórios ou sua baixa
qualidade levou à falta de interesse por parte da indústria devido ao insucesso
exploratório, o que impossibilitou a coleta de novos dados com maior qualidade e em
maior quantidade (ÁVILA, 2010).
Os primeiros estudos aplicados à exploração de petróleo na Bacia do Parnaíba foram
realizados na década de 50, quando o Conselho Nacional do Petróleo (CNP)
desenvolveu estudos de geologia de superfície e perfurou dois poços no Estado do
Maranhão. Entre 1956 e 1966, uma nova fase exploratória foi iniciada, já sobre a
responsabilidade da Petrobras criada em 1953. Nessa ocasião foram desenvolvidas
20
atividades de mapeamento geológico e fotogeológico, gravimetria, levantamentos
localizados de sísmica e a perfuração 22 poços exploratórios. Tal esforço resultou na
detecção de alguns indícios de óleo e gás (GÓES et al., 1990). Em 1975 os trabalhos
foram
retomados
com
uma
nova
campanha
de
levantamento
sísmico,
aeromagnetometria e a perfuração de mais quatro poços pioneiros (GÓES et al.,
1990).
No início dos anos de 1980, a ESSO e a Anschutz, após assinarem contrato de risco,
empreenderam nova campanha exploratória, que possibilitou a obtenção de novos
dados (GÓES, et al., 1990). Essa fase se caracterizou pela implementação do uso da
sísmica de reflexão como ferramenta principal nas atividades exploratórias (ANP,
2007).
A partir de 1988 a Petrobras iniciou nova fase exploratória, que priorizou a
reinterpretação sistemática dos dados disponíveis. A partir desses esforços, vários
indícios de hidrocarbonetos foram encontrados, destacando-se o poço 2-CP-1-MA
(GÓES et al., 1990). Segundo MENDONÇA et al. (2004), a locação do 2-CP-1-MA foi
posicionada em feição antiforme no depocentro da bacia, apoiada por dados sísmicos
de boa qualidade, embora o poço tivesse a finalidade primeira de amostrar os
folhelhos devonianos e verificar suas condições de potencial gerador e maturidade.
Em testes de formação, um intervalo de diabásio fraturado intrudido na rocha geradora
e outro em arenitos da Formação Itaim exibiram surgência de gás. Nos perfis, revelouse um terceiro intervalo possivelmente portador de gás, este na Formação Cabeças,
porém o mesmo não foi testado (Figura 2-8).
Com o advento da lei 9.478, em 1997, conhecida como Lei do Petróleo, a Agência
Nacional do Petróleo, Gás Natural e Biocombustíves (ANP) passou a contratar áreas,
a partir de licitações de blocos exploratórios, que concretizaram a abertura do mercado
petrolífero no Brasil. Entre os objetivos principais, pode-se citar a busca por
investimentos para acelerar a cadeia exploratória, visando atingir a autossuficiência. A
primeira rodada de licitação aconteceu no ano de 1999. Em 2002, durante a quarta
rodada de licitação, foi ofertado o bloco BT-PN-1, com 12.261 km², na Bacia do
Parnaíba, que foi rejeitado pelo mercado sem nenhum lance ofertado.
Em 2007, a ANP lançou o Programa Plurianual de Geologia e Geofísica (PPA 20072011), o qual previa um plano exploratório para as bacias brasileiras. O PPA
contemplou a Bacia do Parnaíba com a previsão de realização de levantamento
geofísico e geoquímico, levantamento sísmico 2D e perfuração de dois poços. Parte
21
dessas atividades já foram concluídas e outras estão atualmente em andamento.
Em 2007, por ocasião da nona rodada de licitação, a ANP ofertou dez blocos
exploratórios do setor SPN-N-NF. Os blocos PN-T-48, PN-T-49, PN-T-50, PN-T-67,
PN-T-68, PN-T-84 e PN-T-85 foram arrematados pela Petra Energia; o PN-T-66 foi
arrematado pela Devon; o PN-T-86 foi arrematado pela Petrobras e o PN-T-102 pela
Comp E&P de Petróleo e Gás S.A. Atualmente, a OGX possui 70% da concessão de
sete blocos até então pertencentes à Petra Energia.
Figura 2-8: Seção sísmica que passa pelo poço 2-CP-1-MA, localizado na região de
Capinzal-MA.
Fonte: ANP/Nona Rodada (2007)
Apesar dos esforços exploratórios desenvolvidos na Bacia do Parnaíba entre 2007 e
2010, pode-se dizer que ainda há uma carência de dados geofísicos e geológicos que
suportem os estudos dessa região sedimentar (Figura 2-9).
Atualmente 35 poços perfurados na Bacia proporcionam uma densidade de 19.285,7
km² por poço perfurado. Quatro destes poços foram perfurados entre 2009 e 2010 e a
concessionária sustenta ainda um cronograma que contempla um total de quinze
poços até 2013. O investimento previsto para a campanha exploratória é de
aproximadamente R$ 700 milhões. Os esforços até então empenhados resultaram na
22
declaração de comercialidade dos campos de Gavião Azul e Gavião Real, cujos
planos de desenvolvimento encontram-se sob análise da ANP (OGX, 2011).
Figura 2-9: Esforço exploratório na Bacia do Parnaíba.
Fonte: Elaboração própria a partir de dados da ANP/BDEP (2011).
23
3. Intrusões ígneas em rochas sedimentares: um problema
físico-geológico
Fenômenos geológicos, como intrusões ígneas, causam anomalias térmicas em
bacias sedimentares, proporcionando um aumento de temperatura nas regiões de
ocorrência. A análise transiente de temperatura pode favorecer a identificação de
regiões propícias à geração e expulsão de petróleo, no caso de sistemas petrolíferos
atípicos (MAGOON & DOW, 1994).
Os tipos mais comuns de intrusões ígneas em bacias sedimentares são diques e
soleiras. Os diques são estruturas discordantes, geralmente perpendiculares ou
inclinadas em relação ao acamamento intrudido. As soleiras são estruturas
concordantes, paralelas ou subparalelas às camadas sedimentares, possuindo
normalmente uma grande razão entre comprimento e espessura. Na Bacia do
Parnaíba e demais bacias paleozoicas brasileiras são comuns manifestações de
magmatismo básico permo-triássico, que ocorrem em sequências espessas de
derrames e soleiras associadas a diques (MIZUSAKI et al., 2008).
Magmas básicos, devido à sua composição mineralógica (geralmente mais pobres em
sílica), são mais quentes, com temperaturas entre 1.000 e 1.200 ºC e têm viscosidade
menor (SZABÓ et al., 2000). As características físicas do magma básico podem
influenciar na disposição e espessura das soleiras intrudidas nas camadas
sedimentares de uma bacia sedimentar.
WANDERLEY FILHO et al. (2006), analisando o mapa de isólitas da Bacia dos
Solimões, notaram que a espessura do pacote intrusivo diminui nos altos estruturais
anteriores à intrusão, ao passo que, no depocentro da bacia, há um espessamento
dessas rochas. Tais autores citam que o diabásio ainda fluido tende a migrar mergulho
abaixo, por gravidade, para o depocentro da bacia, buscando rotas mais acessíveis
para continuar o fluxo no sentido da calha estrutural (Figura 3-1).
Segundo NEUMANN et al. (2003), o conhecimento dos parâmetros que controlam
intrusões magmáticas gera importantes informações sobre os caminhos de migração
de fluidos e sobre o desenvolvimento térmico e estrutural de bacias sedimentares
afetadas por vulcanismo, caracterizadas por conter expressivos complexos intrusivos e
24
extrusivos. Tais informações são importantes em estudos sobre recursos petrolíferos e
hidrogeológicos.
Figura 3-1: Diagrama de ilustração do mecanismo de intrusão de uma soleira de
diabásio.
Fonte: WANDERLEY FILHO et al. (2006).
Os parâmetros que controlam a intrusão de soleiras em bacias sedimentares são:
densidade e pressão do magma; espessura da sobrecarga; barreiras de fluidos e
produção de vapor (interação com sedimentos úmidos); descontinuidades mecânicas
(acamamento); stress horizontalmente estratificado; existência de fraturas e falhas; o
nível de inversão de densidades entre o magma e a rocha encaixante (NEUMANN et
al., 2003).
Três modelos de intrusão de soleiras (Figura 3-2), considerados bem conhecidos são
destacados por NEUMANN et al. (2003): 1) o modelo de FRANCIS (1982), no qual a
intrusão segue o fluxo gravitacional para o depocentro da bacia, com a consequente
inversão da densidade do magma para a da rocha hospedeira; para o posterior
restabelecimento do equilíbrio hidrostático do magma, pode haver ascensão para um
dos flancos da bacia; 2) o modelo de CHEVALLIER & WOODFORD (1999), no qual o
magma, alimentado por um dique, ascende e segue na estratigrafia da bacia formando
a soleira externa; depois, o soerguimento resultante dos sedimentos sobrepostos
àquela soleira gera uma fratura na parte central, em níveis inferiores da estrutura,
formando uma soleira interna; 3) o modelo de MALTHE- SØRENSSEN et al. (2004),
25
baseado em modelagem numérica, que difere dos outros modelos, pois não considera
os diques alimentadores. Este último modelo sugere que em bacias com campo
isotrópico de esforços, as soleiras tendem a adotar a forma de pires. Durante a
intrusão da soleira, campos de tensão anisotrópicos se formam nas bordas, devido à
elevação da sobrecarga dos estratos. Esta assimetria de stress leva à formação de
segmentos de soleiras transgressivas, quando o comprimento do segmento horizontal
superior excede 2 a 3 vezes a espessura da sobrecarga.
Considerando uma soleira de diabásio intrudida em uma sequência sedimentar, podese intuir que existe uma preferência da direção do transporte de calor através desse
corpo ígneo, proporcionando o efeito chaminé. O efeito chaminé consiste no transporte
de calor, através de um corpo mais condutivo, das porções mais profundas para as
mais rasas, como ocorre no efeito do sal. Como rochas magmáticas possuem alta
capacidade térmica, vão aquecendo as camadas sedimentares a sua volta e, no caso
da existência de matéria orgânica podem causar o fenômeno de maturação.
Figura 3-2: Modelos de intrusão de soleiras. a) modelo deFrancis (1982 apud Neumann et
al., 2003); b) modelo de Chevallier & Woodford (1999 apud Neumann et al., 2003); c)
modelo de Malthe-Sørenssen et al. (2004). Os números indicam os estágios individuais
de desenvolvimento da soleira. Note que as geometrias do fluxo do magma dentro da
intrusão são diferentes nos modelos individuais.
Fonte: Modificado de NEUMANN et al. (2003).
26
O tempo de acomodação dos corpos ígneos nas rochas encaixantes é de poucas
horas (GALUSHKIN, 1997), enquanto que seu tempo de resfriamento total dura
poucos milhares de anos. O efeito térmico das intrusões em rochas sedimentares
depende de diversas variáveis, tais como: temperatura inicial e tipo do magma, tempo
de formação e espessura do corpo intrusivo, grau de maturação inicial da encaixante,
além dos fatores que determinam a condutividade térmica das rochas encaixantes,
como composição mineralógica, grau de compactação, teor de matéria orgânica,
porosidade, permeabilidade, saturação de fluidos e tipos de fluidos presentes
(RODRIGUES, 1995; GALUSHKIN, 1997).
O efeito termal que as intrusões ígneas básicas produzem nas rochas sedimentares
pode atingir distâncias superiores à espessura do corpo intrusivo ou ainda ser a ela
superior, conforme analisado por RODRIGUES (1995), na Bacia do Parnaíba, e
ALVES & RODRIGUES (1985), na Bacia do Amazonas. Segundo THOMAZ FILHO et
al. (2007), esse processo pode variar em suas dimensões em função da profundidade
em que se implantou a intrusão, sendo maior o calor transmitido quanto maior for a
profundidade.
De acordo com GALUSHKIN (1997), em relação às rochas encaixantes afetadas por
intrusões, o halo térmico geralmente se estende, a partir do contato, até uma distância
de 50% a 90% da espessura da intrusiva. Este trabalho, baseado em estudos
geoquímicos e petrológicos de diversas partes do mundo, concluiu que raramente o
efeito térmico sobre as encaixantes ultrapassa 100% da espessura da intrusiva.
SOUSA et al. (2008), estudando os efeitos térmicos provocados por intrusões de
basaltos e microgabros em rochas sedimentares da Bacia Potiguar, observaram que
os corpos ígneos mais rasos, com textura fina a média, ainda contendo matriz vítrea
ou criptocristalina, produzem efeitos a pequenas distâncias das encaixantes. Por sua
vez, os corpos hipoabissais, com textura média a grossa (diabásica), com velocidade
de resfriamento mais lenta, ocasionam efeitos mais expressivos.
O estudo do efeito térmico proporciona um histórico da influência do fluxo e de eventos
térmicos nas diversas camadas que compõem uma bacia, até chegar ao estado
estacionário. No caso da Bacia do Parnaíba, a estrutura térmica foi influenciada pelo
fluxo térmico relacionado com sua evolução termomecânica e pelo efeito das intrusões
ígneas.
27
4. Fundamentos físicos envolvidos na transferência de calor
em bacias sedimentares
Este capítulo busca apresentar os fundamentos físicos envolvidos na transferência de
calor, visando ao entendimento do efeito causado por desequilíbrios na estrutura
térmica original e na maturação da matéria orgânica de bacias sedimentares.
4.1
Mecanismos de condução de calor
A energia transferida pelo fluxo térmico não pode ser medida diretamente, porém, por
estar relacionada à temperatura, pode ser inferida indiretamente. O processo através
do qual a energia é transferida é conhecido como transferência de calor. Sempre que
houver um gradiente térmico entre dois pontos, ocorrerá um processo dinâmico que
visa ao estabelecimento do equilíbrio, tendo como resultado a diminuição desse
gradiente. A transferência de calor ocorre do ponto mais quente para o mais frio,
segundo a direção do gradiente térmico, e é estabelecida a partir de três mecanismos:
condução, convecção e radiação (Figura 4-1).
A condução é o tipo de transferência de calor onde a troca de energia ocorre a partir
da região de maior temperatura em direção à região de menor temperatura, através da
propagação da vibração das moléculas em um meio sólido ou líquido estacionário.
A transferência de calor por convecção é particularmente importante quando existe um
fluido em movimento nas vizinhanças de uma superfície sólida.
Portanto este
processo inclui os efeitos combinados da condução e do movimento do fluido. A
transferência de calor, neste caso, é tanto mais elevada quanto mais rapidamente o
fluido se desloca.
A transferência de calor por radiação é a emitida por todos os corpos e transferida no
espaço sob a forma de ondas eletromagnéticas, conforme a teoria clássica de
Maxwell, ou como fótons discretos de acordo com Planck.
28
Figura 4-1: Mecanismos de transferência de calor.
T é a temperatura média dos meios e q o fluxo térmico entre os meios.
Fonte: KING (2003).
4.2
Lei de Fourier e a equação de difusão de calor
A lei básica da condução de calor baseia-se nas observações experimentais de
Fourier. A Lei de Fourier afirma que o calor trocado por condução em uma certa
direção é proporcional à área normal à direção e ao gradiente de temperaturas na tal
direção:
q x = −λ A
dT
dx
,
(1)
onde λ é a condutividade térmica.
Quando há um gradiente térmico, o conhecimento da distribuição da temperatura
permite a determinação do fluxo térmico. Para um objeto unidimensional que
apresenta uma distribuição de temperatura T (x) , a equação do fluxo térmico é dada
por:
Q=
qx
dT
= −λ
A
dx
(2)
29
O fluxo térmico (Q ) é a taxa de transferência de calor na direção x , proporcional ao
gradiente de temperatura ( dT / dx) , por unidade de área perpendicular à direção da
transferência. A constante λ (condutividade térmica), em uma determinada direção x ,
é uma propriedade de transporte de energia, característica de cada material, e vem
exprimir a maior ou menor facilidade que o material apresenta à condução de calor. O
sinal negativo é uma consequência do fato do calor ser transferido no sentido da
diminuição da temperatura. Sob condições estacionárias, a distribuição de temperatura
é linear.
A Lei de Fourier, implicitamente, nos diz que o fluxo térmico é uma grandeza
direcional, o que nos permite escrever a equação de forma abrangente, considerando
um sistema de coordenadas bidimensional:
 ∂T
∂T 

Q = −k∇T = −k  i
+j
∂
x
∂
y


(3)
A direção do fluxo térmico será sempre perpendicular à superfície com temperatura
constante, conhecida como superfície isotérmica. A Lei de Fourier pode ser escrita de
uma forma alternativa:
qn = − λ
∂T
∂n
(4)
Com a aplicação na presente dissertação do modelo de VASCONCELOS (2010), para
uma seção bidimensional, tem-se a seguinte equação obtida da Lei de Fourier:
ρc p
∂T
∂
∂T ∂
∂T
= λx
+ λy
∂t ∂x
∂x ∂y
∂y
,
(5)
onde c é o calor específico e ρ a massa específica do material.
A equação de difusão de calor calcula a distribuição de temperatura de um meio, dada
suas condições de contorno, e é resultante da combinação da Lei de Fourier
(transmissão de calor) com a Lei de Conservação de Energia.
30
A Figura 4-2, obtida de INCROPERA & DEWIT (1998), ajuda na estruturação da
equação e no entendimento do processamento da transferência de calor por difusão.
Deve-se, entretanto, considerar um meio homogêneo, onde a distribuição de
temperatura é representada em coordenadas cartesianas bidimensionais.
qz+dz
qy+dy
dz
qx
z
y
x
qy
dx
qx+dx
dy
qz
Figura 4-2: Volume de controle infinitesimal, para a análise da condução de calor
em coordenadas cartesianas.
Fonte: Modificado de INCROPERA & DEWIT (1998).
Nesta figura, d x e d y são os contornos definidos, enquanto q x e q y representam a
transferência de calor respectivamente, nas direções x e
y por superfícies
perpendiculares às direções de transferências. Temos também que q x + d x e q y + d y
correspondem às taxas de transferências de calor nas superfícies opostas a q x e q y .
A entrada de energia no sistema ou no meio é representada por q x e a saída por
q x + d x , e assim, respectivamente, para q y e q y + d y . Simplificando, podemos
escrever que as taxas de transferência de calor por condução para as superfícies
opostas são:
31
q x + dx = q x +
q y + dy = q y +
∂q x
dx
∂x
∂q y
∂y
(6)
dy
A forma geral da equação de conservação de energia, dada pela primeira lei da
termomecânica é:
Ε& e + Ε& g − Ε& s = Ε& ac ,
(7)
onde: E e é a taxa de condução de calor, que corresponde à entrada de energia no
meio; E g é um termo de fonte de energia térmica que pode ocorrer no meio, gerada a
partir do produto da transformação de outras formas de energia. No modelo
bidimensional aplicado neste trabalho, por simplificação, este termo foi ignorado; E s
refere-se à energia de saída; e E ac refere-se à energia interna acumulada no meio.
Podem ocorrer variações na quantidade de energia térmica acumulada pela matéria
no interior do volume de controle. Supondo que não há mudança de fase e
considerando ρ e c constantes, conforme o previsto no modelo de VASCONCELOS
(2010), o termo E ac pode ser escrito da seguinte forma:
∂T
Ε& ac = ρc
dxdy ,
∂t
onde ρ e c
(8)
são, respectivamente, a massa específica e o calor específico do
material. A expressão ρc ∂T
∂t
é a taxa de variação com o tempo da energia térmica
do meio por unidade do domínio.
Substituindo os termos da equação geral de conservação de energia temos:
q x + q y − q x + dx − q y + dy = ρc
∂T
dxdy
∂t
(9)
32
Substituindo as equações (6) na equação (9), obtém-se:
−
∂q y
∂q x
∂T
dx −
dy = ρc
dxdy
∂y
∂t
∂x
(10)
As taxas de transferência de calor por condução são dadas pela Lei de Fourier:
q x = −λdy
∂T
∂x
∂T
q y = −λdx
∂y
(11)
Substituindo a equação dada pela Lei de Fourier na equação (11), obtém-se a forma
geral da Equação da Difusão do Calor:
∂  ∂T  ∂  ∂T 
∂T
 = ρc
 λx
 +  λ y
∂x  ∂x  ∂y  ∂y 
∂t
4.3
(12)
Parâmetros físicos usados em modelagem térmica
Ao analisar a distribuição da temperatura em uma bacia sedimentar, é preciso levar
em conta os diferentes tipos litológicos que a compõe. As propriedades dessas
litologias relevantes para a análise da distribuição da temperatura são: porosidade,
densidade, condutividade térmica e calor específico. Essas propriedades serão abaixo
descritas.
a) porosidade (φ ) : é definida pela relação entre o volume de poros V p e o volume
total de rocha VT , ou seja,
φ=
Vp
VT
(13)
33
A porosidade dita primária refere-se ao volume, geometria e distribuição de poros
do sedimento no momento de sua deposição, influenciada pelos tamanhos e
formas das partículas, seu grau de seleção e sem a presença de cimentação
(GIANNINI, 2003). Essa feição é facilmente modificada pela suscetibilidade que os
sedimentos têm ao soterramento e consequente compactação.
Quanto maior a porosidade de uma rocha, menor será a sua condutividade
térmica, ou seja, estas duas propriedades físicas possuem relações inversas de
proporcionalidade, que influenciarão nas variações térmicas de uma bacia
sedimentar. A variação da porosidade com a profundidade, durante o soterramento
de uma bacia, foi definida por ATHY (1930) como uma curva exponencial, na
forma:
φ (z ) = φ0e−cz ,
(14)
onde φ é a porosidade na profundidade z , φ 0 é a porosidade superficial ( z = 0 ) e
c é o fator de decréscimo exponencial da porosidade em profundidade.
b) massa específica ( ρ ) : é calculada levando em consideração o valor da
porosidade, da massa específica da água e da massa específica do tipo
litológico, de acordo com a expressão
ρ (z ) = ρwφ ( z )ρ g(1−φ ( z )) ,
(15)
onde ρ w é a massa específica da água, ρ g a do grão, z refere-se à profundidade e φ
é a porosidade.
De fato, a massa específica guarda relação com porosidade. Trabalhos sobre essas
duas grandezas mostram que a compactação de uma rocha tende a aumentar com a
profundidade, com a diminuição da espessura sedimentar, refletindo o aumento na
massa específica e a diminuição da porosidade (ATHY, 1930).
Devido à heterogeneidade das rochas, é necessário considerar a massa específica de
quatro formas (BEICIP FRANLAB, 2011):
a) a massa específica média de um volume de rocha;
34
b) a massa específica de um componente individual da rocha, por exemplo, um
mineral;
c) a massa específica média da matriz sólida;
d) a massa específica média do fluido (água, óleo, etc.) preenchendo os poros (ou
fraturas).
A massa específica de uma rocha que compreende n componentes é dada por:
 Vi 
d = ∑   * di ,
i =1  V 
n
(16)
onde, d i e Vi são a densidade e o volume do componente i , respectivamente.
c) condutividade térmica ( λ ) : indica a qualidade de um material para conduzir
calor. Deste modo, quanto maior o valor de λ , mais condutor de calor é o
material. É um parâmetro que influencia na quantificação da distribuição de
temperatura. Entretanto, a condutividade térmica das rochas é um tema
relativamente complexo, pois depende da condutividade e proporção relativa
dos minerais que as constitui, além de seus fluidos intersticiais (COSTA DE
JESUS, 2004). Deste modo, o cálculo para obtenção da condutividade térmica
de uma rocha pode ser expresso da seguinte forma (ATHY, 1930):
λ ( z ) = λ(r1−φ ( z ))λφw( z ) ,
(17)
onde z é profundidade (m) da camada, λr é a condutividade dos minerais
constituintes da rocha, λw é a condutividade do fluido intersticial e φ é a porosidade
da rocha.
Uma vez que a condutividade dos sedimentos varia com a temperatura, deve-se
definir um parâmetro de dependência da temperatura (BEICIP FRANLAB, 2011). Este
parâmetro é utilizado para calcular a condutividade térmica de uma rocha sedimentar
cujos poros são preenchidos com água:
35
φ
 λw   1 
λ − λs   * 
,
T
λ
1
+
α


 s 
0
onde α é a dependência térmica em 1 ο
C
(18)
, λ é a maior condutividade térmica em
Wm −1 oC −1 , λ s é a condutividade térmica da matriz de sedimentos em Wm −1 oC −1 , λ w
é a condutividade da água em Wm −1 oC −1 , φ é a porosidade e T é a temperatura
em ο C .
d) capacidade térmica (C ) : é uma grandeza física que define a quantidade de
calor requerido, em Jm −3 , para aumentar a temperatura de um corpo em 1o K .
A capacidade térmica é o produto da massa especifica (ρ ) de um corpo, por
seu calor específico (c ) .
C = ρ ⋅c
(19)
O calor específico é a grandeza física, constante para cada substância, cuja unidade
usual é JKg −1 o K −1 , que define a variação térmica ao receber determinada quantidade
de calor. Pode-se dizer que o calor específico caracteriza uma substância em um
determinado estado físico.
36
5. Modelos termomecânicos que descrevem a estruturação
térmica de bacias sedimentares
5.1
Modelos de extensão litosférica
A evolução termomecânica da litosfera durante o processo de formação de uma bacia
envolve duas fases: uma de estiramento, seguida por outra de subsidência térmica. A
fase de estiramento da litosfera é geralmente associada a processos de rifteamento,
com afinamento e falhamento da crosta acompanhado pela ascensão positiva da
litosfera que gera um aumento do fluxo térmico. A fase de subsidência termal é
relacionada ao restabelecimento do equilíbrio térmico no manto litosférico, com o seu
resfriamento e aumento da massa específica. Processos geodinâmicos da litosfera
são suportados por compensação isostática.
A isostasia é justamente a compensação, ou a contrapartida pelo equilíbrio, da placa
litosférica, quando alguma carga geológica é adicionada ou retirada. Os mecanismos
de compensação isostática buscam o equilíbrio de massas para manter uma
distribuição uniforme de tensões na litosfera.
Segundo QUINTAS (2002), o objetivo original desses estudos isostáticos foi
determinar a forma de compensação de massas associadas com feições geológicas
individuais em continentes e oceanos. Deste modo, o modelo de compensação local é
aplicado diretamente sob feições geológicas caracterizadas pelo espessamento da
crosta, como os modelos de AIRY (1855) e PRATT (1855). No modelo de AIRY
(1855), a massa específica da litosfera é constante, porém sem resistência lateral e
com rigidez flexural nula. Já o modelo de PRATT (1855) considera variações laterais
de massa específica.
Para uma escala regional, ocorre o modelo de compensação flexural. Neste modelo, a
litosfera apresenta resistência mecânica às cargas impostas. Assim, quando uma
carga é aplicada, a litosfera comporta-se como uma placa elástica, homogênea e
isotrópica superposta a uma astenosfera fluida.
Os mecanismos de compensação isostática ajudam a entender como funcionam os
modelos aplicados na avaliação da história térmica de bacias sedimentares. Diversos
modelos tratam da história térmica de uma bacia sedimentar, porém serão descritos os
37
modelos clássicos de extensão uniforme e não-uniforme (duas camadas), por estarem
incluídos na proposta metodológica deste trabalho.
Os modelos de extensão litosférica são ferramentas importantes para a análise da
evolução térmica de bacias sedimentares, pois sugerem como a crosta e manto
litosférico podem se comportar quando submetidos a esforços distensivos, muitas
vezes responsáveis pela gênese e por mecanismos de propagação de calor nas
bacias. Os modelos de extensão litosférica são uniformes quando assumem que os
estiramentos crustal e subcrustal são coincidentes na vertical, como também que a
deformação se dá por cisalhamento puro. São ditos não-uniformes quando assumem
comportamento reológico rúptil para a crosta e dúctil para o manto litosférico,
considerando assim, diferentes taxas de estiramento quando submetidas a mesma
tensão.
5.1.1 Modelo de extensão uniforme
O modelo básico de distensão litosférica foi primeiro proposto por MCKENZIE (1978),
admitindo o afinamento de uma litosfera sem rigidez flexural e mecanismos de
compensação isostática local do tipo Airy. Os estiramentos crustal e subcrustal não
são distintos e a quantificação de deformação é expressa pelo fator de afinamento
litosférico ( β ):
β= y
y'
,
(20)
onde y é a espessura litosférica inicial e y ' é a espessura litosférica após a
distensão.
O modelo de Mckenzie assume que, no tempo t = 0 , a litosfera possui condições de
equilíbrio térmico (Figura 5-1). O afinamento litosférico proporcionado pelo estiramento
causa depressões, seguida por uma subsidência tectônica inicial, rápida, que
preenche a bacia sedimentar com água e sedimentos. A diferença de massa
específica desses materiais tenderá a ser compensada localmente pela ascensão da
astenosfera, menos densa que a litosfera. Com o afinamento, a então espessura y da
litosfera passa a
y
β , resultando em alto valor de gradiente térmico, com
comportamento linear. Esta fase corresponde ao desenvolvimento da bacia e é
conhecida como fase rifte, pois ocorre durante e logo após a formação destas
38
estruturas. A subsidência inicial (Si) ou fase rifte está relacionada à falhamentos,
ocasionados pelo afinamento crustal e consequentes reajustes de compensação
isostática, que levam em consideração mudanças de massa específica e expansão
térmica. Contudo, este modelo desconsidera os efeitos de calor radiogênico da crosta
continental e as perdas laterais de calor ocorridas na transição entre a litosfera
estirada e a não estirada.
Duas premissas adotadas por MCKENZIE (1978) são importantes nesta fase: o efeito
extensional é considerado instantâneo no tempo geológico, impedindo que a anomalia
térmica seja dissipada durante a subsidência inicial; além disso a isostasia é mantida
durante e após o estiramento.
Após o reequilíbrio térmico e consecutivo espessamento da litosfera, ocorre uma nova
e lenta fase chamada de subsidência termal (St). A subsidência termal é causada pelo
processo de resfriamento associado à perda de calor por condução e consequentes
contrações térmicas da litosfera. O resfriamento é devido à dissipação da anomalia
térmica e inicia logo após a fase rifte. A anomalia térmica que propaga calor para a
bacia é um fator determinante na história térmica.
A separação entre as fases de Si e St previstas pelo modelo original de MCKENZIE
(1978), foi revisada por JARVIS & MCKENZIE (1980). Estes autores mostram que
existe uma nítida separação entre Si e St para casos de fase de rifte de até 20 M.a. No
entanto, nas fases riftes mais longas (> 20 M.a.) ocorre perda de calor ainda durante o
rifteamento, transferindo parte da subsidência da fase termal para a fase rifte.
39
Figura 5-1: Modelo de Extensão Uniforme de MCKENZIE (1978).
Fonte: CARDOSO (2007).
A história da evolução térmica de uma bacia sedimentar se relaciona com sua
subsidência, já que anomalias térmicas influenciam diretamente as taxas de
estiramento envolvidas nos processos de desenvolvimento de tal subsidência, seja
mecânica ou termal.
40
O modelo de Mckenzie calcula a subsidência mecânica pela seguinte equação:
 *
Tm y c  α v Tm ρ m* 
* yc 
1 − α v
 −
 ρm − ρc
(1 − 1 / β )
y
2
y
2
l 
l 

ys = 
,
*
ρ m (1 − α v Tm ) − ρ w
(
)
(21)
onde ρ m , ρ c e ρ w representam as massas específicas respectivas do manto, crosta
e água à temperatura de 0 ºC, yc a espessura da crosta, α o coeficiente de dilatação
térmica e T a temperatura da astenosfera.
Com o término da fase inicial de subsidência mecânica, onde o efeito extensional é
considerado instantâneo, ocorre a distribuição de temperatura por condução de calor
que dá início a subsidência termal, que é variante no tempo e dependente do fator de
estiramento.
O cálculo da subsidência termal é dado por:
∞ 

(2m + 1)π e−(2m+1)2τ1 
1
β
S (t ) = E0 ∑ 
sen
,

2 
β
m = 0  (2 m + 1)  (2 m + 1)π


onde
τ=
y l2
π 2λ
é uma constante termal de tempo
4 y L ρ m* α v Tm
E0 = 2 *
π ρm − ρw
(
(22)
e
).
A subsidência total também chamada de subsidência tectônica é o somatório de Si e
St, amplificada pelos efeitos da sedimentação, ou seja, é a resposta do embasamento
ao peso dos sedimentos (MCKENZIE,1978; SCLATER & CHRISTIE, 1980). Neste
modelo, para cálculo do fluxo térmico, a distribuição de temperatura assume as
seguintes condições iniciais:
41
T = Tm
em
0 < y < yl −

y
T = Tm β 1 − 
 yl 
em
yl −
yl
β
yl
β
< y < yl
Com base na Lei de Fourier (veja capítulo 4) para obtenção da variação do fluxo
térmico e nas condições de contorno estabelecidas no modelo de Mckenzie, chega-se
à equação do fluxo térmico:
T = Tm
em
y=0
T =0
em
y = yl
T
Q( yl , t ) ) = λ m
yl
∞

 nπ
β
sen
1 + 2∑
n =1 nπ

 β
n 2t
 −τ
e




(23)
5.1.2 Modelo de extensão não-uniforme
O modelo de extensão não-uniforme ou de duas camadas, desenvolvido por ROYDEN
& KEEN (1980), assume os princípios básicos do modelo de MCKENZIE (1978). Ele
traz, entretanto, como diferença essencial, a proposta de que a crosta e o manto
litosférico, sob estiramento, podem se comportar de maneira distinta, levando a
diferentes taxas de afinamento crustal e subcrustal. Este modelo considera que as
diferenças reológicas da crosta rúptil e do manto litosférico dúctil proporcionarão
deformações definidas por fatores de estiramento diferentes. Assim, acima da
interface que limita essas diferenças, na região crustal da litosfera, o fator de
estiramento é δ , enquanto que abaixo, na região subcrustal é β (Figura 5-2).
42
Figura 5-2: Modelo de duas camadas de ROYDEN & KEEN (1980), onde a é a espessura
da litosfera, Tm a temperatura na base da litosfera e Si a subsidência inicial.
Fonte: CARDOSO (2007).
A relação entre os fatores de estiramento influenciará nas subsidências inicial e
térmica da bacia. Deste modo, se δ é menor que β tem-se uma subsidência térmica
mais intensa que no modelo de MCKENZIE (1978). Caso contrário, quando o
estiramento β , subcrustal, é menor, a anomalia térmica não é suficiente para
influenciar uma subsidência de grande porte após o estiramento inicial (rifteamento). A
mesma avaliação é feita para uma subsidência mecânica favorecida por valores
maiores de δ . Se os estiramentos crustal e subcrustal foram iguais, ou seja, δ = β , o
modelo de extensão é uniforme conforme o modelo de MCKENZIE (1978).
Outro aspecto que diferencia o modelo duas camadas diz respeito a uma mudança na
elevação da crosta em resposta ao estiramento, que irá depender da espessura
crustal inicial, da profundidade do limite de diferença reológica e das magnitudes dos
parâmetros δ e β .
ROYDEN & KEEN (1980) alertam que, no modelo de duas camadas, não é possível
haver conservação de massa durante a extensão sem que ocorram consequências
nas regiões adjacentes que não sofreram estiramento. Como uma possível solução, as
autoras sugerem a combinação da extensão com a intrusão magmática durante o
processo de rifteamento.
Neste modelo, como já visto, a subsidência dependerá dos fatores de estiramentos
crustal e subcrustal. A subsidência mecânica será dada pela seguinte equação:
43
Si =
(ρ
)
  1 γ 
− ρ c*
Tm z 

 z 1 − + 1 − α v
*
2 y L 
ρ m (1 − α vTm ) − ρ w   δ δ 
*
m
T  z + yc

1 γ 
+ ( y c − z )1 − + 1 − α v m 
2  yL
 β β 
(24)
 
 

 
A subsidência termal é obtida por:
S (t ) = E 0 ∑
m =0
− ( 2 m +1)2 t
x(2 m +1)
∞
(2m + 1)
2
τ
e
(25)
onde,
E0 =
xn
4 y1α v Tm
π2
(ρ
ρ m*
*
m
− ρw
)
n +1
(
− 1)
= γ + (1 − γ )[(δ − β )sen(nπH ) + sen(nπG )]
,
H = 1−
nπ
z
yl δ
,
G = 1−
z
yl δ
−
1 − z / yl
β
Na equação acima as letras n e m denotam os números inteiros da série de Fourier e
as letras G e H são utilizadas para simplificar a equação para xn .
No modelo de duas camadas, são usadas as mesmas condições de contorno e
condições iniciais usadas no modelo de Mckenzie. Com base na Lei de Fourier (veja
capítulo 4) para obtenção da variação do fluxo térmico e nas condições de contorno
estabelecidas, chega-se à equação do fluxo térmico para o modelo de ROYDEN &
KEEN (1980):
n t 
∞

−

1 + ∑ 2 xn e τ 
 n=1

2
T
Q=K m
yl
(26)
44
5.1.3 Modelo de reconstrução geológica da profundidade do embasamento:
técnica de backstripping
A técnica de backstripping (STECKLER & WATTS, 1978) consiste na remoção das
camadas de uma bacia sedimentar e a consequente descompactação das camadas
adjacentes com o objetivo de obter a subsidência tectônica da bacia. Não obstante
essa técnica seja amplamente aceita no estudo de bacias marginais, sua aplicação em
bacias interiores tem sido contestada pela dificuldade em estabelecer os parâmetros
para análise da subsidência, principalmente a idade dos horizontes, dados
paleobatimétricos e a quantidade de material removido por erosão (BOCARDI et al.,
2008). Segundo estes autores, a dificuldade na estimativa dos eventos erosivos
subsequentes aos períodos de subsidência é um dos aspectos mais importantes no
questionamento do uso do backstripping nestas bacias, que normalmente possuem
expressivas discordâncias, intrínsecas à sua longa história evolutiva. Entretanto, a
partir de estimativas de erosão fundamentadas em análises estratigráficas regionais e
correlação entre poços profundos, estes autores aplicaram o backstripping na Bacia do
Paraná.
A curva de backstripping aproxima-se da curva de subsidência real, uma vez que
considera que a espessura e a densidade dos sedimentos são variáveis a medida que
a técnica é aplicada e a descompactação efetuada. Deste modo, a curva de
backstripping pode ser comparada com a curva de subsidência tectônica modelada a
partir dos modelos de MCKENZIE (1978) e ROYDEN & KEEN (1980). Pode, até
mesmo, constituir uma ferramenta de calibração para estes modelos. A curva de
subsidência resultante dos modelos de estiramento dependerá dos fatores δ e β ,
pois quanto maiores, maior a subsidência tectônica. A comparação das curvas obtidas
utilizando os modelos com a curva de backstripping permite estabelecer um grau de
estiramento, ou seja, a escolha do fator de estiramento necessário para gerar a
subsidência tectônica da bacia (PINTO, 2008). Essa calibração é importante, pois os
fatores de estiramento estão relacionados ao fluxo térmico que compõe, junto com o
efeito termal das intrusivas, a estrutura térmica responsável pela história termal da
bacia. A curva de backstripping é dada pela equação abaixo:
−


ρ
ρ
−
 m
si  

ρm
*
 − ∆
Yi = Wdi + S i  
sli
(ρ m − ρ w )
 ρm − ρw 


(27)
45
onde Wdi , S i e Yi são, respectivamente, a paleobatimetria, a espessura de sedimento
descompactada e a subsidência tectônica das inúmeras (i ) camadas estratigráficas.
A letra ρ indica as massas específicas para o manto (m ) , água (w) e sedimento (si )
referente a cada unidade estratigráfica.
46
6. Metodologia Aplicada
6.1
Introdução
Conforme abordado anteriormente, as bacias paleozoicas brasileiras, embora
possuam extensas áreas sedimentares, são relativamente pouco exploradas. O baixo
esforço exploratório faz com que haja uma escassez de dados e informações, que
muitas vezes dificultam a realização de trabalhos e pesquisas acadêmicas. No caso
desta dissertação, a falta de dados foi tratada como uma premissa, o que contribuiu
para que uma aplicação metodológica simplificada fosse adaptada a essa condição.
Todos os dados e informações utilizados são públicos e disponíveis na literatura.
Os dados e informações angariados contribuíram para a obtenção de seções
geológicas que foram modeladas para verificação da estrutura térmica da Bacia do
Parnaíba, relacionadas aos gradientes geotérmicos e ao efeito térmico de intrusões
ígneas comuns na região. Para isso, foram integradas técnicas de reconstrução
sedimentar e o uso de um aplicativo bidimensional (VASCONCELOS, 2010)
embasado por um modelo matemático, o qual descreve a evolução térmica devido ao
efeito de intrusões ígneas em bacias sedimentares.
Reconhecida a estrutura térmica, partiu-se para a avaliação da maturação da matéria
orgânica e determinação das janelas de geração de óleo e gás pelo método Easy%Ro.
A Figura 6-1 sintetiza a metodologia aplicada nesta dissertação. Em resumo, busca-se
o valor do fluxo térmico ao nível do embasamento, utilizando a técnica de
backstripping e os modelos termomecânicos de estiramento. O fluxo térmico calculado
é utilizado como condição de contorno basal no modelo bidimensional para avaliação
do efeito térmico das intrusões. Paralelamente foi feita a calibração do modelo
bidimensional, mediante a comparação com os resultados de um software
convencional. Tais modelos foram aplicados em seções extraídas do bloco 3D,
construído para a bacia.
47
Técnica de
backstripping
Modelos
termomecânicos
Modelo 2D
de avaliação do
efeito térmico
Calibração com
software
convencional
Fluxo térmico
devido
intrusões
Fluxo térmico
no
embasamento
Seções
Bloco 3D
Figura 6-1: Resumo da metodologia aplicada.
6.2
Base de dados e informações
6.2.1 Construção do bloco 3D para extração das seções geológicas
O bloco 3D foi elaborado com o módulo 3DView do software Temis (BEICIPFRANLAB). O objetivo foi a obtenção de seções geológicas da Bacia do Parnaíba.
Estabeleceu-se um domínio no ponto à extrema esquerda do sul bloco 3D,
coordenadas métricas X = 9003792 e Y = 170112, com 800 km na direção N-S e 600
km na E-W, respeitando a concentração de poços na bacia (Figura 6-2).
48
Figura 6-2: Domínio do bloco 3D construído com o módulo 3DView do software Temis, a
partir de dados de 31 poços com informações públicas disponíveis.
Foram utilizados 30 poços perfurados pela Petrobras até 1985, extraídos de CUNHA
(1986), mais o poço 2-CP-1-MA, perfurado em 1986, retirado de GÓES & FEIJÓ
(1994) (Tabela 6-1). CUNHA (1986), ao estudar a evolução paleozoica da Bacia do
Parnaíba, com base em poços, utilizou para cada uma das unidades: as espessuras
em metros; altura da mesa rotativa; profundidade do topo; espessura das intrusões
ígneas.
49
Com essas informações foi possível correlacionar os poços na seção paleozoica.
Contudo, para as camadas da seção mesozóica, foi necessário fazer uma estimativa
extrapolando as espessuras de um poço de referência, no caso o 2-CP-1-MA (GÓES
& FEIJÓ, 1994). Tal pacote sedimentar vai do EoTriássico ao NeoCretáceo, contempla
a Formação Pastos Bons da Sequência Jurássica e as formações Codó, Grajaú,
Corda e Itapecuru da Sequência Cretácea, conforme a descrição de VAZ et al. (2007)
(Figura 2-3).
Tabela 6-1 – Poços da Bacia do Parnaíba utilizados na construção do Bloco 3D
CoordX
CoordY
Poço
9166247
395280
1-CA-1-MA
9187437
228451
1-CL-1-MA
9285622
742908
1-FL-1-PI
9087614
380160
1-FM-1-MA
9115494
363765
1-FO-1-MA
9619509
274794
1-GI-1-PA
9397051
239527
1-IZ-2-MA
9466039
744110
1-MA-1-PI
9463628
746716
1-MA-2-PI
9294360
577417
1-MD-1-MA
9227147
445792
1-MS-1-MA
9538612
427276
1-PA-1-MA
9414150
548016
1-PD-1-MA
9112264
380990
1-RB-1-MA
9179240
378613
1-TB-1-MA
9178726
382622
1-TB-2-MA
9036854
290219
1-TM-1-MA
9182156
320795
1-VG-IR-MA
9285450
704329
2-BGst-1-MA
9473400
577964
2-CP-1-MA
9388503
224077
2-IZst-1-MA
9357975
375933
2-NGst-1-MA
9380405
767435
2-NLst-1-PI
9598387
455576
2-PMst-1-MA
9558033
442002
2-SLst-1-MA
9173977
355502
2-VBst-1-MA
9607700
623712
2-VGst-1-MA
9603984
515900
9-PAF-1-MA
9636097
480749
9-PAF-3-MA
9634302
564806
9-PAF-7-MA
Fonte: BDEP/ANP (2011).
50
Os poços foram georreferenciados a partir do cruzamento com o mapa de poços do
Banco de Dados de Exploração e Produção (BDEP) e organizados em planilhas
contendo dados estratigráficos, idades, espessuras das formações, porcentagem dos
litotipos e coordenadas geográficas.
Primeiro, as informações foram integradas no modelo, gerando o contorno estrutural
para cada camada. Posteriormente, os horizontes foram interpolados concretizando a
construção do bloco 3D (Figura 6-3). A Figura 6-4 mostra, através de um corte, o bloco
3D com os poços.
Z
Y
X
Figura 6-3: Bloco 3D da Bacia do Parnaíba, em perspectiva, elaborado com dados de 31
poços públicos e disponíveis na literatura.
51
N
600 km
800 km
Z
Y
X
Figura 6-4: Bloco 3D e os poços, em corte.
Os parâmetros de compactação e as propriedades térmicas das rochas podem ser
preenchidos com dados reais ou com os padrões da biblioteca de litologias do
software Temis (BEICIP-FRANLAB, 2011). Os principais litotipos e demais parâmetros
constituintes desta biblioteca de litologias foram elaborados e caracterizados de
acordo com a biblioteca do programa. Na falta de parâmetros específicos das rochas
da bacia, foram utilizados tais padrões. O programa calcula os parâmetros com base
na composição litológica e percentual dos litotipos inseridos como dados de entrada.
Apenas com a intenção de apresentar o resultado do bloco 3D, foi plotada sobre o
mesmo, a linha sísmica 0059-0048 (Figura 2-8). Esta linha foi adquirida em 1980,
passa pelo poço 2-CP-1-MA e possui uma interpretação divulgada pela Petrobras
(MENDONÇA et al., 2004). Isto permitiu a extração de uma seção geológica com
mesmo posicionamento geográfico da linha. Nota-se que, guardadas as devidas
características de cada método, incluindo as diferenças de escalas, as semelhanças
são claras. Ambas retratam camadas tabulares, sem deformações expressivas e com
intrusões ígneas em pontos coincidentes (Figura 6-5). Com isso podemos inferir que o
bloco possui boa aproximação com a realidade, portanto é adequado para a obtenção
das seções a serem utilizadas na modelagem térmica da Bacia do Parnaíba.
52
B as e do
C retác eo
E oT riás s ic oJ urás s ic o
F m. P edra de F og o
F m. P iauí
F m. P oti
F m. L ong á
F m. C abeç as
F m. P imenteiras
F m. Itaim
F m. J aic ós
F m. T ing uá
F m. Ipú
Figura 6-5: Comparação entre seção sísmica que passa pelo poço 2-CP-1-MA com a
seção extraída do bloco 3D da Bacia do Parnaíba.
Diversas seções podem ser extraídas do bloco 3D construído para a Bacia do
Parnaíba. Entretanto, para um melhor aproveitamento dos dados disponíveis nesta
dissertação optou-se por trabalhar com três seções (Figura 6-6):
a) A – A’: seção Norte-Capinzal-Sudoeste (N-CP-SW), que corta a bacia de norte
a sul, considerando a maior concentração de poços. É limitada pelos poços 9PAF-3, 2-CP-1-M e 1-TM-1-MA;
b) B – B’: seção Oeste-Capinzal-Leste (W-CP-E), que corta a bacia de leste a
oeste, passando pelos poços 1-IZ-2MA, 2-CP-1-MA, 1-MA-1-PI;
c) C – C’: seção Nordeste-Capinzal-Sudeste (NE-CP-SE), que corta a bacia na
direção NE do poço 1-VGST-1-MA até o 2-CP-1-MA e continua o corte para SE
até o poço 1-BGST-1-MA.
O poço 2-CP-1-MA foi adotado como ponto central entre as seções por constituir o
perfil tipo da bacia, que deu origem a coluna estratigráfica da Petrobras (GÓES &
FEIJÓ, 1994), posteriormente revisada por VAZ et al. (2007). Além disso, contém os
dados de vitrinita (RODRIGUES, 1995) utilizados na calibração da maturação térmica.
53
Figura 6-6: Seções, em planta, sobre o bloco 3D da Bacia do Parnaíba.
A - A’) seção N-CP-SW; B - B’) seção W-CP-E; C - C’) seção NE-CP-SE.
A correlação entre os poços foi feita a partir das descrições contidas em CUNHA
(1986), porém com limitação de dados estruturais. Contudo, as bacias sedimentares
paleozoicas brasileiras do Parnaíba, Paraná, e Amazonas caracterizam-se pela
carência de deformações estruturais intensas, o que as diferencia das prolíferas
bacias paleozoicas da plataforma do Leste Europeu (MIZUSAKI et al., 2008). Não
obstante, julga-se necessário, em uma próxima versão, agregar a componente
estrutural. As seções escolhidas para a simulação do efeito termal das intrusões
54
ígneas na Bacia do Parnaíba, conforme localização na Figura 6-6, são apresentadas
nas Figuras 6-7 a 6-8.
6.2.2 Estratigrafia
Devido à escassez de informações disponíveis na literatura com relação a datações
geocronológicas da bacia e às simplificações estratigráficas, foi feita uma aproximação
das idades, o que não afeta significativamente o resultado final da simulação
(GONZAGA, 2005). As idades das unidades geocronológicas são referenciadas à
carta estratigráfica oficial da Petrobras (VAZ et al., 2007), conforme Tabela 6-2.
Tabela 6-2: Unidades litológicas e idades geocronológicas das seções modeladas.
Tempo em milhões de anos (M.a.)
Tempo (M.a.)
Unidades litológicas
EoTriássico-Neocretáceo
Recente
Fm Pedra do Fogo
255
Fm Piauí
297
Fm Poti
331
Fm Longa
349
Fm Cabeças
363
Fm Pimenteiras
380
Fm Itaim
400
Fm Jaicós
405
Fm Tianguá
430
Fm Ipu
439
Embasamento
540
Vulcânica (diabásio)
178
Fonte: Modificada de VAZ et al. (2007).
6.2.3 Unidades litológicas, composição litológica, porosidade e constante de
decaimento
Devido à baixa quantidade ou ausência de dados específicos da bacia na bibliografia
consultada, o preenchimento litológico das camadas foi simplificado. Para a seção
paleozoica, cada formação teve a espessura obtida do trabalho de CUNHA (1986).
Entretanto, as litologias foram compiladas de várias publicações, principalmente da
atualização da carta estratigráfica da bacia (VAZ et al., 2007). Para a seção
mesozoica, como citado anteriormente, foi necessário fazer uma estimativa
extrapolando as espessuras das camadas de um poço de referência, no caso o
55
N
SW
2-CP-1-MA
2-CP-1-MA
Seção Mesozóica
Fm. Pimenteiras
Fm. Pedra do Fogo
Fm. Itaim
Fm. Piauí
Fm. Jaicós
Fm. Poti
Fm. Tianguá
Fm. Longá
Fm. Ipu
Fm. Cabeças
Vulcânicas
Figura 6-7: Seção N-CP-SW.
56
E
2-CP-1-MA
W
Seção Mesozóica
Fm. Pimenteiras
Fm. Pedra do Fogo
Fm. Itaim
Fm. Piauí
Fm. Jaicós
Fm. Poti
Fm. Tianguá
Fm. Longá
Fm. Ipu
Fm. Cabeças
Vulcânicas
Figura 6-8: Seção W-CP-E.
57
SE
NE
2-CP-1-MA
Seção Mesozóica
Fm. Pimenteiras
Fm. Pedra do Fogo
Fm. Itaim
Fm. Piauí
Fm. Jaicós
Fm. Poti
Fm. Tianguá
Fm. Longá
Fm. Ipu
Fm. Cabeças
Vulcânicas
Figura 6-9: Seção NE-CP-SE.
58
o 2-CP-1-MA (GÓES & FEIJÓ, 1994).
Os dados de porosidade utilizados na modelagem proposta neste trabalho são
padrões da biblioteca de litologias do programa Temis, estabelecidos a partir da
composição litológica por formação inserida na construção do bloco 3D.
As porosidades estão coerentes com as apresentadas por YOUNG (2006), que,
visando identificar e caracterizar potenciais intervalos de reservatório, analisou
estratigraficamente, com alta-resolução, intervalos da Formação Pimenteiras e suas
formações limítrofes, Itaim e Cabeças, gerando um gráfico de porosidade versus
permeabilidade vertical (Figura 6-10). Também mantêm consistência com a
porosidade variável de até 28% da Formação Uerê, que corresponde ao Devoniano
Superior na Bacia dos Solimões (BARATA & CAPUTO, 2007), bem como com a
c
porosidade
calculada por CORRÊA (2007) para os folhelhos da Formação Irati, c’
na
Bacia do Paraná.
Figura 6-10: Gráfico de porosidade versus permeabilidade vertical, elaborado com
amostras das formações Itaim (A e B), Pimenteiras (C, D e G), e Cabeças (I).
Fonte: YOUNG (2006).
A constante de decaimento da porosidade (c) foi calculada pela equação de ATHY
(1930), conforme equação (14) do capítulo 4. As litologias, porosidades e constantes
de decaimento da porosidade consideradas para cada formação podem ser
consultadas na Tabela 6-3.
59
Tabela 6-3: Comp litológica, porosidade (Φ), e constante de decaimento (c) para cada
unidade litoestratigráfica.
Seção Paleozoica
Seção
Mesozoica
Unidades
Litológicas
(Formações)
Composição Litológica (%)
Φ
(%)
c
km-1
1
40
0,4
Pedra do Fogo
24
37
27
3
9
Piauí
53
40
2
5
Poti
100
Longa
100
Cabeças
100
Pimenteiras
12
88
Itaim
100
Jaicos
85
15
Tiangua
48
52
Ipu
100
Fonte: Modificada de BEICIP-FRANLAB (2011).
34
34
36
22
32
14
29
22
16
26
0,5
0,4
0,2
0,7
0,2
0,6
0,2
0,3
0,4
0,2
Bons Pastos,
Codó, Grajaú,
Itapecuru
Arenito Folhelho Siltito Carbonato Evaporito
43
9
41
6
6.2.4 Massa específica e propriedades termais
Os dados de massa específica, condutividade térmica e capacidade térmica utilizados
na modelagem proposta neste trabalho são padrões da biblioteca de litologias do
software Temis, estabelecidos a partir da composição litológica por formação inserida
na construção do bloco 3D.
Contudo, com relação a estas propriedades, para a rocha vulcânica intrusiva foram
utilizados os valores propostos por HANTSCHEL & KAUERAUF (2009) (Tabela 6-4).
6.2.5 Dados geotérmicos
Os gradientes geotérmicos são utilizados na calibração das temperaturas de contorno
utilizadas na modelagem. As informações sobre os gradientes da Bacia do Parnaíba
foram extraídas do trabalho de ZEMBRUSCKI & CAMPOS (1988). Esses autores, com
base em 27 poços, elaboraram mapas do gradiente geotérmico da Bacia do Parnaíba
para diferentes níveis de profundidade, a fim de estabelecer um panorama térmico
espacial tridimensional. O trabalho de ZEMBRUSCKI & CAMPOS (1988) configura o
mais completo estudo com resultados públicos e disponíveis sobre o gradiente
geotérmico da Bacia do Parnaíba, embora os autores admitam que estes resultados
possam ser considerados preliminares, pela precariedade dos dados geológicos
60
disponíveis e pela pequena quantidade e concentração aleatória de poços. O mapa do
gradiente geotérmico médio total (CGMT) mostra o comportamento térmico médio
regional da bacia, interrelacionando os gradientes geotérmicos médios de todos os
poços, obtidos pela interpolação gráfica dos respectivos valores de temperatura e
profundidades de medição. Também foram preparados mapas do gradiente
geotérmico médio parcial (GGMP) para fatias sucessivas de 500 m, desde o nível do
mar até - 2 500 m, convertendo-se a profundidade correspondente a cada medida de
temperatura em cota relativa ao nível do mar (Figura 6-11).
A temperatura superficial de referência (TSR) foi fixada em 27,7 °C (82°F). A TSR, que
localmente pode alcançar de 28 °C a 30 °C, é superior às encontradas nas bacias do
Tabela 6-4: Parâmetros físicos usados no modelo, aplicados à Bacia do Parnaíba por
unidade litológica.
Unidade Litológicas
k
C
ρ
Formação
(W/m K)
(J/kgK)
(kg/m³)
EoTriássico-Neocretáceo
3,92
750,0
2679,8
Fm Pedra do Fogo
3,40
771,9
2613,4
Fm Piauí
4,10
752,7
2665,5
Fm Poti
6,32
700,0
2675,0
Fm Longa
2,37
815,0
2645,0
Fm Cabeças
6,32
700,0
2675,0
Fm Pimenteiras
2,67
801,2
2648,6
Fm Itaim
6,32
700,0
2675,0
Fm Jaicós
5,46
717,3
2670,5
Fm Tianguá
3,80
759,8
2659,4
Fm Ipu
6,32
700,0
2675,0
Vulcânica (diabásio)
2,60
800,0
2800,0
Fonte: Modificada de BEICIP-FRANLAB (2011). Os parâmetros em vermelho foram
extraídos de HANTSCHEL & KAUERAUF (2009).
Acre e Médio Amazonas, cuja TSR máxima é de 26,6 °C (80 °F), ou na Bacia do
Paraná de 24 °C (75 °F). Os limites mínimo e máximo do gradiente geotérmico da
bacia se encontram entre 13 °C/km (23,5 °F/km) e 27,0 °C/km (48,7 °F/km)
respectivamente. A média corresponde ao gradiente de 19,4 °C/km (35,0 °F/km).
Os valores de gradiente geotérmico encontrados para a Bacia do Parnaíba excedem
os 25 °C/km em 48% dos casos e ocorrem em todas as faixas de profundidade. Essas
características atribuem para a Bacia uma condição geotérmica superior à de outras
paleozoicas intracratônicas brasileiras.
61
Figura 6-11: Gradientes geotérmicos da Bacia do Parnaíba.
Fonte: ZEMBRUSCKI & CAMPOS (1988)
6.2.6 Dados de Maturação
Embora, num contexto amplo, haja poucas informações disponíveis sobre a maturação
térmica na Bacia do Parnaíba, dados preciosos foram obtidos do trabalho de
RODRIGUES (1995). Um trabalho completo acerca da geoquímica orgânica da bacia
foi realizado por este autor com os dados disponíveis na época.
São disponibilizados dados de reflectância de vitrinitas para os poços 1-PA-1-MA; 1CI-1-MA; 1-IZ-2-MA; e 2-CP-1-MA, que foram utilizados na calibração da modelagem
térmica e extrapolados para outros pontos. O efeito térmico das intrusões ígneas pode
ser observado no poço 2-CP-1-MA, em que o índice de reflectância de vitrinita
apresenta um salto chegando ao valor de 3 %Ro na profundidade de 2.350 m, à
medida que se aproxima das intrusões (Figura 6-12). Segundo RODRIGUES (1995),
considerando apenas a subsidência da bacia, este intervalo sedimentar não atingiu
uma evolução térmica compatível a geração de hidrocarbonetos e, neste caso, essa
seção seria praticamente eliminada como potencial geradora de óleo e gás.
Entretanto, o modelo alternativo de geração, que considera o efeito térmico das
intrusões de diabásio, possibilita delinear algumas áreas de interesse segundo os
valores de maturação medidos (RODRIGUES, 1995).
62
Figura 6-12: Dados de carbono orgânico e reflectância de vitrinita do poço 2-CP-1-MA
Fonte: RODRIGUES (1995)
6.3
Modelagem térmica por contato intrusivo
6.3.1 Modelo bidimensional para análise da influência de intrusões ígneas
A principal proposta desse trabalho é aplicação do modelo bidimensional proposto por
VASCONCELOS (2010) para a análise da influência térmica de intrusões de diabásio
na Bacia do Parnaíba. Fenômenos térmicos, inclusive em bacias sedimentares, são
modelados pela equação de transferência de calor.
A equação de transferência de calor é obtida mediante a realização do balanço de
energia dentro de um volume de controle previamente estabelecido. Significa que a
variação de energia interna é uma combinação do calor conduzido para dentro e fora
do volume, da energia transferida por convecção e da energia adicionada ao sistema
devido à radiação ou geração (veja capítulo 4). A análise individualizada de cada
termo da equação permite uma melhor compreensão dessa combinação:
 ∂T 
λ∇
T = ρ p c p ∇ ⋅ (v p T ) +
Q
−∇
1
4⋅2
4
3
,
{r
1
4
4
2
4
4
3
t
∂


Difusão
Fonte
/
Sumikdouro
1424
3
Convecção
ρc r 
(28)
Acumulação
63
onde ρ , λ e c r são, respectivamente, a massa específica, condutividade térmica e
calor específico da rocha; ρ p , c p , v p são, respectivamente, a densidade, calor
específico e velocidade do fluido no poro e Qr é uma densidade de energia produzida
devido à radioatividade.
O modelo aqui aplicado assume as seguintes simplificações: a) ρ , λ e c r são
considerados constantes; b) o termo relativo à convecção é abandonado, pois a baixa
permeabilidade das rochas intrudidas levaria a uma baixa velocidade de escoamento
de fluido, portanto com influência reduzida no balanço global de energia; c) o termo
relativo à radioatividade seria abandonado, devido ao baixo efeito térmico do
decaimento radiométrico de minerais radioativos nas rochas do embasamento, se
comparado ao das intrusões. Pela simplificação, temos a equação difusiva conhecida
como equação de condução do calor (veja capítulo 4).
Os perfis térmicos do modelo bidimensional (VASCONCELOS, 2010) requerem a
adaptação de uma malha que divide as seções em blocos e posteriormente distribui as
propriedades físicas ao longo do domínio discreto (Figura 6-13). A Tabela 6-5,
apresenta o número de blocos gerados para cada perfil, mostrando que a malha foi
diferenciada, variando conforme o do tamanho da seção.
Tabela 6-5: Malha utilizada nas seções geológicas.
Seção
N-CP-SW
W-CP-E
NE-CP-SE
Malha considerada
Nº de blocos
7865 (65 x 121)
7378 (62 x 119)
7623 (63 x 121)
64
Figura 6-13: Exemplificação da malha aplicada na seção N-CP-SW, preparando-a para a
discretização das propriedades físicas. A linha amarela representa os limites dos blocos
que compõem a malha desta seção. O procedimento foi estendido às outras seções
utilizadas no projeto.
6.3.2 Ambiente de desenvolvimento
A avaliação da história térmica da bacia, neste trabalho, foi produto de um modelo
numérico implementado em linguagem C++ (Vasconcelos, 2010). Neste modelo, o
tratamento físico da condução de calor em uma bacia sedimentar influenciada por
intrusões ígneas foi desenvolvido pelo Método das Diferenças Finitas (MDF), mais
especificamente, a classe de Método de Direções Alternadas (ADI). Este método é
geralmente útil na solução de equações diferenciais multi-dimensionais e transientes,
pois consiste na separação de variáveis que são tratadas independentemente. Para
modelos bidimensionais, como o utilizado neste trabalho, em uma malha igualmente
dividida, a aplicação do método ADI resulta na formação de 2n sistemas lineares
tridiagonais (equivalente à solução de 2n problemas unidimensionais), o que leva a
uma resolução extremamente simples e com maior facilidade para implementação
(VASCONCELOS, 2010).
65
6.4
Reconstrução do embasamento (história térmica da bacia)
As seções geológicas extraídas do bloco 3D (Figuras 6-7 a 6-9) foram utilizadas na
aplicação da técnica de backstripping. O objetivo é a reconstrução do embasamento,
obtido pela curva também chamada de backstripping.
A reconstrução do
embasamento é possível porque esta técnica consiste na remoção das camadas de
uma bacia sedimentar e consequente descompactação das camadas subjacentes,
obtendo-se a subsidência tectônica da bacia. Neste trabalho, o backstripping foi obtido
a partir de aplicativo anteriormente implementado. Tal aplicativo consiste no
processamento da equação que define a curva de backstripping (veja capítulo 5).
Do mesmo modo, o cálculo do estiramento crustal, objetivando a obtenção do fluxo
térmico no embasamento a partir modelos termomecânicos, foi obtido a partir de
aplicativo previamente implementado. Tal aplicativo foi desenvolvido em linguagem
CC+ e reproduz analiticamente as formulações publicadas nos trabalhos de
MCKENZIE (1978) e de ROYDEN & KEEN (1980).
6.5
Modelagem da maturação da matéria orgânica
O processo de evolução térmica de uma bacia sedimentar está relacionado
diretamente à maturação térmica da matéria orgânica presente em rochas
sedimentares. A partir do soterramento, a matéria orgânica transformada em
querogênio alcança diversas mudanças composicionais impostas pela ação da
temperatura
e
pressão.
A
evolução
térmica
culmina
com
a
geração
de
hidrocarbonetos, cujo tempo e a profundidade de geração podem ser identificados
pela modelagem térmica da bacia. O conhecimento da evolução térmica e as
temperaturas envolvidas no processo requerem o uso de métodos geoquímicos que
traduzam a história térmica a partir de indicadores de paleotemperaturas.
Neste trabalho, o indicador do estágio de maturação orgânica é a vitrinita, um maceral
de origem lenhosa contido na matéria orgânica, que possui uma reflectância (%Ro)
característica sob luz refletida em miscroscópios petrográficos, o que a difere de
outros macerais. A reflectância da vitrinita (%Ro) constitui um dos mais importantes
parâmetros utilizados para estudos da evolução térmica da matéria orgânica contida
nos sedimentos (SWEENEY & BURNHAM, 1990). Parte-se do princípio que a
reflectância da vitrinita é sensível à variação positiva das temperaturas ao longo do
66
tempo geológico, uma vez que o aumento da temperatura provoca alterações
irreversíveis na estrutura molecular deste maceral.
Em termos práticos, considerando a história térmica da rocha, quanto maiores os
valores de %Ro, maior o estágio de maturação. No processo de evolução térmica da
matéria orgânica, os intervalos de geração de hidrocarbonetos podem ser definidos
pelos índices de reflectância de vitrinitas (Figura 6-14). A “janela de geração de óleo”
está entre 0,6 a 1,3% Ro e a “janela de geração de gás” entre 1,3 a 4,0% Ro, com o
limite entre gás úmido e seco sendo 2,0% Ro (SANTOS NETO, 2004).
Figura 6-14: Diagrama com a evolução térmica da matéria orgânica.
Fonte: SANTOS NETO (2004).
Para o cálculo das reflectâncias de vitrinitas como indicador de maturação de rochas
geradoras, foi usado método EasyRo de SWEENEY & BURNHAM (1990), que será
descrito adiante.
6.5.1 Método Easy%Ro
Atualmente, o modelo Easy%Ro proposto por SWEENEY & BURNHAM (1990) é o
mais aceito nas análises de bacia para cálculo de %Ro. Neste método, se integram
equações de cinética química ao longo do tempo e temperatura, sendo aplicável na
faixa de valores de refletividade da vitrinita (%Ro) de 0,3 a 4,5% e taxas de
67
aquecimento desde condições de laboratório, ºC/semana, a geológicos, ºC/milhão de
anos.
O método consiste em quantificar o grau de maturação da matéria orgânica, a partir de
reações paralelas de cinética química, baseadas em balanços de massa obtidos dos
resultados de pirólise experimental. Sua utilização é permitida em conjunto com
qualquer tipo de história térmica. Modelos baseados em cinética de reatividades
distribuídas, nas quais as reações se processam em taxas dependentes da
temperatura e da quantidade de reagente disponível, são amplamente utilizados.
Essas reações podem ser descritas como de primeira ordem de acordo com a Lei de
Arrhenius, onde a quantidade do componente x em função do tempo dada por:
κ = Ae
−E
RT
(28)
onde κ é a taxa de reação, A = 1,0 × 1013 / s o fator de frequência, T é a temperatura
em o K , E a energia de ativação e R = 8,31447Ws / mol / oK é constante universal dos
gases.
O fator de frequência representa a frequência em que as moléculas são
transformadas. A energia de ativação descreve o limiar de energia necessário para
que a reação inicie.
O modelo Easy%Ro considera um conjunto paralelo de quatro reações de primeira
ordem que compreendem: eliminações de água (H2O), de dióxido de carbono (CO2),
de metano (CH4) de hidrocarbonetos pesados (CHn). Para cada reação há uma
distribuição de energia, porém com um mesmo fator de frequência. Desse modo, cada
uma dessas reações é descrita como uma reação paralela de decomposição que
apresenta um conjunto discreto de energias de ativação:
κ 1i
vitrinita →
vitrinita residual + H2O
2i
vitrinita κ→
vitrinita residual + CO2
3i
vitrinita κ→
vitrinita residual + CH4
4i
vitrinita κ→
vitrinita residual + CHn
68
O modelo Easy%Ro foi implementado no modelo numérico bidimensional para análise
da influência do efeito térmico de intrusões ígneas em bacias sedimentares,
desenvolvido por Vasconcelos (2010), que será aplicado nesse trabalho. O modelo
químico-matemático foi detalhadamente descrito em VASCONCELOS (2010), além de
(SWEENEY & BURNHAM, 1990).
69
7. Modelagem da estrutura térmica da Bacia do Parnaíba
7.1
Calibração do modelo
Os processos físico-químicos atuantes em uma bacia sedimentar que possibilitam a
acumulação do petróleo podem ser simulados a partir de modelos matemáticos
incluídos em programas específicos que descrevem sua evolução geométrica, térmica,
de pressões, além dos fenômenos de geração, expulsão e migração do petróleo
(COUTINHO, 2008). Os modelos em 1D, 2D ou 3D abordam diferentes aspectos do
mesmo problema e devem ser utilizados de forma integrada (COUTINHO, 2008).
Neste trabalho, utilizou-se o programa Temis3D (Instituto Francês do Petróleo) para
construção do bloco 3D (veja item 6.2.1 do capítulo 6), do qual foram extraídas as
seções para a modelagem térmica. Uma vez extraídas as seções (Figura 6-6), utilizouse o programa Temis2D (IFP) para a reprodução da história térmica e da maturação
das rochas geradoras. O objetivo foi a comparação dos resultados do efeito das
intrusões sobre as camadas sedimentares das seções com os obtidos com o modelo
bidimensional de VASCONCELOS (2010).
Na simulação térmica realizada com o Temis2D, utilizou-se os módulos de
descompactação e térmico. O módulo de descompactação permite simular a evolução
geométrica de cada célula da seção que representa a camada sedimentar. Considera
que a alteração do espaço poroso no curso da sedimentação e soterramento pode ser
descrita por leis de compactação normais, invariáveis no tempo geológico. O módulo
térmico calcula a distribuição de temperaturas ao longo das células da seção 2D, que
representa a bacia sedimentar, considerando a evolução geométrica fornecida
previamente pelo módulo de descompactação e a variação do fluxo de calor no
sistema. Desta forma foi obtido o efeito térmico devido a ocorrência da intrusão.
Para a reconstrução da história térmica nas bacias sedimentares, é necessário
estabelecer as condições de contorno do modelo térmico. Para a simulação com o
Temis2D, acerca das intrusões ígneas, essas condições envolveram uma temperatura
de superfície estimada de 22 ºC para a época da intrusão. O fluxo térmico basal
considerado foi de 50 mW/m2, conforme proposto por POLLACK et al., (1993) como
valor aproximado para bacias paleozoicas. O efeito térmico adicional inicia a partir do t
(tempo) = 178 milhões de anos, quando ocorreu a intrusão das rochas básicas
70
eojurássicas (VAZ et al., 2007). No modelo proposto estas intrusões são consideradas
instantâneas (Figura 7-1 a 3).
Os dados disponíveis permitiram, no caso da seção N-CP-SW, inferir intrusões ígneas
de grandes extensões. Como resultado, esta seção foi fortemente influenciada pelos
efeitos térmicos proporcionados pelo calor emanado por estas rochas. As intrusões
estão presentes na Sequência Siluriana na porção basal da bacia, formações Ipu e
Tianguá, e na Sequência Mesodevoniana-Eocarbonífera, porção intermediária,
formações Pimenteiras e Longá. Percebe-se que sob o poço 2-CP-1-MA, ocorrem
várias soleiras sobrepostas, tornando expressivos os efeitos térmicos, que alcançam,
a partir do contato, até o dobro da espessura da intrusão (Figura 7-1).
A palheta de cores ao lado direito da simulação mostra os intervalos de refletividade
da vitrinita. Influenciado pelo aumento da temperatura o índice %Ro registra os
estágios de maturação térmica das rochas sedimentares.
N-CP-SW
Figura 7-1: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas nas
camadas da seção N-CP-SW. Resultados obtidos com o Temis2D. Conforme legenda
que acompanha a seção, a profundidade e o comprimento estão em metros.
As intrusões da seção W-CP-E, com base nas informações disponíveis, ocorrem
localmente. Estão presentes na Sequência Siluriana, formações Ipu e Tianguá, mas
predominam na Sequência Mesodevoniana-Eocarbonífera, nas formações Pimenteiras
e Longá. A simulação térmica mostra que a maior influência está nos contatos das
intrusões, alcançando até o dobro da espessura das mesmas. Nota-se que acima e
71
abaixo das intrusões o efeito é maior que nas laterais devido ao empilhamento das
soleiras. Os intervalos com os índice de %Ro na legenda, registram os estágios de
maturação térmica das rochas sedimentares (Figura 7-2).
W-CP-E
Figura 7-2: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas nas
camadas da seção W-CP-E. Resultados obtidos com o Temis2D. Conforme legenda que
acompanha a seção, a profundidade e o comprimento estão em metros.
As intrusões da seção NE-CP-SE, com base nas informações disponíveis, também
são locais e apresentam similaridade com a seção W-CP-E quanto à ocorrência nas
sequências. A simulação térmica mostra que a maior influência está nos contatos das
intrusões, alcançando até, aproximadamente, o dobro da espessura. Nota-se que
acima e abaixo das intrusões o efeito é maior que nas laterais, devido ao
empilhamento de soleiras. Os intervalos com os índice de %Ro, na legenda, registram
os estágios de maturação térmica (Figura 7-3).
A Figura 7-4 mostra a curva de variação do índice %Ro em profundidade. Os índices
alcançam valores superiores a 4% nas Sequências Siluriana (Formação Tianguá) e
Mesodevoniana-Eocarbonífero (formações, Pimenteiras e Tianguá) à medida que se
aproximam das intrusões ígneas.
72
NE-CP-SE
Figura 7-3: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas nas
camadas da seção NE-CP-SE. Resultados obtidos com o Temis2D. Conforme legenda
que acompanha a seção, a profundidade e o comprimento estão em metros.
Neocretáceo
Eotriássico
Pedra de Fogo
Piauí
Poti
Vulcânica
Cabeças
Vulcânica
Pimenteiras
Itaim
Jaicós
Tianguá
Figura 7-4: Modelagem térmica bidimensional avaliando o efeito de intrusões ígneas no
poço 2-CP-1-MA. Resultados obtidos com o Temis2D, extraídos da seção N-CP-SW.
73
Os pontos na cor laranja correspondem a dados reais de vitrinita do poço 2-CP-1-MA
(RODRIGUES, 1995) que corrobora com um bom ajuste para a curva. A palheta à
direita da curva representa as espessuras aproximadas das formações que compõem
a seção no poço.
O petróleo, que por um processo convencional de soterramento, se forma a uma
temperatura relativamente baixa, porém em um longo período do tempo geológico,
também pode ocorrer quase instantaneamente nas proximidades das intrusões devido
às altas temperaturas ali presentes. A Figura 7-5 mostra a simulação do efeito térmico
das intrusões obtido pelo modelo bidimensional de VASCONCELOS (2010). A escala
à direita mostra a maturação térmica para a seção N-CP-SW, utilizando a técnica
Easy%Ro implementada no modelo. As condições de contorno estabelecidas para
esta simulação envolveram uma temperatura de superfície de 22 ºC. O fluxo térmico
basal considerado foi de 50 mW/m2. O efeito térmico inicia a partir do t (tempo) = 178
milhões de anos, quando ocorreu a intrusão das rochas básicas Eojurássicas (VAZ et
al., 2007). Estas condições são compatíveis com aquelas utilizadas nas simulações do
Temis2D (Figura 7-1), justamente para permitir a comparação entre os resultados.
Os resultados deste modelo, para o efeito térmico das intrusões eojurássicas na
seção N-CP-SW, apresentam, nas proximidades das mesmas, índices de evolução
térmica que alcançam entre 2% a 3,5% representados, segundo a graduação da
palheta, pelas cores azul claro e laranja respectivamente. No contato com as intrusões
e suas adjacências os valores superam 4% (cor marrom). O efeito termal é maior na
vertical, como ocorre também com a simulação do Temis2D.
Figura 7-5: Efeito da maturação térmica através do modelo Easy%Ro após o evento de
intrusão ígnea. A escala da esquerda representa a profundidade em metros e a da direita
o índice %Ro para a refletividade da vitrinita. Resultados obtidos pelo modelo
bidimensional de VASCONCELOS (2010).
74
Os resultados de ambos, Temis2D e do modelo bidimensional, permitem concluir que
nas regiões próximas às intrusões magmáticas de grande extensão, como a seção NCP-SW, a maturação da matéria orgânica foi fortemente controlada pelo calor liberado,
evidenciada pelos altos valores de vitrinita.
Dados teóricos de índices de reflectância da vitrinita do poço 2-CP-1-MA em cada uma
das seções N-CP-SW, NE-CP-SE e W-CP-E, obtidos do perfil de maturação gerado
pela simulação com o modelo bidimensional, foram comparados com dados reais
publicados por RODRIGUES (1995). Na Figura 7-6 observa-se, para um determinado
intervalo de profundidade, a variação nos índices obtidos. A comparação entre os
índices de maturação térmica obtidos é de grande importância na validação do
modelo, pois, embora tenha sido aplicado anteriormente na Bacia do Solimões, é a
primeira vez que pôde ser calibrado com dados reais.
%Ro
1
1,5
2
2,5
3
3,5
2250
Profundidade (m)
2300
2350
2400
2450
2500
W-CP-E
N-CP-SW
NE-CP-SE
Dados Reais
Figura 7-6: Comparação dos índices de reflectância da vitrinita com dados reais obtidos
de RODRIGUES (1995). Simulação considerando o efeito térmico das intrusões e fluxo
térmico constante no embasamento.
A diferença no ajuste da curva pode ser explicada pela resolução da malha. Dada uma
malha única, uma seção menor será mais refinada, e por sua vez terá uma resposta
mais efetiva à influência do fluxo térmico por unidade de área. Este é o caso da seção
NE-CP-SW que possui uma extensão menor que as demais. A seção N-CP-SW possui
uma malha de 122 pontos (em x) no seu comprimento, por 65 pontos (em y) na
75
profundidade. Isto representa a escala de 1:6150 metros (em x) e 1:50 metros (em y),
o que indica que a malha deveria ser refinada, em função da sua extensão. Diferenças
nos ajustes das curvas também podem ser explicadas pelas aproximações assumidas
na elaboração do bloco 3D, devido a interpolação das camadas no Temis3D. Outras
implicações no ajuste podem decorrer do tratamento dado às discordâncias regionais,
sem detalhamento na geometria das seções.
Para esta simulação utilizou-se um fluxo térmico constante, entretanto, de acordo com
a metodologia discutida, as correções para o fluxo térmico basal podem influenciar o
comportamento dos valores, proporcionando um melhor ajuste aos dados reais.
7.2
Modelagem termomecânica
A avaliação termomecânica de uma bacia sedimentar envolve a determinação da
subsidência tectônica e da subsidência termal (veja capítulo 5). A subsidência
tectônica é calculada a partir da reconstrução da sequência evolutiva da bacia que
define o histórico de subsidência da mesma sob o peso dos sedimentos depositados.
Neste trabalho foi utilizada a técnica de backstripping para esta finalidade.
Entretanto, a determinação da subsidência termal define o comportamento do
embasamento considerando apenas os efeitos térmicos atuantes na bacia. Foi
utilizado o modelo de estiramento litosférico não-uniforme de ROYDEN & KEEN
(1980). Esse modelo de estiramento litosférico, permite o cálculo do fluxo térmico no
embasamento, principal aplicação neste trabalho. A Tabela 7-1 apresenta os valores
dos parâmetros utilizados na aplicação dos modelos. Os modelos foram aplicados à
sete poços situados ao longo das seções modeladas (Figura 7-7).
O cálculo do fluxo térmico basal obtido com a restauração do embasamento e com o
modelo termomecânico permitiu o uso de condições de contorno variáveis na
modelagem dos efeitos térmicos de intrusões ígneas na bacia.
76
Tabela 7-1: Valores dos parâmetros utilizados na aplicação dos modelos
Parâmetros Descrição dos parâmetros
Valor
Unidade
ρw
densidade da água
1
ρm
densidade do manto
3,3
ρc
a
tc
densidade da crosta
espessura inicial da litosfera
espessura inicial da crosta
2,8
200
35
α
τ
λ
kw
coeficiente de expansão térmica da litosfera
constante de tempo da litosfera
condutividade térmica do embasamento
condutividade térmica da água
T1
temperatura na base da litosfera
k
difusibilidade da litosfera
3,28 10-5
62,8
4,6
0,56
g/cm³
km
ºC-1
Ma
W/m.K
1333
ºC-1
8,0 10-7
m²/s
Fonte: QUINTAS et al. (1999) e CARDOSO et al. (2007).
Figura 7-7: Localização dos sete poços utilizados na determinação da história
termomecânica da Bacia do Parnaíba. Seções: em vermelho N-CP-SW; em rosa W-CP-E;
em azul NE-CP-SE.
Fonte: Elaboração própria a partir de dados da ANP/BDEP (2011).
77
7.2.1 Reconstrução sedimentar
O objetivo da reconstrução sedimentar é a reconstituição dos movimentos verticais do
embasamento e das camadas sedimentares sobrejacentes, depositadas desde a fase
de formação da bacia, fase rifte, até o tempo Recente, nos fornecendo a subsidência
tectônica da bacia. No caso da Bacia do Parnaíba, a fase inicial de formação da bacia,
está associada ao final do Ciclo Brasiliano, por volta de 500 milhões de anos.
Na avaliação da subsidência tectônica através do processo de backstripping é
necessário adotar, inicialmente, um modelo de ajustamento isostático representativo
do processo de evolução geológica da bacia em questão (CARDOSO, 2007). Nesta
modelagem, o mecanismo de ajustamento isostático indicado é do tipo local, também
denominado Airy.
A aplicação da técnica do backstripping requereu um algoritmo para implementar a
equação 27 (veja capítulo 5). No entanto, neste modelo, as correções para a
batimetria e a eustasia foram desconsideradas. A partir do procedimento do
backstripping foram elaboradas as curvas de subsidência tectônica das camadas
sedimentares e do embasamento para os sete poços que cortam as seções
modeladas. Da Figura 7-8 a 7-14 são retratadas as curvas que caracterizam a
variação vertical das camadas ao longo do tempo geológico. É importante ressalvar
que este modelo não contemplou de forma detalhada o estudo das discordâncias
regionais da bacia.
A curva de subsidência tectônica obtida com o backstripping, também chamada de
subsidência real, é usada na obtenção dos fatores de estiramento dos modelos de
estiramento litosférico, pois as variações destes fatores refletem diretamente no
espaço deposicional criado. Portanto, a subsidência tectônica funciona como uma
calibração para a curva de subsidência termal modelada com os modelos
termomecânicos, que relacionam a taxa de subsidência tectônica com a história do
fluxo térmico no embasamento.
O perfil de subsidência tectônica apresenta-se regular para todos os poços analisados,
o que pode ser evidenciado na similaridade entre os parâmetros de estiramento
encontrados (Tabela 7-2). Estes resultados refletirão no valor da média do fluxo
térmico basal obtido, como veremos à frente.
78
Idade (Ma)
439
405
380
349
297
0
0
400
800
1.600
2.000
Profundidade (m)
1.200
2.400
2.800
2-CP-1-MA
3.200
Subsidência Tectônica
Subsidência Total
Figura 7-8: Curvas de subsidência tectônica e total do embasamento do poço 2-CP-1-MA
que corta as seções N-CP-SW, W-CP-E e NE-CP-SE.
439
405
Idade (Ma)
380
349
297
0
0
400
1200
1600
Profundidade (m)
800
2000
9-PAF-3-MA
2400
Subsidência Tectônica
Subsidência Total
Figura 7-9: Curvas de subsidência tectônica e total do embasamento do poço 9-PAF-3MA que corta a seção N-CP-SW.
79
Idade (Ma)
439
405
380
349
297
0
0
400
1200
Profundidade (m)
800
1600
1-TM-1-MA
2000
Subsidência Tectônica
Subsidência Total
Figura 7-10: Curvas de subsidência tectônica e total do embasamento do poço 1-TM-1MA que corta as seções N-CP-SW.
Idade (Ma)
439
405
380
349
297
0
0
400
1200
1600
Profundidade (m)
800
2000
1-IZ-2-MA
2400
Subsidência Tectônica
Subsidência Total
Figura 7-11: Curvas de subsidência tectônica e total do embasamento do poço 1-IZ-2-MA
que corta a seção W-CP-E.
80
Idade (Ma)
439
405
380
349
297
0
0
400
1200
1600
Profundidade (m)
800
2000
1-MA-1-PI
2400
Subsidência Tectônica
Subsidência Total
Figura 7-12: Curvas de subsidência tectônica e total do embasamento do poço 1-MA-1-PI
que corta as seções W-CP-E.
Idade (Ma)
439
405
380
349
297
0
0
400
1200
1600
2000
Profundidade (m)
800
2400
2-BGST-1-MA
2800
Subsidência Tectônica
Subsidência Total
Figura 7-13: Curvas de subsidência tectônica e total do embasamento do poço 2-BGST1-MA que corta a seção NE-CP-SE.
81
Idade (Ma)
439
405
380
349
297
0
0
400
800
1600
2000
2400
Profundidade (m)
1200
2800
2-VGST-1-MA
3200
Subsidência Tectônica
Subsidência Total
Figura 7-14: Curvas de subsidência tectônica e total do embasamento do poço 2-VGST-1MA que corta a seção NE-CP-SE.
7.3
Subsidência termal
Como visto em detalhe no capítulo 4, a subsidência termal é causada pelo processo
de resfriamento associado à perda de calor por condução e consequentes contrações
térmicas da litosfera. Isto permite determinar a subsidência do embasamento em
consequência apenas dos processos térmicos ocorridos na evolução da bacia. Com
base na evolução tectônica e termal da bacia torna-se possível a avaliação do campo
térmico da litosfera desde o período inicial da formação da bacia.
A subsidência termal, neste trabalho, foi modelada pelo modelo de duas camadas, ou
modelo de extensão não-uniforme de ROYDEN & KEEN (1980). Para isso foram
aplicadas as formulações 24, 25 e 26 (veja capítulo 5) que se referem ao cálculo da
subsidência inicial, subsidência termal e fluxo térmico respectivamente. Os fatores de
estiramento δ e β foram determinados pelo ajuste entre as curvas do backstripping e
a modelada, conforme descrito acima, pelo modelo de duas camadas.
A relação entre as curvas está na proporção direta entre o estiramento e a
subsidência. Entretanto, devido à imprecisão ou ausência de informações sobre
paleobatimetria nem sempre é possível obter um ajuste exato (PINTO, 2008). Uma
medida que ajuda a minimizar a incerteza é calibrar os pontos da profundidade da
subsidência inicial (rifte) e do tempo presente obtida diretamente a partir de dados dos
82
poços. Os valores dos graus de estiramento para δ e β encontrados por este método
estão na Tabela 7-2.
Tabela 7-2: Valores dos graus de estiramento para δ e β obtidos pelo modelo de
ROYDEN & KEEN (1980).
Modelo Não-Uniforme
Poço
Royden & Keen
δ
β
2-CP-1-MA
1,046
1,087
β
δ
9-PAF-3-MA
1,030
1,065
1-TM-1-MA
1,030
1,048
1-IZ-2-MA
1,040
1,070
1-MA-1-PI
1,032
1,070
2-VGST-1-MA
1,026
1,047
2-BGST-1-MA
1,037
1,070
Os estiramentos crustais ( δ ) encontrados estão entre 1,03 e 1,05 e os subcrustais
( β ) entre 1,05 e 1,09. Esses valores variam pouco entre os setes poços
considerados. Valores muito próximos de δ e β , no modelo de duas camadas,
indicam um padrão de subsidência similar do manto litosférico e da crosta (ROYDEN,
& KEEN, 1980). Os ajustes das curvas teóricas de subsidência tectônica determinadas
pelo backstripping e as curvas de subsidência termal obtida pelo modelo
termomecânico de ROYDEN & KEEN (1980) são apresentados da Figura 7-15 à 7-21.
Figura 7-15: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 2-CP-1-MA.
83
Figura 7-16: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 9-PAF-3-MA.
Figura 7-17: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 1-TM-1-MA.
Figura 7-18: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 1-IZ-2-MA.
84
Figura 7-19: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 1-MA-1-PI.
Figura 7-20: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 2-VGST-1-MA.
Figura 7-21: Curvas de subsidência tectônica obtida pelo backstripping e termal obtida
pelo modelo de ROYDEN & KEEN, poço 2-BGST-1-MA.
85
7.4
Fluxo térmico
Uma vez determinados os parâmetros de estiramento, foi aplicada a formulação 25
(veja capítulo 5) para aplicação do modelo de ROYDEN & KEEN (1980) na obtenção
do fluxo térmico e reconstituição da sua história evolutiva. Posteriormente foi a
utilizado o fluxo térmico calculado, para a época da intrusão, na modelagem do efeito
térmico.
A Figura 7-22 apresenta a variação do fluxo térmico após o estiramento inicial até o
Recente, na localização dos sete poços que cortam as seções estudadas (Figura 7-7).
A diminuição do fluxo térmico ao longo do tempo geológico indica a dissipação
gradativa da anomalia térmica, gerada no período do estiramento inicial, nos primeiros
30 milhões de anos da bacia. O fluxo térmico apresenta uma baixa variação no tempo,
contudo no momento inicial os valores apresentam-se mais altos. Os valores máximo
e mínimo encontrados para o fluxo térmico no momento inicial correspondem a 57,69
mW/m² e 57,02 mW/m², respectivamente, para os poços 2-CP-1-MA e 2-VGST-1-MA.
58
Fluxo Térmico (mW/m²)
1-IZ-2-MA
1-MA-1PI
57
1-TM-1MA
56
2-BGST-1-MA
2-CP-1-MA
55
9-PAF-3-MA
2-VGST-1-MA
54
0
100
200
300
400
500
Tempo após estiramento inicial (Ma)
Figura 7-22: Variação temporal do fluxo térmico nos poços que cortam as seções
estudadas, a partir do modelo de ROYDEN & KEEN (1980).
Observa-se ainda que no período de subsidência inicial, ou seja, nos primeiros 10
milhões de anos, o fluxo térmico apresenta uma queda acentuada, característica
dessa fase. Entre 30 e 40 milhões de anos ocorre uma suave elevação.
86
Posteriormente,
com
a
dissipação
da
anomalia,
o
fluxo
térmico
decai
progressivamente até o presente.
Através da observação do comportamento do fluxo térmico ao longo da história da
bacia, é possível notar sua relação com a subsidência termal ocorrida, ou melhor, com
o grau de estiramento da litosfera. Quando ocorre diminuição no grau de estiramento
da litosfera há uma queda no valor do fluxo térmico. Segundo MCKENZIE (1978),
fatores de extensão litosférica menores que 1,5 não induzem variações significativas
no fluxo térmico, o que pode ser constatado na Figura 7-22.
Os resultados obtidos para o fluxo térmico basal apresentam uma regularidade, onde
se conclui que o valor médio de 55,1 mW/m² poderia ser aplicado como constante à
base da bacia na modelagem térmica das intrusões. Entretanto uso de condições de
contorno variáveis, que se propõe, é admitido como uma melhoria na análise da
estrutura térmica de bacias sedimentares.
7.5
Estruturação térmica da Bacia do Parnaíba considerando fluxo
térmico basal e de intrusões ígneas
Visando analisar o efeito térmico das intrusões ígneas nas rochas sedimentares da
bacia, propõe-se o uso do modelo bidimensional implementado por VASCONCELOS
(2010).
Originalmente,
este
modelo
foi
aplicado
na
Bacia
do
Solimões
(VASCONCELOS, 2010), entretanto utilizou-se como condição de contorno um fluxo
térmico basal constante. Para a avaliação da evolução termomecânica da Bacia do
Parnaíba foram implementadas modificações no algoritmo numérico do modelo
bidimensional. Estas modificações possibilitaram a definição de condição de contorno
variável no embasamento, mediante a interpolação dos diferentes valores de fluxo
térmico dos poços existentes ao longo da seção. Na Tabela 7-3 encontram-se os
fluxos térmicos basais utilizados no modelo bidimensional.
A temperatura de superfície considerada é de 27 ºC, calibrada com dados
geotérmicos apresentados em ZEMBRUSCKI & CAMPOS (1988). O efeito térmico
inicia a partir do t (tempo) = 178 milhões de anos, quando ocorreu a intrusão das
rochas básicas eojurássicas (VAZ et al., 2007), consideradas instantâneas.
87
A temperatura da base da bacia foi calculada considerando o fluxo térmico, os
parâmetros físicos e as propriedades das rochas (veja capítulo 6). A Tabela 7-4
apresenta a temperatura no embasamento para os sete poços que cortam as seções.
Tabela 7-3: Fluxo térmico calculado para os sete poços, na idade aproximada de
ocorrência da intrusão.
Fluxo
Poço
Intrusão
Térmico
(Ma)
(mW/m²)
2-CP-1-MA
~180
55,119
9-PAF-3-MA
~180
55,099
1-TM-1-MA
~180
55,090
1-IZ-2-MA
~180
55,107
1-MA-1-PI
~180
55,103
2-VGST-1-MA
~180
55,087
2-BGST-1-MA
~180
55,109
Da Figura 7-23 a 7-25 são apresentados os resultados obtidos com o modelo
bidimensional para a simulação do efeito térmico das intrusões. É possível observar o
contorno das intrusões ígneas nas porções com alto índice de evolução térmica.
Nessas proximidades os índices alcançam valores de reflectância superiores a 4,5%.
Ainda próximo às intrusões, porém fora do contato, apresenta-se um intervalo com
uma maturação térmica progressiva, com um intervalo de índices de 3,5% a 2%,
representados pelas cores laranja e azul claro respectivamente e à medida que se
afastam da intrusão. Observa-se a proeminência do fluxo térmico na vertical.
Tabela 7-4: Temperatura no embasamento para os poços que cortam as seções.
Temperatura em Kelvin.
Seção/poço
Temperatura
basal
(K)
Seção N-CP-SW
9-PAF-3-MA
2-CP-1-MA
1-TM-1-MA
323
340
331
Seção W-CP-E
1-IZ-2-MA
2-CP-1-MA
1-MA-1-PI
331
337
320
Seção NE-CP-SE
2-VGST-1-MA
2-CP-1-MA
2-BGST-1-MA
324
337
330
88
Figura 7-23 representa a influência do calor das intrusões na seção N-CP-SW. Neste
caso, são indicadas nas janelas de geração de gás áreas ainda não exploradas, com
potencial para a existência de hidrocarbonetos. Mostra-se favorável a região situada a
oeste da figura, na profundidade aproximada de 2.300m, localização do poço 2-CP-1MA. Outro ponto de interesse refere-se à porção entre intrusões situada a leste da
figura na profundidade aproximada de 1.700m.
Figura 7-23: Efeito térmico das intrusões ígneas e maturação térmica na seção N-CP-SW.
Obtido a partir do modelo de VASCONCELOS (2010)
A Figura 7-24 representa a influência do calor das intrusões na seção W-CP-E. O
efeito térmico mostra-se pontual, de acordo com a ocorrência de intrusões. Nas
proximidades das intrusões, a uma profundidade aproximada de 2.300m, são
observadas regiões com potencial exploratório, propícias à existência de gás natural.
Figura 7-24: Efeito térmico das intrusões ígneas e maturação térmica na seção W-CP-E.
Obtido a partir do modelo de VASCONCELOS (2010)
89
A Figura 7-25 representa a influência do calor das intrusões na seção NE-CP-SE. O
efeito térmico nesta seção também é localizado, mas a 2000m de profundidade, em
camadas intercaladas por intrusões, são observadas regiões com potencial
exploratório, propícias à existência de gás natural.
Figura 7-25: Efeito térmico das intrusões ígneas e maturação térmica na seção NE-CPSE. Obtido a partir do modelo de VASCONCELOS (2010).
7.6
Maturação térmica
A Figura 7-26 mostra a simulação da maturação térmica para a seção N-CP-SW,
utilizando a técnica Easy%Ro implementada no modelo de VASCONCELOS (2010).
Os valores indicam, no caso da seção avaliada, a favorabilidade para a geração de
gás. Este resultado é corroborado por RODRIGUES (1995), que considerou as áreas
senis, com alta maturação térmica devido às intrusões de diabásio, as melhores para a
prospecção de gás na bacia do Parnaíba.
A análise de gás do poço 2-CP-1-MA, que corta a seção N-CP-SW (Figura 7-1)
demonstra que o mesmo foi gerado em nível de evolução térmica correspondente a
aproximadamente 2% de reflectância de vitrinita a partir do efeito térmico
(RODRIGUES, 1995).
O efeito térmico das intrusões é facilmente visualizado no perfil de maturação invertido
(dados de reflectância da vitrinita), indicando um efeito térmico decrescente à medida
que se afasta do corpo intrusivo (Figura 7-26). Os maiores índices da curva são
90
referentes às profundidades de ocorrência das intrusões nas formações Pimenteiras e
Longá, conforme também observado na Figura 7-4.
Os resultados obtidos no perfil de maturação para o poço 2-CP-1-MA na seção W-CPE (Figura 7-27) e na NE-CP-SE (Figura 7-28) são similares aos da seção N-CP-SW,
com níveis de evolução térmica variáveis, que alcançam até 4,5% de reflectância de
vitrinita nas adjacências das intrusões. Contudo, observa-se que a seção NE-CP-SE
(Figura 7-28) apresenta uma calibração maior com relação ao perfil obtido com o
programa Temis2D (Figura 7-4).
Dados teóricos de índices de reflectância da vitrinita do poço 2-CP-1-MA, em cada
uma das seções N-CP-SW, NE-CP-SE e W-CP-E, obtidos do perfil de maturação
gerado pela simulação com o modelo bidimensional, foram novamente comparados
com dados reais (Figura 7-29). Esta comparação considera as modificações
implementadas no algoritmo numérico, que possibilita a definição de condição de
contorno variável no embasamento. Os resultados obtidos mostram que embora haja
regularidade no fluxo térmico, o uso de condição de contorno variável na base da
bacia permitiram uma melhor calibração com dados reais.
Seção N-CP-SW
0,0
0,5
1,0
1,5
2,0
2,5
3,0
Easy%Ro
3,5
4,0
4,5
5,0
0
Profundidade (m)
500
1000
1500
2000
2500
3000
Figura 7-26: Perfil de maturação térmica para o poço 2-CP-1-MA na seção N-CP-SW.
Obtido pelo método EASY%Ro, implementado no modelo bidimensional de Vasconcelos
(2010).
91
S eç ão W-C P -E
0,0
0,5
1,0
1,5
2,0
2,5
3,0
E a sy%R o
3,5
4,0
4,5
5,0
0
P rofundidade (m )
500
1000
1500
2000
2500
3000
Figura 7-27: Perfil de maturação térmica para o poço 2-CP-1-MA na seção W-CP-E.
Obtido pelo método EASY%Ro implementado no modelo bidimensional de Vasconcelos
(2010).
Seção NE-CP-SE
Easy%Ro
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
0
Profundidade (m)
500
1000
1500
2000
2500
3000
Figura 7-28: Perfil de maturação térmica para o poço 2-CP-1-MA na seção NE-CP-SE.
Obtido pelo método EASY%Ro, implementado no modelo bidimensional de Vasconcelos
(2010).
92
%Ro
1
1,5
2
2,5
3
3,5
Profundidade (m)
2250
2300
2350
2400
2450
2500
W-CP-E
N-CP-SW
NE-CP-SE
Dados Reais
Figura 7-29: Comparação dos índices de reflectância da vitrinita com dados reais obtidos
de RODRIGUES (1995).
93
8. Conclusões
Foi elaborado o bloco 3D para a Bacia do Parnaíba utilizando as espessuras de poços
disponíveis. O objetivo foi utilizar seções extraídas deste bloco para as modelagens
térmicas bidimensionais propostas.
Na modelagem das seções geológicas, relacionou-se a estrutura térmica ao fluxo
térmico basal e ao efeito térmico devido a intrusões ígneas comuns na bacia. Obtevese a história térmica do soterramento e o fluxo térmico no embasamento pela técnica
de backstripping e pelos modelos de extensão litosférica de MCKENZIE (1978) e
ROYDEN & KEEN (1980). Os valores de temperatura calculados na base foram
utilizados nas condições de contorno da modelagem, para avaliação do efeito térmico
devido às intrusões.
Estudos detalhados das discordâncias regionais e do arcabouço estrutural são
recomendados, pois proporcionarão uma melhoria dos resultados da reconstrução
sedimentar, logo das curvas de subsidência tectônica, que ajustam os modelos
teóricos.
Utilizou-se o modelo numérico bidimensional implementado por VASCONCELOS
(2010) na avaliação do efeito térmico das intrusões eojurássicas ocorridas na bacia.
Este modelo permitiu extrair perfis de temperatura e avaliar a maturação térmica da
bacia pelo método Easy%RO.
As simulações mostraram que o fluxo térmico do embasamento não foi suficiente para
a maturação térmica da bacia. Contudo, a soma do fluxo térmico basal com o fluxo
emanado das intrusões é responsável pela sua maturação térmica. Estas duas fontes
estão diretamente relacionadas com a geração de hidrocarbonetos confirmada pelos
sistemas petrolíferos lá existentes.
O fluxo térmico obtido possui regularidade, portanto, na modelagem do efeito térmico
por intrusões, poderia ter seu valor médio aplicado como condição de contorno
constante na base da bacia. Contudo, a definição de uma condição de contorno
variável no embasamento, mediante a interpolação dos diferentes valores de fluxo
térmico dos poços existentes ao longo da seção, proporcionou perfis de maturação
térmica com melhores ajustes com dados reais.
94
As simulações com o modelo bidimensional permitiram a verificação da abrangência
do efeito térmico das intrusões nas seções, a história térmica a partir de perfis de
maturação térmica pelo modelo Easy%Ro, e a identificação de janelas de gás.
Os valores de %Ro obtidos mostram que as intrusões foram fundamentais para o
potencial de geração hidrocarbonetos da bacia. Indicam potencial exploratório de
regiões ainda não exploradas e a favorabilidade para gás natural.
A influência do efeito térmico de intrusões ígneas na maturação térmica da Bacia do
Parnaíba mostra-se determinante para a geração de hidrocarbonetos, validando os
sistemas ditos não convencionais.
95
9. Referências Bibliográficas
AIRY, G.B. “On the Computation of the Effect of the Attraction of Mountain-Masses, as
Disturbing the Apparent Astronomical Latitude of Stations in Geodetic Surveys”,
Phil. Trans. R. Soc., London; v.145; pp. 101-104, 1855.
ALMEIDA, F. F. M., CARNEIRO, C. D. R. “Inundações Marinhas Fanerozóicas no
Brasil
e
Recursos
Minerais
Associados”.
In:
MANTESSO-NETO,
V.,
BARTORELLI, A., CARNEIRO, C. D. R., BRITO-NEVES, B. B. (eds). Geologia do
Continente Sul-Americano: Evolução da obra de Fernando Flávio Marques
de Almeida. 1 ed. capítulo 3, São Paulo, Beca, 2004.
ALVES D.B., RODRIGUES R. “Infuência das Intrusões Ígneas nos Folhelhos
Devonianos da Bacia do Baixo Amazonas”, Revista Brasileira de Geociências
v.15, n. 2, pp. 110-115, Fev. 1985.
ALVES, D. B., RODRIGUES, R. “Influência das Intrusões Ígneas nos Folhelhos
Devonianos da Bacia do Amazonas”. Simpósio Sobre Vulcanismo e Ambientes
Associados, 2, Belém, Pará, Brasil, 51-51, nov, 2002.
ANP. Agência Nacional do Petróleo, Gás e Biocombustíveis. Boletim Mensal da
Produção
de
Petróleo
e
Gás
Natural,
2011.
Disponível
em:
<http://www.anp.gov.br/?pg=57291&m=&t1=&t2=&t3=&t4=&ar=&ps=&cachebust=
1314470245590>. Acesso: em 27 de agosto de 2011, 22:30:00.
ANP. Agência Nacional do Petróleo, Gás e Biocombustíveis. Plano Plurianual de
Geologia e Geofísica da ANP (PPA 2007-2011), 2007. Disponível em:
<http://www.anp.gov.br/?pg=42186&m=plano+plurianual&t1=&t2=plano+plurianual
&t3=&t4=&ar=0&ps=1&cachebust=1314482882653>. Acesso: em 25 de agosto de
2011, 21:30:30
ANP. Agência Nacional do Petróleo, Gás e Biocombustíveis. Sítio das Rodadas de
licitações.
Nona
Rodada
de
Licitação,
2007.
Disponível
em:
<http://www.anp.gov.br/?pg=42186&m=plano+plurianual&t1=&t2=plano+plurianual
&t3=&t4=&ar=0&ps=1&cachebust=1314482882653>. Acesso: em 30 de maio de
2011, 20:30:00.
ATHY, L.F., “Density, porosity, and compaction of sedimentary rocks”, AAPG Bulletin
v.14, n.1, pp. 1-24, Jan. 1930.
96
ÁVILA, R. M., 2010, Reprocessamento de Dado Sísmico 2D da Bacia do Parnaíba.
Dissertação de M.Sc., COPPE/UFRJ, Rio de Janeiro, RJ, Brasil.
BACOCCOLI et al., 2003, Situação da Sísmica Terrestre no Brasil. ONIP/GEO, Rio
de Janeiro, RJ.
BARATA, C. F., CAPUTO, M. V. “Geologia do petróleo da Bacia do Solimões: o
Estado da Arte”. 4º Congresso Brasileiro de P&D em Petróleo e Gás,
Campinas, São Paulo, Brasil, 21-24, out. 2007.
BDEP. Banco de Dados de Exploração e Produção, 2002. Disponível em
<http://www.bdep.gov.br/cgi-bin/bacias/acervo?name=parnaiba&> Acesso: em 22
de agosto de 2010.
BEICIP-FRANLAB. Manual do Usuário para o programa Temis, 2011.
BENDER, A. A., EIRAS, J. F., WANDERLEY FILHO, J. R., BARBOSA FILHO, C. M.
“Quantificação 3D da evolução termal da Bacia do Solimões e suas implicações
petrolíferas”. Simpósio de Geologia da Amazônia, 7, Belém : SBG, nov, 2001.
BOCARDI, L.B., ROSTIROLLA, S.P., DEGUCHI, M.G.F., MANCINI, F., “História de
Soterramento e Diagênese em Arenitos do Grupo Itararé – Implicações na
Qualidade de Reservatórios”, Revista Brasileira de Geociências, v. 38, n.1, pp.
207-216, março, 2008.
CARDOSO, R. A., 2007, Evolução Termo-Tectônica da Bacia da Plataforma
Continental da Plataforma do Estado do Rio de Janeiro. Dissertação de M.Sc.,
Observatório Nacional, Rio de Janeiro, RJ, Brasil.
CORRÊA, L. M. S. A, 2007, Avaliação do Efeito térmico das Soleiras de Diabásio
nas Rochas Geradoras da Formação Irati (Bacia do Paraná, Brasil) Através
de Técnicas de Modelagem Numérica. Dissertação de M.Sc., IGEO/UERJ, Rio
de Janeiro, RJ, Brasil.
COSTA DE JESUS, C. L., 2004, Determinação da Condutividade Térmica de
Rochas Sedimentares a Partir de Perfilagem Elétrica de Poços. Dissertação
de M.Sc., IGEO/UFBA, Salvador, BA, Brasil.
97
CUNHA, F.M.B., 1986, Evolução Paleozoica da Bacia do Parnaíba e Seu
Arcabouço Tectônico. Dissertação de M.Sc., IGEO/UFRJ, Rio de Janeiro, RJ,
Brasil.
GALUSHKIN, Y. I. “Thermal Effects of Igneous Intrusions on Maturity of Organic
Matter: a Possible Mechanism of Intrusion”, Organic Geochemistry, v. 26, n. 11-12,
pp. 645-658, julho, 1997.
GIANNINI, P. C. “Depósitos e Rochas Sedimentares”. In: TEIXEIRA, W., TOLEDO, M.
C., FAIRCHILD, T. R., TAIOLI, F. (eds). Decifrando a Terra. 2 ed. capítulo 14,
São Paulo, Oficina de Textos, 2003.
GÓES, A.M.O., FEIJÓ, F.J. “A Bacia do Parnaíba”, Boletim de Geociências da
Petrobras, v.8, n.1, pp. 57-67, jan/mar. 1994.
GÓES, A.M.O., SOUZA, J.M.P., TEIXEIRA, L.B. “Estágio Exploratório e Perspectivas
Petrolíferas da Bacia do Parnaíba”, Boletim de Geociências da Petrobras, Rio
de Janeiro, v.4, n.1, pp. 55-64, jan/mar.1990.
GONZAGA, F. G., 2005, Simulação Geoquímica 1D ao Longo de uma Seção
Geológica da Bacia de Campos. Dissertação de M.Sc., COPPE/UFRJ, Rio de
Janeiro, RJ, Brasil.
HANTSCHEL, T., KAUERAUF, A. I., 2009, Fundamentals of Basin and Petroleum
Systems Modeling. 1 ed. Berlin, Heidelberg, Springer–Verlag.
INCROPERA, F. P., DEWITT, D. P., 1998, Fundamentos de Transferência de Calor
e de Massa. 4 ed., Rio de Janeiro, Livros Técnicos e Científicos Editora.
JARVIS, G.T., MCKENZIE, D.P, 1980, “Sedimentary basin formation with finite
extension rates”. Earth and Plan. Sci. Letters, v. 48, p. 42-52.
KING, V.P.S., 2003, Análise Térmica Transiente e Tridimensional em Rochas
Sedimentares. Dissertação de M.Sc., COPPE/UFRJ, Rio de Janeiro, RJ, Brasil.
LUTHI, S. M., O’BRIEN, D. P. “A Quantitative Thermodynamic Model for Diabase
Intrusions in the Amazonas Basin – Brazil, and their Effect on Maturation of
Organic Matter”, 3rd International Congress SBGF, v. 45, pp. 255–282, 1993.
98
MAGOON, L.B., DOW, W.G., 1994, “The petroleum system”. AAPG Memoir n.60, p. 324.
MCKENZIE, D. “Some Remarks on the Development of Sedimentary Basins”, Earth
and Plan., Sci. Letters, v. 40, p. 25-32, 1978.
MENDONÇA P.M.M., SPADINI R.A., MILANI J.E. “Exploração na Petrobras: 50 anos
de sucesso”, Boletim de Geociências da Petrobras, v.12, n.1, pp.9-58,
nov.2003/maio 2004.
MIZUSAKI, A. M. P, THOMAZ FILHO, A. “O Magmatismo Pós-Paleozóico no Brasil”.
In: MANTESSO-NETO, V., BARTORELLI, A., CARNEIRO, C. D. R., BRITONEVES, B. B. (eds). Geologia do Continente Sul-Americano: Evolução da
obra de Fernando Flávio Marques de Almeida. 1 ed. capítulo 17, São Paulo,
Beca, 2004.
MIZUSAKI, A. M. P, THOMAZ FILHO, A., ROISENBERG, A. “Rochas Ígneo-Básicas
das Bacias Sedimentares Brasileiras Como Potenciais Reservatórios de
Hidrocarbonetos”. 4º simpósio de Vulcanismo e Ambientes Associados, Foz
do Iguaçu, Paraná, PR, Brasil, p.4, abril, 2008.
NEUMANN E.R., PLANKE S., SØRENSSEN A.M., 2003. Emplacement mechanisms
and magma flows in sheet intrusions in sedimentary basins. In: Sill EmplacementNFR
Application,
Oslo.
VBPR
Report,
p.
1-10.
Disponível
em:
http://folk.uio.no/polteau/sill_application1.pdf. Acesso em 06 de setembro de 2011,
20:30:00.
OGX PETRÓLEO E GÁS PARTICIPAÇÕES S.A., 2011. Plano de Negócios para
Desenvolvimento das Descobertas de Campos e Parnaíba. Disponível em
<http://ri.ogx.com.br/Show.aspx?IdMateria=IyEEIUl8HAvH+Mx0t/PyWA==>
Acesso: em 25 de agosto de 2011, 21:00:00.
PINTO, V.H.G., 2008, Importância da Modelagem Termomecânica para o Sistema
Petrolífero. Estudo 2D na Parte Central da Bacia de Santos. Dissertação de
M.Sc., IGEO/UFF, Niterói, RJ, Brasil.
POLLACK, H.N., HURTER, S.J., JOHNSON, J.R. “Heat flow from the Earth´s interior:
Analysis of the global data set”, Reviews of Geophysics, v.31, n.3, pp. 267- 280,
1993.
99
PRATT, J. H., “On the Attraction of the Himalaya Mountains, and of the Elevated
Regions Beyond Them, Upon the Plumb Line in India”, Phil. Trans. R. Soc.
London, vol. 145, pp. 53-100, 1855.
QUINTAS, M. C. L., MANTOVANI, M. S. M., ZALÁN, P. V. “Contribuição para o Estudo
da Evolução Mecânica da Bacia do Paraná”, Boletim de Geociências da
Petrobras, v.11, n.1/2, pp. 48-73, jan/dez. 1997.
QUINTAS, M.C.L., “Um Estudo de Compensação Isostática para a Bacia do Paraná”,
Boletim de Ciências Geodésicas, v.8, n.2, pp. 93-108, out. 2002.
RODRIGUES, R., 1995, A Geoquímica Orgânica na Bacia do Parnaíba. Tese de
D.Sc., Instituto de Geociências/Universidade Federal do Rio Grande do Sul, Porto
Alegre, RS, Brasil.
ROYDEN, L., KEEN, C.E. “Rifting Process and Thermal Evolution of the Continental
Margin of Eastern Canada Determined from Subsidence Curves”. Earth and
Plan., Sci. Letters, 51, p. 343-361, 1980.
SANTOS NETO, E.V. “Geoquímica de Gases: uma Nova Tecnologia em Avaliação de
Sistemas Petrolíferos”, Boletim de Geociências da Petrobras, v.12, n.2, pp.
357-383, maio/nov. 2004.
SANTOS, V.H., LIMA FILHO, M.F., NEUMANN, V.H. “Quais as possibilidades de um
sistema petrolífero na Bacia do Parnaíba?” 4º Congresso Brasileiro de P&D em
Petróleo e Gás. Campinas, São Paulo, Brasil, 1-10, 2007.
SCLATER, J.G., CHRISTIE, P.A.F. “Continental Stretching: an Explanation of the PreMid-Cretaceous Subsidence of the Central North Sea Basin”, Journal of
Geophys. Res., v. 85, n.B7, pp. 3711-3739, fev. 1980.
SILVA, A. J. P., LOPES, R. C., VASCONCELOS, A. M., BAHIA, R. B. C. “Bacias
Sedimentares Paleozoicas e Meso-Cenozóicas Interiores”. In: BIZZI, L. A.,
SCHOBBENHAUS, C., VIDOTTI, R. M., GONÇALVES, J. H. G. (eds.), Geologia,
Tectônica e Recursos Minerais do Brasil, capítulo 2, Brasília, CPRM, 2003.
SOUSA, V. F. C., NOBRE, H. A., SOUZA, Z. S. et al. “Efeitos Termais Provocados por
Intrusões Básicas Cenozóicas em Rochas Sedimentares da Bacia Potiguar, RN”.
In: Congresso Brasileiro de Geologia, 44, Curitiba, PR, pp. 26-31, out. 2008.
100
STECKLER, M. S., WATTS, A. B., 1978, “Subsidence of the Atlantic-type continental
margin off New York”, Earth and Planetary Science Letters, v. 41, pp. 1-13,
1978.
SWEENEY, J. J., BURNHAM, A. K. “Evaluation of a Simple Model of Vitrinite
Reflectance Based on Chemical Kinetics”, The American Association of
Petroleum Geologists Bulletin, v. 74, pp. 1559–1570, 1990.
SZABÓ, G. A. J., BABINSKI, M., TEIXEIRA, W. “Rochas Ígneas”. In: TEIXEIRA, W,
TOLEDO, M. C., FAIRCHILD, T. R., TAIOLI, F. (eds). Decifrando a Terra. 2 ed.
capítulo 16, São Paulo, Oficina de Textos, 2003.
THOMAZ FILHO, A., MIZUSAKI, A. M. P., ANTONIOLI, L., “Magmatismo nas Bacias
Sedimentares e sua Influência na Geologia do Petróleo”, Revista Brasileira de
Geociências, v.38, n.15, pp. 128-137, junho, 2007.
VASCONCELOS, D. F. M., 2010, Modelo Numérico para Análise da Influência de
Intrusões Magmáticas na Estrutura Térmica e na Maturação da Matéria
Orgânica de Bacias Sedimentares. Projeto de Graduação, UFRJ/ESCOLA
POLITÉCNICA, Rio de Janeiro, RJ, Brasil.
VAZ, P. T., REZENDE, N. G. A. M., WANDERLEY FILHO, J. R., et al.,, “A Bacia do
Parnaíba”, Boletim de Geociências da Petrobras, v.15, n.2, pp. 253-263,
maio/nov. 2007.
WANDERLEY FILHO, J. R., TRAVASSO, W. A. S., ALVES, D. B. “O Diabásio nas
Bacias Paleozoicas Amazônicas - Herói ou Vilão?”, Boletim de Geociências da
Petrobras, v.14, n.1, pp. 177-184, nov.2005/maio 2006.
WATTS, A.B. “An analysis of Isostasy in the World’s Oceans. 1- Hawaiian-Emperor
Seamount Chain”, Journal of Geophys. Res., v. 83, pp. 5989-6004, fev.1978.
YOUNG C.G.K., BORGHI, L. “Pimenteira Formation (Devonian, Parnaíba Basin): a
New Prospect for Hydrocarbon Reservoirs”. 2º Congresso Brasileiro de P&D em
Petróleo e Gás. Campinas, São Paulo, Brasil, 1-6, 2003.
YOUNG, C.G.K., 2006, Contribuição à Análise da Formação Pimenteira
(Devoniano, Bacia do Parnaíba): Caracterização de um Potencial Intervalo de
101
Rochas Reservatório. Trabalho de Conclusão de Curso, IGEO/UFRJ, Rio de
Janeiro, RJ, Brasil.
YOUNG, C.G.K., 2006, Estratigrafia de Alta-Resolução da Formação Pimenteiras
(Devoniano, Bacia do Parnaíba). Dissertação de M.Sc., IGEO/UFRJ, Rio de
Janeiro, RJ, Brasil.
ZÁLAN, P. “Evolução Fanerozóica das Bacias Sedimentares Brasileiras”. In:
MANTESSO-NETO, V., BARTORELLI, A., CARNEIRO, C. D. R., BRITO-NEVES,
B. B., Geologia do Continente Sul-Americano: Evolução da obra de Fernando
Flávio Marques de Almeida. 1 ed. capítulo 33, São Paulo, Beca, 2004.
ZEMBRUSCKI, S. G., Campos, J. N. P. “Provável Movimentação de Fluidos na Bacia
do Parnaíba, Maranhão”, Boletim de Geociências da Petrobras, v. 2, n. 2/41,
pp. 133-145, abril/dez. 1988.
102