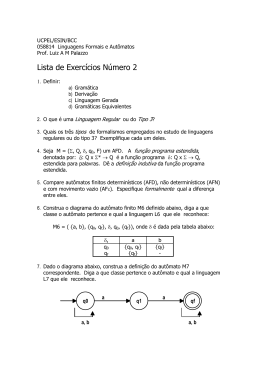
INF 1626 – Linguagens Formais e Autômatos
P1 – 11/05/01
José Lucas Rangel
Responda cinco das seis questões.
1. Mostre que a linguagem { xR c yR | x,y ∈ { a,b }*} é uma linguagem livre de
contexto, no alfabeto Σ = {a,b,c }.
Como x e y são cadeias quaisquer, podemos usar a gramática
S → TcT
T → aT | bT |ε
ou mesmo a gramática regular
S → aS | bS | cT
T → aT | bT |ε
ou até mesmo a expressão regular
(a∨b)*c(a∨b)*
Nota: Esta questão sofreu um “erro de datilografia”, e acabou ficando mais fácil do
que o previsto. A intenção era usar a linguagem { x c xR | x ∈ { a,b }* }, que é uma
linguagem livre de contexto, como pode ser visto pela gramática abaixo, mas não é
regular.
S → aSb | bSa |ε
2. Mostre que a linguagem { 0i 1j 2k | i=j=k } é sensível ao contexto, no alfabeto Σ=
{ 0,1,2 }.
Esta linguagem é semelhante à linguagem, {an bn cn | n≥0 }, usada como exemplo em
aula. Uma gramática sensível ao contexto para esta linguagem pode ser
S→T|ε
T → ZUDT | ZUD’
UZ → ZU
DZ → ZD
DU → UD
DD’ → D’2
UD’ → U’2
UU’ → U’1
ZU’ → Z’ 1
ZZ’ → Z’0
Z’ → 0
/* Z=zero, U=um, D=dois */
A justificativa para esta questão é semelhante à da gramática citada.
3. Dada a expressão regular α = ab*a ∨ ba*b, construa um autômato finito
determinístico mínimo que aceite a linguagem denotada por α.
Podemos obter um afd (não necessariamente mínimo) usando o método da árvore. A
expressão
α$ = (ab*a ∨ ba*b)$
corresponde à árvore
•
/ \
∨
$
/ \
/
\
/
\
/
\
•
•
/ \
/ \
•
a3
•
b6
/ \
/ \
a1 |
b4 |
*
*
|
|
b2
a5
a partir da qual podemos gerar o autômato
14
23
56
$
∅
a
23
$
56
∅
∅
b
56
23
$
∅
∅
(Note que ∅ também é conjunto.) 14 é o estado inicial e $ é o único estado final. Uma
forma mais legível pode ser obtida renomeando os estados:
A
B
C
D
E
a
B
D
C
E
E
b
C
B
D
E
E
/* A=14; B=23; C=56; D=$; E=∅ */
A é o estado inicial, e D o único estado final.
Para provar que este autômato é mínimo, basta mostrar que cada estado só é equivalente a
ele mesmo, por exemplo indicando cadeias para distinguir os pares de estados:
Estados
A, B
A, C
A, D
A, E
B, C
B, D
B, E
C, D
C, E
D, E
Cadeia
a
b
ε
aa
a
ε
a
ε
b
ε
4. Mostre que a classe das linguagens livres de contexto é fechada para a união.
Sejam L1 e L2 linguagens livres de contexto. Portanto, existem gramáticas livres de
contexto G1=<N1, Σ, P1, S1> e G2=<N2, Σ, P2, S2> tais que L1=L(G1) e L2=L(G2). Sem
perda de generalidade, podemos supor que N1∩N2=∅. (Se necessário, basta renomear
os símbolos não terminais de uma das duas gramáticas.)
Seja S um símbolo novo, não pertencente nem a N1, nem a N2.
Defina G=<N1∪N2∪{S}, Σ, P1∪P2∪{S→S1, S→S2}, S>.
Podemos mostrar que L(G)=L(G1)∪L(G2), da seguinte maneira:
(1) Se x∈L(G), x pode ser derivado a partir de S por uma derivação S⇒S1⇒*x ou
S⇒S2⇒*x. No primeiro caso, temos S1⇒*x e x∈L1, e no segundo caso, S2⇒*x e
x∈L2. Em qualquer dos dois casos, x pertence à união das duas linguagens.
(2) Se x∈pertence à união, ou x∈L1, ou x∈L2. Portanto, ou S1⇒*x ou S2⇒*x.
Acrescentando a regra apropriada, temos S⇒S1⇒*x ou S⇒S2⇒*x, e x∈L(G).
5. Mostre que a interseção de conjuntos recursivos é recursiva.
Sejam R1 e R2 conjuntos recursivos. Portanto existem algoritmos (sempre param!) A1
e A2 que determinam se um valor de entrada x pertence a R1 ou R2. (Por exemplo, se
x∈R1, A1 com entrada x pára e diz SIM; caso contrário, pára e diz NÃO.) Podemos
construir um algoritmo semelhante para a interseção dos dois conjuntos da seguinte
maneira.
(com entrada x)
1. Execute R1 com entrada x. (Quando R1 parar, pode dizer SIM ou NÃO.)
Se disser SIM, vá para 2. Se disser NÃO, pare e diga NÃO.
2. Execute R2 com entrada x. (Quando R2 parar, pode dizer SIM ou NÃO.)
Se disser SIM, pare e diga SIM. Se disser NÃO, pare e diga NÃO.
6. Mostre que Li • Lj = Li+j, para qualquer linguagem L, e naturais i, j.
Temos:
(1) a concatenação das linguagens é associativa.
(2) A definição de potência é
L0={ε}
caso i=0.
Li=L•Li-1.
caso i>0.
Vamos provar o resultado desejado
∀i P(i)
∀i∈Nat, ∀L⊆Σ*, Li•Lj=Li+j.
por indução em i. Ou seja, vamos provar
P(i)
∀L⊆Σ*, Li•Lj=Li+j.
(Note que, para a demonstração, j é um natural qualquer, constante.)
(base da indução)
P(0) ∀L⊆Σ*, L0•Lj=L0+j.
Isto decorre do fato de que 0+j=j e de que L0={ε} é a identidade da concatenação de
linguagens.
(passo de indução)
P(i) ⇒ P(i+1)
Ou seja, a partir da propriedade P(i) acima, devemos provar
P(i+1)
∀L⊆Σ*, Li+1•Lj=Li+1+j.
Temos:
Li+1•Lj = (L•Li) •Lj = (definição de potência)
= L•(Li •Lj) =
(associatividade da concatenação de linguagens)
= L•Li+j =
P(i)
i+1+j
=L
(definição de potência)