Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
1. Se a + b = 1, então a3 + b3 é igual a
(a) (a + b)3 + (a − b)3
√3
0
b
3
(b) 0 3 √0 a 0
3
3
(c) a3 + 3a2 b + 3ab2 + b3
√3
0
b 3
(d) 0 −3 √0 a
3
0
3
(e) a3 − 3a2 b + 3ab2 − b3
2. Dada uma função f , chamamos de valor de ponto fixo de f um valor x no domı́nio
da função tal que f (x) = x. Ordenando o conjunto dos valores positivos de ponto
fixo de f (x) = x − 2sen(x) obtemos
(a) uma progressão aritmética de razão π.
(b) uma progressão geométrica de razão π.
(c) uma progressão aritmética de razão π2 .
(d) uma progressão geométrica de razão π2 .
(e) uma progressão aritmética de razão 2π.
3. O gráfico da função f (x) = x − 2cos(x) está contido no conjunto de todos os pontos
do plano cujas coordenadas (x; y) satisfazem
(a) a equação |y − x| > 2.
(b) a equação |y + x| > 2.
(c) a equação |y − x| 6 2.
(d) a equação |y + x| 6 2.
(e) simultaneamente as equações |x| 6 2 e |y| 6 2.
√
4. Suponha que o lado do quadrado maior na figura abaixo seja igual a 2 2 cm.
Considere que cada uma das regiões da figura acima deve ser pintada com uma das
duas cores: vermelho ou amarelo. Se duas regiões vizinhas não podem ser pintadas
com mesma cor, então a soma de todas as áreas das regiões pintadas em vermelho
é igual a
1
Vestibular Ibmec 2003 2
(a)
√
Análise Quantitativa e Lógica - Prova A
2 cm2 .
(b) 2 cm2 .
√
(c) 2 2 cm2 .
(d) 4 cm2 .
√
(e) 4 2 cm2 .
5. Considere na figura abaixo um cubo de lado 4 cm, sua diagonal AB e o plano α
constituı́do de todas as retas perpendiculares a AB passando por A.
α
A
B
Se o plano α atravessar o cubo partindo de A, seguindo paralelamente à sua posição
inicial, até chegar em B, então as interseccões sucessivas do plano com o cubo serão
√
(a) triângulos equiláteros de lado crescente até atingir a medida 4 2 cm, seguidos
√
de hexágonos não regulares, seguidos de um hexágono regular de lado 2 2 cm,
seguido de hexágonos não regulares, seguidos
√ de triângulos equiláteros de lado
decrescente começando com a medida de 4 2 cm.
√
(b) triângulos equiláteros de lado crescente até atingir a medida 4 2 cm, seguidos de√quadrados de lado decrescente, seguidos de um hexágono regular de
lado 2 2 cm, seguido de quadrados de lado crescente, seguidos
√ de triângulos
equiláteros de lado decrescente começando com a medida de 4 2 cm.
√
(c) triângulos equiláteros de lado crescente até atingir a medida 2 2 cm, seguidos
√
de hexágonos não regulares, seguidos de um hexágono regular de lado 4 2 cm,
seguido de hexágonos não regulares, seguidos
√ de triângulos equiláteros de lado
decrescente começando com a medida de 2 2 cm.
2
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
√
(d) triângulos equiláteros de lado crescente até atingir a medida 4√ 2 cm, seguidos
de quadrados de lado decrescente até atingir a medida de 2 2 cm, seguidos
de quadrados de lado crescente, seguidos√de triângulos equiláteros de lado
decrescente começando com a medida de 4 2 cm.
√
de hexágonos
(e) quadrados de lado crescente até atingir a medida 4 2 cm, seguidos
√
não regulares, seguidos de um hexágono regular de lado 2 2 cm, seguido de
hexágonos não regulares,
seguidos quadrados de lado decrescente começando
√
com a medida de 4 2 cm.
6. Considere as imagens geométricas dos números complexos da forma z = n + 2n i,
com n ∈ Z, no plano Argand-Gauss. Desenhado neste mesmo plano, passaria por
todos esses pontos o gráfico de
(a) uma função modular.
(b) uma função logarı́tmica.
(c) uma função quadrática.
(d) uma função polinomial de grau 4.
(e) uma função exponencial.
1
7. Se m = logπ (sec(x) + tg(x)) e n = logπ ( sec(x)−tg(x)
), com 0 6 x 6 π2 , então m − n é
igual a
(a) sen( π6 ).
(b) cos( π6 ).
(c) sen( π4 ).
(d) cos(0).
(e) sen(0).
8. No plano cartesiano os conjuntos
{(x; y) ∈ R2 ||x| + |y| = 1},
{(x; y) ∈ R2 |x2 + y 2 = 1}
e
{(x; y) ∈ R2 |max{x, y} = 1},
(em que maxA denota o maior elemento de um conjunto finito A), estão representados na figura abaixo.
3
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
1
−1
1
−1
Assim, no espaço euclidiano tridimensional, os conjuntos
{(x; y; z) ∈ R3 ||x| + |y| + |z| 6 1},
{(x; y; z) ∈ R3 |x2 + y 2 + z 2 6 1}
e
{(x; y; z) ∈ R3 |max{x, y, z} 6 1}
podem ser identificados, respectivamente, com
(a) um octaedro regular de volume
volume 8.
2
,
3
uma esfera de volume
8π
3
e um cubo de
(b) um octaedro regular de volume 43 , uma esfera de volume 4π
e um cubo de
3
volume 8.
√
e um octaedro regular de
(c) um cubo √de volume 2 2, uma esfera de volume 4π
3
8 2
volume 3 .
(d) um cubo√de volume 2, uma esfera de volume
volume 8 3 2 .
(e) um octaedro regular de volume
√
volume 16 2.
4
,
3
8π
3
e um octaedro regular de
uma esfera de volume
8π
3
e um cubo de
(Considere as informações a seguir para os testes 9 e 10). Um designer especialista
em embalagens projetou uma casquinha de sorvete na forma de um cone com raio
da base igual a r a partir das seguintes condições estabelecidas:
• uma bola de sorvete de raio R deve caber apoiada na casquinha de tal forma
que sua superfı́cie tangencie a superfı́cie do cone exatamente na circunferência
máxima do cone, isto é, a bola não “cai”dentro do cone e nem “sobra”bola
caindo para fora da casquinha;
4
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
• o volume interno do cone deve ser igual ao volume da bola de raio R, isto é, se
o sorvete derreter totalmente sem pingar para fora caberá totalmente dentro
da casquinha e sem sobrar espaço (para seus cálculos, despreze a espessura
da casquinha e a variação do volume do sorvete no processo de variação da
temperatura).
Assim, um corte por um plano passando pelo centro da base do cone e pelo centro
da esfera, na bola apoiada no cone, pode ser representado através da seguinte figura.
R
R
r
r
a
9. Segue da condição de tangência dos sólidos que o valor de a é igual a
(a)
(b)
(c)
(d)
(e)
√
R2 −r 2
.
Rr
√ Rr
.
R2 +r 2
√ Rr
.
R2 −r 2
√
R2 +r 2
.
Rr
2 2
√R r
.
R2 −r 2
10. Segue das duas condições que R e r satisfazem a relação dada através equação
(a) 16R6 =
r8
.
R2 +r 2
(b) 4R3 =
r8
.
R2 +r 2
(c) 4R3 =
r4
.
R2 −r 2
(d) 16R6 =
(e) 4R3 =
r8
.
R2 −r 2
r4
.
R2 +r 2
11. Para que o conjunto imagem da função f (x) = asen(x) + bcos(x) esteja contido no
intervalo [−1; 1] é suficiente que a e b sejam, respectivamente, iguais a
5
Vestibular Ibmec 2003 2
(a)
(b)
(c)
√
3
2
√
3
3
√
Análise Quantitativa e Lógica - Prova A
e 21 .
√
e 3.
3e
√
3
.
3
(d) 1 e 1.
√
√
(e) 22 e 2.
12. Considere 8 pontos distintos sobre uma circunferência. Suponha que
• A é o número de triângulos que podem ser formados com vértices sobre quaisquer três desses pontos;
• B é o número de quadriláteros que podem ser formados com vértices sobre
quaisquer quatro desses pontos;
• C é o número de pentágonos que podem ser formados com vértices sobre quaisquer cinco desses pontos;
• D é o número de hexágonos que podem ser formados com vértices sobre quaisquer seis desses pontos e
• E é o número de heptágonos que podem ser formados com vértices sobre quaisquer sete desses pontos.
Então A + B + C + D + E é igual a
(a) 28 − 37.
(b) 27 − 38.
(c) 28 − 38.
(d) 27 − 37.
(e) 28 − 27 .
13. Um investimento de alto risco propicia um rendimento de 25% em um mês se o
ı́ndice de fechamento de mercado do mês supera a marca dos 5%. Caso contrário o
total investido fica 60% menor naquele mês. Para que sobre apenas um décimo do
que foi investido, para uma conveniente configuração do mercado naqueles meses,
são necessários
(a) 5 meses.
(b) 6 meses.
(c) 7 meses.
(d) 8 meses.
(e) 9 meses.
14. Na figura abaixo temos o quadrado ABCD de lado 4. Dividimos cada lado na razão
1:3 e, com os pontos obtidos, obtemos um outro quadrado A1 B1 C1 D1 inscrito no
maior. Dividimos cada lado do quadrado A1 B1 C1 D1 na mesma razão e repetimos
o processo obtendo o quadrado A2 B2 C2 D2 , e assim sucessivamente.
6
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
A1
A
B
A2
B1
B2
D2
D1
C2
D
C1
C
Se S1 é a área do triângulo AD1 A1 , S2 é a área do triângulo A1 D2 A2 e assim
sucessivamente, então o limite da soma
S1 + S2 + ...
é igual a
(a) 1.
√
(b) 2.
(c) 2.
√
(d) 2 2.
(e) 4.
15. Se a e b são números reais positivos, então
s
2ab +
r
2a2 b2
+
q
2a4 b4 +
é igual a
(a) a − b.
(b) ab.
(c) 2ab.
(d) a + b.
(e) (a + b)2 .
7
√
a16 + 2a8 b8 + b16
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
16. Se a equação da reta r é
y=
y=
e a equação da reta s é
com a não nulo e diferente de 1, então
x
x,
a−1
a
a
1−a
(a) essas retas são ambas decrescentes.
(b) r e s são perpendiculares qualquer que seja o valor de a.
(c) essas retas são ambas crescentes.
(d) r e s são paralelas para algum valor de a.
(e) uma dessas retas é horizontal para um conveniente valor de a.
17. Dizemos que o conjunto de todos os economistas do mundo é uniforme em determinado momento se, e somente se, qualquer que seja a localização de um economista sobre a face da terra existe um outro economista localizado a menos de 50 quilômetros
dessa localização. Para que o conjunto de todos os economistas do mundo não seja
uniforme às 12 horas do dia 01 de junho de 2003
(a) é necessário que, às 12 horas do dia 01 de junho de 2003, o único economista
do mundo fora dos continentes esteja num avião sobre o Atlântico aproximadamente na metade do caminho entre Brasil e Portugal.
(b) é necessário que, às 12 horas do dia 01 de junho de 2003, todos os economistas
do mundo estejam distantes mais que 50 quilômetros dois a dois.
(c) é suficiente que, às 12 horas do dia 01 de junho de 2003, o único economista
do mundo fora dos grandes continentes esteja num avião sobre o Atlântico
aproximadamente na metade do caminho entre Brasil e Portugal.
(d) é suficiente que, às 12 horas do dia 01 de junho de 2003, todos os economistas
do mundo estejam distantes menos que 50 quilômetros dois a dois.
(e) é necessário que, às 12 horas do dia 01 de junho de 2003, todos os economistas
do mundo estejam distantes menos que 50 quilômetros dois a dois.
18. Se x, y e z representam grandezas inteiras positivas tais que x é diretamente proporcional à y e inversamente proporcional ao quadrado de z, então quanto vale x se
y = z = 2?
Considere que
(I) x = 3 pode acontecer quando y = 6.
(II) x = 3 pode acontecer quando z = 2.
Assim, para responder a pergunta acima, é correto afirmar que
(a) I sozinha é suficiente, mas II sozinha não é.
(b) II sozinha é suficiente, mas I sozinha não é.
(c) I e II juntas são suficientes, mas cada uma sozinha não é.
(d) cada uma das afirmações sozinha é suficiente.
8
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
(e) I e II juntas não são suficientes, sendo necessário mais dados.
19. Suponha que as premissas do raciocı́nio apresentado abaixo sejam verdadeiras.
Está equivocado quem afirma que a essência dos padrões estéticos presentes na arte
ocidental atual foi moldada pelos alemães e italianos no perı́odo pós-Renascimento,
porque os italianos evidentemente apresentam nas suas obras padrões estéticos primordialmente estabelecidos 3000 anos antes pelos gregos e os alemães tentaram
começar do zero no século XVI, mas sucumbiram gradativamente à influência da
arte genuı́na grega.
A partir desse raciocı́nio, é correto afirmar que
(a) a essência dos padrões estéticos presentes na arte ocidental atual foi moldada
exclusivamente pelos italianos no perı́odo pós-Renascimento.
(b) a conclusão é verdadeira.
(c) a essência dos padrões estéticos presentes na arte ocidental atual foi moldada
exclusivamente pelos alemães no perı́odo pós-Renascimento.
(d) a conclusão é falsa.
(e) a essência dos padrões estéticos presentes na arte ocidental atual foi moldada
exclusivamente pelos gregos no perı́odo pós-Renascimento.
20. Considere verdadeiras as afirmações abaixo.
(I) Todo bom tomador de decisões possui intuição e domina os métodos quantitavivos dos processos decisórios gerenciais.
(II) Quem tem raciocı́nio lógico tem intuição.
(III) Há candidatos com raciocı́nio lógico dentre os admitidos em nossa faculdade.
Então
(a) não podemos formar bons tomadores de decisão se ensinarmos para alguns
dos admitidos em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(b) certamente formaremos bons tomadores de decisão se ensinarmos para todos
os admitidos em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(c) certamente formaremos bons tomadores de decisão se ensinarmos para alguns
dos admitidos em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(d) podemos formar bons tomadores de decisão se ensinarmos a todos os admitidos
em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(e) certamente formaremos bons tomadores de decisão se ensinarmos para os admitidos em nossa faculdade que tem intuição os métodos quantitavivos dos
processos decisórios gerencias.
9
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
21. Na noite anterior à prova de vestibular do IBMEC, um candidato dormiu pensando
tanto na faculdade que teve um estranho sonho: ele estava em frente ao local de
exame que era um prédio de cinco andares denominados I, B, M, E, C, não necessariamente nessa ordem. Entrou no prédio, que estava completamente vazio porque
ainda era muito cedo e percebeu que cada sala estava identificada com um anagrama da palavra IBMEC sem faltar nenhum anagrama e que, em cada andar, a
identificação de todas as salas começava com a letra do andar. De repente, apareceu
seu colega de estudos, que também faria a prova na manhã seguinte, e antes que
os dois pudessem se cumprimentar ecoou por todo o prédio uma voz muito grave
profetizando: “Se vocês fizerem a prova em salas começadas com letras diferentes
e terminadas com a mesma letra suas mentes irão se iluminar, mas lembrem-se,
somente se fizerem a prova em salas começadas com letras diferentes e terminadas
com a mesma letra.”Neste exato momento eles acordaram, aprontaram-se ansiosamente e foram para o local do exame, que era exatamente igual ao do sonho, mas
com muita gente. Suponha que as salas em que os candidatos farão a prova foram
determinadas aleatoriamente.
(a) Quantas salas tinha cada andar do prédio?
(b) Calcule a probabilidade de ambos fazerem a prova na mesma sala.
(c) Calcule a probabilidade de os dois candidatos terem suas mentes iluminadas.
10
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
22. Suponha que o gráfico da função f : [−1; 1] −→ [0; 1] seja dada pela figura abaixo.
1
C
B
D
A
E
−1
1
Suponha que AB seja um arco da circunferência de centro (−1; 0, 5) e raio 0,5, que
BCD seja a semicircunferência de centro (0; 0, 5) e raio 0,5 e que DE seja um arco
da circunferência de centro (1; 0, 5) e raio 0,5.
Considere a função área A : [−1; 1] −→ R que para cada x0 ∈ [−1; 1] associa a
medida da área entre o eixo Ox e o gráfico de f limitada pelas retas x = −1 e
x = x0 , denotada por A(x0 ), conforme figura abaixo.
1
B
A
−1
C
D
A(x0 )
E
x = x0
(a) Determine a fórmula da função f .
11
1
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
(b) Calcule A(0, 5) − A(−0, 5) e indique no gráfico abaixo a área que está representada por essa subtração.
1
B
C
D
A
E
−1
1
12
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
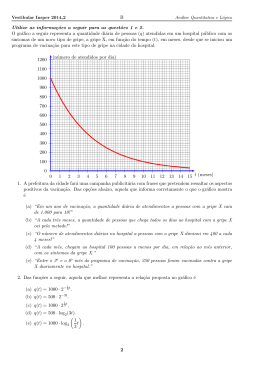
23. Suponha que a quantidade mensal (d) que uma comunidade queira comprar de um
determinado produto seja uma função do primeiro grau em termos do preço (p) do
respectivo produto. Considere que nos últimos dois meses os preços praticados foram
R$10,00 e R$20,00 e que as respectivas quantidades adquiridas pela comunidade
foram 180 e 80 unidades do produto. O fabricante desse produto calcula que cada
unidade produzida custa-lhe R$2,00, e que o custo fixo operacional mensal é de
R$690,00 (isto é, independente da quantidade produzida, ele gasta R$690,00 para
manter sua empresa funcionando).
(a) Determine a fórmula que estabelece a função de d em termos de p.
(b) Defina a função lucro total mensal (l) do fabricante como a função que, para
cada preço p praticado, associa o resultado da receita total mensal (dada pelo
produto do preço pela quantidade) subtraindo o custo total mensal (dado pela
soma do custo fixo operacional mensal com o custo de produzir d unidades); e
determine a fórmula da função l em termos de p.
(c) Determine o preço que o fabricante deve praticar no próximo mês para que seu
lucro total mensal seja o maior possı́vel.
13
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
24. Considere uma circunferência (C1 ) inscrita em um quadrado de lado 2. Dentro de C1
inscreva outro quadrado, com os lados paralelos ao maior, e dentro desse quadrado
inscreva outra circunferência (C2 ), como na figura abaixo.
C1
C2
Seja S1 a medida da área compreendida entre C1 e C2 e repita a mesma construção
dentro de C2 , obtendo S2 a medida da área compreendida entre C3 e C4 e assim
sucessivamente, como na figura abaixo.
C1
C2
C3
C4
14
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
Se Sn é a medida da área compreendida entre C2n−1 e C2n , determine o limite da
soma
S = S1 + S2 + S3 + ... + Sn + ...
15
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
25. Considere a matriz A4×4 cujas entradas aij são dadas por
ai1
ai2
ai3
ai4
= pi−1
= q i−1
= ri−1
= si−1
i = 1, 2, 3, 4
i = 1, 2, 3, 4
i = 1, 2, 3, 4
i = 1, 2, 3, 4
em que p,q,r e s são números naturais não nulos e distintos dois a dois.
(a) Exiba a matriz A.
(b) Calcule det(A), o determinante da matriz A.
(c) Mostre que det(A) é um múltiplo de 6, quaisquer que sejam p, q, r, s ∈ N.
16
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
26. Na figura abaixo, suponha que as medidas dos segmentos BC, BD, CF, BG e CG
−→ −−→
sejam todas iguais a 2 e que CF e BD sejam, respectivamente, as bissetrizes dos
b e CBG.
b
ângulos BCE
A
E
G
F
D
B
C
(a) Determine a medida do segmento BE.
(b) Calcule sen(750 ). (Sugestão: 750 = 450 + 300 .)
(c) Determine a medida da área do triângulo ACE.
17
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
27. Um banco irá construir uma sede com um cofre cilı́ndrico para armazenar seus mais
preciosos valores. A parede, o piso e o teto deverão ser constituı́dos de uma camada
de um metro de espessura de um material cujo custo é R$1.000,00 por metro cúbico.
Suponha que devam ser gastos R$88.000,00 com esse material e que, internamente,
o raio da base (R) do cofre deva ser igual à altura. Determine o valor de R. (Utilize
28π ∼
= 88.)
18
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
28. Considere a matriz
R(θ) =
cosθ senθ
−senθ cosθ
(a) Resolva a equação
4
[R(θ)] =
para θ ∈ [0; π2 ].
−1 0
0 −1
.
,
(b) Se as colunas da matriz
Q=
1 1 −1 −1
1 −1 −1 1
representam as coordenadas dos vértices de um quadrado, determine o quadrilátero
cujos vértices são as colunas da matriz R(θ).Q, para o valor de θ obtido no
item anterior.
19
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
29. Considere as seqüências
(a1 , a2 , a3 , ..., an , an+1 , ...)
e
(g1 , g2 , g3 , ..., gn , gn+1 , ...)
que satisfazem as leis de formação
an+1 − an =
e
1
para n = 1, 2, 3, ...; com a1 = 1
2
1
gn+1
= para n = 1, 2, 3, ...; com g1 = 2,
gn
2
respectivamente.
(a) Mostre que a seqüência
(2a1 , 2a2 , 2a3 , ..., 2an , 2an+1 , ...)
é uma progressão geométrica e exiba a fórmula do termo geral dessa progressão.
(b) Mostre que a seqüência
(log2 (g1 ), log2 (g2 ), log2 (g3 ), ..., log2 (gn ), log2 (gn+1 ), ...)
é uma progressão aritmética e exiba a fórmula do termo geral dessa progressão.
20
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
30. Considere que foi estabelecida no Olimpo da Homérica Odisséia a seguinte regra:
“Se, na divina assembléia, os deuses atendem a um pedido de Atena somente se
Posı́don estiver ausente (e, obviamente, Atena presente), então Zeus obriga os deuses
a executar o contrário de todo pedido que Posı́don fizer somente se Atena estiver
ausente (e, obviamente, Posı́don presente).”
(a) Se Atena e Posı́don estiverem presentes numa mesma assembléia e ambos fizerem pedidos distintos e não contráditórios, como os deuses devem proceder?
(b) Desejando acabar com essa regra, Posı́don comparece exatamente na assembléia
em que Atena pede o regresso de Ulisses e faz o mesmo pedido. O que Zeus, o
lógico dos lógicos, deve fazer para que a regra prevaleça?
21
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
Rascunho
Rascunho
Rascunho
22
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
Rascunho
Rascunho
Rascunho
23
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica - Prova A
Nome:
No. de inscrição:
Rascunho
Rascunho
Rascunho
24
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
1. Um investimento de alto risco propicia um rendimento de 25% em um mês se o
ı́ndice de fechamento de mercado do mês supera a marca dos 5%. Caso contrário o
total investido fica 60% menor naquele mês. Para que sobre apenas um décimo do
que foi investido, para uma conveniente configuração do mercado naqueles meses,
são necessários
(a) 5 meses.
(b) 6 meses.
(c) 7 meses.
(d) 8 meses.
(e) 9 meses.
2. Se a e b são números reais positivos, então
s
2ab +
r
2a2 b2
+
q
2a4 b4 +
√
a16 + 2a8 b8 + b16
é igual a
(a) a − b.
(b) ab.
(c) 2ab.
(d) a + b.
(e) (a + b)2 .
3. Se a equação da reta r é
y=
y=
e a equação da reta s é
x
x,
a−1
a
a
1−a
com a não nulo e diferente de 1, então
(a) essas retas são ambas decrescentes.
(b) r e s são perpendiculares qualquer que seja o valor de a.
(c) essas retas são ambas crescentes.
(d) r e s são paralelas para algum valor de a.
(e) uma dessas retas é horizontal para um conveniente valor de a.
4. Na figura abaixo temos o quadrado ABCD de lado 4. Dividimos cada lado na razão
1:3 e, com os pontos obtidos, obtemos um outro quadrado A1 B1 C1 D1 inscrito no
maior. Dividimos cada lado do quadrado A1 B1 C1 D1 na mesma razão e repetimos
o processo obtendo o quadrado A2 B2 C2 D2 , e assim sucessivamente.
1
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
A1
A
B
A2
B1
B2
D2
D1
C2
D
C1
C
Se S1 é a área do triângulo AD1 A1 , S2 é a área do triângulo A1 D2 A2 e assim
sucessivamente, então o limite da soma
S1 + S2 + ...
é igual a
(a) 1.
√
(b) 2.
(c) 2.
√
(d) 2 2.
(e) 4.
(Considere as informações a seguir para os testes 5 e 6). Um designer especialista
em embalagens projetou uma casquinha de sorvete na forma de um cone com raio
da base igual a r a partir das seguintes condições estabelecidas:
• uma bola de sorvete de raio R deve caber apoiada na casquinha de tal forma
que sua superfı́cie tangencie a superfı́cie do cone exatamente na circunferência
máxima do cone, isto é, a bola não “cai”dentro do cone e nem “sobra”bola
caindo para fora da casquinha;
• o volume interno do cone deve ser igual ao volume da bola de raio R, isto é, se
o sorvete derreter totalmente sem pingar para fora caberá totalmente dentro
da casquinha e sem sobrar espaço (para seus cálculos, despreze a espessura
da casquinha e a variação do volume do sorvete no processo de variação da
temperatura).
Assim, um corte por um plano passando pelo centro da base do cone e pelo centro
da esfera, na bola apoiada no cone, pode ser representado através da seguinte figura.
2
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
R
R
r
r
a
5. Segue da condição de tangência dos sólidos que o valor de a é igual a
(a)
(b)
(c)
(d)
(e)
√
R2 −r 2
.
Rr
√ Rr
.
R2 +r 2
√ Rr
.
R2 −r 2
√
R2 +r 2
.
Rr
2 2
√R r
.
R2 −r 2
6. Segue das duas condições que R e r satisfazem a relação dada através equação
(a) 16R6 =
r8
.
R2 +r 2
(b) 4R3 =
r8
.
R2 +r 2
(c) 4R3 =
r4
.
R2 −r 2
(d) 16R6 =
(e) 4R3 =
r8
.
R2 −r 2
r4
.
R2 +r 2
7. Para que o conjunto imagem da função f (x) = asen(x) + bcos(x) esteja contido no
intervalo [−1; 1] é suficiente que a e b sejam, respectivamente, iguais a
(a)
(b)
(c)
√
3
2
√
3
3
√
e 21 .
√
e 3.
3e
√
3
.
3
(d) 1 e 1.
√
√
(e) 22 e 2.
8. Considere 8 pontos distintos sobre uma circunferência. Suponha que
3
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
• A é o número de triângulos que podem ser formados com vértices sobre quaisquer três desses pontos;
• B é o número de quadriláteros que podem ser formados com vértices sobre
quaisquer quatro desses pontos;
• C é o número de pentágonos que podem ser formados com vértices sobre quaisquer cinco desses pontos;
• D é o número de hexágonos que podem ser formados com vértices sobre quaisquer seis desses pontos e
• E é o número de heptágonos que podem ser formados com vértices sobre quaisquer sete desses pontos.
Então A + B + C + D + E é igual a
(a) 28 − 37.
(b) 27 − 38.
(c) 28 − 38.
(d) 27 − 37.
(e) 28 − 27 .
9. Considere na figura abaixo um cubo de lado 4 cm, sua diagonal AB e o plano α
constituı́do de todas as retas perpendiculares a AB passando por A.
α
A
B
Se o plano α atravessar o cubo partindo de A, seguindo paralelamente à sua posição
inicial, até chegar em B, então as interseccões sucessivas do plano com o cubo serão
4
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
√
(a) triângulos equiláteros de lado crescente até atingir a medida 4 2 cm, seguidos
√
de hexágonos não regulares, seguidos de um hexágono regular de lado 2 2 cm,
seguido de hexágonos não regulares, seguidos
√ de triângulos equiláteros de lado
decrescente começando com a medida de 4 2 cm.
√
(b) triângulos equiláteros de lado crescente até atingir a medida 4 2 cm, seguidos de√quadrados de lado decrescente, seguidos de um hexágono regular de
lado 2 2 cm, seguido de quadrados de lado crescente, seguidos
√ de triângulos
equiláteros de lado decrescente começando com a medida de 4 2 cm.
√
(c) triângulos equiláteros de lado crescente até atingir a medida 2 2 cm, seguidos
√
de hexágonos não regulares, seguidos de um hexágono regular de lado 4 2 cm,
seguido de hexágonos não regulares, seguidos
√ de triângulos equiláteros de lado
decrescente começando com a medida de 2 2 cm.
√
(d) triângulos equiláteros de lado crescente até atingir a medida 4√ 2 cm, seguidos
de quadrados de lado decrescente até atingir a medida de 2 2 cm, seguidos
de quadrados de lado crescente, seguidos√de triângulos equiláteros de lado
decrescente começando com a medida de 4 2 cm.
√
(e) quadrados de lado crescente até atingir a medida 4 2 cm, seguidos
de hexágonos
√
não regulares, seguidos de um hexágono regular de lado 2 2 cm, seguido de
hexágonos não regulares,
seguidos quadrados de lado decrescente começando
√
com a medida de 4 2 cm.
10. Considere as imagens geométricas dos números complexos da forma z = n + 2n i,
com n ∈ Z, no plano Argand-Gauss. Desenhado neste mesmo plano, passaria por
todos esses pontos o gráfico de
(a) uma função modular.
(b) uma função logarı́tmica.
(c) uma função quadrática.
(d) uma função polinomial de grau 4.
(e) uma função exponencial.
1
11. Se m = logπ (sec(x) + tg(x)) e n = logπ ( sec(x)−tg(x)
), com 0 6 x 6 π2 , então m − n é
igual a
(a) sen( π6 ).
(b) cos( π6 ).
(c) sen( π4 ).
(d) cos(0).
(e) sen(0).
12. No plano cartesiano os conjuntos
{(x; y) ∈ R2 ||x| + |y| = 1},
e
{(x; y) ∈ R2 |x2 + y 2 = 1}
{(x; y) ∈ R2 |max{x, y} = 1},
(em que maxA denota o maior elemento de um conjunto finito A), estão representados na figura abaixo.
5
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
1
−1
1
−1
Assim, no espaço euclidiano tridimensional, os conjuntos
{(x; y; z) ∈ R3 ||x| + |y| + |z| 6 1},
{(x; y; z) ∈ R3 |x2 + y 2 + z 2 6 1}
e
{(x; y; z) ∈ R3 |max{x, y, z} 6 1}
podem ser identificados, respectivamente, com
(a) um octaedro regular de volume
volume 8.
2
,
3
uma esfera de volume
8π
3
e um cubo de
e um cubo de
(b) um octaedro regular de volume 43 , uma esfera de volume 4π
3
volume 8.
√
(c) um cubo √de volume 2 2, uma esfera de volume 4π
e um octaedro regular de
3
8 2
volume 3 .
(d) um cubo√de volume 2, uma esfera de volume
volume 8 3 2 .
(e) um octaedro regular de volume
√
volume 16 2.
4
,
3
13. Se a + b = 1, então a3 + b3 é igual a
(a) (a + b)3 + (a − b)3
√3
3 0 b
(b) 0 3 √0 a 0
3
3
(c) a3 + 3a2 b + 3ab2 + b3
6
8π
3
e um octaedro regular de
uma esfera de volume
8π
3
e um cubo de
Vestibular Ibmec 2003 2
√3
0
3
(d) 0 −3
a
0
3
2
Análise Quantitativa e Lógica Objetiva - Prova B
3
b
0
√
3
(e) a − 3a b + 3ab2 − b3
√
14. Suponha que o lado do quadrado maior na figura abaixo seja igual a 2 2 cm.
Considere que cada uma das regiões da figura acima deve ser pintada com uma das
duas cores: vermelho ou amarelo. Se duas regiões vizinhas não podem ser pintadas
com mesma cor, então a soma de todas as áreas das regiões pintadas em vermelho
é igual a
√
(a) 2 cm2 .
(b) 2 cm2 .
√
(c) 2 2 cm2 .
(d) 4 cm2 .
√
(e) 4 2 cm2 .
15. Dada uma função f , chamamos de valor de ponto fixo de f um valor x no domı́nio
da função tal que f (x) = x. Ordenando o conjunto dos valores positivos de ponto
fixo de f (x) = x − 2sen(x) obtemos
(a) uma progressão aritmética de razão π.
(b) uma progressão geométrica de razão π.
(c) uma progressão aritmética de razão π2 .
(d) uma progressão geométrica de razão π2 .
(e) uma progressão aritmética de razão 2π.
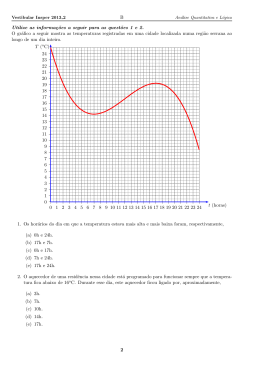
16. O gráfico da função f (x) = x − 2cos(x) está contido no conjunto de todos os pontos
do plano cujas coordenadas (x; y) satisfazem
(a) a equação |y − x| > 2.
(b) a equação |y + x| > 2.
(c) a equação |y − x| 6 2.
(d) a equação |y + x| 6 2.
7
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
(e) simultaneamente as equações |x| 6 2 e |y| 6 2.
17. Se x, y e z representam grandezas inteiras positivas tais que x é diretamente proporcional à y e inversamente proporcional ao quadrado de z, então quanto vale x se
y = z = 2?
Considere que
(I) x = 3 pode acontecer quando y = 6.
(II) x = 3 pode acontecer quando z = 2.
Assim, para responder a pergunta acima, é correto afirmar que
(a) I sozinha é suficiente, mas II sozinha não é.
(b) II sozinha é suficiente, mas I sozinha não é.
(c) I e II juntas são suficientes, mas cada uma sozinha não é.
(d) cada uma das afirmações sozinha é suficiente.
(e) I e II juntas não são suficientes, sendo necessário mais dados.
18. Considere verdadeiras as afirmações abaixo.
(I) Todo bom tomador de decisões possui intuição e domina os métodos quantitavivos dos processos decisórios gerenciais.
(II) Quem tem raciocı́nio lógico tem intuição.
(III) Há candidatos com raciocı́nio lógico dentre os admitidos em nossa faculdade.
Então
(a) não podemos formar bons tomadores de decisão se ensinarmos para alguns
dos admitidos em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(b) certamente formaremos bons tomadores de decisão se ensinarmos para todos
os admitidos em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(c) certamente formaremos bons tomadores de decisão se ensinarmos para alguns
dos admitidos em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(d) podemos formar bons tomadores de decisão se ensinarmos a todos os admitidos
em nossa faculdade os métodos quantitavivos dos processos decisórios gerencias.
(e) certamente formaremos bons tomadores de decisão se ensinarmos para os admitidos em nossa faculdade que tem intuição os métodos quantitavivos dos
processos decisórios gerencias.
19. Dizemos que o conjunto de todos os economistas do mundo é uniforme em determinado momento se, e somente se, qualquer que seja a localização de um economista sobre a face da terra existe um outro economista localizado a menos de 50 quilômetros
dessa localização. Para que o conjunto de todos os economistas do mundo não seja
uniforme às 12 horas do dia 01 de junho de 2003
8
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
(a) é necessário que, às 12 horas do dia 01 de junho de 2003, o único economista
do mundo fora dos continentes esteja num avião sobre o Atlântico aproximadamente na metade do caminho entre Brasil e Portugal.
(b) é necessário que, às 12 horas do dia 01 de junho de 2003, todos os economistas
do mundo estejam distantes mais que 50 quilômetros dois a dois.
(c) é suficiente que, às 12 horas do dia 01 de junho de 2003, o único economista
do mundo fora dos grandes continentes esteja num avião sobre o Atlântico
aproximadamente na metade do caminho entre Brasil e Portugal.
(d) é suficiente que, às 12 horas do dia 01 de junho de 2003, todos os economistas
do mundo estejam distantes menos que 50 quilômetros dois a dois.
(e) é necessário que, às 12 horas do dia 01 de junho de 2003, todos os economistas
do mundo estejam distantes menos que 50 quilômetros dois a dois.
20. Suponha que as premissas do raciocı́nio apresentado abaixo sejam verdadeiras.
Está equivocado quem afirma que a essência dos padrões estéticos presentes na arte
ocidental atual foi moldada pelos alemães e italianos no perı́odo pós-Renascimento,
porque os italianos evidentemente apresentam nas suas obras padrões estéticos primordialmente estabelecidos 3000 anos antes pelos gregos e os alemães tentaram
começar do zero no século XVI, mas sucumbiram gradativamente à influência da
arte genuı́na grega.
A partir desse raciocı́nio, é correto afirmar que
(a) a essência dos padrões estéticos presentes na arte ocidental atual foi moldada
exclusivamente pelos italianos no perı́odo pós-Renascimento.
(b) a conclusão é verdadeira.
(c) a essência dos padrões estéticos presentes na arte ocidental atual foi moldada
exclusivamente pelos alemães no perı́odo pós-Renascimento.
(d) a conclusão é falsa.
(e) a essência dos padrões estéticos presentes na arte ocidental atual foi moldada
exclusivamente pelos gregos no perı́odo pós-Renascimento.
9
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
21. Na noite anterior à prova de vestibular do IBMEC, um candidato dormiu pensando
tanto na faculdade que teve um estranho sonho: ele estava em frente ao local de
exame que era um prédio de cinco andares denominados I, B, M, E, C, não necessariamente nessa ordem. Entrou no prédio, que estava completamente vazio porque
ainda era muito cedo e percebeu que cada sala estava identificada com um anagrama da palavra IBMEC sem faltar nenhum anagrama e que, em cada andar, a
identificação de todas as salas começava com a letra do andar. De repente, apareceu
seu colega de estudos, que também faria a prova na manhã seguinte, e antes que
os dois pudessem se cumprimentar ecoou por todo o prédio uma voz muito grave
profetizando: “Se vocês fizerem a prova em salas começadas com letras diferentes
e terminadas com a mesma letra suas mentes irão se iluminar, mas lembrem-se,
somente se fizerem a prova em salas começadas com letras diferentes e terminadas
com a mesma letra.”Neste exato momento eles acordaram, aprontaram-se ansiosamente e foram para o local do exame, que era exatamente igual ao do sonho, mas
com muita gente. Suponha que as salas em que os candidatos farão a prova foram
determinadas aleatoriamente.
(a) Quantas salas tinha cada andar do prédio?
(b) Calcule a probabilidade de ambos fazerem a prova na mesma sala.
(c) Calcule a probabilidade de os dois candidatos terem suas mentes iluminadas.
10
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
22. Na figura abaixo, suponha que as medidas dos segmentos BC, BD, CF, BG e CG
−→ −−→
sejam todas iguais a 2 e que CF e BD sejam, respectivamente, as bissetrizes dos
b e CBG.
b
ângulos BCE
A
E
G
F
D
B
C
(a) Determine a medida do segmento BE.
(b) Calcule sen(750 ). (Sugestão: 750 = 450 + 300 .)
(c) Determine a medida da área do triângulo ACE.
11
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
23. Um banco irá construir uma sede com um cofre cilı́ndrico para armazenar seus mais
preciosos valores. A parede, o piso e o teto deverão ser constituı́dos de uma camada
de um metro de espessura de um material cujo custo é R$1.000,00 por metro cúbico.
Suponha que devam ser gastos R$88.000,00 com esse material e que, internamente,
o raio da base (R) do cofre deva ser igual à altura. Determine o valor de R. (Utilize
28π ∼
= 88.)
12
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
24. Considere a matriz
R(θ) =
cosθ senθ
−senθ cosθ
(a) Resolva a equação
4
[R(θ)] =
para θ ∈ [0; π2 ].
−1 0
0 −1
.
,
(b) Se as colunas da matriz
Q=
1 1 −1 −1
1 −1 −1 1
representam as coordenadas dos vértices de um quadrado, determine o quadrilátero
cujos vértices são as colunas da matriz R(θ).Q, para o valor de θ obtido no
item anterior.
13
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
25. Considere as seqüências
(a1 , a2 , a3 , ..., an , an+1 , ...)
e
(g1 , g2 , g3 , ..., gn , gn+1 , ...)
que satisfazem as leis de formação
an+1 − an =
e
1
para n = 1, 2, 3, ...; com a1 = 1
2
1
gn+1
= para n = 1, 2, 3, ...; com g1 = 2,
gn
2
respectivamente.
(a) Mostre que a seqüência
(2a1 , 2a2 , 2a3 , ..., 2an , 2an+1 , ...)
é uma progressão geométrica e exiba a fórmula do termo geral dessa progressão.
(b) Mostre que a seqüência
(log2 (g1 ), log2 (g2 ), log2 (g3 ), ..., log2 (gn ), log2 (gn+1 ), ...)
é uma progressão aritmética e exiba a fórmula do termo geral dessa progressão.
14
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
26. Suponha que o gráfico da função f : [−1; 1] −→ [0; 1] seja dada pela figura abaixo.
1
C
B
D
A
E
−1
1
Suponha que AB seja um arco da circunferência de centro (−1; 0, 5) e raio 0,5, que
BCD seja a semicircunferência de centro (0; 0, 5) e raio 0,5 e que DE seja um arco
da circunferência de centro (1; 0, 5) e raio 0,5.
Considere a função área A : [−1; 1] −→ R que para cada x0 ∈ [−1; 1] associa a
medida da área entre o eixo Ox e o gráfico de f limitada pelas retas x = −1 e
x = x0 , denotada por A(x0 ), conforme figura abaixo.
1
B
A
−1
C
D
A(x0 )
E
x = x0
(a) Determine a fórmula da função f .
15
1
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
(b) Calcule A(0, 5) − A(−0, 5) e indique no gráfico abaixo a área que está representada por essa subtração.
1
B
C
D
A
E
−1
1
16
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
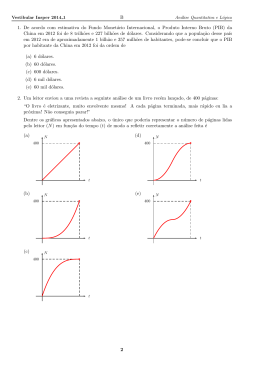
27. Suponha que a quantidade mensal (d) que uma comunidade queira comprar de um
determinado produto seja uma função do primeiro grau em termos do preço (p) do
respectivo produto. Considere que nos últimos dois meses os preços praticados foram
R$10,00 e R$20,00 e que as respectivas quantidades adquiridas pela comunidade
foram 180 e 80 unidades do produto. O fabricante desse produto calcula que cada
unidade produzida custa-lhe R$2,00, e que o custo fixo operacional mensal é de
R$690,00 (isto é, independente da quantidade produzida, ele gasta R$690,00 para
manter sua empresa funcionando).
(a) Determine a fórmula que estabelece a função de d em termos de p.
(b) Defina a função lucro total mensal (l) do fabricante como a função que, para
cada preço p praticado, associa o resultado da receita total mensal (dada pelo
produto do preço pela quantidade) subtraindo o custo total mensal (dado pela
soma do custo fixo operacional mensal com o custo de produzir d unidades); e
determine a fórmula da função l em termos de p.
(c) Determine o preço que o fabricante deve praticar no próximo mês para que seu
lucro total mensal seja o maior possı́vel.
17
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
28. Considere uma circunferência (C1 ) inscrita em um quadrado de lado 2. Dentro de C1
inscreva outro quadrado, com os lados paralelos ao maior, e dentro desse quadrado
inscreva outra circunferência (C2 ), como na figura abaixo.
C1
C2
Seja S1 a medida da área compreendida entre C1 e C2 e repita a mesma construção
dentro de C2 , obtendo S2 a medida da área compreendida entre C3 e C4 e assim
sucessivamente, como na figura abaixo.
C1
C2
C3
C4
18
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
Se Sn é a medida da área compreendida entre C2n−1 e C2n , determine o limite da
soma
S = S1 + S2 + S3 + ... + Sn + ...
19
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
29. Considere a matriz A4×4 cujas entradas aij são dadas por
ai1
ai2
ai3
ai4
= pi−1
= q i−1
= ri−1
= si−1
i = 1, 2, 3, 4
i = 1, 2, 3, 4
i = 1, 2, 3, 4
i = 1, 2, 3, 4
em que p,q,r e s são números naturais não nulos e distintos dois a dois.
(a) Exiba a matriz A.
(b) Calcule det(A), o determinante da matriz A.
(c) Mostre que det(A) é um múltiplo de 6, quaisquer que sejam p, q, r, s ∈ N.
20
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
30. Considere que foi estabelecida no Olimpo da Homérica Odisséia a seguinte regra:
“Se, na divina assembléia, os deuses atendem a um pedido de Atena somente se
Posı́don estiver ausente (e, obviamente, Atena presente), então Zeus obriga os deuses
a executar o contrário de todo pedido que Posı́don fizer somente se Atena estiver
ausente (e, obviamente, Posı́don presente).”
(a) Se Atena e Posı́don estiverem presentes numa mesma assembléia e ambos fizerem pedidos distintos e não contráditórios, como os deuses devem proceder?
(b) Desejando acabar com essa regra, Posı́don comparece exatamente na assembléia
em que Atena pede o regresso de Ulisses e faz o mesmo pedido. O que Zeus, o
lógico dos lógicos, deve fazer para que a regra prevaleça?
21
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
Rascunho
Rascunho
Rascunho
22
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
Rascunho
Rascunho
Rascunho
23
Vestibular Ibmec 2003 2
Análise Quantitativa e Lógica Objetiva - Prova B
Nome:
No. de inscrição:
Rascunho
Rascunho
Rascunho
24