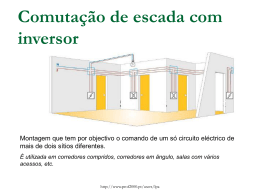
ELECTROMAGNETISMO
2006/07
APRESENTAÇÃO
• Docente: Margarida Facão
Gab. 13.2.12
[email protected]
• Regime de avaliação contínua
presença obrigatória em 2/3 das aulas
3 testes ( 2 ao longo do período lectivo e 1 no
período de exames)
• Laboratórios – notas válidas desde 2002/03
• Informações e documentos no ELEARNING
BIBLIOGRAFIA
• Fundamentals of Electricity and
Magnetism, Arthur Kip
• Introdução à electricidade e magnetismo,
S.K. Mendiratta
• Electricidade e magnetismo, cursos de
física de Berkeley, vol. 2
ELECTROSTÁTICA
• Electrostática = Estudo dos fenómenos
decorrentes de cargas eléctricas estacionárias.
• Carga eléctrica = propriedade de alguns corpos
que os divide em 2 classes (positivos e
negativos) de tal forma que componentes da
mesma classe se repelem entre si e de classes
diferentes se atraem.
Propriedades da carga eléctrica
• Conservação da carga - válido num
sistema isolado.
• Quantização da carga – carga total é
sempre igual a múltiplos inteiros da carga
do electrão
e=1.6X10-19 Coulomb
Charles Augustin de Coulomb
•
•
Nasceu a 14 de Junho de 1736 em
Angoulême
Morreu a 23 de Agosto de 1806 em
Paris
•
Em sua homenagem, deu-se seu
nome à unidade de carga elétrica, o
coulomb.
•
Engenheiro de formação, ele foi
principalmente físico. Publicou 7
tratados sobre a Eletricidade e o
Magnetismo, e outros sobre os
fenômenos de torção, o atrito entre
sólidos, etc.
•
Experimentador genial e rigoroso,
realizou uma experiência histórica com
uma balança de torsão para
determinar a força exercida entre duas
cargas elétricas - Lei de Coulomb.
Wikipedia
LEI DE COULOMB
1 q1q2
F1 = F2 =
2
4πε0 d
Direcção – linha que une as cargas
ε 0 = 8.84 × 10 −12 C 2 N −1m −2
1
4πε 0
= 9 ×109 Nm 2C − 2
Sentido - atractivo para cargas de
sinal contrário
- repulsivo para cargas do
mesmo sinal
Princípio da sobreposição
(distribuição discreta de cargas)
• A força eléctrica total sobre a carga q0 devida à
presença de n cargas q1,q2,...,qn é igual à soma
vectorial das forças exercidas por cada uma
das cargas, ou seja,
n
G
q0
qi
ˆ
F0 =
r
∑
2 i
4πε0 i =1 ri
onde rˆ i é um vector unitário que aponta de qi para q0.
Exercícios
•
•
Três cargas pontuais iguais de valor Q encontram-se nos vértices
de um triângulo equilátero de 10 cm de lado. Calcule a força em
cada uma delas.
Três cargas pontuais +Q1, -Q2 e +Q3 estão igualmente espaçadas
ao longo de uma linha. Se os módulos Q1 e Q2 forem iguais qual
terá que ser o módulo Q3 para que a força total na carga Q1 seja
zero?
+Q1
•
-Q2
+Q3
Qual a força exercida numa carga de valor 2Q colocada no centro
de um quadrado de 20 cm de lado se 4 cargas idênticas de valor Q
estiverem colocadas uma em cada vértice? Refaça os cálculos para
o caso em que uma das cargas dos vértices é removida.
Distribuição contínua de cargas
• Nas distribuições contínuas de
carga é conveniente usar a
noção de densidade de carga:
– Densidade linear de carga
– Densidade superficial de carga
– Densidade volúmica de carga
dq
λ = (Cm −1 )
dl
dq
σ = (Cm − 2 )
da
dq
ρ = (Cm −3 )
dv
Exercícios
• Uma carga Q está uniformemente
distribuída numa esfera de raio 2 cm.
– Qual é a densidade volúmica de carga?
– Qual é a carga total contida na coroa esférica
externa desde o raio 1 cm ao raio 2 cm.
• Exercício 1 das folhas.
• TPC – exercício 3 das folhas
Princípio da sobreposição
(distribuição contínua de cargas)
• Quando a distribuição de carga é contínua, a
força total na carga q0 é igual ao integral
seguinte:
G
q0 dq
ˆ
F0 =
r
2
∫
4πε 0 r
onde r̂ é um vector unitário que aponta da carga
elementar dq para a carga q0 e o integral se
estende a todo o comprimento, área ou volume
carregado.
Exercício
• Um anel circular de 3 cm de raio tem uma
carga total de 10-3 C uniformemente
distribuída.
– Qual a força numa carga de 10-2 C colocada
no seu centro?
– Qual a força na mesma carga agora colocada
no eixo do anel a uma distância de 4 cm do
centro do mesmo?
Campo eléctrico
Campo eléctrico = quantidade vectorial definida em
cada ponto do espaço e que representa a força
que actuaria numa carga positiva unitária
colocada no mesmo ponto.
G
EP =
1
q
ˆ
r
2
4πε 0 r
(N / C)
Princípio de sobreposição aplicado
ao campo eléctrico
G
E=
G
E=
n
qi
ˆ
r
∑
2 i
4πε 0 i =1 ri
1
1
dq
ˆ
r
2
∫
4πε 0 r
Caso de distribuições
discretas de cargas
Caso de distribuições
contínuas de cargas
Exercícios
• Oito cargas pontuais idênticas de valor Q C
estão colocadas uma em cada um dos vértices
de um cubo cujos lados medem 10 cm.
– Calcule o campo eléctrico no centro do cubo.
– Calcule o campo eléctrico no centro das faces
do cubo.
– Recalcule o campo eléctrico no centro do
cubo para o caso em que uma das cargas é
removida.
• Ex. 6
• Ex. 10
Linhas de campo eléctrico
O campo elétrico é usualmente representado por linhas
tais que:
• Em cada ponto a direcção do campo eléctrico é
tangente a essa linha
• A sua densidade numa dada região é proporcional à
intensidade do campo nessa região.
• Começam nas cargas positivas e terminam nas cargas
negativas
• O número de linhas que começam ou terminam numa
carga é proporcional ao valor dessa carga
Possível devido ao facto do campo eléctrico ser descrito
por uma lei inversamente proporcional ao quadrado da
distância.
http://qbx6.ltu.edu/s_schneider/physlets/main/efield.shtml
FLUXOG
Fluxo de um campo vectorial F através de uma
superfície S é dado pelo integral
G G
Φ = ∫∫ F .dS
S
G
onde dS é um vector perpendicular ao elemento de área dS
cuja intensidade é igual a dS e sentido para fora.
G
• F é o campo nesse pedaço elementar (considerado
constante porque o pedaço é muito pequeno)
G G
G
• F .dS é um escalar conhecido como fluxo de F através de dS
(é o produto interno entre estes dois vectores)
G
F
S
θ
Φ = FS cos θ
Fluxo do campo eléctrico
Fluxo do campo eléctrico produzido por uma carga
pontual através de uma superfície esférica de
centro na carga
q
Φesfera
de raio R
G G
= ∫ E.dS
G
G
(campo E é sempre paralelo a dS )
= ∫ EdS = ∫
q
4πε 0 R
2
dS
(função integranda é constante em toda a superfície)
=
q
4πε 0 R 2
∫ dS =
q
4πε 0 R
Fluxo não depende do raio da esfera.
2
×
R
=
π
4
2
q
ε0
G
dS 2
θ
• fluxo através do elemento externo
q
dS 2 cos θ
4πε 0 R22
G
dS1
• fluxo através do elemento esférico
q
dS1
2
4πε 0 R1
• Relação entre os dois elementos de área
dS
dS
cosθ × 22 = 21
R2
R1
O fluxo através dos dois elementos é o mesmo
Como existe uma correspondência biunívoca entre os
elementos da superfície da esfera e os da superfície
arbitrária.
O fluxo através da superfície arbitrária é igual ao fluxo
através da esfera.
G G q
∫SF E.dS = ε 0 , para uma carga pontual
∫
G G
E.dS =
SF
∫
SF
∑q
i
i
ε0
, para várias cargas discretas
G G ∫ dq
, para uma distribuição contínua de carga
E.dS =
ε0
Lei de Gauss
O fluxo do campo eléctrico através de uma
superfície fechada é igual à carga total no interior
dessa superfície dividida por ε0
∫
SF
G G Q
E.dS =
ε0
- Lei equivalente à lei de Coulomb.
- Formulação inversa – através do conhecimento do campo podemos conhecer
a carga total.
-Permite-nos calcular o campo em problemas com distribuições simétricas
de carga.
Carl Friedrich Gauss
• Nasceu em Braunschweig a 30 de Abril de 1777 e
morreu em Göttingen a 23 de Fevereiro de 1855.
• Matemático, astrônomo e físico alemão.
• Desenvolveu teorias e métodos na área dos erros
de observação. Entre eles, o método de mínimos
quadrados (que inventou aos 18 anos) e a lei de
distribuição normal de erros com a sua curva em
formato de sino a que se dá o mome de Gaussiana.
Exercícios
• Calcule o campo eléctrico produzido por
uma esfera de raio R uniformemente
carregada com densidade de carga ρ.
Faça os cálculos para dentro e fora da
esfera.
• Exercícios 16 e 17.
Trabalho da Força Eléctrica
Para aproximarmos uma carga de outra do mesmo sinal é
necessário realizar trabalho. O trabalho efectuado é igual em
módulo mas de sinal contrário ao trabalho da força eléctrica
o qual neste caso é negativo.
A
B
W =∫
+
+
B
A
G G
Fel .dl < 0
A carga afasta-se de B para A pela açção da força eléctrica. Neste caso o
trabalho da força eléctrica é positivo.
B
+
+
A
W =∫
B
A
G G
Fel .dl > 0
Energia Potencial Eléctrica
Como a força eléctrica é conservativa, o trabalho da força
eléctrica não depende do caminho. Assim é possível
definir uma energia potencial eléctrica. Nos casos do
slide anterior:
• A energia potencial eléctrica aumentou no primeiro
caso,
• A energia potencial eléctrica diminuiu no segundo
caso.
G G
U B − U A = − ∫ Fel .dl
B
A
Potencial Eléctrico
Como a energia potencial eléctrica depende da quantidade
de carga que se está a mover é útil definir energia
potencial eléctrica por unidade de carga a que se dá o
nome de potencial eléctrico.
G G
∫ Fel .dl
B
VBA
G G
UB −U A
A
=
=−
= − ∫ E.dl
qmóvel
qmóvel
A
B
Se escolhermos um ponto de referência (ponto A fixo) a função só depende
do ponto B. Usualmente usamos o ponto fixo no infinito a não ser que
tenhamos uma distribuição contínua de carga com carga até ao infinito. Esse
ponto fixo fica assim a um potencial zero.
G G
VB = − ∫ E.dl
B
∞
Potencial do ponto P relativamente
ao infinito devido a:
• Uma carga pontual q a
uma distância r do
ponto P.
• Uma distribuição
discreta de cargas.
VP =
VP =
q
4πε 0 r
qi
∑
4πε 0 i ri
1
(onde ri é a distância da
carga qi ao ponto P )
• Uma distribuição
contínua de carga.
dq
VP =
4πε 0 ∫ r
1
(onde r é a distância do
elemento de carga dq ao ponto P )
Potencial eléctrico (cont.)
Reciprocamente o campo eléctrico pode ser definido a
partir do potencial da seguinte forma:
G
⎛ ∂V G ∂V G ∂V G ⎞
E = −⎜
ux +
uy +
u z ⎟ = − grad V
∂y
∂z ⎠
⎝ ∂x
O gradiente de V aponta na direcção e sentido do maior
crescimento de V e o seu módulo é a taxa de crescimento
nessa direcção.
Exercício 11
Superfícies equipotenciais
Superfícies equipotenciais são superfícies onde o potencial
é constante e às quais o campo eléctrico é
perpendicular.
Energia de uma distribuição de carga
• Distribuição discreta de 4 cargas
A energia desta distribuição de cargas é igual ao trabalho
necessário para trazer cada uma das cargas do infinito na
presença do campo eléctrico devido às que já lá se encontram.
W1 = 0
W2 = q2V21
W3 = q3 (V31 + V32 )
W4 = q4 (V41 + V42 + V43 )
i
⎛
⎞
U = W = ∑ Wi = ∑ ⎜ qi ∑ Vij ⎟
i =1
i =1 ⎝
j = i −1
⎠
(onde Vij representa o potencial em i devido à carga q j )
4
4
Energia de uma distribuição de carga (cont.)
O trabalho será igual se transportarmos as cargas na sequência
q1, q2, q3 e q4 ou na sequência inversa q4, q3, q2 e q1. Assim a
soma das parcelas à esquerda é igual à soma das parcelas à
direita.
W1 = 0
q2 ⎛ q1 ⎞
W2 =
⎜ ⎟
4πε 0 ⎝ r21 ⎠
q3 ⎛ q1 q2 ⎞
W3 =
⎜ + ⎟
4πε 0 ⎝ r31 r32 ⎠
q ⎞
q ⎛q q
W4 = 4 ⎜ 1 + 2 + 3 ⎟
4πε 0 ⎝ r41 r42 r43 ⎠
q1 ⎛ q4 q3 q2 ⎞
W1 =
⎜ + + ⎟
4πε 0 ⎝ r14 r13 r12 ⎠
W2 =
q2 ⎛ q4 q3 ⎞
⎜ + ⎟
4πε 0 ⎝ r24 r23 ⎠
q3 ⎛ q4 ⎞
W3 =
⎜ ⎟
4πε 0 ⎝ r34 ⎠
W4 = 0
Energia de uma distribuição de carga (cont.)
2W =
q1 ⎛ q2 q3 q4 ⎞
⎜ + + ⎟+
4πε 0 ⎝ r12 r13 r14 ⎠
q2 ⎛ q1 q3 q4 ⎞
+
⎜ + + ⎟+
4πε 0 ⎝ r21 r23 r24 ⎠
q3 ⎛ q1 q2 q4 ⎞
+
⎜ + + ⎟+
4πε 0 ⎝ r31 r32 r34 ⎠
q4 ⎛ q1 q2 q3 ⎞
+
⎜ + + ⎟
4πε 0 ⎝ r41 r42 r43 ⎠
⎛ 4
⎞
q
1 ⎜
1 4
j
⎟
= ∑ qiVi
U = W = ∑ qi ∑
2 i =1 ⎜⎜ j =1 4πε 0 rij ⎟⎟ 2 i =1
⎝ j ≠i
⎠
(onde Vi é o potencial em ri devido às restantes cargas)
4
Generalização a n cargas pode ser consultada na bibliografia: Mendiratta pag. 22
Energia de uma distribuição de carga
Generalização para distribuições contínuas
Q
U = ∫ Vdq
Onde V é o potencial devido à carga
já presente na distribuição.
0
1
U = ∫ ρVdv
2
Exercícios 30 e 33.
Onde V é o potencial devido a
toda a distribuição de carga.
Condutores e isoladores
• Isoladores
Fraca condutibilidade
eléctrica
Exemplo: vidro
• Condutores
Boa condutibilidade
eléctrica.
Exemplo: metais
A condutibilidade eléctrica pode variar com:
• a temperatura como no caso dos semicondutores,
• a humidade como no caso do ar,
• muitas outras condições.
Condutor perfeito = material onde o deslocamento das
cargas, quando sujeito a um campo eléctrico, se pode fazer
sem qualquer restrição à excepção dos limites físicos do
condutor.
Campo eléctrico em condutores
Situação de equilíbrio
• Cargas em repouso → Forças nulas → Eint=0
• Distribuição de cargas na superfície tal que a soma do
campo por elas criadas com o campo criados por cargas
exteriores é nula.
• Potencial é igual em todos os pontos. A sua superfície é
uma superfície equipotencial → Esup é perpendicular à
superfície.
Campo eléctrico em condutores
•
•
Cavidades dentro de condutores
Cavidade sem carga:
- Eint é nulo
- Não existem cargas na superfície interna
Cavidade com carga:
- Cargas de sinal contrário na superfície interna do
condutor para garantir campo eléctrico nulo no
interior do condutor
- Eint não é nulo
Forma diferencial da lei de Gauss
O teorema da divergência aplica-se a campos vectoriais e
é dado por
G G
G
∫ F .dS = ∫ divFdv
SF
Vol .
SF
ε 0 Vol .
G
onde, em coordenadas cartesianas, divF é dado por
G ∂Fx ∂Fy ∂Fz
+
+
divF =
∂x
∂y
∂z
Usando o teorema da divergência na lei de Gauss
G G 1
∫ E.dS = ∫ ρ dv
obtemos
G ρ
divE =
ε0
Carácter conservativo de E
O teorema de Stokes aplica-se a campos vectoriais
e é dado por
G G
G G
v∫ F .dl = ∫ rotF .dS
LF
S
G
onde, em coordenadas cartesianas, o rotF é dado por
G ⎛ ∂Fz ∂Fy ⎞
⎛ ∂Fy ∂Fx
⎛ ∂Fx ∂Fz ⎞
−
−
−
uˆ y + ⎜
rotF = ⎜
⎟ uˆ x + ⎜
⎟
∂z ⎠
∂x ⎠
∂y
⎝ ∂z
⎝ ∂y
⎝ ∂x
Aplicando o teorema de Stokes a
G G
v∫ E.dl = 0 (válido para campos eléctrostáticos)
LF
obtemos
G
rot E = 0
⎞
⎟ uˆ z
⎠
Equações de Laplace e Poisson
Usando a forma diferencial da lei de Gauss
G ρ
div E =
ε0
e a relação entre o campo eléctrico e o potencial, ou seja
G
E = − grad V
obtemos
ρ
lap V = −
ε0
(Equação de Poisson)
onde, em coordenadas cartesianas, lap V é dado por
∂ 2 Fy
∂ Fx
∂ 2 Fz
lap V =
+ 2 + 2
2
∂x
∂y
∂z
Em regiões onde não existe carga
2
lap V = 0
(Equação de Laplace)
As funções grad, div, rot e lap
Usando operador nabla, definido da forma
∂
∂
∂
ˆ
ˆ
∇ = u x + u y + uˆ z
∂x
∂y
∂z
podemos escrever
∇f = grad f
G
G
∇.F = div F
G
G
∇ × F = rot F
G
G
2
∇ F = lap F
Estas funções têm expressões diferentes quando escritas em
Coordenadas esféricas ou cilíndricas.
Pode, por exemplo, ver
http://mathworld.wolfram.com/SphericalCoordinates.html
http://mathworld.wolfram.com/CylindricalCoordinates.html
Energia do campo electrostático
(outra formulação)
A partir da expressão
1
ρVdv
∫
2
pode-se chegar a uma nova formulação para a energia
U=
electrostática que é dada por
U=
ε0
2
E dv
∫
2
Condensadores
• Condensador = conjunto de dois
condutores muito próximos de tal forma
que o campo entre eles não é afectado
por outros corpos carregados
Capacidade de um condensador
C=Q/V (Faraday)
onde Q é a carga em cada um deles e V é a
diferença de potencial entre os dois.
Cálculo da capacidade
Capacidade de um condensador de placas paralelas
(dimensão das placas é grande relativamente à distância
entre as placas).
Consideremos A a área de cada placa, d a distância
ente placas e Q = σ A a carga total em cada placa.
Campo produzido por cada placa (supostamente infinita)
E=
σ
2ε 0
Entre as placas as duas contribuições do campo somam-se,
obtendo-se
d
σ
Q
E= =
ε 0 Aε 0
A diferença de potencial entre as placas é dada por
d
V =∫
0
Q
Qd
dy =
Aε 0
Aε 0
Assim a capacidade é igual a
C=
Aε 0
d
Exercício 1 da 2ª série
Leis de associação de
condensadores
• Condensadores em
paralelo
CT = ∑ Ci
• Condensadores em
série
1
1
=∑
CT
i Ci
i
Campo eléctrico em
isoladores/dieléctricos
• Matéria polariza-se na presença de um
campo eléctrico.
Na ausência de campo eléctrico, as
cargas negativas estão sobrepostas
às cargas positivas.
Na presença de campo eléctrico,
as cargas negativas estão afastadas
da posição de equilíbrio.
Matéria Polarizada
• Cada átomo ou molécula constitui um dipolo que pode
ser caracterizado por um momento dipolar (induzido).
-q
G
a
G
G
p = qa
+q
• Para melhor caracterizar a polarização podemos definir
um momento dipolar por unidade de volume ao qual se
dá o nome de densidade de polarização (ou apenas
polarização):
G
G
P = np
(onde n é o número de dipolos por unidade de volume)
P = neΔ
(onde e é a carga do electrão e Δ o deslocamento relativo das cargas)
Polarização
• Nos casos mais simples a polarização é proporcional
ao campo eléctrico médio existente no material.
• Note que este campo eléctrico médio se deve à soma
do campo eléctrico externo (ou aplicado) com o campo
eléctrico devido a esta polarização do material (sendo
este contrário ao aplicado).
• A polarização depende ainda do grau de
polarizibilidade do material.
• Assim podemos escrever:
G
G
P = ε0χ E
onde χ é a susceptibilidade eléctrica do material
Como calcular este campo médio?
Note que o campo médio depende da polarização, no entanto, a
polarização é proporcional ao campo médio → problema implícito.
G
G G G
P = ε 0 χ E ( Eapl , P)
1. Qual o campo criado pela matéria polarizada?
Suponhamos o caso mais simples em que a polarização é perpendicular
a duas faces do material.
-
Δ
+ ++
+
+ ++
+ + ++ +
+ + ++ +
+ + ++ +
+ + ++ +
+ +
-P
Eapl
As cargas no interior cancelam e a
polarização cria, em média, o mesmo
campo que duas superfícies carregadas
situadas nas faces perpendiculares
à polarização.
A densidade superficial de carga é,
neste caso, dada por
σ p = neΔ = P
No caso genérico de faces não perpendiculares à polarização, a densidade
superficial de carga é dada por:
σ p = neΔ cos θ = P⊥
G
P⊥ representa a componente de P perpendicular à superfície
(ver Kip página 130)
2. Ao campo médio total aplica-se uma lei de Gauss generalizada
∫
SF
G G 1
E.dS = (ql + q p )
ε0
carga de polarização
carga livre
Aplicação: condensador
preenchido com material dieléctrico
Seja um condensador de placas paralelas de área A e distância entre placas d
preenchido com um dieléctrio de susceptibilidade χ .
Pela lei de Gauss generalizada, o campo no interior é dado por
1
(σ + σ p )
ε0 l
σ l = ε 0 E − σ p = ε 0 E + ε 0 χ E = ε 0 (1 + χ ) E
E=
A capacidade do condensador é dada por
Ql σ l A ε 0 (1 + χ ) A ε 0ε r A
=
=
=
Ed
d
d
V
onde ε r é a permitividade eléctrica relativa ou constante dieléctrica.
C=
A ε =ε 0ε r dá-se o nome de permitividade eléctrica.
Vector deslocamento eléctrico
G
G G
D = ε0E + P
G G
G G
∫ D.dS = ε 0 ∫ E.dS +
SF
SF
∫
G G
P.dS = qtotal − q p = ql
SF
O vector deslocamento eléctrico tem como fonte apenas as cargas livres.
No vazio
No dieléctrico
Exercícios 3 e 7.
G
G
D = ε0E
G
G
D =εE
Corrente eléctrica
• Corrente eléctrica é um fluxo de cargas através de
condutores.
• Usualmente medida em termos da intensidade de
corrente = quantidade de carga que atravessauma
determinada área (ex. secção recta de um fio) por
unidade de tempo.
dq
I=
dt
(Ampere = Cs-1 )
• O sentido positivo da corrente é o sentido do fluxo de
cargas positivas. Embora na maior parte dos casos, a
corrente seja produzida pelo movimento das cargas
negativas.
Corrente eléctrica (cont.)
•
Define-se uma quantidade vectorial associada a cada ponto do
condutor onde flui a corrente,a que se chama densidade de
corrente = vector cuja direcção e sentido coincidem com o fluxo de
cargas positivas no ponto e cujo módulo é a intensidade de corrente
por unidade de área.
G
G
-2
j = nev (Am )
G G
I = ∫ j .dS
S
Se a densidade for constante em módulo e
em orientação relativa à superfície, fica
GG
I = j .S
Se o fluxo for perpendicular à superfície, fica
I = jS
Lei de Ohm
• A corrente eléctrica consegue-se à custa da actuação de
uma força eléctrica sobre as cargas.
• Assim, existe um campo eléctrico dentro do condutor
(note que já não estamos em regime estacionário).
• Existe também uma diferença de potencial entre as
extremidades do condutor.
• Usualmente a intensidade de corrente é proporcional a
esta diferença de potencial de tal forma que
V= R I
onde R é uma característica eléctrica do condutor
designada resistência (depende do seu material
constituinte, tamanho e forma) . Esta lei é conhecida
com lei de Ohm.
• A unidade SI de resitência é Ohm (Ω).
Georg Simon Ohm
•
•
•
•
Nasceu a 16 de Março de 1789 em
Erlangen, Bavaria (Alemanha actual)
Morreu a 6 Julho de 1854 em
Munique, Bavaria.
O pai de Georg Ohm era um autodidata
notável e ele próprio educou
cientificamente os seus filhos.
Curiosidade: em 1805 Ohm entrou para
a Universidade de Erlangen onde em
vez de se concentrar nos estudos
ocupava o seu tempo com a dança, a
patinagem no gelo e o bilhar. O pai de
Ohm, zangado pelo filho desperdiçar a
oportunidade de estudar que ele nunca
tinha tido, retirou-o da Universidade
passados 3 semestres.
O que é hoje conhecido como lei de
Ohm foi publicada num livro onde ele
descreve a sua teoria completa da
electricidade (1827).
Determinação da resistência
• Localmente a lei de Ohm pode escrever-se
G 1 G
G
j =σE = E
ρ
Resistividade do material
Condutividade do material
• Considere um cilindro de comprimento L, área de secção
recta A e resistividade ρ
A
1
L
1 dV
A dV
j=
E =
,
I = jA =
ρ
ρ dy
ρ dy
ρL
ρI
ρL
dV =
dy ⇒ V =
I ⇒ R =
A
A
A
Leis de associação de resistências
• Resistências em série
RT = ∑ Ri
i
• Resistências em
paralelo
• Exercício 11
1
1
=∑
RT
i Ri
Circuito eléctrico
• Circuito eléctrico = configuração de condutores
no qual a corrente flui por um ou mais caminhos
fechados constituído por:
– Fontes - repoêm a energia separando a carga contra
o campo eléctrico
- as fontes de tensão ideais são
caracterizadas pela d.d.p aos terminais =f.e.m
– Carga – parte do circuito que gasta a energia (ex.
resistências, motor, lâmpada)
– Fios de resistência baixa que ligam os vários
elementos.
Nomenclatura
•
•
•
•
•
Nó – junção de 3 ou mais condutores
Ramo – porção do circuito entre 2 nós
Malha – qualquer caminho fechado
Intensidade de corrente – um valor por cada ramo
Tensão ou diferença de potencial (d.d.p) – associada
aos terminais de cada elemento.
1Ω
6Ω
10 V
4Ω
12 Ω
8Ω
Leis de Kirchhoff
• Lei dos nós – a
soma das correntes
que entram num nó é
igual à soma das que
saem.
Resulta da conservação
da carga.
I1
I2
I3
I1=I2+I3+I4
I4
Leis de Kirchhoff (cont.)
• Lei das malhas – numa malha
a soma das f.e.m. das fontes é
igual à soma das d.d.p. aos
terminais das resistências.
Tanto as f.e.m. como as d.d.p.
são somadas com as
polaridades adquadas. Note
qual o sinal do trabalho da
força eléctrica.
Resulta do carácter conservativo
do campo eléctrico, ou seja,
G G
v∫ E.dl = 0
4V
2Ω
I1
2V
I3
3Ω
A•
•
I2
3Ω
2V
Malha 1
3xI3+2+2xI1-4=0
Malha 2
3I3+3xI2-2=0
B
Análise de circuitos
Método de Maxwell (das correntes fictícias)
• Atribui-se uma
corrente a cada
malha.
• Aplica-se a lei das
malhas a cada malha,
usando a lei de Ohm
em cada resistência.
• Aplica-se a lei dos
nós aos ramos
comuns a duas
malhas.
R1
a
R3
V1
V2
R2
I1
I2
b
−V1 + I1 R1 + ( I1 − I 2 ) R2 = 0
V2 + I 2 R3 + ( I 2 − I1 ) R2 = 0
Campo magnético
• É criado por cargas em movimento
• Actua sobre cargas em movimento
História:
• Imans permanentes usados para navegação.
• Oersted observa o movimento da agulha de uma
bússola na presença de uma corrente eléctrica durante
uma apresentação pública sobre electricidade e
magnetismo (1819). Na altura, estes fenómenos
julgavam-se independentes.
• Ampère estuda a força entre dois fios paralelos
transportando corrente (1820)
• Einstein explica que o campo magnético é a parte
relativista do campo eléctrico.
Lei de Biot-Savart
Campo magnético criado pelo elemento
G
de corrente Idl a uma distância r
G
G μ0 Idl × rˆ
dB =
4π r 2
− rˆ aponta do elemento de corrente para o
ponto onde se está a calcular o campo
− μ0 é a permeabilidade magnética do vazio
μ0
= 10−7
4π
x G
dB
G
dl
r̂
Linhas de campo magnético
• Indicam a direcção do campo magnético
• Indicam a grandeza do campo magnético pela
sua densidade
• Não têm fontes
• São contínuas e fechadas
Exercício 1 – Fio que transporta corrente
Exemplos de linhas de campo
magnético
Exercício 3 – anel de corrente
Campo magnético do solenóide
Força produzida pelo campo magnético
G G
G
dF = Idl × B
G
G G
F = qv × B
• Sobre elementos de
corrente
• Sobre a carga q com
velocidade v
Equivalência entre as 2 expressões:
I=
l=vΔt
Q lAnq vΔtAnq
=
=
= nqvA
Δt
Δt
Δt
n = cargas por unidade de volume
v = velocidade média
A = área da secção recta do condutor
Exercícios 6 e 9
G
G G
dF = nAdl qv × B
G
G G
F = qv × B
Movimento de cargas na presença de
campos magneticos uniformes
•
Campo magnético
perpendicular à velocidade
inicial – movimento circular
F = qvB
v2
F = man = m
R
vm
R=
qB
B
F
v
Este tipo de comportamento é usado em espectrómetros de massa onde se
determina a massa de partículas carregadas medindo o seu raio num campo
magnético
•
Campo magnético não perpendicular à velocidade – movimento
helicoidal – componente da velocidade paralela a B mantem-se
constante e a componente perpendicular produz o movimento
circular.
Lei de Ampère
•
Qual o valor da circulação (=integral de
linha ao longo de um caminho fechado) do
campo magnético?
1. Caso do fio infinito
1.1 Ao longo de uma circunferência de raio r
G G
μ0 I
μ0 I
.
=
=
=
B
dl
Bdl
dl
dl =μ0 I
v
∫
v
∫
v
∫
v
∫
π
π
2
2
r
r
circunf.
raio r
1.2 Ao longo de um caminho qualquer.
O caminho pode ser subdividido em
componentes de arco centrado no fio e
componentes radiais.
•
Componentes de arco - dl aumenta com r
- B diminui com
•
Componentes radiais – contribuição nula
para a circulação.
v∫
Caminho
arbitrário
G G
B.dl = μ0 I
G G
v∫ B.dl
G
BG
dl
Lei de Ampère
Pode provar-se que para qualquer configuração de corrente a
circulação de B é sempre dada por:
G G
G G
B
.
dl
=
μ
I
=
μ
j
.
dS
0
0
v∫
∫
L
A
Área definida
por L
Qualquer caminho fechado
Soma das correntes
que atravessam uma área
definida por L
Em situações de simetria, esta lei pode ser usada para calcular o
campo magnético.
Campo magnético devido a um
solnóide
Anel de corrente
Solenóide muito comprido
Campo magnético de uma bobina
toroidal
Pela simetria do problema, as linhas do
campo serão circunferências concêntricas
com o eixo da bobina toroidal.
Forma integral da lei de Ampère
Partindo da lei de Ampère
G G
G G
v∫ B.d l=μ0 ∫ j .dS
e usando o teorema de Stokes
G G
G G
v∫ F .dl = ∫ rot F .dS
obtemos
G
G
rot B = μ 0 j
Fluxo do campo magnético
• O fluxo do campo magnético através de uma
superfície fechada é nulo, ou seja,
∫
G G
B.dS = 0
SF
E, usando o teorema da divergência
G G
G
∫ F .dS = ∫ div Fdv
SF
vol
obtemos
G
div B = 0
Relembramos que as linhas de campo magnético são contínuas.
Força electromotriz induzida
Aparecimento de uma força electromotriz induzida numa espira:
v
• Quando esta é colocada
numa região de campo
magnético variável no tempo.
• Quando o campo magnético é
constante no tempo mas a
área definida pela espira varia
no tempo.
• Quando a espira se
movimenta numa região onde
o campo magnético varia
espacialmente.
• Quando a orientação relativa
entre o plano da espira e o
campo magnético variam no
tempo.
N
B
S
v
v
B
N
S
Lei de Faraday
Todas os efeitos descritos anteriormente têm em comum uma variação
temporal do fluxo do campo magnético através da superfície definida
pelas espiras onde aparece a f.e.m. Matematicamente escrevemos
G G
dφ
ε =−
onde φ = ∫ B.dS
dt
A
A é a área definida pela espira onde aparece a f.e.m.
Princípio de Lenz: a f.e.m. tem sinal tal que a corrrente eléctrica induzida produz
campo magnético que contraria a variação do fluxo.
Energia magnética
•
Suponhamos um circuito contendo uma fonte de tensão, uma
resistência e uma bobina, do tipo
V0
R
Enquanto a corrente passa de I=0 até ao valor final
I é necessário produzir trabalho contra a tensão
em L que se opõe à variação de fluxo. Esta tensão
é, em cada instante, dada por
VL = − L
L
dI
dt
O trabalho é dado pelo produto da diferença de potencial pela carga que a atravessa.
tal que
dI
dq
dW = −VL dq = L dq = L dI = LIdI
dt
dt
I
W = ∫ dW = ∫ LIdI =
0
1 2
LI
2
Este valor é igual à energia armazenada na bobina e esta está associada ao campo
magnético criado pela bobina.
Energia Magnética (cont.)
Qual a expressão da energia armazenada na bobina em termos
do campo magnético?
Supomos que a bobina é um solenóide comprido cujo coeficiente
de auto-indução é dado por
N2
π R2 .
L = μ0
l
Usando a expressão de energia encontrada no slide anterior, obtemos
para a energia
μ0 2 N 2 I 2
1 N2
1 B2
2 2
2
U = μ0
vol
πR I =
πR l =
2
2
l
2 μ0 l
2 μ0
A densidade de energia magnética obtida acima é válida para
outros indutores sendo dada por:
U
1 B2
=
vol 2 μ0
Transformadores
•
O funcionamento de um transformador baseia-se no fenómeno de indução
mútua. O transformador é composto por um enrolamento primário e um
enrolamento secundário, ambos contendo um núcleo de ferro para uma
melhor eficiência. O enrolamento primário é alimentado por uma tensão AC
e o secundário tem menos ou mais espiras que o primário consoante
queiramos diminuir ou aumentar a tensão, respectivamente.
O núcleo de ferro permite que quase todo o fluxo do enrolamento primário
atravesse o enrolamento secundário. Assim:
dφ
dφ
e V2 = − N 2
dt
dt
A razão entre as duas tensões é igual à razão entre o número de espiras, ou seja
V1 = − N1
V1 N1
=
V2 N 2
Gerador de corrente alternada
Conversor de energia mecânica (rotação da bobina) em energia eléctrica.
A f.m.e. Obtida é do tipo sinusoidal, ou seja,
ε = − BAω sin(ωt )
(como foi obtido no exercício 1 da 4ª série)
Motor eléctrico DC
• Conversor de energia eléctrica em energia mecânica.
• Espira com corrente num campo
magnético uniforme sofre um torque
que a faz rodar.
• Um comutador é usado para inverter
a corrente quando o torque é zero,
para que a rotação não inverta o
sentido.
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/motdc.html
Correntes de Foucault = Correntes de Eddy
• Correntes induzidas em condutores de secção
finita por campos magnéticos variáveis no
tempo.
• Seguindo o princípio de Lenz, estas correntes
tendem a cancelar as variações do campo
magnético.
• São usados em travões magnéticos, detectores
de metal, etc.
• São desvantajosas quando, por exemplo, se
estabelecem nos núcleos de transformadores
porque provocam perdas.
Efeito pelicular = Skin effect
• Efeito que consiste na distribuição de correntes
alternadas preferencialmente à superfície dos
cabos condutores. Este efeito aumenta com a
frequência.
Causa: correntes de Foucault que contrariam a
variação do fluxo, o qual se consegue se a
corrente se concentrar na superfície.
Consequência: resistência aumenta com a
frequência. Porquê?
Circuitos corrente alternada (a.c.)
• Circuitos cuja fonte de tensão varia
sinusoidalmente no tempo.
• Vamos estudar o comportamento de
circuitos constituídos por resistências (R),
bobinas (L) e condensadores (C).
Funções sinusoidais
v = V0 sin(ωt )
V0
Amplitude V0
Frequência Angular ω
0
ω
Frequência
2π
-V0
0
π/ω
2π/ω
t
Comportamento da resistência
v(t ) = Ri (t )
• Continua válida a
lei de Ohm
V0
v(t ) = V0 cos(ωt ) ⇒ i (t ) = cos(ωt )
R
V0
V0/R
0
-V0/R
v(t)
i(t)
-V0
0
π/ω
2π/ω
t
• intensidade de corrente e tensão têm a mesma frequência e estão em fase
• as amplitudes obedecem à lei de Ohm
Comportamento da bobina
di
vL (t ) = L
dt
V0
π⎞
⎛
cos ⎜ ωt − ⎟
vL (t ) = V0 cos(ωt ) ⇒ i (t ) =
2⎠
ωL
⎝
+
I
V0
V0/(ωL)
0
-V0/(ωL)
v(t)
i(t)
-V0
0
π/ω
2π/ω
t
A corrente na bobina está atrasada de π/2 relativamente à tensão aos seus terminais.
Comportamento do condensador
q (t ) ∫ i (t )dt
=
vC =
C
C
π⎞
⎛
vC (t ) = V0 cos(ωt ) ⇒ i (t ) = V0ωC cos ⎜ ωt + ⎟
2⎠
⎝
+
-
I
V0
V0ωC
0
-V0ωC
v(t)
i(t)
-V0
0
π/ω
2π/ω
t
A corrente no condensador está adiantada de π/2 relativamente à tensão
aos seus terminais
Os elementos têm tensões e correntes com variação temporal sinusoidal
de frequência igual à da fonte.
No entanto, as amplitudes e as fases relativas variam.
Num dado circuito, cada uma das tensões ou correntes pode
ser representada por uma amplitude e uma fase relativa a um
sinal de referência
Para isso, usa-se um número complexo ou vector –
usualmente designado por fasor
z = x + iy = ρ cis (θ ) = ρ eiθ = ρ θ
onde
ρ= x +y
2
2
⎛ y⎞
e θ = arctg ⎜ ⎟
⎝x⎠
ρ
θ
Fasores e impedâncias
Cada tensão ou corrente pode ser representada por um fasor
V (t ) = V0 cos(ωt + δ ) ⇒ V = V0 eiδ
I (t ) = I cos(ωt + α ) ⇒ I = I eiα
0
0
Nesta nova notação, as relações entre tensão e intensidade para cada
um dos elementos são algébricas
À constante complexa característica de cada elemento
V = RI
R
i π2 VL = ω Le I = iω LI
1 − i π2 1 VC =
e I=
I
iωC
ωC
que é a razão entre o fasor tensão e o fasor intensidade
dá-se o nome de impedância e designa-se por Z .
ZR = R
Z L = iω L
ZC =
1
iωC
Análise de circuitos a.c.
• Continuam válidas as leis de Kirchoff.
• Estas leis aplicadas aos fasores têm como
resultado equações algébricas.
• Leis de associação de impedâncias:
Impedâncias em série
Z eq = ∑ Z i
i
1
1
Impedâncias em paralelo
=∑
Z eq
i Zi
Circuito RLC série
R
V ( t ) = V 0 co s( ω t )
Aplicando a lei das malhas aos fasores,
~
obtemos
C
L
1 ⎞
⎛
V0 0 = ⎜ iω L + R +
⎟I
iωC ⎠
⎝
2
1 ⎞
⎛
2
V0 0 = R + ⎜ ω L −
⎟ θI
ωC ⎠
⎝
I =
I (t ) =
V0
1 ⎞
⎛
R2 + ⎜ ω L +
ωC ⎟⎠
⎝
V0
2
−θ
1 ⎞
⎛
R + ⎜ωL −
⎟
ω
C
⎝
⎠
2
⎛ ω L − 1 ωC ⎞
θ = arctg ⎜
⎟
R
⎝
⎠
2
cos(ωt − θ )
Exercício: circuito RLC paralelo
Potência em circuitos a.c.
• Resistências gastam energia
• Condensadores armazenam energia sob a
forma de campo eléctrico enquanto carregam
mas dispensam a energia de volta ao circuito
quando descarregam.
• Bobinas armazenam energia sob a forma de
campo magnético enquanto a corrente aumenta
mas dispensam a energia de volta ao circuito
quando acorrente diminui para zero.
Em estado estacionário, condensadores e bobinas armazenam
e libertam energia mas não dissipam energia.
Potência em circuitos a.c. (cont.)
dW dW dq
=
= VI
P=
dt
dq dt
Seja uma resistência atravessada por uma intensidade
I = I 0 sin(ωt )
A potência instantânea é dada por
P = VI = RI 2 = RI 02 sin 2 (ωt )
Usualmente define-se potência média, dada por
T
2
2
RI
RI
1
T
P = RI 02 sin 2 (ωt ) = RI 02 ∫ sin 2 (ωt )dt = 0 = 0
T 0
T 2
2
Potência em circuitos a.c. (cont.)
A potência média dissipada por um circutito é
igual
• à soma das potências dissipadas por cada
resistência ou
• P = VT (t ) IT (t )
sendo VT (t ) = VT 0 cos(ωt ) e IT (t ) = IT 0 cos(ωt + θ )
a tensão e a corrente na fonte, respectivamente
T
1
1
P = ∫ VT 0 IT 0 cos(ωt ) cos(ωt + θ )dt = VT 0 IT 0 cos θ
T 0
2
Factor de potência
Nomenclatura de circuitos a.c.
• Valores de tensão e
corrente eficazes =
valores de tensão e
corrente d.c. que
provocariam a mesma
dissipação média de
energia.
Pd.c. = P
I0
1 2
RI = RI 0 ⇒ I ef =
2
2
De modo semelhante obteríamos:
V0
Vef =
2
2
ef
• Frequência de ressonância = frequência para a qual a
impedância total do circuito é puramente resistiva. Nesta
situação a tensão e a corrente na fonte estão em fase.
Magnetismo na matéria
• À semelhança do que acontece com o campo
eléctrico, a matéria reage ao campo magnético
externo funcionando também como fonte de
campo magnético – resultando num campo
magnético médio diferente do externo.
• No entanto, neste caso a contribuição da
matéria nem sempre é contrária ao campo
magnético externo.
• Assim, temos 3 tipos de fenómenos:
diamagnetismo, paramagnetismo e
ferromagnetismo.
Diamagnetismo
• Ocorre em todos os materiais. No entanto, o efeito pode ser cancelado pelos
efeitos paramagnéticos e ferromagnéticos que são mais fortes.
• Resulta num decréscimo do campo magnético externo.
• É provocado pela perturbação do movimento orbital dos electrões. Seguindo
o princípio de Lenz esta perturbação é de forma a contrariar o campo
magnético aplicado.
Paramagnetismo
• Ocorre em materiais que têm electrões desemparelhados (electrões com
spin por emparelhar).
• Resulta num acréscimo do campo magnético externo.
• O spin do electrão tem propriedades idênticas a uma espira de corrente. Na
ausência de campo magnético externo, os vários electrões desemparelhados
apresentam-se como espiras de corrente com orientação aleatória. Na
presença do campo magnético estas espiras orientam-se com o campo da
forma descrita abaixo.
Torque sobre uma espira de corrente
na presença de um campo magnético
F
•
I
Bext
X I
F
Bespira
O torque é tal que orienta o campo
magnético da espira segundo o seu
eixo com o campo magnético externo.
Ferromagnetismo
• Materiais ferromagnéticos são materiais em que o spin
do electrão origina um campo magnético que tende a
alinhar os spins dos outros electrões, estabelecendo-se
domínios onde todos os spins estão alinhados.
• Na presença de um campo magnético, os vários
domínios alinham-se com o campo.
• Resulta num acréscimo significativo do campo
magnético externo.
• Exemplos de ferromagnéticos: ferro, níquel e cobalto.
• Os ferromagnetes têm tendência para manter a sua
magnetização depois de retirado o campo
externo→efeito usado em memórias magnéticas.
Fenómeno que deriva do seu comportamento mais geral
designado de histerese.
Os campos magnetização e H
• Define-se o campo vectorial M que se designa por
magnetização que descreve as fontes de campo
magnético na matéria.
• Define-se ainda o campo H que descreve apenas as
fontes externas de campo magnético.
G
G G
B = μ0 ( H + M )
G
G
G
Na ausência de matéria M=0 ⇒ B=μ0 H
G
G
Em alguns materiais M é proporcional a H
G
G
M = χm H
Susceptibilidade
G
G G
G
G
Permeabilidade
magnética
B = μ0 ( H + M ) = μ0 H + μ0 χ m H =
magnética
G
= μ0 (1 + χ m ) H =
Permeabilidade
G
G
magnética relativa
= μ0 μ r H = μ H
Valores típicos da susceptibiladade magnética:
cobre
alumínio
zinco
ferro
−1.0 ×10−5
2.3 × 10−5
−2.0 ×10−5
~ 103
O diamagnetismo e o paramagnetismo não são observáveis no nosso laboratório.
Curva de histerese para uma
ferromagnete
• Campos
magnéticos variáveis no tempo
dão origem a campos eléctricos.
Pela lei de Faraday
G
G G
∂B G
v∫ E.dl = −∫ ∂t .dS
•Campos eléctricos variáveis no tempo darão
origem a campos magnéticos?
G G
G G
A lei de Ampère dita v∫ B.dl = μ0 ∫ j .dS
∫
G G
j .dS ≠ 0
Sup.
cinzenta
~
∫
G G
j .dS = 0
Sup.
branca
Resultado que parece violar a lei de Ampère.
Maxwell postulou uma nova fonte de campo magnético –
o campo eléctrico variável
Neste caso, e considerando um condensador
de placas paralelas infinitas.
Em geral:
j=
dσ
dE
= ε0
dt
dt
G
G G
G G
∂E G
v∫ B.dl = μ0ε 0 ∫ ∂t .dS +μ0 ∫ j .dS
Equações de Maxwell no vazio
Forma integral
Forma diferencial
Lei de Faraday – equação do campo magnético induzido
G
G G
∂B G
v∫ E.dl = −∫ ∂t .dS
G
G
∂B
rot E = −
∂t
Lei de Ampère – equação do campo magnético induzido
G
G
G
G
G G
G G
∂E
∂E G
rot B = μ0ε 0
+ μ0 j
v∫ B.dl = μ0ε 0 ∫ ∂t .dS +μ0 ∫ j .dS
∂t
Equação do fluxo eléctrico
∫
G G 1
E.dS =
ε0
SF
∫ ρ dv
G ρ
divE =
ε0
Equação do fluxo magnético
∫
SF
G G
B.dS = 0
G
d iv B = 0