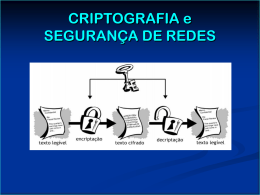
Criptografia:
Algoritmo RSA
por: Bernardino Sant’ Ana Júnior
Objetivos
- Apresentar uma revisão histórica da criptografia até
surgimento do RSA
- Descrição do RSA e apresentação da matemática
envolvida
Sumário
Introdução
Desenvolmento
Breve Histórico
Cifras assimétricas
RSA e Aritmética Modular
Conclusão
Por milhões de anos a humanidade viveu como os animais.
Então aconteceu algo, que despertou o poder de nossas mentes:
aprendemos a falar.
Stephen Hawking
Três pessoas só conseguem manter um segredo se duas delas já estiveram
mortas
Benjamim Franklin
Histórico
- Objetivos da Criptografia : SIGILO e AUTENTICAÇÃO
- Processos : transposição e substituição
- Cifra de César e Códigos antigos de substituição. Eram
quebrados por análise de frequência.
- 1563 - Criador Blaise de Viginère
- 1821 - Charles Babbage criptonalista
- A partir do século XX e principalmente na Segunda Guerra
Mundial os métodos de transposição e substituição
começaram a ser mecanizados e com o desenvolvimento do
computador tornaram-se informatizados.
Máquinas utilizadas na II GM: Enigma e Purple
FREQUÊNCIA APROXIMADA DAS LETRAS NO PORTUGUÊS.
Letra Freq Letra
(%)
Freq
(%)
A
B
C
D
E
F
G
H
I
J
K
L
M
5.05
10.73
2.52
1.20
6.53
7.81
4.34
4.63
1.67
0.01
0.21
0.01
0.47
14.63
1.04
3.88
4.99
12.57
1.02
1.30
1.28
6.18
0.40
0.02
2.78
4.74
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
Textos eram
criptoanalisados
comparando-se a
frequência com que
as letras apareciam
no texto
criptografado com a
frequência com que
apareciam num
determinado idioma.
Até 1976, os sistemas criptográficos eram baseados nos
chamados algoritmos simétricos, onde remetente e destinatário
possuíam a mesma chave.
A segurança do sistema encontrava-se no fato de a chave ser
transmitida de forma segura. Para a troca de chaves é necessário
um canal seguro. Mas se existe um canal seguro então é
necessário criptografar ?
Outra questão é o gerenciamento das chaves.
Exemplo: Para que 50 pessoas possam comunicar-se utilizando
a criptografia simétrica são necessárias:
(50 * 49) / 2 = 1.255 chaves diferentes.
No início da década de 70 a Indústria e Comércio
adotam o DES (Data Encryption Standard)
Diffie e Hellman, em 1976, criam a concepção de
chave pública
Em 1977 a criação do RSA (Rivest, Shamir, Adleman)
implementa de forma prática as idéias de chave
pública
Surgimento do PGP na década de 80
Nos algoritmos de Chave Pública:
Criptografia garante o SIGILO
Assinatura Digital garante a AUTENTICIDADE
Criptografia
A
Texto
Claro
Texto
Cript
o
B
Texto
Claro
Ch Pub B
Meio de
Transmissão
Texto
Cript
o
Ch Pr B
Assinatura digital
A
B
Texto
Claro
Texto
Claro
Ch Pr A
Texto
assinad
o
Meio de
Transmissão
Texto
assinad
o
Ch Pub A
Criptografia e Assinatura Digital
A
Texto
Claro
Texto
Cripto
assinad
o
B
Ch Pub B
Ch Pr A
Meio de
Transmissão
Texto
Claro
Texto
Cripto
assinad
o
Ch Pr B
Ch Pub A
RSA
Adi Shamir, Ronald Rivest e Leonard Adlman
http://www.usc.edu/dept/molecular-science/RSApics.htm
Algoritmo criado em 1977 por:
Ron Rivest, Adi Shamir e Leonard Adleman
Idéia da chave pública colocado em prática
Utilizado até os dias atuais e de grande segurança
Aritmética Modular: a ≡ b mod
A notação a ≡ b mod
divisível por m.
m, indica que (a-b) é
O Módulo 3, por exemplo, representa o conjunto
dos inteiros formados por 0, 1 e 2, sendo que
qualquer operação neste módulo não pode
ultrapassar 3. Exemplo:
2 + 2 = 4 , mas em MOD 3 o resultado 2 + 2 = 1.
Pois 4 é dividido por 3 e tem resto 1.
Matematicamente: 4 ≡ 1 MOD 3.
Algoritmo RSA
1) escolher p e q , dois números primos;
2) calcular n=p*q;
3) calcular Φ(n) = (p-1)(q-1);
4) escolher e
5) calcular d, com o Algoritmo de Euclides Estendido
6) Chave pública = (e,n)
7) Chave privada = (d,n)
8) Transformar a frase em ASCII e separar os blocos
9) Aplicar ci = bie mod n
Algoritmo de Euclides Estendido
NÍCIO
Procedimento Euclides Estendido
INÍCIO
R0= Φ(n), R1= e, x0=1, y0=0, x1=0, y1=1;
R0= Φ(n), R1= e, x0=1, y0=0, x1=0, y1=1;
Repita o procedimento abaixo enquanto R<>0;
Repita o procedimento abaixo enquanto R<>0;
R= R0 mod R1;
R= R0 mod R1;
q = inteiro de (Φ(n)/e);
q = inteiro de (Φ(n)/e);
x = x0 – q.x1;
x = x0 – q.x1;
x0 = x1;
x1 x0
= x; = x1;
y =x1
y0 –q.=y1;x;
= y0 –q. y1;
y0 y
= y1,
y1 y0
= y; = y1,
se y1
R=0=
apresentar
y; os valores de x e y
FIM
se R = 0 apresentar os valores de x e y
FIM
Algoritmo AKS
Os pesquisadores Manindra Agarwal, Nitin
Saxena e Neeraj Kayal, do Departamento de
Ciência da Computação e Engenharia do
Instituto de Tecnologia Indiano de Kanpur,
divulgaram em 6 de agosto de 2002, um
algoritmo para testar se números ímpares
grandes são primos em tempo polinomial.
<http://www.cse.iitk.ac.in/news/primality.html>.
EXEMPLO
p = 41, q = 29, logo n = p*q = 1189
Φ(n) = (p-1).(q-1), logo Φ(1189) = 1120.
Escolhendo e = 17 e calculando d = 593
chave pública: (e, n) = (17, 1189)
chave privada: (d, n) = (593, 1189)
equação: c = me ( mod n ).
Mensagem:
HORA
H
72
O
79
R
82
A
65
Chave Pública (17, 1189)
ASCII: 72 79 82 65; BLOCOS: 727 982 65
ci = bie mod n
bie mod n
Resultado
72717mod 1189
833
98217mod 1189
661
6517mod 1189
691
BLOCOS: 833 661 691
Chave Privada (593, 1189)
mi = cie mod n
cie mod n
Resultado
833593mod 1189
727
661593mod 1189
928
691593mod 1189
65
BLOCOS: 72 79 82 65
BLOCOS UNIDOS: 72798265
72
H
79
O
82
R
65
A
Analogia:
E = 69
=> ((69)17)1 / 17 = 69
Assinatura Digital:
Mensagem: E ; ASCII => 69
Alice envia mensagem para Bob
ALICE
p = 41, q = 29, n = 1189, Φ(n) = 1120)
chave pública: (e, n) = (17, 1189)
chave privada: (d, n) = (593, 1189)
BOB
p = 31, q = 37, n = 1147, Φ(n) = 1080)
chave pública: (e, n) = (11, 1147)
chave privada:(d, n) = (491, 1147)
CRIPTOGRAFIA (ALICE)
DECRIPTOGRAFIA (BOB)
6911mod 1147
92417mod 1189 => 516
=> 516
516593mod 1189 => 924
516491mod 1147 => 69
Simétricos x Assimétricos
As vantagens dos algoritmos simétricos são:
Não precisam transmitir a chave privada
Permitem a assinatura digital
E as desvantagens são relativas a velocidade de
processamento, que é mais lenta que os simétricos
EXEMPLOS DE CHAVES:
e
51755
136866879
10781
d
911
40471
4247405
n
93953
155975371
9687191
Chave pública
Chave Privada
(51755, 93953)
(911, 93953)
(136866879, 155975371)
(40471, 155975371)
(10781, 9687191)
(4247405, 9687191)
Algoritmos de fatoração
- Algoritmo de Fermat
- Algoritmo Pollard p-1
RSA 576
Fatorado em 03 Dez 2003, por uma equipe da Agência Federal para Segurança
de Tecnologia da Informação da Alemanha. Prêmio de $ 10,000.00. Total de
dígitos 174.
188198812920607963838697239461650439807163563379417382700763356422988
859715234665485319060606504743045317388011303396716199692321205734031
879550656996221305168759307650257059
Resultado:
398075086424064937397125500550386491199064362342526708406385189575946
388957261768583317
472772146107435302536223071973048224632914695302097116459852
171130520711256363590397527
Para Saber Mais:
http://www.rsasecurity.com
http://www.numaboa.com.br
http://www.geocities.com/dicaseduvidas
REFERÊNCIAS BIBLIOGRÁFICAS
AGRAWAL, Maindra; KAYAL, Neeraj; SAXENA, Nitin. Primes is in P. Indian Institute
of Technology: 2002. Disponível em: <http://www.cse.iitk.ac.in/news/primality.html>.
Acesso em: 09 mar. 2004.
COUTINHO, Severino Collier. Números Inteiros e Criptografia RSA, Rio de Janeiro:
Sociedade Brasileira de Matemática, 2000.
EVARISTO, Jaime; PERDIGÃO, Eduardo. Álgebra Abstrata, Maceió: EDUFAl, 2002.
KAHN, David. The Codebreakers: The history of secret writing, New York: Scribner,
1967, 1996.
LUCCHESI, Cláudio Leonardo. Introdução à Criptografia Computacional, Campinas:
Papirus, 1986.
SANT’ ANA JÚNIOR, Bernardino. Introdução à matemática aplicada à criptologia.
2004. Trabalho de Conclusão de Curso (Licenciatura em Matemática) - Universidade
Castelo Branco, Rio de Janeiro, 2004.
SINGH, Simon. O livro dos Códigos. Rio de Janeiro: Record, 1999.
CONCLUSÃO