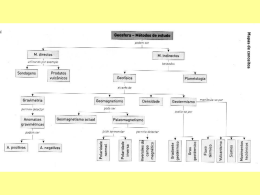
Formulação do Problema Direto Estrutura • Exemplos – – – – Movimento uniformemente acelerado Ajuste de rede Perfilagem Sísmica Vertical Sísmica de Reflexão • Refletor plano paralelo • Refletor plano inclinado (Perpendicular ao strike) – Determinação Epicentral – Sinal Climático • Perturbação Abrupta • Perturbação Linear – Gravimetria • Bacia Triangular • Bacia Trapezoidal – Magnetometria • Separação regional-residual • Esfera Movimento uniformemente acelerado Problema Geofísico Cálculo da aceleração da gravidade Movimento uniformemente acelerado • Sabe-se que uma massa atirada para cima sofre efeito da aceleração da gravidade • A massa experimenta um movimento uniformemente acelerado • As observações são medições da posição da massa em diferentes instantes no decorrer de sua trajetória Movimento uniformemente acelerado t4 t3 t5 t2 t1 t6 t7 t0 Movimento uniformemente acelerado • Sabe-se que uma massa atirada para cima sofre efeito da aceleração da gravidade • A massa experimenta um movimento uniformemente acelerado • As observações são medições da posição da massa em diferentes instantes no decorrer de sua trajetória Movimento uniformemente acelerado • Sabe-se que uma massa atirada para cima sofre efeito da aceleração da gravidade • A massa experimenta um movimento uniformemente acelerado • As observações são medições da posição da massa em diferentes instantes no decorrer de sua trajetória Movimento uniformemente acelerado z t Movimento uniformemente acelerado Parametrização Desconsiderando a resistência do ar, o movimento de uma massa atirada para cima pode ser descrito em termos da: • Posição inicial S0 da massa • Velocidade inicial V0 com que a massa foi atirada • Aceleração da Gravidade g Movimento uniformemente acelerado Relação funcional Nessas condições, a relação entre a posição da massa em diferentes instantes e os parâmetros S0, V0 e g pode ser escrita como: z(S0 ,V0 , g ) S0 V0 t 0,5gt 2 Movimento uniformemente acelerado Relação funcional Nessas condições, a relação entre a posição da massa em diferentes instantes e os parâmetros S0, V0 e g pode ser escrita como: =0 z(S0 ,V0 , g ) S0 V0 t 0,5gt =0 2 Movimento uniformemente acelerado Relação funcional Nessas condições, a relação entre a posição da massa em diferentes instantes e os parâmetros S0, V0 e g pode ser escrita como: =0 z(V0 , g ) V0 t 0,5gt 2 Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p vetor de dados preditos Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p vetor de parâmetros Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p matriz de sensibilidade Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: derivada (sensibilidade) do dado predito 1 em relação ao parâmetro 1 z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p matriz de sensibilidade Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: derivada (sensibilidade) do dado predito 1 em relação ao parâmetro 2 z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p matriz de sensibilidade Movimento uniformemente acelerado Problema Direto Sendo assim, para posições em diferentes instantes: derivada (sensibilidade) do dado predito N em relação ao parâmetro 2 z1 (V0 , g ) V0 t1 0,5gt12 z2 (V0 , g ) V0 t2 0,5gt22 ... z N (V0 , g ) V0 t N 0,5 g t N2 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p matriz de sensibilidade Movimento uniformemente acelerado Norma Para quantificar a diferença entre os dados observados e os dados preditos é comum utilizar a norma L2: ( p) z obs z ( p) z T obs z ( p) z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p Movimento uniformemente acelerado Norma Para quantificar a diferença entre os dados observados e os dados preditos é comum utilizar a norma L2: ( p) z obs z ( p) z T obs z ( p) z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p Movimento uniformemente acelerado Norma Para quantificar a diferença entre os dados observados e os dados preditos é comum utilizar a norma L2: ( p) z obs z ( p) z T obs z ( p) Função escalar e que depende dos parâmetros z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p Movimento uniformemente acelerado Norma Para quantificar a diferença entre os dados observados e os dados preditos é comum utilizar a norma L2: ( p) z obs ( p) z obs z ( p) z obs Ap z ( p) obs Ap z T T z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p Movimento uniformemente acelerado Norma Para quantificar a diferença entre os dados observados e os dados preditos é comum utilizar a norma L2: ( p) z obs ( p) z obs z ( p) z obs Ap z ( p) obs Ap N z T T ( p) [ ziobs zi ( p)]2 i 1 z1 (V0 , g ) t1 z (V , g ) 2 0 t2 z N (V0 , g ) t N 0,5 t12 0,5 t 22 V0 g 2 0,5 t N z ( p) A p Perfilagem Sísmica Vertical Problema Geofísico Cálculo da velocidade sísmica (vertical) dos materiais ao redor do poço Perfilagem Sísmica Vertical • Uma fonte localizada na superfície do poço gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de receptores localizados dentro do poço • As observações são medições do tempo de chegada da primeira onda em cada receptor Perfilagem Sísmica Vertical Fonte Receptor Poço Perfilagem Sísmica Vertical • Uma fonte localizada na superfície do poço gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de receptores localizados dentro do poço • As observações são medições do tempo de chegada da primeira onda em cada receptor Perfilagem Sísmica Vertical t z Perfilagem Sísmica Vertical Parametrização Considerando raios sísmicos sem curvatura e que a subsuperfície é formada por uma sucessão de camadas homogêneas, o tempo gasto para uma onda atingir um receptor pode ser descrito em termos dos parâmetros: • Espessura s de cada camada • Velocidade v em cada camada Perfilagem Sísmica Vertical Relação funcional Nessas condições, a relação entre o tempo gasto para uma onda atingir um receptor e os parâmetros s e v em cada camada pode ser escrita como: sj s1 s2 t j (s , v ) v1 v2 vj Perfilagem Sísmica Vertical Tempo até o sexto receptor s1 s2 s3 s4 s5 s6 t6 (s , v ) v1 v2 v3 v4 v5 v6 Perfilagem Sísmica Vertical s1 v1 s2 v2 s3 v3 s4 v4 s5 v5 s6 v6 s1 s2 s3 s4 s5 s6 t6 (s , v ) v1 v2 v3 v4 v5 v6 Perfilagem Sísmica Vertical Relação funcional Como as espessuras s são conhecidas, uma vez que representam o espaçamento entre a fonte e o primeiro receptor e entre receptores adjacentes: sj s1 s2 t j (s , v ) v1 v2 vj sj s1 s2 t j (v ) v1 v2 vj Perfilagem Sísmica Vertical Problema Direto Sendo assim, para todos os receptores: t1 (v ) s1 v1 s1 s2 t2 (v ) v1 v2 ... s1 s2 sN t N (v ) v1 v2 vN Perfilagem Sísmica Vertical Problema Direto Sendo assim, para todos os receptores: t1 (v ) s1 v1 s1 s2 t2 (v ) v1 v2 ... s1 s2 sN t N (v ) v1 v2 vN s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN Perfilagem Sísmica Vertical Problema Direto Sendo assim, para todos os receptores: t1 (v ) s1 v1 s1 s2 t2 (v ) v1 v2 ... s1 s2 sN t N (v ) v1 v2 vN s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN t (v ) Bv Perfilagem Sísmica Vertical Norma A norma L2 entre os dados observados e os dados preditos é dada por: (v ) t obs t (v ) t T obs t (v ) s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN t (v ) Bv Perfilagem Sísmica Vertical Norma A norma L2 entre os dados observados e os dados preditos é dada por: (v ) t obs t (v ) t T obs t (v ) s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN t (v ) Bv Perfilagem Sísmica Vertical Norma A norma L2 entre os dados observados e os dados preditos é dada por: (v ) t obs (v ) t t (v ) obs Bv t T t T obs obs t (v ) Bv s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN t (v ) Bv Perfilagem Sísmica Vertical Norma A norma L2 entre os dados observados e os dados preditos é dada por: (v ) t obs (v ) t t (v ) obs Bv t T t T obs obs t (v ) Bv s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN t (v ) Bv Perfilagem Sísmica Vertical Norma A norma L2 entre os dados observados e os dados preditos é dada por: (v ) t obs (v ) t t (v ) obs Bv N t T t T obs obs t (v ) Bv 2 (v ) [t obs t ( v )] j i j 1 s1 v1 t1 (v ) t ( v ) s v s v 1 1 2 2 2 t N (v ) s1 v1 s2 v2 s N vN t (v ) Bv Sísmica de Reflexão (Refletor plano-paralelo) Problema Geofísico Cálculo da profundidade do embasamento e da velocidade da camada sobrejacente Sísmica de Reflexão (Refletor plano-paralelo) • Uma fonte localizada na superfície gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de receptores que também são localizados na superfície • As observações são medições do tempo de chegada da onda refletida em cada receptor Sísmica de Reflexão (Refletor plano-paralelo) Fonte Receptor R4 R5 R6 arenito embasamento R1 R2 R3 Sísmica de Reflexão (Refletor plano-paralelo) • Uma fonte localizada na superfície gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de receptores que também são localizados na superfície • As observações são medições do tempo de chegada da onda refletida em cada receptor Sísmica de Reflexão (Refletor plano-paralelo) R4 R5 R6 R1 R2 R3 Fonte tempo Receptor R4 R5 R6 arenito embasamento R1 R2 R3 Sísmica de Reflexão (Refletor plano-paralelo) Parametrização Considerando raios sísmicos sem curvatura, que a camada sobre o embasamento é homogênea, isotrópica e plano-paralela, o tempo gasto para uma onda refletida atingir um receptor pode ser descrito em termos dos parâmetros: • Espessura h da camada • Velocidade v da camada • Distância x entre a fonte e o receptor Sísmica de Reflexão (Refletor plano-paralelo) Relação funcional Nessas condições, a relação entre o tempo de chegada de uma onda refletida e os parâmetros h, v e x em cada receptor: 2 i 2 2 x 4h ti (h, v) 2 v v Sísmica de Reflexão (Refletor plano-paralelo) R4 R5 R6 R1 R2 R3 Fonte tempo Receptor R4 R5 R6 v embasamento R1 R2 R3 h 2 i 2 2 x 4h ti (h, v) 2 v v Sísmica de Reflexão (Refletor plano-paralelo) Problema Direto Sendo assim, para todos os receptores: x12 4h 2 t1 (h, v) 2 2 v v x22 4h 2 t2 (h, v) 2 2 v v ... x N2 4h 2 t N (h, v) 2 2 v v Sísmica de Reflexão (Refletor plano-paralelo) Problema Direto Sendo assim, para todos os receptores: x12 4h 2 t1 (h, v) 2 2 v v x22 4h 2 t2 (h, v) 2 2 v v ... x N2 4h 2 t N (h, v) 2 2 v v t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) Sísmica de Reflexão (Refletor plano-paralelo) Problema Direto Sendo assim, para todos os receptores: x12 4h 2 t1 (h, v) 2 2 v v x22 4h 2 t2 (h, v) 2 2 v v t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) ... x N2 4h 2 t N (h, v) 2 2 v v t ( p) B p Sísmica de Reflexão (Refletor plano-paralelo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T obs t ( p) t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) t ( p) B p Sísmica de Reflexão (Refletor plano-paralelo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T obs t ( p) t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) t ( p) B p Sísmica de Reflexão (Refletor plano-paralelo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs ( p) t t ( p) obs t obs t ( p) t obs B p B p T T t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) t ( p) B p Sísmica de Reflexão (Refletor plano-paralelo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs ( p) t t ( p) obs t obs t ( p) t obs B p B p T T t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) t ( p) B p Sísmica de Reflexão (Refletor plano-paralelo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs ( p) t t ( p) obs t obs t ( p) t obs B p B p N T T 2 ( p) [t obs t ( p )] j i j 1 t1 (h, v) ( x1 v) 2 ( 2h v) 2 t ( h, v ) 2 2 ( x v ) ( 2 h v ) 2 2 2 2 t N ( h, v) ( x N v) (2h v) t ( p) B p Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Problema Geofísico Cálculo da profundidade e mergulho do embasamento e também da velocidade da camada sobrejacente Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) • Uma fonte localizada na superfície gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de receptores que também são localizados na superfície • As observações são medições do tempo de chegada da onda refletida em cada receptor Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Fonte Receptor R4 R5 R6 arenito embasamento R1 R2 R3 Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) • Uma fonte localizada na superfície gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de receptores que também são localizados na superfície • As observações são medições do tempo de chegada da onda refletida em cada receptor Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) R4 R5 R6 R1 R2 R3 Fonte tempo Receptor R4 R5 R6 arenito embasamento R1 R2 R3 Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Parametrização Considerando raios sísmicos sem curvatura e que a camada sobre o embasamento é homogênea e isotrópica, o tempo gasto para uma onda refletida atingir um receptor pode ser descrito em termos dos parâmetros: • Espessura h ao longo do perfil sísmico • Velocidade v da camada • Distância x entre a fonte e o receptor • Mergulho β do embasamento Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Relação funcional Nessas condições, a relação entre o tempo de chegada de uma onda refletida e os parâmetros h, v, x e β em cada receptor: 2 i 2 2 i 2 x 4h ti (hi , v, ) 4 hi xi sen v v Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) R4 R5 R6 R1 R2 R3 Fonte tempo Receptor R4 R5 R6 h1 h2 h3 R1 R2 R3 h4 h5 h6 v embasamento β xi2 4hi2 ti (hi , v, ) 2 2 4 hi xi sen v v Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Problema Direto Sendo assim, para todos os receptores: x12 4h12 t1 (h1 , v, ) 2 2 4 h1 x1 sen v v x22 4h22 t2 (h2 , v, ) 2 2 4 h2 x2 sen v v ... xN2 4hN2 t N (hN , v, ) 2 2 4 hN xN sen v v Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Problema Direto Sendo assim, para todos os receptores: x12 4h12 t1 (h1 , v, ) 2 2 4 h1 x1 sen v v x22 4h22 t2 (h2 , v, ) 2 2 4 h2 x2 sen v v ... xN2 4hN2 t N (hN , v, ) 2 2 4 hN xN sen v v t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Problema Direto Sendo assim, para todos os receptores: x12 4h12 t1 (h1 , v, ) 2 2 4 h1 x1 sen v v x22 4h22 t2 (h2 , v, ) 2 2 4 h2 x2 sen v v t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) ... xN2 4hN2 t N (hN , v, ) 2 2 4 hN xN sen v v t ( p) B p Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T obs t ( p) t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) t ( p) B p Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T obs t ( p) t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) t ( p) B p Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T T obs t ( p) ( p) t obs B p t obs B p t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) t ( p) B p Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T T obs t ( p) ( p) t obs B p t obs B p t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) t ( p) B p Sísmica de Reflexão (Refletor inclinado – perpendicular ao strike) Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs t ( p) t T obs t ( p) T ( p) t obs B p t obs B p N 2 ( p) [t obs t ( p )] j i j 1 t1 (h1 , v, ) ( x1 v) 2 (2h1 t ( h , v, ) 2 ( x v ) (2h2 2 2 2 2 t ( h , v , ) N N ( x N v) (2hN v) 2 (4h1 x1sen ) v) 2 (4h2 x2 sen ) 2 v) (4hN x N sen ) t ( p) B p Determinação Epicentral Problema Geofísico Cálculo das coordenadas de um epicentro Determinação Epicentral • Um terremoto gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de estações sismográficas localizadas na superfície • As observações são medições da diferença entre o tempo de chegada das ondas P e S em cada estação Determinação Epicentral superfície Determinação Epicentral superfície fonte do terremoto Determinação Epicentral superfície fonte do terremoto estação sismográfica Determinação Epicentral • Um terremoto gera ondas, que se propagam em subsuperfície e são detectadas por um arranjo de estações sismográficas localizadas na superfície • As observações são medições da diferença entre o tempo de chegada das ondas P e S em cada estação Determinação Epicentral B superfície A C fonte do terremoto estação sismográfica Determinação Epicentral onda S estação sismográfica onda P ∆tA A ∆tB B ∆tC C tempo Determinação Epicentral estação sismográfica A B C ∆t Determinação Epicentral Parametrização Considerando raios sísmicos sem curvatura, que a profundidade do terremoto pode ser desprezada e que o meio é homogêneo e isotrópico, a diferença de tempo entre as ondas P e S em uma determinada estação pode ser descrito em termos dos parâmetros: • Velocidades vP e vS • Coordenadas x e y da estação • Coordenadas x0 e y0 da estação Determinação Epicentral Relação funcional Nessas condições, a relação entre a diferença de tempo de chegada das ondas P e S e os parâmetros vP, vS, x, y, x0, e y0 em uma estação: 1 1 2 2 12 ti ( x0 , y0 ) [(xi x0 ) ( yi y0 ) ] v P vS Determinação Epicentral B superfície A (xB, yB) (xA, yA) C (x0, y0) (xC, yC) vP vS fonte do terremoto estação sismográfica 1 1 1 ti ( x0 , y0 ) [(xi x0 ) 2 ( yi y0 ) 2 ] 2 v P vS Determinação Epicentral Problema Direto Sendo assim, para todas as estações: tA ( x0 , y0 ) [(xA x0 )2 ( yA y0 )2 ] 2 1 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 2 2 2 1 ... tC ( x0 , y0 ) [(xC x0 )2 ( yC y0 )2 ] 2 1 1 1 v P vS Determinação Epicentral Problema Direto Sendo assim, para todas as estações: tA ( x0 , y0 ) [(xA x0 )2 ( yA y0 )2 ] 2 1 tB ( x0 , y0 ) [(xB x0 )2 ( yB y0 )2 ] 2 1 ... tC ( x0 , y0 ) [(xC x0 )2 ( yC y0 )2 ] 2 1 1 1 v P vS 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 Determinação Epicentral Problema Direto Sendo assim, para todas as estações: tA ( x0 , y0 ) [(xA x0 )2 ( yA y0 )2 ] 2 1 tB ( x0 , y0 ) [(xB x0 )2 ( yB y0 )2 ] 2 1 ... 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 tC ( x0 , y0 ) [(xC x0 )2 ( yC y0 )2 ] 2 1 1 1 v P vS t ( p) B p Determinação Epicentral Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs T t ( p) t obs t ( p) 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 t ( p) B p Determinação Epicentral Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs T t ( p) t obs t ( p) 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 t ( p) B p Determinação Epicentral Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs T t ( p) t obs t ( p) 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 T obs obs ( p) t B p t B p t ( p) B p Determinação Epicentral Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs T t ( p) t obs t ( p) 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 T obs obs ( p) t B p t B p t ( p) B p Determinação Epicentral Norma A norma L2 entre os dados observados e os dados preditos é dada por: ( p) t obs T t ( p) t obs t ( p) 2 2 12 tA ( x0 , y0 ) [(xA x0 ) ( yA y0 ) ] 2 2 12 tB ( x0 , y0 ) [(xB x0 ) ( yB y0 ) ] 1 tC ( x0 , y0 ) [(xC x0 ) 2 ( yC y0 ) 2 ] 2 T obs obs ( p) t B p t B p ( p) tAobs tA ( p) tBobs tB ( p) tCobs tC ( p) 2 2 2 t ( p) B p Sinal Climático (Perturbação Abrupta) Problema Geofísico Cálculo da amplitude e do tempo em que ocorreu uma perturbação climática Sinal Climático (Perturbação Abrupta) • Uma mudança abrupta no clima gera uma perturbação na temperatura da superfície, que se propaga em subsuperfície e é detectada por um sensor movido ao longo de um poço • As observações são medições da diferença entre a temperatura ao longo do poço e a temperatura predita pelo campo térmico regional Sinal Climático (Perturbação Abrupta) subsuperfície Sinal Climático (Perturbação Abrupta) t subsuperfície Sinal Climático (Perturbação Abrupta) T t subsuperfície Sinal Climático (Perturbação Abrupta) T t0 tempo em que ocorreu a perturbação climática t0 subsuperfície t Sinal Climático (Perturbação Abrupta) T t0 tempo em que ocorreu a perturbação climática t0 subsuperfície t o tempo é positivo em direção ao presente Sinal Climático (Perturbação Abrupta) T t0 tempo em que ocorreu a perturbação climática t0 subsuperfície t Sinal Climático (Perturbação Abrupta) T t0 tempo em que ocorreu a perturbação climática mudança abrupta na temperatura t0 subsuperfície t Sinal Climático (Perturbação Abrupta) T t0 tempo em que ocorreu a perturbação climática t0 t a mudança abrupta na temperatura, induzida por uma perturbação climática, propaga-se em subsuperfície subsuperfície Sinal Climático (Perturbação Abrupta) • Uma mudança abrupta no clima gera uma perturbação na temperatura da superfície, que se propaga em subsuperfície e é detectada por um sensor movido ao longo de um poço • As observações são medições da diferença entre a temperatura ao longo do poço e a temperatura do campo térmico regional Sinal Climático (Perturbação Abrupta) T t0 t medidas da temperatura ao longo do poço Sinal Climático (Perturbação Abrupta) T temperatura t profundidade t0 Sinal Climático (Perturbação Abrupta) T temperatura campo térmico regional t profundidade t0 Sinal Climático (Perturbação Abrupta) T 0 t profundidade t0 sinal climático Sinal Climático (Perturbação Abrupta) Parametrização Considerando que a subsuperfície é um semi-espaço infinito e homogêneo, o sinal climático em uma determinada profundidade pode ser descrito em termos dos parâmetros: • Difusividade térmica λ • Tempo t’ decorrido desde a perturbação climática • Amplitude A da perturbação climática • Profundidade z dentro do poço Sinal Climático (Perturbação Abrupta) Relação funcional Nessas condições, a relação entre o sinal climático em uma determinada profundidade e os parâmetros λ, t’ e A é dada por: z i Ti ( A, t ' ) A 1 erf 4 t ' Sinal Climático (Perturbação Abrupta) T 0 A sinal climático t' t0 t z λ profundidade z z i Ti ( A, t ' ) A 1 erf 4 t ' Sinal Climático (Perturbação Abrupta) Problema Direto Sendo assim, para diferentes profundidades: z T1 ( A, t ' ) A 1 erf 1 4 t ' z T2 ( A, t ' ) A 1 erf 2 4 t ' ... z TN ( A, t ' ) A 1 erf N 4 t ' Sinal Climático (Perturbação Abrupta) Problema Direto Sendo assim, para diferentes profundidades: z T1 ( A, t ' ) A 1 erf 1 4 t ' z T2 ( A, t ' ) A 1 erf 2 4 t ' ... z TN ( A, t ' ) A 1 erf N 4 t ' T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Abrupta) Problema Direto Sendo assim, para diferentes profundidades: z T1 ( A, t ' ) A 1 erf 1 4 t ' z T2 ( A, t ' ) A 1 erf 2 4 t ' T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N ... z TN ( A, t ' ) A 1 erf N 4 t ' T ( p) B p 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Abrupta) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N T ( p) B p 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Abrupta) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N T ( p) B p 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Abrupta) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N T obs obs ( p) T B p T B p T ( p) B p 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Abrupta) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N T obs obs ( p) T B p T B p T ( p) B p 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Abrupta) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T1 ( A, t ' ) A[1 erf ( z1 T2 ( A, t ' ) A[1 erf ( z2 TN ( A, t ' ) A[1 erf ( z N T obs obs ( p) T B p T B p ( p) Ti obs Ti ( p) N i 1 2 T ( p) B p 4 t ' )] 4 t ' )] 4 t ' )] Sinal Climático (Perturbação Linear) Problema Geofísico Cálculo da amplitude e do tempo em que ocorreu uma perturbação climática Sinal Climático (Perturbação Linear) • Uma mudança linear no clima gera uma perturbação na temperatura da superfície, que se propaga em subsuperfície e é detectada por um sensor movido ao longo de um poço • As observações são medições da diferença entre a temperatura ao longo do poço e a temperatura predita pelo campo térmico regional Sinal Climático (Perturbação Linear) subsuperfície Sinal Climático (Perturbação Linear) t subsuperfície Sinal Climático (Perturbação Linear) T t subsuperfície Sinal Climático (Perturbação Linear) T t0 tempo em que ocorreu a perturbação climática t0 subsuperfície t Sinal Climático (Perturbação Linear) T t0 tempo em que ocorreu a perturbação climática t0 subsuperfície t o tempo é positivo em direção ao presente Sinal Climático (Perturbação Linear) T t0 tempo em que ocorreu a perturbação climática t0 subsuperfície t Sinal Climático (Perturbação Linear) T t0 tempo em que ocorreu a perturbação climática mudança linear na temperatura t0 subsuperfície t Sinal Climático (Perturbação Linear) T t0 tempo em que ocorreu a perturbação climática t0 t a mudança linear na temperatura, induzida por uma perturbação climática, propaga-se em subsuperfície subsuperfície Sinal Climático (Perturbação Linear) • Uma mudança linear no clima gera uma perturbação na temperatura da superfície, que se propaga em subsuperfície e é detectada por um sensor movido ao longo de um poço • As observações são medições da diferença entre a temperatura ao longo do poço e a temperatura do campo térmico regional Sinal Climático (Perturbação Linear) T t0 t medidas da temperatura ao longo do poço Sinal Climático (Perturbação Linear) T temperatura t profundidade t0 Sinal Climático (Perturbação Linear) T temperatura campo térmico regional t profundidade t0 Sinal Climático (Perturbação Linear) T 0 t profundidade t0 sinal climático Sinal Climático (Perturbação Linear) Parametrização Considerando que a subsuperfície é um semi-espaço infinito e homogêneo, o sinal climático em uma determinada profundidade pode ser descrito em termos dos parâmetros: • Difusividade térmica λ • Tempo t’ decorrido desde a perturbação climática • Amplitude A da perturbação climática • Profundidade z dentro do poço Sinal Climático (Perturbação Linear) Relação funcional Nessas condições, a relação entre o sinal climático em uma determinada profundidade e os parâmetros λ, t’ e A é dada por: 2 z 2 z 2 zi2 z i i i Ti ( A, t ' ) A 1 erfc exp 4 t ' 4 t ' 4 t ' 4 t ' Sinal Climático (Perturbação Linear) T A t' t0 t z λ 2 z 2 z 2 zi2 z i i exp i erfc Ti ( A, t ' ) A 1 4 t ' 4 t ' 4 t ' 4 t ' Sinal Climático (Perturbação Linear) Problema Direto Sendo assim, para diferentes profundidades: ... 21 21 e T1 ( A, t ' ) A 1 21 erfc1 22 2 2 e T2 ( A, t ' ) A 1 2 2 erfc 2 2 N 2 e TN ( A, t ' ) A 1 2 N erfc N N i zi 4 t ' Sinal Climático (Perturbação Linear) Problema Direto Sendo assim, para diferentes profundidades: ... 21 21 e T1 ( A, t ' ) A 1 21 erfc1 22 2 2 e T2 ( A, t ' ) A 1 2 2 erfc 2 21 2 e A[(1 21 )erfc (1 )] 1 T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] 2 N 2 e TN ( A, t ' ) A 1 2 N erfc N N i zi 4 t ' Sinal Climático (Perturbação Linear) Problema Direto Sendo assim, para diferentes profundidades: ... 21 21 e T1 ( A, t ' ) A 1 21 erfc1 22 2 2 e T2 ( A, t ' ) A 1 2 2 erfc 2 21 2 e A[(1 21 )erfc (1 )] 1 T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] 2 N 2 e TN ( A, t ' ) A 1 2 N erfc N N i zi 4 t ' T ( p) B p Sinal Climático (Perturbação Linear) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) A[(1 21 )erfc (1 )] T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] T ( p) B p i zi 21 e 21 4 t ' Sinal Climático (Perturbação Linear) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) A[(1 21 )erfc (1 )] T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] T ( p) B p i zi 21 e 21 4 t ' Sinal Climático (Perturbação Linear) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T obs obs ( p) T B p T B p A[(1 21 )erfc (1 )] T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] T ( p) B p i zi 21 e 21 4 t ' Sinal Climático (Perturbação Linear) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T obs obs ( p) T B p T B p A[(1 21 )erfc (1 )] T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] T ( p) B p i zi 21 e 21 4 t ' Sinal Climático (Perturbação Linear) Norma A norma L2 entre os dados observados e os dados preditos é dada por: T obs obs ( p ) T T ( p ) T T ( p ) T obs obs ( p) T B p T B p ( p) Ti N i 1 obs Ti ( p) 2 A[(1 21 )erfc (1 )] T1 ( A, t ' ) 22 21 e T ( A , t ' ) 2 A [( 1 2 ) erfc ( )] 2 2 T ( A , t ' ) N 2 N 2 e N A[(1 2 N )erfc ( N )] T ( p) B p i zi 21 e 21 4 t ' Gravimetria (Bacia Triangular) Problema Geofísico Cálculo da profundidade do embasamento Gravimetria (Bacia Triangular) • O relevo do embasamento sob uma bacia sedimentar produz uma anomalia na Aceleração da Gravidade • As observações são medições da componente vertical da Anomalia de Gravidade Gravimetria (Bacia Triangular) Modificado de Allen e Allen (2005) Gravimetria (Bacia Triangular) Modificado de Allen e Allen (2005) Gravimetria (Bacia Triangular) bacia Gravimetria (Bacia Triangular) • O relevo do embasamento sob uma bacia sedimentar produz uma anomalia na Aceleração da Gravidade • As observações são medições da componente vertical da Anomalia de Gravidade Gravimetria (Bacia Triangular) Parametrização Considerando que o pacote sedimentar e o embasamento são homogêneos, a anomalia de gravidade pode ser descrita em termos dos parâmetros: • Contraste ρ de densidade dos sedimentos • Relevo do embasamento Gravimetria g (Bacia Triangular) A bacia sedimentar pode ser aproximada por um polígono triangular posição Gravimetria g (Bacia Triangular) posição Cujo formato é definido pelas coordenadas do vértice inferior (x, z) Gravimetria (Bacia Triangular) Relação funcional Nessas condições, a relação entre a anomalia de gravidade em uma determinada posição e os parâmetros ρ, x e z é dada por uma função: g i ( x , z ) G f i ( x, z ) Que pode ser baseada, por exemplo, no trabalho de Talwani (1959) Gravimetria g (Bacia Triangular) x ρ g i ( x , z ) G f i ( x, z ) z (x, z) Gravimetria (Bacia Triangular) Problema Direto Sendo assim, para diferentes posições: g1 ( x, z ) G f1 ( x, z ) g 2 ( x, z ) G f 2 ( x, z ) ... g N ( x, z ) G f N ( x, z ) Gravimetria (Bacia Triangular) Problema Direto Sendo assim, para diferentes posições: g1 ( x, z ) G f1 ( x, z ) g 2 ( x, z ) G f 2 ( x, z ) ... g N ( x, z ) G f N ( x, z ) g1 ( x, z ) G f1 ( x, z ) g 2 ( x, z ) G f 2 ( x, z ) g N ( x, z ) G f N ( x, z ) Gravimetria (Bacia Triangular) Problema Direto Sendo assim, para diferentes posições: g1 ( x, z ) G f1 ( x, z ) g 2 ( x, z ) G f 2 ( x, z ) ... g1 ( x, z ) G f1 ( x, z ) g 2 ( x, z ) G f 2 ( x, z ) g N ( x, z ) G f N ( x, z ) g N ( x, z ) G f N ( x, z ) g ( p) B p Gravimetria (Bacia Triangular) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( x, z ) G f1 ( x, z ) T obs obs ( p) g g ( p) g g ( p) g 2 ( x, z ) G f 2 ( x, z ) g N ( x, z ) G f N ( x, z ) g ( p) B p Gravimetria (Bacia Triangular) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( x, z ) G f1 ( x, z ) T obs obs ( p) g g ( p) g g ( p) g 2 ( x, z ) G f 2 ( x, z ) g N ( x, z ) G f N ( x, z ) g ( p) B p Gravimetria (Bacia Triangular) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( x, z ) G f1 ( x, z ) T obs obs ( p) g g ( p) g g ( p) g 2 ( x, z ) G f 2 ( x, z ) T g N ( x, z ) G f N ( x, z ) ( p) g obs B p g obs B p g ( p) B p Gravimetria (Bacia Triangular) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( x, z ) G f1 ( x, z ) T obs obs ( p) g g ( p) g g ( p) g 2 ( x, z ) G f 2 ( x, z ) T g N ( x, z ) G f N ( x, z ) ( p) g obs B p g obs B p g ( p) B p Gravimetria (Bacia Triangular) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( x, z ) G f1 ( x, z ) T obs obs ( p) g g ( p) g g ( p) g 2 ( x, z ) G f 2 ( x, z ) T g N ( x, z ) G f N ( x, z ) ( p) g obs B p g obs B p ( p) g N i 1 obs i gi ( p ) 2 g ( p) B p Gravimetria (Bacia Trapezoidal) Problema Geofísico Cálculo da profundidade do embasamento Gravimetria (Bacia Trapezoidal) • O relevo do embasamento sob uma bacia sedimentar produz uma anomalia na Aceleração da Gravidade • As observações são medições da componente vertical da Anomalia de Gravidade Gravimetria (Bacia Trapezoidal) crosta Gravimetria (Bacia Trapezoidal) crosta estiramento Gravimetria (Bacia Trapezoidal) crosta falhamento normal Gravimetria (Bacia Trapezoidal) subsidência Gravimetria (Bacia Trapezoidal) bacia sedimentar Gravimetria (Bacia Trapezoidal) • O relevo do embasamento sob uma bacia sedimentar produz uma anomalia na Aceleração da Gravidade • As observações são medições da componente vertical da Anomalia de Gravidade Gravimetria g (Bacia Trapezoidal) posição Gravimetria (Bacia Trapezoidal) Parametrização Considerando que o pacote sedimentar e o embasamento são homogêneos, a anomalia de gravidade pode ser descrita em termos dos parâmetros: • Contraste ρ de densidade dos sedimentos • Relevo do embasamento Gravimetria g (Bacia Trapezoidal) posição A bacia sedimentar pode ser aproximada por um polígono trapezoidal Gravimetria g (Bacia Trapezoidal) posição Cujo formato é definido pela profundidade dos vértices inferiores Gravimetria (Bacia Trapezoidal) Relação funcional Nessas condições, a relação entre a anomalia de gravidade em uma determinada posição e os parâmetros ρ, z1 e z2 é dada por uma função: gi ( z1 , z2 ) G f i ( z1 , z2 ) Que pode ser baseada, por exemplo, no trabalho de Talwani (1959) Gravimetria g (Bacia Trapezoidal) posição z1 ρ z2 Gravimetria (Bacia Trapezoidal) Problema Direto Sendo assim, para diferentes posições: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) ... g N ( z1 , z2 ) G f N ( z1 , z2 ) Gravimetria (Bacia Trapezoidal) Problema Direto Sendo assim, para diferentes posições: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) ... g N ( z1 , z2 ) G f N ( z1 , z2 ) g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) Gravimetria (Bacia Trapezoidal) Problema Direto Sendo assim, para diferentes posições: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) ... g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g ( p) B p Gravimetria (Bacia Trapezoidal) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g ( p) B p Gravimetria (Bacia Trapezoidal) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g ( p) B p Gravimetria (Bacia Trapezoidal) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) T g N ( z1 , z2 ) G f N ( z1 , z2 ) ( p) g obs B p g obs B p g ( p) B p Gravimetria (Bacia Trapezoidal) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) T g N ( z1 , z2 ) G f N ( z1 , z2 ) ( p) g obs B p g obs B p g ( p) B p Gravimetria (Bacia Trapezoidal) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) T g N ( z1 , z2 ) G f N ( z1 , z2 ) ( p) g obs B p g obs B p ( p) g N i 1 obs i gi ( p ) 2 g ( p) B p Magnetometria (Dipolo) Problema Geofísico Determinação da localização de um dipolo em subsuperfície Magnetometria (Dipolo) • Um corpo magnetizado em subsuperfície produz um campo magnético • O campo magnético produzido é uma grandeza vetorial, que é somado ao campo Geomagnético e produz um campo resultante • As observações são medições da intensidade do campo magnético resultante na superfície (Anomalia de Campo Total) Magnetometria (Dipolo) Magnetometria (Dipolo) O corpo adquire magnetização Magnetometria (Dipolo) E produz um campo magnético Magnetometria (Dipolo) • Um corpo magnetizado em subsuperfície produz um campo magnético • O campo magnético produzido é uma grandeza vetorial, que é somado ao campo Geomagnético e gera um campo resultante • As observações são medições da intensidade do campo magnético resultante na superfície (Anomalia de Campo Total) Magnetometria (Dipolo) Campo Geomagnético Campo do corpo Magnetometria (Dipolo) O campo resultante é uma soma vetorial Magnetometria (Dipolo) • Um corpo magnetizado em subsuperfície produz um campo magnético • O campo magnético produzido é uma grandeza vetorial, que é somado ao campo Geomagnético e gera um campo resultante • As observações são medições da intensidade do campo magnético resultante na superfície (Anomalia de Campo Total) Magnetometria B (Dipolo) posição Magnetometria (Dipolo) Parametrização Considerando que a rocha encaixante é não-magnética, que o campo geomagnético é constante, que a magnetização é induzida e que o corpo pode ser aproximado por um dipolo, a anomalia de campo total pode ser descrita em termos dos parâmetros: • Suscetibilidade magnética χ do corpo • Componentes Bx, By e Bz do campo geomagnético • Coordenadas x, y e z do dipolo Magnetometria g (Dipolo) posição A bacia sedimentar pode ser aproximada por um polígono trapezoidal Magnetometria g (Dipolo) posição Cujo formato é definido pela profundidade dos vértices inferiores Magnetometria (Dipolo) Relação funcional Nessas condições, a relação entre a anomalia de gravidade em uma determinada posição e os parâmetros ρ, z1 e z2 é dada por uma função: B 0 (1 ) H M H M 0 (1 ) B Bx 3 B M y Bz Magnetometria g (Dipolo) posição z1 ρ z2 Magnetometria (Dipolo) Problema Direto Sendo assim, para diferentes posições: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) ... g N ( z1 , z2 ) G f N ( z1 , z2 ) Magnetometria (Dipolo) Problema Direto Sendo assim, para diferentes posições: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) ... g N ( z1 , z2 ) G f N ( z1 , z2 ) g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) Magnetometria (Dipolo) Problema Direto Sendo assim, para diferentes posições: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) ... g1 ( z1 , z2 ) G f1 ( z1 , z2 ) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g ( p) B p Magnetometria (Dipolo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g ( p) B p Magnetometria (Dipolo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) g N ( z1 , z2 ) G f N ( z1 , z2 ) g ( p) B p Magnetometria (Dipolo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) T g N ( z1 , z2 ) G f N ( z1 , z2 ) ( p) g obs B p g obs B p g ( p) B p Magnetometria (Dipolo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) T g N ( z1 , z2 ) G f N ( z1 , z2 ) ( p) g obs B p g obs B p g ( p) B p Magnetometria (Dipolo) Norma A norma L2 entre os dados observados e os dados preditos é dada por: g1 ( z1 , z2 ) G f1 ( z1 , z2 ) T obs obs ( p) g g ( p) g g ( p) g 2 ( z1 , z2 ) G f 2 ( z1 , z2 ) T g N ( z1 , z2 ) G f N ( z1 , z2 ) ( p) g obs B p g obs B p ( p) g N i 1 obs i gi ( p ) 2 g ( p) B p
Download