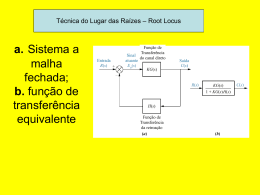
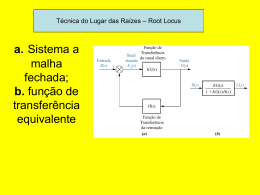
Disciplina: Sistemas de Controle 1 - ET76H
Prof. Dr. Ismael Chiamenti
2014/2
Aula 9
• CONTATOS PARA DÚVIDAS
- Email: [email protected]
-Local: DAELT/UTFPR
• PLANO DE ENSINO, PLANO DE AULAS E INFORMAÇÕES:
https://paginapessoal.utfpr.edu.br/chiamenti
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Conceitos básicos de sistemas de controle;
Sistemas em malha aberta e malha fechada;
(Revisão TL) e Simplificação de diagrama de blocos;
Funções de transferência ;
Modelo na forma de variáveis de estado;
Caracterização da resposta de sistemas de
primeira ordem, segunda ordem e ordem superior;
Erro de estado estacionário;
Estabilidade;
Introdução a controladores PID;
Sintonia de controladores PID;
Método do lugar das raízes (root locus);
Projeto PID via método do lugar das raízes;
Resposta em frequência;
Margens de ganho e fase e estabilidade relativa;
Projeto de controlador por avanço e atraso de fase;
Controlabilidade e Observabilidade.
T(s): Função de
Transferência do
Sistema (função de
transferência global):
T ( s) 
G1 ( s)G2 ( s)
1  G1 ( s)G2 ( s) H1 ( s)
Quais serão as variações na localização dos pólos quando um ou
mais parâmetros do controlador são variados ?
• O Método do Lugar das Raízes foi desenvolvido
por W. R. Evans (1953);
• Permite que o “lugar das raízes”, no plano s, de uma
equação seja analisado em função da variação
contínua de um parâmetro;
• A obtenção do lugar das raízes permite que seja
escolhido um valor específico do parâmetro variado
para obtenção dos requisitos desejados;
• O método pode ser empregado tanto em sistemas contínuos
quanto em sistemas digitais.
Considerando o seguinte sistema realimentado:
Sendo a função de transferência
de malha aberta:
KG ( s) H ( s)
E a função de transferência de
malha fechada:
OBJETIVO: Determinar a reação
devido a variação do ganho
K  (0 < K < ∞) sobre a localização dos
pólos em malha fechada.
T ( s) 
KG ( s)
1  KG ( s) H ( s)
Em outras palavras, aplicar procedimentos para determinação do lugar
geométrico formado pelas raízes de 1 +KG(s)H(s) = 0 quando K variar de
0 < K < ∞.
Exemplo: Determinar o lugar das raízes (pólos de malha fechada em
função de K) para o seguinte sistema:
K5
s ( s  20)
T ( s) 
K5
1
s ( s  20)
T (s) 
K5
s 2  20 s  K 5
Exemplo: continuação....
s 2  20s  K 5
raízes....
K →∞
s1, 2  10  100 K 5
K →∞
Serão considerados 10 passos para a construção e verificação do lugar
das raízes.
REGRA 1: os ramos do lugar das raízes iniciam nos pólos de G(s)H(s), nos
quais K = 0 e terminam nos zeros de G(s)H(s), para quando K → ∞,
incluindo os zeros no infinito.
O número de zeros no infinito é determinado por:
Pólos explícitos de malha aberta: N p
Zeros explícitos de malha aberta: N z
N z  N p  N z
Exemplo (comprovação quanto a origem e destino do lugar das raízes
conforme declarado na regra 1) Considere que G e H são:
s2
s5
G (s)  2
H ( s) 
s
s4
1  KG(s) H (s)  0
1 K
( s  2)(s  5)
0
2
s ( s  4)
Para K = 0 (origem):
s 2 (s  4)  K (s  2)(s  5)  0
s 2 (s  4)  0
Que são os pólos de G(s)H(s).
s1  s2  0;
s3  4.
Exemplo: Continuação...
Para K → ∞ (destino)
A condição acima é analisada escrevendo a equação sob análise como:
s 2 (s  4)  K (s  2)(s  5)  0
s 2 ( s  4)
K 
( s  2)(s  5)
Para a igualdade ser válida é necessário que:
s  2, pela
esquerda( 2) ;
s  5, pela
esquerda( 5);
s  
Onde -2 e -5 são os zeros de G(s)H(s).
O termo s → -∞ indica um zero no
infinito, uma vez que
N z  N p  N z  N z  3  2  1
REGRA 2: as regiões sobre o eixo real, à esquerda de um número ímpar de
pólos mais zeros de KG(s)H(s), pertencem ao lugar das raízes. (iniciando a
contagem a partir do zero ou pólo localizado na extrema direita do plano s).
Exemplo: Considerando os valores do exemplo anterior:
K
Zeros: s1 = -2 e s2 = -5
Pólos: p1 = p2 = 0 e p3 = -4.
( s  2)(s  5)
0
2
s ( s  4)
Exemplo: Continuação...
No plano s
OBS.: Dois pólos na origem!
REGRA 3: A medida que K se aproxima de ∞, os ramos do lugar
das raízes se aproximam de assíntotas com inclinação
(2i  1)180o
; i  0,1,2,...
N p  Nz
Exemplo: Considere um sistema com:
KG ( s) H ( s) 
K
s( s  1)(s  4)
Para o sistema considerado, temos que: N p  3;
Nz  0
Exemplo: Continuação....
(2i  1)180o
; i  0,1,2,...
N p  Nz
(2i  1)180o
 (2i  1)60o ;0,1,2,...
30
Assim, as assíntotas terão ângulos, no
sentido anti-horário a partir do eixo
real, de 60º, -60º e 180º. Qual a
origem das assíntotas ?
REGRA 4: O ponto de partida das assíntotas é o centro de
gravidade (C.G.) da distribuição dos pólos e zeros, calculado por:
polos  zeros

C.G. 
N p  Nz
Exemplo: Considerando o sistema do exemplo anterior:
KG ( s) H ( s) 
C.G. 
K
s( s  1)(s  4)
0 1 4  0
5

30
3
Exemplo:
Continuação...
C.G.
REGRA 5: os locais de chegada e saída dos ramos no eixo real do
plano s são determinados a partir da seguinte expressão:


d
G ( s) H ( s)1  0
ds
Exemplo: Considerando o seguinte sistema:
G( s) H ( s) 

1
s( s  1)(s  4)

d
G ( s) H ( s)1  0
ds
G(s)H (s)1  s(s 1)(s  4)  s3  5s2  4s
3s 2  10s  4  0
3s 2  10s  4  0
s1  0,465;
s2  2,869
-0,465
REGRA 6: as ramificações do local das raízes deixam ou entram
no eixo real com ângulos de ± 90º.
REGRA 7: o local das raízes é simétrico em relação ao eixo real
porque as raízes são números complexos conjugados.
REGRA 8: os ângulos de saída e de chegada de pólos e zeros são
determinados a partir da seguinte condição geral de ângulos:
 p1  p 2  p3....  z1   z 2   z 3...  (2i 1)180o
Exemplo: Determinar o ângulo de saída do pólo 1
Exemplo: Continuação....
 p1   p2  p3   z1  (2i 1)180o
 p1   p 2  p3   z1 180o
 p 2  90o
 p 3  tg 1 (1 / 2)  26,56o
 z1  tg 1 (1 / 1)  45o
 p1  90o  26,56o  45o 180o
 p1  108,44o
REGRA 9: o ponto onde o lugar das raízes cruza o eixo imaginário é obtido
fazendo s = jω na equação característica : 1 + KG(s)H(s) = 0, igualando a parte
imaginária a zero para determinar ω e, com este valor, igualar a parte real a zero
para determinar o valor de K. Exemplo:
Im :  3  2  0
K
1  0,
Frequências onde o
KG ( s) H ( s)  3
2
s  3s  2s
 2,3  1,41 lugar das raízes cruza
o eixo jω.
1  KG( j ) H ( j )  0
1
K
0
3
2
( j )  3( j )  2 j
Re : 3 2  K  0
p / 1  0  K  0,
p / 2,3  1,41  3 1,41  K  0
2
 j 3  3 2  2 j  K  0
K 6
K=0 e K = 6Valores do ganho para
deslocar os pólos de malha fechada
para os pontos de cruzamento sobre
o eixo jω (ω1, ω2, ω3,) .
Exercício: Construa o lugar das raízes (root locus) para o seguinte sistema:
Im :  3  2  0
1  0,
 2,3  1,41
Re : 3 2  K  0
p / 1  0  K  0,
p / 2,3  1,41 
 3 1,41  K  0
K 6
2
REGRA 10: Se pelo menos dois ramos do lugar das raízes vão para o
infinito, então a soma dos pólos de malha fechada correspondente a um
mesmo K é uma constante independente de K.
Exemplo: Considerando o seguinte sistema:
G( s) H ( s) 
K
s( s  1)(s  2)
Exemplo: Continuação...
 3,26  0,13  j1,68  0,13  j1,68  3
K  9,3
 2,77  0,114 j1,16  0,114 j1,16  3
K  3,75
LOCALIZAÇÃO DO PÓLO ASSOCIADO AO GANHO: a determinação
do ganho K associado a um ponto P do lugar das raízes é obtida a partir do
cálculo do módulo da equação
1  KG(s) H (s)  0
Que é reescrita para determinação do módulo como
KG(s) H (s)  1
KG(s) H (s)  1
Uma vez que 0 < K < ∞:
K G(s)H (s)  1
K
1
G( s ) H ( s ) s  p
Exemplo: Considerando o seguinte sistema:
G( s) H ( s) 
1
s( s  1)(s  2)
Qual o valor de K associado ao ponto sobre o root locus s1,2 = -0,179±j1,01?
1
K
  0,179 j1,01 0,179 j1,01 1 0,179 j1,01 2
G( s) H ( s)
K  2,76
Exercício:
(a) Construa o lugar das raízes (root locus) para o seguinte sistema.
(b) Desloque os pólos complexos do sistema de tal forma que passem pelo
ponto p= -1,5±1,47j, determinando o ganho K relacionado a tal posição.
s 2  4s  3
KG(s) H (s)  K 3
s  4s 2  3,5s  10
Exercício: continuação...
s 2  4s  3
KG(s) H (s)  K 3
s  4s 2  3,5s  10
Regra1:
Regra3:
(2i  1)180o
; i  0,1,2,...
N p  Nz
Regra4:
polos  zeros

C.G. 
N p  Nz
C.G. 
Regra2: Sobre eixo real
 3,77  0,113  1,62 j  0,113  1,62 j  1  3
3 2
C.G.  0
Exercício: continuação...
Regra5:

s 2  4s  3
KG(s) H (s)  K 3
s  4s 2  3,5s  10

d
G ( s) H ( s)1  0
ds
REGRA 6: as ramificações do
local das raízes deixam ou entram
no eixo real com ângulos de ± 90º.
REGRA 7: o local das raízes é
simétrico em relação ao eixo real
porque as raízes são números
complexos conjugados.
Exercício: continuação...
s 2  4s  3
KG(s) H (s)  K 3
s  4s 2  3,5s  10
Regra 8:
 p1  p 2  p3....  z1   z 2   z 3...  (2i 1)180o
 p1  p 2  p3   z1   z 2  180o
 p1   p 2  p3   z1   z 2 180o
Regra 9 e 10: Não são
necessárias neste exemplo.
Exercício: continuação...
Ganho K para pólo em p:
p= -1,5±1,47j
K
1
G( s ) H ( s ) s  p
Exercício: continuação...pólos para K=3,93
p= -1,5±1,47j