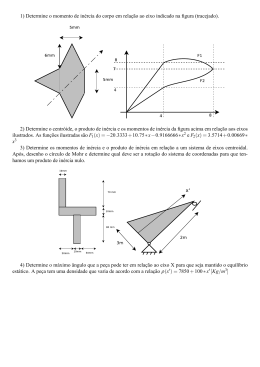
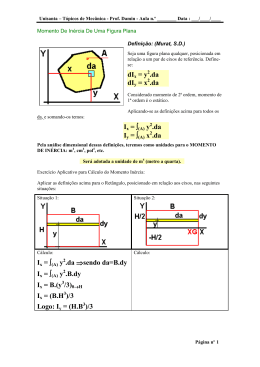
52
CAPÍTULO VI
MOMENTOS ESTÁTICOS, BARICENTROS E MOMENTOS DE INÉRCIA
I.MOMENTOS ESTÁTICOS
Momento Estático de um elemento de superfície, em relação a um eixo,
situado no mesmo plano que a superfície considerada, é o produto da área do
elemento pela sua distância ao eixo considerado.
Sejam:
dA - elemento de área componente da superfície
x e y - coordenadas deste elemento em relação ao sistema de eixos
sx = y. dA
sy = x. dA
Momento Estático de uma superfície, em relação a um eixo, situado no mesmo
plano que a superfície considerada, é a integral dos momentos estáticos de todos os
elementos de superfície, contidos na superfície finita.
Sx =
y. dA
A
Sy =
x. dA
A
II. DETERMINAÇÃO DO BARICENTRO DE SUPERFÍCIE
A utilização dos conceitos de momento estático se dá no cálculo da posição
do centro de gravidade de figuras planas.
Seja:
G - baricentro da superfície com coordenadas à determinar (xG; yG)
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini
53
por definição:
Sx =
y. dA
A
se o baricentro da superfície fosse conhecido
poderíamos calcular o momento estático desta
superfície pela definição:
Sx = yG . A
∴
yG =
Sx
A
ou
como A (área total) pode ser calculado pela soma dos elementos de área que a
constituem:
A =
dA
então :
A
y. dA
yG =
A
dA
A
analogamente:
x. dA
xG =
A
dA
A
O centro de gravidade de uma superfície é o ponto por onde passam todas as
retas do plano da superfície, em relação as quais é nulo o momento estático.
Para algumas figuras é obvia a posição do centro de gravidade; assim, se a
figura é simétrica, o centro de gravidade coincide com o centro geométrico da figura.
Nos casos mais comuns, quando a superfície em estudo for a seção
transversal de um elemento estrutural, normalmente seções constituidas por
elementos de área conhecidos (perfilados), podemos substituir nas equações a
integral por seu similar que é o somatório, e as expressões ficam:
n
yG =
1
n
Ai . yi
n
1
Ai
ou
xG =
1
Ai . xi
n
1
Ai
III. MOMENTO DE INÉRCIA
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini
54
Momento de inércia de um elemento de superfície, em relação a um eixo de
seu plano, é o produto da área deste elemento pelo quadrado de sua distância ao
eixo considerado.
jx = y2 . dA
jy = x2 . dA
Momento de inércia de uma superfície em relação a um eixo é a soma dos
momentos de inércia em relação ao mesmo eixo dos elementos de área que a
constituem.
2
Jx =
A
y . dA
ou
2
Jy =
A
x . dA
IV. TRANSLAÇÃO DE EIXOS (TEOREMA DE STEINER)
Este teorema nos permite relacionar momentos de inércia em relação a eixos
quaisquer com momentos de inércia relativos a eixos baricêntricos, desde que eles
sejam paralelos.
Jx = JxG + A.dy2
Jy = JyG + A.dx2
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini
55
V. DECOMPOSIÇÃO DE SUPERFÍCIES
O momento de inércia de uma superfície é a soma dos momentos de inércia
das diversas superfícies nas quais ela pode ser decomposta.Isto evita, muitas vezes,
a necessidade de integrações,desde que se decomponha a superfície dada em
figuras geométricas básicas tais como retângulos, círculos, etc, para os quais já se
conhecem previamente o valor dos momentos de inércia.
VI.RAIO DE GIRAÇÃO
Sendo J o momento de inércia de uma superfície, de área A, em relação a um
eixo, então:
i= J/A
é, por definição, o raio de giração, relativamente a este eixo.
VII. EIXOS E MOMENTOS PRINCIPAIS CENTRAIS DE INÉRCIA
Vimos que o Momento de Inércia de uma área A muda com a mudança do
eixo em que o mesmo é calculado.Denomina-se EIXOS PRINCIPAIS CENTRAIS DE
INÉRCIA os eixos que passam pelo baricentro da área A e em relação aos quais o
Momento de Inércia admite valores extremos (máximo e mínimo).
Com o objetivo de projetar de forma mais racional possível, nos interessa
conhecer os eixos em relação aos quais a peça estrutural apresenta maior e menor
Momento de Inércia, assim como o valor destes Momentos de Inércia.
O estudo da variação desta grandeza nos permite demonstrar e concluir que:
-Os EIXOS PRINCIPAIS CENTRAIS DE INÉRCIA são ortogonais.
-Se a área A apresentar 2 (dois) eixos de simetria os eixos baricêntricos
horizontal e vertical serão os EIXOS PRINCIPAIS CENTRAIS DE INÉRCIA.
-Se a área A apresentar somente 1(um) eixo de simetria este eixo é um EIXO
PRINCIPAL CENTAL DE INÉRCIA o outro eixo é perpendicular a ele passando pelo
baricentro.
EXERCÍCIOS:
1. Determinar a posição do centro de gravidade das figuras abaixo (medidas em
cm):
a.
b.
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini
56
c.
R: XG = 5,00
YG = 9,66
R: YG = 2,60
XG = 6,57
d.
R: XG = 6,00
YG = 9,17
R: YG = 27
XG = 25
2. Determinar o momento de inércia das figuras em relação aos eixos baricêntricos
horizontal e vertical.
(medidas em cm)
a.
b.
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini
57
R: Jx = 3.541,33 cm4
Jy= 1.691,33 cm4
c.
R: Jx = 553 cm4
Jy = 279,08 cm4
d.
R: Jx = 687,65 cm4
Jy= 207,33 cm4
R: Jx = 1.372,29 cm4
Jy= 1.050,27 cm4
TABELAS:
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini
58
Jx =
b. h 3
3
J xG =
Jy =
b. h 3
12
h. b 3
3
JyG =
h. b 3
12
Jx =
b. h 3
12
Jy =
J xG =
b. h 3
36
JyG =
Jx =
h. b 3
12
h. b 3
36
b. h 3
12
J xG =
b. h 3
36
Jx = Jy =
JyG =
h. b 3
48
π. R 4
4
Resistência dos Materiais E – DECivil . PUCRS- Profas: Sílvia Baptista Kalil / Maria Regina Leggerini